Towards accurate and precise positions of hydrogen atoms bonded to heavy metal atoms

Abstract

A comparison of five X-ray structures of transition-metal-bound hydride complexes, successfully refined using Hirshfeld Atom Refinement (HAR) against low resolution X-ray diffraction data (including the positions and ADPs of all hydrogen atoms), with neutron structures shows that using aspherical atomic scattering factors instead of spherical ones results in systematic elongation of metal–hydrogen bonds, which in the case of the highest-quality data leads to excellent agreement of the X-ray and the neutron-derived bond lengths.

---

The Independent Atom Model (IAM)¹ is the most commonly applied model of electron density in the structural refinement of X-ray diffraction data. It treats atomic electron densities as spherical densities of isolated atoms and thus does not allow to take into account aspherical deformations of density arising from bond formation and other interactions between molecules in crystals. Hydrogen atoms are severely affected by the lack of asphericity in this model since they possess only one valence electron with the density strongly shifted towards the atom they are bonded to. As a consequence, the lengths of bonds involving hydrogen atoms are considerably underestimated and usually anisotropic thermal motions of hydrogen atoms cannot be refined within the IAM formalism. For bond types common in crystals of organic compounds, IAM underestimates the distance of hydrogen atom to its bonding partner roughly by 0.12 Å.² The Hirshfeld model implemented in the procedure of Hirshfeld Atom Refinement (HAR)³ has been confirmed to significantly increase accuracy and precision of determining hydrogen positions based on X-ray diffraction data of not only high but also standard resolution. For bond types common in organic compounds, mean X–H bond lengths obtained with HAR are underestimated by 0.01–0.02 Å compared to the neutron values,² which on average results only in a 0.014 Å difference.⁴ HAR also enables refinement of anisotropic displacement parameters (ADPs) of hydrogen atoms, with the proviso that the HAR ADPs are less accurate than the ones derived from neutron diffraction or estimated with other methods.^2,5

Transition metal (TM) bound hydrides pose a challenge for X-ray crystallography. They can be used as hydrogen storage materials,⁶ and play an important role in the search for superconductivity,⁷ for example, palladium hydrides. TM hydrides participate in a variety of chemical processes – as catalysts or intermediate compounds – such as energy conversion,⁸ catalytic hydrogenation, and reactions involving C–H bond activation.⁹ The position of the hydrogen atom in the vicinity of a TM atom is particularly difficult to determine with X-ray diffraction due to strong screening by the electron rich metal atoms. A few attempts of using HAR to tackle X-ray structures containing heavy metals, including relativistic effects, have been made.¹⁰ Nevertheless, to date, only 5 structures of complexes with TM–H bonds have been successfully refined with HAR,^2,13 for only two of which a complementary neutron data set is available. Refinement of such structures demands a flexible HAR procedure, which initiated integration of HAR with Olex2,¹¹ such as HARt,¹² NoSPherA2 (Non-Spherical Atoms in Olex2)¹³ – implementing relativistic effects and anharmonicity refinement, and DiSCaMB (Densities in Structural Chemistry and Molecular Biology) – introducing a choice of electron density partitions and also enabling relativistic effects.¹⁴

In this study, the DiSCaMB version of HAR developed in our group (further called DiSCaMB-HAR) is challenged to refine positions and thermal motions of hydrogen atoms in 5 X-ray data sets collected for TM bound hydride complexes (CCDC refcodes: QOSZON, MIGKIY, NOBBOX, SITKUB, XAXMEP), for which also neutron data sets are available. The structures were retrieved from the Cambridge Structural Database (CSD) and the exact refcodes and literature references for the utilized structures can be found in the ESI.† The selected data sets include complexes of metals from periods IV, V and VI (Fe, Ru, Rh and Os), which enables a study of performance of HAR in establishing the position of H atoms bonded to TMs with an increasing number of electrons. The structure factor data utilized in this study were either those deposited in the CSD or available on the webpage of the corresponding publication and were used in the refinements carried out in an unchanged form. The method used to obtain the molecular wave function and derive the atomic scattering factors used in HAR was DFT/B3LYP in combination with the basis sets chosen according to the heavy atom present in the structure: cc-pVDZ for the Fe complex, cc-pVTZ-DK for Ru and Rh, and jorge-DZP¹⁵ for Os. Additionally, for the Fe and Os complex, refinement with the triple-ζ version of the basis set was also performed. The refinement was started from the retrieved IAM structure. Positions of all hydrogen atoms were freely refined. The adjustment of weighting scheme was a crucial factor allowing to obtain the best quality of the final structure and in some cases to successfully complete the refinement. The detailed description of the computationally demanding DiSCaMB-HAR procedure is available in the ESI,† where we present how, compared to the IAM and neutron values, refinement statistics (max(parameter shift/Sigma)), goodness of fit, R, wR₂, (minimum and maximum residual density) and TM–H or Si–H bond lengths change in each DiSCaMB-HAR cycle and how they stabilize to prove that the criterion max(parameter shift/Sigma) <1 between the subsequent DiSCaMB-HAR cycles is enough to finish refinement. It is stopped when the specified quantities stabilize, not when the results are better than the ones from IAM. The most significant improvement of bond lengths is usually observed in the first DiSCaMB-HAR cycle and the subsequent cycles bring minor changes. Additionally, IAM re-refinement of the retrieved structures was performed using olex2.refine against all the available reflections, as in HAR, and resulted in improvement of TM–H bond lengths for XAXMEP and no change in this respect for the other structures.

Both neutron and X-ray data quality and the quality of the models obtained in the course of refinement is crucial for a reliable comparison of TM–H bond lengths. At the same time, crystal structures with TM-bonds for which both neutron and X-ray data have been collected are scarce and we have to take into account the fact that there may be some factors related to data collection, which will obstruct determination of hydrogen positions both with IAM and HAR. In order to make the reader take notice of this problem, we ranked neutron and X-ray data and the models obtained as a result of refinement of those data according to their quality and combined it into the overall ranking of the 5 analyzed structures according to their neutron/X-ray data/refined model quality (details in the ESI†). The ranking lists at the top the NOBBOX and QOSZON structures, then SITKUB followed by MIGKIY and is closed by XAXMEP. One can notice that this ranking corresponds with the increasing number of electrons in the TM. It can be predicted that the neutron-HAR bond lengths comparison will be the most favorable for the structures at the top of this ranking and divergences will increase towards the end of the ranking. Therefore, TM–H bond lengths from the optimized geometries were used as an additional benchmark (details in the ESI†). The evaluation of general quality of all hydrogen positions in the 5 structures obtained with the DiSCaMB-HAR method in comparison with IAM can be found in the ESI† (Table S2).

Unfortunately, in all the cases the temperatures at which X-ray data were collected (100–293 K) are substantially higher than the data collection temperature of the neutron data sets (20 K in all the cases), which may hinder comparison of bond lengths, let alone parameters characterizing thermal motions. In order to verify the influence of problematic refinement of hydrogen ADPs on the resulting hydrogen positions, an attempt of HAR with hydrogen ADPs estimated with SHADE2¹⁶ was made (using SHADE3 would require geometry optimization under periodic boundary conditions which would be problematic for such large challenging systems). For all the systems but one (QOSZON), the SHADE2-HAR approach was unsuccessful, resulting in the structure falling apart in the first cycles of least squares refinement. Refinement of thermal ellipsoids of hydrogen atoms is a problematic aspect of HAR, however, isotropic and anisotropic treatment² or even using SHADE⁵ result in comparable positions of hydrogen atoms.

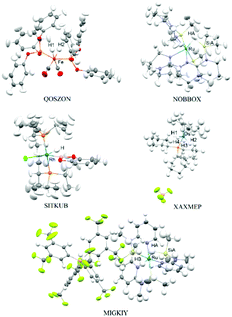
Anisotropic refinement of hydrogen thermal motions was achieved for 3 structures from the top of the data-refinement quality ranking (QOSZON, NOBBOX, SITKUB – see Fig. 1). In the case of QOSZON, full anisotropic refinement resulted in non-positive definite (N.P.D.) thermal ellipsoids for the two hydrogen atoms (H1 and H2) bonded to Fe, both when cc-pVDZ and cc-pVTZ basis sets were used. Therefore, we also performed HAR with H1 and H2 refined isotropically. The best result in terms of Fe–H bond lengths was achieved for the cc-pVTZ refinement with isotropic H1 and H2 and we use this structure in further discussion. Using SHADE for estimating hydrogen ellipsoids did not bring further improvement. Still, the SHADE-estimated ellipsoids for QOSZON may be used to assess the quality of hydrogen ADPs refined with HAR. Statistics from all 6 versions of refinement of QOSZON are presented in the ESI.†

Fig. 1 The structures obtained in the course of DiSCaMB-HAR with the names of TMs, TM-bound H and Si atoms marked. H atoms refined anisotropically: QOSZON (with H1 and H2 refined isotropically), NOBBOX, SITKUB. H atoms refined isotropically: XAXMEP, MIGKIY.

In the case of the 3 X-ray structures for which anisotropic refinement of hydrogen thermal motions was feasible, the DiSCaMB-HAR method improves the accuracy of determination of the positions of hydrogen atoms bonded to TM atoms (see the values in Table 1), as shown by comparison of the DiSCaMB-HAR, IAM and neutron values. DiSCaMB-HAR also results in improved precision of the discussed bond lengths – the DiSCaMB-HAR bond length errors are up to two times smaller than for IAM. Still, the DiSCaMB-HAR errors are one order of magnitude higher than the neutron ones, unless the neutron bond length precision is decreased, as it is in the case of SITKUB. The most outstanding agreement was achieved between the DiSCaMB-HAR and the neutron position of the TM-bound hydrogen atom in the case of the NOBBOX structure (see Table 1). The difference between both values is equal to 0.005 Å, which is less than 2 neutron esds. The IAM bond length in this case is also quite close to the neutron length. However, the difference between the IAM and the neutron value is 0.038 Å (within 13 neutron esds), which is a much bigger difference than in the case of DiSCaMB-HAR. The HA atom is also bound to a Si atom and in the case of the SiA-HA bond length the comparison between the neutron and HAR value is equally favorable for HAR, whereas for IAM the level of similarity is decreased. The DiSCaMB-HAR Si–HA bond length compared to the neutron ones is underestimated by 0.006 Å, which is less than 50% of the average shortening achieved with HAR for X–H bonds in organic compounds.⁴ In the case of IAM, the bond length is underestimated by 0.064 Å, which is much worse than the DiSCaMB-HAR result, but still much better than the average underestimation made by IAM.² What is more, all thermal ellipsoids of hydrogen atoms, including the one bonded to Ru, have regular shapes. The excellent outcome achieved for the NOBBOX structure corresponds with its highest position in the data-refinement quality ranking of structures (see the ESI†).

Table 1 TM–H and Si–H bond lengths (units: Å) obtained with various methods

Structure	Bond	Optimized	Neutron	IAM	HAR
Bold – HAR closer to neutron than IAM, italic – HAR further from neutron than IAM, regular – no difference.a Refinement with cc-pVTZ basis set, H1 and H2 refined isotropically and the remaining H atoms refined anisotropically.
QOSZON^a	Fe–H1	1.530	1.529(2)	1.44(2)	1.522(15)
	Fe–H2	1.517	1.521(2)	1.42(2)	1.505(14)
NOBBOX	Ru–HA	1.590	1.598(3)	1.55(2)	1.593(11)
	SiA–HA	1.879	1.874(3)	1.82(2)	1.868(13)
SITKUB	Rh–H1	1.531	1.531(11)	1.40(2)	1.433(13)
MIGKIY	Ru–HA	1.596	1.600(8)	1.55(4)	1.58(6)
	Ru–HB	1.579	1.587(7)	1.47(4)	1.47(4)
	SiA–HA	1.750	1.737(10)	1.62(4)	1.72(6)
XAXMEP	Os–H1	1.636	1.606(17)	1.60(7)	1.68(3)
	Os–H2	1.632	1.632(15)	1.60(6)	1.66(5)
	Os–H3	1.627	1.599(21)	1.61(5)	1.68(5)
	Os–H4	1.622	1.626(19)	1.63(4)	1.66(5)

---

In the case of QOSZON, which is ranked as the second structure, using the cc-pVTZ basis set and isotropic refinement of H1 and H2, allows to obtain the difference between the neutron and DiSCaMB-HAR result as low as 0.007 Å for Fe–H1 (within 4 neutron esds) and to 0.016 Å in the case of Fe–H2 (the level on average expected for X–H bonds in organic compounds⁴), which is within 8 neutron esds. The conventional HAR² performed with Tonto was even more successful than DiSCaMB-HAR in refinement of H1 position (bond length equal to 1.531(9) Å), however, establishing H2 position, conventional HAR performed even slightly worse than IAM (1.414(8) Å).

All hydrogen ADPs in SITKUB could be refined isotropically. However, despite the fact that DiSCaMB-HAR elongates the Rh-H1 bond by 0.033 Å, as compared to IAM, the bond length is still too short by 0.098 Å in comparison with the neutron one. Instead, the thermal ellipsoid of H1 is elongated in the direction of the bond. This structure is positioned in the middle of the data-refinement quality ranking due to, i.e., higher negative residual density resulting from refinement of X-ray data than for QOSZON and NOBBOX and the 0.474 data completeness and wR₂ = 16.62% in the case of the neutron structure (see ESI,† Table S1). This suggests that quality of the X-ray data collected for SITKUB is insufficient to refine the position of the hydrogen atom bonded to Rh, whereas the results of geometry optimization confirm the neutron Rh–H1 bond value.

In the case of the MIGKIY and XAXMEP (Fig. 1), which are placed at the end of the data-refinement quality ranking, only isotropic refinement of hydrogen thermal motions was possible (Table 1). The low position in the ranking is caused by i.e. high residual density maxima/minima obtained in the course of X-ray data refinement (−0.47/0.95 e Å⁻³ for MIGKIY and −1.54/1.00 e Å⁻³ for XAXMEP, see ESI,† Table S1), high R = 12.9% characterizing the neutron data refinement for XAXMEP. In the X-ray structure of MIGKIY, residual density maps allow to detect a minor disorder within one of the CF₃ groups. The disorder was not modeled due to its small magnitude and significant distance from the metallic center, however it could influence all the reflections. The X-ray structure of XAXMEP, in turn, is characterized by significant amounts of residual density in the vicinity of the Os atom and Os–H bonds (<−1 e Å⁻³). The detailed discussion of Ru–H and Si–H bonds in MIGKIY and Os–H bonds in XAXMEP is available in the ESI.†

To summarize, this study presents the problem of obtaining accurate and precise positions of hydrogen atoms bonded to TMs based on X-ray diffraction experiments. To this end, 5 standard resolution X-ray data sets for crystal structures containing hydrogen atoms bonded to IV, V and VI-period TMs (Fe, Ru, Rh and Os) were processed using HAR in the version offered by the DiSCaMB library interfaced with Olex2. The resulting bond lengths were compared to the IAM values, to the bond lengths obtained in neutron experiments and in the course of geometry optimization. The key factor deciding about the accuracy and precision of locating hydrogen atoms in the vicinity of TMs is the electronic structure of the TM, the quality of experimental data and the electron density model refined against it. For the structures from the top of the X-ray and neutron data-refinement quality ranking (QOSZON and NOBBOX), using an advanced model of atomic scattering factors provided by HAR, brings the TM–H bond lengths considerably closer to the neutron values compared to IAM. Individual adjustments in the refinement procedure (exploring different basis sets, refining selected H atoms isotropically) might help to obtain better results (QOSZON). For the structures lower in the ranking HAR brings certain improvement of the position of TM-bonded hydrogen atoms (SITKUB, MIGKIY) compared to IAM. Finally, for the lowest in the ranking structure of XAXMEP, which one would expect the most problematic in terms of determining Os–H bond lengths, IAM results in high agreement with the neutron values; HAR, although not as accurate as IAM, still performs relatively well. There is still room for advancement of the technical side of the refinement method in the aspects of testing various basis sets and more sophisticated computational methods (MP2, CCSD). Accounting for relativistic effects could bring improvement particularly for heavier TMs. The described results were obtained as a part of a larger project aimed at exploration of the capabilities of HAR in terms of determination of positions of hydrogen atoms bonded to TMs. The outcome of the full analysis including a wider variety of structures and heavy elements will be published as a separate study.

This work was funded by the Polish National Science Centre (NCN) under Opus grant DEC-2018/31/B/ST4/02142 and carried out at the Core Facility for crystallographic and biophysical research to support the development of medicinal products sponsored by the Foundation for Polish Science (FNP). Wroclaw Centre for Networking and Supercomputing of Wroclaw University of Technology and the PL-Grid infrastructure are gratefully acknowledged for providing computational facilities.

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. A. H. Compton, Nature, 1915, 95, 343–344.
2. M. Woińska, S. Grabowsky, P. M. Dominiak, K. Woźniak and D. Jayatilaka, Sci. Adv., 2016, 2(5), e1600192.
3. (a) D. Jayatilaka and B. Dittrich, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 383–393; (b) S. C. Capelli, H.-B. Bürgi, B. Dittrich, S. Grabowsky and D. Jayatilaka, IUCrJ, 2014, 1, 361–379.
4. K. K. Jha, B. Gruza, P. Kumar, M. L. Chodkiewicz and P. M. Dominiak, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2020, 76, 296–306.
5. L. A. Malaspina, A. A. Hoser, A. J. Edwards, M. Woińska, M. J. Turner, J. R. Price, K. Sugimoto, E. Nishibori, H.-B. Bürgi, D. Jayatilaka and S. Grabowsky, CrystEngComm, 2020, 22, 4778–4789.
6. (a) L. Schlapbach and A. Züttel, Nature, 2001, 414, 353–358; (b) S. Fukuzumi and T. Suenobu, Dalton Trans., 2013, 42, 18–28; (c) H. W. Langmi, J. Ren, B. North, M. Mathe and D. Bessarabov, Electrochim. Acta, 2014, 128, 368–392.
7. (a) D. V. Semenok, I. A. Kruglov, I. A. Savkin, A. G. Kvashnin and A. R. Oganov, Curr. Opin. Solid State Mater. Sci., 2020, 24(2), 100808; (b) X. Li and F. Peng, Inorg. Chem., 2017, 56(22), 13759–13765; (c) T. Skoskiewicz, Phys. Status Solidi A, 1972, 11, K123.
8. (a) R. M. Bullock, A. M. Appel and M. L. Helm, Chem. Commun., 2014, 50, 3125–3143; (b) M. Rakowski DuBois and D. L. DuBois, Acc. Chem. Res., 2009, 42, 1974–1982; (c) V. S. Thoi, Y. Sun, J. R. Long and C. J. Chang, Chem. Soc. Rev., 2013, 42, 2388–2400; (d) D. Wang and D. Astruc, Chem. Rev., 2015, 115, 6621–6686.
9. (a) G. Hilt, ChemCatChem, 2014, 6, 2484–2485; (b) T. W. Lyons and M. S. Sanford, Chem. Rev., 2010, 110, 1147–1169; (c) J. A. Labinger and J. E. Bercaw, Nature, 2002, 417, 507–514; (d) J. Choi, A. H. R. MacArthur, M. Brookhart and A. S. Goldman, Chem. Rev., 2011, 111, 1761–1779.
10. (a) L. Bučinský, D. Jayatilaka and S. Grabowsky, J. Phys. Chem. A, 2016, 120, 6650–6669; (b) L. Bučinský, D. Jayatilaka and S. Grabowsky, Acta Crystallogr., Sect. A: Found. Adv., 2019, 75, 705–717; (c) L. A. Malaspina, E. K. Wieduwilt, J. Bergmann, F. Kleemiss, B. Meyer, M. F. Ruiz-López, R. Pal, E. Hupf, J. Beckmann, R. O. Piltz, A. J. Edwards, S. Grabowsky and A. Genoni, J. Phys. Chem. Lett., 2019, 10, 6973–6982.
11. O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Cryst., 2009, 42, 339–341.
12. M. Fugel, D. Jayatilaka, E. Hupf, J. Overgaard, V. R. Hathwar, P. Macchi, M. J. Turner, J. A. K. Howard, O. V. Dolomanov, H. Puschmann, B. B. Iversen, H.-B. Bürgi and S. Grabowsky, IUCrJ, 2018, 5, 32–44.
13. F. Kleemiss, O. V. Dolomanov, M. Bodensteiner, N. Peyerimhoff, L. Midgley, L. J. Bourhis, A. Genoni, L. A. Malaspina, D. Jayatilaka, J. L. Spencer, F. White, B. Grundkötter-Stock, S. Steinhauer, D. Lentz, H. Puschmann and S. Grabowsky, Chem. Commun., 2014, 50, 3125–3143.
14. (a) M. L. Chodkiewicz, S. Migacz, W. Rudnicki, A. Makal, J. A. Kalinowski, N. W. Moriarty, R. W. Grosse-Kunstleve, P. V. Afonine, P. D. Adams and P. M. Dominiak, J. Appl. Cryst., 2018, 51, 193–199; (b) M. L. Chodkiewicz, M. Woińska and K. Woźniak, IUCrJ, 2020, 7, 1199–1215.
15. (a) N. B. Balabanov and K. A. Peterson, J. Chem. Phys., 2005, 123, 064107; (b) T. H. J. Dunning, Chem. Phys., 1989, 90, 1007–1023; (c) A. C. Neto, E. P. Muniz, R. Centoducatte and F. E. Jorge, THEOCHEM, 2005, 718, 219–224; (d) A. C. Neto and F. E. Jorge, Chem. Phys. Lett., 2013, 582, 158–162.
16. A. Ø. Madsen, J. Appl. Crystallogr., 2006, 39, 757–758.

---

Footnote

† Electronic supplementary information (ESI) available: Crystallographic data refinement, references to the X-ray and neutron data sets used. CCDC 2044020–2044026, 2068736–2068739 and 2069603–2069606. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0cc07661a

---