Dysprosium-directed metallosupramolecular network on graphene/Ir(111)

Abstract

The interest in exploiting the unique properties of lanthanides has led to the recent design of two-dimensional coordination networks incorporating f-block elements on metallic surfaces. In order to take this field to the next step of progression, it is necessary to electronically decouple these two-dimensional architectures from the metallic surface underneath. As a first step in this direction, we report the formation of dysprosium-directed metal–organic networks employing three-fold ligands as molecular linkers equipped with terminal carbonitrile functional groups on weakly interacting substrates such as Au(111) and graphene/Ir(111). We observe on both substrates identical quasi-hexagonal Dy–carbonitrile coordination networks based on majority five-fold nodes. Our findings provide perspectives for the formation of lanthanide coordination networks on graphene and related sp² materials grown on metals.

---

During the last two decades, the bottom-up fabrication of two-dimensional surface-confined metal–organic coordination networks (MOCNs) has been a fundamental object of research envisioning many potential applications for gas sensing, heterogeneous catalysis, molecular electronics, nanomagnetism or photovoltaics.^1–4 The coordination of organic ligands with s- and d-block metal atoms on metallic surfaces has provided a plethora of MOCNs with versatile topologies and distinct structural, electronic and magnetic properties.^3–5 Only recently, significant efforts have been dedicated to the study of coordination nanoarchitectures directed by f-block metal atoms.^4,6–9

The quantum-mechanic nature of lanthanide metals favors their widespread presence in today's technology. Due to their high spin–orbit coupling and their inner localized 4f orbitals, the rare-earths show unique and versatile physico-chemical properties, making them appealing in different sectors including magnets, photonic devices, rechargeable batteries, alloys and solar cells among others.¹⁰ The combination of the properties of such metals with the design potential from metal–organic coordination chemistry paves new avenues for the development of novel functional materials. The morphology of these MOCNs is considered to be governed by the dominant ionic character of the lanthanide–ligand coordination bond,¹⁰ which determines the maximum coordination number allowed by intermolecular steric hindrance.^10,11

Notably, for many disruptive potential applications such as single atom magnetism or quantum information, it would be desirable to diminish as much as possible the influence of the metallic substrate. In this context, the growth of decoupling layers on metal surfaces provides an appealing playground to sustain the electronic and magnetic structures, sensing or catalytic activity of targeted MOCNs, which otherwise are quenched or modified due to their strong interaction with the substrate. In the last years, the growth on single-crystal metal surfaces of several sp²-hybridized sheets displaying high structural quality such as graphene (Gr)^12–14 or hexagonal boron nitride (h-BN)¹⁵ was obtained. These achievements open new routes towards the investigation of chemical and physical properties of adsorbates with a varying degree of perturbation by the substrate. However, only recently, the design of some coordination networks employing d-block transition metals on decoupling supports has been reported.^16–18 Despite these striking advances, the engineering of lanthanide-based MOCNs on decoupling layers has not been yet explored. Progress in this area is required to exploit the full potential of lanthanides.¹⁰

In this work we provide a scanning tunnelling microscopy (STM) study complemented with density functional theory (DFT) calculations of the design and characterization of a lanthanide-based metallosupramolecular network, first on Au(111) and second on a decoupling layer of graphene grown on Ir(111).¹⁹ We demonstrate the feasibility of embedding lanthanide elements in coordinative environments on decoupling supports. We also reveal that such assemblies are mostly directed by lanthanide–ligand coordinative interactions, with a negligible role of the substrate. The designed coordinative network is similar on both surfaces and it is based on the coordination of dysprosium atoms with a three-fold ligand (1,3,5-tris(4′-biphenyl-4′′-carbonitrile)benzene (BCNB))²⁰ equipped with a cyano substituent at the para-positions of the three terminal phenyl groups. Our results show the formation of quasi-hexagonal lattices relying mainly on five-fold nodes and directed by the coordinative interactions between the lanthanide and the nitrogen atoms of the ligands.

The sublimation of BCNB on a clean Au(111) surface held at room temperature gives rise to the formation of large self-assembled islands (cf.Fig. 1a and b), to be termed α phase, In these islands, the molecules form a hexagonal lattice with unit cell vector values of |a⃑₁| = 17.4 ± 0.5 Å and |a⃑₂| = 17.5 ± 0.5 Å, spanning an angle of θ = 59 ± 5°, as shown in Fig. 1b and c. Herein, the molecular arrangement is stabilized by the establishment of CN⋯H–C intermolecular interactions between adjacent molecules. The average projected CN⋯H–C length is 2.6 ± 0.5 Å.^20,21 An analogous coverage of BCNB deposited on clean Au(111) and annealed to 373 K gives rise to a metal–organic phase, termed β phase, forming large coordination patches all over the surface, which is rationalized to be based on 3-fold^5,20,22 and two distinct 4-fold coordination nodes between the nitrile substituents of BCNB and gold adatoms,²³ where the metallic centres remain invisible to the STM (Fig. 1d).

Fig. 1 Self-assembly of BCNB species on Au(111). (a) Long range STM image of α phase. The inset depicts a ball and stick atomistic model of a BCNB molecule, where nitrogen, carbon and hydrogen atoms are represented in blue, light blue and white colours, respectively. V_b = −1.0 V, I_t = 100 pA. Scale bar: 10 nm. (b) High-resolution STM image of the molecular self-assembly. V_b = −1.0 V, I_t = 100 pA. The blue arrows represent the unit cell vectors. Scale bar: 2 nm. (c) Atomistic model of (b). (d) High resolution STM image showing β phase. V_b = 0.7 V, I_t = 130 pA. Scale bar: 3.0 nm.

The subsequent deposition of Dy onto a BCNB sample featuring only α phase and subsequent annealing to 373 K to promote diffusion results in a drastic change of the self-assembly, giving rise to the formation of a metal–organic coordination network, to be termed γ phase (cf.Fig. 2a). This new coordinative network is interpreted to be mostly composed by 5-fold nodes, representing 65% of the total (see left image of Fig. 2b). The Dy-nodes have a projected CN⋯Dy average length of 2.5 ± 0.5 Å, which is in good agreement with the values reported for other lanthanide-directed MOCNs on metals.⁶ Furthermore, the DFT simulated CN⋯Dy length is in the range from 2.6 to 2.7 Å (cf.Fig. 2c and Fig. S1, ESI†), which match with the experimental results. The Bader analysis of the DFT calculations assigns a positive charge of 2.35 e⁻ to the Dy atom. This is consistent with a +3 oxidation state, similar to Dy- and Gd-carboxylate reticulated architectures on Cu(111).⁴ Importantly, every five-fold coordination centre exhibits a sixth BCNB molecule (highlighted in purple in Fig. 2b left) relatively close to the node, though it does not participate in the coordination (projected CN⋯Dy average length of 5.0 ± 0.5 Å),² but it seems to be engaged in CN⋯C–H interactions with two adjacent BCNB ligands. In addition to the 5-fold coordinated centres, two other coordination motifs are observed. The second most frequent node type represents 23% of the metallic centres, being rationalized to be 4-fold and similar to the observed ones in β phase (cf. middle of Fig. 2b and Fig. S2a, Fig. S3, ESI†), that we assign to the coordination of BCNB species with concomitant gold adatoms coming from the substrate.²³ This assignment is supported by the projected cyano–Au average bond length of 2.2 ± 0.5 Å, which is shorter than the analogous CN⋯Dy coordination bond. Finally, the third coordination motif, representing 12% of the centres, is interpreted to be a 6-fold Dy–Dy binuclear node, in which each Dy atom is interacting with three BCNB molecules (cf. right of Fig. 2b and left of Fig. S1, ESI†). The presence of Dy binuclear nodes is ascribed to the symmetry of the ligands surrounding the node, which is compatible with previous results of binuclear Dy-based carboxylate nanomeshes.²⁴ The distribution of the cyano groups around the Dy centres gives a projected CN⋯Dy average distance of 2.6 ± 0.5 Å. A mononuclear centre for this type of node is discarded since it would imply a CN⋯Dy average distance of 4.5 ± 0.5 Å (cf. right of Fig. S2b, ESI†).

Fig. 2 γ phase: Dy–BCNB metal–organic coordination network on Au(111). (a) Long range STM image of the supramolecular architecture formed after Dy deposition on a sample featuring α phase. Scanning parameters: V_b = 0.5 V, I_t = 15 pA. Scale bar: 10 nm. (b) High-resolution STM images and corresponding atomistic models of the three kind of nodes found in the lattice. The yellow circle represents a gold adatom, while green circles represent Dy atoms. Molecules marked in purple are not contributing to the coordination bond, but interact through CN⋯H–C bonds with the two closest carbonitrile groups, depicted by green ovals. Scanning parameters: V_b = 0.5 V, I_t = 15 pA. Scale bar: 1 nm. (c) DFT calculations illustrating the coordination between the carbonitrile functional groups and the Dy in a 5-fold coordination node. (d) Zoom-in of the green square depicted in (a) with the corresponding atomistic model superimposed. The nodes are connected by black lines to emphasize the quasihexagonal order. Scale bar: 2 nm.

Notably, the nodes are disposed forming a slightly distorted hexagonal lattice, which results from the competition between coordination schemes, steric repulsion and molecular flexibility (Fig. 2d).

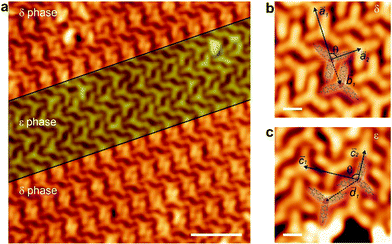
Once the lattice has been produced on top of a metal, which, although weakly interacting, generates unwanted metal adatoms that coordinate with the molecules, the next step is to explore the growth of such architecture on the decoupling layer of high quality graphene on Ir(111) (cf. Fig. S4, ESI†). BCNB species were deposited on the graphene/Ir(111) substrate held at room temperature. STM imaging reveals that the molecules are self-assembled in two different phases, to be termed δ and ε phases, respectively (cf.Fig. 3a). The δ phase exhibits a rectangular packing that can be described by a lattice with basis (cf.Fig. 3b). Two molecules are aligned antiparallel in the basis, separated by a basis vector b⃑₁, with module |b⃑₁| = 14.5 ± 0.5 Å. The unit cell vectors (a⃑₁ and a⃑₂) of δ phase form an angle θ = 88 ± 5° between them (cf.Fig. 3b), presenting modules of |a⃑₁| = 29.4 ± 0.5 Å and |a⃑₂| = 17.1 ± 0.5 Å. The ε phase also displays a rectangular packing (cf.Fig. 3c), featuring again two antiparallel aligned molecules in the basis of the unit cell, separated by a basis vector with module |d⃑₁| = 20.7 ± 0.5 Å. The vectors that define the unit cell (c⃑₁ and c⃑₂) span an angle θ = 89 ± 5° between them, with modules |c⃑₁| = 30.2 ± 0.5 Å and |c⃑₂| = 17.6 ± 0.5 Å. Both δ and ε phases are stabilized by CN⋯H–C bonds between adjacent molecules,⁶ though featuring a distinct fashion in each phase.

Fig. 3 BCNB self-assembly on Gr/Ir(111). (a) STM image of the BCNB arrangement on graphene. V_b = −1.0 V, I_t = 100 pA. Scale bar: 5 nm. (b and c) High-resolution STM images of δ and ε phases, respectively. The two molecules that form the basis of the lattice for each phase are highlighted in purple. Black arrow represents the basis vector and blue arrows represent the unit cell vectors. Scanning parameters: (b) V_b = 0.8 V, I_t = 400 pA, (c) V_b = 0.8 V, I_t = 10 pA. Scale bar: 1 nm.

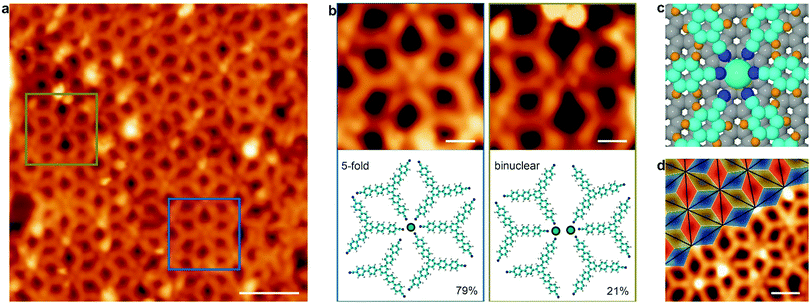
Finally, Dy atoms were deposited on the sample containing the self-assembled BCNB molecules holding the Gr/Ir(111) substrate at 338 K, and then post-annealed to 473 K to increase the diffusion of the molecules and to favour the formation of the network. In this range of temperatures, intercalation of dysprosium below graphene can be discarded as explained in the ESI.† This procedure leads to the formation of a Dy–BCNB MOCN on the graphene surface, to be termed ζ phase (cf.Fig. 4a). Notably, in this case only two different types of metallic-nodes were observed (cf.Fig. 4b). The predominant node (79% of the centres) is interpreted as a 5-fold coordination node, with an average projected length of 2.9 ± 0.5 Å for the CN⋯Dy bond (cf. left of Fig. 4b and right of Fig. S1, ESI†). This value is in agreement with DFT calculations, which show a slightly larger bond length of the Dy–BCNB network grown on Gr/Ir(111) in comparison to the one grown on Au(111) (cf.Fig. 4c). The Bader analysis reveals a positive charge of +2.26 e⁻ in the Dy centre, very similar to the one assigned on pristine Au(111), i.e. a +3 oxidation state. Note that a divalent configuration is observed for direct adsorption of Dy atoms on graphene/Ir(111) featuring atomic magnetic remanence, thus anticipating implications in the magnetic properties of Dy (+3)-directed coordinative architectures.²⁵ In analogy to the former Dy-directed network on Au(111), there is a sixth molecule close to the node, with a projected CN⋯Dy average bond length of 6.9 ± 0.5 Å, considered too large to contribute to the coordination nodes. The 6-fold binuclear node represents the remaining 21% of the centres observed in the lattice (cf. right of Fig. 4b and Fig. S1, ESI†), with a projected CN⋯Dy average distance of 2.5 ± 0.5 Å. The network shows a very similar architecture to the one formed on Au(111), with the metallic centres featuring quasi-hexagonal order and the molecular species covering the substrate with a porous rhombille tilling (cf.Fig. 4d). Importantly, the 4-fold coordination node is now missing, which confirms the necessary participation of Au adatoms to form these nodes and the absence of unwanted metal atoms from the substrate once the decoupling layer of graphene is in place.

Fig. 4 ζ Phase: Dy-BCNB metal–organic coordination network on Gr/Ir(111). (a) Medium range STM image showing the MOCN governed by 5-fold coordination motifs. V_b = 0.5 V, I_t = 10 pA. Scale bar: 4 nm. (b) The left panel shows a zoom-in of the Dy–BCNB 5-fold node highlighted with a blue square in (a) and the corresponding atomistic model. The right panel shows the binuclear node highlighted with a green square in (a). V_b = 0.5 V, I_t = 10 pA. Scale bar: 1 nm. (c) DFT calculations showing the coordination between the carbonitrile groups and the Dy in a 5-fold node on Gr/Ir(111). (d) STM image with the rhombille tilling superimposed. V_b = −0.4 V, I_t = 5 pA. Scale bar: 1 nm.

The fact that the Dy–BCNB assembly on different substrates has similar lattices and the same tilling suggests that its formation is mainly driven by the metal–ligand and ligand–ligand interactions with a low or negligible contribution of the surface.

In summary, we have investigated the formation of surface-confined metal–organic networks based on the coordination of cyano functional group of BCNB species with Dy atoms, both on Au(111) and, for the first time, on graphene/Ir(111). In both cases, the resulting coordinative architectures are very similar featuring quasi-hexagonal order, and exhibiting a porous rhombille tiling, which is based on 5-fold coordination nodes. Our findings reveal the feasibility of engineering lanthanide-based networks on graphene, paving avenues to explore the promising properties of rare-earths in low dimensional systems.

Author contribution: D. M., B. C. and D. E. conceived the project. D. M., B. C., S. O. P. and K. L. carried out the experiments. N. G., J. R. G.-M. and P. B. synthesized the molecular precursor. The experimental data were analysed by D. M., B. C., S. O. P., J. I. U., J. M. G., J. I. M., R. M. and D. E. and discussed by all the authors. J. I. M. performed the DFT calculation. The manuscript was written with contributions from all the authors.

This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement no. 766555). This work has also been financed by the Spanish Ministerio de Ciencia, Innovación y Universidades (projects PGC 2018-098613-B-C21, SpOrQuMat, MAT2017-85089-C2-1-R) and the Comunidad de Madrid (projects S2018/NMT-4321, NanoMagCost). IMDEA Nanociencia thanks support from the “Severo Ochoa” Programme for Centers of Excellence in R&D (MINECO, Grant SEV-2016-0686).

Conflicts of interest

There are no conflicts of interest to declare.

Notes and references

1. R. Gutzler, S. Stepanow, D. Grumelli, M. Lingenfelder and K. Kern, Acc. Chem. Res., 2015, 48, 2132–2139.
2. J. V. Barth, Annu. Rev. Phys. Chem., 2007, 58, 375–407.
3. L. Dong, Z. A. Gao and N. Lin, Prog. Surf. Sci., 2016, 91, 101–135.
4. D. Écija, J. I. Urgel, A. P. Seitsonen, W. Auwärter and J. V. Barth, Acc. Chem. Res., 2018, 51, 365–375.
5. S. Stepanow, N. Lin, D. Payer, U. Schlickum, F. Klappenberger, G. Zoppellaro, M. Ruben, H. Brune, J. V. Barth and K. Kern, Angew. Chem., Int. Ed., 2007, 46, 710–713.
6. D. Écija, J. I. Urgel, A. C. Papageorgiou, S. Joshi, W. Auwärter, A. P. Seitsonen, S. Klyatskaya, M. Ruben, S. Fischer, S. Vijayaraghavan, J. Reichert and J. V. Barth, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 6678–6681.
7. J. I. Urgel, D. Ecija, W. Auwärter, D. Stassen, D. Bonifazi and J. V. Barth, Angew. Chem., Int. Ed., 2015, 54, 6163–6167.
8. J. I. Urgel, D. Écija, G. Lyu, R. Zhang, C. A. Palma, W. Auwärter, N. Lin and J. V. Barth, Nat. Chem., 2016, 8, 657–662.
9. M. Uphoff, G. S. Michelitsch, R. Hellwig, K. Reuter, H. Brune, F. Klappenberger and J. V. Barth, ACS Nano, 2018, 12, 11552–11560.
10. J. C. G. Bünzli, J. Coord. Chem., 2014, 67, 3706–3733.
11. D. G. Karraker, J. Chem. Educ., 1970, 47, 424–430.
12. J. Wintterlin and M. L. Bocquet, Surf. Sci., 2009, 603, 1841–1852.
13. M. Garnica, D. Stradi, S. Barja, F. Calleja, C. Díaz, M. Alcamí, N. Martín, A. L. Vázquez De Parga, F. Martín and R. Miranda, Nat. Phys., 2013, 9, 368–374.
14. A. L. Vázquez De Parga, F. Calleja, B. Borca, M. C. G. Passeggi, J. J. Hinarejos, F. Guinea and R. Miranda, Phys. Rev. Lett., 2008, 100, 1–4.
15. W. Auwärter, Surf. Sci. Rep., 2019, 74, 1–95.
16. A. Kumar, K. Banerjee, A. S. Foster and P. Liljeroth, Nano Lett., 2018, 18, 5596–5602.
17. J. I. Urgel, M. Schwarz, M. Garnica, D. Stassen, D. Bonifazi, D. Ecija, J. V. Barth and W. Auwärter, J. Am. Chem. Soc., 2015, 137, 2420–2423.
18. J. Li, L. Solianyk, N. Schmidt, B. Baker, S. Gottardi, J. C. Moreno Lopez, M. Enache, L. Monjas, R. Van Der Vlag, R. W. A. Havenith, A. K. H. Hirsch and M. Stöhr, J. Phys. Chem. C, 2019, 123, 12730–12735.
19. S. Barja, M. Garnica, J. J. Hinarejos, A. L. Vázquez De Parga, N. Martín and R. Miranda, Chem. Commun., 2010, 46, 8198–8200.
20. T. Sirtl, S. Schlögl, A. Rastgoo-Lahrood, J. Jelic, S. Neogi, M. Schmittel, W. M. Heckl, K. Reuter and M. Lackinger, J. Am. Chem. Soc., 2013, 135, 691–695.
21. B. D. Baker Cortés, N. Schmidt, M. Enache and M. Stöhr, J. Phys. Chem. C, 2019, 123, 19681–19687.
22. U. Schlickum, R. Decker, F. Klappenberger, G. Zoppellaro, S. Klyatskaya, M. Ruben, I. Silanes, A. Arnau, K. Kern, H. Brune and J. V. Barth, Nano Lett., 2007, 7, 3813–3817.
23. T. A. Pham, F. Song, M. N. Alberti, M. T. Nguyen, N. Trapp, C. Thilgen, F. Diederich and M. Stöhr, Chem. Commun., 2015, 51, 14473–14476.
24. J. I. Urgel, B. Cirera, Y. Wang, W. Auwärter, R. Otero, J. M. Gallego, M. Alcamí, S. Klyatskaya, M. Ruben, F. Martín, R. Miranda, D. Ecija and J. V. Barth, Small, 2015, 11, 6358–6364.
25. R. Baltic, M. Pivetta, F. Donati, C. Wäckerlin, A. Singha, J. Dreiser, S. Rusponi and H. Brune, Nano Lett., 2016, 16, 7610–7615.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental methods. Theoretical calculations. Models for minority nodes on Dy-BCNB MOCN/Au(111). Characterization of Graphene/Ir(111) substrate. See DOI: 10.1039/d0cc07315f

---