Efficient Brownian oscillators and nanoheaters based on gallium-doped ε-Fe₂O₃

Abstract

Wireless actuation at the nanoscale is vital in many contexts, and magnetic fields acting on nanoparticles (NPs) are among the most effective tools when actuation concerns linear forces. However, effective tools to apply torques at the nanoscale are still missing, because NPs where the magnetic moment is strongly coupled to the lattice agglomerate due to their high magnetic moment. Here, we show that gallium-doped ε-iron oxide NPs have small interparticle magnetic interactions and huge lattice-coupling for efficiently applying torques at the nanoscale. In this view, they are expected to be useful tools to efficiently apply mechanical forces to induce cellular apoptosis and to discern between mechanical and thermal contributions to cellular apoptosis currently under debate.

---

Wireless actuation such as magnetic separation and detection of molecules,¹ manipulation with optical tweezers,² acoustic trapping³ and patterning⁴ is especially attractive in the context of nanotechnology. Concerning magnetic actuation on magnetic nanoparticles (NPs), a field constant in space generates a torque on the magnetic moment, whereas a field gradient generates also an attraction force. The generated torque that tends to align the magnetic moment and field can be translated (or not) as a torque on the NP itself depending on the coupling between the magnetic moment and the crystalline lattice. If the coupling is weak, the magnetic moment will rotate “freely” across all the crystalline directions of the NP with no torque being transmitted to the NP. If the coupling is strong, the magnetic moment will transmit the torque to the NP, which will then be able to actuate mechanically on the surrounding media (Fig. SI8, ESI†).⁵ In the context of biomedical applications, these actuations can intervene in a cellular process either by a mechanical effect⁶ or by a heat dissipation mechanism.⁷

NPs with strong magnetic-lattice coupling, enabling a mechanical-thermal wireless actuation, have a high coercivity and behave essentially as a permanent magnet. This is the case of cobalt, cobalt ferrite and iron cobalt NPs,⁸ for instance. However, in the NPs explored so far, this high coercivity is generally associated with a high magnetization, which is of interest for applications such as magnetic recording but not that much for biomedical applications and wireless actuation at the nanoscale, due to the propensity of these NPs to aggregate by magnetic dipolar interactions⁹ Therefore, a full exploitation of the exciting possibilities offered by mechanical magnetic actuation calls for NPs with both high coercivity and low magnetization. Here we show that this unique combination can be achieved by gallium-substituted ε-iron oxide NPs, where strong magnetic-lattice coupling of the ε-iron oxide phase grants a high coercivity and gallium doping the tuning of saturation magnetization.

Saturation magnetization of the ε-Ga_xFe_2−xO₃ NPs can be tuned between 10 and 28.5 Am² kg⁻¹ as the Ga molar ratio is varied between x = 0 and x = 0.46^10,11 (Fig. 1 and Fig. SI1, ESI†). The maximum dipolar interaction between two neighboring particles with magnetic moments m₁ and m₂ at a distance d can be estimated as:¹²

that for a minimum distance d equal to the hydrodynamic size of the NPs gives 370 K (5.1 × 10⁻²¹ J) and 70 K (1.0 × 10⁻²¹ J) for x = 0.46 and x = 0, respectively. These values are of the same order of magnitude as thermal fluctuations (4.1 × 10⁻²¹ J) at room temperature (300 K). Thus, Edipolar of ε-Ga_xFe_2−xO₃ NPs can be adjusted within a range where thermal fluctuations dominate over dipolar interactions to be of the same order of magnitude, leading anyway to obtaining stable ferrofluids of isolated NPs, in accordance with the DLS sizes close to those of individual NPs observed by TEM, and DLS monomodal size distribution (Fig. 2, and Fig. SI4, ESI†). These values of Edipolar are quite a bit lower than those of other hard magnetic NPs having a high coercivity like ε-Ga_xFe_2−xO₃ NPs, but a high magnetization. Fig. 3 demonstrates the M_Svs. H_C diagram of several types of hard magnetic NPs at 300 K,^13–17 including ε-Ga_xFe_2−xO₃ (x = 0, 0.10, 0.15, 0.22, 0.29, 0.35, 0.40) taken from data in ref. 10 and 18 (see Fig. SI1, ESI†). For instance, cobalt ferrites with a coercivity of 80 kA m⁻¹ have a typical saturation magnetization of 80 Am² kg⁻¹ (from ref. 19), which for similar nanoparticle sizes and distances give Edipolar more than 7 times higher than that of ε-Ga_0.46Fe_1.54O₃. In cobalt ferrites (and other high coercive NPs), a decrease of Edipolar is achieved by decreasing the size of the NPs but then coercivity is also reduced toward zero and thus the magnetic moment of such NPs is able to follow the external field direction without a physical rotation. On the contrary, the intrinsic coercivity of the ε-Ga_0.46Fe_1.54O₃ is still quite high (H_c = 621 kA m⁻¹, Fig. 1) whereas the saturation magnetization is still low (M_S = 28.5 Am² kg⁻¹) enabling torque actuations while avoiding aggregation by dipolar magnetic interactions, thus opening the way for a torque-driven mechanical and mechano-thermal wireless actuation on individual NPs, as discussed below.

Fig. 1 Hysteresis loops of ε-Ga_0.46Fe_1.54O₃ NPs in frozen (200 K), liquid (300 K), and powder (300 K) forms.

Fig. 2 (a) TEM image of the Ga-substituted ε-Fe₂O₃ NPs deposited on a copper grid, (b) electron diffraction pattern, (c) nanoparticle size distribution from the TEM images and lognormal fitting (μ = 3.26, σ = 0.48), and (d) distribution of hydrodynamic diameters from dynamic light scattering (DLS) measurements.

Fig. 3 M _S vs. H _C diagram of different kinds of hard magnetic NPs at 300 K, showing that the ε-Ga_xFe_2−xO₃ have a unique combination of H_c and M_s values, leading to unique behavior as efficient Brownian oscillators and Brownian nanoheaters, as explained in the text.

The application of a constant magnetic field below H_c on a water suspension of ε-Ga_0.46Fe_1.54O₃ NPs leads to a physical rotation of the NPs until their magnetic moment aligns with the direction of the magnetic field. If this magnetic field oscillates with a given frequency, the rotation can follow the field totally in-phase or with a delay. The frequency dependence of magnetic susceptibility at room temperature (Fig. 4) shows that a full in-phase rotation occurs below 1000 Hz, whereas above this value an out-of-phase component emerges, meaning that above 1000 Hz the mechanical rotation is accompanied by heat dissipation. This means that 2 types of actuation are possible: mechanical-only and mechano-thermal, opening new opportunities of actuation beyond the usually explored magneto-thermal.²⁰ These new opportunities may enlighten the current debate on mechanical effects disrupting cellular membranes and leading to cell apoptosis.⁶

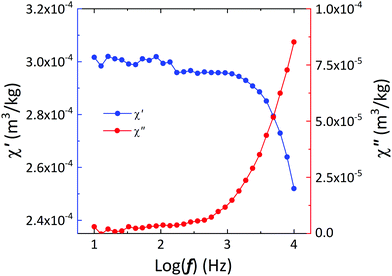Fig. 4 Variation of the in-phase and out-of-phase magnetic AC susceptibilities with the frequency of the alternating magnetic field of the ε-Ga_0.46Fe_1.54O₃ NPs water-suspension.

In the mechanical-only regime (f <1000 Hz), a torque actuation on individual ε-Ga_xFe_2−xO₃ NPs is possible for external field amplitudes below the intrinsic H_c; in the case of actuation in water, a field amplitude as low as 20 kA m⁻¹ is sufficient to overcome thermal fluctuations and rotate the magnetic moment of the nanoparticle in the direction of the field (Fig. 1), i.e. a 180° rotation of the nanoparticle per each external field cycle.

In the mechano-thermal actuation frequency regime, the physical rotation is dephased from the external field and dissipates heat with a specific absorption rate (SAR) that depends on frequency and field amplitude (Fig. 5a), with values of 200 W g⁻¹, at the H·f limit for in vivo applications.²¹ These values are higher than those previously obtained for γ-Fe₂O₃ NPs of similar size (Fig. 5b, 160 W g⁻¹),¹⁸ in which the heat dissipated under an ac magnetic field is mostly due to the rotation of the magnetic moment inside the nanoparticle across the magnetic hard axis, as explained below.

Fig. 5 SAR values at low frequencies of ε-Ga_0.46Fe_1.54O₃ (a) and γ-Fe₂O₃ (b) NPs in water suspensions as a function of Hf quantifying the performance of these systems as nanoheaters. The safety limit is marked as a dotted line. Solid lines are guides for the eyes.

In general, heat dissipation in isolating magnetic NPs under an external field can be due: (i) to a dissipating physical rotation governed by a characteristic Brownian relaxation time (τ_B = 3ηV_h/kT, with η the viscosity of the medium, and V_h the hydrodynamic volume²²) or (ii) to the internal rotation of the magnetic moment governed by a characteristic Néel relaxation time (τ_N = τ₀e^KV/kT, with K the anisotropy constant and V the volume of the NP).²³ Estimation of τ_B and τ_N, as a function of the size of NPs (Fig. SI8, ESI†), shows that τ_B < <τ_N within the size range studied here meaning that the magnetic moment of the NPs will follow the external field by mechanical rotation of the NP. This mechanical rotation results in heat dissipation if the period of the external magnetic field, (t_field = 1/f) is of the order of the characteristic time, τ_B, i.e., if τ_B ∼1/f. Our estimations (Fig. SI8, ESI†) show that this condition occurs for frequencies between 5 and 390 kHz confirming that the observed heat dissipation in that range is due to mechanical rotations only.

In summary, Ga-doped ε-Fe₂O₃ NPs have unique lower magnetization and higher coercivity when compared with magnetic NPs explored for bio applications so far: they are hard NPs for soft applications. As a result, these NPs have low tendency to aggregate due to small magnetic interactions and, at the same time, a high coercivity that allows an effective mechanical and mechano-thermal actuation. Although lower than usual, the magnetization is still high enough for an effective mechano-thermal actuation, with specific heating power values identical to those obtained with γ-Fe₂O₃ NPs which are currently in clinical trials as an effective route of cancer remission.²⁴ In this view, Ga-doped ε-Fe₂O₃ NPs can offer a similar heating power with an added mechanical effect that may further contribute to cancer remission. In the long pathway to applications, the Ga-doped ε-Fe₂O₃ NPs are also useful to understand the separate contributions of the mechanical and heating effects.

Gallium-substituted ε-Fe₂O₃ NPs were synthesized by using the sol–gel method.¹⁰ Briefly, an aqueous solution of Fe(NO₃)₃ (0.38 mol L⁻¹) and Ga(NO₃)₃ (0.12 mol L⁻¹) was mixed with a 5 mol L⁻¹ NH₃ aqueous solution under rapid stirring, followed by adding tetraethoxysilane (TEOS) into the solution to reach a final molar ratio of [Si]/[Fe + Ga] = 1.5 : 1. After being stirred for 20 h, the resulting materials were then sintered at 1100 °C for 4 h in air. The SiO₂ shells were removed by etching with a NaOH solution for 24 h at 60 °C, and then the NPs were dispersed in tetramethylammonium hydroxide (TMAH) to obtain a stable suspension.

XRD measurement was carried out for the powder-form sample. All of the peaks can be readily indexed to metal-substituted ε-Fe₂O₃.^{10,11,25–27} Fig. SI2 (ESI†) shows the Rietveld analysis of the XRD pattern indicating an orthorhombic crystal structure in the Pna2₁ space group. The refined structural parameters are shown in Table SI1 (ESI†).

Results of DLS and TEM characterization studies of the ε-Ga_0.46Fe_1.54O₃ NPs are presented in Fig. 2. The DLS plot shows a monomodal particle size distribution with an average hydrodynamic diameter D_H = 37 nm (PDI = 0.218), which is larger than the D_TEM ± SD = 24.9 ± 15.0 nm (N = 400), as it should be expected; yet, it is clear that the NPs are individually dispersed in water. TEM images of the sample show NPs with spherical or ellipsoidal shape (Fig. 2a). In accordance with the electron diffraction pattern (Fig. 2b), the iron oxide NPs are in the crystalline state. The TEM particle size distribution and its fitting to a lognormal function are shown in Fig. 2c. Since the NPs are well dispersed and since the average TEM size and XRD crystalline size are close, a single spin model where τ_B and τ_N are dominated by the size and anisotropy of a single NP is fully justified.

SAR measurements with frequencies below 120 kHz of the magnetic field were carried out on a homemade magnetic generator, the field intensity and frequency of which were varied in the ranges 10 to 100 mT and 19 to 120 kHz, respectively. The measurements with frequencies from 400 to 800 kHz were investigated on a device from Nanoscale Biomagnetics, where the magnetic field intensity was ranged from 0 to 30 mT. The investigation was performed in water suspensions of uncoated ε-Ga_0.46Fe_1.54O₃ NPs at room temperature.

Financial support by European Union's Horizon 2020 FET Open program [Grants no: 801305 and 829162] Spanish Ministry of Science Innovation and Universities [Grant no: PGC2018_095795_B_I00], Diputación General de Aragón [E11/17R], FCT/MEC and co-financed by FEDER [Grants no: P2020-PTDC/CTMNAN-4511-2014, UIDB/50011/2020 and UIDP/50011/2020] and support of the publication fee by the CSIC Open Access Publication Support Initiative (URICI) are gratefully acknowledged. Authors would like to acknowledge the use of Servicio General de Apoyo a la Investigación-SAI, Universidad de Zaragoza.

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. S. S. Leong, S. P. Yeap and J. Lim, Interface Focus, 2016, 6, 20160048.
2. J. R. Moffitt, Y. R. Chemla, S. B. Smith and C. Bustamante, Annu. Rev. Biochem., 2008, 77, 205–228.
3. S. C. Takatori, R. De Dier, J. Vermant and J. F. Brady, Nat. Commun., 2016, 7, 10694.
4. L. Tian, N. Martin, P. G. Bassindale, A. J. Patil, M. Li, A. Barnes, B. W. Drinkwater and S. Mann, Nat. Commun., 2016, 7, 13068.
5. P. C. Fannin and S. W. Charles, J. Phys. D: Appl. Phys., 1989, 22, 187.
6. E. Zhang, M. F. Kircher, M. Koch, L. Eliasson, S. N. Goldberg and E. Renström, ACS Nano, 2014, 8, 3192–3201.
7. S. Hyun Noh, S. H. Moon, T. H. Shin, Y. Lim and J. Cheon, Nano Today, 2017, 13, 61–76.
8. Z. Zhang, X. Chen, X. Zhang and C. Shi, Solid State Commun., 2006, 139, 403–405.
9. K. Butter, P. H. H. Bomans, P. M. Frederik, G. J. Vroege and A. P. Philipse, Nat. Mater., 2003, 2, 88–91.
10. S. Ohkoshi, S. Kuroki, S. Sakurai, K. Matsumoto, K. Sato and S. Sasaki, Angew. Chem., Int. Ed., 2007, 46, 8392–8395.
11. S. Ohkoshi, A. Namai and S. Sakurai, J. Phys. Chem. C, 2009, 113, 11235–11238.
12. J. M. D. Coey, Magnetism and magnetic materials, Cambridge university press, 2010.
13. J. Jin, S. Ohkoshi and K. Hashimoto, Adv. Mater., 2004, 16, 48–51.
14. B. Shen, C. Yu, A. A. Baker, S. K. McCall, Y. Yu, D. Su, Z. Yin, H. Liu, J. Li and S. Sun, Angew. Chem., Int. Ed., 2019, 58, 602–606.
15. H. Zhang, S. Peng, C. B. Rong, J. P. Liu, Y. Zhang, M. J. Kramer and S. Sun, J. Mater. Chem., 2011, 21, 16873–16876.
16. A. Das, A. Roychowdhury, S. P. Pati, S. Bandyopadhyay and D. Das, Phys. Scr., 2015, 90, 025802.
17. M. A. Ahmed, N. Helmy and S. I. El-Dek, Mater. Res. Bull., 2013, 48, 3394–3398.
18. Y. Gu, M. Yoshikiyo, A. Namai, D. Bonvin, A. Martinez, R. Piñol, P. Téllez, N. J. O. Silva, F. Ahrentorp, C. Johansson, J. Marco-Brualla, R. Moreno-Loshuertos, P. Fernández-Silva, Y. Cui, S. Ohkoshi and A. Millán, RSC Adv., 2020, 10, 28786–28797.
19. A. López-Ortega, E. Lottini, C. D. J. Fernández and C. Sangregorio, Chem. Mater., 2015, 27, 4048–4056.
20. S. Dutz and R. Hergt, Int. J. Hyperthermia, 2013, 29, 790–800.
21. R. Hergt and S. Dutz, J. Magn. Magn. Mater., 2007, 311, 187–192.
22. W. F. Brown Jr., Phys. Rev., 1963, 130, 1677.
23. Q. A. Pankhurst, J. Connolly, S. K. Jones and J. Dobson, J. Phys. D: Appl. Phys., 2003, 36, 167–181.
24. B. Thiesen and A. Jordan, Int. J. Hyperthermia, 2008, 24, 467–474.
25. S. Ohkoshi, A. Namai, K. Imoto, M. Yoshikiyo, W. Tarora, K. Nakagawa, M. Komine, Y. Miyamoto, T. Nasu, S. Oka and H. Tokoro, Sci. Rep., 2015, 5, 14434.
26. A. Namai, M. Yoshikiyo, K. Yamada, S. Sakurai, T. Goto, T. Yoshida, T. Miyazaki, M. Nakajima, T. Suemoto, H. Tokoro and S. Ohkoshi, Nat. Commun., 2012, 3, 1035.
27. S. Ohkoshi, M. Yoshikiyo, K. Imoto, K. Nakagawa, A. Namai, H. Tokoro, Y. Yahagi, K. Takeuchi, F. Jia, S. Miyashita, M. Nakajima, H. Qiu, K. Kato, T. Yamaoka, M. Shirata, K. Naoi, K. Yagishita and H. Doshita, Adv. Mater., 2020, 32, 2004897.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cc07309a

---