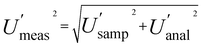How reliable is my uncertainty estimate?
Analytical Methods Committee AMCTB No. 105
First published on 10th June 2021
Abstract
It has become accepted practice for laboratories to report the value of the uncertainty of each measured quantity value (i.e. measurement uncertainty, MU). Informally, the MU expresses the range of values within which the true value of the analyte concentration (i.e. the value of the measurand) is asserted to lie. It is much less widely appreciated that the estimate of MU is also not an exact or ‘true’ value. The quoted MU is actually only an estimate, and has its own uncertainty which also can be expressed using a confidence interval (CI) for a specified confidence level (e.g. 95%).
It was perhaps understandable that the existence of a confidence interval (CI) for each value of measurement uncertainty (MU) was not widely discussed in the initial phase of getting the concept of MU accepted by both laboratories and their customers. Now, however, making sure that the CI of the MU is small enough, can be very important for making reliable decisions based upon measurement results. This document aims to explain the existence of a CI on every MU estimate, and how it can be evaluated, using a worked example that includes primary sampling within the measurement process. In particular this Technical Brief aims to explain how and when it is helpful to calculate the CI of MU estimates using the software RANOVA3. Furthermore, situations will be identified for which a knowledge of this CI is important.
Why uncertainty estimates have confidence intervals
Each estimate of MU is usually based upon a value of the standard deviation (SD) of a number of observations (usually called a Type A evaluation). Statisticians have long been aware that an estimate of SD has its own uncertainty, sometimes called the standard error of the standard deviation, that can be expressed as a confidence interval (CI). This CI can be written as two numbers called confidence limits (LCL and UCL), that give the lower and upper limits, respectively, of the range within which the population value of the SD (σ) lies for a specified confidence level (such as 95%). Equations exist to calculate the CLs on any estimate of SD made using a specified number of observations (n), when the population is assumed to have a normal (i.e. Gaussian) frequency distribution.1For example, if we have 10 observations (3.3, 4.6, 3.5, 6.6, 6.9, 4.1, 5.3, 4.8, 4.9, 4.9) generated for a population with a mean (μ) of 5 and SD (σ) of 1, the estimated SD (s) of this ‘sample’ is 1.17. We can calculate the confidence limits of s using the chi-squared distribution1 (χ2), with the equations:
| LCLs = √(νs2/χ2(1−α/2),ν) = 0.80 |
| UCLs = √(νs2/χ2(α/2),ν) = 2.14 |
When an estimate of SD is used to estimate MU, the CI of the SD (or more strictly on the variance, [SD]2) can be used to express explicitly the CI of the MU estimate (CIU), which is bound by LCLU and UCLU. In many situations with low degrees of freedom e.g. <30, we use percentage points of the Student’s ‘t’ rather than the normal distribution, to calculate what is effectively expanded uncertainty, to implicitly allow for the uncertainty in the estimated SD. However, Student’s ‘t’ is not applicable to more complex situations, such as the output from analysis of variance (ANOVA) discussed below.
Evaluation of the confidence interval of an uncertainty estimate
MU is usually estimated using one, or both, of two different approaches; (a) empirical, by taking repeated measurements at various stages of the process, under operating conditions that vary realistically, or (b) modelling, by summing a list of individual variance components from all steps in the measurement process, including sampling. Using the empirical (or ‘top down’) approach the repeated measurement results can be used to calculate not just the MU but also the CIU, using known equations.1 The calculation of the MU estimates, for various stages of the measurement process, can be made typically using a balanced experimental design followed by the statistical procedure of ANOVA.2 Software packages exist to make these estimates of MU, but generally they do not provide estimates of the corresponding values of the CIU. This situation can be complicated if the measured quantity values are fundamentally normally distributed, but also contain a small proportion (e.g. < 10%) of outlying values. In this case, robust ANOVA can be applied to accommodate the outlying values and to provide an estimate of the MU for the underlying normal distribution.3 A procedure to calculate the CI of a robust estimate of MU has only recently been devised using a bootstrapping approach.1 A slightly different situation can occur if the underlying population distribution is log-normal, rather than normal. This can be overcome using log-transformation of the measured quantity values prior to classical ANOVA, and expressing the MU as an uncertainty factor,4 which also has its own CI. The calculation of CIs for MU estimates for each of these situations is possible within the program RANOVA3,5 which is an Excel macro based upon published methods and validation.1Using the modelling (or ‘bottom up’) approach to estimating MU, it should be possible to enter the CI of each of the component variances into a summation, or a Monte Carlo simulation, to calculate CIU on the resultant estimate of the overall MU.
Worked example of confidence intervals on MU estimates
An example that illustrates the process and the usefulness of calculating CIU, as well as an MU estimate, is that for the determination of nitrate in glasshouse lettuce.6 Eight sampling targets (i.e. bays A–H each of around 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 lettuces) were sampled using a composite sample made up of 10 lettuce heads taken on a ‘W’ shape walked across the bay. An independent duplicate sample was taken of each target by applying the ‘W’ in the opposite spatial orientation. Both duplicate samples for all eight targets were analysed in duplicate for nitrate by HPLC (results in Table 1).
000 lettuces) were sampled using a composite sample made up of 10 lettuce heads taken on a ‘W’ shape walked across the bay. An independent duplicate sample was taken of each target by applying the ‘W’ in the opposite spatial orientation. Both duplicate samples for all eight targets were analysed in duplicate for nitrate by HPLC (results in Table 1).
| Sample target | S1A1 | S1A2 | S2A1 | S2A2 |
|---|---|---|---|---|
| A | 3898 | 4139 | 4466 | 4693 |
| B | 3910 | 3993 | 4201 | 4126 |
| C | 5708 | 5903 | 4061 | 3782 |
| D | 5028 | 4754 | 5450 | 5416 |
| E | 4640 | 4401 | 4248 | 4191 |
| F | 5182 | 5023 | 4662 | 4839 |
| G | 3028 | 3224 | 3023 | 2901 |
| H | 3966 | 4283 | 4131 | 3788 |
Measurement uncertainty (MU) was calculated by placing these 32 measured quantity values (Table 1) into RANOVA3. Robust ANOVA was selected as there was an evident outlier in the sample (target C). The MU is expressed in Table 2 as both standard uncertainty (u = SD) and expanded relative uncertainty (U′ = 100 × 2 × SD/mean). The respective confidence intervals are expressed as the 95% confidence limits (LCLU, UCLU). The basic interpretation of the estimates of the expanded relative uncertainty (U′) for all 8 sampling targets (Table 2), ignoring CIU, is that the U′ estimate for the whole measurement process 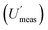 is 16.4%, whilst that for sampling alone
is 16.4%, whilst that for sampling alone 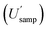 is 14.5%. However, when the CIU of
is 14.5%. However, when the CIU of  is examined (Table 2) it becomes clear that the population value of
is examined (Table 2) it becomes clear that the population value of  lies somewhere between 13.7% and 35.3%. This CIU is strongly asymmetric, with a positive skew, as the MU estimate (16.4%) is much closer to the LCLU (13.7%) than to the UCLU (35.3%). This skewed CI is typical of all of these uncertainty estimates, both classical and robust, and is caused by its frequency distribution (which is either exactly or approximately chi-squared).
lies somewhere between 13.7% and 35.3%. This CIU is strongly asymmetric, with a positive skew, as the MU estimate (16.4%) is much closer to the LCLU (13.7%) than to the UCLU (35.3%). This skewed CI is typical of all of these uncertainty estimates, both classical and robust, and is caused by its frequency distribution (which is either exactly or approximately chi-squared).
| Sampling | Confidence limits | Analysis | Confidence limits | Measurement | Confidence limits | |
|---|---|---|---|---|---|---|
| u (SD) | 319 | (251, 762) | 168 | (140, 208) | 361 | (301, 777) |
| U′ (95%) | 14.5 | (11.4, 34.6) | 7.6 | (6.3, 9.4) | 16.4 | (13.7, 35.3) |
Interestingly, the CIU for 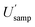 lies between a similarly wide 11.4% to 34.6%. This CIU overlaps substantially with that for
lies between a similarly wide 11.4% to 34.6%. This CIU overlaps substantially with that for 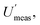 showing that no significant difference has been found between these two estimates, of
showing that no significant difference has been found between these two estimates, of  (16.4%) and
(16.4%) and 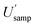 (14.5%). By contrast, the CIU of
(14.5%). By contrast, the CIU of 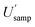 does not overlap with that for
does not overlap with that for 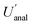 (7.6%), which lies between 6.3% and 9.4%, indicating that their population values are significantly different from each other.
(7.6%), which lies between 6.3% and 9.4%, indicating that their population values are significantly different from each other.
Incidentally, it is worth pointing out that, although the 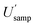 appears to be only twice the size of
appears to be only twice the size of 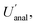 it actually contributes four times as much variance to
it actually contributes four times as much variance to 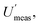 because they add using their variances, i.e.,
because they add using their variances, i.e.,
Generally, the width of the CIU reduces as the number of duplicated measurements used in the estimation process increases, but is more marked for the sampling uncertainty (Fig. 1).
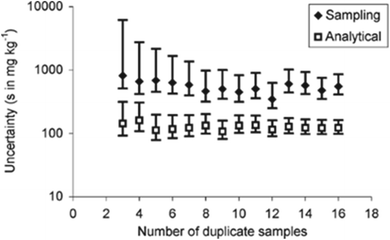 | ||
| Fig. 1 Estimates of uncertainty, with their CIU, arising from sampling (usamp) and analysis (uanal) from a previous study of glasshouse-grown lettuce for nitrate (mg kg−1). Standard, rather than relative uncertainty, and a log scale, are used to enable the comparison. Increasing the number of duplicate samples clearly reduces the CI of the uncertainty estimates in both cases, but is more marked for the sampling uncertainty.7 | ||
When is knowing the CI important?
It is clear from this example, that one important reason for knowing the CIU of a MU estimate, is to decide whether the experimental design is adequate. It becomes possible to see in Fig. 1 that for low numbers of duplicate samples, the CIU is too large to give a reliable estimate of MU. This reliability clearly increases, as the CIU decreases, for a greater number of sample duplicates. The main limitation arises from financial constraints, but also from the evidence that as the number of duplicates increases further there is progressively less decrease in CIU. The recommended minimum number of duplicated samples7 has been set at 8, which gives acceptably small values of CIU on the MU and both of its component values, but not at excessive expense.The estimate of MU can be used in compliance assessment, by comparing the measured quantity value (x) against a threshold value. This requires the use of the confidence interval of the concentration estimate (CIx), which is bound by LCLx (e.g. x − Umeas) and UCLx (e.g. x + Umeas). For the example of nitrate in lettuce, the regulatory threshold is 4500 mg kg−1. For rejection of a batch with 97.5% confidence (at the lower tail of distribution), the LCLx of the concentration estimate (x) for the single composite sample with single analysis routinely taken (e.g. S1A1) needs to exceed this threshold value. Applying this criterion to the eight batches of lettuce (Table 1), seven batches would have been accepted for human consumption. Only one batch (C, x = 5708 mg kg−1) would have been rejected, using  of 16.4%, giving the LCLx as 4774 mg kg−1 (i.e. 5708 × 1 − [
of 16.4%, giving the LCLx as 4774 mg kg−1 (i.e. 5708 × 1 − [ /100]), which is above 4500 mg kg−1.
/100]), which is above 4500 mg kg−1.
The suitability of a minimum of 8 duplicated samples is confirmed by the fact that this compliance decision is barely affected using any of the different estimates of  within its CIU. However, if a smaller number of targets had been used in the estimation of MU, to apparently save money, it is clear from Fig. 1 that there would have been both a different estimate of MU, but more importantly a much wider CIU, making this estimate much less reliable. For example, if only four duplicated samples were used, the CIU is substantially widened to the point where an estimate of Umeas could arise that would cause the rejection of a second batch (F). This erroneously rejected batch of 20
within its CIU. However, if a smaller number of targets had been used in the estimation of MU, to apparently save money, it is clear from Fig. 1 that there would have been both a different estimate of MU, but more importantly a much wider CIU, making this estimate much less reliable. For example, if only four duplicated samples were used, the CIU is substantially widened to the point where an estimate of Umeas could arise that would cause the rejection of a second batch (F). This erroneously rejected batch of 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 lettuces, caused by the insufficiently reliable estimate of MU, would be worth far more than the small apparent saving achieved by taking fewer duplicated samples.
000 lettuces, caused by the insufficiently reliable estimate of MU, would be worth far more than the small apparent saving achieved by taking fewer duplicated samples.
A second advantage of knowing CIU, is for the comparison of estimates of MU made by different approaches, to see whether they are significantly different. This topic will be discussed in a subsequent and related Technical Brief.
The task of combining CIU into the uncertainty statement for the measurand, if required, will need further research.
Conclusions
Quoted statements of measurement uncertainty (MU) are only estimates, not ‘true’ values. For some non-routine applications it is useful to know the confidence interval (CIU) of the estimated MU. The CIU of the MU estimates that are made by empirical methods can be calculated using known equations, if the frequency distribution is normal. When there are a small proportion of outlying values, robust statistical approaches can be applied, and the CIU on MU estimates can be calculated using special software, such as RANOVA3. Knowing the size of the CIU can improve the reliability of decisions made that are based upon measured quantity values, by identifying sufficiently reliable estimates of their MU.Michael H. Ramsey
This Technical Brief was prepared for the Analytical Methods Committee with contributions from members of the AMC Sampling Uncertainty and Statistics Expert Working Groups, and the Eurachem Working Group on Uncertainty from Sampling, and approved on 19th March 2021.
References
- P. D. Rostron, T. Fearn and M. H. Ramsey, Confidence intervals for robust estimates of measurement uncertainty, Accreditation and Quality Assurance: Journal for Quality, Comparability and Reliability in Chemical Measurement, 2020, DOI:10.1007/s00769-019-01417-4.
- AMC, The Duplicate Method for the estimation of measurement uncertainty arising from sampling, Technical Brief No. 40, 2009, https://rsc.li/amc.
- AMC, TB Robust statistics: a method of coping with outliers, Technical Brief No. 6, 2001, https://rsc.li/amc.
- AMC, Why do we need the uncertainty factor? Technical Brief No. 88, Anal. Methods, 2019, 11, 2105–2107, 10.1039/C9AY90050K.
- https://www.rsc.org/Membership/Networking/InterestGroups/Analytical/AMC/Software/ .
- Eurachem/EUROLAB/CITAC/Nordtest/AMC Guide: Measurement uncertainty arising from sampling: a guide to methods and approach, ed. M.H.Ramsey, S. L. R. Ellison and P. Rostron, Eurachem, ISBN 978-0-948926-35-8 http://www.eurachem.org/index.php/publications/guides/musamp, Example A1, 2nd edn, 2019, pp.39–42 Search PubMed.
- J. A. Lyn, M. H. Ramsey, S. Coad, A. P. Damant, R. Wood and K. A. Boon, The duplicate method of uncertainty estimation: are eight targets enough?, Analyst, 2007, 132, 1147–1152, 10.1039/b702691a.
| This journal is © The Royal Society of Chemistry 2021 |