Simplex optimisation in practice

Abstract

While the underlying principles of simplex optimisation are easy to understand and the small number of trial experiments involved make the approach very attractive, there are several important issues to be considered in the practical application of the method to the analytical sciences and other areas. These include the selection of suitable factor levels to set the size and position of the initial simplex, and the variation of the step sizes used to find the positions of subsequent simplexes. The possibility of accidentally finding a local maximum rather than a global maximum must also be considered.

---

In a previous Technical Brief (No. 95)¹ the simplex approach to the optimisation of analytical methods was outlined. Contour diagrams were used to demonstrate the principles of the method in the simplest situation where two experimental factors are involved. The initial simplex in such cases is a triangle, and subsequent simplexes are calculated by rejecting the vertex of the triangle that gives the poorest system response, a new vertex being obtained by reflecting the position of the rejected one through the line joining the other two.

An immediate problem seems to arise in deciding the size and position of this first simplex. If the initial triangle is too small, an unnecessarily large number of experiments are needed to approach the optimum, while if it is too big the new vertices of successive simplexes will soon hop alternately from one side of the optimum to the other, with the optimum itself being poorly defined between those positions. This concern, which inevitably extends to systems with more than two factors, can be minimised in two distinct ways.

Prior knowledge and common sense

In practice it is very unlikely that we would try to optimise an analytical system of which we had little or no prior knowledge. The following example demonstrates this, and also shows how the positions of new vertices are calculated when more than two experimental factors are studied. In our example we are trying to achieve the best possible limit of detection when analysing a fluorescein labelled compound in diluted blood serum samples, using a conventional fluorescence spectrometer with a broad band light source and grating monochromators in the excitation and emission beams. Fluorescein is intensely fluorescent and can be detected at attomolar levels in pure solution, but in biological samples the limits of detection are adversely affected by two factors. The serum matrix may have a significant background fluorescence of its own (albumin-bound bilirubin is a likely culprit); and Rayleigh scattering background – damaging here as the excitation and emission wavelengths of fluorescein are separated by only about 25 nm – will be enhanced by proteins and other macromolecules in the diluted serum. We seek the conditions in which the fluorescein emission minus the total background is at a maximum level. The experimental factors studied will be the excitation and emission wavelengths and the bandwidths of the two monochromators. To minimise the background it may be advisable to use excitation and emission wavelengths that are not the optimal ones for fluorescein. Monochromator bandwidths should not be too small (that would reduce the fluorescence intensity) or too big (giving too much scattered light interference). With four factors there will be five vertices for each simplex. Table 1 shows hypothetical values and responses for the initial simplex: the background-subtracted fluorescence response is recorded in arbitrary units. Note that it is not necessary when setting up the optimisation process for each factor to have different values at each vertex of the initial simplex. The second part of the table shows how the position of the new vertex (vertex 6) can be calculated after the rejection of vertex 3, which gives the lowest response.

Table 1 Simplex optimisation example

Fluorescence	Excitation wavelength (nm)	Emission wavelength (nm)	Excitation bandwidth (nm)	Emission bandwidth (nm)	Background-corrected fluorescence
Vertex 1	470	515	10	10	59
Vertex 2	475	520	10	5	64
Vertex 3	480	520	5	5	38
Vertex 4	480	525	5	10	52
Vertex 5	485	530	10	15	46
(a) Sum (excluding vertex 3)	1910	2090	35	40
(b) Sum/4 (excluding vertex 3)	477.5	522.5	8.75	10
(c) Vertex 3	480	520	5	5
(d) Displacement, i.e. (b) − (c)	−2.5	2.5	3.75	5
New vertex 6 = (b) + (d)	475	525	12.5	15

---

This calculation suggests that the best limits of detection might be achieved using large monochromator bandwidths, coupled with quite widely separated excitation and emission wavelengths (see also below). Subsequent vertices are found in the same way. Software for performing such calculations is available in programs such as Minitab® and MATLAB®, and also through Microsoft® Excel® add-ins.

Variable step size simplex

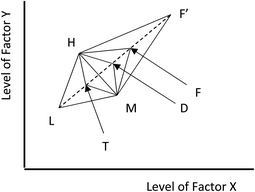
One important modification of the basic method reduces the problem of setting the size and position of the initial simplex. We can vary the rate of movement towards the optimum using the extent to which the response at each new vertex compares with the responses at other vertices. In the fluorescence example above, if new vertex 6 yields a much improved fluorescence response of (e.g.) 81 units, we could assume that we are making good progress towards the optimum and could extend the simplex in the same direction by (normally) twice the usual distance. On the other hand, if vertex 6 produces a fluorescence response of only 66 units, not much better than the response at vertex 2, we could conclude that we might already be close to the optimum response, and subsequent steps would be smaller than usual, say half the size. Returning to the simple situation with only two factors, the principles of this modified approach are shown in Fig. 1. The initial simplex is the triangle with vertices L, M and H, with vertex L giving the lowest response and vertex H the highest. To start we use the usual reflection calculation to yield the vertex labelled F to replace the vertex L. If the response at F is better than the response at H, i.e. is the best response so far, then we extend the reflection process to give a vertex F′ at twice the distance from the line joining vertices M and H. Sometimes the response at F′ will be worse than that at vertex H, so the expansion of the simplex has evidently failed, and we return to using the triangle MHF as the basis for the next step. There are three other possibilities. If the response at F lies between the responses at M and H, we can again use the triangle MHF as the basis for the next reflection. The response at F might be poorer than that at M but better than that at L: this means that the simplex has already moved too far, and we can halve its expansion to generate a new point D. If the response at F is actually lower than that at L we can establish a new simplex using a point, T, inside the original simplex. Overall this flexible approach allows us to begin the optimisation with quite a large simplex, with rapid progress towards the optimum, where the simplexes become smaller.

Fig. 1 Principles of variable-size simplex optimisation for two factors; for details see text.

Pluses and minuses

The advantages of simplex optimisation are clear. The underlying principles are easy to grasp and the calculations are readily performed. Most importantly the number of trial experiments involved does not increase markedly with the number of experimental factors, so we can fearlessly include in the process all the factors that might conceivably affect the outcome. But there are some limitations too. Because of the small number of trials involved we do not get a clear picture of the shape of the response surface near the optimum. We can, however, check the optimisation and establish the factors whose levels affect the optimum most crucially by slightly altering the factor levels one at a time, leaving the other factor levels at their optimum values. In practice the slope of the response surface near the optimum may be similar to or less than the random errors in the measurements, so we may have to be content to arrive at a point that is close to the optimum rather than exactly on it.

A separate problem is that the response surface may have more than one maximum, so we may light upon a subsidiary maximum rather than the true optimum (this may in practice be the case in the fluorescence experiment described above). The conventional way of addressing this problem is to perform a second simplex optimisation with a quite different starting simplex, hoping that the two distinct simplexes arrive at more or less the same optimum. Again the economy of effort characteristic of simplex methods is valuable here. An entirely distinct approach to the problem of subsidiary maxima is provided by simulated annealing, a natural computation method that allows an optimisation process to continue even when a system response is poorer than the previous one.

Applications

Simplex optimisation has been applied to many analytical techniques, including all the major spectroscopic, electrochemical and chromatographic methods, and in other areas of chemistry such as calculations of protein folding, X-ray crystallography, and quantitative structure–activity relationships (QSAR). There is very extensive literature on the method,² including some YouTube videos.

James Miller (Loughborough University)

This Technical Brief was written on behalf of the Statistics Expert Working Group and approved by the Analytical Methods Committee on 17 ^th December 2020.

Further reading

1. AMC TB 95, Experimental design and optimisation (5): an introduction to optimisation, Anal. Methods, 2020, 12, 2422–2424,  10.1039/D0AY90037K.
2. R. G. Brereton, Chemometrics: Data Driven Extraction for Science, John Wiley, 2018.

---