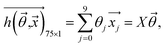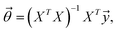A surface-based calibration approach to enable dynamic and accurate quantification of colorimetric assay systems

Abstract

Colorimetry is widely used in assay systems for its low-cost, ease-of-use, rapidity, moderate storage requirements and intuitively visible effects. However, the application is limited due to its relatively low sensitivity. Conventional colorimetric calibration methods often use a fixed incubation time that can limit the detection range, system robustness and sensitivity. In this paper, we used color saturation to measure the accumulation of product (correlation coefficient R² = 0.9872), and we created a novel “calibration mesh” method based on an expanded sigmoid function to enhance sensitivity. The novel calibration mesh method can be adapted for a wide variety of assay systems to improve robustness and detection range, and provide a dynamic and faster output.

---

1. Introduction

Colorimetric analyses have been widely used in various types of assays, including tests for pregnancy,¹ bacteria,² toxicity,³ pH,⁴ soil,^5,6 industry waste water⁷ and many common biomarkers in blood⁸ and sweat.^9,10 The development of low-cost point-of-care devices, such as those that use simple paper pads,¹⁷ could help address health disparity issues related to inadequate access to care.¹⁶ Colorimetry offers a low-cost, accessible measurement technique that does not require complex imaging modalities or burdensome data storage. However, compared to fluorescence or other modern detection methods, the biggest disadvantage of colorimetry is low sensitivity and high noise. Most colorimetric data analyses are based on light absorption,¹¹ gray-scale intensity,¹² red, green, blue (RGB) color space measurements,^8,9 or analyses based on the hue channel of the hue, saturation, value (HSV) color space.¹³ Analyses based on the saturation channel of HSV color space can outperform other channels when a colored product accumulates in an assay¹⁴ and is less dependent on ambient light conditions.¹⁵

A linear or non-linear fit of measured values (e.g., intensity, absorption, impedance) to known concentrations is often used to establish a conventional calibration curve in an assay system. Readings based on this curve often require a fixed incubation time, which limits both the detection time and the detection range. Low concentration samples may require more incubation time to be distinguished from blank samples; high concentration samples may exceed the upper limit of detection of the reader after a fixed incubation time. Also, using a fixed incubation time provides only a single readout per sample. Technical replicates are often utilized to overcome single measurement inaccuracies, but this requires additional sample and reagents.

In this study, we developed a colorimetric paper pad sensing unit and analysis technique to quantify the concentration of the enzyme invertase. Our technique utilizes an innovative “calibration mesh” method that uses a temporal analysis of colorimetric saturation to replace the conventional fixed-time calibration method. To demonstrate the robustness of this method, we compared the performance of the “calibration mesh” to the conventional calibration approach.

2. Experimental methods

(a) Reagents and solutions

Sucrose was purchased from VWR. Glucose oxidase (G2133-50KU, 242 776 U g⁻¹), peroxidase from horseradish (P8125-25KU, 50–150 U mg⁻¹), and invertase (I4504-250MG, ≥300 U mg⁻¹) were purchased from Sigma. D-Trehalose, 99% anhydrous was from Acros Organics (NJ). Sodium acetate was purchased from Fisher Scientific. Phosphate buffered saline (28 372) was purchased from Thermo Scientific. Sodium iodide (409286-1G) was purchased from Aldrich. Acetic acid was purchased from Sigma-Aldrich. Cellulose fiber sample pad strips (CFSP203000) were purchased from Millipore. Deionized water (18.0 MΩ) was used in all procedures. Details of buffer preparation are available in ESI.†

(b) Sensing paper pad procedure

Paper pad fabrication. The cellulose fiber paper was cut into round paper pads using a quarter size hole puncher (Walmart), and the edge was trimmed to remove burrs. The pad was then sealed in a plastic storage bag for future use.

Reaction cocktail solution. This solution was made immediately before use and was modified from a glucose sensing method.⁹ Briefly, the final solution consisted of 1.2 mg (291 units) glucose oxidase, 0.12 mg (6–18 units) HRP, 105.2 mg trehalose, 92 mg sodium iodide, 171 mg sucrose and 1 mL 0.05 M cold sodium acetate buffer, pH = 5.55.¹⁸ The vial was covered with foil to protect it from light. More details are available in the ESI.†

Substrate treated paper pad fabrication. We used a 100 μL pipette tip holder as the paper pad reaction holding plane. Twenty-four paper pads were placed on top of the holes of the holder in 8 rows and 3 columns. Each paper pad covered a pipette tip hole, promoting faster, uniform drying of the pads. 100 μL of the cocktail solution was pipetted onto each paper pad and allowed to dry at room temperature overnight.

Colorimetric mechanism. Invertase was used to hydrolyze the conversion of sucrose to glucose (eqn (1)).¹⁹ Next, glucose was catalyzed by glucose oxidase to produce hydrogen peroxide (eqn (2)).²⁰ The subsequent peroxidase catalyzed reaction between iodide (colorless) and hydrogen peroxide produced iodine (brown color) for colorimetric analysis (eqn (3)).²¹ A standard stock solution was prepared using 2 mg invertase dissolved into 1 mL PBS. This stock was gradually diluted with PBS into standard concentrations of 10, 5, 2.5, 1, 0.5, 0.25, 0.1 and blank 0 μg mL⁻¹ (PBS only). Finally, 360 μL of each standard solution was added into a column of a 96-well plate.

(c) Experiment and camera setup

The whole experiment was carried out under a stable and uniform white illumination area. All steps were as follows:

Step 1: place 24 substrate-treated paper pads on a cleaned pipette tip holder as described above (8 rows and 3 columns). Fix the camera (details in ESI†) 20 cm above the paper pads.

Step 2: after focusing the image, turn off all camera automatic adjustment and balance functions, and acquire images at 5, 20, 30, 40, and 72 min.

Step 3: use an 8-channel pipette to add 100 μL invertase solution to the center of each paper pad in the first column avoiding touching or moving the paper pads.

Step 4: repeat step 3 for the second and third columns. The time interval between each addition is 20 s.

(d) Image processing

After capturing the images of paper pads, we converted the captured image to a gray scale image, an R, G, B color space image, and an H, S, V color space image (Fig. 1).

Fig. 1 Response image captured at 30 min. From left to right are raw image, gray image, red channel, green channel, blue channel, hue channel, saturation channel and value channel.

To calculate the average saturation value of HSV color space for each paper pad, the pad area was selected using a circular mask, and the saturation values of regions outside of the paper pads were set to 0. The average saturation value of all pixels in a paper pad was calculated as follows:

where s_k is the saturation value of each pixel, N is the number of pixels in a paper pad, s is the average of saturation value of all pixels in a paper pad. The background was selected as the average saturation value of each paper pad at the 5 min time point. Unless otherwise specified, all saturation data are given after subtracting the background.

(e) Correlation coefficients calculation

Similar to the saturation channel processing described above, we calculated both raw data and data with the background subtracted for the gray image, and all channels of R, G, B, H, and V. We then calculated the correlation coefficient between the target concentration and magnitude of each of these channels (Table 1).

Table 1 Correlation coefficient between the concentration of detection target and each channel

R squared value	Grey	Red	Green	Blue	Hue	Saturation	Value
Average value of raw image	0.9004	0.7110	0.9166	0.9588	0.4258	0.9790	0.7111
Average value – background	0.6414	0.2836	0.6354	0.9628	0.5953	0.9872	0.2873

---

(f) Calibration method

The data obtained from the standard concentrations of 0.1, 0.5, 1, 2.5, and 10 μg mL⁻¹ were used as training dataset to establish conventional calibration curve or calibration mesh. The dataset obtained from the standard concentrations of 0.25 and 5 μg mL⁻¹ were used as testing data to evaluate the performance of the algorithm and different methods.

1. Conventional calibration curve. We established a conventional calibration curve by linearly fitting the training dataset obtained at 30 min. Three technical replicates were acquired for each concentration (0.1, 0.5, 1, 2.5, and 10 μg mL⁻¹) to yield 15 data points in total.

2. Calibration mesh. We established the calibration mesh by using training dataset at 5 min, 20 min, 30 min, 40 min, and 72 min with three technical replicates for each concentration (0.1, 0.5, 1, 2.5, and 10 μg mL⁻¹). This yielded 75 total data points. The time and the concentration data were set as inputs. The saturation data were set as outputs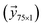. Two different models were proposed for establishing the calibration mesh:
2.1. Linear regression model. In this model, we generated the prediction function as a polynomial function:

The t and c here were normalized by dividing each time and concentration by the maximum values of time and concentration, respectively.

First, we defined an input matrix:

where each of to is a 75 × 1 vector

Then, the prediction function can be rewritten as:

where .

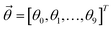Next, we defined the cost function as:

where m = 75

The goal was to solve the coefficient to make the predicted output saturation value 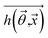as close as possible to the training saturation values by finding the minimum of Since the dataset was not large, we used a normal equation approach to solve for theta:

Note: if X^TX is not inversable, we apply a pseudo inverse.

A regularization was applied to prevent over fitting. Then,

where λ was choosen as 0.01.

D is a 10 by 10 matrix, which is similar to the identity matrix except that the first element is 0.

2.2. Sigmoid model. Plotting the saturation value vs. concentration and time (Fig. S4, S5† and 2) revealed a sigmoidal curve. Therefore, we expanded the basic sigmoid model as follows:

where is a 7 × 1 vector of [k(1), k(2), …, k(7)]

Fig. 2 Contour plot of average saturation raw data for each time vs. time and concentration.

The function retains a sigmoid shape but is shifted and stretched by the coefficients. To extend the sigmoidal function (s) to a surface, we define z(t,c) to capture the relationship between time and concentration.

Next, we defined the cost function:

where m = 75.

The training goal was to find an optimal solution of to minimize the cost of . Since the training dataset was discrete, we used the fminsearch function within Matlab.

For both the linear regression model and the sigmoid model, once the optimal solution for or was obtained, we could build the calibration mesh within the given range of time (0–74 min) and concentration (0–10 μg mL⁻¹).

(g) Performance evaluation

Evaluation of calibration mesh with training dataset. We first plotted the average training dataset on the calibration mesh (Fig. 3), and qualitatively evaluated the performance of the mesh, where the average training saturation data was calculated by taking the average of saturation data of 3 different paper pads at a single capture time. Quantitively, by using the optimal solution within the respective cost function, we compared the total errors or difference between the predicted values and the output values (Table 2).

Fig. 3 Calibration mesh with average of training data set. Linear regression model (A) vs. sigmoid model (B). The yellow dots were the average training data set.

Table 2 Comparison of two models' performance

Calibration Mesh Model	Linear Regression	Sigmoid
Error or cost	1.7067 × 10^−4	4.7337 × 10^−5

---

Compare conventional calibration curve to calibration mesh. To evaluate the performance of traditional conventional calibration curve methods, we used the saturation data for the 0.25 and 5 μg mL⁻¹ samples collected at 30 min in the linear fit equation to calculate the predicted concentration.

For the calibration mesh, we used the saturation data obtained from 0.25 and 5 μg mL⁻¹ concentrations measured at 20 min, 30 min 40 min and 72 min in the calibration mesh model and used our algorithm presented in Fig. 4 for mapping the predicted concentration.

Fig. 4 Flow chart for using calibration mesh. t_i: the i^th input time for capture of paper pads. S_i: the i^th saturation value (raw data). S_BG: the background saturation value. SR_i: data. CalMesh: calibration mesh. ARD: absolute relative difference. ***If there were N duplication inputs, we will calculate the average value of c_i as: .

Absolute relative difference (ARD) for each of these methods was then calculated as:

3. Results and discussion

(a) Saturation channel performance

Rather than working in the orthogonal RGB space, which depends on linear combinations of red, green, and blue values to describe a color, saturation data obtained in the HSV space does not depend on the color produced in a reaction (Fig. S7†). The accumulation of any color product yields a saturation value that can be directly related to concentration.

By observing the histogram and normal distribution of pixel saturation (Fig. S1 to S3†) and the comparison between the raw image and the data channels shown in Fig. 1, we found that the average saturation value of all pixels from a paper pad represents the color change of the paper pad well.

The correlation coefficient values in Table 1 show that the saturation channel had the best correlation with concentration among all channels. Also, the saturation data with background subtracted gave a higher correlation coefficient than the raw data. Therefore, we selected the average saturation value of the raw image minus background as our training or testing saturation data in this study.

(b) Calibration curve and calibration mesh development

A conventional calibration curve (Fig. 5) was established using a linear fit based on the 30 minutes training dataset. These data yielded the following fit:

y = 0.0159x + 0.0075

Fig. 5 Conventional calibration curve established based on 30 minutes training data.

Next, we developed the first calibration mesh model using a linear regression technique. After training, the optimal solution of was [−0.0017, –0.0986, −0.0442, 0.3161, 0.8425, 0.0059, −0.1326, −0.1963, −0.3172, 0.0067]. After plotting the mesh (Fig. 3A), we observed that the average training dataset (“yellow dots”) did not fit the calibration mesh well.

From the contour plot of average saturation raw data vs. time and concentration (Fig. 2), we observed that when both time and concentration are small (left bottom corner) or large (top right corner), the distance between contour lines are relatively large, while the density of contour lines in the middle is higher. This indicates that the slope in the middle is higher than the lower left or the upper right regions of the plot. Based on the slopes observed in the contour plot data, we hypothesized that a sigmoidal function may provide a more appropriate fit for our calibration mesh.

After training the sigmoid model, the optimal solution of was [0.5294 1.4278 1.2644, 5.0479, −0.6219, 0.7222, −0.0043]. The sigmoid model calibration mesh fit the average training saturation data well (Fig. 3B, “yellow dots”). As shown in Table 2, the error of the sigmoid model (4.7337 × 10⁻⁵) was smaller than the error obtained using the linear regression model (1.7067 × 10⁻⁴). Therefore, we concluded that the sigmoid model outperformed the linear regression model in this study.

The linear regression model, however, has some advantages that should be considered. First, as a common method, the linear regression model could be used for general situations, especially when the detection range of interest demonstrates a linear relationship between saturation and both concentration and time. Second, the linear regression model does not require optimization to account for variations in mesh shape. Third, training by solving the normal equation is more cost-effective than “fminsearch”. In this study, the training time (averaged over 10 runs) for the linear regression model was 0.0002 s, while the average training time of the sigmoid model was 0.0323 s. Therefore, the linear regression model may be more appropriate for platforms in which computational effort is a major concern.

(c) Calibration mesh utilization

For the conventional calibration method, we can map a saturation value at a fixed time (e.g., 30 min) on the calibration curve to determine the associated concentration. Similarly, for the “calibration mesh”, we can map a saturation value (s) at a time (t) on the “calibration mesh” and find the associated concentration (c). The added benefit of the calibration mesh method is the ability to capture images at multiple time points and increase the accuracy of the concentration measurement (Fig. 4).

(d) Performance of the conventional calibration curve vs. calibration mesh models

As shown in Table 3, although the conventional calibration curve method did well in identifying concentration for 5 μg mL⁻¹ (ARD = 0.48%), it was unable to accurately identify the 0.25 μg mL⁻¹ condition (ARD = 410.22%). The calibration mesh using the sigmoid model accurately calculated both concentrations (ARDs were 0.67% and 0%, respectively).

Table 3 Predicted concentration value of three different models with ARD

Model		Conventional calibration method	Calibration mesh via linear regression model	Calibration mesh via sigmoid model
For concentration	Prediction	0.0490 μg mL^−1	0.2167 μg mL^−1	0.25 μg mL^−1
0.25 μg mL^−1 testing	ARD	410.22%	13.32%	0%
For concentration	Prediction	4.9761 μg mL^−1	5.6667 μg mL^−1	4.9667 μg mL^−1
5 μg mL^−1 testing	ARD	0.48%	11.77%	0.67%

---

(e) Merits of calibration mesh

In this study, the conventional calibration curve was constructed based on a fixed time (30 min). However, from the calibration mesh (Fig. 3), we can see that a higher concentration sample has a faster chemical reaction and a rapid increase in saturation value, which requires a shorter time to be distinguished from the blank. On the other hand, as shown in the results presented above, the conventional calibration curve may be inaccurate for low concentration prediction. The calibration mesh can overcome this limitation by extending the reaction time so that the lower concentration samples would eventually exhibit and increase in saturation to improve the signal-to-noise ratio. Using this method, an investigator does not need to determine the incubation time a priori. Further, if multiple samples with large concentration differences are being assayed simultaneously (or perhaps several biomarkers with drastically different concentrations in a multiplex assay), the calibration mesh technique can provide reliable quantification without the need to perform separate incubation times for each sample or biomarker. The designed algorithm for utilizing the calibration mesh can give a robust and accurate output by setting conversion criteria for the predicted concentration over time. The calibration mesh can expand the detection range and provide an earlier output.

4. Conclusions

We have demonstrated that color saturation has a higher correlation to accumulated product in a paper pad assay system. We have also shown that the calibration mesh method has an improved dynamic range and accuracy compared to a conventional calibration curve. The utilize of calibration mesh is simple and can be adapted for a wide variety of assay systems.

There are several things we can do to improve the performance of the calibration mesh method in future iterations. First, increasing the standard concentrations and automating image capture with higher frequency could provide better model inputs and achieve higher resolution calibration mesh in both concentration and temporal axis. Second, instead of using saturation only, we could explore using a combination of gray, R, G, B, hue, saturation, and value data to obtain a combined output, which may further enhance the correlation between the imaged data and the concentration. Third, since temperature changes can affect chemical reactions, we can also integrate temperature as a variable in the training model. Fourth, for the calibration mesh utilization algorithm, we can also introduce a factor that changes the weight of a single measurement based on the ARD at particular time points in the assay. Fifth, we can utilize the slope of calibration mesh to eliminate potential background error. Utilization and iterative improvements of the calibration mesh technique could yield a robust algorithm that will enhance the accuracy and sensitivity of colorimetric assays.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was funded by the NSF Engineering Research Center, Precise Advanced Technologies and Health Systems for Underserved Populations (PATHS-UP) – award no. 1648451. The authors also acknowledge helpful discussions with Daniel Chaparro and other members of the Cardiovascular Matrix Remodeling Laboratory.

References

1. S. L. Cohen, A Method for the Rapid Colorimetric Assay of Total Estrins in Pregnancy Urine1, J. Clin. Endocrinol. Metab., 1966, 26(9), 994–1004,  DOI:10.1210/jcem-26-9-994.
2. K. Methee, X. Zhu and E. Almeide, et al., Paper based point-of-care testing disc for multiplex whole cell bacteria analysis, Biosens. Bioelectron., 2011, 26(11), 4342–4348,  DOI:10.1016/j.bios.2011.04.035.
3. X. Zhu, E. Hondroulis, W. Liu and C. Li, Biosensing Approaches for Rapid Genotoxicity and Cytotoxicity Assays upon Nanomaterial Exposure, Small, 2013, 9(9–10), 1821–1830,  DOI:10.1002/smll.201201593.
4. A. R. C. Haas, Colorimetric Determination of the Hydrogen Ion Concentration in Small Quantities of Solution, J. Biol. Chem., 1919, 38(1), 49–55,  DOI:10.1016/s0021-9258(18)87373-2.
5. S. R. Dickman and R. H. Bray, Colorimetric Determination of Phosphate, Ind. Eng. Chem., Anal. Ed., 1940, 12(11), 665–668,  DOI:10.1021/ac50151a013.
6. W. E. Baethgen and M. M. Alley, A manual colorimetric procedure for measuring ammonium nitrogen in soil and plant Kjeldahl digests, Commun. Soil Sci. Plant Anal., 1989, 20(9–10), 961–969,  DOI:10.1080/00103628909368129.
7. K. Shrivas, S. Sahu, G. K. Patra, N. K. Jaiswal and R. Shankar, Localized surface plasmon resonance of silver nanoparticles for sensitive colorimetric detection of chromium in surface water, industrial waste water and vegetable samples, Anal. Methods, 2016, 8(9), 2088–2096,  10.1039/c5ay03120f.
8. C. M. McGeough and S. O'Driscoll, Camera Phone-Based Quantitative Analysis of C-Reactive Protein ELISA, IEEE Trans. Biomed. Circuits Syst., 2013, 7(5), 655–659,  DOI:10.1109/TBCAS.2012.2234122.
9. A. Koh, D. Kang and Y. Xue, et al., A soft, wearable microfluidic device for the capture, storage, and colorimetric sensing of sweat, Sci. Transl. Med., 2016, 8(366), 366ra165,  DOI:10.1126/scitranslmed.aaf2593.
10. R. Ghaffari, J. A. Rogers and T. R. Ray, Recent progress, challenges, and opportunities for wearable biochemical sensors for sweat analysis, Sens. Actuators, B, 2021, 332(October 2020), 129447,  DOI:10.1016/j.snb.2021.129447.
11. J. Riemer, H. H. Hoepken, H. Czerwinska, S. R. Robinson and R. Dringen, Colorimetric ferrozine-based assay for the quantitation of iron in cultured cells, Anal. Biochem., 2004, 331(2), 370–375,  DOI:10.1016/j.ab.2004.03.049.
12. J. C. Jokerst, J. A. Adkins, B. Bisha, M. M. Mentele, L. D. Goodridge and C. S. Henry, Development of a paper-based analytical device for colorimetric detection of select foodborne pathogens, Anal. Chem., 2012, 84(6), 2900–2907,  DOI:10.1021/ac203466y.
13. S. T. Krauss, A. Q. Nauman, G. T. Garner and J. P. Landers, Color manipulation through microchip tinting for colorimetric detection using hue image analysis, Lab Chip, 2017, 17(23), 4089–4096,  10.1039/C7LC00796E.
14. K. Su, Q. Zou and J. Zhou, et al., High-sensitive and high-efficient biochemical analysis method using a bionic electronic eye in combination with a smartphone-based colorimetric reader system, Sens. Actuators, B, 2015, 216, 134–140,  DOI:10.1016/j.snb.2015.04.052.
15. B. Coleman, C. Coarsey and W. Asghar, Cell phone based colorimetric analysis for point-of-care settings, Analyst, 2019, 144(6), 1935–1947,  10.1039/c8an02521e.
16. K. R. King, L. P. Grazette and D. N. Paltoo, et al., Point-of-Care Technologies for Precision Cardiovascular Care and Clinical Research: National Heart, Lung, and Blood Institute Working Group, J. Am. Coll. Cardiol. Basic Trans. Science, 2016, 1(1–2), 73–86,  DOI:10.1016/j.jacbts.2016.01.008.
17. Z. S. Ballard, H. A. Joung and A. Goncharov, et al., Deep learning-enabled point-of-care sensing using multiplexed paper-based sensors, NPJ Digit. Med., 2020, 3(1), 1–8,  DOI:10.1038/s41746-020-0274-y.
18. AAT Bioquest I. Acetate Buffer (pH 3.6 to 5.6) Preparation. https://www.aatbio.com/resources/buffer-preparations-and-recipes/acetate-buffer-ph-3-6-to-5-6.
19. E. Roemer, M. K. Schorp, J. J. Piadé, J. I. Seeman, D. E. Leyden and H. J. Haussmann, Scientific assessment of the use of sugars as cigarette tobacco ingredients: A review of published and other publicly available studies, Crit. Rev. Toxicol., 2012, 42(3), 244–278,  DOI:10.3109/10408444.2011.650789.
20. E. P. Golikova, N. V. Lakina, O. V. Grebennikova, V. G. Matveeva and E. M. Sulman, A study of biocatalysts based on glucose oxidase, Faraday Discuss., 2017, 202, 303–314,  10.1039/C7FD00042A.
21. E. L. Thomas and T. M. Aune, Cofactor Role of Iodide in Peroxidase Antimicrobial Action Against Escherichia coli, Antimicrob. Agents Chemother., 1978, 13(6), 1000–1005,  DOI:10.1128/AAC.13.6.1000.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ay01130h

---