Multivariate statistics in the analytical laboratory (1): an introduction

Abstract

Modern analytical techniques can harvest large amounts of multi-analyte data from multiple sample materials in extremely short periods. Such methods offer much more than major gains in efficiency, cost and time. They can yield information not otherwise available – classification, discrimination, cluster analysis and pattern recognition. Multivariate regression methods are also widely used. All these applications are available in software packages and are readily implemented. The calculations use matrix algebra, but here we outline the basic principles that underpin some of the methods, and show the types of information available.

---

The landmark Analytical Methods Committee (AMC) Technical Brief (TB) No. 100 is published below. Approximately 67% of published TBs are ‘statistical’, so the AMC considered it appropriate to also make this milestone TB statistically orientated. It provides an introduction to a major series of future TBs dealing with multivariate statistics. Multivariate statistics are increasingly being used by the analytical community and if implemented correctly can furnish the user/analyst with significant advantages and benefits. Instigated by Professor Michael Thompson (Birkbeck College), AMC TBs have been published by the Royal Society of Chemistry since 2000. Initially they were circulated in hard-copy to members of the Royal Society of Chemistry Analytical Division, but now all TBs are publicly available electronically from the AMC website¹ and, since 2012 also in, the Royal Society of Chemistry AMC Technical Briefs themed collection platform.² Areas covered by AMC TBs mainly reflect activities of the various AMC Expert Working Groups (EWGs) as well as the AMC itself. AMC TBs focus on subjects considered important for analytical scientists, which are currently topical or not readily available from other sources. AMC TBs are mainly drafted by EWG members, then separately peer-reviewed by the relevant EWG and by the whole of the AMC prior to publication. It should be noted that apart from their general application, AMC TBs comprise a very useful addition to CPD records. They are a great open-access resource, and provide an excellent foundation for most of what an analytical scientist needs to know in modern (bio-)analytical measurement science.

Dr Andrew P Damant

AMC Technical Briefs Editor

Heaps of data

The trend towards acquiring large amounts of multi-sample data can be traced back to the use of auto-analysers in clinical chemistry, which began in the 1950s. Air-segmented flow systems with colorimetric detection were used to analyse up to a dozen clinically important compounds at up to 90 samples per hour. Many automatic analysers are now available, and their use has been extended to water and other environmental materials. The use of array detectors in spectroscopy allows complete spectra for a sample to be recorded more or less instantly, and high-speed chromatographic separations provide rapid quantitative data on multiple analytes, as do solid state and bio-specific array detectors. As a result, multivariate methods have been applied to many areas of analytical science – studies of food authenticity and adulteration; characterising archaeological and other heritage objects; the composition of essential oils; the solution of forensic problems; and the examination of environmental and ecological data. Common measurement techniques include UV-visible, middle and near infra-red, NMR, fluorescence and Raman spectroscopies, and perhaps unexpected methods such as differential scanning calorimetry. The same techniques are also used in process analytical technology, the on-line monitoring of industrial manufacturing methods. The statistical methods used to extract information from data-rich experiments are based on matrix algebra: but by using smaller data sets we can illustrate the potential of the methods without delving into the detailed mathematics.

Principal components

Food materials are often studied using near infrared spectroscopy. Suppose that 12 samples of fat are studied at wavelengths of 1100, 1200, 1300 and 1400 nm, with the transmission percentages shown in Table 1. The table contains 48 separate measurements: in reality the materials would be studied at hundreds of wavelengths, giving thousands of measurements, so we would welcome significant data reduction if that could be achieved with no loss of chemical information. One approach utilises the likelihood of a significant correlation between the results at different wavelengths, so that some of the information obtained is redundant: in our example the results at 1100 nm and 1200 nm are strongly correlated, with a product–moment correlation coefficient of 0.95. When (and only when) such correlations occur, can we use principal components analysis (PCA) to give the desired data reduction. In this case, with four variables (transmission percentages) X₁–X₄, we seek four principal components Z₁–Z₄, defined by:

Z₁ = a₁₁X₁ + a₁₂X₂ + a₁₃X₃ + a₁₄X₄etc.

Table 1 NIR spectroscopy of fat samples: transmission percentages

Sample	1100 nm	1200 nm	1300 nm	1400 nm
1	19	68	75	30
2	18	66	77	34
3	16	65	76	34
4	18	67	78	34
5	16	66	78	33
6	16	65	77	33
7	20	69	76	32
8	19	68	75	31
9	18	66	80	33
10	20	69	77	30
11	20	68	76	31
12	21	70	75	32

---

So each principal component is a linear combination of the four transmission percentages X₁–X₄. The coefficients a₁₁, a₁₂etc. are chosen so that the Z values are not correlated with each other. Superficially it seems that we have simply replaced four original variables with four new ones, but the key point is that the coefficients are also calculated so that the first principal component Z₁ (PC1) accounts for most of the variation in the data, PC2 shows the next biggest variation, and so on. In a more realistic situation where there are many Z values, the number of useful principal components is far less than the number of variables, and significant data reduction has been achieved. PCA results for the data in Table 1 (from standard statistics software or Excel add-ins) show that Z₁ accounts for 74.2% of the total variance and Z₂ for a further 15.4%. The analysis calculates the coefficients of the principal components, a₁₁etc., so each principal component for each sample can be found using the above equation. Such values are called scores. When the scores for the first two principal components for the Table 1 data are expressed graphically (Fig. 1) they show that the samples fall into two distinct groups, a result not apparent in the original data.

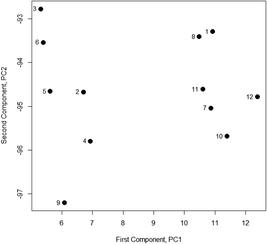Fig. 1 Scores for PC1 and PC2 for Table 1 data.

PCA makes no assumptions about the distribution of the data, so it is a general method for data reduction. It has been applied to a vast range of analytical problems and is regarded as a key tool in exploratory data analysis. It has been extended to regression calculations: as expected principal components regression is most valuable when the predictor variables are highly correlated, for example in spectroscopy.

Cluster analysis

The example above shows that PCA may reveal groups or clusters in a data set, but quite often the first few principal components do not resolve such groups properly. Dedicated cluster analysis methods are designed to classify a group of objects so that similar ones fall into the same class. Again these methods make no assumptions about the distribution of the measured variables, and the number of groups is not initially known. To identify objects that are close together in n-dimensional space we need a method to find the distance, d, between them. For two points with coordinates x₁, x₂, … x_n and y₁, y₂, … y_n the Euclidean distance is commonly used:

d = [(x₁ − y₁)² + (x₂ − y₂)² + … (x_n − y_n)²]^0.5

Before calculating d, the data are often standardised, so that each variable has zero mean and unit variance, thus ensuring that all the variables carry an equal weight (this procedure is also common in PCA). Initially pairs of objects separated by small values of d are grouped together to form clusters of two objects. The distances between such pairs are recalculated using the smallest distance between individual members of each pair (the single linkage method – other approaches are available). This procedure is applied iteratively so that the clusters become ever larger, and eventually all the objects are joined in a single cluster. The calculations are summarised in a dendrogram, which looks a little like an inverted tree. A judgement is then made on where the tree should be “cut” to show how many realistic clusters there are. Fig. 2 shows the dendrogram for the data in Table 1. The broken line near the top of the diagram shows that the tree can be convincingly cut to confirm that the data fall into two clusters, as already shown by PCA. The vertical scale in a dendrogram can be based on d values, but standard software often uses a similarity scale, the similarity between two points s_ij being given by s_ij = 100(1 − d_ij/d_max), where d_max is the greatest distance between two objects.

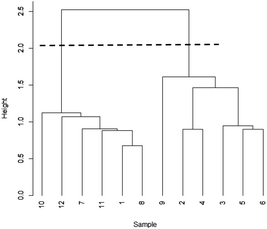Fig. 2 Dendrogram for Table 1 data.

This type of cluster analysis is described as hierarchical, because once an object has been assigned to a particular cluster it cannot be moved to another cluster. (Non-hierarchical methods are also available.) Cluster analysis has been used successfully with many analytical problems, and is an important area of exploratory data analysis. An important and recent application pinpointed the geographical origin of the sarsen stones at Stonehenge, using trace element data obtained with hand-held X-ray fluorescence instrumentation (see Technical Brief 89 (ref. 1 and 2)). The methods outlined here are described as unsupervised pattern recognition or classification, as we have no prior knowledge of any groups that may occur. There are also supervised methods, in which the starting point is a training set of sample materials with a group membership that is known; that set’s properties are used to place new materials (the test set) in an appropriate group.

Regression methods for multiple analytes

Regression methods to determine single analyte concentrations using standard materials to establish a calibration graph are well known, but the analysis of multiple components of a mixture using an analogous approach is far more complex. The absorbance (for example) of a mixture of compounds may not be the sum of the absorbances of the components: the latter may interact with each other causing spectral changes, and in real-world samples other materials may contribute to the measured absorbance. We therefore need to use real world samples for calibrations, and to use inverse calibration, in which the concentration of each analyte is expressed as a function of the spectrum, in the form

c_i = b_0i + b_1iA₁ + b_2iA₂ + … b_niA_n

where the A values are absorbances at n different wavelengths and the coefficients b are wavelength dependent. This is the opposite of the usual situation, in which we model the data (absorbances etc.) as a function of concentration: the absorbances have now become the predictor variables and the analyte concentrations are now the response variables.

Several methods for finding regression equations in the above form have been developed. They have at least two features in common. Just as in univariate regression it is important to study the residuals, the differences between the actual concentrations of the analytes in the calibration materials and the concentrations predicted by the regression model. Such residuals should not show any particular pattern or trend. The performance of each method can also be evaluated using cross-validation. This technique, also used to study supervised pattern recognition methods, has been less elegantly called the leave one out method. The measured values for the first calibration material are omitted and the other values are used to find a new equation for c₁ (for example). This new value for c₁ is compared with the actual value, and the process is repeated for each calibration material in turn. The sum of the squares of the differences between the predicted and actual c_i values is the predicted residual error sum of squares (PRESS). As the predictive power of the regression model increases, the PRESS value becomes closer to zero: PRESS data can thus be used to compare the performance of different regression methods. (There are alternative measures of predictive power, such as the root mean square error, RMSE.)

Partial least squares

The main multivariate regression methods used in the analytical sciences are principal components regression (PCR), which is related to PCA (see above), and partial least squares (PLS). Each method uses linear combinations of the predictor variables such as absorbance values, but in different ways. In PCR, the principal components are selected to describe as much as possible of the variations in the predictors, without regard for the relationship between the predictor and response variables. By contrast PLS chooses linear combinations of predictor variables that are highly correlated with the response variables, as well as explaining variations in the predictor variables themselves. In both cases it is expected that only a few linear combinations of the predictor variables will be needed to describe most of the variation, the PRESS statistic being used to select the optimum number. The better approach will depend on the nature of the data, such as the degree of correlation between the predictor variables. Given the general availability of suitable software it may be wise to apply both calculations to a given data set and use PRESS or a similar statistic to indicate which is more successful.

A PLS result for a small and simple data set is provided in ref. 4. The data describe the study of ten sample materials, each containing different amounts of three analytes studied by absorption spectroscopy at six wavelengths. The aim of the PLS calculation is to provide an equation for the concentration (c₁etc.) of each analyte in the form given above, with coefficients (b₀, b₁etc.) for the absorbance values at each of the wavelengths. For each of the three concentrations there will be an analysis of variance table of the type familiar in univariate regression; the outcome of the cross-validation calculation with PRESS values to show the optimum number of linear combinations of the six sets of wavelength data (once this optimum is exceeded the PRESS value starts to rise from its minimum); and the resulting coefficients which give the full equation for the concentration. This form of PLS, with separate outputs for each response variable, is called PLS1. If the response variables are correlated with each other they can be treated collectively; this is known as PLS2. Many applications of PLS in analytical work have arisen from molecular spectroscopy, where the spectra of sample components may overlap strongly, and where measurements at different wavelengths may be significantly correlated.

Subsequent technical briefs will give further details of the methods summarised above, and introduce additional techniques of multivariate analysis (also see ref. 3 and 4).

James Miller (Loughborough University)

This Technical Brief was written on behalf of the Statistics Expert Working Group and approved by the Analytical Methods Committee on 15th September 2020.

Further Reading

1. AMC Technical Briefs webpage, https://www.rsc.org/Membership/Networking/InterestGroups/Analytical/AMC/TechnicalBriefs.asp.
2. Royal Society of Chemistry themed collection platform, Analytical Methods Committee Technical Briefs, http://rsc.li/amctb.
3. T. Naes, T. Isaksson, T. Fearn and T. Davies, A User-Friendly Guide to Multivariate Calibration and Classification, IM Publications LLP, 2nd edn, 2017.
4. J. N. Miller, J. C. Miller and R. D. Miller, Statistics and Chemometrics for Analytical Chemistry, Pearson Education, 7th edn, 2018.

---