Open Access Article
Open Access ArticleQuantitative analysis of binary and ternary organo-mineral solid dispersions by Raman spectroscopy for robotic planetary exploration missions on Mars†
L.
Demaret
ab,
I. B.
Hutchinson
c,
G.
Eppe
 a and
C.
Malherbe
a and
C.
Malherbe
 *abc
*abc
aMass Spectrometry Laboratory, MolSys Research Unit, University of Liège, Liège, Belgium. E-mail: c.malherbe@uliege.be
bEarly Life Traces & Evolution Laboratory, UR Astrobiology, University of Liège, Liège, Belgium
cDepartment of Physics and Astronomy, University of Leicester, Leicester, UK
First published on 2nd November 2021
Abstract
The Mars 2020 and ExoMars 2022, rover-based missions are specifically dedicated to the search for evidence of life and will both utilise Raman spectrometers on the surface of Mars. Raman spectroscopy is indeed a valuable analytical technique for planetary exploration that enables in situ characterisation of rocks and soils collected directly from the surface or retrieved as cores and subsequently crushed when extracted from the subsurface with a drill. On Mars, the miniaturised spectrometers will interrogate ancient geological deposits, in order to try and identify hydrated or aqueously altered minerals and organic matter to assess the habitability of Mars. While the identification of relevant hydrous minerals and organic components is the primary analytical objective of the missions, quantifying their abundances would be of particular significance for interpreting past geological conditions (e.g. formation or alteration processes) and for ascertaining the putative presence of biosignatures. Therefore, we have developed quantitative models that enable the quantification of both mineral proportions from crushed mixtures of geological components and spiked mixtures containing organic analytes dispersed in mineral matrices. Based on data normalisation with appropriate standards (internal and external), we demonstrate that robust quantitative models can be (1) applied for solid dispersions of various complexities relevant to planetary exploration; and (2) applied to different Raman set-ups, including an instrument representative of the ExoMars Raman Laser Spectrometer. With important Raman-active minerals (calcite, gypsum, baryte, quartz), we demonstrate that using a correction factor Fϕ2/ϕ1, based on the ratio of apparent Raman scattering coefficients, the relative proportion of minerals in binary mixtures can be accurately determined. Regarding the organics, evaluated in clay-rich sediments (Fe-smectite) and crushed rocks of coarse-grained fraction (>100μm), we establish calibration curves in the concentration range 2–20 wt% for non-resonant compounds (L-cysteine, phthalic acid, adenine) and even lower (<1 wt%) for pre-resonant anthracene. Despite large levels of heterogeneity, the Raman analyses of these solid dispersions verify that quantitative Raman analyses can be performed in the context of robotic exploration studies.
1. Introduction
Raman spectroscopy is a well-established analytical technique that provides information about the molecular composition of samples, both qualitatively and quantitatively, based on the inelastic scattering of light by matter (Raman effect). Despite the low sensitivity of the technique, laser excitation sources enable fast and non-destructive Raman analyses to be performed on samples allowing the discrimination of various constituents, both organic and inorganic. In addition, miniaturised Raman spectrometers can be utilised remotely, outside of the laboratory facilities, enabling in situ measurements for various applications, including: geosciences, archaeometry and forensic analyses;1in vivo clinical applications;2 on-line process/quality control;3 stand-off Raman analyses of hazardous substances (e.g. explosives or biological agents),4 and finally, for exploring environments not accessible to humans (e.g. deep sea or extra-terrestrial bodies).5,6 Space exploration applications rely mostly on remote, high-technology robotic instruments, and Raman spectrometers have been included in the payloads of the exploration rovers for both the Mars 2020 and ExoMars 2022 missions.7,8The robotic exploration of Mars has long been guided by the search for water. More recently, the scientific priority became the search for possible habitable environments.9 Besides the presence of liquid water (in the past or present), habitable environments are also characterised by the presence of relevant minerals representing potential sources of energy or nutrients to support the activity of micro-organisms, and capable of preserving organic biomarkers from extinct life. Therefore, a comprehensive identification of the minerals in a specific location on Mars, and the detection of any putative organic signature, which are both feasible by Raman spectroscopy, will help in understanding the past geological processes of the planet and the conditions necessary for habitability. As a consequence, three Raman spectrometers are soon to be deployed on Mars. The Raman Laser Spectrometer (RLS), included in the analytical laboratory drawer of the Rosalind Franklin rover for the ESA/Roscosmos mission ExoMars2022, will analyse crushed core samples with a 532 nm (continuous excitation) laser, focused onto the flattened surface of the powdered geological samples with a spot size diameter of ∼50 μm.7 The RLS instrument will interrogate the samples utilising two possible operating modes: a pre-configured multi-measurement sequence (with a line or a grid pattern on the sample surface), or a single-measurement on a specific location of interest identified in a co-operative mode with the MicrOmega instrument (a visible-near infrared hyperspectral imager).10 The NASA Perseverance rover, already operating on the surface of Mars, includes two instrument suites with Raman modalities: SuperCam and SHERLOC. The SuperCam instrument comprises a Raman spectrometer capable of remote sample analyses from distances up to ∼7 m, with a pulsed 532 nm laser excitation source.11 The SHERLOC instrument, mounted on the robotic arm of the rover, is an imager instrument for the close-up analysis of rock specimens, combining fluorescence and resonance Raman analyses using a UV excitation laser at 248.6 nm.12 Raman mapping is performed using pulsed laser spots (∼100 μm beam diameter), with a spatial resolution of 30 μm, over a 7 mm2 area on the samples.13 A substantial part of the preparatory analytical work for Raman planetary exploration missions has focused on qualitative analyses, such as the creation of spectral databases for relevant minerals and biomolecules14–18 or the characterisation of (bio)geological samples from extreme habitable niches on Earth, presenting some analogies with expected scenarios for extant microbial life on Mars (Mars analogue samples).19–23
While quantitative Raman studies are considered the next logical step in terms of remote analytical research,19,24 developments in quantitative Raman analyses remain limited in the context of planetary exploration, either on Earth or on another planet. Nonetheless, quantitative analyses can provide specific information on the concentrations of organic molecules and/or minerals, which can reveal additional information regarding the biogenicity of a tested sample, when the co-occurrence of specific markers is determined.8 The significance of some compounds as biosignatures is indeed ascertained from the accurate quantities determined, not solely from their identification. Simultaneous quantitative Raman analyses for minerals and organics are feasible, but both quantifications are often examined separately. On the one hand, for quantitative Raman analyses of minerals, two approaches are considered. The first approach consists of evaluating the occurrence of a specific mineral spectral signature within a set of Raman spectra obtained randomly on the samples of rock or soil, which is similar to a standard petrographic approach.25 This type of analysis is best suited to instruments with a small laser footprint and enables the heterogeneity of complex geological specimens to be determined. For instance, the quantification of mineral proportions was successfully achieved using the point count method on Atacama soil samples evaluated with a flight-like instrument designed for planetary exploration.26 The second approach consists of evaluating the signal intensity for quantifications based on calibration curves developed from homogeneous, powdered mineral mixtures, with fine grains.27 This approach is best suited for analyses of transparent fine-grain mineral mixtures (e.g. mixtures of gypsum, calcite, aragonite or quartz) with large laser footprints on the sample surface.28,29 Actually, this approach is compatible with the RLS automatic operating mode and has been applied to demonstrate that semi-quantitative analyses can be obtained from planetary exploration mission instruments with binary calibration mixtures, such as gypsum-calcite, nitrate-oxalate salts or pyroxene-olivine systems.30,31 However, only a limited number of studies have focused on the quantitative Raman analyses of organics in minerals, especially for planetary mission scenarios. Those studies were mainly dedicated to the determination of the lower concentration levels enabling a qualitative detection of organic molecules of interest for planetary or astrobiological research, such as pigments (e.g. carotenoids), amino acids, carboxylic acids, nucleobases and polyaromatic hydrocarbons (PAH).32–37 These studies have identified a series of organics that can possibly be observed on Mars, if life ever developed on its surface. However, in a previous quantitative study on solid dispersions of L-cysteine in gypsum, we underlined that the analytical procedure, including the subsampling of the sample by the laser during a Raman analyses, is critical for quantitative evaluations.38 In particular, the signal observed (either absolute or relative) in one spectrum is not necessarily representative of the entire sample composition, which is especially the case for powder mixtures and highly dependent on the sample structure (e.g. grain size, compaction of the dispersions, heterogeneity of the mixture).
In this study, we present a general quantitative approach that enables the simultaneous determination of (a) the relative weight proportion of minerals in rock-powder mixtures and (b) the amounts of organic analytes dispersed into these mixtures, utilising Raman spectroscopy under the operating constraints associated with remote exploration missions. In particular, for the quantification of binary mineral mixtures, we introduce a correction factor (Fϕ2/ϕ1) allowing the consideration of binary mixtures prepared with minerals characterised by significantly different apparent Raman scattering efficiencies with a simple linear quantitative model. This correction factor not only enables the quantification of binary mineral mixtures, it also provides an effective normalisation of the Raman signal assigned to the organic analytes when they are dispersed in binary mineral mixtures. Calibration models obtained for different classes of organic compounds of interest for Mars exploration dispersed in complex geological substrates are reported, enabling the discussion of critical parameters for quantitative Raman analyses on solid dispersions (e.g. grain size, sample heterogeneity and signal variability), using two different instruments, including a miniaturised spectrometer with operating parameters similar to the RLS instrument. Finally, we comment on the sensitivity of Raman measurements for non-resonant and (pre-)resonant organic components in the frame of Mars exploration missions.
2. Materials and methods
2.1. Materials
The materials used for this study are listed in Table 1. Analytical grade L-cysteine, adenine, anthracene and phthalic acid were purchased from chemical companies. These organic molecules correspond to various classes of chemical substances identified in meteorites and interplanetary dust particles, which could therefore also be observed on Mars.39 Synthetic standards of gypsum, baryte, calcite and quartz were purchased from chemical companies. Natural samples of gypsum, calcite (all crystallised samples) and an Fe-rich smectite (nontronite, powder) were provided by collaborators. These minerals were selected for the present study as they have been identified as being relevant to the exploration of Mars.40,41| Class | Formula | Origin | |
|---|---|---|---|
| Organic components | Amino acids | ||
| L-Cysteine | C3H7NO2S | Merck 2838 (for biochemistry), purity 99% | |
| Nucleobases | |||
| Adenine | C5H5N5 | Sigma-Aldrich A8626, purity ≥99% | |
| Polyaromatic hydrocarbons | |||
| Anthracene | C14H10 | Sigma-Aldrich 141062, purity 99% | |
| Carboxylic acids | |||
| Phthalic acid | C8H6O4 | Sigma-Aldrich 80010, purity ≥99.5% | |
| Inorganic components | Sulphates | ||
| Gypsum | CaSO4·2H2O | Honeywell C3771, purity ≥99% | |
| Gypsum | CaSO4·2H2O | Environmental specimen (Carresse, FR) | |
| Baryte | BaSO4 | BDH Chemicals Ltd. 27304 | |
| Carbonates | |||
| Calcite | CaCO3 | Sigma-Aldrich 398101, purity ≥99.95% | |
| Calcite | CaCO3 | Environmental specimen (Leffe, BE) | |
| Silica | |||
| Quartz | SiO2 | Merck 7530 (pro analysis) | |
| Clay minerals | |||
| Nontronite | Na0.3Fe2((Si,Al)4O10)(OH)2·nH2O | Environmental specimen (Westerwald, DE) | |
The desired grain size fractions for the inorganic matrices were obtained using test sieves (Retsch – 200 × 50 mm) with mesh sizes of 100 or 50 μm. The synthetic inorganic reactants and the clay material were directly collected as powders with grain size <50 μm. The bulk crystals of gypsum and calcite, on the other hand, were crushed with a pestle in an agate mortar, and the three fractions were separated on the test sieves according to their grain sizes (<50 μm, between 50 and 100 μm and >100 μm in diameter). The average grain-size of inorganic matrices, either synthetic or environmental, were verified by measurement with scanning electron microscopy (SEM) (ESI, Table A†). The organic constituents were employed without additional preparation or grain size separation and a wide distribution of crystalline organic morphologies and grain sizes can be observed by SEM (ESI, Table A†). Every item of crushing and sieving equipment was cleaned with deionised water, methanol and acetone (analytical grade solvents) before use.
Various powder mixtures were prepared by homogeneously mixing the powdered constituents together. Three different types of mixtures were prepared: mixtures of two minerals in varying proportions (binary mixtures), mixtures of a single mineral dispersion spiked with an organic analyte (binary mixtures) and mixtures of binary mineral dispersions spiked with an organic analyte (ternary mixtures). All the dispersions were prepared by accurately weighing masses of inorganic and organic powders using an analytical balance (Mettler Toledo – mass reading error ± 0.0001 g) and reporting the sample concentrations in relative weight proportions (weight percentage, wt%). The weighed amounts of powder were successively added in polypropylene falcon tubes and mixed using a multifunctional tube rotator (grant PTR-35). A mixing programme combining different modes (reciprocal rotation and vibration motions) was applied for a minimum of 15 minutes prior to measurements in order to ensure the homogeneity of the mixtures. A few mg of each dispersion were then placed in circular wells (10 mm in diameter) engraved in aluminium blocks and the surface of the powders was flattened with a spatula. Various aliquots of the same dispersion were evaluated by repeating this last step using fresh quantities of material from the stock dispersion.
2.2. Raman spectroscopy
Raman measurements were performed in macroscopic mode using a benchtop LabRAM 300 spectrometer (Horiba Jobin Yvon) coupled to a Superhead Raman probe (Horiba) with optical fibres. The Superhead system, previously described in Grignard et al.,42 was employed with a 532 nm laser source (Coherent DPSS) focused on the sample at a focal distance of 12 cm, with a laser footprint on the sample surface larger than 100 μm in diameter and a laser power of ∼4 mW. Spectra were recorded with a spectral resolution of 3 cm−1 and typically averaged from 4 scans with a recording time of 4 seconds.Measurements were also performed with a DeltaNu Advantage 532 portable spectrometer interfaced with the 532 nm Coherent DPSS laser, enabling Raman analyses with operating parameters similar to those of flight-representative spectrometers, in particular the RLS instrument.17,43 These parameters are summarised in Table 2. The space mission instruments implement automatic Raman measurement procedures, which involve the collection of several Raman spectra along line or grid patterns at the surface of the samples. For instance, the RLS instrument will interrogate the samples with between 20 and 39 measurements, depending on the resources allocated to the Raman instrument during mission operations.31
| Analysis parameters | Miniaturised spectrometer | Raman laser spectrometer57 |
|---|---|---|
| a More acquisitions required for analyses on clay samples. | ||
| Laser wavelength (nm) | 532 – CW | 532 – CW |
| Laser power on sample (mW) | 6–12 | 20–30 |
| Laser spot size (μm) | ∼50 | ∼50 |
| Spectral range (cm−1) | 200–3400 | 200–3800 |
| Spectral resolution (cm−1) | ∼10 | 6–8 |
| Automated operating mode | Grid scanning (i = 36 points) | Grid/line scanning (i = 20–39 points) |
| Spectral acquisition parameters | 3 × 4 s (4 × 4 s)a | Adjustable according to intensity responses |
The collection of Raman data from the various dispersions was accomplished using a grid pattern at the flattened surface of powders (without using an autofocus). A set of 36 spectra (i = 36) were recorded per sample. The spectra were baseline-corrected using bespoke software, fitting the spectral baseline with a Savitzky–Golay polynomial fit (4th to 7th degree) in the spectral region of interest. Raman band intensities were estimated using the maximum height of each spectral peak. Each sample was evaluated using three independent aliquots (n = 3). With the Superhead configuration, the grid pattern covered 2.5 mm2 of the sample surface, and the spectra were recorded from sample locations with a lateral separation distance of 500 μm. With the miniaturised spectrometer, the grid pattern covered an area of 1.25 mm2 of the sample surface, and the spectra were recorded from sample locations with a lateral separation distance of 250 μm. The difference in lateral separation between consecutive locations, where spectra were collected with each instrument prevent oversampling (partial collection of the signal from identical area of the samples in two consecutive spectra). Assuming independent spectra are collected on the homogeneous dispersions, quantitative models can be established owing to the proportionality between the Raman intensity attributed to a compound, and the number of molecules of that compound probed by the instrument.
2.3. Scanning electron microscopy
Micrographs of the reference powders were obtained using Scanning Electron Microscopy (SEM). The inorganic and organic particles were gold-metallised and characterised with an ESEM-FEG XL 30 microscope (FEI) operating at 15 kV. Images were obtained using magnifications in the range 250 to 2500×, depending on the size of the crystals under investigation.2.4. Raman data normalisation
The normalisation of data is essential for the development of Raman quantitative models in the frame of planetary exploration in order to account for variations between instruments (e.g. laser stability, optical alignment) and/or environmental variations (e.g. temperature).44 Normalisation can be performed with an internal standard (i.e. a reference compound present in each sample in constant or controlled quantity, such as the solvent) or with an external standard (i.e. a reference material, such as a calibrating polymeric material) if no internal standard is available. The normalisation of signals used for the quantification of analytes is based on eqn (1) by dividing, for each pre-processed spectrum, the absolute intensity of the analyte signal IAna with the absolute intensity of the appropriate standard IStd (internal or external), arbitrarily set to 100. Normalised intensities with values INorma >100 (associated with hotspots) or obtained from saturated spectra were discarded from the datasets. | (1) |
In the frame of this study, three cases are developed concerning the normalisation of the analyte signal for quantification.
Case 1: If the main constituent of a binary mixture (mineral matrix, assimilated to the solvent) is not Raman active or is not observed, the normalisation of the analyte signal is determined from an external standard of poly(methyl methacrylate) (PMMA).
Case 2: If the main constituent of a binary mixture (mineral matrix assimilated to the solvent) is Raman active and characterised by a strong Raman signal, the normalisation of the analyte signal is performed using the response of the mineral matrix as an internal standard. The normalisation was performed on each independent spectrum recorded (i).
Case 3: If the mixture is composed of three components (ternary mixtures), with two main constituents ϕ1 and ϕ2 (binary mineral matrix, assimilated to the solvent) that are both Raman active and characterised by distinct strong Raman bands, the normalisation of the analyte signal is then determined by the response of both minerals constituting the matrix. In this case, a correcting factor, Fϕ2/ϕ1, must be applied as shown in eqn (2).
 | (2) |
The correction factor introduced in eqn (2) accounts for the variation of the apparent scattering efficiency of the mineral phase ϕ2, relative to the mineral phase ϕ1. The Fϕ2/ϕ1 factor is defined in eqn (3) as the ratio of apparent Raman scattering coefficients (r) evaluated from the two minerals constituting the solid dispersion. The apparent Raman scattering coefficient for a mineral phase (e.g. rϕ1) is calculated from eqn (4) and corresponds to a proportionality factor between the concentration of that mineral phase (Cϕ1) and its Raman intensity (Iϕ1). That experimental coefficient depends on the applied methodology and describes the apparent Raman scattering capacity of a mineral phase as measured by the instrument. The use of the ratios, hence the Fϕ2/ϕ1 factor, enables a constant value for a given binary system to be determined, which is then independent of the instrument used.
 | (3) |
| Iϕ1 = rϕ1Cϕ1 | (4) |
3. Results and discussion
3.1. Qualitative description of Raman spectra
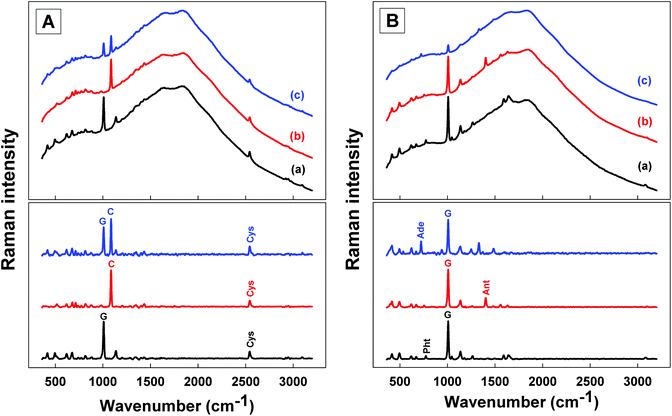
The main characteristic Raman bands for each of the mineral phases considered in this study are readily distinguished, even in mixtures (i.e. calcite-baryte, calcite-gypsum or gypsum-quartz mixtures; Fig. S1†). A strong Raman band is observed for calcite at 1085 cm−1 (CO32− symmetric stretching mode),45 for baryte at 988 cm−1 (SO42− symmetric stretching mode),46 for gypsum at 1008 cm−1 (SO42− symmetric stretching mode)47 and for quartz at 464 cm−1 (O–Si–O symmetric bending mode).48 Additional Raman bands can be observed in the wavenumber offset range 1000–3400 cm−1 when organic analytes are added to the mineral dispersions. Representative Raman spectra obtained for the binary and ternary mixtures (organic compound into one- or two-mineral matrices) with the miniaturised spectrometer are presented in Fig. 1. Typical spectral profiles for dispersions of L-cysteine in gypsum, calcite and a mixture of both minerals are presented in panel A (both the raw and baseline corrected spectra are shown). The main characteristic band for L-cysteine at 2544 cm−1 (S–H stretching mode)49 can be followed in each of these matrices. Similarly, typical spectra obtained for gypsum dispersions containing adenine, phthalic acid or anthracene are presented in panel B. The strong and distinct Raman bands selected for quantitative development include the Raman band at 772 cm−1 for the phthalic acid (out-of-plane ring bending),50 the Raman band at 1401 cm−1 for anthracene (ring deformation and C–C stretching)51 and the Raman band at 723 cm−1 for adenine (C–C and C–N stretching, in-phase breathing).52 For the samples composed of Fe-rich clay material spiked with L-cysteine, it was often the case that no specific Raman bands were observed from the mineral matrix (Fig. S2†). Consequently, the diagnostic bands of cysteine, which could be observed, were used and the value of the band at 2544 cm−1 employed for quantitative development using an external standard for signal normalisation.3.2. Calibration curves for binary organo-mineral mixtures
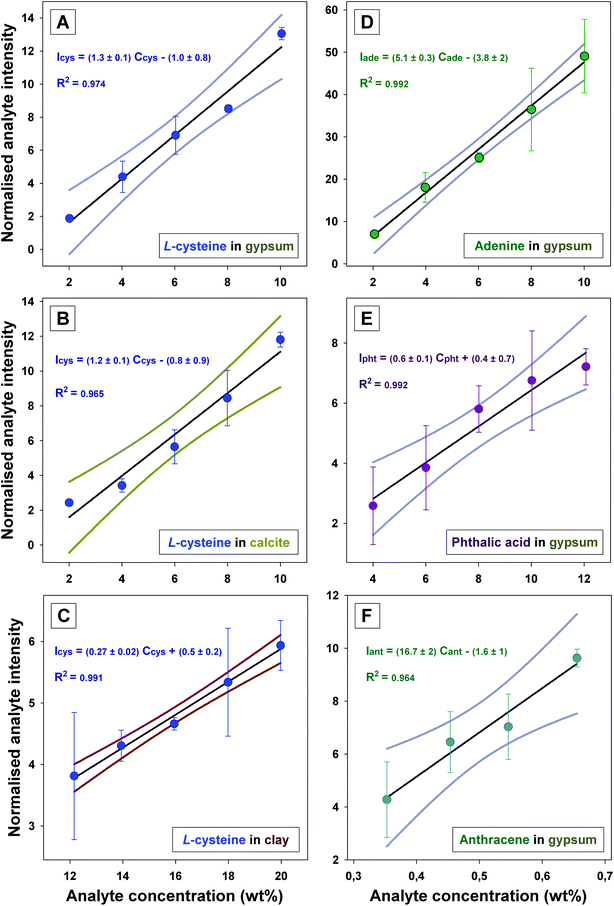
Calibration curves were obtained for binary powder mixtures by evaluating the normalised Raman intensity of organic compounds (i.e.L-cysteine, adenine, phthalic acid or anthracene) as a function of their concentration when dispersed in different mineral matrices (i.e. gypsum, calcite or clay), and are presented in Fig. 2. For all binary mixtures, linear regression models (at 95% confidence intervals) were developed with a coefficient of determination, R2 >0.95. The error bars express the variation of the average intensities estimated from 3 replicates (each obtained from 36 spectra), which are reported in Table B (ESI†). In most cases, the relative standard deviation (RSD) associated to the averaged normalised intensities of the organic analytes was estimated to be below 25%. These RSD values account for procedural variations (e.g. sample surface flattening and focus optimisation between replicates) and essentially the signal variation due to the intrinsic heterogeneity of each powdered replicate analysed by the Raman instruments, especially when laser footprints on the sample surfaces are smaller than the size of the grains in the samples. Furthermore, the intrinsic heterogeneity is exacerbated when the mineral matrix is characterised by a strong absorption coefficient (e.g. dark Fe-rich clay), by reducing the effective volume of materials probed by the spectrometer (i.e. the depth of field).Calibration curves for L-cysteine in gypsum, calcite or clay are presented in Fig. 2A, B and C, respectively. When the L-cysteine is dispersed in either gypsum or calcite (2 white matrices, with the grain size fraction >100 μm), similar linear regression models are obtained, in the range of concentrations 2–10 wt%, in both matrices. In gypsum and calcite, the signal of L-cysteine was normalised, using the signals of the mineral matrix as an internal standard (eqn (1) – Case 2). When the L-cysteine was dispersed in dark clay, the normalisation of the L-cysteine was performed using an external PMMA standard (eqn (1) – Case 1) A linear calibration model was also obtained but in the 10–20 wt% range of concentrations. The lower sensitivity of the quantitative model developed for dark clay is due to the higher absorption of the excitation laser light, and the scattered Raman light, by the Fe-rich clay in comparison to gypsum or calcite. The calibration curves presented in Fig. 2D and E demonstrate that linear calibration curves can also be derived for the quantitation of other organic analytes in gypsum. Linear regressions in the concentration range 2–12 wt% were achieved for mixtures of either adenine or phthalic acid in a gypsum matrix. For these analytes, comprising strong polarisable molecular functions (e.g. the presence of polarisable heteroatom in L-cysteine, the presence of a monoaromatic cycle in phthalic acid or the heterocyclic structure of adenine), the linear dynamic ranges (LDR) are all within 2–12 wt% (or higher for the dark Fe-rich matrix).
Finally, the calibration curve obtained for anthracene in gypsum is presented in Fig. 2F. The quantitation of the signal of anthracene was shown to be possible in gypsum down to 0.35 wt%. Indeed, the Raman signal of anthracene, a polyaromatic hydrocarbon (PAH), is enhanced by pre-resonance effects, which enables quantification of anthracene at lower concentrations, in this case below 1 wt%. However, the gain in sensitivity is not as high as expected for true resonant analytes (typically 103 to 106 enhancement53). Actually, the (pre-)resonance and/or self-absorption of PAH has previously been reported to cause deviations in the linear dependence between the Raman responses and PAH concentrations.37
3.3. Limitations of the classical quantification models for binary mineral mixtures
For binary mixtures obtained by mixing two mineral phases together in relative proportions, calibrations have been previously reported in the literature based on normalised intensities following eqn (5),28,30,31 While this normalisation procedure appears efficient for binary mixtures where both minerals are characterised with similar Raman scattering coefficients, the model should be adapted when the Raman scattering coefficients of the minerals are not identical. Indeed, Fig. 3A shows that, when minerals have similar apparent Raman scattering coefficients (e.g. calcite and baryte), the normalised intensity of one phase (ϕ1) with respect to the sum of intensities for both phases (ϕ1 and ϕ2) follows a linear relationship with the weighted fraction. As a result, a linear trend (R2 = 0.99) can be obtained for the normalised intensities of ϕ1 (calcite) tested at various proportions. The same linear function is obtained for the mineral phase ϕ2 (baryte), and the trend appears complementary. Conversely, Fig. 3B shows that, when two minerals exhibit significantly different Raman scattering coefficients, the normalised intensities do not follow a linear relationship with the relative weighted proportions of the mineral phases in the mixtures. Actually, quartz is a poorer Raman scatterer than gypsum, which leads to intensity ratios that differ significantly from the weight proportions, when the intensities are normalised to 1.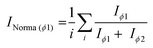 | (5) |
 | ||
Fig. 3 Calibration curves for binary mixtures of minerals in varying weighed proportions obtained with the Superhead set-up. Intensity ratios are calculated using eqn (5) for varying relative proportions (20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80, 40 80, 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60, 50 60, 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50, 60 50, 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40, 80 40, 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 wt%) of calcite and baryte (A); gypsum and quartz (B). The normalised intensities for each mineral phase have been connected by a solid line to emphasise their (non)linear alignment. 20 wt%) of calcite and baryte (A); gypsum and quartz (B). The normalised intensities for each mineral phase have been connected by a solid line to emphasise their (non)linear alignment. | ||
The difference between the apparent Raman scattering efficiencies of two minerals and its implication on the calculated relative intensities is apparent in the values reported in Table C (ESI†), particularly for mixtures at 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 wt% (i.e. equal masses of ϕ1 and ϕ2). For instance, equal amounts of calcite and baryte lead to almost identical Raman responses with intensity ratios calculated at 50.9 ± 0.5 and 49.1 ± 0.5 (expressed in %). Conversely, for gypsum and quartz, despite equivalent concentrations, the Raman signal collected for gypsum is higher than the Raman signal for quartz, with relative intensities of 76.9 ± 0.6 and 23.1 ± 0.6 respectively. This discrepancy in Raman response between the two minerals explains the lack of linearity observed between the relative intensities and the weight fraction, as presented in Fig. 3B. In the context of planetary exploration, where various associations of minerals can be encountered in mixtures, minerals presenting similar apparent scattering efficiencies only represent a limited number of situations. For the other cases, non-linear regression models are commonly applied.28,31 However, we propose a data normalisation enabling to apply linear models for any binary mixtures, regardless of the relative intrinsic Raman activity of the minerals in presence.
50 wt% (i.e. equal masses of ϕ1 and ϕ2). For instance, equal amounts of calcite and baryte lead to almost identical Raman responses with intensity ratios calculated at 50.9 ± 0.5 and 49.1 ± 0.5 (expressed in %). Conversely, for gypsum and quartz, despite equivalent concentrations, the Raman signal collected for gypsum is higher than the Raman signal for quartz, with relative intensities of 76.9 ± 0.6 and 23.1 ± 0.6 respectively. This discrepancy in Raman response between the two minerals explains the lack of linearity observed between the relative intensities and the weight fraction, as presented in Fig. 3B. In the context of planetary exploration, where various associations of minerals can be encountered in mixtures, minerals presenting similar apparent scattering efficiencies only represent a limited number of situations. For the other cases, non-linear regression models are commonly applied.28,31 However, we propose a data normalisation enabling to apply linear models for any binary mixtures, regardless of the relative intrinsic Raman activity of the minerals in presence.
3.4. Correction factors for binary mineral mixtures
Clearly, the classical model (i.e. using eqn (5)) is not appropriate for obtaining simple linear calibration curves for every binary mineral mixture, especially when the apparent Raman scattering coefficients of the minerals are not similar. We propose here to take the apparent scattering coefficient of both minerals into account by introducing the correction factor Fϕ2/ϕ1, as defined in eqn (3). The correction factor Fϕ2/ϕ1 was calculated for three types of binary mineral mixtures (i.e. calcite-baryte, calcite-gypsum and gypsum-quartz, prepared from purchased synthetic compounds), where the minerals were present in different weighted proportions (i.e. ϕ1/ϕ2 = 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80, 40
80, 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60, 50
60, 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50, 60
50, 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 and 80
40 and 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20). The Fϕ2/ϕ1 values obtained with the Superhead set-up are presented in Fig. 4. Distinct Fϕ2/ϕ1 values were obtained for each type of binary mineral mixture, and the more the value of Fϕ2/ϕ1 departed from 1, the higher the difference in the apparent Raman scattering coefficients. Furthermore, the Fϕ2/ϕ1 value appears to remain constant for each type of binary mixture, regardless of the relative proportions of each mineral component: FCalcite/Baryte = 1.06 ± 0.05, FCalcite/Gypsum = 1.35 ± 0.01 and FGypsum/Quartz = 3.40 ± 0.06.
20). The Fϕ2/ϕ1 values obtained with the Superhead set-up are presented in Fig. 4. Distinct Fϕ2/ϕ1 values were obtained for each type of binary mineral mixture, and the more the value of Fϕ2/ϕ1 departed from 1, the higher the difference in the apparent Raman scattering coefficients. Furthermore, the Fϕ2/ϕ1 value appears to remain constant for each type of binary mixture, regardless of the relative proportions of each mineral component: FCalcite/Baryte = 1.06 ± 0.05, FCalcite/Gypsum = 1.35 ± 0.01 and FGypsum/Quartz = 3.40 ± 0.06.
The values of FCalcite/Gypsum determined from binary mixtures of calcite and gypsum, in various proportions, and prepared with minerals of different origins and granulometries, are reported in Table 3. The values indicate that FCalcite/Gypsum is moderately dependent on the origin of the minerals (i.e. synthetic or natural rocks). Multiple causes (crystallisation, density, impurities, etc.) could account for the variations observed between these inorganic materials of different origin. However, the values of FCalcite/Gypsum reported in Table 3 do not seem to be affected by the mineral grain size (crushed natural rocks of fractions <50 μm and >100 μm). Only the standard deviation of the mean FCalcite/Gypsum values increases with the average grain size. Finally, the addition of 4 to 10 wt% of L-cysteine in the mineral mixtures does not affect the value obtained for the FCalcite/Gypsum, but again, the standard deviation of the mean is higher when an organic analyte is added, which is probably due to the increase of the variation of the local molecular composition interrogated for each spectrum.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80, 40
80, 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60, 50
60, 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50, 60
50, 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40, 80
40, 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 wt%)
20 wt%)
| Spectrometer – Superhead set-up | |||
|---|---|---|---|
| F (5) | ± | SD | Type of gypsum – calcite dispersions |
| 1.35 | ± | 0.01 | Synthetic inorganic reactants (<50 μm) |
| 1.22 | ± | 0.03 | Natural crystals (<50 μm) |
| 1.21 | ± | 0.05 | Natural crystals (>100 μm) |
| 1.15 | ± | 0.04 | Natural crystals (>100 μm) spiked with cysteine at 10 wt% |
| 1.17 | ± | 0.04 | Natural crystals (>100 μm) spiked with cysteine at 8 wt% |
| 1.10 | ± | 0.10 | Natural crystals (>100 μm) spiked with cysteine at 6 wt% |
| 1.12 | ± | 0.08 | Natural crystals (>100 μm) spiked with cysteine at 4 wt% |
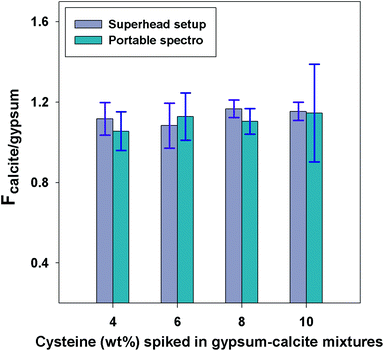
By definition, the factor Fϕ2/ϕ1 is described as a ratio of apparent Raman scattering coefficients (eqn (3)), which should be constant for a given binary mineral mixture and independent of the type of instrument employed. This was verified for the calcite-gypsum system using the mineral fraction with the average grain size >100 μm (a plausible scenario for the binary mixtures expected during remote planetary exploration) using the two Raman instruments: a benchtop spectrometer coupled to the Superhead and a miniaturised instrument. Fig. 5 shows that the FCalcite/Gypsum values obtained for both instruments are not statistically different (p-value >0.05), even when the calcite-gypsum mixtures are spiked with L-cysteine (4 different concentrations). The standard deviations obtained for the average FCalcite/Gypsum values appear, however, to be higher with the portable instrument than those observed with the Superhead, even when the analytical protocols were identical. Differences in laser footprint size and the collection optics are expected to be the cause of this difference.
3.5. Quantification of binary mineral mixtures using the correction factor
Given the Fϕ2/ϕ1 constant values determined from our calibrations of multi-mineral mixtures, we are now able to correct the signal of one of the mineral species with respect to the other, for any given relative proportion, as if a single phase was involved. The relative proportions of both mineral phases in a binary mixture, Cϕ1 and Cϕ2 (i.e. concentrations in weight percentage), can be determined from the combined equations given in eqn (6). The correction factor also makes it possible to account for the fact that the relative normalised intensities diverge from linearity in Fig. 3B, by inserting the correction factor into eqn (5) (ESI†). The corrected data are presented in Fig. 6 and demonstrate that the corrected intensity ratios follow a linear function with the weight fraction, characterised with a unitary slope (R2 >0.999), for all binary mixtures considered.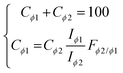 | (6) |
3.6. Calibration curves for ternary mixtures of an organic analyte in a binary mineral matrix
The calibration curves established with the miniaturised spectrometer for L-cysteine dispersed in a binary gypsum-calcite matrix (prepared from mineral grain-size fraction >100 μm and in various proportions) are presented in Fig. 7. The intensity of cysteine was normalised using the response of both calcite and gypsum (eqn (1) – Case 3). For each concentration level of cysteine (i.e. binary mineral mixtures spiked at 10, 8, 6 or 4 wt%), the normalised intensities using the appropriate correction factor (FCalcite/Gypsum) were plotted in the Fig. 7A (for 5 calcite/gypsum matrix compositions at 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80, 40
80, 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60, 50
60, 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50, 60
50, 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 and 80
40 and 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 wt%). This figure shows that the correction coefficient, which was introduced in eqn (2) to express the Raman signal of both minerals as if only one was present in the matrix, allows an effective normalisation of the analyte signal, independently of the relative proportions of these minerals in the matrix. The averaged normalised cysteine intensities and the associated standard deviations are presented in Fig. 7B, along with the derived linear regression fit (R2 = 0.995). The results demonstrate that the quantification of organic analytes can be performed in multi-mineral mixtures, irrespective of the proportions at which these mineral phases are present.
20 wt%). This figure shows that the correction coefficient, which was introduced in eqn (2) to express the Raman signal of both minerals as if only one was present in the matrix, allows an effective normalisation of the analyte signal, independently of the relative proportions of these minerals in the matrix. The averaged normalised cysteine intensities and the associated standard deviations are presented in Fig. 7B, along with the derived linear regression fit (R2 = 0.995). The results demonstrate that the quantification of organic analytes can be performed in multi-mineral mixtures, irrespective of the proportions at which these mineral phases are present.
3.7. Implications for planetary exploration
We successfully developed simple quantitative (univariate) models to determine the molecular composition of organo-mineral, binary and ternary mixtures by Raman spectroscopy, under the constraints of robotic planetary exploration instrumentation and operation, in particular in preparation for the ExoMars 2022 mission. Indeed, our quantitative models were developed from complex crushed rock powders (grain size >100 μm, which are relevant to the ExoMars delivery system of crushed samples7) by using two different instruments with similar operating parameters to those used for the miniaturised ExoMars RLS instrument (Table 2) and presenting similar responses (see Fig. 5). This suggests that our quantitative models can be transferred to data sets obtained during planetary missions with dedicated instrumentation. Quantitative analyses, which will be performed in situ at the surface of Mars, will help with the interpretation of the geological context (i.e. the formation and alteration of the matrix). The applicability of our quantitative models with miniaturised instruments, and under the constraints of automatic procedures, can also find utility for analytical investigations on Earth, for instance for environmental, pharmaceutical or material sciences.To enable quantification with different instruments and to reduce the influence of instrument-based fluctuations over time, the data were normalised using the appropriate standards, either external or internal. When at least one component of the matrix is not active in Raman spectroscopy (e.g. halides, which are not active in Raman spectroscopy, or clay minerals, which are active in Raman spectroscopy but no signal is actually detected due to a high fluorescence background and a poor crystallinity), quantitative measurements of a dispersed analyte can be performed resorting to an external standard of intensity, such as a polymer like the polyethylene terephthalate (PET) calibration target included in the analytical laboratory drawer of the ExoMars rover.54 When all components of a complex multi-mineral matrix are active in Raman spectroscopy, the mineral matrix can play the role of internal standards. We introduce a correction factor, Fϕ2/ϕ1, that allows both the quantification of binary mineral mixtures and the normalisation of the analyte signal in ternary organo-mineral mixtures, even if one component is characterised by a higher (or lower) scattering efficiency than the other component of the matrix. Both types of normalisation are compatible with the operation of a Raman spectrometer on Mars, however the normalisation that utilises an internal standard should be preferred over normalisation that utilises an external standard, especially for quantitative development on powder samples for which the light absorption and diffusion can differ importantly from those observed for the external standard. Nonetheless, the normalisation using identical external polymer targets can be useful for adjusting the instrument response of a remote system on Mars (which experiences significant shock loads during launch and landing) or provided prototype instruments operated on Earth for comparison purposes.
Finally, the introduction of the correction factor, Fϕ2/ϕ1, enables the quantification of both mineral constituents in all proportions for binary mixtures, and the quantification of non-resonant organics, typically in the concentration range 1–10 wt%, when dispersed in complex binary mineral matrices (ternary mixtures). These levels of organics concentration are relevant to the recognition of important organic matter deposits in complex geological matrices analogous to materials on Mars. However, in the context of planetary exploration and the search for preserved organics, possibly attesting from extinct life on Mars, lower concentrations of organics are expected, down to the μg g−1 level. Actually, higher sensitivity for organic components could be achieved using a UV excitation laser instead of a green laser at 532 nm, owing to the fact that the Raman cross section increases with the frequency of the excitation source.37 Besides, the sensitivity can also be increased by utilising the resonance effect of specific molecules, often containing chromophores, under specific excitation wavelengths. For instance, with a 532 nm excitation source, a significant enhancement of signals can be promoted for carotenoids and carbonaceous matter,55 enabling a detection down to the μg g−1 levels.22,56
4. Conclusions
We have developed a combined quantitative approach using Raman spectroscopy to determine the organo-mineral molecular composition of solid dispersions relevant to robotic planetary exploration missions dedicated to the search for biosignatures. We present simple quantitative models using Raman active minerals and non-resonant organics. The models were transposed from a Raman benchtop set-up to a miniaturised instrument representative of the ExoMars RLS, and using both fine clay substrates and crushed rocks with an average grain size larger than the instrument laser footprint. The micro-heterogeneity of the solid dispersions, due to the presence of micro-grains in the samples, was considered by recording multiple spectra at different locations at the surface of the samples. Important analytical developments regarding the proposed models concerned the utilisation of a correction factor (Fϕ2/ϕ1), describing the apparent Raman scattering efficiencies of mineral mixtures, for quantitative evaluations. Most notably, accurate relative proportions of minerals were determined from a variety of associated compounds (binary mixtures) using effective linear relationships obtained from the data normalisation based on Fϕ2/ϕ1. Quantitative determinations of organic analyte in complex geological matrices were also achieved following appropriate data normalisations (internal and external standards), including corrections of the matrix effects on the analyte responses using Fϕ2/ϕ1 for mixtures of minerals with different apparent Raman scattering efficiencies. The analytical developments presented in this study provide a strong foundation for Raman quantitative applications for solid dispersions with calibrations based on a large diversity of samples (combined minerals or organo-minerals). Owing to the versatility of the models using adaptable normalisation procedures, further quantitative investigations can be dedicated to planetary exploration missions in the future, for instance including resonant Raman analytes or extending the normalisation to quaternary mixtures (one organic dispersed in three minerals).Conflicts of interest
There are no conflicts to declare.Acknowledgements
L. D. and C. M. acknowledge support from the F. R. S. – FNRS (FRIA doctoral grant and Research Associate fellowship, respectively). I. B. H. acknowledges support from the UK Space Agency. The authors thank the UR AGEs – Argiles, Géochimie et Environnements sédimentaires of the University of Liège for providing the clay sample and Raymond Vanderlinden for the mineral specimens (private collection). The authors also thank Valérie Collard from the Centre d'Etude et de Recherche sur les Macromolécules (CERM) of the University of Liège for providing the SEM images.References
- P. Vandenabeele, H. G. M. Edwards and J. Jehlička, The role of mobile instrumentation in novel applications of Raman spectroscopy: archaeometry, geosciences, and forensics, Chem. Soc. Rev., 2014, 43(8), 2628 RSC . Available from: http://xlink.rsc.org/?DOI=c3cs60263j.
- E. Cordero, I. Latka, C. Matthäus, I. W. Schie and J. Popp, In vivo Raman spectroscopy: from basics to applications, J. Biomed. Opt., 2018, 23(07), 1 Search PubMed.
- F. Adar, R. Geiger and J. Noonan, Raman spectroscopy for process/quality control, Appl. Spectrosc. Rev., 1997, 32(1–2), 45–101 CrossRef CAS.
- A. P. Lister, W. J. Sellors, C. R. Howle and S. Mahajan, Raman Scattering Techniques for Defense and Security Applications, Anal. Chem., 2021, 93(1), 417–429 CrossRef CAS PubMed.
- A. Wang, L. A. Haskin and E. Cortez, Prototype Raman spectroscopic sensor for in situ mineral characterization on planetary surfaces, Appl. Spectrosc., 1998, 52(4), 477–487 CrossRef CAS.
- P. G. Brewer, G. Malby, J. D. Pasteris, S. N. White, E. T. Peltzer and B. Wopenka, et al., Development of a laser Raman spectrometer for deep-ocean science, Deep Sea Res., Part I, 2004, 51(5), 739–753 CrossRef CAS.
- J. L. Vago, F. Westall, Pasteur Instrument Teams, S. Landing, A. J. Coates, R. Jaumann and O. Korablev, et al., Habitability on Early Mars and the Search for Biosignatures with the ExoMars Rover, Astrobiology, 2017, 17(6–7), 471–510 CrossRef PubMed . Available from: http://online.liebertpub.com/doi/10.1089/ast.2016.1533.
- K. A. Farley, K. H. Williford, K. M. Stack, R. Bhartia, A. Chen and M. de la Torre, et al., Mars 2020 Mission Overview, Space Sci. Rev., 2020, 216, 142, DOI:10.1007/s11214-020-00762-y.
- J. Grotzinger, Beyond water on Mars, Nat. Geosci., 2009, 2(April), 1–3 Search PubMed . Available from: http://papers://bcab5980-e9b6-4eaf-b643-294662106260/Paper/p1021.
- F. Rull, S. Maurice, I. Hutchinson, A. Moral, C. Perez and C. Diaz, et al., The Raman Laser Spectrometer for the ExoMars Rover Mission to Mars, Astrobiology, 2017, 17(6–7), 627–654 CrossRef CAS . Available from: http://online.liebertpub.com/doi/10.1089/ast.2016.1567.
- R. C. Wiens, S. Maurice, S. H. Robinson, A. E. Nelson, P. Cais and P. Bernardi, et al., The SuperCam Instrument Suite on the NASA Mars 2020 Rover: Body Unit and Combined System Tests, Space Sci. Rev., 2021, 217, 4, DOI:10.1007/s11214-020-00777-5.
- L. Beegle, R. Bhartia, M. White, L. Deflores, W. Abbey, Y. H. Wu, et al., SHERLOC: Scanning habitable environments with Raman & luminescence for organics & chemicals, IEEE Aerosp. Conf. Proc., 2015, pp. 1–11, DOI:10.1109/AERO.2015.7119105.
- K. H. Williford, K. A. Farley, K. M. Stack, A. C. Allwood, D. Beaty and L. W. Beegle, et al., The NASA Mars 2020 Rover Mission and the Search for Extraterrestrial Life, in From Habitability to Life on Mars, ed. N.A Cabrol and E.A Grin, Elsevier Inc., 2018, pp. 275–308, DOI:10.1016/B978-0-12-809935-3.00010-4.
- H. G. M. Edwards, S. E. J. Villar, J. Jehlicka and T. Munshi, FT-Raman spectroscopic study of calcium-rich and magnesium-rich carbonate minerals, Spectrochim. Acta, Part A, 2005, 61(10), 2273–2280 CrossRef PubMed.
- A. Wang, J. J. Freeman, B. L. Jolliff and I. M. Chou, Sulfates on Mars: A systematic Raman spectroscopic study of hydration states of magnesium sulfates, Geochim. Cosmochim. Acta, 2006, 70(24), 6118–6135 CrossRef CAS.
- J. J. Freeman, A. Wang, K. E. Kuebler, B. L. Jolliff and L. A. Haskin, Characterization of natural feldspars by raman spectroscopy for future planetary exploration, Can. Mineral., 2008, 46(6), 1477–1500 CrossRef CAS.
- H. G. M. Edwards, I. Hutchinson and R. Ingley, The ExoMars Raman spectrometer and the identification of biogeological spectroscopic signatures using a flight-like prototype, Anal. Bioanal. Chem., 2012, 404(6–7), 1723–1731 CrossRef CAS PubMed . Available from: http://link.springer.com/10.1007/s00216-012-6285-z.
- M. Veneranda, J. Sáiz, A. Sanz-Arranz, J. A. Manrique, G. Lopez-Reyes and J. Medina, et al., Planetary Terrestrial Analogues Library (PTAL) project: Raman data overview, J. Raman Spectrosc., 2020, 51(9), 1731–1749 CrossRef CAS.
- J. L. Bishop, E. Murad, M. D. Lane and R. L. Mancinelli, Multiple techniques for mineral identification on Mars: A study of hydrothermal rocks as potential analogues for astrobiology sites on Mars, Icarus, 2004, 169(2), 311–323 CrossRef CAS.
- H. G. M. Edwards, P. Vandenabeele, S. E. Jorge-Villar, E. A. Carter, F. R. Perez and M. D. Hargreaves, The Rio Tinto Mars Analogue site: An extremophilic Raman spectroscopic study, Spectrochim. Acta, Part A, 2007, 68(4), 1133–1137 CrossRef PubMed.
- N. Bost, F. Westall, C. Ramboz, F. Foucher, D. Pullan and A. Meunier, et al., Missions to Mars: Characterisation of Mars analogue rocks for the International Space Analogue Rockstore (ISAR), Planet. Space Sci., 2013, 82–83, 113–127, DOI:10.1016/j.pss.2013.04.006.
- P. Vítek, J. Jehlička, H. G. M. Edwards, I. Hutchinson, C. Ascaso and J. Wierzchos, Miniaturized Raman instrumentation detects carotenoids in Mars-analogue rocks from the Mojave and Atacama deserts, Philos. Trans. R. Soc., A, 2014, 372, 20140196, DOI:10.1098/rsta.2014.0196.
- C. Malherbe, I. B. Hutchinson, R. Ingley, A. Boom, A. S. Carr and H. Edwards, et al., On the Habitability of Desert Varnish: A Combined Study by Micro-Raman Spectroscopy, X-ray Diffraction, and Methylated Pyrolysis–Gas Chromatography–Mass Spectrometry, Astrobiology, 2017, 17(11), 1123–1137 CrossRef CAS PubMed . Available from: http://online.liebertpub.com/doi/10.1089/ast.2016.1512.
- J. Razzell Hollis, D. Rheingold, R. Bhartia and L. W. Beegle, An Optical Model for Quantitative Raman Microspectroscopy, Appl. Spectrosc., 2020, 74(6), 684–700 CrossRef CAS PubMed.
- L. A. Haskin, A. Wang, K. M. Rockow, B. L. Jolliff, R. L. Korotev and K. M. Viskupic, Raman spectroscopy for mineral identification and quantificafion for in situ planetary surface analysis: A point count method, J. Geophys. Res., 1997, 102(97), 19293–19306 CrossRef CAS.
- J. Wei, A. Wang, J. L. Lambert, D. Wettergreen, N. Cabrol and K. Warren-Rhodes, et al., Autonomous soil analysis by the Mars Micro-beam Raman Spectrometer (MMRS) on-board a rover in the Atacama Desert: A terrestrial test for planetary exploration, J. Raman Spectrosc., 2015, 46(10), 810–821 CrossRef CAS.
- C. G. Kontoyannis, M. G. Orkoula and P. G. Koutsoukos, Quantitative analysis of sulfated calcium carbonates using Raman spectroscopy and X-ray powder diffraction, Analyst, 1997, 122(1), 33–38 RSC.
- N. Noguchi, K. Shinoda and K. Masuda, Quantitative analysis of binary mineral mixtures using Raman microspectroscopy: Calibration curves for silica and calcium carbonate minerals and application to an opaline silica nodule of volcanic origin, J. Mineral. Petrol. Sci., 2009, 104(4), 253–262 CrossRef CAS . Available from: http://joi.jlc.jst.go.jp/JST.JSTAGE/jmps/080714?from=CrossRef.
- P. Kristova, L. Hopkpkinson, K. Rutt, H. Hunter and G. Cressey, Quantitative analyses of powdered multi-minerallic carbonate aggregates using a portable raman spectrometer, Am. Mineral., 2013, 98(2–3), 401–409 CrossRef CAS.
- G. Lopez-Reyes, F. Rull, G. Venegas, F. Westall, F. Foucher and N. Bost, et al., Analysis of the scientific capabilities of the ExoMars Raman Laser Spectrometer instrument, Eur. J. Mineral., 2013, 25(5), 721–733 CrossRef CAS . Available from: http://www.scopus.com/inward/record.url?eid=2-s2.0-84892491047&partnerID=40&md5=5134faa8eb7613aa999767d0b7114d4e%5Cn, http://openurl.ingenta.com/content/xref?genre=article&issn=0935-1221&volume=25&issue=5&spage=721.
- M. Veneranda, G. Lopez-Reyes, J. A. Manrique-Martinez, A. Sanz-Arranz, E. Lalla and M. Konstantinidis, et al., ExoMars Raman Laser Spectrometer (RLS): development of chemometric tools to classify ultramafic igneous rocks on Mars, Sci. Rep., 2020, 10(1), 1–14, DOI:10.1038/s41598-020-73846-y.
- P. Vítek, K. Osterrothová and J. Jehlička, Beta-carotene-A possible biomarker in the Martian evaporitic environment: Raman micro-spectroscopic study, Planet. Space Sci., 2009, 57(4), 454–459 CrossRef.
- A. I. Alajtal, H. G. M. Edwards and I. J. Scowen, Raman spectroscopic analysis of minerals and organic molecules of relevance to astrobiology, Anal. Bioanal. Chem., 2010, 397(1), 215–221 CrossRef CAS PubMed.
- K. Osterrothová and J. Jehlička, Raman spectroscopic identification of phthalic and mellitic acids in mineral matrices, Spectrochim. Acta, Part A, 2010, 77(5), 1092–1098 CrossRef PubMed.
- A. Culka, J. Jehlička, P. Vandenabeele and H. G. M. Edwards, The detection of biomarkers in evaporite matrices using a portable Raman instrument under Alpine conditions, Spectrochim. Acta, Part A, 2011, 80(1), 8–13 CrossRef CAS PubMed.
- J. H. Hooijschuur, M. F. C. Verkaaik, G. R. Davies and F. Ariese, Raman spectroscopy for future planetary exploration: Photodegradation, self-absorption and quantification of carotenoids in microorganisms and mineral matrices, J. Raman Spectrosc., 2015, 46(10), 856–862 CrossRef CAS.
- W. J. Abbey, R. Bhartia, L. W. Beegle, L. DeFlores, V. Paez and K. Sijapati, et al., Deep UV Raman spectroscopy for planetary exploration: The search for in situ organics, Icarus, 2017, 290, 201–214, DOI:10.1016/j.icarus.2017.01.039.
- L. Demaret, I. B. Hutchinson, G. Eppe and C. Malherbe, Analytical strategy for representative subsampling of Raman-based robotic planetary exploration missions: The case study of solid dispersions of β-carotene and L-cysteine in gypsum, J. Raman Spectrosc., 2020, 51(9), 1624–1635 CrossRef CAS.
- O. Botta and J. L. Bada, Extraterrestrial organic compounds in meteorites, Surv. Geophys., 2002, 23(5), 411–467 CrossRef.
- T. A. Goudge, R. E. Milliken, J. W. Head, J. F. Mustard and C. I. Fassett, Sedimentological evidence for a deltaic origin of the western fan deposit in Jezero crater, Mars and implications for future exploration, Earth Planet. Sci. Lett., 2017, 458, 357–365, DOI:10.1016/j.epsl.2016.10.056.
- J. Razzell Hollis, S. Ireland, W. Abbey, R. Bhartia and L. W. Beegle, Deep-ultraviolet Raman spectra of Mars-relevant evaporite minerals under 248.6 nm excitation, Icarus, 2021, 357, 114067, DOI:10.1016/j.icarus.2020.114067.
- B. Grignard, B. Gilbert, C. Malherbe, C. Jerome and C. Detrembleur, Online Monitoring of Heterogeneous Polymerizations in Supercritical Carbon Dioxide by Raman Spectroscopy, ChemPhysChem, 2012, 13, 2666–2670 CrossRef CAS PubMed.
- C. Malherbe, I. B. Hutchinson, M. McHugh, R. Ingley, J. Jehlička and H. G. M. Edwards, Accurate Differentiation of Carotenoid Pigments Using Flight Representative Raman Spectrometers, Astrobiology, 2017, 17(4), 351–362 CrossRef CAS PubMed . Available from: http://online.liebertpub.com/doi/10.1089/ast.2016.1547.
- M. J. Pelletier, Quantitative Analysis Using Raman Spectrometry, Appl. Spectrosc., 2003, 57(1), 20–42 CrossRef PubMed . Available from: http://asp.sagepub.com/lookup/doi/10.1366/000370203321165133.
- S. Gunasekaran, G. Anbalagan and S. Pandi, Raman and infrared spectra of carbonates of calcite structure, J. Raman Spectrosc., 2006, 37(9), 892–899 CrossRef CAS.
- J. Jehlička, P. Vítek, H. G. M. Edwards, M. Heagraves and T. Čapoun, Application of portable Raman instruments for fast and non-destructive detection of minerals on outcrops, Spectrochim. Acta, Part A, 2009, 73(3), 410–419 CrossRef PubMed.
- C. P. Marshall and A. Olcott Marshall, Challenges Analyzing Gypsum on Mars by Raman Spectroscopy, Astrobiology, 2015, 15(9), 761–769 CrossRef CAS PubMed . Available from: http://online.liebertpub.com/doi/10.1089/ast.2015.1334.
- J. Etchepare, M. Merian and L. Smetankine, Vibrational normal modes of SiO2. I. α and βquartz, J. Chem. Phys., 1974, 60(5), 1873–1876 CrossRef CAS.
- A. Pawlukojć, J. Leciejewicz, A. J. Ramirez-Cuesta and J. Nowicka-Scheibe, L-Cysteine: Neutron spectroscopy, Raman, IR and ab initio study, Spectrochim. Acta, Part A, 2005, 61(11–12), 2474–2481 CrossRef PubMed.
- D. S. Dunn, N. Sridhar, M. A. Miller, K. T. Price, R. Pabalan and T. A. Abrajano, Development of a surface-enhanced Raman technique for biomarker studies on mars, Appl. Spectrosc., 2007, 61(1), 25–31 CrossRef CAS PubMed.
- E. Cloutis, P. Szymanski, D. Applin and D. Goltz, Identification and discrimination of polycyclic aromatic hydrocarbons using Raman spectroscopy, Icarus, 2016, 274, 211–230, DOI:10.1016/j.icarus.2016.03.023.
- M. Mathlouthi, A. M. Seuvre and J. L. Koenig, F.t.-i.r. and laser-Raman spectra of adenine and adenosine, Carbohydr. Res., 1984, 131(1), 1–15 CrossRef CAS.
- J. C. Merlin, Resonance Raman spectroscopy of carotenoids and carotenoid- containing systems, Pure Appl. Chem., 1985, 57(5), 785–792 CAS.
- G. Lopez-Reyes, C. Pilorget, A. G. Moral, J. A. Manrique, A. Sanz and A. Berrocal, et al., Raman Laser Spectrometer (RLS) calibration target design to allow onboard combined science between the RLS and MicrOmega instruments on the ExoMars rover, J. Raman Spectrosc., 2020, 51(9), 1718–1730 CrossRef CAS.
- F. Foucher, Detection of biosignatures using Raman spectroscopy, in Biosignatures for Astrobiology, ed. B. Cavalazzi and F. Westall, Springer I, 2019, pp. 267–282 Search PubMed.
- I. B. Hutchinson, J. Parnell, H. G. M. Edwards, J. Jehlicka, C. P. Marshall and L. V. Harris, et al., Potential for analysis of carbonaceous matter on Mars using Raman spectroscopy, Planet. Space Sci., 2014, 103, 184–190, DOI:10.1016/j.pss.2014.07.006.
- A. G. Moral, F. Rull, S. Maurice, I. B. Hutchinson, C. P. Canora and L. Seoane, et al., Design, development, and scientific performance of the Raman Laser Spectrometer EQM on the 2020 ExoMars (ESA) Mission, J. Raman Spectrosc., 2020, 51(9), 1771–1781 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1an01514a |
| This journal is © The Royal Society of Chemistry 2021 |