Simultaneous measurement of neurite and neural body mass accumulation via quantitative phase imaging

Abstract

Measurement of neuron behavior is crucial for studying neural development and evaluating the impact of potential therapies on neural regeneration. Conventional approaches to imaging neuronal behavior require labeling and do not separately quantify the growth processes that underlie neural regeneration. In this paper we demonstrate the use of quantitative phase imaging (QPI) as a label-free, quantitative measurement of neuron behavior in vitro. By combining QPI with image processing, our method separately measures the mass accumulation rates of soma and neurites. Additionally, the data provided by QPI can be used to separately measure the processes of maturation and formation of neurites. Overall, our approach has the potential to greatly simplify conventional neurite outgrowth measurements, while providing key data on the resources used to produce neurites during neural development.

---

Introduction

Neuronal wiring and growth is a fundamental process for the functional nervous system. Quantitative measurement of neuronal growth is essential to understand and develop an accurate model for these neural development/regeneration processes. For example, quantitative neurite growth revealed long-range inhibitory signaling facilitates single axon formation,¹ axon guidance control in neural circuits,² the role of dendritic tree in neurological disorders,³ and extracellular cues for neurite growth.^4–6 Furthermore, recent computational work has demonstrated the need to correlate neurite growth and cell body signals.⁷

Conventional approaches to quantify neuronal growth are based on phase-contrast imaging,^8,9 fluorescence microscopy,¹⁰ or other staining methods. Phase contrast can be used to measure the changing morphology of neurons and neurites in culture, cell–cell interaction, and neural toxicity.^11–13 However, in phase contrast imaging, the intensity in the image itself is not directly related to a physiologically relevant measure of the cell behavior, making additional quantification difficult. Fluorescence microscopy can be used to tag or label specific cellular components with intensity proportional to the quantity of the tagged components or expression level of a fluorescence label. Fluorescence can therefore provide an additional quantitative dimension to analysis of cell behavior.^14–16 However the requirement of adding tags or labels makes it more difficult to work with primary cells, fluorescence signal often degrades over time due to photobleaching or loss of expression, and fluorescent tags or labels can alter cell behavior (ex. GFP¹⁷). Dendritic growth has traditionally been studied with the Golgi method but it remains unknown if this introduces bias due to uneven staining.¹⁸

Quantitative phase imaging (QPI) offers a label-free method to study neuronal behavior. QPI measures the amount that light slows down as it passes through a cell.¹⁹ This phase shift is related to cell dry mass by the specific refractive increment, which defines the relationship between cell refractive index and density.^19,20 Unlike phase contrast, the intensity at each pixel in a quantitative phase image is related to a physical parameter, cell dry mass at that location. With no requirement for labeling, QPI also does not suffer from the limitations of fluorescence imaging. Significant advances in QPI have enabled direct measurement of cell morphology, dynamics, and behavior.²¹ QPI data reveal changes in cell mass due to proliferation or death^22–25 and changes in the distribution of mass due to transport^26,27 or neural activity.²⁸ As a wide-field microscopy technique, QPI enables simultaneous monitoring of 100s–1000s of cells, for example to determine structure or response to stimulations,^29–32 or emergence of interconnected networks of cells.³³ QPI has also been use to study dynamic responses of neurons. For example, measurements at the scale of ∼1 s detect subtle changes in phase shift of neurites during neural activity,³⁴ possibly due to organelle transport.³⁵ High speed QPI at a time scale of 1 ms measures neuron membrane fluctuations,³⁶ while measurements at ∼0.1 ms has been applied to directly measure neuron deformation during neuronal spikes.³⁷ Label-free QPI can also be used to nondestructively monitor neural growth and transport, with machine-learning approaches providing cell-compartment specificity and removing the need for fluorescent labeling.³⁸ These applications of QPI to study neural behavior may indicate possible treatments for neural disorders based on responses of individual cells to therapy.³⁹

In this paper we demonstrate the use of QPI data to separately monitor the mass of both soma and neurites in primary rat hippocampal neurons over hours to days in culture. This data quantifies the continued growth of neurites after a decrease in soma mass accumulation rate. Additionally, an image processing approach we develop here quantifies the mass increase due to the formation and maturation of neurites consistent with axonal maturation. Overall, as a contactless, label-free approach, our method has potential applications in the development of new methods for neural regeneration as well as in the study of degenerative disease.

Experimental

Neural cell culture

Two E18 Sprague Dawley rat Hippocampi were acquired from BrainBits (BrainBits animal protocol #32-08-013, approved by the Southern Illinois University School of Medicine Laboratory Animal Care and Use Committee under National Institutes of Health, Office of Laboratory Animal Welfare assurance ID D16-00132) and plated following the BrainBits suggested protocol into a total of 5 dishes for imaging. Briefly, E18 hippocampus was dissociated in 2 mg mL⁻¹ papain in Hibernate E media without calcium for 8 min at 37 °C then transferred to Hibernate E/B27/GlutaMAX media and gently dissociated with a Pasteur pipette for 1 min. After settling 1 min, the supernatant was removed and spun at 200 G for 1 min. The pellet was resuspended in Neurobasal/B27/GlutaMax media and cells were counted with a hemocytometer. Primary neurons were then plated at 16 000 cells per cm² in ibidi 35 mm high-sided cell culture dishes and cultured at 37 °C, 5% CO₂ for 2 days prior to transferring to the microscope stage-top incubator for QPI.

Quantitative phase imaging

Live cell imaging was performed using an Olympus IX83 microscope with automated stage (Prior H117), stage top incubator with gas and humidity control (Oko-Lab H301), and red LED illumination (ThorLabs Solis 623 nm). A 20× 0.45 NA objective with 1.2× magnification (for a total 24× image magnification) was used for all QPI acquisition. Microscope control was automated in custom Micromanager and MATLAB scripts. A Phasics SID4BIO-4MP camera based on quadriwave lateral shearing interferometry (QWLSI)^40,41 was used for all QPI data acquisition. Images were captured at 50 imaging locations every 10 min for 5 days. Unless otherwise stated, time t = 0 refers to time after the start of imaging. After the experiment, raw interferograms were processed to phase data using the SID4BIO-SDK in MATLAB.

Image processing

Raw phase images were initially segmented using Sobel edge detection and the remaining data were fit to a 4^th order polynomial surface. This surface was subtracted from the phase image as an initial correction for nonuniformities in the imaging system (Fig. S1†).

Soma and neurites were then separately segmented from rolling-ball filtered QPI data to remove low frequency background phase shifts using the MATLAB imtophat function with a spherical structuring element via the strel function. The rolling ball algorithm is equivalent to rolling a ball of the specified size across the 3D surface described by the phase data and recording the location of the bottom of the ball. This surface is then the background that is subtracted from the original data.^42,43 The size of the ball determines the feature size that the ball can ‘roll’ into. A smaller rolling ball filter kernel will identify smaller structures as background. The soma filter was a 7 pixel radius (8.3 μm) rolling ball filter that retained soma and neurites but eliminated background phase shifts. The neurite filter was a 2 pixel radius (2.4 μm) rolling ball filter that retained neurites but eliminated soma and background phase shifts. A soma mask, M_S was then generated by applying Sobel edge detection (threshold 100 nm) to I_S − I_N, where I_S is the soma filtered image, and I_N is the neurite filtered image. A neurite mask, M_N, was generated by applying Sobel edge detection (threshold 25 nm) and complementing with the soma filter, M_S, to remove soma-masked regions from M_N. Dry mass of soma, m_S, and neurites, m_N, were computed as

where α is the specific refractive increment and the sum was taken pixelwise over each image, and p is the area represented by each pixel in the object plane. In this expression, the product of the binary mask, M, and the phase image, I, represented in phase shift [length] is a discrete representation of the integral of the phase shift, or optical volume of the soma or neurite fraction. Dry mass was computed assuming a specific refractive increment of 1.8 × 10⁻⁴ m³ kg⁻¹ as an effective average over cell contents.¹⁹ An image generated with an intermediate filter (I_I) with a 3 pixel radius (3.6 μm) was used for calculation of neurite mass to prevent errors due to the more aggressive rolling ball filter used to isolate neurites for M_N. Soma and neurite mass was normalized by the number of distinct soma regions in each image, excluding debris from dead cells.

The slope of this total soma or neurite mass as a function of time was computed using a linear least squares fit to data from each imaging location, then averaged across all locations to determine mass accumulation rates. Rates of increase of neurite phase shift and area were computed from linear least squares fits to the total area and phase shift of masked neurite regions in QPI images. To determine the increase in neurite phase shift with age, age was determined as the sum of all previous frames in which a given pixel had been included in M_N multiplied by the time between frames.

Immunofluorescence

Following QPI imaging, culture media was completely removed from the dish and replaced with 1× PBS before preparing the cells for immunofluorescence staining. The preparation procedure was based on two protocols provided by Santa Cruz Biotechnology⁴⁴ and Abcam.⁴⁵ Cells were washed 3× with PBS and fixed with 4% paraformaldehyde in PBS for 10 min. After fixation, cells were washed 3× with ice-cold PBS and incubated with 0.1% Triton X-100 in PBS for 10 min to permeabilize the cell membranes. The fixed cells were washed 3× with PBS after permeabilization and incubated with blocking solution for 30 min to prevent unspecific binding of the antibodies. After blocking, the cells were washed 3× with PBS and incubated in the dark with fluorophore-conjugated primary antibody (MAP2 and GFAP) overnight at 4 °C. 4 μg ml⁻¹ of antibody was used to stain the cells and the antibody was diluted in blocking agent. The stained cells were rinsed with PBS 3× before incubation with DAPI (0.1 μg ml⁻¹ in PBS) for 5 min at room temperature.

An indirect immunofluorescence staining protocol was followed for Synapsin Ia/b. After blocking the cells with the blocking agent, the incubation with Synapsin Ia/b primary antibody took place overnight at 4 °C. The primary antibody solution was replaced by PBS and the cells were washed with PBS 3×. The cells were then incubated with secondary antibody m-IgG_κ-FL 647 for 60 min in a dark chamber. 1 μg ml⁻¹ antibody solution in the blocking agent was used for both primary and secondary antibody incubation. Finally, cells were incubated with DAPI, the same as in the direct method.

Immunostained cells were stored in the dark at 4 °C before imaging by the Nikon A1R confocal microscope in the health science facility of the University of Utah. All primary and secondary antibodies were purchased from Santa Cruz Biotechnology.

Results & discussion

QPI for monitoring mass of neurons during development

We used fresh, dissociated primary Sprague-Dawley E18 hippocampal cells as a model system to study axonal growth and neurite development. Cells were cultured on poly-D-lysine coated coverslips using established protocols.^46,47 Developing neurons were then imaged repeatedly with QPI for 5 days post seeding (Fig. 1a). QPI provides label-free images of the distribution of mass within neurons (Fig. 1b). Neurites are visible as extensions from individual soma in QPI data. The formation of cell–cell connections over the 5 d imaging is clearly visible from QPI data with no degradation of signal because the QPI signal is based on intrinsic biophysical properties of the cells themselves (Movie M1†).

Fig. 1 Overview of experimental setup. (a) Sprague-Dawley rat embryo day 18 (E18) hippocampal neurons were isolated and cultured for 2 days prior to imaging via QPI for 5 days. The start of imaging is defined as t = 0 for analysis. (b) Sample QPI image showing the distribution of mass within soma and neurites.

To confirm the development of E18 hippocampal cells, we performed immunohistochemistry of cells after QPI (Fig. 2). MAP2 and Synapsin are expressed in neuronal cells and used to confirm neuronal growth from hippocampal tissue.^48,49 Cells stained positive with MAP2 and Synapsin confirmed cytoskeletal proteins in neuronal dendrites and axons (green in Fig. 2a) and densely distributed synapses over the surface of neurons (red in Fig. 2c). DNA in the nuclei were stained by DAPI (blue) present in all the immunofluorescence images in Fig. 2. Cells were also stained with GFAP Alexa 488. However, the GFAP was not detected in the cell culture (Fig. 2b) as GFAP expression is selective to astrocytes.⁵⁰Fig. 2d displays the phase contrast image of the cells of Fig. 2c confirming that all cells were labeled. The dendritic growth and the abundance of synapses in the immunofluorescence data established that the E18 hippocampal cells can successfully develop into neuronal cells.

Fig. 2 Immunofluorescence data confirms neural lineage development. Primary neurons stained by (a) MAP-2 Alexa 488 and DAPI (b) GFAP Alexa 488 and DAPI (c) Synapsin-m-IgG_κ-FL 647 and DAPI (d) phase contrast image of (c). Scalebars are 20 μm.

Image processing to detect soma and neurites

QWLSI data is acquired using a wavefront-sensor like approach in which phase shifts are referenced to a background image.^40,41 This data typically has residual background phase shifts due to dust and other irregularities within the optical system.^51,52 Residual background phase shifts due to these optical irregularities are visible as the nonuniform ‘cloudy’ structures visible underneath individual neurons in QPI data (Fig. 3a). These cloudy structures interfere with quantification of mass from fine cell structures such as neurites. To properly segment soma and neurites, we applied a rolling ball filter to remove low frequency perturbations in QPI images. The rolling ball algorithm removes structures with a size significantly larger than the ball diameter, while retaining smaller structures. A rolling ball filter with a size of 8.3 μm effectively detected soma in QPI images (Fig. 3b). From this image, edges of individual soma were easily detected using standard edge-finding methods⁴² (Fig. 3c). QPI data processed with a more aggressive, 2.4 μm rolling ball filter effectively detected neurites (Fig. 3d). Neurite edges, which are difficult to detect in the original image (Fig. 3a) or soma filtered image (Fig. 3b), were also easily segmented via edge detection (Fig. 3e).

Fig. 3 Overview of image processing to mask soma and neurites. (a) QPI data at t = 83 h of imaging after initial background correction with residual background phase shifts that interfere with quantification of neurite mass. (b) QPI data after applying a 7 pixel radius (8.3 μm) rolling ball filter (soma filter) to remove phase shifts due to everything other than soma. (c) After applying the soma filter, soma are readily segmented via edge detection. (d) QPI data after applying a 2 pixel radius (2.4 μm) rolling ball filter (neurite filter). This filter is used for calculation of both soma and neurite mass. (e) Neurites are readily filtered via edge detection from the neurite filtered data. Soma mask (c) is removed from neurite mask (e) to prevent overestimation of soma mass.

Soma and neurite growth can then observed over time using filtered QPI images (Fig. 4). These data reveal the relatively small motion of soma (Fig. 4a and b) as well as a moderate increase in soma mass. Additionally, comparatively large motions and growth of neurites can be observed (Fig. 4c and d). These motions are clearly visible as neurite networks form and develop over time (Movie M2†).

Fig. 4 Soma and neurite dynamic behavior. (a) Soma filtered image at t = 0 h, (b) soma filtered image at 120 h (5 d) showing increase in mass of individual cell bodies. (c) Neurite filtered image at t = 0 h, and (d) neurite filtered image at 120 h showing development of neurite interconnections over the 5 d differentiation protocol.

Mass of soma and neurites during development

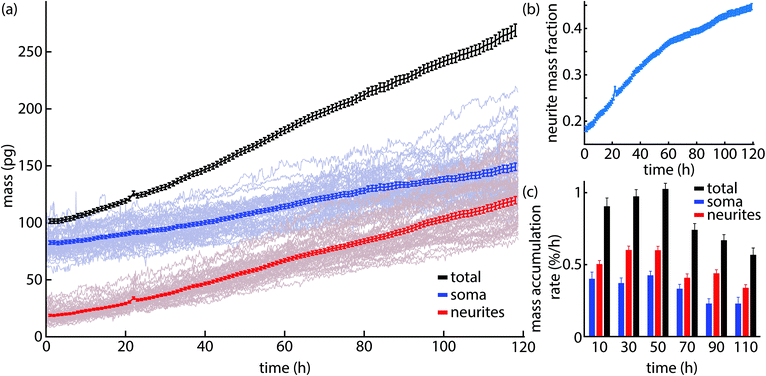
Masks of the location of soma and neurites can be used to compute total mass of each from QPI data. These data were then normalized by the number of soma per image to obtain the mass of each per cell body. This enables the mass of both soma and neurites to be tracked over time (Fig. 5a). Initially, soma account for 20% of the overall cell mass, but by the end of the experiment this fraction has risen to almost 45% of total mass (Fig. 5b). This is consistent with visible trends in QPI (Fig. 4) that show soma increasing moderately in size and mass (Fig. 4a and b) but a dramatic increase in neurite size and number during cell development in culture.

Fig. 5 Measurement of neurite and soma mass accumulation. (a) Total (black), soma (blue), and neurite (red) mass per cell body over time. Total mass of each category within each frame was normalized by the number of soma bodies per frame. Average of all data shown as solid lines with error bars, individual soma and neurite traces shown as lightly colored lines. (b) Neurite mass fraction (mass of neurites over total mass) as a function of time indicating a transition around 60 h. Error bars show standard error of the mean. (c) Mass accumulation rates normalized by total mass of total (soma + neurite, black), soma (blue), and neurite (red) mass over 20 h periods. These data show mass accumulation rate is primarily due to dendrite growth and that soma and neurite mass accumulation both decrease around t = 60 h.

We can also estimate the rate of mass accumulation per cell from QPI data as well (Fig. 5c). These data show that soma mass accumulation peaks around 60 h after the start of imaging (4.5 d post plating). In contrast, neurite mass accumulation is primary driver of mass accumulation across all time periods (Fig. 5c and Fig. S2†). The observed 0.5% mass added per hour is consistent with other estimates based on QPI³⁸ and the estimated 10% soma mass added per day in vivo.⁵³

Formation and maturation of neurites tracked with label-free QPI

QPI results show neurite mass accumulation is a primary source of overall neuron mass accumulation. This increase in neurite mass is driven by two processes: maturation of existing neurites, as occurs during axon formation, and formation of new neurites leading to an increase in number of connections.¹⁸ We can observe these two processes with QPI (Fig. 6a and b). Over time, some locations within QPI data demonstrate neurite maturation as an increase in phase shift due to the addition of new neurite mass. Simultaneously, other locations demonstrate formation of entirely new neurites (Fig. 6b).

Fig. 6 QPI captures neurite mass increase due to maturation and formation. (a and b) Neurites at t = 24 and 120 h with marked locations indicating maturation and formation of neurites. (c) Average mass neurite accumulation rate due to maturation (blue) vs. formation (red), and total neurite mass accumulation rate (black) from n = 643 neurons. (d) Mean phase shift versus neurite age of shows gradual average increase over time due to maturation. (e) Histograms of mean neurite phase shift for different ages shows maturation as the distribution of phase shifts spreads to higher values.

In order to quantify the rates of mass accumulation due to neurite formation and maturation, we can start by writing the total neurite network mass as:

where α is the specific refractive increment, A is the area of the network and is the average phase shift of the network. Then, the rate of mass accumulation (dm/dt) can be split into two components by the product rule:

This shows that at a given time point, one component of mass accumulation is proportional to the rate of increase of phase shift of the existing network while the other component is proportional to the rate of increase of area. The increase in phase shift corresponds to an increase in mass of individual neurites, so we will call the first term maturation. The second term reflects an increase in neurite area due to formation of new neurites, so we call this term formation.

Applying this metric to QPI data of n = 643 developing neurons yields a formation rate that is substantially greater than the maturation rate (Fig. 6c). Additionally, during the first 30 h, the overall change in phase shift is negative (Fig. S3†). This suggests that formation of new neurites accounts for substantially more addition of mass, and consequent metabolic activity, than maturation of existing neurites. In addition to this overall view, we can also capture maturation rate using QPI by looking at the average phase shift of individual neurites versus the age of neurites (Fig. 6d). This data demonstrates a moderate average increase of phase shift due to maturation in the overall neurite population, consistent with what we observe in individual locations within QPI data (Fig. 6a and b). We also performed a histogram analysis of phase shifts recorded by QPI to confirm that neurite phase shifts increase with age. Histogram analysis enables measurement of changes in morphology shift population phase shifts of cells or cell features and has been previously used to characterize adherent cell response to capsaicin-loaded nanocapsules.⁵⁴ This analysis shows a broadening of phase shift histograms with age (Fig. 6e). When grouped by age, the low end of the phase shift histogram peak is always roughly the same (∼10 nm), implying that new neurites are being added and formed with roughly consistent mass, while a fraction of older neurites steadily increase in mass due to maturation.

Discussion

Overall, the primary advantage of our analytical approach is that it allows for separate quantification of soma and neurite mass. This work therefore builds on and extends previous analytical methods that used QPI to measure cell mass, morphology, and dynamics.²¹ For example, growth can be measured from QPI data as the rate of increase of mass over time.^21,22 Here we extend that approach to determine the changing growth rate of soma during differentiation (Fig. 5). Additionally, the separate measurement of neurite mass allows histogram analysis⁵⁴ to be applied to the neurite fraction to quantify the influence of aging (Fig. 6e). In contrast to other applications of QPI to study neurite mass and growth our method is based on morphological image processing and so does not require training with pre-labeled fluorescence images.³⁸ We also leverage the quantitative data provided by QPI to apply a new analytical method to separately determine the contribution of neurite aging and outgrowth to neurite mass (Fig. 6c). This result indicates that, although soma growth and neurite maturation is measurable (Fig. 5 and 6), the majority of mass accumulation by the end of a 5 d in vitro neural differentiation protocol goes towards the production of new connections rather than strengthening of existing ones.

The major limitation of our approach is the requirement of a relatively uniform background for measurement of soma and neurite mass. We have therefore demonstrated this method on 2-dimensional cell cultures. However, 3-dimensional QPI approaches such as those based on tomography are increasingly available.²¹ Extension of our approach to this data may enable similar quantification in the context of more extensive cell–cell and cell–microenvironment interactions such as are experienced in vivo. This would be especially relevant for studies of how mass accumulation is split among soma growth, neurite formation, and neurite maturation in more mature neural networks.

Conclusions

We demonstrated that quantitative, label-free QPI data can be used to track the mass of both neurites and soma during in vitro neuronal development. The long-term stability of QPI signals, relative to a stain or possible variable expression of a fluorescent protein, enables continuous tracking over days in culture. We presented methods to separate soma and neurites from each other and from the image background based on their characteristic feature size and phase shift. This separate segmentation allows for separate observation and quantification of both soma and neurite mass over time. Our method therefore reveals the relative rates of mass accumulation of both soma and neurites during neuronal growth.

Additionally, neurite outgrowth is most often quantified from microscopy data in terms of length,⁵⁵ often based on staining.⁵⁶ Neurite length measurements are also possible from label-free QPI data,⁵⁷ and our study indicates that the quantitative data from QPI can be used to track neurite maturation and formation rates as a method to quantify neurite outgrowth without staining. This label free method can therefore be used to complement to other measurements of neurite outgrowth⁵⁸ to understand development of the nervous system and repair after injury.

Author contributions

Investigation and writing, S.P., T.T., H.Z., and T.A.Z.; formal analysis, validation, and data curation, S.P. and T.A.Z.; software and visualization, T.A.Z.; conceptualization, methodology, project administration, resources, funding acquisition, and supervision, H.Z. and T.A.Z.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by funds in conjunction with NIH grant P30 CA042014 awarded to the Huntsman Cancer Institute and to the CRR Program at the Huntsman Cancer Institute, the Utah Science Technology and Research (USTAR) fund, Grant No. UTAP-172163.f, as well as the University of Utah office of the Vice President for Research. We also acknowledge the Cell Imaging Core at the University of Utah for use of the Nikon A1R confocal microscope.

References

1. T. Takano, M. Y. Wu, S. Nakamuta, H. Naoki, N. Ishizawa, T. Namba, T. Watanabe, C. D. Xu, T. Hamaguchi, Y. Yura, M. Amano, K. M. Hahn and K. Kaibuchi, Nat. Commun., 2017, 8, 33.
2. E. T. Stoeckli, Development, 2018, 145, dev151415.
3. V. A. Kulkarni and B. L. Firestein, Mol. Cell. Neurosci., 2012, 50, 10–20.
4. K. Tsaneva-Atanasova, A. Burgo, T. Galli and D. Holcman, Biophys. J., 2009, 96, 840–857.
5. D. M. Suter and K. E. Miller, Prog. Neurobiol., 2011, 94, 91–101.
6. I. Song and A. Dityatev, Brain Res. Bull., 2018, 136, 101–108.
7. B. A. Bicknell, Z. Pujic, P. Dayan and G. J. Goodhill, PLoS Comput. Biol., 2018, 14, e1006218.
8. R. Kasprowicz, R. Suman and P. O'Toole, Int. J. Biochem. Cell Biol., 2017, 84, 89–95.
9. J. Pang, N. Ozkucur, M. Ren, D. L. Kaplan, M. Levin and E. L. Miller, Biomed. Opt. Express, 2015, 6, 4395–4416.
10. A. Miyawaki, Neuron, 2005, 48, 189–199.
11. R. Suman, G. Smith, K. E. Hazel, R. Kasprowicz, M. Coles, P. O'Toole and S. Chawla, Sci. Rep., 2016, 6, 22032.
12. A. Lannuzel, P. P. Michel, G. U. Hoglinger, P. Champy, A. Jousset, F. Medja, A. Lombes, F. Darios, C. Gleye, A. Laurens, R. Hocquemiller, E. C. Hirsch and M. Ruberg, Neuroscience, 2003, 121, 287–296.
13. B. A. Wilt, L. D. Burns, E. T. W. Ho, K. K. Ghosh, E. A. Mukamel and M. J. Schnitzer, Annu. Rev. Neurosci., 2009, 32, 435–506.
14. J. C. Waters and J. R. Swedlow, Cell, 2007, online, 37–42.
15. J. C. Waters, J. Cell Biol., 2009, 185, 1135–1148.
16. W. Yang and R. Yuste, Nat. Methods, 2017, 14, 349–359.
17. A. M. Ansari, A. K. Ahmed, A. E. Matsangos, F. Lay, L. J. Born, G. Marti, J. W. Harmon and Z. Sun, Stem Cell Rev. Rep., 2016, 12, 553–559.
18. A. Holtmaat and K. Svoboda, Nat. Rev. Neurosci., 2009, 10, 647–658.
19. T. A. Zangle and M. A. Teitell, Nat. Methods, 2014, 11, 1221–1228.
20. R. Barer, Nature, 1953, 172, 1097–1098.
21. Y. Park, C. Depeursinge and G. Popescu, Nat. Photonics, 2018, 12, 578–589.
22. J. Reed, J. Chun, T. A. Zangle, S. Kalim, J. S. Hong, S. E. Pefley, X. Zheng, J. K. Gimzewski and M. A. Teitell, Biophys. J., 2011, 101, 1025–1031.
23. J. Chun, T. A. Zangle, T. Kolarova, R. S. Finn, M. A. Teitell and J. Reed, Analyst, 2012, 137, 5495–5498.
24. T. A. Zangle, D. Burnes, C. Mathis, O. N. Witte and M. A. Teitell, PLoS One, 2013, 8, e68916.
25. N. Pavillon, J. Kühn, C. Moratal, P. Jourdain, C. Depeursinge, P. J. Magistretti and P. Marquet, PLoS One, 2012, 7, e30912.
26. T. A. Zangle, J. Chun, J. Zhang, J. Reed and M. A. Teitell, Biophys. J., 2013, 105, 593–601.
27. M. Mir, T. Kim, A. Majumder, M. Xiang, R. Wang, S. C. Liu, M. U. Gillette, S. Stice and G. Popescu, Sci. Rep., 2014, 4, 4434.
28. Z. Wang, L. Millet, V. Chan, H. Ding, M. U. Gillette, R. Bashir and G. Popescu, J. Biomed. Opt., 2011, 16, 026019–026019.
29. P. Jourdain, N. Pavillon, C. Moratal, D. Boss, B. Rappaz, C. Depeursinge, P. Marquet and P. J. Magistretti, J. Neurosci., 2011, 31, 11846–11854.
30. S. A. Levesque, J. M. Mugnes, E. Belanger and P. Marquet, Methods, 2018, 136, 90–107.
31. E. Bélanger, S. A. Lévesque, É. Rioux-Pellerin, P. Lavergne and P. Marquet, Front. Phys., 2019, 7, 172.
32. P. Marquet, B. Rappaz, P. J. Magistretti, E. Cuche, Y. Emery, T. Colomb and C. Depeursinge, Opt. Lett., 2005, 30, 468–470.
33. C. Yin, X. Xiao, V. Balaban, M. E. Kandel, Y. J. Lee, G. Popescu and P. Bogdan, Sci. Rep., 2020, 10, 15078.
34. C. Hu, R. Sam, M. Shan, V. Nastasa, M. Wang, T. Kim, M. Gillette, P. Sengupta and G. Popescu, J. Biophotonics, 2019, 12, e201800269.
35. C. C. Overly, H. I. Rieff and P. J. Hollenbeck, J. Cell Sci., 1996, 109, 971–980.
36. H. Majeed, L. Ma, Y. J. Lee, M. Kandel, E. Min, W. Jung, C. Best-Popescu and G. Popescu, Opt. Express, 2018, 26, 5423–5440.
37. T. Ling, K. C. Boyle, V. Zuckerman, T. Flores, C. Ramakrishnan, K. Deisseroth and D. Palanker, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 10278–10285.
38. M. E. Kandel, E. Kim, Y. J. Lee, G. Tracy, H. J. Chung and G. Popescu, Multiscale assay of unlabeled neurite dynamics using phase imaging with computational specificity (PICS), arXiv, 2020, arXiv:2008.00626 [eess.IV].
39. P. Marquet, C. Depeursinge and P. J. Magistretti, Neurophotonics, 2014, 1, 020901.
40. P. Bon, G. Maucort, B. Wattellier and S. Monneret, Opt. Express, 2009, 17, 13080–13094.
41. P. Bon, J. Savatier, M. Merlin, B. Wattelier and S. Monneret, J. Biomed. Opt., 2012, 17, 076004.
42. R. C. Gonzalez, R. E. Woods and S. L. Eddins, Digital Image Processing Using MATLAB, Gatesmark Publishing, Knoxville, TN, 2nd edn, 2009.
43. S. R. Sternberg, IEEE Comput., 1983, 16, 22–34.
44. Immunofluorescence Cell Staining, Santa Cruz Biotechnology, https://www.scbt.com/resources/protocols/immunofluorescence-cell-staining, (accessed 10-December-2020).
45. Immunochemistry and immunofluorescence Protocol, Abcam, https://www.abcam.com/protocols/immunocytochemistry-immunofluorescence-protocol, (accessed 10-December-2020).
46. G. J. Brewer, J. R. Torricelli, E. K. Evege and P. J. Price, J. Neurosci. Res., 1993, 35, 567–576.
47. G. J. Brewer and P. J. Price, NeuroReport, 1996, 7, 1509–1512.
48. G. V. Johnson and R. S. Jope, J. Neurosci. Res., 1992, 33, 505–512.
49. G. Thiel, P. Greengard and T. C. Südhof, Proc. Natl. Acad. Sci. U. S. A., 1991, 88, 3431–3435.
50. H. Baba, K. Nakahira, N. Morita, F. Tanaka, H. Akita and K. Ikenaka, Dev. Neurosci., 1997, 19, 49–57.
51. S. Liu, Q. Lian and Z. Xu, Optics and Lasers in Engineering, 2019, vol. 115, pp. 238–242.
52. C. Leiping, W. Xiao, L. Xiaoping, J. Liu, F. Pan and P. Ferraro, OSA Continuum, 2020, 3, 1856–1868.
53. L. Ma and D. A. Gibson, in Cellular Migration and Formation of Neuronal Connections, Academic Press, 2013, ch. 3, pp. 51–68,  DOI:10.1016/B978-0-12-397266-8.00056-9.
54. M. Kaiser, L. Pohl, S. Ketelhut, L. Kastl, C. Gorzelanny, M. Gotte, J. Schnekenburger, F. M. Goycoolea and B. Kemper, PLoS One, 2017, 12, e0187497.
55. M. H. Longair, D. A. Baker and J. D. Armstrong, Bioinformatics, 2011, 27, 2453–2454.
56. P. J. Mitchell, J. C. Hanson, A. T. Quets-Nguyen, M. Bergeron and R. C. Smith, J. Neurosci. Methods, 2007, 164, 350–362.
57. Y. J. Lee, P. Cintora, J. Arikkath, O. Akinsola, M. Kandel, G. Popescu and C. Best-Popescu, J. Biomed. Opt., 2017, 22, 66015.
58. A. I. M. Athamneh, Y. He, P. Lamoureux, L. Fix, D. M. Suter and K. E. Miller, Sci. Rep., 2017, 7, 7292.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0an01961e

---