Open Access Article
Open Access ArticleMicrosecond timescale MD simulations at the transition state of PmHMGR predict remote allosteric residues†
Taylor R.
Quinn
 ab,
Calvin N.
Steussy
ab,
Calvin N.
Steussy
 c,
Brandon E.
Haines
c,
Brandon E.
Haines
 d,
Jinping
Lei
ef,
Wei
Wang
e,
Fu Kit
Sheong
e,
Cynthia V.
Stauffacher
d,
Jinping
Lei
ef,
Wei
Wang
e,
Fu Kit
Sheong
e,
Cynthia V.
Stauffacher
 c,
Xuhui
Huang
c,
Xuhui
Huang
 e,
Per-Ola
Norrby
e,
Per-Ola
Norrby
 ag,
Paul
Helquist
ag,
Paul
Helquist
 a and
Olaf
Wiest
a and
Olaf
Wiest
 *ah
*ah
aDepartment of Chemistry and Biochemistry, University of Notre Dame, Notre Dame, IN 46556, USA. E-mail: owiest@nd.edu
bEarly TDE Discovery, Early Oncology, Oncology R&D, AstraZeneca, Boston, USA
cDepartment of Biological Sciences, Purdue Center for Cancer Research, Purdue University, West Lafayette, IN 47907, USA
dDepartment of Chemistry, Westmont College, Santa Barbara, CA 93108, USA
eDepartment of Chemistry, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China
fSchool of Pharmaceutical Sciences, Sun Yat-sen University, Guangzhou 510006, China
gData Science and Modelling, Pharmaceutical Sciences, R&D, AstraZeneca Gothenburg, Pepparedsleden 1, SE-431 83, Mölndal, Sweden
hLab of Computational Chemistry and Drug Design, School of Chemical Biology and Biotechnology, Peking University, Shenzhen Graduate School, Shenzhen, China
First published on 1st April 2021
Abstract
Understanding the mechanisms of enzymatic catalysis requires a detailed understanding of the complex interplay of structure and dynamics of large systems that is a challenge for both experimental and computational approaches. More importantly, the computational demands of QM/MM simulations mean that the dynamics of the reaction can only be considered on a timescale of nanoseconds even though the conformational changes needed to reach the catalytically active state happen on a much slower timescale. Here we demonstrate an alternative approach that uses transition state force fields (TSFFs) derived by the quantum-guided molecular mechanics (Q2MM) method that provides a consistent treatment of the entire system at the classical molecular mechanics level and allows simulations at the microsecond timescale. Application of this approach to the second hydride transfer transition state of HMG-CoA reductase from Pseudomonas mevalonii (PmHMGR) identified three remote residues, R396, E399 and L407, (15–27 Å away from the active site) that have a remote dynamic effect on enzyme activity. The predictions were subsequently validated experimentally via site-directed mutagenesis. These results show that microsecond timescale MD simulations of transition states are possible and can predict rather than just rationalize remote allosteric residues.
Introduction
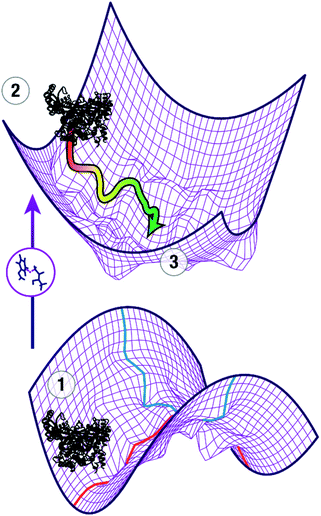
The question of how enzymes catalyze chemical reactions is a core topic of biophysical chemistry. Moving beyond the classical picture of enzyme catalysis by stabilization of the transition state,1 numerous models have been proposed to understand the modes of catalysis. While there is widespread agreement that the biological function of an enzyme depends on dynamic properties, the precise relationship of conformational dynamics and enzyme catalysis has been a topic of vigorous debate.2–5 Computational studies have played an important role in these studies because they can provide a level of atomistic detail that is difficult to obtain using experimental methods alone. Due to the conformational dynamics of enzymes, it is important that the simulations cover an appropriate time domain to allow for relaxation of the initial structure to represent the enzyme structure at the transition state and to generate the correct conformational ensemble at the transition state.To locate the transition state of the enzymatic reaction, the first order saddle point in the reaction coordinate (red) needs to be calculated while minimizing the 3n − 7 perpendicular coordinates (blue) as shown on the lower potential energy surface in Fig. 1. In addition, the conformational ensemble in these perpendicular coordinates needs to be appropriately sampled. In a typical study, an initial guess of the transition state of the reaction of interest, e.g. from appropriate electronic structure calculations of a model system, is spliced into the ground state crystal structure ①. This leads to a non-equilibrium structure (②), projected for clarity onto a potential energy surface of coordinates perpendicular to the reaction coordinate (upper part of Fig. 1). In ②, all parts of the enzyme except the active site are in a nonreactive conformation whereas the active site approximates a reactive conformation that enables catalysis. As a first approximation, the reorganization of the protein in response to the presence of the transition state and the changes in the transition state structure in response to the presence of the protein provide an understanding of how the enzyme stabilizes the transition state through a combination of electrostatic and van der Waals forces. Adequate treatment of these long- and short-range interactions requires both sampling of the conformational space that maximizes interaction with the substrates in the active site, and short-range electrostatics, which require capturing how small distortions in the transition state affect the energetics of the reaction. It is important to note that the initial guess ② is not necessarily a good model of the actual transition state ③ and may require extensive MD simulations to escape local minima and relax to ③. Depending on the movements involved to adopt the catalytically active conformation, this requires timescales from nanoseconds (for side chain movements) to microseconds (for loop and helix motions).
The dual challenges of preparing the system through sufficient MD sampling to allow the conformational changes of the initial model structure ② to adapt to the presence of the transition state in the active site and to adequately sample the transition state ③ long enough to obtain an accurate description of the ensemble are widely recognized.6–8 A number of methods have been developed to approximate the transition state in an efficient manner. Transition state “mimics”, i.e. systems in a pseudo-intermediate state,9 have been used to approximate the reactant state at a consistent MM level that allows for long simulations, but these mimics necessarily capture conformational changes in the active site towards the reactive conformation only at an approximate level. The empirical valence bond (EVB) method10 has been very successful in studying catalysis in enzymes2,11 using a mix of ground state force fields describing the reactant and product of the reaction. This implies the assumption that the transition state (TS) is a weighted average of ground states. In particular for charges, this is not always the case12 as can be seen when considering charge distribution in many transition states that are more polar than either the reactant or the product of a reaction.
The use of transition state force fields (TSFFs) is a promising alternative to QM/MM methods because they treat the entire system at a consistent level of theory, provide an accurate description of the transition state, and allow long time-scale MD simulations. TSFFs have been shown to be highly accurate compared to high-level DFT calculations and experimental data for a wide range of small-molecule reactions,13,14 but have only been used for the study of enzyme reactivity in an approximate fashion15,16 and, to the best of our knowledge, never for the study of enzyme dynamics or mechanism. Conceptually, this approach has some similarities to the EVB method. The key difference is that rather than using a mix of the reactant and product ground state force field (FF) and adjusting the parameters using empirical information to represent the transition state, the TSFF approach reparameterizes a FF at the transition state using data from electronic structure methods that are more accurate than those used in typical QM/MM calculations. Because this includes geometric and electronic features that might not be represented well by either the reactant or the product, the resulting TSFF is expected to be more accurate. Furthermore, the calculation of the [2 × 2] interaction matrix is not necessary, making TSFFs as fast as a traditional FF. Finally, TSFFs are truly predictive in that they do not use any experimental information in the parameterization. The increased speed of the classical FF then allows long simulation times to allow the complete protein to better sample the protein in a reactive configuration as discussed above.
It should be noted that TSFFs use different energy functions for the starting material and the transition state and are therefore not suitable for the calculation of absolute activation energies. Rather, they focus on the key question of how the structure of the protein changes from the non-reactive crystal structure to the reactive conformation to catalyze a reaction, e.g. by changing the direction and magnitude of dipoles that stabilize active site interactions as well as longer-range interactions.
Results and discussion
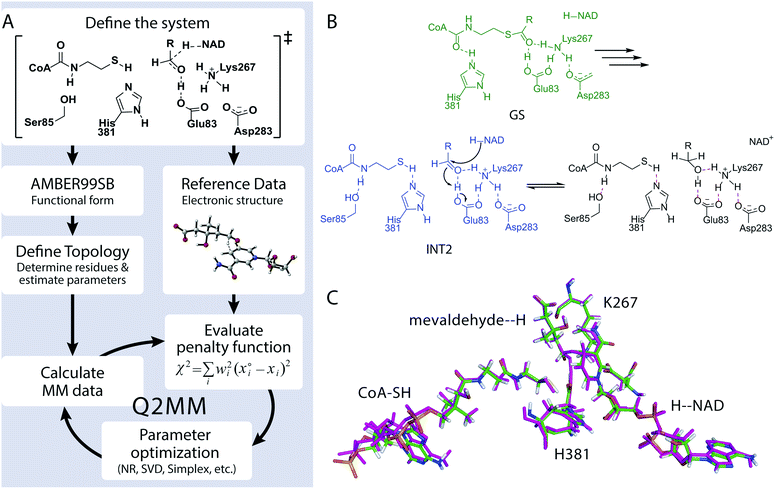
We developed the Quantum-Guided Molecular Mechanics (Q2MM) method13,14 for the automated fitting of TSFFs to high-level electronic structure calculations and applied it to a variety of transition metal catalyzed reactions.17,18 The details of adapting the Q2MM method to the parameterization of TSFFs for enzymes have also been described.19 The general philosophy of the Q2MM approach as applied to enzymes, shown in Fig. 2A, is reminiscent of a transfer learning approach in that the extensively validated parameters of an existing force field are reparametrized for a small subset of atoms to reproduce the electronic structure calculations. Specifically, the parameters of a small number of atoms representing the active site of the enzyme (Fig. 2C) are fitted to the reference data from electronic structure calculations by minimizing the penalty function χ2. In addition to geometric data such as bond lengths, angles or dihedrals, Q2MM also fits to the QM Hessian elements, with special treatment of the reaction coordinate to give it a positive curvature in the TSFF,13 to properly account for energy costs of small distortions in the active site. Because only a few structures are calculated for the training set, larger active site models than in a typical QM/MM study can be treated at a higher level of theory. The TSFF, in combination with standard force field parameters for the remainder of the protein, is then used in MD simulations to study the crucial question of how the enzyme responds to the presence of the transition state and thus catalyzes the reaction, and then to sample the conformational ensemble at the transition state.To demonstrate this novel approach to the study of enzymatic reaction mechanisms, we investigated HMG-CoA reductase from Pseudomonas mevalonii (PmHMGR) which uses two equivalents of NADH to convert HMG-CoA to mevalonate via sequential hydride transfer steps in a single active site.20 This obligate homodimer is the point of feedback control for poly-isoprenoid biosynthesis21 and its human homolog is the target of the widely used statin drugs. More importantly, it has an extraordinarily complex reaction mechanism (Fig. S1†) that despite decades of study continues to provide novel insights into enzyme catalysis.22,23 Based on our previous QM/MM study of PmHMGR at the ONIOM-(B3LYP/6-31g(d,p):AMBER) level of theory,22 a TSFF was created for the second hydride transfer from the NADH to mevaldehyde by Q2MM. Fig. 2B shows the active site residues for which the FF parameters were fitted to the results from the Q2MM calculations in addition to the NADH cofactor and the HMG-CoA substrate shown in Fig. 2C. The resulting TSFF shows excellent agreement between the active site structure calculated by the QM/MM22 and TSFF (Fig. 2C). The TSFF was used to perform 10 μs of adaptive sampling24 followed by 3–5 μs of MD simulation in an NVT ensemble in AMBER14.25 For comparison, the ternary complex of the starting material, NADH, and PmHMGR (constructed from the non-productive ternary complex, PDB code 1QAX with 2.8 Å resolution)26 as well as the intermediate immediately preceding the hydride transfer (Fig. 2B, GS and INT2) were also calculated.
The trajectories from these long-timescale MD simulations were analyzed using time-lagged Independent Component Analysis (tICA) to identify residues that contribute the most to the slowest dynamics of the system in the ground state and transition state, respectively. tICA is a variation of the linear variational approach that transforms the input coordinates (such as Euclidean distances, torsion angles) into collective coordinates (time structure-based independent components, tICs) sorted by “slowness”.27
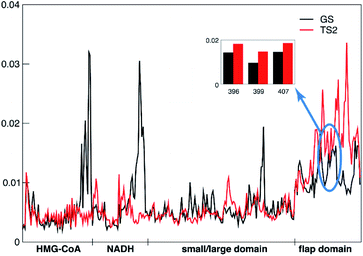
The tICA analysis indeed shows that the transition state MD simulations of PmHMGR need to be at the μs timescale in order to capture the allosteric role of remote residues on enzymatic functions that cannot be captured using shorter timescale simulation (Fig. S4–S6†). The largest differences in the per-residue contributions (Fig. 3), between the ground state and transition state are observed in the flap domain and substrates HMG-CoA and NADH. For example, the remote residues R396, E399 and L407 (inset in Fig. 3) on the flap domain have significantly larger tICA values in the transition state than in the ground state, suggesting that they are important to the allosteric effect during PmHMGR's enzymatic catalysis. This is noteworthy because the flap domain has been postulated to be involved in catalysis,23 but there has been no previous suggestion of allostery of remote residues.
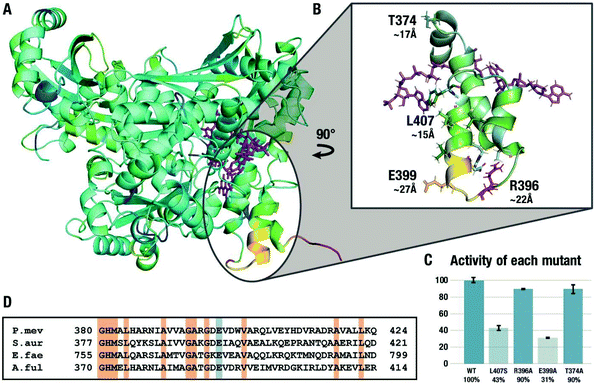
Fig. 4A shows the difference between the RMSD values for the ground state and the transition state of the second hydride transfer color-coded on the structure of HMGR where yellow/red coloring indicates areas where the RMSD of the GS calculated over the μs trajectory is larger than in the TS, i.e. the residues rigidify in the TS. The results from this analysis of the flexibility of the entire protein are in line with the ones from the local tICA analysis, indicating the decreased movement of certain residues on the flap domain in the transition state. We focused the investigation on four specific residues. L407 is the center of a solvent-exposed hydrophobic patch of residues on the last two α-helices approximately 15 Å away from the active site. R396 is located on the first loop of the flap domain, ∼22 Å away from the active site and uses the side chain to hydrogen bond to residues on the last two helices. E399 is positioned at the end of the second helix, ∼27 Å away from the active site. It is an excellent test case for the computational predictions because it is not engaged in any significant non-bonded interactions in the crystal structure but exhibited very high flexibility in the GS compared to the TS and has a large contribution in the tICA.
To test the hypothesis that the changes in the flexibility of the remote residues between ground- and transition-states have a functional role in enzyme catalysis, three residues in the second α-helix on the flap domain discussed above were chosen for experimental mutagenesis. L407 was mutated to a serine in order to disrupt the electronics in the area while keeping the surface area of the residue similar while R396 and E399 were replaced by alanine residues. As a negative control, we studied the alanine mutant of T374, a residue that showed virtually no difference in the tICA values between the GS and TS2 states. The effect of the four point mutations on the relative maximum rate of the conversion of mevalonate, CoA and two equivalents of NAD+ to HMG-CoA were averaged over eight experiments and are shown in Fig. 4C. In agreement with the simulations, the activity of the L407S decreased by 57% compared to the wild type. The R396A mutant experiences little change, possibly because the flexible loop region is more tolerant of mutations. The E399A mutant experienced the greatest decline in activity with 69%, despite being the furthest from the active site in the crystal structure and only engaging in interactions with the solvent. These results cannot be predicted based on the crystal structure or rationalized using short-timescale simulations but are in line with the results from long-timescale MD simulations at the transition state. They are also in line with the surprising observation that this glutamate residue is conserved in all Class II HMGRs (Fig. 3D),28 which is hard to explain based on the available crystal structures. As predicted by the RMSF and tICA analysis of the trajectories, the T374A mutant is virtually indistinguishable from the wild type despite also being part of the flap domain and at a similar distance from the active site.
This work demonstrates that TSFFs derived by the Q2MM method allow conformational sampling at the transition states of enzyme catalyzed reactions on the μs timescale, 2–3 orders of magnitude longer than what can be reached using traditional QM/MM methods. Computational enzymology in this time regime provides experimentally verifiable predictions on properties such as dynamic allosteric effects on catalysis, a topic of intense interest in biophysics and drug design29 thus going beyond the more typical computational rationalization of experimental observations. Given the widely discussed role of dynamics on enzyme catalysis,30e.g. by slow conformational changes to reach the reactive conformation, we expect that HMGR is a typical case rather than an exception in requiring long-timescale simulations at the transition state. The general availability of the Q2MM code31 will allow future applications of TSFFs to computational enzymology on the μs timescale.
Author contributions
T. R. Q., B. E. H. and P.-O. N. generated the TSFF and performed the MD simulations, T. R. Q. and C. N. S. performed the experimental studies of the enzyme mutants, and J. L., W. W., F. K. S. and X. H. performed the analysis of the MD trajectories. X. H., P.-O. N., P. H. and O. W. conceived and supervised the projects. All authors contributed to the analysis of the data and the writing of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Marcus Arieno for preliminary simulations and Moumita Sen for the T374A mutant data. This work was supported by the National Institutes of Health (1R01GM111645 and T32GM075762) and the Hong Kong Research Grant Council (AoE/P-705/16).References
- L. Pauling, Chem. Eng. News, 1946, 24, 1375–1377 CrossRef CAS
.
- K. F. Wong, T. Selzer, S. J. Benkovic and S. Hammes-Schiffer, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 6807–6812 CrossRef CAS
.
- E. Z. Eisenmesser, D. A. Bosco, M. Akke and D. Kern, Science, 2002, 295, 1520–1523 CrossRef CAS PubMed
.
- M. H. Olsson, W. W. Parson and A. Warshel, Chem. Rev., 2006, 106, 1737–1756 CrossRef CAS
.
- S. Hammes-Schiffer and S. J. Benkovic, Annu. Rev. Biochem., 2006, 75, 519–541 CrossRef CAS PubMed
.
- H. M. Senn and W. Thiel, Angew. Chem., Int. Ed., 2009, 48, 1198–1229 CrossRef CAS
.
- M. P. Frushicheva and A. Warshel, ChemBioChem, 2012, 13, 215–223 CrossRef CAS PubMed
.
- J.-K. Hwang and A. Warshel, J. Am. Chem. Soc., 1996, 118, 11745–11751 CrossRef CAS
.
- M. W. van der Kamp, E. J. Prentice, K. L. Kraakman, M. Connolly, A. J. Mulholland and V. L. Arcus, Nat. Commun., 2018, 9, 1177 CrossRef PubMed
.
- J. Åqvist and A. Warshel, Chem. Rev., 1993, 93, 2523–2544 CrossRef
.
- M. Lee, C. Bai, M. Feliks, R. Alhadeff and A. Warshel, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 10321–10326 CrossRef CAS PubMed
.
- F. Jensen and P.-O. Norrby, Theor. Chem. Acc., 2003, 109, 1–7 Search PubMed
.
- A. R. Rosales, T. R. Quinn, J. Wahlers, A. Tomberg, X. Zhang, P. Helquist, O. Wiest and P.-O. Norrby, Chem. Commun., 2018, 54, 8294–8311 RSC
.
- E. Hansen, A. R. Rosales, B. Tutkowski, P.-O. Norrby and O. Wiest, Acc. Chem. Res., 2016, 49, 996–1005 CrossRef CAS PubMed
.
- P. Rydberg, S. M. Hansen, J. Kongsted, P.-O. Norrby, L. Olsen and U. Ryde, J. Chem. Theory Comput., 2008, 4, 673–681 CrossRef CAS PubMed
.
- P. Rydberg, L. Olsen, P.-O. Norrby and U. Ryde, J. Chem. Theory Comput., 2007, 3, 1765–1773 CrossRef CAS PubMed
.
- P. J. Donoghue, P. Helquist, P.-O. Norrby and O. Wiest, J. Am. Chem. Soc., 2009, 131, 410–411 CrossRef CAS PubMed
.
- A. R. Rosales, S. P. Ross, P. Helquist, P.-O. Norrby, M. S. Sigman and O. Wiest, J. Am. Chem. Soc., 2020, 142, 9700–9707 CAS
.
- T. R. Quinn, H. N. Patel, K. H. Koh, B. E. Haines, P.-O. Norrby, P. Helquist and O. Wiest, ChemRxiv, 2020 DOI:10.26434/chemrxiv.13206038.v1
.
- C. M. Lawrence, V. W. Rodwell and C. V. Stauffacher, Science, 1995, 268, 1758–1762 CrossRef CAS
.
- J. L. Goldstein and M. S. Brown, Nature, 1990, 343, 425–430 CrossRef CAS PubMed
.
- B. E. Haines, C. N. Steussy, C. V. Stauffacher and O. Wiest, Biochemistry, 2012, 51, 7983–7995 CrossRef CAS PubMed
.
- B. E. Haines, O. Wiest and C. V. Stauffacher, Acc. Chem. Res., 2013, 46, 2416–2426 CrossRef CAS PubMed
.
- F. K. Sheong, D.-A. Silva, L. Meng, Y. Zhao and X. Huang, J. Chem. Theory Comput., 2014, 11, 17–27 CrossRef PubMed
.
-
D. A. Case, V. Babin, J. Berryman, R. Betz, Q. Cai, D. Cerutti, T. Cheatham III, T. Darden, R. Duke and H. Gohlke, AMBER 2014, University of California, San Francisco, 2014 Search PubMed
.
- L. Tabernero, D. A. Bochar, V. W. Rodwell and C. V. Stauffacher, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 7167–7171 CrossRef CAS PubMed
.
- J. D. Chodera and F. Noé, Curr. Opin. Struct. Biol., 2014, 25, 135–144 CrossRef CAS PubMed
.
- M. Hedl, L. Tabernero, C. V. Stauffacher and V. W. Rodwell, J. Bacteriol., 2004, 186, 1927–1932 CrossRef CAS PubMed
.
- N. M. Goodey and S. J. Benkovic, Nat. Chem. Biol., 2008, 4, 474 CrossRef CAS PubMed
.
- K. A. Henzler-Wildman, M. Lei, V. Thai, S. J. Kerns, M. Karplus and D. Kern, Nature, 2007, 450, 913–916 CrossRef CAS PubMed
.
-
http://github.com/q2mm
.
Footnote |
| † Electronic supplementary information (ESI) available: Details of TSFF parameterization, MD simulations and analysis, and experimental mutagenesis studies; TSFF parameters, model coordinates; and accompanying movie. See DOI: 10.1039/d1sc00102g |
| This journal is © The Royal Society of Chemistry 2021 |