Open Access Article
Open Access ArticleTowards a traceable enhancement factor in surface-enhanced Raman spectroscopy†
Eleonora
Cara
 *a,
Luisa
Mandrile
a,
Alessio
Sacco
*a,
Luisa
Mandrile
a,
Alessio
Sacco
 a,
Andrea M.
Giovannozzi
a,
Andrea M.
Rossi
a,
Federica
Celegato
a,
Natascia
De Leo
a,
Philipp
Hönicke
a,
Andrea M.
Giovannozzi
a,
Andrea M.
Rossi
a,
Federica
Celegato
a,
Natascia
De Leo
a,
Philipp
Hönicke
 b,
Yves
Kayser
b,
Yves
Kayser
 b,
Burkhard
Beckhoff
b,
Davide
Marchi
c,
Alberto
Zoccante
b,
Burkhard
Beckhoff
b,
Davide
Marchi
c,
Alberto
Zoccante
 c,
Maurizio
Cossi
c,
Maurizio
Cossi
 c,
Michele
Laus
c,
Luca
Boarino
a and
Federico
Ferrarese Lupi
c,
Michele
Laus
c,
Luca
Boarino
a and
Federico
Ferrarese Lupi
 a
a
aIstituto Nazionale di Ricerca Metrologica (INRiM), Strada delle Cacce 91, 10135 Torino, Italy. E-mail: e.cara@inrim.it
bPhysikalisch-Technische Bundesanstalt (PTB), Abbestr. 2-12, 10587 Berlin, Germany
cDipartimento di Scienze e Innovazione Tecnologica, Università del Piemonte Orientale (UPO), Via T. Michel 11, 15100 Alessandria, Italy
First published on 2nd November 2020
Abstract
The enhancement factor (EF) is an essential parameter in the field of surface-enhanced Raman spectroscopy (SERS), indicating the magnification of the Raman signal of molecules interacting with the surface of plasmonic nanostructures. The calculation of EF requires a careful evaluation of both the signal intensities and the number of molecules in SERS and normal Raman conditions. The determination of the surface density of molecules adsorbed on the plasmonic substrate is a challenging task, but essential for the estimation of the number of SERS-active molecules. This paper describes the determination of EF using 7-mercapto-4-methylcoumarin (MMC) as the probe molecule on gold-coated silicon nanowires, integrating SERS and normal Raman spectroscopy with X-ray fluorescence (RF-XRF) data that provide a reference-free quantitative measurement of the molecular surface density. In addition, the surface coverage of MMC on the substrate is modelled by molecular mechanics (MM) and molecular dynamics (MD) simulations.
1 Introduction
Surface-enhanced Raman spectroscopy (SERS) is a vibrational spectroscopic technique belonging to the vast category of plasmon-enhanced molecular spectroscopies (PEMS). The intensity of the fingerprint Raman spectrum of a molecule is amplified by strong local electromagnetic fields on a plasmonic substrate and, to a minor extent, by chemical interaction with its surface.1 Since its discovery in 1974, SERS has attracted remarkable interest concerning both the fundamental mechanism governing the amplification of Raman scattering and its applications from materials science to biomedicine. Currently, the engineering of electromagnetic hot spots at sub-nanometric spatial resolution2–7 allows SERS quantification capability down to the single-molecule regime.The enhancement factor (EF) is the key parameter for the assessment of SERS substrate performances. A great effort has been addressed to the definition of EF.8–10Eqn (1) reports the most commonly employed definition:
 | (1) |
| NSERS = μM·μmol·AM·Aeff | (2) |
This work reports on the determination of EF for the model system consisting of 7-mercapto-4-methylcoumarin (MMC) as the probe molecule on gold-coated silicon nanowires, by combining SERS and normal Raman measurements with reference-free X-ray fluorescence (RF-XRF) to estimate the molecular surface density. The surface coverage of MMC on the substrate is further modelled by molecular mechanics (MM) and molecular dynamics (MD) simulations. A comparison among the EFs so calculated with those estimated using different approaches is also carried out, thus clearly highlighting the extremely high sensitivity of EF to the μmol parameter.
2 Results and discussion
2.1 Structure of the SERS substrate
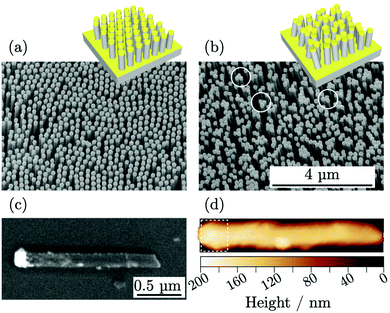
A three-dimensional SERS substrate was fabricated by a combination of nanospheres lithography (NSL) and metal-assisted chemical etching (MACE) leading to high-aspect-ratio silicon nanowires ordered over large areas. Then, the nanowires were coated with gold by e-beam evaporation to form plasmonic caps on their tops as shown in Fig. 1a. The morphology of the nanowires was characterized by scanning electron microscopy (SEM), obtaining diameter of (155 ± 15) nm, lateral spacing of (250 ± 4) nm, and height of the top gold cap of (100 ± 9) nm. The top-view SEM micrographs were processed to identify the single objects and to determine the number of nanowires per unit area, μM = 14.8 μm−2, useful for NSERS calculation through eqn (2). The nanowires presented an aspect ratio of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and exhibited high flexibility forming bundles and generating hot spots at the tip-to-tip sites.19,20,25Fig. 1b shows a SEM micrograph of the substrate where some hot spots are highlighted with white circles.
1 and exhibited high flexibility forming bundles and generating hot spots at the tip-to-tip sites.19,20,25Fig. 1b shows a SEM micrograph of the substrate where some hot spots are highlighted with white circles.
Atomic force microscopy (AFM) was used to characterize the metallic surface area AM on single nanowires spread horizontally on the solid substrate as shown in Fig. 1d. The analysis was limited to the apical part of the nanowires coated with gold, visible in the SEM image in Fig. 1c. Few metallic nanoparticles located on the length of the nanowires were observed but were not accounted for in the metallic surface area evaluation. The surface area for single nanowire, contributing to eqn (2), was estimated AM = (0.52 ± 0.09) μm2.
2.2 SERS experiment
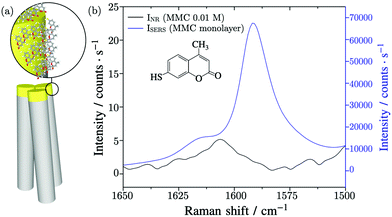
For the SERS experiment, thanks to the specific interaction of MMC molecules with Au surface, the substrate with standing nanowires was incubated in a solution of MMC in ethanol for 120 minutes and then the unbounded MMC was removed by rinsing the substrate with ethanol. Finally, the nanowires were induced to bend by soaking the substrate in water and letting it evaporate so as to trap the molecules inside the hot spots regions.25Fig. 2a shows a graphical scheme of the bending gold-coated nanowires covered with MMC.The substrate was probed with a 780 nm laser beam focalized on the tips of the nanowires by a 20 × long working distance microscope (LWD) objective. Under these conditions, the effective area of the excitation volume,10 included in eqn (2), was calculated to be Aeff = 4.4 μm2 and includes 65.1 nanowires. The vibrational peak of MMC at 1593 cm−1, assigned to the conjugated –C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C– symmetric stretching, was measured to find the value of ISERS = (6.6 ± 0.7) × 104 counts per s, as shown in Fig. 2b. The intensity of the normal Raman signal, obtained by performing the measurements in a MMC solution with a concentration cNR = 10 mM, was INR = (5.2 ± 0.3) counts per s, as shown in Fig. 2b. Normally, the Raman intensity of a signal is calculated as the sum of the counts under a given band in the spectrum, however, in this case the nearby signals limit this approach, because their fitting and deconvolution add variability and subjectivity in the peak analysis and determination of the peak integral. In this study, the peak height was employed instead because the ratio of the same band, varying by a proportionality factor in the two conditions (SERS and non-amplified Raman), is calculated in the EF. The number of Raman active molecules contributing to INR was calculated as NNR = cNR·V = (2.2 ± 0.1) × 109, where V is the value of the laser–probe interaction volume V = (364 ± 20) μm3, determined experimentally through the dimension of the focal depth26,27 (further details in the ESI file†).
C– symmetric stretching, was measured to find the value of ISERS = (6.6 ± 0.7) × 104 counts per s, as shown in Fig. 2b. The intensity of the normal Raman signal, obtained by performing the measurements in a MMC solution with a concentration cNR = 10 mM, was INR = (5.2 ± 0.3) counts per s, as shown in Fig. 2b. Normally, the Raman intensity of a signal is calculated as the sum of the counts under a given band in the spectrum, however, in this case the nearby signals limit this approach, because their fitting and deconvolution add variability and subjectivity in the peak analysis and determination of the peak integral. In this study, the peak height was employed instead because the ratio of the same band, varying by a proportionality factor in the two conditions (SERS and non-amplified Raman), is calculated in the EF. The number of Raman active molecules contributing to INR was calculated as NNR = cNR·V = (2.2 ± 0.1) × 109, where V is the value of the laser–probe interaction volume V = (364 ± 20) μm3, determined experimentally through the dimension of the focal depth26,27 (further details in the ESI file†).
Then, the determination of the number of molecules contributing to the SERS signal requires the molecular surface density μmol. This quantity was estimated by different approaches.
2.3 Determination of the molecular surface density by geometrical considerations
Various geometrical assumptions are carried out in literature to estimate the number of molecules contributing to the SERS signal, considering in general the molecules adsorbed in a monolayer or submonolayer. To test the reliability of such an approach, we evaluated the monolayer density with some simple geometrical models. First, using the tabulated molecular weight and density of MMC, we computed the molar volume Vmol = (148 ± 3) × 1012 μm3 mol−1 and the volume of a single molecule VMMC = Vmol/NA = (2.45 ± 0.05) × 10−10 μm3, where NA is the Avogadro constant. Considering the molecules as spherical objects, as the simplest approximation, their circular area projected on the surface was estimated AMMC = (4.7 ± 0.1) × 10−7 μm−2 (Fig. S2a, ESI†) and the surface density, i.e., the reciprocal of AMMC, resulted in μMMC/geom1 = (2.1 ± 0.1) × 106 μm−2. This is the maximum surface density that can be obtained when no specific information about the molecular shape and orientation in space is available, and a sphere is used to roughly approximate the actual molecular hindrance.A second geometrical model considered the MMC molecule, with an end-to-end length of 0.73 nm, freely rotating around the thiol group bound to the gold surface (Fig. S2b, ESI†). In this way, a single molecule spans an area of 1.7 × 10−6 μm2 leading to a density of μMMC/geom2 = 0.6 × 106 μm−2. An alternative description was based on an ordered arrangement of MMC molecules, as close as possible given the gold–gold distances on the Au(111) surface and a reasonable estimate of atomic van der Waals radii. This approach, illustrated in the ESI file,† leads to maximum densities of μMMC/geom3 = 3.6 × 106 μm−2 or μMMC/geom4 = 5.0 × 106 μm−2, depending on the lateral or vertical arrangements assumed by the MMC in the monolayer, respectively (see the ESI file†).
2.4 Determination of the molecular layer density by MM and MD simulations
To gain more insights into the MMC layer structure and interactions, we performed molecular mechanics (MM) and molecular dynamics (MD) theoretical simulations, based on suitable force fields, as described in the Experimental details section. To evaluate the most plausible density, several monolayers were optimized, with N MMC molecules anchored to the gold surface, with N = 1, 9, 18, 24, 27 (Fig. 3a–c). The nature of the S–Au chemical bond in this kind of interface is still debated. Most models assume that the thiol hydrogen is lost giving rise to a covalent sulphur–gold bond,28 while others propose that the thiol group is undissociated and a donor–acceptor bond is formed between –SH and Au.29 Here, we adopt the former model, so that the MMC molecules lose their thiol hydrogen homolytically before anchoring to the surface.The MM energies, referred to the bare surface and N isolated molecules, are plotted in Fig. 3d with respect to the molecular layer density. The minimum energy is found for μMMC/simul = 4.3 × 106 μm−2, corresponding to a monolayer of 23 molecules packed on the model surface. During the optimization of the monolayers with 24 or 27 MMC molecules, one or three molecules were expelled from the organic layer, respectively, returning to the most favourable density. Clearly, above the density μMMC/simul, the intermolecular repulsion in the crowded monolayer prevails on the MMC/surface attractive interaction. This result was refined by adding kinetic energy contributions, with MD runs at 298 K performed on all the previously optimized monolayers, to verify whether the thermal motions could induce some other MMC to leave the surface. All the monolayers, however, were found stable at this temperature, as no molecules were detached from the surface during the 3 ns simulations. Then the most stable monolayer density is expected to be 4.3 × 106 μm−2. It is worth noting that this value is only slightly lower than the maximum density (μMMC/geom4) obtained by considering only geometrical restraints in an ordered packing of MMC, as mentioned above.
2.5 Determination of the molecular surface density by X-ray fluorescence
The experimental quantification of the surface density of MMC was performed by the reference-free X-ray fluorescence to target the sulphur atom present in the molecules. RF-XRF offers a well-established tool which requires little or no sample preparation, for non-destructive and quantitative characterization of virtually any material for the determination of the elemental composition, layer thickness, mass deposition and contamination.30 With the atomic fundamental parameters (FPs) method proposed by Sherman,31 the sulphur K fluorescence line photon count PS,K can be converted to its mass per unit area σS, expressed in g cm−2. This can be obtained by using the physical modelling of the characteristic fluorescence radiation emitted by the sample while including atomic FPs32–34 and physically-calibrated instrumentation. The calculation for σS is reported in eqn (3):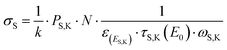 | (3) |
The RF-XRF measurements were performed on the substrate without MMC (NWbg) and on the substrate on which ISERS was measured. The latter substrate was named NWMMC. NWbg was used to measure the background content of sulphur that has to be subtracted to the signal of NWMMC. The two substrates were probed with monochromatised synchrotron radiation, as schematically represented in Fig. 4a, to excite their fluorescence radiation (Fig. 4b). The content of sulphur per unit area on NWMMC is σS(NWMMC) = (3.9 ± 0.5) × 10−8 g cm−2, while the background content evaluated on the non-functionalized substrate was σS(NWbg) = (0.60 ± 0.08) × 10−8 g cm−2. Thus, the amount of sulphur per unit area results σS = (3.3 ± 0.5) × 10−8 g cm−2. Absorption effects within the Si nanowires and the thin Au layer were considered to be negligible. From σS, the number of sulphur atoms per unit area can be derived from the following relation μS = σS·NA/wS, where wS is the atomic weight of sulphur and NA is the Avogadro constant. Given that to each atom of sulphur there corresponds one molecule of MMC, μS is equal to μMMC/XRF = (6.1 ± 1.0) × 106 μm−2.
The XRF elemental specificity to target the sulphur present in MMC along the nanostructure and quantitatively measure its mass per unit area, which was related to the surface density of MMC molecules. The thiols in MMC are bound preferentially to the gold surface and it is common to assume that any unbound excess is removed from the silicon surface by rinsing the substrate. This assumption could be further verified by performing the quantification of MMC on silicon nanostructures prepared without the gold features. However, the residual MMC on silicon, if any, was neglected. The values of the molecular surface density obtained with different geometrical methods, reported in Table 1, exhibited large differences with respect to μMMC/XRF, varying from 1.2 to 10 times its value. Among the geometrical calculations, it is possible to observe that the packing density of vertically arranged molecules is larger than the density of rotating molecules by a factor 8.4, marking the largest difference among the geometrical results.
| μ MMC [μm−2] | N SERS | EF | |
|---|---|---|---|
| Geom. calc. 1 circular area | (2.1 ± 0.1) × 106 | (0.7 ± 0.2) × 108 | (3.9 ± 1.0) × 105 |
| Geom. calc. 2 rotating molecule | 0.6 × 106 | (0.20 ± 0.04) × 108 | (14 ± 3) × 105 |
| Geom. calc. 3 lateral arrangement | 3.6 × 106 | (1.2 ± 0.3) × 108 | (2.3 ± 0.5) × 105 |
| Geom. calc. 4 vertical arrangement | 5 × 106 | (1.7 ± 0.4) × 108 | (1.7 ± 0.4) × 105 |
| Theoretical simulations | 4.3 × 106 | (1.4 ± 0.3) × 108 | (1.9 ± 0.5) × 105 |
| RF-XRF | (6.1 ± 1.0) × 106 | (2.0 ± 0.5) × 108 | (1.4 ± 0.4) × 105 |
The MD simulations could be used to interpret these values. Both the assumptions leading to μMMC/geom1 and μMMC/geom2 correspond to energetically inefficient configurations of submonolayer coverage where the molecules are isolated, respectively laying flat on the gold surface and rotating around the anchor group. On the other hand, the density μMMC/geom3 and μMMC/geom4 correspond to a closely packed monolayer of molecules with the same occupancy but different spatial arrangement, laterally or vertically oriented molecules, respectively. The value of μMMC/geom4 corresponds to the maximum theoretical density of the molecules monolayer. The surface density μMMC/simul, obtained from theoretical simulations including the lateral interaction of the molecules, corresponds to a compact self-assembled monolayer (SAM) presenting strong interactions and average orientation which is intermediate between the vertical and lateral alignments.
2.6 Calculation of the enhancement factor
The calculation of the EF requires the value of NSERS as in eqn (2), for which the surface area of the gold caps was used together with the nanostructure density, effective laser excitation area and MMC surface density μMMC determined by the different approaches. The outcomes are reported in Table 1. It was then possible to evaluate the enhancement factor by combining the signal intensities and number of molecules as in the eqn (1), these values are also reported in Table 1. The comparison among the resulting EFs is independent of the surface area. Different estimations of the molecular surface density affected the calculation of NSERS and, consequently, the enhancement factor resulting in significant variability of its value. The value of the EFgeom1 and EFgeom2 are not comparable within the uncertainty with each other, neither with the EFgeom3 and EFgeom4 nor with EFsimul and EFXRF. The largest difference among the reported values is seen as a consequence of the assumptions of the sub-monolayer coverage. The RF-XRF experimental measurements led to the estimation of a compact monolayer coverage of MMC on gold and to EFXRF, in agreement with EFsimul within the uncertainty, thus supported by molecular dynamics computational calculations. For the compact monolayer EFgeom3 and EFgeom4 were found comparable with each other within the uncertainty, because corresponding to the same assumption on the occupancy of the MMC molecule but different spatial arrangement. Of these two, the EF calculated in the case of vertically-arranged molecules (geom4) in a compact monolayer is comparable within the uncertainty with both EFsimul and EFXRF. The quite large relative uncertainty associated with EFXRF should be read as an inclusive estimation of all the relevant contributions to the uncertainty budget rather than as a lack of precision. A complete description of the derivation and uncertainty budget analysis for these quantities is reported in the ESI file.†The proposed RF-XRF method constitutes a suitable solution for the experimental determination of the molecular surface density which is performed with fully calibrated instrumental setup and physical traceability to the International System of Units. This solid method fills the absence of experimental analytical techniques supporting the calculation of the SERS enhancement factor.
3 Conclusions
In summary, we proposed reference-free X-ray fluorescence as a viable experimental methodology to evaluate the surface density of molecules adsorbed on a surface. This absolute quantitative information is fundamental to estimate the number of active molecules contributing to the enhanced Raman signal on a plasmonic substrate and, for this reason, strongly impacts the estimation of the enhancement factor. Despite relying on a specialized synchrotron radiation facility with radiometrically calibrated instrumentation, RF-XRF could be extended to commonly available XRF laboratory setup with the use of proper reference standards, so that an accurate molecular quantification could be widely implemented. This analytical methodology for the quantification of SERS-active adsorbates complies with the necessity to obtain a more reliable EF evaluation with high accuracy. It could be extended to other molecules or common analytes for SERS, independently of the presence of a thiol group. In fact, RF-XRF could be used to quantify any substance in which a convenient target element, with atomic number higher than 5, could be identified. In addition to this, we stress the importance to include a thorough uncertainty analysis in the characterization of the EF as well as the complete description of the experimental or theoretical adopted methods.36 Reporting the relevant parameters systematically and adopting standardized methodologies would promote the comparison among different nanostructured systems and boosting the applicability and progress of SERS.4 Experimental details
4.1 SERS substrate: fabrication and characterisation
The details on the fabrication protocol are reported in ref. 37. The SEM measurements, performed with FEI Inspect F field emission gun SEM (FEG-SEM), and uncertainty evaluation were carried out in comparison to a calibrated reference standard.38 The AFM height micrographs were acquired with a Bruker Multimode V AFM in tapping mode with resonance frequency of 88.8 kHz. The micrographs were analysed by Gwyddion freeware.39 The surface area was extracted by means of a built-in statistical tool. Additional details on the surface area characterization are reported in the ESI file.†4.2 SERS experiment
For the preparation of the SERS experiment, the substrate was incubated in a 1 mM solution of MMC (Sigma-Aldrich 63759 7-Mercapto-4-methylcoumarin) in ethanol for 120 minutes. For normal Raman measurements, a concentration cNR of 10 mM concentration was used to prepare the analyte solution. The Raman spectra were acquired using a Thermo Scientific DXR xi Raman Imaging confocal microscope, where the excitation laser source was chosen at 780 nm with a power of 8 mW. The exposure time was set to 1 s for 20 scans.4.3 Reference-free XRF experiments
The RF-XRF characterization was performed at the laboratory of Physikalische-Technische Bundesanstalt (PTB), the German national metrology institute, with a dedicated beamline at BESSY II electron storage ring, a third-generation synchrotron radiation source. A thorough description of the experimental setup used at PTB can be found in ref. 40, while a scheme of the adopted experimental condition is visible in Fig. S6 in the ESI.† The employed beamline41 is equipped with a four crystals monochromator (FCM) which allows varying the energy of the incident beam from 1.75 keV to 10.5 keV. To quantify the amount of sulphur, the low-divergence monochromatic incident X-ray beam was set to have energy E0 = 2.5 keV, larger than the X-ray absorption edge for sulphur K shell 2.472 keV. The instrumental setup, contained in an ultra-high vacuum (UHV) chamber, was equipped with both calibrated and other photodiodes used to perform the alignment procedure and to measure some characteristics of the incoming beam, including the full-width at half maximum beam width equal to (361 ± 18) μm and the photon flux ϕ0 = (4.5 ± 0.1) × 108 photons per s. The sample was mounted on a manipulator and moved along three translational axes and one rotational axis, varying the angle of incidence θ between the beam and the sample surface in the range from 27.5 and 45 with a step width of 0.5. The zero angle motor position θ0, at which the beam is parallel to the sample surface, was measured for each sample. The emitted fluorescence was detected utilizing an energy-dispersive silicon drift detector (SDD), mounted at 90 with respect to the incident beam and fully calibrated. The solid angle of detection Ω/4π was equal to 0.01134sr in the angular range of the measurement. The knowledge of the detector response functions and detection efficiency at different energies42 allowed the XRF spectral deconvolution, reported in Fig. 4b, to obtain the photon counts for the elemental fluorescence lines. The vicinity of the strong Au–M peak does not influence the sulphur peak deconvolution since it is adjusted for the peak height, rather than position and shape, reducing the degree of freedom and making it more reliable.4.4 Theoretical simulations
A model of the gold substrate was prepared with CRYSTAL17 code by cleaving a three layers thick (111) surface out of the bulk structure and by optimizing the top layer at the DFT level with PW91 functional. During the molecular mechanics (MM) and molecular dynamics (MD) simulations an 8 × 8 supercell was used, comprising 91 gold atoms per layer. The force field (FF) parameters were checked, and fitted when necessary, against ab initio model calculations, as detailed in the ESI file.† During the MM energy minimizations, the geometry of the gold slab was kept fixed. MD calculations were performed with NVT ensemble at 298 K with 0.5 fs time step, and included 1 ns equilibration and 3 ns production runs.Authors contributions
E. C. prepared the samples, L. M., A. S., A. M. G. conducted the SERS experiments, F. C. conducted the AFM measurements, P. H., Y. K. and E. C. conducted the XRF experiments, D. M., A. Z. and M. C. conducted the theoretical simulations, E. C., L. M., P. H. and Y. K. performed data analysis, all authors contributed to writing the manuscript, F. F. L., M. L., M. C., A. M. R., N. D. L., B. B. and L. B. provided research infrastructure support and revised the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The project 16ENV07 AEROMET has received funding from the EMPIR programme co-financed by the Participating States and from the European Unions Horizon 2020 research and innovation programme. Part of this work has been carried out in the framework of the EMPIR Researcher Mobility Grant 16ENV07-RMG1. Part of this work has been carried out at Nanofacility Piemonte INRiM, a laboratory supported by the “Compagnia di San Paolo” Foundation.Notes and references
- S.-Y. Ding, E.-M. You, Z.-Q. Tian and M. Moskovits, Chem. Soc. Rev., 2017, 46, 4042–4076 RSC.
- S.-Y. Ding, J. Yi, J.-F. Li, B. Ren, D.-Y. Wu, R. Panneerselvam and Z.-Q. Tian, Nat. Rev. Mater., 2016, 1, 1–16 Search PubMed.
- C. Chen, Y. Li, S. Kerman, P. Neutens, K. Willems, S. Cornelissen, L. Lagae, T. Stakenborg and P. Van Dorpe, Nat. Commun., 2018, 9, 1–9 CrossRef.
- D. O. Sigle, S. Kasera, L. O. Herrmann, A. Palma, B. de Nijs, F. Benz, S. Mahajan, J. J. Baumberg and O. A. Scherman, J. Phys. Chem. Lett., 2016, 7, 704–710 CrossRef CAS.
- S. Laing, L. E. Jamieson, K. Faulds and D. Graham, Nat. Rev. Chem., 2017, 1, 1–19 CrossRef.
- J. E. Park, N. Yonet-Tanyeri, E. Vander Ende, A.-I. Henry, B. E. Perez White, M. Mrksich and R. P. Van Duyne, Nano Lett., 2019, 19, 6862–6868 CrossRef CAS.
- N. Kim, M. R. Thomas, M. S. Bergholt, I. J. Pence, H. Seong, P. Charchar, N. Todorova, A. Nagelkerke, A. Belessiotis-Richards and D. J. Payne, et al. , Nat. Commun., 2020, 11, 1–12 Search PubMed.
- M. J. Natan, Faraday Discuss., 2006, 132, 321–328 RSC.
- M. D. Porter and J. H. Granger, Faraday Discuss., 2017, 205, 601–613 RSC.
- E. Le Ru, E. Blackie, M. Meyer and P. G. Etchegoin, J. Phys. Chem. C, 2007, 111, 13794–13803 CrossRef CAS.
- X. Wang, S.-C. Huang, S. Hu, S. Yan and B. Ren, Nat. Rev. Phys., 2020, 1–19 Search PubMed.
- M. F. Cardinal, E. Vander Ende, R. A. Hackler, M. O. McAnally, P. C. Stair, G. C. Schatz and R. P. Van Duyne, Chem. Soc. Rev., 2017, 46, 3886–3903 RSC.
- A. Sivanesan, W. Adamkiewicz, G. Kalaivani, A. Kamińska, J. Waluk, R. Hołyst and E. L. Izake, Analyst, 2014, 140, 489–496 RSC.
- S. He, J. Chua, E. K. M. Tan and J. C. Y. Kah, RSC Adv., 2017, 7, 16264–16272 RSC.
- F. Xu, F. Ma, Z. Ding, L. Xiao, X. Zhang, Q. Lu, G. Lu and D. L. Kaplan, ACS Appl. Mater. Interfaces, 2019, 11, 42896–42903 CrossRef CAS.
- P. Wang, L. Wu, Z. Lu, Q. Li, W. Yin, F. Ding and H. Han, Anal. Chem., 2017, 89, 2424–2431 CrossRef CAS.
- D.-K. Lim, K.-S. Jeon, J.-H. Hwang, H. Kim, S. Kwon, Y. D. Suh and J.-M. Nam, Nat. Nanotechnol., 2011, 6, 452 CrossRef CAS.
- Y. S. Hu, J. Jeon, T. J. Seok, S. Lee, J. H. Hafner, R. A. Drezek and H. Choo, ACS Nano, 2010, 4, 5721–5730 CrossRef CAS.
- M. S. Schmidt, J. Hubner and A. Boisen, Adv. Mater., 2012, 24, 11–18 Search PubMed.
- M. Hu, F. S. Ou, W. Wu, I. Naumov, X. Li, A. M. Bratkovsky, R. S. Williams and Z. Li, J. Am. Chem. Soc., 2010, 132, 12820–12822 CrossRef CAS.
- D. Lin, Z. Wu, S. Li, W. Zhao, C. Ma, J. Wang, Z. Jiang, Z. Zhong, Y. Zheng and X. Yang, ACS Nano, 2017, 11, 1478–1487 CrossRef CAS.
- J.-A. Huang, Y.-Q. Zhao, X.-J. Zhang, L.-F. He, T.-L. Wong, Y.-S. Chui, W.-J. Zhang and S.-T. Lee, Nano Lett., 2013, 13, 5039–5045 CrossRef CAS.
- J. Langer, et al. , ACS Nano, 2020, 14(1), 28–117 CrossRef CAS.
- S. E. Bell, G. Charron, E. Cortés, J. Kneipp, M. L. de la Chapelle, J. Langer, M. Procházka, V. Tran and S. Schlücker, Angew. Chem., Int. Ed., 2020, 59, 5454–5462 CrossRef CAS.
- S. Kara, A. Keffous, A. Giovannozzi, A. Rossi, E. Cara, L. D’Ortenzi, K. Sparnacci, L. Boarino, N. Gabouze and S. Soukane, RSC Adv., 2016, 6, 93649–93659 RSC.
- C. Korzeniewski, J. P. Kitt, S. Bukola, S. E. Creager, S. D. Minteer and J. M. Harris, Anal. Chem., 2018, 91, 1049–1055 CrossRef.
- A. D’Agostino, A. M. Giovannozzi, L. Mandrile, A. Sacco, A. M. Rossi and A. Taglietti, Talanta, 2020, 216, 120936 CrossRef.
- C. Vericat, M. Vela, G. Benitez, P. Carro and R. Salvarezza, Chem. Soc. Rev., 2010, 39, 1805–1834 RSC.
- M. S. Inkpen, Z.-F. Liu, H. Li, L. M. Campos, J. B. Neaton and L. Venkataraman, Nat. Chem., 2019, 11, 351–358 CrossRef CAS.
- B. Beckhoff, J. Anal. At. Spectrom., 2008, 23, 845–853 RSC.
- J. Sherman, Spectrochim. Acta, 1955, 7, 283–306 CrossRef CAS.
- B. Beckhoff, B. Kanngießer, N. Langhoff, R. Wedell and H. Wolff, Handbook of practical X-ray fluorescence analysis, Springer Science & Business Media, 2007 Search PubMed.
- B. Beckhoff, R. Fliegauf, M. Kolbe, M. Müller, J. Weser and G. Ulm, Anal. Chem., 2007, 79, 7873–7882 CrossRef CAS.
- M. Müller, P. Hönicke, B. Detlefs and C. Fleischmann, Materials, 2014, 7, 3147–3159 CrossRef.
- T. Schoonjans, A. Brunetti, B. Golosio, M. S. del Rio, V. A. Solé, C. Ferrero and L. Vincze, Spectrochim. Acta, Part B, 2011, 66, 776–784 CrossRef CAS.
- J. E. Millstone, W. C. Chan, C. R. Kagan, L. M. Liz-Marzán, N. A. Kotov, P. A. Mulvaney, W. J. Parak, A. L. Rogach, P. S. Weiss and R. E. Schaak, Redefining the Experimental and Methods Sections, ACS Nano, 2019, 13(5), 4862–4864 CrossRef CAS.
- E. Cara, L. Mandrile, F. Ferrarese Lupi, A. M. Giovannozzi, M. Dialameh, C. Portesi, K. Sparnacci, N. De Leo, A. M. Rossi and L. Boarino, Sci. Rep., 2018, 8, 11305 CrossRef.
- G. Aprile, F. Ferrarese Lupi, M. Fretto, E. Enrico, N. De Leo, L. Boarino, F. G. Volpe, G. Seguini, K. Sparnacci and V. Gianotti, et al. , ACS Appl. Mater. Interfaces, 2017, 9, 15685–15697 CrossRef CAS.
- D. Necas and P. Klapetek, Gwyddion: an open-source software for SPM data analysis (http://gwyddion.net/), Cent. Eur. J, 2012 Search PubMed.
- J. Lubeck, B. Beckhoff, R. Fliegauf, I. Holfelder, P. Hönicke, M. Müller, B. Pollakowski, F. Reinhardt and J. Weser, Rev. Sci. Instrum., 2013, 84, 045106 CrossRef CAS.
- M. Krumrey and G. Ulm, Nucl. Instrum. Methods Phys. Res., Sect. A, 2001, 467, 1175–1178 CrossRef.
- F. Scholze and M. Procop, X-Ray Spectrom., 2009, 38, 312–321 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Evaluation of the scattering volume, description of the geometrical considerations on the molecular surface density, determination of the force field for MM and MD simulations, description of the reference free XRF experiment, uncertainty evaluation for the metallic surface area and other uncertainty budgets presented in this manuscript. See DOI: 10.1039/d0tc04364h |
| This journal is © The Royal Society of Chemistry 2020 |