Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
In silico design of 2D polymers containing truxene-based platforms: insights into their structural and electronic properties†
Sergio
Gámez-Valenzuela
a,
Marcelo
Echeverri
 b,
Berta
Gómez-Lor
b,
Berta
Gómez-Lor
 *b,
José I.
Martínez
*b,
José I.
Martínez
 *b and
M. Carmen
Ruiz Delgado
*b and
M. Carmen
Ruiz Delgado
 *a
*a
aDepartment of Physical Chemistry, University of Malaga, Campus de Teatinos s/n, 29071, Malaga, Spain. E-mail: carmenrd@uma.es
bInstituto de Ciencia de Materiales de Madrid, CSIC. C/Sor Juana Inés de la Cruz 3, Cantoblanco, Madrid 28049, Spain. E-mail: bgl@icmm.csic.es; joseignacio.martinez@icmm.csic.es
First published on 10th September 2020
Abstract
In the present work, we investigate two-dimensional (2D) conjugated polymers based on C3-symmetric truxene-based cores at the density functional theory (DFT) level. In total, 27 different 2D polymers have been exhaustively studied with the aim to explore the impact of the following effects on the electronic and charge-transport properties: (i) the nature of the conjugated platform, going from electron-rich truxene (Tx) and triindole (Tr) units to electron-deficient truxenone (To) cores, (ii) the spacing of the cores with different bridges, i.e., phenylene (Ph) or ethynylene (A) units, (iii) the linker position (2,7,12-substitution in the T2 polymers and 3,8,13-substitution in T3 polymers), and (iv) the increased number of π-bridges connecting the cores, from three linkers in T2 and T3 to six linkers in T2,3. To this end, we have carried out a large battery of DFT calculations on fragments extracted from the 2D polymers (dimers and trimers) as well as on the corresponding periodic 2D structures (infinite monolayers and self-assembled monolayers) using periodic boundary conditions. Our results show that simultaneous manipulation of the pore surface size and band-gap engineering together with charge-transport parameters can be achieved in these truxene-based 2D polymers by fine-tuning their structural features. The contributions of this study to the overall understanding of the structure–electronic property relationships of these semiconducting polymers and its correlation with available experimental work are highlighted. Our results provide interesting guidelines to design novel 2D materials with applications ranging from sensing to photocatalysis or electronics.
Introduction
After three decades of enormous research effort, the field of organic semiconductors is currently a mature workbench that has already reached the market.1–3 Advances in this area have been closely related to the continuous improvement in the ability of organic semiconductors to transport charge carriers (holes or electrons), which is quantified by their charge carrier mobility μ. While the highest mobilities are usually observed in crystalline or liquid crystalline materials, in the pursuit of an optimal balance between mobility and processability, semiconducting polymers are the preferred candidates.4 These materials are usually constituted by conjugated one-dimensional (1D) chains and offer continuous electronic delocalization along the chain axis, and favor the efficient one-dimensional migration of charge carriers. However, hopping of charge carriers between chains is significantly hindered, thus resulting in slow down.Expanding the π-conjugation has emerged as an efficient strategy to address the aforementioned drawback; this expansion permits the achievement of equally efficient electron delocalization in two dimension (2D) or three dimension (3D). This possibility has focused increasing attention on 2D organic polymers as semiconducting materials with enhanced transport dimensionality.5
2D covalent organic frameworks (COFs) are porous crystalline solids obtained by the polymerization of organic building blocks functionalized with reactive groups that predetermine their growth along two or more directions through dynamic covalent chemistry.6,7 This design strategy gives rise to well-defined, high-surface-area materials whose final properties, topologies and porosities can be conveniently tuned by the choice of monomers and linking groups and by the position of the reactive groups, which determines the growth direction.
Achieving crystalline order in COFs relies on the reversibility of the chemical reactions used to connect the constituting molecular units via an error-correction mechanism.8 Among the small number of chemical reactions that are sufficiently dynamic to enable the synthesis of COFs, Schiff base (imine) formation is the only chemical transformation that gives rise to π-conjugated structures.9 However, imine linkages are far from ideal to induce efficient π-delocalization between connected units owing to their high polarization.10,11 In order to facilitate exciton migration and carrier transportation across these frameworks, efforts are being focused on the search for linkages that promote π-electron delocalization. Interestingly, the choice of planar π-conjugated monomers has allowed the synthesis of 2D conjugated microporous polymers (CMPs), even in irreversible coupling conditions, by performing the coupling reactions on the surface12–14 or in confined liquid–liquid interfaces.10,15,16 This strategy has demonstrated crystalline sheet-like organic frameworks with building units directly linked or connected through bridges and are prone to efficient electronic delocalization (diyne, phenyl, alkyne, etc.).17
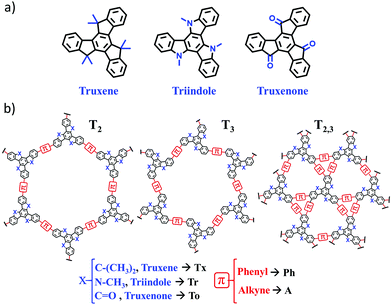
Our group has long been involved in the development of high-mobility self-assembling molecular materials based on different heptacyclic truxene-related platforms. Truxene can be considered as a 1,3,5-triphenylbenzene planarized through three bridging methylene groups, giving rise to a π-conjugated heptacyclic system with three additional fused 5-member rings. Varying the nature of the bridging groups (i.e., changing methylene units to amino or ketone units) allows us to obtain molecules that share the truxene-like geometry but show completely different redox and semiconducting behaviors. Thus, while triindole18,19 and truxene20 are p-type semiconductors, truxenone21 behaves as a high-mobility n-type semiconductor.
Because of their flat trigonal topology, these molecules have recently aroused interest as building units in the construction of functional COFs and CMPs. In fact, recently, microporous polymers based on these semiconducting monomers have been reported, with photocatalytic properties,22–24 sensing ability,25,26 thermoelectric,27 supercapacitor behavior28 or field effect behavior.16 Optimizing materials for these applications requires the fine-tuning of different parameters, such as energy levels, π-conjugation or exciton/charge transport. In this sense, theoretical calculations are found to be very useful to predict or rationalize the relationships between chemical structural modifications and the properties of the resulting materials. DFT calculations on the electronic structures of different 2D conjugated polymers have been previously reported, with an emphasis on the role played by the network topology,29–31 lattice symmetry32 or structural differences between 1D and 2D,33–35 among other structural factors.36–39 However, while isolated truxene-based molecules have been amply theoretically explored, a systematic study of their 2D conjugated polymers has not yet been reported.40–42
In this work, we performed an exhaustive investigation of truxene-based 2D conjugated polymers with the aim to explore their chemical structure–electronic property relationships to guide the design of novel optimized 2D materials. To this end, we combined an oligomer approach with periodic boundary conditions (PBC) calculations for the 2D lattices. Our selection of truxene-based 2D polymers for this work is shown in Fig. 1. A total of 27 different 2D polymers were investigated with the ultimate goal of exploring how their electronic and charge-transport properties can be tuned by engineering the organic building blocks (i.e., by changing the nature of the core from Tx to Tr or To or by using different π-bridges, from phenylene to alkyne) and the connecting mode (i.e., by changing the linkage position from T2 to T3 or by increasing the number of π-bridges from three units in T2 and T3 to six units in T2,3). Among the selected 2D polymers, four truxene-based (i.e., Tx2, Tx3, Ph-Tx2 and Ph-Tx3)25 and one triindole-based (Ph-Tr2) polymer have been successfully reported16 and showed promising applications in sensing and electronics, respectively. We anticipate that this class of truxene-based 2D conjugated networks are potential versatile semiconducting materials for optoelectronic applications.
It is worth noting that most of the first-principles theoretical frameworks adopted here have been very recently used to rationalize similar compounds, such as the first example of a solid-state fluorescent 2D-COF bonded via imine linkage37 or highly-efficient metal-free COF catalysts towards the oxygen reduction reaction and hydrogen evolution processes.43 Taking advantage of this not-yet-fully-harvested theoretical workbench, this exhaustive and systematic study provides a powerful protocol for prefiltering of novel candidate materials towards different potential application fields according to the targeted functionality.
Results and discussion
The structural and electronic properties of 2D conjugated polymers containing truxene-based platforms were theoretically investigated using a canonical bottom-up approach. First, molecular equivalent fragments extracted from the 2D polymeric structures were investigated in order to evaluate the impact produced by the nature of the core as well as the influence of the nature, number and linkage positions of the bridging connectors on the electronic communication between the conjugated C3-symmetric platforms. To this end, we focused on the relationships between the HOMO–LUMO gaps, topologies and structural reorganization energies for hole and electron transport and the chemical structures of these 2D materials. Second, these molecular fragments were then sequentially assembled to form larger subsystems, and truxene-based 2D lattices were generated. The structural features (pore size, geometry of the monolayer, interlayer stacking) and electronic band structures of these 2D COFs were investigated in detail. This study allowed us to explore the pore surface size and band-gap engineering of these promising 2D materials and their potential as charge-transport materials, with important implications for their application in fields ranging from electronics to photocatalysis or sensing.1. Molecular fragments
We first focused on performing DFT calculations for the molecular fragments of the 2D polymers under study (Fig. S1 and S2, ESI†). Note that it has been recently demonstrated that calculations of fragments of molecules provide important information about the molecular and electronic structures of 2D conjugated networks.44–50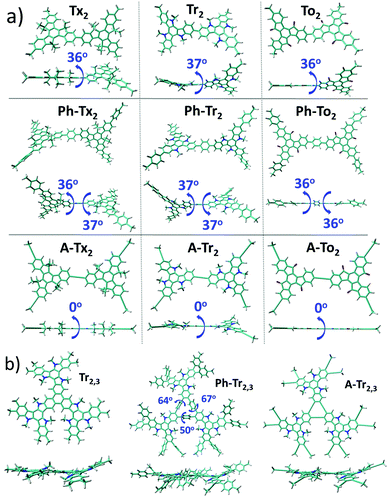 | ||
| Fig. 2 Top and lateral views of the DFT-optimized structures (PBE0/6-31G** level) for the (a) T2 dimeric models (see Fig. S3a (ESI†) for the T3 systems) and (b) Tr2,3 trimeric models chosen as representatives for the series of the hexa-substituted T2,3 systems under study (see Fig. S3b (ESI†) for the rest of the T2,3 systems). The dihedral angles between the conjugated cores and the π-bridges (in absolute values) are also shown. | ||
Interestingly, the nature of the C3-symmetric conjugated platforms plays a key role in their internal disorder: (i) in the truxene (Tx) cores, each methyl group is oriented out of the plane of the conjugated platform and therefore does not sterically hinder the planarity of the overall system, (ii) the trivalent nature of the nitrogen atoms of the triindole (Tr) core results in a moderate distortion of the platform due to the steric hindrance caused by the only existing methyl groups and the outermost benzene rings, and (iii) the truxenone (To) cores are totally coplanar as a consequence of the favorable intramolecular interactions between the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups and adjacent hydrogen atoms of the outermost benzene rings (with C
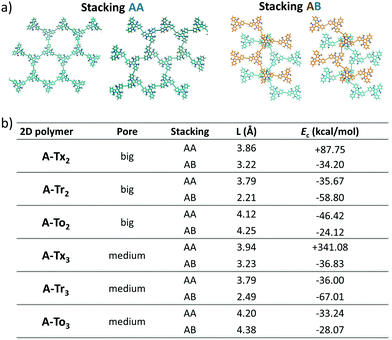
O groups and adjacent hydrogen atoms of the outermost benzene rings (with C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯H distances of 2.12 Å). The change of the linkage position from para (2,7,12) connections in T2 to meta (3,8,13) connections in T3 yields very similar geometrical distortions (Fig. S4, ESI†). Importantly, an increase of the number of peripheral linkers from three to six units in T2,3 results in more extended and coplanar skeletons when the cores are directly linked due to the formation of fully fused benzene rings between the platforms or when alkyne groups are connecting the cores (see Fig. 2b). However, in the hexaphenyl-substituted Ph-T2,3 polymers, three-dimensional cyclic cavities are created between the three external phenylene units connecting the cores that are significantly distorted by ∼50–67° (see Ph-Tr2,3 taken as a model in Fig. 2b).
O⋯H distances of 2.12 Å). The change of the linkage position from para (2,7,12) connections in T2 to meta (3,8,13) connections in T3 yields very similar geometrical distortions (Fig. S4, ESI†). Importantly, an increase of the number of peripheral linkers from three to six units in T2,3 results in more extended and coplanar skeletons when the cores are directly linked due to the formation of fully fused benzene rings between the platforms or when alkyne groups are connecting the cores (see Fig. 2b). However, in the hexaphenyl-substituted Ph-T2,3 polymers, three-dimensional cyclic cavities are created between the three external phenylene units connecting the cores that are significantly distorted by ∼50–67° (see Ph-Tr2,3 taken as a model in Fig. 2b).
 | ||
| Fig. 3 (a) DFT-calculated (PBE0/6-31G** level) HOMO–LUMO gaps (a) and frontier molecular orbital energies (b) for the T2 (solid circles), T3 (open circles) and T2,3 (solid triangle) models. (b) HOMO and LUMO topologies of the directly connected T2 dimeric models and Tr2,3 trimeric models chosen as representatives (see Fig. S6 (ESI†) for the remaining compounds). | ||
The nucleus-independent chemical shift (NICS) values for the T2 and T3 fragment models were calculated at the geometrical centers of all the phenyl rings (NICS(0)) and at 1 Å above (NICS(1)); see Fig. S8 and S9 (ESI†). The NICS methodology is a widely employed indicator of chemical aromaticity;51,52 the more negative the NICS value, the more aromatic the system. On the basis of the calculated data, the aromaticity of these systems is significantly affected by the nature of the core but is barely influenced by the linker units or linkage position. When compared to the reference Tx-based derivatives: (i) the presence of electron-rich Tr platforms results in more negative NICS values (around 2 ppm), suggesting that the platforms become more aromatic. (ii) The insertion of To cores leads to less negative NICS values, and this effect is more important in the innermost benzene rings (with NICS(0) values of around −1.2 ppm in the To-based systems compared to values of around −6.8 ppm for the Tx-based systems); this can be explained in terms of the electron-withdrawing character of the ketone groups, which decreases the aromaticity of the structure in consonance with better electronic delocalization, as previously pointed out by their lowest HOMO–LUMO gap values in the series.
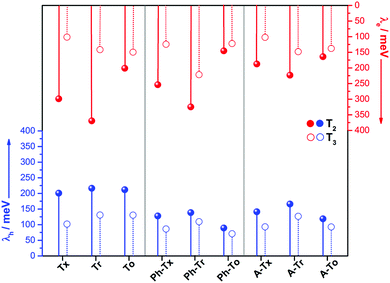
The intramolecular reorganization energy is one of the key molecular parameters governing charge transport,53 and it reveals the geometrical adjustments necessary to accommodate a positive or a negative charge. The smaller the value of λ, the larger the expected charge mobility. With this in mind, we analyzed the effects of the electronic nature of the conjugated platforms on the intramolecular reorganization energies associated with hole (λh) and electron (λe) transfer. Fig. 4 shows the computed λ values for the T2 and T3 dimeric models. The calculated λh [λe] values are in the range of 71–217 [102–369] meV. Note that these values are on the same order of those previously obtained for 2D COF fragments based on pyrene (with λh = 134 meV and λe = 192 meV) or porphyrin (with λh = 54 meV and λe = 170 meV) cores for which high charge-carrier mobility values were predicted.49 Among the series, the Tr-based and To-based systems exhibit the largest and lowest λ values, respectively; this can be attributed to the large distortion found in Tr platforms due to the steric hindrance between the N-methyl groups and the outermost benzene rings, whereas the To cores exhibit totally coplanar skeletons, allowing for better geometrical relaxation upon charging. The insertion of π-bridges results in smaller λ values, especially for alkyne groups. For instance, linking the cores with phenyl [alkyne] groups results in λh and λe decreases of 123 [56] and 93 [37] meV, respectively, for the To2 derivatives; this behavior can be related to the previously observed enhancement of the π-electron delocalization between the heptacyclic platforms and to the overall relaxation of the structure upon core elongation. Finally, the structural reorganization needed to accommodate both positive and negative charges decreases by an average of 30% and 40%, respectively, when the linkage position changes from T2 to T3; this effect is more pronounced when the cores are directly linked.
2. 2D conjugated polymer networks
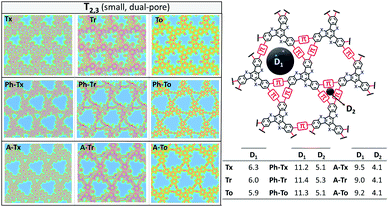
We next investigated the electronic structures of single-layer truxene-based 2D polymers built by sequentially assembling the previously studied molecular fragments. For all the materials under study, honeycomb-Kagome-like hexagonal lattices were observed, where within the primitive unit cell, the connection between the conjugated platforms exhibits an arrangement of a kagome sublattice while the centers of the cores form a honeycomb sublattice.54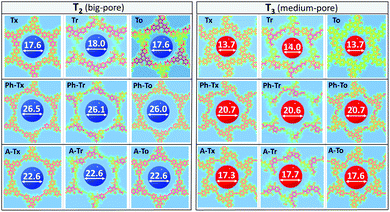 | ||
| Fig. 5 DFT-PBE-calculated surface charge density colour maps in the xy-plane (at the z-position) for all the T2 and T3 2D COFs under study. Accessible pore diameter (Å) values are also shown. | ||
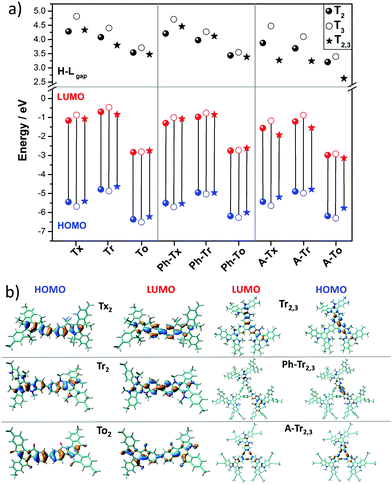
In accordance with the optimized molecular fragments, the optimized periodic single layers predict that the Tx- and To-based COF structures are planar, while the Tr-homologues have a moderately distorted configuration as a consequence of the steric repulsions between the N-methyl groups and the hydrogen atoms of the adjacent phenyl groups. This structural feature plays a role in the electronic total charge distribution of these 2D materials. Fig. 5 and 6 depict colour total electronic density maps (increasing charge density from the light green to the red/purple regions) associated with the cutting-planes of the 3D total charge isodensity, which becomes slightly inhomogeneous in specific regions of some of the compounds due to out-of-plane distortions of the structures. The distorted configuration of the Tr-based COF monolayer will have a strong implication for the preferential interlayered bulk stacking, as discussed below.
The DFT-PBE0 band structures of the T2 and T2,3 COFs are displayed in Fig. 8. The three-armed platforms in the T2 COFs lead to the formation of highly symmetric kagome-like lattices,32 which results in a totally flat top of the valence band (VB) and bottom of the conduction band (CB); this affords fully localized charge carriers and infinitive carrier effective masses, which translates into vanishing charge carrier mobilities (Fig. 8a). Only a very slight gain of the valence band dispersion is observed when the cores are directly connected through meta connections in T3 (Fig. S10, ESI†). The insertion of phenylene or alkyne π-bridges between the cores retained the totally flat character of the bands around the Fermi level in both the T2 and T3 COFs (Fig. S10 and S11, ESI†). These predicted flat bands contrast with the high mobility values experimentally obtained for Ph-Tr2 COFs, one of the benchmark hole transport 2D conjugated polymers reported to date.16 In this case, the high mobility values probably reflect the favorable electronic coupling between the cores of the adjacent layers, which may increase the bandwidths along the vertical direction. To reinforce this hypothesis, we analyzed the preferential interlayer stacking of different selected 2D COFs (see the Discussion in Section 2.3).
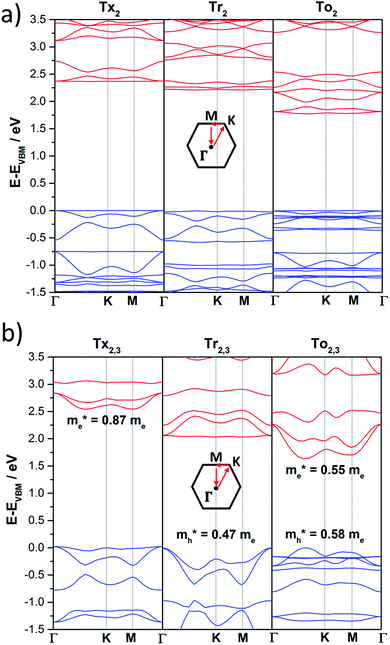 | ||
| Fig. 8 DFT-PBE-calculated electronic band structures of directly core-connected 2D polymers: Tx2, Tr2 and To2 (a) and Tx2,3, Tr2,3 and To2,3 (b). The valence and conduction bands are marked in blue and red, respectively. The zero energy is taken to correspond to the valence band maximum, EVBM, while the x-axis labels denote a path through the 3D space of the k-vectors. Points of high symmetry in the Brillouin zone are labeled as Γ (0,0,0), M (0,1/2,0) and K (1/3,2/3,0), all in reciprocal space coordinates. For the electronic band structures of the remaining 2D polymers under study, see Fig. S10–S13 (ESI†). | ||
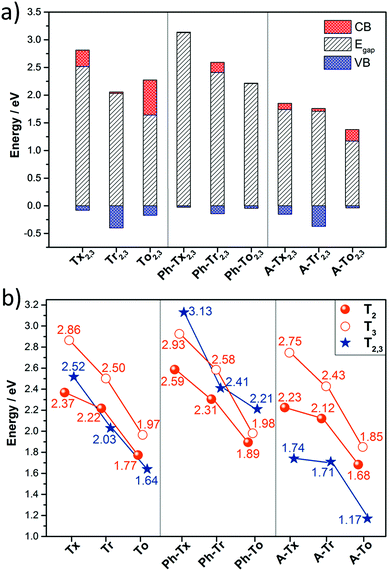
On the other hand, the electronic structures of COFs based on six-armed cores result in more dispersive bands (Fig. 7a and 8b). In this context, it is worth noting that the more dispersive the valence band [conduction band] at the VB maximum [BC minimum], the larger the expected hole [electron] charge carrier mobility. Interestingly, a large variation of the bandwidths was found in the T2,3 COFs (i.e., in the range of 26–400 meV and 6–633 meV for the CB and VB, respectively). Particularly large CB [VB] bandwidths and low effective masses for holes [electrons] were found for the Tr2,3 [A-To2,3] polymers; therefore, these systems are promising hole and electron charge-transport 2D materials, respectively. On the other hand, large bandwidths for both CB and VB (and low hole and electron effective masses) were obtained for To2,3, A-Tx2,3 and A-Tr2,3; therefore, they are attractive ambipolar charge carrier materials (see Fig. 8b for the directly connected T2,3 COFs and Fig. S12 (ESI†) for the alkyne-substituted A-T2,3 COFs).
At this point, it is interesting to remark that all the compounds analyzed in this study mainly exhibit π-type semiconducting character, with the Fermi energy almost pinning the valence band in some cases. The 3D isosurfaces of the orbital electronic densities corresponding to the valence and conduction bands of the different extended 2D COF systems studied here provide valuable information about the spatial localization and delocalization degrees of these states, the homogeneity in the spatial distribution of the states, and the preferential carrier transport paths across the compounds (Fig. S13–S16, ESI†). For instance, the engineered A-Tr2,3 system, which is predicted to have narrower band-gaps and pronounced electronic k-dispersions, exhibits similar morphologies for the valence and conduction bands, with a more delocalized spatial distribution of the valence band (Fig. S16, ESI†).
The time-dependent DFT-based UV-Vis absorption spectra of the T2 and T3 2D polymers were also calculated (Fig. S17, ESI†). A good correlation can be found with the experimental results previously reported for truxene-based (Tx2, Tx3, Ph-Tx2 and Ph-Tx3)25 polymers. Please note that UV-Vis absorption (photoexcitation) spectra are of fundamental importance for applications ranging from sensing to photocatalysis and photovoltaics. We have found that in these systems, it is possible to modulate the absorption spectral response from the UV region to the near infrared region through suitable chemical modification, such as from 325 nm in Tx3 to 726 nm in A-To2 (a more detailed explanation can be found in the ESI†). These differences are also of fundamental interest for their sensing behavior, as we recently demonstrated for some of these truxene-related-materials.25 The character of the symmetry of these valence and conduction orbital states (see Fig. S13–S16, ESI†) will be crucial to yield the permitted optical transitions captured by the computed photoabsorption spectra (see Fig. S17, ESI†) because the main contribution to the primary electronic excitation in these compounds comes from excitation of an electron from the valence band towards the conduction band (see the ESI†).
Interestingly, this variety of possible scenarios predicted by our theoretical protocol leads to high versatility in selecting candidates for different applications: going from easy-to-delaminate systems, allowing the transfer of a 2D single layer to more interesting inert technological substrates, up to highly robust stacked crystals with potential use in optoelectronic applications or for interpore gas-sensing purposes.
Conclusions
In summary, we have performed a comprehensive and exhaustive investigation at the DFT level of the structural and electronic features of 27 different 2D conjugated polymer networks based on C3-symmetric platforms (i.e., truxene, triindole and truxenone). The conjugated cores are connected directly or through alkyne or phenylene spacers, whose number and linkage position (from para to meta) have also been explored. Semiconductors band-gap values in the range between 1.17 and 3.13 eV are predicted.Our results show that wide tuning of the structural properties (i.e., geometry or pore size) and electronic properties (i.e. HOMO–LUMO levels, band-gap or band dispersion) can be achieved in these truxene-based 2D polymers by suitable selection of the trigonal building blocks and the nature and position of the connecting moieties. In the same line, a strong modulation of the absorption spectral response from the UV region to the near infrared region is found through suitable chemical modification. Please note that the above parameters will determine properties such as the selectivity/sensitivity of sensing polymers towards analytes of interest and will dictate their photocatalytic activity.
On the other hand, large bandwidths and low effective masses (and thus, high carrier mobilities) are predicted for 2D polymers with six-armed triindole and truxenone cores, connected directly (Tr2,3 and To2,3) or through alkyne bridges (A-Tr2,3 and A-To2,3). Preferential interlayered stacking is also expected to result in favorable electronic couplings between the cores and may increase the bandwidths along the vertical direction, thus positively affecting the charge-carrier mobilities. This probably explains the high mobility experimentally determined for Ph-Tr216 in spite of the fact that flat bands are predicted for polymers with three-armed cores (T2 and T3). In fact, the calculations suggest preferred AB stacking between layers for the related triindole-based polymers, which would lead to a staggered arrangement of neighbouring cores. This organization has been previously demonstrated to result in pronounced electronic coupling and high hole mobilities in triindole self-assembling systems.18,59,60 The synthesis of selected candidates (particularly those with monomers connected via six ethynyl linkers) is now actively ongoing in our laboratories in an attempt to obtain high mobility semiconductors and validate our theoretical results.
Overall, our findings shed light on the structure–property relationships of 2D truxene-based conjugated polymers and provide interesting guidelines to design novel 2D materials with applications ranging from sensing to photocatalysis or electronics. Additionally, this computational first-principles-based strategy emerges as a powerful tool to achieve in silico pre-filtering of future similar 2D materials, which, by adequate and careful selection of building blocks, will permit the prediction, within the limits of the level of theory employed, of emerging optoelectronic features as a lighthouse to experimentalists according to the desired targeted functionality.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by the MINECO (CTQ2016-78557-R) and MICINN (PID2019-104125RB-I00) of Spain. JIM acknowledges financial support from Spanish MINECO (MAT2017-85089-C2-1-R, RYC-2015-17730), Comunidad de Madrid via Programa de Investigación Tecnologías 2018 (FOTOART-CM S2018/NMT-4367), and the innovation program under grant agreements 785219 and 881603 (GrapheneCore2 and GrapheneCore3-Graphene-based disruptive technologies, respectively). The work at the University of Málaga was funded by the MICINN (PID2019-110305GB-I00) and by the Junta de Andalucıa (P09-FQM-4708, UMA18-FEDERJA-080). S. G.-V. thanks the MINECO for a FPU predoctoral fellowship (FPU17/04908). Computer resources, technical expertise and assistance provided by the SCBI (Supercomputing and Bioinformatics) centre of the University of Málaga are gratefully acknowledged.Notes and references
- P. Samorí and V. Palermo, Flexible Carbon-based Electronics, Wiley-VCH, Weinheim, 2018 Search PubMed.
- H. Klauk, Organic electronics: materials, manufacturing, and applications, Wiley-VCH, Weinheim, 2006 Search PubMed.
- H. Klauk, Organic electronics II: more materials and applications, Wiley-VCH, Weinheim, 2012 Search PubMed.
- S. Fratini, M. Nikolka, A. Salleo, G. Schweicher and H. Sirringhaus, Nat. Mater., 2020, 19, 491–502 Search PubMed.
- D. F. Perepichka and F. Rosei, Science, 2009, 323, 216–217 Search PubMed.
- M. S. Lohse and T. Bein, Adv. Funct. Mater., 2018, 28, 1705553 Search PubMed.
- H. V. Babu, M. G. M. Bai and M. Rajeswara Rao, ACS Appl. Mater. Interfaces, 2019, 11, 11029–11060 Search PubMed.
- Y. Li, W. Chen, G. Xing, D. Jiang and L. Chen, Chem. Soc. Rev., 2020, 49, 2852–2868 Search PubMed.
- J. L. Segura, M. J. Mancheño and F. Zamora, Chem. Soc. Rev., 2016, 45, 5635–5671 Search PubMed.
- D. Zhou, X. Tan, H. Wu, L. Tian and M. Li, Angew. Chem., Int. Ed., 2019, 58, 1376–1381 Search PubMed.
- M. R. Rao, Y. Fang, S. De Feyter and D. F. Perepichka, J. Am. Chem. Soc., 2017, 139, 2421–2427 Search PubMed.
- W. Liu, X. Luo, Y. Bao, Y. P. Liu, G. H. Ning, I. Abdelwahab, L. Li, C. T. Nai, Z. G. Hu, D. Zhao, B. Liu, S. Y. Quek and K. P. Loh, Nat. Chem., 2017, 9, 563–570 Search PubMed.
- L. Cardenas, R. Gutzler, J. Lipton-Duffin, C. Fu, J. L. Brusso, L. E. Dinca, M. Vondráček, Y. Fagot-Revurat, D. Malterre, F. Rosei and D. F. Perepichka, Chem. Sci., 2013, 4, 3263–3268 Search PubMed.
- D. Cui, D. F. Perepichka, J. M. MacLeod and F. Rosei, Chem. Soc. Rev., 2020, 49, 2020–2038 Search PubMed.
- S. Wu, M. Li, H. Phan, D. Wang, T. S. Herng, J. Ding, Z. Lu and J. Wu, Angew. Chem., Int. Ed., 2018, 57, 8007–8011 Search PubMed.
- C. Li, Y. Wang, Y. Zou, X. Zhang, H. Dong and W. Hu, Angew. Chem., Int. Ed., 2020, 59, 9403–9407 Search PubMed.
- C. Ruiz, J. T. López Navarrete, M. C. Ruiz Delgado and B. Gómez-Lor, Org. Lett., 2015, 17, 2258–2261 Search PubMed.
- C. Ruiz, U. K. Pandey, R. Termine, E. M. García-Frutos, G. López-Espejo, R. P. Ortiz, W. Huang, T. J. Marks, A. Facchetti, M. C. Ruiz Delgado, A. Golemme and B. Gómez-Lor, ACS Appl. Mater. Interfaces, 2016, 8, 26964–26971 Search PubMed.
- A. Benito-Hernández, U. K. Pandey, E. Cavero, R. Termine, E. M. García-Frutos, J. L. Serrano, A. Golemme and B. Gómez-Lor, Chem. Mater., 2013, 25, 117–121 Search PubMed.
- K. Q. Zhao, C. Chen, H. Monobe, P. Hu, B. Q. Wang and Y. Shimizu, Chem. Commun., 2011, 47, 6290–6292 Search PubMed.
- S. Gómez-Esteban, A. Benito-Hernandez, R. Termine, G. Hennrich, J. T. L. Navarrete, M. C. Ruiz Delgado, A. Golemme and B. Gómez-Lor, Chem. – Eur. J., 2018, 24, 3576–3583 Search PubMed.
- J. Guadalupe, A. M. Ray, E. M. Maya, B. Gómez-Lor and M. Iglesias, Polym. Chem., 2018, 9, 4585–4595 Search PubMed.
- V. R. Battula, H. Singh, S. Kumar, I. Bala, S. K. Pal and K. Kailasam, ACS Catal., 2018, 8, 6751–6759 Search PubMed.
- A. Valverde-González, C. G. López Calixto, M. Barawi, M. Gomez-Mendoza, V. A. De La Peña O’Shea, M. Liras, B. Gómez-Lor and M. Iglesias, ACS Appl. Energy Mater., 2020, 3, 4411–4420 Search PubMed.
- M. Echeverri, S. Gámez-Valenzuela, R. C. González-Cano, J. Guadalupe, S. Cortijo-Campos, J. T. López Navarrete, M. Iglesias, M. C. Ruiz Delgado and B. Gómez-Lor, Chem. Mater., 2019, 31, 6971–6978 Search PubMed.
- X. Liu, Y. Xu and D. Jiang, J. Am. Chem. Soc., 2012, 134, 8738–8741 Search PubMed.
- A. E. Sadak, E. Karakuş, Y. M. Chumakov, N. A. Dogan and C. T. Yavuz, ACS Appl. Energy Mater., 2020, 3, 4983–4994 Search PubMed.
- X. C. Li, Y. Zhang, C. Y. Wang, Y. Wan, W. Y. Lai, H. Pang and W. Huang, Chem. Sci., 2017, 8, 2959–2965 Search PubMed.
- A. V. Kuklin, G. V. Baryshnikov, B. F. Minaev, N. Ignatova and H. Ågren, J. Phys. Chem. C, 2018, 122, 22216–22222 Search PubMed.
- Y. Jing and T. Heine, J. Am. Chem. Soc., 2019, 141, 743–747 Search PubMed.
- M. A. Springer, T. J. Liu, A. Kuc and T. Heine, Chem. Soc. Rev., 2020, 49, 2007–2019 Search PubMed.
- S. Thomas, H. Li, C. Zhong, M. Matsumoto, W. R. Dichtel and J. L. Bredas, Chem. Mater., 2019, 31, 3051–3065 Search PubMed.
- R. Gutzler and D. F. Perepichka, J. Am. Chem. Soc., 2013, 135, 16585–16594 Search PubMed.
- J. Wen, D. Luo, L. Cheng, K. Zhao and H. Ma, Macromolecules, 2016, 49, 1305–1312 Search PubMed.
- R. Gutzler and Phys Chem, Chem. Phys., 2016, 18, 29029–29100 Search PubMed.
- D. J. Rizzo, Q. Dai, C. Bronner, G. Veber, B. J. Smith, M. Matsumoto, S. Thomas, G. D. Nguyen, P. R. Forrester, W. Zhao, J. H. Jørgensen, W. R. Dichtel, F. R. Fischer, H. Li, J. L. Bredas and M. F. Crommie, Nano Lett., 2020, 20, 963–970 Search PubMed.
- P. Albacete, J. I. Martínez, X. Li, A. López-Moreno, S. Mena-Hernando, A. E. Platero-Prats, C. Montoro, K. P. Loh, E. M. Pérez and F. Zamora, J. Am. Chem. Soc., 2018, 140, 12922–12929 Search PubMed.
- P. Zhu and V. Meunier, J. Chem. Phys., 2012, 137, 244703 Search PubMed.
- S. Thomas, H. Li, R. R. Dasari, A. M. Evans, I. Castano, T. G. Allen, O. G. Reid, G. Rumbles, W. R. Dichtel, N. C. Gianneschi, S. R. Marder, V. Coropceanu and J. L. Brédas, Mater. Horiz., 2019, 6, 1868–1876 Search PubMed.
- M. Reig, G. Bagdziunas, A. Ramanavicius, J. Puigdollers and D. Velasco, Phys. Chem. Chem. Phys., 2018, 20, 17889–17898 Search PubMed.
- A. Tripathi and C. Prabhakar, J. Phys. Org. Chem., 2019, 32, e3944 Search PubMed.
- A. Benito-Hernández, M. T. El-Sayed, J. T. López Navarrete, M. C. Ruiz Delgado and B. Gómez-Lor, Org. Chem. Front., 2018, 5, 1748–1755 Search PubMed.
- S. Royuela, E. Martínez-Periñán, M. P. Arrieta, J. I. Martínez, M. M. Ramos, F. Zamora, E. Lorenzo and J. L. Segura, Chem. Commun., 2020, 56, 1267–1270 Search PubMed.
- L. Li, Z. Cai, Q. Wu, W. Y. Lo, N. Zhang, L. X. Chen and L. Yu, J. Am. Chem. Soc., 2016, 138, 7681–7686 Search PubMed.
- G. V. Baryshnikov, B. F. Minaev, N. N. Karaush and V. A. Minaeva, RSC Adv., 2014, 4, 25843–25851 Search PubMed.
- L. Li, W. Y. Lo, Z. Cai, N. Zhang and L. Yu, Macromolecules, 2016, 49, 6903–6909 Search PubMed.
- J. Wen, D. Luo, L. Cheng, K. Zhao and H. Ma, Macromolecules, 2016, 49, 1305–1312 Search PubMed.
- R. Gutzler and D. F. Perepichka, J. Am. Chem. Soc., 2013, 135, 16585–16594 Search PubMed.
- S. Thomas, H. Li, R. R. Dasari, A. M. Evans, I. Castano, T. G. Allen, O. G. Reid, G. Rumbles, W. R. Dichtel, N. C. Gianneschi, S. R. Marder, V. Coropceanu and J. L. Brédas, Mater. Horiz., 2019, 6, 1868–1876 Search PubMed.
- S. Jhulki, A. M. Evans, X. L. Hao, M. W. Cooper, C. H. Feriante, J. Leisen, H. Li, D. Lam, M. C. Hersam, S. Barlow, J. L. Brédas, W. R. Dichtel and S. R. Marder, J. Am. Chem. Soc., 2020, 142, 783–791 Search PubMed.
- P. V. R. Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. R. Van Eikema Hommes, J. Am. Chem. Soc., 1996, 118, 6317–6318 Search PubMed.
- T. K. Zywietz, H. Jiao, P. V. R. Schleyer and A. De Meijere, J. Org. Chem., 1998, 63, 3417–3422 Search PubMed.
- V. Coropceanu, J. Cornil, D. A. da Silva Filho, Y. Olivier, R. Silbey and J. L. Brédas, Chem. Rev., 2007, 107, 926–952 Search PubMed.
- C. Barreteau, F. Ducastelle and T. Mallah, J. Phys.: Condens. Matter, 2017, 29, 465302 Search PubMed.
- R. R. Liang, S. Q. Xu, L. Zhang, A. Ru-Han, P. Chen, F. Z. Cui, Q. Y. Qi, J. Sun and X. Zhao, Nat. Commun., 2019, 10, 4609 Search PubMed.
- T. Y. Zhou, S. Q. Xu, Q. Wen, Z. F. Pang and X. Zhao, J. Am. Chem. Soc., 2014, 136, 15885–15888 Search PubMed.
- A. Nagai, Z. Guo, X. Feng, S. Jin, X. Chen, X. Ding and D. Jiang, Nat. Commun., 2011, 2, 536 Search PubMed.
- W. Shockley and H. J. Queisser, J. Appl. Phys., 1961, 32, 510–519 Search PubMed.
- E. M. García-Frutos, E. Gutierrez-Puebla, M. A. Monge, R. Ramírez, P. de Andrés, A. de Andrés, R. Ramírez and B. Gómez-Lor, Org. Electron., 2009, 10, 643–652 Search PubMed.
- E. M. García-Frutos, G. Hennrich, E. Gutierrez, A. Monge and B. Gómez-Lor, J. Org. Chem., 2010, 75, 1070–1076 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Theoretical methods and computational details; chemical structures of the molecular fragments studied theoretically and Study of 2D conjugated polymer networks. See DOI: 10.1039/d0tc03139a |
| This journal is © The Royal Society of Chemistry 2020 |