Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
High harmonic generation in graphene–boron nitride heterostructures
Zi-Yu
Chen†
 *a and
Rui
Qin†
*a and
Rui
Qin†
 *b
*b
aKey Laboratory of High Energy Density Physics and Technology (MoE), College of Physics, Sichuan University, Chengdu 610064, China. E-mail: ziyuch@scu.edu.cn
bNational Key Laboratory of Shock Wave and Detonation Physics, Institute of Fluid Physics, China Academy of Engineering Physics, Mianyang 621999, China. E-mail: qinrui.phy@outlook.com
First published on 30th June 2020
Abstract
van der Waals heterostructures formed by stacking various atomically thin crystals have been proved to be a powerful approach to explore designer materials with nearly limitless new properties. Here, we report nonperturbative high harmonic generation (HHG) in two-dimensional (2D) heterostructures combining graphene and hexagonal boron nitride (G/hBN). First-principles calculation results reveal that the G/hBN bilayer extends the HHG properties of the constituent layers. Harmonic intensity can be significantly enhanced by several orders of magnitude by tuning the Berry curvature of G/hBN via pressure-controlled interlayer interaction. The result offers a new way to enhance HHG in graphene. It also demonstrates that van der Waals heterostructures and their novel degrees of freedom can be used to control the HHG process and open up more possibilities to manipulate strong-field ultrafast physical properties in such 2D materials.
1 Introduction
Since the discovery of graphene, various two-dimensional (2D) materials have been intensively investigated due to their exceptional properties and great potential for many applications. Among them, the distinctive optical properties of 2D materials provide exciting opportunities in many device applications in optoelectronics and nanophotonics. For example, many 2D materials have been demonstrated to be useful in ultrashort laser applications.1 Besides, strong excitonic, spin- and valley-dependent effects in 2D materials may have impacts for novel photonic devices.2,3 Recently, there has been great interest in advancing the study of nonlinear optical properties of 2D materials into the strong-field nonperturbative regime. High harmonic generation (HHG) in 2D materials has attracted much attention, alongside the emergence of the new research frontier of HHG in solids,4,5 which is of great importance for the exploration of strong-field physics in condensed matter systems6–11 and for the development of novel ultrafast optoelectronic and photonic applications.12–16 HHG in graphene,17–28 silicene,29 black phosphorous,30 transition metal dichalcogenides,31–34 and hexagonal boron nitride (hBN)35–37 has been investigated theoretically and/or experimentally. Yet, these studies only focus on 2D materials in the form of monolayers or multilayers composed of the same material.Besides, the highest harmonic order in graphene from the reported experimental results is relatively low, e.g., up to the 9th order by Yoshikawa et al.23 and 5th order by Taucer et al.24 Enhancement of HHG in this most popular 2D material is of great interest. Note that sapphire substrates are typically used in the experiments, which substantially degrade the electronic properties of graphene owing to the amorphous nature of the oxide.38 Improving the substrate to maintain the remarkably high quality of graphene may provide a solution to benefit the HHG process.
A great advantage of 2D materials is the possibility to combine and mix various different atomically thin layers to create new materials, i.e., the so-called van der Waals heterostructures.39 Owing to weak van der Waals interlayer interactions between the layers, 2D materials with different compositions can be readily assembled without the usual interfacial lattice-matching constraints of conventional crystal growth. This ability opens a new paradigm in material design. Moreover, entirely new degrees of freedom, such as relative rotation and interlayer spacing between the stacked materials, are introduced to the system that can be critical in determining its physical properties, and thus can be used as additional knobs to control the material properties. However, the strong-field nonlinear optical properties of such van der Waals heterostructures have not been studied to date.
In this work, we report HHG in bilayer van der Waals heterostructures combining graphene and hBN (G/hBN) monolayers38 using ab initio simulations based on the framework of real-time time-dependent density-functional theory (TDDFT).40–42 We find that the G/hBN bilayer exhibits distinctive HHG properties from those of the constituent layers. We also demonstrate that interlayer spacing can be an important degree of freedom to tune the electronic properties and the related HHG process in heterostructures. Harmonic intensity in G/hBN can be significantly enhanced by up to three orders of magnitude with decreasing interlayer spacing using hydrostatic pressure. This study also offers a new path to enhance HHG in graphene, since the presence of atomically flat hBN not only serves as an ideal passive substrate for graphene that maintains its high quality, but also actively modifies the band structure and Berry curvature of graphene and affects HHG in new ways, as we will show later.
2 Methods
The G/hBN bilayer structure is studied by using a periodical supercell model and modelled by the hexagonal primitive cell containing two carbon atoms, one boron atom and one nitrogen atom. The lattice constant along the direction perpendicular to the bilayer plane is taken to be 12 Å for ground state properties calculations to eliminate the interactions between adjacent bilayer images. The geometric structure relaxation and ground state electronic structure are investigated within the density functional theory framework with the local density approximation (LDA) using the CASTEP package43 which uses the plane wave basis set and ultrasoft pseudopotentials. A plane wave cutoff energy of 310 eV and an 18 × 18 × 1 Monkhorst–Pack k-point mesh for Brillouin zone sampling is used during the calculation. The atomic positions are relaxed until the maximum force on each atom is less than 0.01 eV Å−1.The calculations of the time evolution of the wave functions and the time-dependent total electronic current are studied by propagating the Kohn–Sham equations in real time and real space within the framework of TDDFT with the adiabatic LDA (ALDA) using the OCTOPUS code44,45 which uses the real space grid representation. For the study of the time evolution properties, the lattice constant along the direction perpendicular to the bilayer plane is taken to be 30 Bohr, which includes 3 Bohr of absorbing regions on each side of the heterostructure to avoid the reflection error in the spectral region of interest. The grid spacing of the real-space box is 0.4 Bohr, and the time step for time propagation is 6.05 attosecond. An 80 × 80 × 1 Monkhorst–Pack k-point mesh for Brillouin zone sampling and the fully relativistic Hartwigsen, Goedecker, and Hutter pseudopotentials are used in the calculations.
The driving laser field is described in the velocity gauge. The laser wavelength is 1800 nm (corresponding to a photon energy of 0.69 eV). The laser field is linearly polarized in the plane of the 2D samples with an electric field along the x-direction, i.e., fundamental field perpendicular to a mirror plane of the samples (see Fig. 1). The laser pulse has a sine-square envelope f(t) = sin2(πt/2τ) with τ = 20 fs and the carrier-envelope phase is set to be zero. The peak laser intensity is 2 × 1011 W cm−2. Previously, the reported damage threshold of monolayer graphene in experiments is about 3 × 1012 W cm−2.46 Besides, the pump laser intensity in the experiments of HHG in monolayer graphene reaches 1.7 × 1012 W cm−2.23 Moreover, considering the damage threshold of insulating hBN being higher than that of semimetallic graphene, we deem that the laser intensity in this study is below the damage threshold of the heterostructure.
The HHG spectrum is calculated from the time-dependent electronic current j(r,t) as:
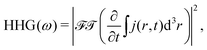 | (1) |
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif)
![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) denotes the Fourier transform.
denotes the Fourier transform.
The Berry curvature is calculated using the maximally localized Wannier functions (MLWF). First, we perform ab initio electronic-structure calculations using the PWSCF package.47,48 Then, we construct MLWF based on the Bloch states from the ab initio calculations and calculate the Berry curvature using MLWF with the Wannier90 package.49 For 2D materials, the Berry curvature is along the out-of-plane direction (z-direction), and the Berry curvature of all occupied bands is written as:
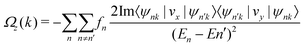 | (2) |
3 Results
3.1 Crystal structures
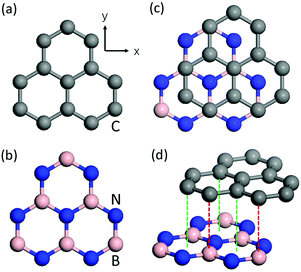
The structures of graphene monolayer, hBN monolayer, and G/hBN bilayer are schematically illustrated in Fig. 1. Graphene monolayers are composed of sp2 hybridized carbon (C) atoms arranged in a 2D honeycomb lattice and exhibit inversion symmetry (see Fig. 1(a)). Single-layer hBN has a similar honeycomb geometry in a 2D plane, while the lattice is alternatively arranged by boron (B) atoms and nitride (N) atoms and thus the inversion symmetry is no longer preserved (see Fig. 1(b)). For the G/hBN bilayer, we assume that the graphene and hBN single layers are commensurate since the lattice mismatch between them is only about 1.5%. We use a Bernal (A–B) stacking pattern with the C atoms of one graphene sublattice on the top of B atoms while those of the other sublattice are right above the centers of the hBN lattice (see Fig. 1(c) and (d)). As revealed by previous and our own calculations, such a stacking configuration is the most stable one.50,51 A high-quality large-area epitaxial G/hBN heterostructure with a 0° stacking angle and size extending to a few hundred micrometers has been successfully grown experimentally.52 The G/hBN bilayer also lacks inversion symmetry. The equilibrium interlayer distance between graphene and the hBN layers is about 3.2 Å, in good agreement with the previous results.50,513.2 High harmonic spectra
High harmonic spectra from graphene, hBN, and G/hBN samples are shown in Fig. 2. For the harmonic component parallel to the fundamental field (see Fig. 2(a)), only odd harmonic orders are present in the spectra for the three samples. In contrast, for the harmonic component perpendicular to the fundamental field (see Fig. 2(b)), only even harmonic orders appear for the hBN monolayer and G/hBN bilayer, while no harmonic generation is found in the graphene monolayer.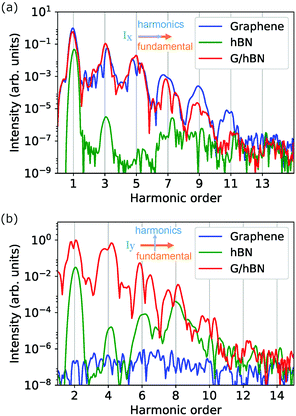 | ||
| Fig. 2 High harmonic spectra from the G/hBN bilayer and its constituent layers. Harmonic components (a) parallel and (b) perpendicular to the laser polarization direction, i.e., polarized along the x- and y-direction, respectively. The x and y directions are the same as those in Fig. 1(a). | ||
To explain similar observations of HHG in MoS2, Liu et al. presented a semiclassical model considering intraband dynamics of carrier motion within a single band with the Berry curvature term included:31
ħ![[k with combining dot above]](https://www.rsc.org/images/entities/b_char_006b_0307.gif) = −eE; = −eE; | (3) |
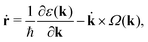 | (4) |
The results of appearing harmonic orders are also consistent with symmetry requirements. For example, mirror symmetry requires even harmonic radiation parallel to the driving field to vanish when the fundamental field is perpendicular to the mirror plane. hBN and G/hBN show even order harmonics perpendicular to the fundamental field because of nonzero Berry curvature as a result of inversion symmetry breaking in both samples. In comparison, symmetry in graphene results in a zero Berry curvature and thus no even harmonics are allowed in the perpendicular direction.
For the harmonic intensity, it can be seen from Fig. 2 that the overall HHG efficiency from G/hBN is much higher than that from hBN for both parallel and perpendicular components, while it is comparable to and much higher than that from graphene for the parallel and perpendicular component, respectively. On the one hand, the physical properties of the constituent layers in the heterostructure remain to a great extent due to the weak van der Waals interactions. HHG from G/hBN in the parallel direction is mainly from the contribution of graphene. On the other hand, the presence of hBN modifies the fundamental properties of the bilayer. One significant consequence is the breakage of inversion symmetry. This leads to a strong HHG in the perpendicular direction from G/hBN, much stronger than that from hBN. Thus the G/hBN heterostructure as a new layered material combines and extends the HHG properties of the constituent layers. Apart from these, by orienting the linearly polarized laser field along the zigzag and armchair directions, we have observed anisotropic harmonic emission in G/hBN, similar to that being reported in graphene28 and hBN.36
3.3 Pressure-enhanced high harmonics
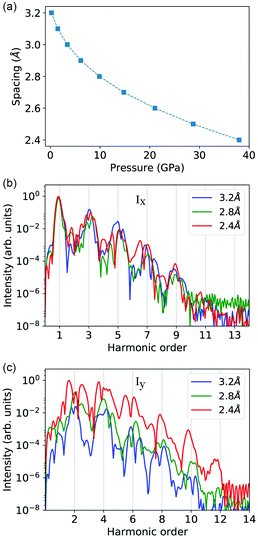
One of the fascinating features of van der Waals heterostructures lies in the various novel degrees of freedom existing to control their physical properties. Next, we show that HHG in G/hBN can be greatly enhanced by decreasing the interlayer separation with pressure. Experimentally, the techniques to control interlayer spacing with hydrostatic pressure in hBN-encapsulated graphene heterostructure53 and trilayer graphene54 have been demonstrated. High pressure up to hundreds of GPa can be created with the help of the diamond anvil cell (DAC) technique.55,56 The diamonds can also be utilized as transparent optical windows allowing the laser pumping and transmitted harmonic measurement to be accessible. The sample can be transferred onto the diamond surface of the DAC using a polydimethylsiloxane (PDMS) stamping technique as shown in the experiments by Ke et al.54 The effect of pressure medium intercalation between the graphene and hBN layer should be negligible, since the interlayer spacing between the graphene and hBN layer is extremely small. Fig. 4(a) shows results of equilibrium interlayer spacing as a function of pressure from ambient up to about 40 GPa using first-principles calculations. Generally, the interlayer spacing decreases with pressure with a sublinear scaling, with a spacing decrement of 12.5% (i.e., 2.8 Å) at about 10 GPa and 25% (i.e., 2.4 Å) at about 38 GPa. When pressure is applied to the G/hBN system along the out-of-plane stacking direction, the in-plane lattice constants increase with decreasing interlayer spacing due to the Poisson effect. However, the interlayer interaction is the weak van der Waals interaction, while the interaction between atoms in the same layer is the much stronger chemical bonding. Thus, the change in the in-plane dimensions is very small. For example, when interlayer spacing decreases by 25% from 3.2 to 2.4 Å, the bond length and in-plane lattice constants only increase by 9 × 10−5. Hence the pressure primarily results in a c-axis compression. The effect of such a small change in the in-plane dimension on the harmonic intensity is negligible.HHG in the x- and y-direction at these representative pressures and interlayer spacings is shown in Fig. 4(b) and (c), respectively. With the increase of pressure or decrease of interlayer spacing, the harmonic intensity of parallel component (Ix) shows little change. In contrast, the harmonic intensity of perpendicular component (Iy) is dramatically enhanced with pressure. Compared to ambient conditions, the enhancement at a spacing of 2.4 Å reaches two orders of magnitude for lower (≤8th) harmonic orders and even three orders of magnitude for higher (≥10th) harmonic orders. In addition to intensity enhancement, the cutoff energy of high harmonics is also improved under compression.
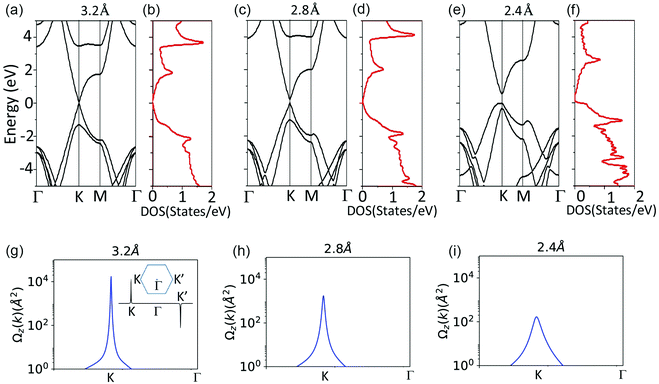
To understand the effect of pressure on HHG, we investigate how the electronic structures of the bilayer can be altered with different interlayer coupling strengths. Fig. 5(a)–(f) show the band structure and density of state (DOS) of the G/hBN with different interlayer spacings. Without pressure, i.e., at an interlayer spacing of 3.2 Å, the band structure is similar to that of monolayer graphene around the Dirac point albeit with a small bandgap, i.e., quasi-linear band dispersion and nearly vanishing DOS at the Fermi level. With the decrease of interlayer spacing, evidently large bandgap opening can be seen that increases with pressure. At a spacing of 2.4 Å, the top of valence band maximum exhibits a much flatter band dispersion that leads to a large DOS at the Fermi level. However, the effects of increasing both bandgap and DOS near the Fermi level tend to cancel each other out with respect to carrier excitation. Moreover, it is seen that the band shape of the conduction band minimum (CBM) changes little with pressure. Now that the band shape of CBM and the number of carriers being excited to CBM change little with pressure, the dependence of intraband current on pressure is weak. Since the parallel harmonics (Ix) are mainly generated by an intraband mechanism, this may explain the results that the parallel harmonics also show little change with pressure, as shown in Fig. 4(b).
As the generation mechanisms of perpendicular harmonics (Iy) are related with Berry curvatures, we calculate the Berry curvature Ωz along the K–K′ line and show the results in Fig. 5(g)–(i). Note the Berry curvature in the conduction band is opposite to that in the valence band. Under low pressure, Ωz mainly peaks around the K (K′) point, where the DOS near the Fermi level is very small. The amplitude of Ωz decays rapidly away from the K (K′) point. As pressure increases, although the peak amplitude of Ωz decreases, Ωz becomes broader in the momentum space and is smeared to areas away from the K (K′) point. Thus Ωz enhances in more areas in the momentum space. With a decreasing interlayer spacing, a wider region of carriers in the Brillouin zone experiences the enhanced Berry curvature. Combined with the enhanced DOS, it is favorable for the formation of a larger intraband anomalous current perpendicular to the driving field. Consequently, the perpendicular high harmonics also enhances under pressure.
4 Conclusion
In conclusion, we have investigated HHG in bilayer G/hBN heterostructures using an ab initio approach. G/hBN extends the high harmonic properties of its building blocks, i.e., graphene and hBN monolayers. Harmonic intensity can be significantly enhanced up to three orders of magnitude by controllably tuning the interlayer spacing of the heterostructure using high pressure. A similar HHG can also be expected in other heterostructures that exhibit broken inversion symmetry and nonzero Berry curvature. It can lead to many potential applications such as the development of a solid-state attosecond photonic source and compact high pressure sensing. Though maintaining the system under high pressure is challenging at present, further development of novel advanced technology may allow better implementation. Even if the exceptional properties under high pressure are not preservable under ambient conditions, the knowledge gained at high pressure is very useful for guiding the search and synthesis of materials exhibiting similar structures and properties with alternative approaches. Our findings demonstrate that van der Waals heterostructures provide a new platform to study the strong-field ultrafast physical properties in 2D materials. It is of great interest to explore the possibilities to control the strong-field properties in heterostructures with many novel degrees of freedom, such as stacking pattern, valley, and lattice twisting in particular, which may lead to many unexpected new results. As revealed by previous studies, at a small relative twist angle, the band structures can be profoundly altered by the resulting moiré superlattice. Unusual electronic properties can emerge, which will certainly have a significant influence on the HHG properties. Beyond this, the HHG properties of other novel 2D materials, such as MXenes57 and 2D perovskite,58 are also of high interest to investigate due to their unique structures.Data availability
The data that support the findings of this study are available from the corresponding authors upon request. The OCTOPUS code is available from http://www.octopus-code.org.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported in part by the National Natural Science Foundation of China (Grant No. 11705185) and the Fundamental Research Funds for the Central Universities (YJ202025).Notes and references
- J. He, L. Tao, H. Zhang, B. Zhou and J. Li, Nanoscale, 2019, 11, 2577–2593 RSC.
- K. F. Mak and J. Shan, Nat. Photonics, 2016, 10, 216–226 CrossRef CAS.
- J. Pei, J. Yang, T. Yildirim, H. Zhang and Y. Lu, Adv. Mater., 2019, 31, 1706945 CrossRef PubMed.
- S. Ghimire, A. D. DiChiara, E. Sistrunk, P. Agostini, L. F. DiMauro and D. A. Reis, Nat. Phys., 2011, 7, 138–141 Search PubMed.
- S. Ghimire and D. A. Reis, Nat. Phys., 2019, 15, 10–16 Search PubMed.
- G. Vampa, C. R. McDonald, G. Orlando, D. D. Klug, P. B. Corkum and T. Brabec, Phys. Rev. Lett., 2014, 113, 073901 CrossRef CAS PubMed.
- G. Vampa, T. Hammond, N. Thiré, B. Schmidt, F. Légaré, C. McDonald, T. Brabec, D. Klug and P. Corkum, Phys. Rev. Lett., 2015, 115, 193603 CrossRef CAS PubMed.
- T. T. Luu, M. Garg, S. Y. Kruchinin, A. Moulet, M. T. Hassan and E. Goulielmakis, Nature, 2015, 521, 498–502 CrossRef CAS PubMed.
- Y. S. You, D. A. Reis and S. Ghimire, Nat. Phys., 2017, 13, 345–349 Search PubMed.
- N. Tancogne-Dejean, O. D. Mücke, F. X. Kärtner and A. Rubio, Phys. Rev. Lett., 2017, 118, 087403 CrossRef PubMed.
- T. T. Luu and H. J. Wörner, Nat. Commun., 2018, 9, 916 CrossRef PubMed.
- N. Tancogne-Dejean, O. D. Mücke, F. X. Kärtner and A. Rubio, Nat. Commun., 2017, 8, 745 CrossRef PubMed.
- F. Langer, M. Hohenleutner, U. Huttner, S. W. Koch, M. Kira and R. Huber, Nat. Photonics, 2017, 11, 227–231 CrossRef CAS PubMed.
- T. J. Hammond, S. Monchocë, C. Zhang, G. Vampa, D. Klug, A. Y. Naumov, D. M. Villeneuve and P. B. Corkum, Nat. Photonics, 2017, 11, 594–599 CrossRef CAS.
- M. Sivis, M. Taucer, G. Vampa, K. Johnston, A. Staudte, A. Y. Naumov, D. M. Villeneuve, C. Ropers and P. B. Corkum, Science, 2017, 357, 303–306 CrossRef CAS PubMed.
- M. Garg, H. Y. Kim and E. Goulielmakis, Nat. Photonics, 2018, 12, 291–296 CrossRef CAS.
- S. A. Mikhailov, EPL, 2007, 79, 27002 CrossRef.
- K. L. Ishikawa, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 201402(R) CrossRef.
- H. K. Avetissian, A. K. Avetissian, G. F. Mkrtchian and K. V. Sedrakian, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 115443 CrossRef.
- I. Al-Naib, J. E. Sipe and M. M. Dignam, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 245423 CrossRef CAS.
- L. A. Chizhova, F. Libisch and J. Burgdörfer, Phys. Rev. B, 2017, 95, 085436 CrossRef.
- J. D. Cox, A. Marini and F. J. G. de Abajo, Nat. Commun., 2017, 8, 14380 CrossRef CAS PubMed.
- N. Yoshikawa, T. Tamaya and K. Tanaka, Science, 2017, 356, 736–738 CrossRef CAS PubMed.
- M. Taucer, T. J. Hammond, P. B. Corkum, G. Vampa, C. Couture, N. Thiré, B. E. Schmidt, F. Légaré, H. Selvi, N. Unsuree, B. Hamilton, T. J. Echtermeyer and M. A. Denecke, Phys. Rev. B, 2017, 96, 195420 CrossRef.
- M. Baudisch, A. Marini, J. D. Cox, T. Zhu, F. Silva, S. Teichmann, M. Massicotte, F. Koppens, L. S. Levitov, F. J. García de Abajo and B. Jens, Nat. Commun., 2018, 9, 1018 CrossRef PubMed.
- H. K. Avetissian and G. F. Mkrtchian, Phys. Rev. B, 2018, 97, 115454 CrossRef CAS.
- C. Liu, Y. Zheng, Z. Zeng and R. Li, Phys. Rev. A, 2018, 97, 063412 CrossRef CAS.
- Z.-Y. Chen and R. Qin, Opt. Express, 2019, 27, 3761–3770 CrossRef CAS PubMed.
- R. Qin and Z.-Y. Chen, Nanoscale, 2018, 10, 22593–22600 RSC.
- Z.-Y. Chen and R. Qin, Nanoscale, 2019, 11, 16377–16383 RSC.
- H. Liu, Y. Li, Y. S. You, S. Ghimire, T. F. Heinz and D. A. Reis, Nat. Phys., 2017, 13, 262–265 Search PubMed.
- N. Yoshikawa, K. Nagai, K. Uchida, Y. Takaguchi, S. Sasaki, Y. Miyata and K. Tanaka, Nat. Commun., 2019, 10, 1–7 Search PubMed.
- M.-X. Guan, C. Lian, S.-Q. Hu, H. Liu, S.-J. Zhang, J. Zhang and S. Meng, Phys. Rev. B, 2019, 99, 184306 CrossRef CAS.
- M. Guan, S. Hu, H. Zhao, C. Lian and S. Meng, Appl. Phys. Lett., 2020, 116, 043101 CrossRef.
- N. Tancogne-Dejean and A. Rubio, Sci. Adv., 2018, 4, eaao5207 CrossRef PubMed.
- G. Le Breton, A. Rubio and N. Tancogne-Dejean, Phys. Rev. B, 2018, 98, 165308 CrossRef CAS.
- M. S. Mrudul, N. Tancogne-Dejean, A. Rubio and G. Dixit, npj Comput. Mater., 2020, 6, 1–9 CrossRef.
- M. Yankowitz, Q. Ma, P. Jarillo-Herrero and B. J. LeRoy, Nat. Rev. Phys., 2019, 1, 112–125 CrossRef CAS.
- A. K. Geim and I. V. Grigorieva, Nature, 2013, 499, 419–425 CrossRef CAS PubMed.
- E. Runge and E. K. U. Gross, Phys. Rev. Lett., 1984, 52, 997–1000 CrossRef CAS.
- R. van Leeuwen, Phys. Rev. Lett., 1998, 80, 1280–1283 CrossRef CAS.
- A. Castro, M. Marques, J. A. Alonso and A. Rubio, J. Comput. Theor. Nanosci., 2004, 1, 231–255 CrossRef CAS.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567–570 CAS.
- X. Andrade, D. A. Strubbe, U. D. Giovannini, A. H. Larsen, M. J. T. Oliveira, J. Alberdi-Rodriguez, A. Varas, I. Theophilou, N. Helbig, M. Verstraete, L. Stella, F. Nogueira, A. Aspuru-Guzik, A. Castro, M. A. L. Marques and A. Rubio, Phys. Chem. Chem. Phys., 2015, 17, 31371–31396 RSC.
- N. Tancogne-Dejean, M. J. T. Oliveira, X. Andrade, H. Appel, C. H. Borca, G. Le Breton, F. Buchholz, A. Castro, S. Corni, A. A. Correa, U. De Giovannini, A. Delgado, F. G. Eich, J. Flick, G. Gil, A. Gomez, N. Helbig, H. Hübener, R. Jestädt, J. Jornet-Somoza, A. H. Larsen, I. V. Lebedeva, M. Lüders, M. A. L. Marques, S. T. Ohlmann, S. Pipolo, M. Rampp, C. A. Rozzi, D. A. Strubbe, S. A. Sato, C. Schäfer, I. Theophilou, A. Welden and A. Rubio, J. Chem. Phys., 2020, 152, 124119 CrossRef PubMed.
- A. Roberts, D. Cormode, C. Reynolds, T. Newhouse-Illige, B. J. LeRoy and A. S. Sandhu, Appl. Phys. Lett., 2011, 99, 051912 CrossRef.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. D. Corso, S. de Gironcoli, P. Delugas, R. A. D. Jr, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. O. de-la Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS PubMed.
- A. A. Mostofi, J. R. Yates, G. Pizzi, Y.-S. Lee, I. Souza, D. Vanderbilt and N. Marzari, Comput. Phys. Commun., 2014, 185, 2309–2310 CrossRef CAS.
- G. Giovannetti, P. A. Khomyakov, G. Brocks, P. J. Kelly and J. van den Brink, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 073103 CrossRef.
- Y. Fan, M. Zhao, Z. Wang, X. Zhang and H. Zhang, Appl. Phys. Lett., 2011, 98, 083103 CrossRef.
- W. Yang, G. Chen, Z. Shi, C.-C. Liu, L. Zhang, G. Xie, M. Cheng, D. Wang, R. Yang, D. Shi, K. Watanabe, T. Taniguchi, Y. Yao, Y. Zhang and G. Zhang, Nat. Mater., 2013, 12, 792–797 CrossRef CAS PubMed.
- M. Yankowitz, J. Jung, E. Laksono, N. Leconte, B. L. Chittari, K. Watanabe, T. Taniguchi, S. Adam, D. Graf and C. R. Dean, Nature, 2018, 557, 404–408 CrossRef CAS PubMed.
- F. Ke, Y. Chen, K. Yin, J. Yan, H. Zhang, Z. Liu, J. S. Tse, J. Wu, H.-K. Mao and B. Chen, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 9186–9190 CrossRef CAS PubMed.
- H.-K. Mao, X.-J. Chen, Y. Ding, B. Li and L. Wang, Rev. Mod. Phys., 2018, 90, 015007 CrossRef CAS.
- H.-K. Mao, B. Chen, J. Chen, K. Li, J.-F. Lin, W. Yang and H. Zheng, Matter Radiat. Extremes, 2016, 1, 59–75 CrossRef.
- X. Jiang, A. V. Kuklin, A. Baev, Y. Ge, H. Ågren, H. Zhang and P. N. Prasad, Phys. Rep., 2020, 848, 1–58 CrossRef CAS.
- Y. Zhang, C.-K. Lim, Z. Dai, G. Yu, J. W. Haus, H. Zhang and P. N. Prasad, Phys. Rep., 2019, 795, 1–51 CrossRef CAS.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2020 |