Synergy effect of co-doping Sc and Y in Sb2Te3 for phase-change memory†
Abstract
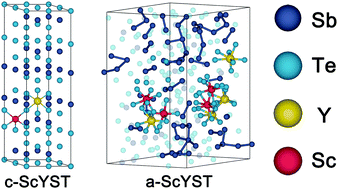
Sb2Te3 phase-change material possesses the highest crystallization speed and hence the highest operating speed among investigated phase-change systems. Doping with Y or Sc has been exploited to optimize the performance of Sb2Te3, yet the substituted Y atoms are strongly clustered, while Sc is extremely expensive and thus is unfavourable for commercialization. In this work, we have successfully obtained better-performance and moderate-cost phase-change materials by co-doping Sc and Y based on ab initio calculations and ab initio molecular-dynamics simulations (AIMD). Sc can shrink the lattice while Y expands the lattice, which makes a perfect match between original and co-doped configurations and hence can benefit by maximizing the release of lattice strain. The co-doping increases the band gap to around 0.5 eV, and the concentration ratio of Sc and Y dopants provides an advantageous tool for controlling the electronic structure. Results of calculations using the BoltzTraP code show that co-doping can result in a significant reduction in the electrical conductivity at room temperature. AIMD simulation of amorphous co-doped Sb2Te3 shows that the incorporation of Sc and Y atoms can effectively improve the thermal stability of amorphous Sb2Te3. Overall, co-doping Sc and Y is a feasible way to improve the properties of Sb2Te3 for phase-change memory applications.


 Please wait while we load your content...
Please wait while we load your content...