Open Access Article
Open Access ArticleA probe of the radiation field magnetic component based on octahedral Yb3+ in the CaNbGa garnet – CNGG – single crystal†
Jorge Omar
Álvarez-Pérez
 ,
José María
Cano-Torres
,
José María
Cano-Torres
 ,
María Dolores
Serrano
,
María Dolores
Serrano
 ,
Concepción
Cascales
,
Concepción
Cascales
 and
Carlos
Zaldo
and
Carlos
Zaldo
 *
*
Instituto de Ciencia de Materiales de Madrid, Consejo Superior de Investigaciones Científicas, c/Sor Juana Inés de la Cruz 3, 28049 Madrid, Spain. E-mail: cezaldo@icmm.csic.es
First published on 15th May 2020
Abstract
In a disordered Yb3+-doped CaNbGa garnet – CNGG – single crystal, it is shown that octahedral Yb centers exist up to a solubility limit of about 5 × 1018 cm−3 in addition to the well known dodecahedral Yb which incorporates to a much larger density ∼1021 cm−3. Despite the low density of the octahedral Yb, the presence of a symmetry center for this garnet site forbids electric dipole (ED) transitions, thus magnetic dipole (MD) spectroscopic contributions are observed with an intensity similar to that of ED ones. Because of the easy growth of this garnet, the potential application of these two contributions for probing the magnetic field component radiated by plasmonic structures is discussed on the basis of time-resolved spectroscopy, since ED Yb3+ photoluminescence is about one order of magnitude faster than MD 2F5/2 → 2F7/2 (ΔJ = +1) emissions for the 0.3 at%Yb:CNGG crystal. Channels appropriated for room temperature operation can be excited at λEXC = 960.3 nm, while sensed at λEMI = 1022 nm for the short-lived ED reference channel and λEMI = 998, 1011, 1068 or 1080 nm for the long-lived MD signal channel.
1. Introduction
Energy levels of trivalent lanthanides (Ln3+) are characterized by 2S+1LJ multiplets further split by the crystal field (CF) of a host in mJ levels. Intraconfigurational electronic transitions between these multiplets are most often induced by light–matter interactions mediated by electric fields through forced electric dipole (ED) transitions, but also include magnetic dipole (MD) interactions, particularly notable for transitions between multiplets with ΔJ = 0 or ±1.1 Although it is usually assumed that MD transitions are ∼105 times weaker than ED ones, their relative intensity in fact depends on the specific selection rules. In hosts where ED transitions are weak or even strictly forbidden, as when Ln3+ are incorporated at sites with a center of symmetry, the intensity of MD transitions can be dominant.Stimulated by recent advances in optical plasmonic-based metamaterials and nanophotonics, a variety of ways to exploit MD transitions of Ln3+ have been proposed: theoretically, as the building blocks for homogeneous negative index materials,2 or experimentally, as probes for the study of local magnetic fields in metamaterials, in a very simple approach that consists of placing the MD probe at the metamaterial surface, and if this resonance frequency corresponds to the spectral range of the field enhancement, spectral changes in intensity or shape may be observed in comparison with other magnetic dipoles outside the system or with some reference ED emission in the same system.3–7 Furthermore, experimental studies by using the competition between ED and MD processes have shown the way for achieving a strong enhancement of MD emission8 and also to broadly tune the emission spectra.9
For the above indicated sensing purposes, previous studies have involved mainly the visible 5D0 → 7F1 MD transition of Eu3+, in probing systems based on Eu-doped Y2O3 thin films,7–9 dispersions of Eu-doped organic systems in polymeric thin films,3,4,6 or Eu-doped Y2O3 NPs (about 60 nm).10 The specific advantage of using Eu3+ is the coexistence of the nearly pure MD 5D0 → 7F1 (λ ≈ 590 nm) transition and the ED 5D0 → 7F2 (λ ≈ 615 nm) transition used as the reference. Other Ln3+ emissions which have been tested with the same aim are mixed MD–ED transitions in the near-infrared (NIR) range, for instance the overlapping 4F9/2 → 6F11/2 + 6H9/2 (λ ≈ 734 nm) emissions of Dy3+,11 the also overlapping 1G4 → 3H5 (λ ≈ 784 nm) and 3H4 → 3H6 (λ ≈ 800 nm) emissions of Tm3+,11 or the 4I13/2 → 4I15/2 (λ ≈ 1.5 μm) transition of Er3+,12 in all cases by using the corresponding doped Y2O3 thin films.
The near-infrared (NIR) range from 800 to 1100 nm has several advantages over other spectral regions. As compared to the visible (characteristic of Eu3+), micron-sized plasmonic nanostructures are much easier to fabricate than nano-sized ones and their resonances exhibit higher-quality factors due to lower ohmic losses. However, as compared with the 4I13/2 → 4I15/2 Er3+ transition at λ ≈ 1.5 μm, emissions at λ < 1100 nm can be observed using standard Si photodetector technology, which simplifies the detection process. Moreover, among MD Ln3+ emissions at this wavelength range, those that can be pumped at the NIR will be the better candidates to be used. From the above considerations the 2F5/2 ↔ 2F7/2 transitions of Yb3+ (typically λEXC ≈ 940–980 nm and λEMI ≈ 980–1060 nm) in a centrosymmetric crystal site are very interesting options. The simple two-state energy structure of Yb3+ means that MD emission can account for a significant contribution to the overall decay. In fact, relatively long Yb3+ lifetime (τ) characteristics of MD transitions have been measured for Yb-doped BaF2 and SrF2 fluorites (τ = 9.72 ms and 8.20 ms, respectively), as well as for Rb2NaYF6 elpasolite (τ = 10.84 ms) crystals, with Yb3+ at centrosymmetric sites of cubic eightfold and perfect octahedral coordination,13 respectively, in both cases with calculated MD branching ratios of ∼50%.12
Cubic garnets A3M2N3O12 with space group Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d (No. 230) offer simultaneously non centrosymmetric dodecahedral 24c sites (A) and octahedral 16a centrosymmetric sites (M) to host Ln. An illustration of the garnet structure can be seen in the general view given in Fig. 1a. Fig. 1b shows the coordination of dodecahedral AO8 and octahedral MO6 garnet sites. Further drawings showing other atomic arrangements can be seen for instance in ref. 14. The Ln3+ distribution over 24c and 16a garnet sites is a topic which has been addressed with several purposes and under different approaches.15–23 The main factor governing the site preference of Ln3+ in the garnet structure is the ionic size, in such a way that garnets with any Ln3+ cation occupying the dodecahedral 24c site are known,15 and only the smallest size Ln3+ cations, typically Dy3+ to Lu3+ and also Y3+ or Sc3+, are able to enter into the octahedral 16a site, even up to its complete filling, but in this case a 24c cation with a considerably large size, for example Ca2+ in the germanate series Ca3Ln2Ge3O12,18 including Ca3Y2Ge3O12,20 is required, thus the relative sizes of 24c and 16a cations also play a role. The presence of Yb3+ in both garnet sites would offer the possibility of having the MD probe and ED reference ions in the same tested volume minimizing uncertainties related to excitation and detection processes, but so far the properties of Yb coexisting in both garnet sites have not been properly documented. Either the studies are limited to crystallographic aspects,16,17,20 or the spectroscopic-based proposals21,23 are not soundly supported by crystallographic data and/or crystal field (CF) interaction calculations.
d (No. 230) offer simultaneously non centrosymmetric dodecahedral 24c sites (A) and octahedral 16a centrosymmetric sites (M) to host Ln. An illustration of the garnet structure can be seen in the general view given in Fig. 1a. Fig. 1b shows the coordination of dodecahedral AO8 and octahedral MO6 garnet sites. Further drawings showing other atomic arrangements can be seen for instance in ref. 14. The Ln3+ distribution over 24c and 16a garnet sites is a topic which has been addressed with several purposes and under different approaches.15–23 The main factor governing the site preference of Ln3+ in the garnet structure is the ionic size, in such a way that garnets with any Ln3+ cation occupying the dodecahedral 24c site are known,15 and only the smallest size Ln3+ cations, typically Dy3+ to Lu3+ and also Y3+ or Sc3+, are able to enter into the octahedral 16a site, even up to its complete filling, but in this case a 24c cation with a considerably large size, for example Ca2+ in the germanate series Ca3Ln2Ge3O12,18 including Ca3Y2Ge3O12,20 is required, thus the relative sizes of 24c and 16a cations also play a role. The presence of Yb3+ in both garnet sites would offer the possibility of having the MD probe and ED reference ions in the same tested volume minimizing uncertainties related to excitation and detection processes, but so far the properties of Yb coexisting in both garnet sites have not been properly documented. Either the studies are limited to crystallographic aspects,16,17,20 or the spectroscopic-based proposals21,23 are not soundly supported by crystallographic data and/or crystal field (CF) interaction calculations.
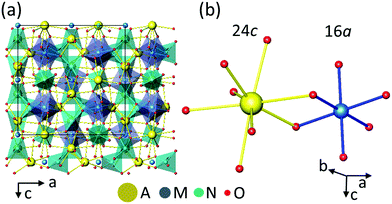 | ||
| Fig. 1 (a) General view of the A3M2N3O12 garnet structure. (b) Oxygen coordinations of the AO8 24c dodecahedra and MO6 16a octahedra. | ||
In this work we present the first report and characterization of the 2F5/2(n′) ↔ 2F7/2(n) MD transitions of Yb3+ at the octahedral 16a (centrosymmetric C3i symmetry) site of the CaNbGa garnet (thereafter CNGG). The host selection is based on the large Ca2+ ionic size filling the dodecahedral site, see before, while a large variety of ionic filling (Nb5+, Ga3+ and even vacancies) is found for the octahedral and tetrahedral sites of this garnet composition. The occupancy of the 24c dodecahedral site of the CNGG garnet by Yb3+ is well documented from both crystallographic and spectroscopic points of view.24–27
The emphasis of the present work is the study of Yb3+ in the octahedral 16a CNGG garnet site. Through low temperature (6 K) optical absorption (OA) and photoluminescence (PL) spectra followed by the modeling of CF interactions, it has been possible to establish the sequence of 16a Yb3+ energy levels as a well-separated set with regards to those of Yb3+ at the 24c dodecahedral site. The lifetime associated with the 16a Yb3+ 2F5/2 → 2F7/2 MD emissions has been also measured, and the MD branching ratio has been calculated as βMD = 50%, a value that equals those of previously indicated for Yb3+ in centrosymmetric sites of fluoride-based hosts.12 Furthermore, by using their different kinetics, ED and MD Yb3+ PL contributions have been separated even at room temperature (RT), opening the possibility of its application as a sensor for the magnetic field radiation in plasmonic systems.
2. Methods
2.1 Crystal growth
The crystal precursor polycrystalline material with a nominal cationic composition Ca2.991Yb0.009Nb1.6875Ga3.1875 (0.3 at%Yb:CNGG) was prepared by mixing CaCO3 (Alfa Aesar 99.5%), Yb2O3 (99.99%, acquired through Shangai Zimei International Co., Ltd), Nb2O5 (Aldrich 99.9%) and Ga2O3 (Aldrich 99.99%) in a 36.33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.21
0.21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 27.21
27.21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 36.25 weight% ratio. This off-stoichiometry formula is within the composition range with congruent melting that allows garnet crystal growth from the melt.28 The mixture was heated in air to 1648–1673 K for several hours with intermediate regrinding. The garnet phase purity of the synthesized crystal precursor material was checked at RT using powder X-ray diffraction using a Bruker AXS D-8 Advance diffractometer with Cu Kα radiation. From this polycrystalline powder the single crystal was grown in air by the Czochralski technique. For this purpose we used a Cyberstar crystal growth equipment incorporating a radiofrequency (RF) coil fed by a Huttinger TruHeat MF 3020 power supply operated at 9.2 kHz. The crucible (40 mm in diameter and height) was made of platinum, and a platinum wire was used as the seed, which was rotated and pulled simultaneously. Samples for optical purposes were obtained by crystal cutting and polishing using conventional methods.
36.25 weight% ratio. This off-stoichiometry formula is within the composition range with congruent melting that allows garnet crystal growth from the melt.28 The mixture was heated in air to 1648–1673 K for several hours with intermediate regrinding. The garnet phase purity of the synthesized crystal precursor material was checked at RT using powder X-ray diffraction using a Bruker AXS D-8 Advance diffractometer with Cu Kα radiation. From this polycrystalline powder the single crystal was grown in air by the Czochralski technique. For this purpose we used a Cyberstar crystal growth equipment incorporating a radiofrequency (RF) coil fed by a Huttinger TruHeat MF 3020 power supply operated at 9.2 kHz. The crucible (40 mm in diameter and height) was made of platinum, and a platinum wire was used as the seed, which was rotated and pulled simultaneously. Samples for optical purposes were obtained by crystal cutting and polishing using conventional methods.
2.2 Structural and compositional analyses
Due to the low Yb3+ doping (nominally 0.3 at% with regard to the dodecahedral site occupancy) of the currently studied 0.3 at%Yb:CNGG crystal, its structure should be very similar to that described for the undoped CNGG single crystal in one of our previous studies.14 So, we shall adopt the crystal formula previously determined by the refinement of single crystal X-ray diffraction (XRD) data, i.e. {Ca0.985□D}3[Nb0.625Ga0.372□O]2(Ga0.821Nb0.102□T)3O12, □ stating for vacancies at 24c dodecahedral (curly brackets), 16a octahedral (square brackets) and 24d tetrahedral (parentheses) sites.The low concentration of Yb in the studied garnet prevents their compositional determination using XRD or X-ray fluorescence methods. However, these methods were successfully used for heavily (>10 at%) Yb-doped crystals. Thus, the actual Yb content of the used 0.3 at%Yb:CNGG crystal was determined by comparison of the integrated RT OA in this and in heavily Yb-doped crystals. This methodology provides a 0.08 at%Yb content for the grown crystal with regards to the dodecahedral occupancy.
2.3 Spectroscopic techniques
OA in the visible and NIR region was determined by using a Varian spectrophotometer, model Cary 5E, with a limiting spectral resolution of 0.04 nm at λ ≈ 1000 nm. An extensive 6 K OA study in the whole visible region using a thick (≈5.1 mm) 0.3 at%Yb:CNGG sample discarded the contamination with any Ln different to the studied Yb3+. PL was excited either in a continuous wave (cw) with a tunable Ti-sapphire laser or pulsed (10 Hz) with a tunable Quanta-Ray MOPO-HF system providing ns laser pulses. PL light was dispersed in a SPEX (f = 34 cm) spectrometer and detected using a 77 K cooled Ge photodiode in cw experiments, or with a Hamamatsu InP/InGaAs phototube (model H10330A-75) in lifetime measurements and time-resolved spectroscopy. In cw PL experiments the laser beam was chopped at ≈200 Hz and the PL signal recovered with a lock-in amplifier. Yb3+ lifetime measurements were carried out using a thin crystal plate (60 μm) in order to minimize emission reabsorption. Time-resolved spectroscopy was discriminated by a Stanford Research SR400 photon counter. For 6 K optical spectroscopic measurements a He close-cycle cryostat connected to a suitable temperature controller was used.3. Results
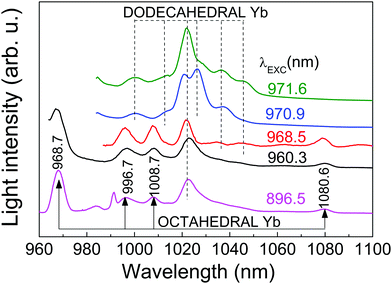
The OA and PL spectra of Yb3+ in the CNGG host originate from electronic transitions between ground 2F7/2 and excited 2F5/2 Yb3+ multiplets. Both, the D2 and C3i local symmetries of the dodecahedral 24c and octahedral 16a garnet sites, respectively, split these multiplets into four 2F7/2 (n = 0, 1, 2, 3) and three 2F5/2 (n′ = 0′, 1′, 2′) Kramers doublets.The Yb3+ spectra of heavily doped (>1 at%Yb) CNGG crystals have been previously studied in detail.14,24–27 So far, the crystallographic and spectroscopic studies only provided evidence for Yb incorporation in the dodecahedral 24c site. The 6 K OA and PL spectra consist in inhomogeneously and thermally broadened bands which hamper the accurate determination of some Yb3+ energy levels. Fig. 2 and 3 show selected examples of the optical contributions of dodecahedral Yb in CNGG, while a more extensive dodecahedral Yb spectroscopic review is provided in the ESI.†
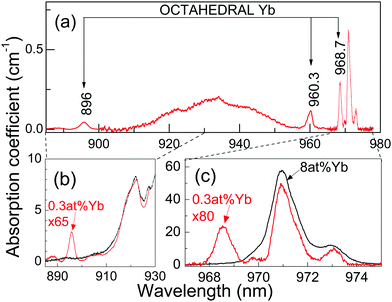
The only well resolved band in the 6 K spectra of 8 at%Yb:CNGG crystals is 2F7/2(0) ↔ 2F5/2(0′) (shortly, 0 ↔ 0′) at λ = 970.9 nm (see Fig. 2c). Even this band is largely broadened by the different crystalline environments coexisting around the dodecahedral 24c site of Yb3+, since the spectral position of this 0 ↔ 0′ transition is mainly related to the electric charge of cations/vacancies occupying the two edge-sharing tetrahedra at the shortest distance (∼3.12 Å) from the central 24c Yb3+.24 In fact, the small OA band at λ = 973 nm corresponds to a dodecahedral Yb3+ center linked to a vacant edge-sharing tetrahedron.24
The 6 K OA (Fig. 2) and PL (Fig. 3) spectra of the 0.3 at%Yb:CNGG crystal show bands not observable in the corresponding spectra for heavily doped >1 at%Yb:CNGG crystals. The new well-resolved OA bands peak at 968.7 nm (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 323 cm−1), 960.3 nm (10
323 cm−1), 960.3 nm (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 413 cm−1) and 896 nm (11
413 cm−1) and 896 nm (11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 161 cm−1), while characteristic PL emissions at 968.7 nm, 996.7 nm, 1008.7 nm and 1080.6 nm are observed when exciting any of the three above listed OA bands (see Fig. 3). The absorption intensity of this new band set reaches 40% when the 968.7 nm new OA is compared with that of the dodecahedral Yb 0 ↔ 0′ transition at λ = 970.9 nm, see Fig. 2c. These new OA and PL band sets indicate the actual presence of a second type of Yb center coexisting in the garnet structure with the main dodecahedral Yb3+ center but with a much lower solubility limit, and thus, although present with low density, its contribution is not observable in the spectrum of the heavily doped Yb:CNGG crystals. In the following we show that this new center is compatible with the assumption of Yb3+ located at the octahedral 16a garnet site, and hereafter we shall refer to it as octahedral Yb.
161 cm−1), while characteristic PL emissions at 968.7 nm, 996.7 nm, 1008.7 nm and 1080.6 nm are observed when exciting any of the three above listed OA bands (see Fig. 3). The absorption intensity of this new band set reaches 40% when the 968.7 nm new OA is compared with that of the dodecahedral Yb 0 ↔ 0′ transition at λ = 970.9 nm, see Fig. 2c. These new OA and PL band sets indicate the actual presence of a second type of Yb center coexisting in the garnet structure with the main dodecahedral Yb3+ center but with a much lower solubility limit, and thus, although present with low density, its contribution is not observable in the spectrum of the heavily doped Yb:CNGG crystals. In the following we show that this new center is compatible with the assumption of Yb3+ located at the octahedral 16a garnet site, and hereafter we shall refer to it as octahedral Yb.
Therefore, from the OA and PL bands experimentally determined for the octahedral Yb3+ center in CNGG, the complete set of Yb3+ energy levels can be established as 0, 290, 410 and 1069 cm−1 for the ground 2F7/2 (0, 1, 2, 3), and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 323, 10
323, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 413 and 11
413 and 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 161 cm−1 for the excited 2F5/2 (0′, 1′, 2′) multiplets.
161 cm−1 for the excited 2F5/2 (0′, 1′, 2′) multiplets.
In a further attempt to correlate these energy levels with the octahedral C3i (≡S6) symmetry of the 16a garnet site, a parametrization of CF effects in this site has been carried out. Since the large number of CF parameters accounting for the C3i symmetry makes it unrealistic for any CF modeling to reproduce the sequence of Yb3+ energy levels, the often followed “descent of symmetry” procedure has considered the tetragonal bypiramidal D4h symmetry as the better approach, i.e. the higher symmetry polyhedron with coordination number CN = 6 that can be regarded as a distortion of an octahedron Oh whose fourfold rotation axis is chosen as the main axis. For the D4h symmetry the CF potential is described by B20, B40, B44, B60 and B64 CF parameters, preliminary Oh, B40 and B60 being the only independent parameters whose values were initially obtained by using the semi-empirical Simple Overlap Model.29 Details of the procedure for the CF parametrization of 16a Yb3+ energy levels in CNGG are given in the ESI.† The energy levels of 16a Yb3+ in CNGG were adequately reproduced by using the set of free ion and D4h CF parameters included in Table 1.
| Parameter | Yb3+ energy levels | |||
|---|---|---|---|---|
| Label | Observed (cm−1) | Calculated (cm−1) | ||
| E 0 | 4809.4 | 2F7/2(0) | 0 | −3.4 |
| ζ | 2905.3 | 2F7/2(1) | 290 | 288 |
| B 20 | −64 | 2F7/2(2) | 410 | 409 |
| B 40 | 2375 | 2F7/2(3) | 1069 | 1076 |
| B 44 | 1844 | 2F5/2(0′) | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 323 323 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 328 328 |
| B 60 | −210 | 2F5/2(1′) | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 413 413 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 416 416 |
| B 64 | 251 | 2F5/2(2′) | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 161 161 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 153 153 |
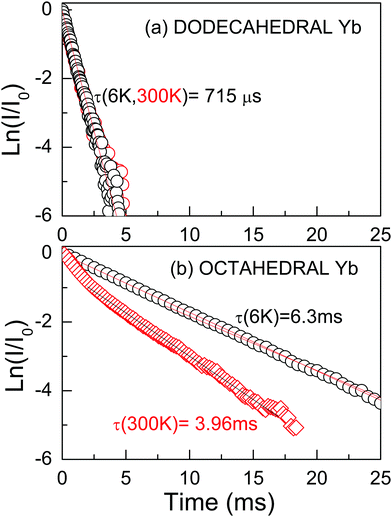
The 2F5/2 Yb3+ PL intensity decay kinetics has been also studied as a further signature of the different symmetry of the two (octahedral and dodecahedral) Yb3+ centers observed in the 0.3 at%Yb:CNGG crystal. The 2F5/2 Yb3+ PL time constant (τ) after 970–973 nm excitation through the 2F7/2(0) → 2F5/2(0′) Yb3+ transition in the dodecahedral centers was shown to vary in the τ = 800–450 μs range depending on the selected excitation/emission wavelength, i.e. the inhomogenously modified dodecahedral center selected.24 The increase of the Yb concentration further reduces this time constant. An example of the PL kinetics is shown in Fig. 4a.
The octahedral Yb center of the 0.3 at%Yb:CNGG crystal exhibits completely different PL intensity decay kinetics, see Fig. 4b. Its time extent widely covers the 10 ms range, it is more sensitive to the sample heating from 6 K to RT than in the dodecahedral case and most often a non-single exponential behavior is observed. The PL decay kinetics excited at λEXC = 960.3 nm are basically independent of the monitored wavelength (λEMI = 968.7 nm, 996.7 nm, 1008.7 nm or 1080.6 nm), see the ESI† (Fig. S4). They most typical show a fast decay for t < 2 ms and later a rather slow decay for the rest of the monitored time. This is understood as the overlapped contributions of the dodecahedral (short-lived) and octahedral (long-lived) Yb3+ centers. The long time tail of the decay can be fit to a single exponential law with a time constant τ ≈ 6–7 ms at 6 K and τ ≈ 4 ms at 300 K, i.e. the PL lifetime of the octahedral Yb3+ center is nearly one order of magnitude larger than that of the dodecahedral Yb one in the same crystal. This strong difference is consistent with the expected ED or MD Yb3+ PL contributions of these centers. For the non-centrosymmetric 24c D2 dodecahedral site the contribution of ED transitions is expected to dominate the PL emission; thus the obtained 2F5/2 Yb3+ lifetime is in the range observed for crystals hosting Yb3+ in similar non-centrosymmetric sites, like YAG, τ ≈ 950 μs,30 NaLn(WO4)2τ ≈ 300–500 μs,31 or LnVO4τ ≈ 250–350 μs.32 However, as stated in the Introduction, the presence of a center of symmetry forbids ED transitions, thus MD ones are observed with similar or even larger intensities than for the ED contributions. Such MD transitions are characterized by long PL lifetimes, thus the much larger lifetime obtained for the so-called Yb octahedral center may be regarded as the ultimate probe of the occupancy by Yb3+ in the centrosymmetric 16a crystal site of the CNGG host.
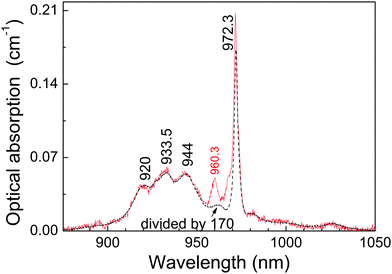
Once the origin of the described OA and PL features of the 0.3 at%Yb:CNGG crystal has been clarified thanks to 6 K spectroscopy, its application as a probe of plasmonic induced radiation fields requires operation at RT. Fig. 5 shows a comparison of the OA spectra corresponding to 0.3 at% and 11.6 at%Yb:CNGG crystals, the spectroscopy of the latter being purely dominated by the dodecahedral Yb3+ contributions. It is obvious that excitation of the octahedral Yb3+ center at RT through its 0 → 0′ transition at λ = 968.7 nm is not possible because with increasing temperature the relative intensity of this band decreases and overlaps with the 0 → 0′ (at λ = 972.3 nm) band tail corresponding to the dodecahedral Yb3+ center. However, the comparison of the spectra at both Yb doping concentrations shows that the octahedral Yb3+ 0 → 1′ transition at λ = 960.3 nm is clearly resolved from the background dodecahedral Yb contribution, the latter amounts to about 50% at this wavelength. Although the standard (integrated over time) cw PL spectra show little difference for excitation at the octahedral Yb3+ (λ = 960.3 nm) or in the side bands corresponding to the dodecahedral Yb3+ centers (see Fig. S3, ESI†), taking advantage of the different PL kinetics of both Yb3+ garnet centers, time-resolved spectroscopy can disclose the separate contributions of these two Yb3+ garnet centers.
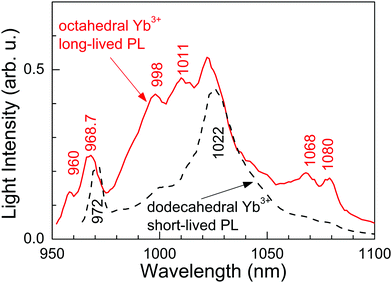
Fig. 6 shows the RT time-resolved PL emission obtained for different delays and gate widths after the laser pulse (<5 ns of duration, tuned at λ = 960.3 nm) excitation. For short times (5 μs of delay and 250 μs of gate width) the PL is dominated by the short-lived ED contributions of the dodecahedral Yb3+ center. Correspondingly, the emission spectrum shows a broad peak at 1022 nm characteristic of the PL observed in highly doped Yb:CNGG,24,26 which is also shown in Fig. 3 (λEXC = 971.6 nm). However, over a long time (2.5 ms of delay and 8 ms of gate width) the spectrum is quite different, and matches the emission of the octahedral Yb3+ shown in Fig. 3. Although the contribution of the λ = 1022 nm band is still present, this PL spectrum contains four well resolved emissions at λ = 998, 1011, 1068 and 1080 nm, with intensities 2.80, 2.56, 2.94 and 3.76 times those corresponding to the dodecahedral Yb3+ contributions at the same wavelengths, respectively. The origin of the 1068 nm RT emission is related to the thermal redistribution of the 2F5/2 electronic population, and corresponds to the 2F5/2(1′) → 2F7/2(3) transition of the octahedral Yb3+ center.
4. Discussion
From 6 K OA and the excitation/emission PL spectra shown in Fig. 2 and 3, it has been disclosed that along the predominant dodecahedral Yb3+ optical center associated with 24c D2 symmetry in YAG-like garnets, another minority Yb3+ center with very different spectroscopic characteristics coexists in the 0.3 at%Yb:CNGG crystal.Several CF considerations support the above conclusion. On one side, the experimental energies determined for the mJ levels of the so called 16a octahedral Yb3+ center are well reproduced by using a CF parameter set describing a centrosymmetric center, see Table 1. On the other side, the absolute CF splittings of 1069 cm−1 and 838 cm−1 for ground 2F7/2 and excited 2F5/2 Yb3+ multiplets and their corresponding barycenters, lying at 442 cm−1 and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 632 cm−1 energies, respectively, are consistent with those found in other 6-fold oxygen coordinated Yb ionic oxides: in Yb-doped sexquioxides the 2F7/2 splitting ranges from 1193 cm−1 in Lu2O3,33 to 1076 cm−1 in Sc2O3.34 ΔE(2F7/2) = 1023 cm−1 is found for Ca4YO(BO3)3 (with 6O-Yb-2B coordination),35 964 cm−1 in Y2SiO5,34 and 900 cm−1 in Ba3Lu(BO3)3.34 Smaller ΔE(2F7/2) values in 6-fold oxygen coordinated Yb compounds are also found, for instance 788 cm−1 in LiNbO3,36 or even below 600 cm−1 in Yb metalorganic complexes,37 indicating a reduction of the CF strength on Yb3+. In the latter case, a reduction of the effective Yb charge due to covalent bonds of oxygen to the neighboring organic ligands may contribute to the observed CF reduction, while in ionic crystals such CF strength reductions are partially ascribed to larger Yb3+ bond distances.
632 cm−1 energies, respectively, are consistent with those found in other 6-fold oxygen coordinated Yb ionic oxides: in Yb-doped sexquioxides the 2F7/2 splitting ranges from 1193 cm−1 in Lu2O3,33 to 1076 cm−1 in Sc2O3.34 ΔE(2F7/2) = 1023 cm−1 is found for Ca4YO(BO3)3 (with 6O-Yb-2B coordination),35 964 cm−1 in Y2SiO5,34 and 900 cm−1 in Ba3Lu(BO3)3.34 Smaller ΔE(2F7/2) values in 6-fold oxygen coordinated Yb compounds are also found, for instance 788 cm−1 in LiNbO3,36 or even below 600 cm−1 in Yb metalorganic complexes,37 indicating a reduction of the CF strength on Yb3+. In the latter case, a reduction of the effective Yb charge due to covalent bonds of oxygen to the neighboring organic ligands may contribute to the observed CF reduction, while in ionic crystals such CF strength reductions are partially ascribed to larger Yb3+ bond distances.
Even when the same Yb3+ coordination occurs in a given material the site symmetry influences the 2S+1LJ multiplet splitting. Sesquioxides sharing 6-fold oxygen coordinated Yb3+ with and without a center of symmetry are a case similar to the present 0.3 at%Yb:CNGG that can guide us for the spectroscopic assignments. While efforts have been made in the assignment of usually experimentally incomplete Yb3+ energy level sets both for C2 and C3i Yb centers of cubic sesquioxides,38,39 mainly through the application of the barycenter plot law,34 only CF analyses of 24c dodecahedral Yb3+ energy levels have been attempted for garnet hosts.40,41 These previously known data for cubic sesquioxides indicate that CF splittings of 2F7/2 and 2F5/2 are always wider and their corresponding barycenters are located at higher energies for centrosymmetric C3i Yb3+ centers than for the C2 ones, see Table 2 in ref. 38 and the ESI† (Table S1). The above indicated splittings for the C3i 16a Yb3+ center in the 0.3 at%Yb:CNGG crystal are considerably larger than those of Yb3+ in the noncentrosymetric D2 24c site in other garnet hosts, for instance, 766 cm−1 and 352 cm−1 for 2F7/2 and 2F5/2, respectively, in YbAG, or 624 cm−1 and 434 cm−1 for YbGG, see Table S2 (ESI†). It could be assumed that larger CF splitting amplitudes for the centrosymmetric C3i 16a Yb3+ center are associated with the cooperative effect of considerably smaller bond distances for 16a Yb3+ than for Yb3+ in the dodecahedral environment as well as with an increase of the symmetry in the 16a center with regard to the 24c one.
The solubility limit for Yb3+ incorporation at 16a positions in the CNGG crystal is rather low, obviously below 0.3 at% of the dodecahedral site. From the facts that the background optical absorption at λ = 960.3 nm of dodecahedral Yb3+ centers in the 0.3 at%Yb:CNGG crystal is about 50% of the total, see Fig. 5, and that the total Yb content was estimated from OA comparison as 0.08 at% of the dodecahedral site, the Yb density in the octahedral 16a garnet site can be roughly estimated to be ≈5 × 1018 cm−3. Such a low limit is in fact expected due to the large Yb3+ ionic radii (0.868 Å for VI coordination) compared to those of Nb5+ and Ga3+ (0.64 Å and 0.62 Å, respectively, also for VI coordination). Due to the low solubility limit for Yb incorporation in the octahedral garnet site, direct evidence of corresponding MD transitions in the OA spectrum will diminish with the increase of Yb content in the crystal, and in fact the same OA bands from 16a Yb3+ can be also perceived with very low intensity in the 77 K OA spectrum of the 2 at%Yb:CNGG crystal reported by Voronko et al.,25 while they are no longer observed in the OA spectrum of the 8 at%Yb:CNGG crystal, see Fig. 2b, since for these latter crystals ED transitions of Yb3+ in the dodecahedral garnet site have intensities several orders of magnitude stronger than those of the MD of Yb3+ in the octahedral garnet site.
Given that forced ED intraconfigurational f–f Ln3+ transitions from the centrosymmetric sites are strictly forbidden, the 2F5/2 → 2F7/2 emission from 16a Yb3+ has a predominant MD character. Consequently, Yb:CNGG is able to provide simultaneously well-differentiated sets of Yb3+ 2F7/2 ↔ 2F5/2 ED and MD transitions, arising from 24c and 16a garnet sites, respectively.
The evaluation of the MD contribution of the 16a Yb3+ 2F5/2(0′) → 2F7/2(1, 2, 3) (λEMI = 996.7, 1008.7 and 1080.6 nm) transitions can be performed by comparing the total decay rate derived from the measured lifetime value, Γtotal = 1/τ, with the MD spontaneous emission rate, AMD = A′MD × nr3, where the vacuum value A′MD is predicted in ref. 12 and nr = 1.96 is the measured refractive index for CNGG at λ ≈ 1000 nm.14 The MD branching ratio, defined as βMD = AMD/Γtotal, results in βMD ≈ 50% for 16a Yb3+ in CNGG if the room temperature center lifetime is taken as τ ≈ 4 ms, see Fig. 4b. This value is similar to previous βMD values indicated for the 2F5/2(0′) → 2F7/2(0) Yb3+ emission in crystals hosting Yb3+ in lattice sites with a center of symmetry, such as SrF2, Rb2NaYF6 or ScBO3.12 Such crystals are difficult to grow and are not easily available with specific Yb doping, while unfortunately the MD branching ratio of Yb3+ in standard YAG is only 10.8%.12 Therefore, even though the 16a Yb3+ center is present in the CNGG garnet with a low density, the strong MD character of its transitions makes them observable, which highlights the interest of the 0.3 at%Yb:CNGG crystal to be used for probing local magnetic fields in plasmonic resonances and metamaterials.
5. Conclusions
A new centrosymmetric octahedral Yb3+ center has been identified in the disordered CaNbGa garnet crystal with spectroscopic properties clearly different, both at 6 K and 300 K, from the usual dodecahedral Yb3+ center found in this and similar garnets. This new center, which shows favorable properties to be used as a probe for the intensity of magnetic fields radiated by plasmonic structures, operates around λ = 1 μm which is a good compromise for lithographic fabrication and optical detection techniques. It is characterized by 2F7/2(0–3) = 0, 290, 410, 1069 cm−1 and 2F5/2(0′–2′) = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 323, 10
323, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 413, 11
413, 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 161 cm−1 Yb3+ mJ energy levels, which are consistent with the large CF splittings and barycenter energies expected for centrosymetric Yb3+ centers in ionic compounds, their individual positions being well reproduced by a CF simulation assuming a lower, but still with inversion center, D4h symmetry.
161 cm−1 Yb3+ mJ energy levels, which are consistent with the large CF splittings and barycenter energies expected for centrosymetric Yb3+ centers in ionic compounds, their individual positions being well reproduced by a CF simulation assuming a lower, but still with inversion center, D4h symmetry.
The probe center can be operated at room temperature by excitation at λ = 960.3 nm and with best sensitivity detection near λ = 1080 nm, although other additional detection channels are found at λ = 998, 1011 and 1068 nm. The coexistence of dodecahedral and octahedral Yb3+ centers in the same crystal with roughly similar densities allows the detection of reference ED and signal MD PL contributions corresponding to the above centers, respectively. Separation of both contributions has been conveniently made by using time-resolved spectroscopy, since ED Yb3+ PL is short-lived (τ < 0.8 ms) and the MD one is long-lived (τ ≈ 4 ms). The measured MD branching ratio in the studied garnet, β ≈ 50%, is equivalent to those previously reported in other centrosymmetric hosts, but the easy growth in air of the present CaNbGa garnet with congruent melting at ≈1470 °C will facilitate the fabrication of the required plasmonic or metamaterial structures in comparison for instance with Y2O3 whose crystal availability is very limited due to its high melting point of ≈2490 °C.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by the Spanish Ministry of Economy and Competitiveness and by the European Regional Development Fund through project RTI2018-094859-B-I00. CSIC support for Open Access publication and advice of Prof. Rafael Valiente on time-resolved spectroscopic measurements are acknowledged.References
- W. T. Carnall, P. R. Fields and K. Rajnak, J. Chem. Phys., 1968, 49, 4424 CrossRef CAS.
- Q. Thommen and P. Mandel, Opt. Lett., 2006, 31, 1803 CrossRef CAS PubMed.
- N. Noginova, G. Zhu, M. Mavy and M. A. Noginov, J. Appl. Phys., 2008, 103, 07E901 CrossRef.
- N. Noginova, Y. Barnakov, H. Li and M. A. Noginov, Opt. Express, 2009, 17, 10767 CrossRef CAS PubMed.
- N. Yang, Y. Tang and A. E. Cohen, Nano Today, 2009, 4, 269 CrossRef CAS.
- X. Ni, G. V. Naik, A. V. Kildishev, Y. Barnakov, A. Boltasseva and V. M. Shalaev, Appl. Phys. B: Photophys. Laser Chem., 2011, 103, 553 CrossRef CAS.
- T. H. Taminiau, S. Karaveli, N. F. van Hulst and R. Zia, Nat. Commun., 2012, 3, 979 CrossRef PubMed.
- S. Karaveli and R. Zia, Opt. Lett., 2010, 35, 3318 CrossRef CAS PubMed.
- S. Karaveli and R. Zia, Phys. Rev. Lett., 2011, 106, 193004 CrossRef PubMed.
- M. Kasperczyk, S. Person, D. Ananias, L. D. Carlos and L. Novotny, Phys. Rev. Lett., 2015, 114, 163903 CrossRef PubMed.
- C. M. Dodson, J. A. Kurvits, D. Li, M. Jiang and R. Zia, Opt. Mater. Express, 2014, 4, 2441 CrossRef CAS.
- C. M. Dodson and R. Zia, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 125102 CrossRef.
- L. DeLoach, S. Payne, L. Chase, L. Smith and W. Kway, IEEE J. Quantum Electron., 1993, 29, 1179 CrossRef CAS.
- E. Castellano-Hernández, M. D. Serrano, R. J. Jiménez-Riobóo, C. Cascales, C. Zaldo, A. Jezowski and P. A. Loiko, Cryst. Growth Des., 2016, 16, 1480 CrossRef.
- S. Geller, Z. Kristallogr., 1967, 125, S1 CrossRef (and refs. therein).
- L. Suchow, M. Kokta and V. J. Flynn, J. Solid State Chem., 1970, 2, 137 CrossRef CAS.
- L. Suchow and R. Mondegarian, J. Solid State Chem., 1973, 6, 553 CrossRef CAS.
- B. V. Mill’, Sov. Phys. Crystallogr., 1975, 19, 653 Search PubMed.
- M. Asano and J. A. Koningstein, Chem. Phys., 1979, 42, 369 CrossRef CAS.
- D. Lévy and J. Barbier, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1999, 55, 1611 CrossRef.
- M. O. Ramírez, L. E. Bausá, E. Cavalli and E. Bovero, J. Appl. Phys., 2006, 99, 013507 CrossRef.
- H. G. Liu, W. C. Zheng and W. L. Feng, Philos. Mag., 2008, 88, 3075 CrossRef CAS.
- A. Kaminska, M. G. Brik, G. Boulon, M. Karbowiak and A. Suchocki, J. Phys.: Condens. Matter, 2010, 22, 255501 CrossRef CAS PubMed.
- M. D. Serrano, J. O. Álvarez, C. Zaldo, J. Sanz, I. Sobrados, J. A. Alonso, C. Cascales, M. T. Fernández-Díaz and A. Jezowski, J. Mater. Chem. C, 2017, 5, 11481 RSC.
- Y. K. Voronko, A. V. Popov, A. A. Sobol and S. N. Ushakov, Inorg. Mater., 2006, 42, 1133 CrossRef CAS.
- V. E. Shukshin, Phys. Wave Phenom., 2009, 17, 165 CrossRef.
- V. Lupei, A. Lupei, C. Gheorghe, L. Gheorghe, A. Achim and A. Ikesue, J. Appl. Phys., 2012, 112, 063110 CrossRef.
- K. Shimamura, M. Timoshechkin, T. Sasaki, K. Hoshikawa and T. Fukuda, J. Cryst. Growth, 1993, 128, 1021 CrossRef CAS.
- P. Porcher, M. C. dos Santos and O. Malta, Phys. Chem. Chem. Phys., 1999, 1, 397 RSC.
- D. S. Sumida and T. Y. Fan, Opt. Lett., 1994, 19, 1343 CrossRef CAS PubMed.
- E. V. Zharikov, C. Zaldo and F. Díaz, MRS Bull., 2009, 34, 271 CrossRef CAS (and refs. therein).
- J. Liu, X. Mateos, H. Zhang, J. Wang, M. Jiang, U. Griebner and V. Petrov, Opt. Lett., 2005, 30, 3162 CrossRef CAS PubMed.
- D. C. Brown, Z. Fleischman, L. D. Merkle, L. D. Sanjeewa, C. D. McMillen and J. W. Kolis, Appl. Phys. B: Photophys. Laser Chem., 2020, 126, 62 CrossRef CAS.
- P. Haumesser, R. Gaumé, B. Viana, E. Antic-Fidancev and D. Vivien, J. Phys.: Condens. Matter, 2001, 13, 5427 CrossRef CAS.
- A. Lupei, G. Aka, E. Antic-Fidancev, B. Viana, D. Vivien and P. Aschehoug, J. Phys.: Condens. Matter, 2002, 14, 1107 CrossRef CAS.
- E. Montoya, J. A. Sanz-García, J. Capmany, L. E. Bausá, A. Diening, T. Kellner and G. Huber, J. Appl. Phys., 2000, 87, 4056 CrossRef CAS.
- J. Wang, J. J. Zakrzewski, M. Heczko, M. Zychowicz, K. Nakagawa, K. Nakabayashi, B. Sieklucka, S. Chorazy and S. Ohkoshi, J. Am. Chem. Soc., 2020, 142, 3970 CrossRef CAS PubMed (and ref. 78 and 79 therein).
- Y. Guyot, M. Guzik, G. Alombert-Goget, J. Pejchal, A. Yoshikawa, A. Ito, T. Goto and G. Boulon, J. Lumin., 2016, 170, 513 CrossRef CAS.
- E. Antic-Fidancev, J. Holsa and M. Lastusaari, J. Phys.: Condens. Matter, 2003, 15, 863 CrossRef CAS.
- L. Hong-Gang, Z. Wen-Chen and F. Wen-Lin, J. Lumin., 2010, 130, 103 CrossRef.
- L. Hong-Gang, G. Paweł and R. Czesław, J. Lumin., 2011, 131, 2690 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: (i) Detailed comparative optical spectroscopy of dodecahedral and octahedral Yb3+ centers in CNGG crystals. (ii) Detailed procedures of crystal field analyses applied to octahedral Yb3+ centers in 0.3 at%Yb:CNGG crystals. (iii) Crystal field splitting of 2FJ Yb3+ levels and the barycenter law. See DOI: 10.1039/d0tc01608j |
| This journal is © The Royal Society of Chemistry 2020 |