The origin and nature of killer defects in 3C-SiC for power electronic applications by a multiscale atomistic approach†
Abstract
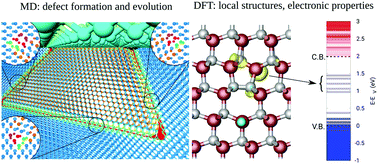
3C-SiC epitaxially grown on Si displays a large wealth of extended defects. In particular, single, double and triple stacking faults (SFs) are observed to coexist in several experiments. Overabundance of defects has so far limited the exploitation of 3C-SiC/Si for power electronics, in spite of its several ideal properties (mainly in terms of the wide gap, high breakdown fields and thermal properties) and the possibility of direct integration in the Si technology. Here we use a multiscale approach, based on both classical molecular dynamics (MD) simulations and first-principles calculations, for the in-depth investigation of the origin, nature and properties of most common 3C-SiC/Si(001) extended defects. Our MD simulations reveal a natural path for the formation of partial dislocation complexes terminating both double and triple SFs. The MD results are used as an input for superior DFT calculations, allowing us to better determine the core structure and to investigate electronic properties. It turns out that the partial dislocation complexes terminating double and triple SFs are responsible for the introduction of electronic states significantly filling the band gap. On the other hand, individual partial dislocations terminating single SFs only induce states very close to the gap edge. We conclude that partial dislocation complexes, in particular the most abundant triple ones, are killer defects in terms of favoring leakage currents. Suggestions coming from theory/simulations for devising a strategy to lower their occurrence are discussed.


 Please wait while we load your content...
Please wait while we load your content...