Using resonant energy X-ray diffraction to extract chemical order parameters in ternary semiconductors†
Abstract
II–IV–V2 materials, ternary analogs to III–V materials, are emerging for their potential applications in devices such as LEDs and solar cells. Controlling cation ordering in II–IV–V2 materials offers the potential to tune properties at nearly fixed compositions and lattice parameters. While tuning properties at a fixed lattice constant through ordering has the potential to be a powerful tool used in device fabrication, cation ordering also creates challenges with characterization and quantification of ordering. In this work, we investigate two different methods to quantify cation ordering in ZnGeP2 thin films: a stretching parameter calculated from lattice constants 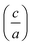 , and an order parameter determined from the cation site occupancies (S). We use high resolution X-ray diffraction (HRXRD) to determine
, and an order parameter determined from the cation site occupancies (S). We use high resolution X-ray diffraction (HRXRD) to determine 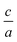 and resonant energy X-ray diffraction (REXD) to extract S. REXD is critical to distinguish between elements with similar Z-number (e.g. Zn and Ge). We found that samples with a
and resonant energy X-ray diffraction (REXD) to extract S. REXD is critical to distinguish between elements with similar Z-number (e.g. Zn and Ge). We found that samples with a 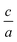 corresponding to the ordered chalcopyrite structure had only partially ordered S values. The optical absorption onset for these films occurred at lower energy than expected for fully ordered ZnGeP2, indicating that S is a more accurate descriptor of cation order than the stretching parameter. Since disorder is complex and can occur on many length scales, metrics for quantifying disorder should be chosen that most accurately reflect the physical properties of interest.
corresponding to the ordered chalcopyrite structure had only partially ordered S values. The optical absorption onset for these films occurred at lower energy than expected for fully ordered ZnGeP2, indicating that S is a more accurate descriptor of cation order than the stretching parameter. Since disorder is complex and can occur on many length scales, metrics for quantifying disorder should be chosen that most accurately reflect the physical properties of interest.


 Please wait while we load your content...
Please wait while we load your content...