Controlling the formation of heliconical smectic phases by molecular design of achiral bent-core molecules†
Abstract
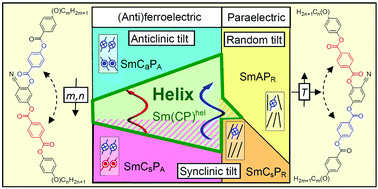
Fluids with spontaneous helical structures formed by achiral low molecular mass molecules is a newly emerging field with great application potential. Here, we explore the chemical mechanisms of the helix formation by systematically modifying the structure of a bent 4-cyanoresorcinol unit functionalized with two different phenyl benzoate based aromatic rods and terminated with two alkyl chains of variable length. The majority of these achiral compounds self-assemble, forming a short-pitch heliconical liquid crystalline phase in broad temperature ranges. In some cases, it occurs without any competing low-temperature phase. We demonstrate that the mirror symmetry broken mesophase occurs at the paraelectric–(anti)ferroelectric transition if the tilt angle of the molecules in the smectic layers is around 18–20° and if this transition coincides with a change of the tilt correlation between the layers. In the close vicinity of this transition, a field-induced heliconical phase develops as well as a new heliconical phase with polarization-randomized structure. These investigations provide a blueprint for the future design of achiral molecules capable of spontaneous mirror symmetry breaking by the formation of heliconical liquid crystalline phases.
- This article is part of the themed collection: Journal of Materials Chemistry C HOT Papers


 Please wait while we load your content...
Please wait while we load your content...