High stress-driven voltages in net-like layer-supported organic–inorganic perovskites†
Abstract
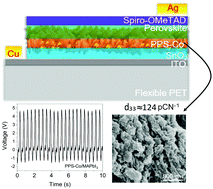
Hybrid organo-metal halide perovskites (OMHPs) have been extensively explored for photo or photo-enhanced applications, which are time, location or light-limited. Unlike in other works, herein, methylammonium lead iodide (MAPbI3) perovskite was employed as a small area (<1 cm2) stress-driven energy converter. Briefly, MAPbI3 was infiltrated into a net-like composite scaffold, having three constituents; polyvinylidene fluoride (PVDF), polylactic acid (PLA) and tin dioxide (SnO2) electrospun nanofibres. A systematic vertical ultrasonic vibration was optimized and applied to each sample, followed by ice quenching. Addition of MAPbI3 and vertical vibration altered the morphotropic phase nature of the composite towards desirable electroactive forms, without further poling, revealed by XRD, FTIR, and Raman studies. When the device was subjected to bending/compression-release forces, high output voltage of 4.82 V and current of 29.7 nA were obtained over an area of 0.0625 cm2. The champion device also registered high piezoelectric strain coefficients (d33) of 123.93 pC N−1 and 118.85 pC N−1 (with and without a SnO2 nanoparticle underlayer, respectively). We further elucidate the mechano-electrical outputs of MAPbI3 devices grown on other distinctive underlayers. This work advances the drive towards all-day–all-night energy harvesting using OMHPs, the force being applied from ubiquitous motions or artificial movements.
- This article is part of the themed collection: Editor’s choice collection: luminescent metal halides


 Please wait while we load your content...
Please wait while we load your content...