Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Dendrimeric calcium-sensitive MRI probes: the first low-field relaxometric study
Francesca
Garello
 a,
Serhat
Gündüz
b,
Sandip
Vibhute
c,
Goran
Angelovski
a,
Serhat
Gündüz
b,
Sandip
Vibhute
c,
Goran
Angelovski
 *b and
Enzo
Terreno
*b and
Enzo
Terreno
 *a
*a
aMolecular and Preclinical Imaging Centers, Department of Molecular Biotechnology and Health Sciences, University of Torino, Via Nizza 52, 10126 Torino, Italy. E-mail: enzo.terreno@unito.it
bMR Neuroimaging Agents, Max Planck Institute for Biological Cybernetics, Max-Planck-Ring 11, 72076 Tuebingen, Germany. E-mail: goran.angelovski@tuebingen.mpg.de
cPhysiology of Cognitive Processes, Max Planck Institute for Biological Cybernetics, Max-Planck-Ring 8, 72076 Tuebingen, Germany
First published on 2nd January 2020
Abstract
Different classes of small- or nano-sized calcium-sensitive probes for magnetic resonance imaging (MRI) have been proposed in the last two decades. These compounds have been developed mainly for functional MRI purposes and tested in vivo in different animal models. Most of them are paramagnetic systems that change their relaxivity in the presence of the divalent ion calcium, resulting in increased T1 or T2 contrast. In this work, we report the investigation of their relaxometric behavior at low magnetic fields, specifically the comparison of the monomeric Ca-sensitive probe and the corresponding dendrimer conjugates of generations 0, 1 and 2 (G0, G1 and G2, respectively). As a result, a relaxivity hump between 10 and 100 MHz of the Larmor frequency progressively appeared with an increase in the size of the investigated contrast agent, indicative of a restricted rotational motion of the complexes as long as the size of the molecule increases. The same trend with a more pronounced effect was detectable in the presence of calcium. The relaxivity enhancement for the Ca2+ adducts, primarily caused by an increase of the hydration state of Gd3+, went from ca. 130% for the monomeric probe to ca. 310% for the G2 dendrimer conjugate at 0.5 T and 25 °C. T1 weighted magnetic resonance images acquired at 1 T displayed the strong ability of these systems to change their contrast according to the presence of calcium at this field, thus laying the basis for promising future in vivo applications.
Introduction
Molecular imaging is gaining increasing attention in clinical and preclinical research due to its ability to non-invasively visualize biological processes at the cellular and molecular levels. Among the various imaging techniques that can be employed to this end, magnetic resonance imaging (MRI) stands out among the rest because of its superlative spatial resolution (μm), ability to distinguish between hard and soft tissues, and the absence of ionizing radiation. However, the low sensitivity associated with MRI requires the use of specific contrast agents able to report on various pathophysiological processes. These agents generally act through contrast-mediated alteration of tissue relaxation-times for the detection and localization of molecular disease markers, cells and therapeutic drugs.1 Recently, many so-called smart contrast agents (SCAs), which generate contrast as a response to a change in their chemical or physical environment, have been developed.2,3 The mechanism of action of SCAs generally resides in either (1) reversible conformational changes that modulate water accessibilities to the agents' metal ions (e.g. changes in the number of coordinated water molecules in the inner-coordination sphere or in water exchange time between the inner-sphere and bulk water molecules) or (2) reversible intermolecular associations that change the agents' rotational correlation time.4,5 It must be taken into account that if these variations are faster than the relatively slow MRI acquisition timeframe, an averaging effect can be obtained, further limiting the sensitivity of the agent's response. SCAs can be sensitive to pH-variations,6–9 enzymatic activity,10–12 glucose uptake,13,14 lactate or nitric oxide concentrations,15,16 partial oxygen pressure,17 the redox status18 and metal ion coordination states19 or concentrations.3,20,21 Among SCAs responsive to metal ions, compounds sensitive to copper,22,23 zinc24,25 and calcium26,27 have been mainly developed. Monitoring metal ions by MRI, in fact, requires at least an intra- or extracellular metal ion concentration in the micromolar range, due to the intrinsic low sensitivity of the technique. Calcium and zinc, the first and second most abundant metal ions in the body, respectively, are the most attractive examples due to their sufficient concentration and irreplaceable role in neuronal signalling, muscle contraction, and enzymatic reactions (extracellular magnesium concentration is also in the micromolar range; however, this metal has been less studied, as its concentration remains constant during neuronal activity). Calcium imaging, in particular, attracts considerable interest for functional MRI applications as it can aid tracking the neuronal activity in vivo. SCAs designed for calcium real-time MRI are generally composed of a calcium chelator linked to one or two MR reporting moieties. The first paramagnetic calcium sensitive compound developed was based on the common BAPTA (1,2-bis(o-aminophenoxy)ethane-N,N,N′,N′-tetraacetic acid) calcium chelator attached to two units of the highly paramagnetic Gd3+ complex of 1,4,7,10 tetraazacyclododecane-1,4,7-tricarboxylic acid (Gd-DO3A).28 Subsequently, SCAs composed of a modified EGTA chelator linked to two macrocyclic DO3A-derived moieties that bear a pair of Gd3+ ions were synthesized, resulting in excellent relaxivity performance.29 A recent study with this smart probe demonstrated the capability to detect and monitor the time course of cerebral ischemia, thus announcing the exciting prospects of this class of functional biomarkers for future advancements in molecular imaging.30Development of even more potent SCAs with appropriate biocompatibility is desired in order to progress further in functional MRI. To this end, existing probes may undergo synthetic modifications that lead to improved properties for their future application. In such cases, the EGTA-derived chelator remains a standard building block for the preparation of Ca-sensitive SCAs, due to its very high selectivity towards calcium. On the other hand, the existence of two macrocyclic chelators provides sufficient flexibility for various structural alterations in SCAs, which may result in different types of multimeric and nanosized systems.3,20 Following the initial preparation of the potent SCA mentioned above, this bifunctional chelator was synthetically modified and coupled to the poly(amidoamine) (PAMAM) dendrimer, aiming to modulate the pharmacokinetic properties of the SCA.31 The obtained system retained calcium sensitivity and displayed a slower diffusion in rat cerebral cortex in comparison to the monomeric equivalent, thus suggesting that dendrimeric systems can have great advantages over monomeric ones. On this wave, a calcium bioresponsive generation 4 (G4) dendrimer was developed and tested at high field (7 T). Thanks to the variations of the r2/r1 ratio at different calcium concentrations, an almost four times greater signal gain per unit of time as compared to conventional T1 weighted imaging with small sized contrast agents was obtained.32 Recently, a series of novel dendrimeric calcium sensitive MRI probes were designed and examined in terms of size change, electrostatic behavior and relaxometric performance at high field (7 T). The study was carried out on different G4 dendrimers based on DO3A-, DO3A-monoamide or DOTA (1,4,7,10 tetraazacyclododecane-1,4,7,10-tetraacetic acid) complexes and indicated that a combination of changes in size, hydration number, and rigidity of the system is required to maximize an increase in the r2/r1 ratio change.33
Interestingly, all these macromolecular systems reported so far were assessed at high magnetic field (7 T). Although a specific set of properties should be expected due to their large molecular size, almost none of them were studied at low fields, except for the liposome-based SCA.34 In the present work, we aimed to add more insights into the relaxometric behaviour of calcium sensitive dendrimeric contrast agents at magnetic fields that are closer to the ones currently more diffuse in clinics (1.5 and 3 T). More specifically, we coupled monomeric SCAs to three different generations of dendrimers, G0, G1 and G2, and compared their properties in terms of calcium responsivity at 0.5 and 1 T.
Materials and methods
Synthesis of DCAs
Dendrimeric contrast agents (DCAs) were prepared following the previously reported procedure for G1 dendrimers.31 Specifically, a protected monomeric ligand L was coupled via an aryl-isothiocyanate group to the amine surface Starburst®PAMAM G0 (4 amine surface groups), G1 (8 amine surface groups) or G2 (16 amine surface groups) dendrimers to yield the dendrimer conjugates D0a, D1a and D2a, respectively. Their hydrolysis in formic acid provided the dendrimeric conjugate ligands D0b, D1b and D2b, which were complexed with Gd3+ to result in dendrimeric contrast agents DCA0, DCA1 and DCA2, respectively. Dendrimers D0-2a and D0-2b were purified by size-exclusion chromatography using Sephadex®LH-20 (bead size: 25–100 μm) and methanol or Sephadex®G-15 (bead size: 40–120 μm) and water as an eluent, respectively. DCA0-2 samples were treated with ethylenediaminetetraacetic acid (EDTA) to remove the excess of Gd3+, while formed GdEDTA and remaining EDTA were removed from DCA0-2 by centrifugation using centrifugal filter units (3 kDa molecular weight cut-off). Following the same literature procedure, the monomeric Gd3+ complex GdL was also prepared and its properties were compared to those of DCA0-2. Purity of GdL and DCA0-2 dendrimers was assessed by the Evans method on a Bruker Avance 600 spectrometer equipped with a 5 mm probe and a standard temperature control unit.35MALDI analysis
MALDI-ToF spectra were recorded at the Center for Metabolomics and Mass Spectrometry of The Scripps Research Institute, La Jolla, USA. All DCA0-2 samples were obtained as a mixture of dendrimeric products with different numbers of monomeric SCA units coupled to the dendrimer surface. Analytical data for DCA1 were reported previously.31DCA0: a mixture of products with 3 and 4 SCA monomeric units. With 3 SCA units: [M + 3Na + 3H2O]+ calcd for C142H228Gd3N37Na3O46S3(H2O)3 3880, found 3878. With 4 SCA units: [M + 4Na]+ calcd for C182H288Gd4N46Na4O60S4 4929, found 4930.
DCA2: the spectrum with broad signals indicated the presence of multiple species, and the average number of SCA monomeric units was 9. [M + 14Na + 34H2O]+ calcd for C502H828Gd9N139Na14O154S9(H2O)34 13911, found 13911.
r 1 titrations with CaCl2
GdL, DCA0, DCA1 and DCA2 were dissolved in HEPES buffer at 0.70 mM Gd3+ concentration and the pH was adjusted to 7.0 ± 0.1. Starting longitudinal relaxivity (r1,0) was measured at 21.5 MHz (0.5 T) and 25 °C on a Stelar Spinmaster (Stelar S. R. L., Mede (PV), Italy). Stepwise additions of 10 mM CaCl2 solution were then carried out for each sample, until a Ca2+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Gd3+ ratio of 2.5 was reached. Variations in longitudinal relaxivity (r1,obs) at 21.5 MHz were monitored 15 min after each addition to let the system equilibrate. The pH was maintained constant at 7.0 ± 0.1 before each measurement and addition. Nuclear magnetic relaxation dispersion (NMRD) profiles were acquired before and after the addition of CaCl2. 1H NMRD profiles were recorded at 25 °C on a Stelar Field Cycling relaxometer (FFC2000), operating at a magnetic field strength ranging from 0.01 to 20 MHz (2.4 × 10−4 to 0.47 T). The additional points measured in the range 20–70 MHz (0.47–1.65 T) were acquired on a tunable magnet (Stelar). The uncertainty of T1 measurements was ± 1%. For each measurement, the longitudinal relaxation (r1p) was calculated according to eqn (1).
Gd3+ ratio of 2.5 was reached. Variations in longitudinal relaxivity (r1,obs) at 21.5 MHz were monitored 15 min after each addition to let the system equilibrate. The pH was maintained constant at 7.0 ± 0.1 before each measurement and addition. Nuclear magnetic relaxation dispersion (NMRD) profiles were acquired before and after the addition of CaCl2. 1H NMRD profiles were recorded at 25 °C on a Stelar Field Cycling relaxometer (FFC2000), operating at a magnetic field strength ranging from 0.01 to 20 MHz (2.4 × 10−4 to 0.47 T). The additional points measured in the range 20–70 MHz (0.47–1.65 T) were acquired on a tunable magnet (Stelar). The uncertainty of T1 measurements was ± 1%. For each measurement, the longitudinal relaxation (r1p) was calculated according to eqn (1).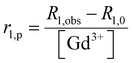 | (1) |
r 1 titration with EDTA
GdL, DCA0, DCA1 and DCA2 were dissolved in HEPES buffer at 0.70 mM Gd3+ concentration and the pH was adjusted to 6.0 ± 0.1. Starting longitudinal relaxivity was measured at 21.5 MHz (25 °C), and then stepwise additions of 20 mM EDTA solution were carried out for each sample. Variations in longitudinal relaxivity at 21.5 MHz were monitored 15 min after each addition. The pH was maintained constant at 6.0 ± 0.1 before each measurement and addition. When a molar concentration ratio of EDTA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Gd3+ of 3
Gd3+ of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 was reached, samples were exhaustively dialysed against isotonic HEPES/NaCl buffer (pH 7.3) to remove Gd-EDTA and the excess of EDTA ligand. Then the amount of residual Gd3+ was relaxometrically determined through the glass vial test. Briefly, aliquots of each dialysed sample were diluted 1
1 was reached, samples were exhaustively dialysed against isotonic HEPES/NaCl buffer (pH 7.3) to remove Gd-EDTA and the excess of EDTA ligand. Then the amount of residual Gd3+ was relaxometrically determined through the glass vial test. Briefly, aliquots of each dialysed sample were diluted 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in volume with HCl 37%, transferred to pre-scored glass ampoules and centrifuged for 3 min at 2000 rpm. Then the glass vials were sealed and placed at 120 °C for 16 hours to achieve the complete mineralization of the samples. Longitudinal relaxivity (R1,obs) was then measured and the amount of residual gadolinium was determined according to eqn (2), where R1,dia is the diamagnetic contribution of water (R1,dia = 0.5 s−1). Finally, titration with CaCl2 was performed as reported in the previous paragraph.
1 in volume with HCl 37%, transferred to pre-scored glass ampoules and centrifuged for 3 min at 2000 rpm. Then the glass vials were sealed and placed at 120 °C for 16 hours to achieve the complete mineralization of the samples. Longitudinal relaxivity (R1,obs) was then measured and the amount of residual gadolinium was determined according to eqn (2), where R1,dia is the diamagnetic contribution of water (R1,dia = 0.5 s−1). Finally, titration with CaCl2 was performed as reported in the previous paragraph.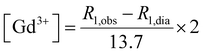 | (2) |
Variable-temperature 17O NMR measurements
Variable-temperature 17O NMR measurements of GdL were recorded on a Bruker Avance 600 spectrometer equipped with a 5 mm probe and a standard temperature control unit. The GdL sample contained 5% of 17O water (Cambridge Isotope) and 12.76 mM Gd3+. The paramagnetic contribution was calculated using HEPES buffer containing 5% of 17O water. 17O NMR measurements were also performed after calcium addition (Gd![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ca ratio 1.5
Ca ratio 1.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) both on the GdL sample and on the control suspension (19.14 mM CaCl2). The observed transverse relaxation rates were calculated from the signal width at half-height. Measurements were performed in a temperature interval ranging from 278 to 343 K.
1) both on the GdL sample and on the control suspension (19.14 mM CaCl2). The observed transverse relaxation rates were calculated from the signal width at half-height. Measurements were performed in a temperature interval ranging from 278 to 343 K.
Analysis of relaxometric data
NMRD profiles were analyzed using a single relaxation model based on Solomon–Bloembergen–Morgan and Freed theories.36The model considered the relaxivity as the sum of three contributions arising from (i) the water protons in the inner-sphere (is) of Gd3+, (ii) the water protons in the second-coordination sphere (ss) of Gd3+, and (iii) the water protons that diffuse around the paramagnetic species (outer sphere, os) and do not interact with any molecular site of the SCA.
| r1 = ris1 + rss1 + ros1 | (3) |
The inner sphere contribution can be described as
 | (4) |
The second-sphere contribution is supposed to follow a similar model:
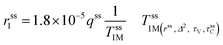 | (5) |
The contribution from the outer-sphere water protons can be modeled as
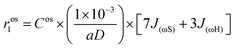 | (6) |
The analysis of the NMRD data for the calcium-free agents was carried out putting q = 0 and, and therefore, only second- and outer-sphere contributions were considered. The fitting was performed keeping constant the values of a and D (3.8 Å and 2.24 × 10−5, respectively, as determined for most of the Gd-based agents reported in the literature).
For the calcium-adducts, q was switched to 1 and the inner-sphere contribution was considered. This mechanism introduced τR and τM, which were varied, and r, which was kept fixed at 3 Å.
Magnetic resonance imaging
Magnetic resonance images of GdL, DCA0, DCA1 and DCA2 were acquired with an Aspect M2 MRI System (Aspect Magnet Technologies Ltd, Netanya, Israel) working at 1 Tesla. To this end, GdL, DCA0, DCA1 and DCA2 were suspended in HEPES buffer at a Gd3+ concentration of 0.57 mM. Another set of GdL, DCA0, DCA1 and DCA2 was incubated with CaCl2 (Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Gd 1.5
Gd 1.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and then suspended in HEPES buffer at a Gd3+ concentration of 0.57 mM. The samples were placed into specific plastic tube vials and imaged at 1T. Bidistilled water was used as a reference. T2-weighted (T2w) images were acquired with a fast spin echo sequence with the following parameters: Repetition Time (TR) 2500 ms, Echo Time (TE) 49 ms, Number of Averages (NAV) 4, Matrix 160 × 152 pixel units, Field Of View (FOV) 40 × 40 mm, slice thickness 1.00 mm, and acquisition time 3 min 20 s. T1-weighted (T1w) images were acquired with a T1 spin echo multislice sequence with the following parameters: TR 50 ms, TE 9 ms, NAV 24, flip angle 90, matrix 128 × 128 pixel units, FOV 40 mm × 40 mm, slice thickness 1.00 mm, and acquisition time 3 min 50 s. Finally, the contrast to noise ratio (CNR) was calculated at 1 T for GdL and DCA0-2 using the following equation:
1) and then suspended in HEPES buffer at a Gd3+ concentration of 0.57 mM. The samples were placed into specific plastic tube vials and imaged at 1T. Bidistilled water was used as a reference. T2-weighted (T2w) images were acquired with a fast spin echo sequence with the following parameters: Repetition Time (TR) 2500 ms, Echo Time (TE) 49 ms, Number of Averages (NAV) 4, Matrix 160 × 152 pixel units, Field Of View (FOV) 40 × 40 mm, slice thickness 1.00 mm, and acquisition time 3 min 20 s. T1-weighted (T1w) images were acquired with a T1 spin echo multislice sequence with the following parameters: TR 50 ms, TE 9 ms, NAV 24, flip angle 90, matrix 128 × 128 pixel units, FOV 40 mm × 40 mm, slice thickness 1.00 mm, and acquisition time 3 min 50 s. Finally, the contrast to noise ratio (CNR) was calculated at 1 T for GdL and DCA0-2 using the following equation: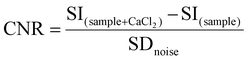 | (7) |
Results and discussion
Rationale and DCA preparation
Dendrimers are multivalent macromolecules with a regular, highly branched structure and nanoscopic dimensions (2–10 nm).37 These structures were first patented in 1980s by Denkewalter et al., who reported a “cascade” synthesis of L-lysine based dendrimers.38–40 However, the first dendrimeric systems that attracted considerable attention were Tomalia's PAMAM dendrimers and Newkome's “arborols”.41 PAMAM dendrimers, firstly prepared in 1984, are still considered promising “smart agents” due to their ability to (1) participate in intracellular drug delivery, (2) cross the biological membranes/barriers, (3) circulate in the body, and (4) target specific cellular and tissue structures.42 In the last decades the use of PAMAM dendrimers for imaging purposes has been widely reported. Due to their branched and extended structure, they can be easily modified and used also for dual imaging techniques.43 A special attention, however, has been dedicated to the use of PAMAM dendrimers in MRI.44 To overcome the sensitivity drawback of MRI, many attempts to load several paramagnetic molecules onto a single system have been carried out. In this regard PAMAM dendrimers, due to their nanoscopic dimensions and tunable size, attract considerable interest. The possibility of implementing a discrete number of MRI labels and targeting units at well-defined positions within the same macromolecular structure is one of the unique features of dendrimers and gives the opportunity to improve both the sensitivity and specificity of MRI.As far as functional imaging is concerned, the first dendrimeric system sensitive to calcium was developed from the G1 dendrimer and was successfully tested in vivo at 7 T. The advantage of this macromolecular system consisted in the slower diffusion, in comparison to the monomeric one.31 Subsequently, a G4 dendrimeric SCA was prepared and tested at 7 T, exhibiting both T1 and T2 shortening effects.32 The relaxometric behaviour of these calcium sensitive macromolecules, however, has never been reported at low field, where, due to the supposed restricted rotational motion, the relaxivity should be higher. For this purpose, in this work, a set of macrocyclic dendrimer conjugates of different sizes were prepared by coupling the monomacrocyclic SCA precursor and G0–G2 PAMAM dendrimers according to the previously established procedure.31 The coupling efficiency varied with the size of the dendrimers: a conjugate of the low molecular weight G0 dendrimer was obtained as a mixture containing 3 and 4 macrocyclic SCA units, and a mid-size G1 dendrimer resulted in a mixture of conjugates bearing mainly 6, 7 and 8 SCA units, while the largest G2 dendrimer resulted in a mixture of species with the average number of 9 SCA units. This observation is in line with those previously established on the same type of PAMAM dendrimers and the macrocyclic units where coupling is performed via the isothiocyanate group.31–33 Subsequently, the product formation was confirmed by the analysis of MALDI-ToF spectra, which indicated the existence of species with different masses, i.e. different numbers of monomacrocyclic SCA units on the dendrimer surface (data not shown).
The dendrimeric contrast agents DCA0, DCA1 and DCA2 thus obtained varied in their molecular weight, i.e. sizes of the molecules. This allowed studying their relaxometric properties, considering the differences in their size. In order to have a better comparison with the dendrimeric SCAs, we used also the monomeric SCA version GdL, which has an identical structure to macrocyclic units coupled to the dendrimers and should interact with Ca2+ in the same manner (Fig. 1).
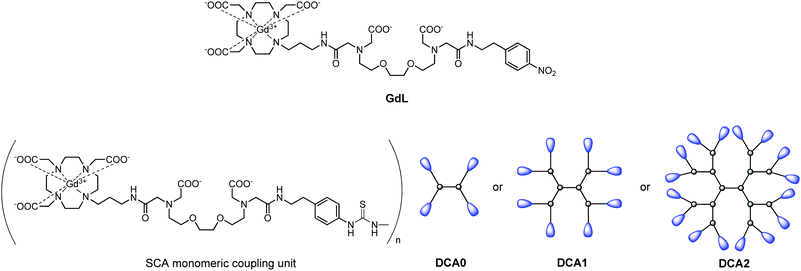 | ||
| Fig. 1 Structures of the monomeric complex GdL and illustrations of the dendrimeric conjugates DCA0, DCA1 and DCA2 studied in this work. | ||
Relaxometric titrations at low magnetic field
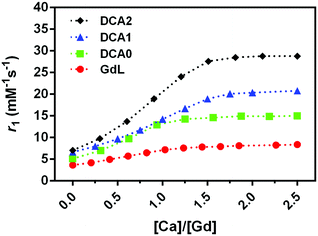
An important aspect of the characterization of SCAs was monitoring their relaxivity variation upon increasing the Ca2+ concentration. Hence, the relaxometric titration experiments were performed at the low magnetic fields, and the SCA behaviour was studied considering their size combined with the investigations at this specific magnetic field strength. The result of this experiment, carried out at 0.5 T, 25 °C, and pH 7, confirmed the excellent sensitivity of the GdL, DCA0, DCA1 and DCA2 for this bivalent ion (Fig. 2). A relaxivity enhancement was observed for all the agents, and it was characterized by an initial rise followed by a stable plateau that was reached at a [Ca2+]/[Gd3+] ratio ranging from 1 to 1.5.As expected, the sensitivity to calcium and the subsequent r1 enhancement followed the order GdL < DCA0 < DCA1 < DCA2, resulting in a 130% increase for GdL and up to ca. 310% for the DCA2. Interestingly, the r1 value measured for DCA2, 28.8 mM−1 s−1, was not too far from the corresponding value reported under the same experimental conditions using Ca-sensitive liposomes (37.0 mM−1 s−1).34 However, as it has been widely reported previously,45 the relaxivity obtained at 0.5 T for a slowly tumbling agent is substantially higher than that measured for the same system at high field, e.g. at 7 T. Furthermore, a drop in relaxivity at high field can be quite prominent to make this agent less efficient than a fast tumbling agent. Representative examples are agents GdL and DCA1, whose longitudinal relaxivities for the Ca-adducts were measured at 7 T; in turn, the relaxivity of the monomer was slightly higher than that of the dendrimer (7.4 mM−1 s−1vs. 6.5 mM−1 s−1).31 In this work, the relaxivity values for the two Ca-adducts were measured at 0.5 T, and, as expected, DCA1 displayed a relaxivity much higher than that of the GdL (20 mM−1 s−1vs. 6.5 mM−1 s−1). Hence, these observations highlight the relevant role played by the magnetic field of the MRI scanner in defining the detection sensitivity of these calcium-sensitive CAs. Apart from pharmacokinetic considerations, large-sized agents may be superior at lower fields, whereas small-sized agents may be superior at higher fields.
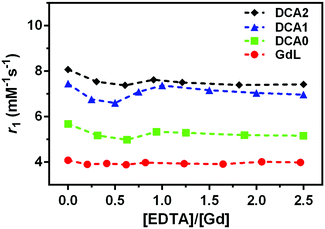
The stability of the Gd3+ complexation for the monomer and dendrimers was monitored by measuring the relaxivity upon addition of EDTA. Almost no variations in pH values were detected and no decrease in relaxivity was observed, thus suggesting that EDTA, as the competing ligand, did not cause destruction of the initially prepared Gd-complexes, i.e.GdL and DCA0-2 (Fig. 3).
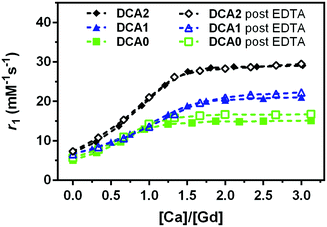
In the next step, we dialysed DCA0-2 (note: GdL cannot be collected due to the large pore size of the membrane) and titration with Ca2+ was carried out again. As expected, no significant differences in the DCA0-2 response towards Ca2+ were detected before and after treatment with EDTA (Fig. 4). These results confirm that DCA0-2 remained intact upon the treatment with EDTA, thereby also excluding the transmetallation of Gd3+ and the presence of GdEDTA species.
Variable temperature 17O NMR and NMRD experiments
The ditopic ligand L, characteristic of the Ca-sensitive SCAs investigated in this work, contains a macrocyclic cage designed for hosting the Gd3+ ion responsible for the generation of the MRI contrast, which is linked to a bis-amide EGTA-derived ligand for the successive coordination of the Ca2+ ion. For the GdL, the coordination of Gd3+ (coordination number 9) is expected to be saturated by the 4 nitrogens of the macrocycle, the 3 oxygens of the pendant carboxylates, and the 2 oxygens coming from one amide and one carboxylate group on the proximal end (with respect to the macrocyclic cage) of the EGTA-derived ligand. Such coordination behavior was already observed for different mono- and bismacrocyclic complexes that bear the same type of the EGTA-derived chelator.29,46The confirmation of the GdL not having a water molecule coordinated to the metal (i.e. it acts as a non-hydrated, q = 0 complex) was gained from the acquisition of the temperature-dependent transverse relaxation rates of water 17O nuclei in a solution of the GdL (Fig. 5, red circles). This technique is the first choice to get information about the number and the dynamics of the water molecules coordinated to a paramagnetic center. In fact, the 17O transverse relaxation rate of water is proportional to the fraction of the water molecule bound to the metal, and to the number q of metal coordinated water. Furthermore, it is modulated by several variables such as the T2 of the water molecule at the metal site T2M, the chemical shift of the water oxygen induced by the metal ΔωM2, and the residence lifetime of the water molecule in the inner coordination sphere τM. However, due to the very small chemical shift effect induced by Gd(III), the relaxation model simplifies in a form already seen for the inner-sphere contribution to the 1H paramagnetic relaxation (eqn (4)), though here the predominant relaxation mechanism arises from contact interaction:
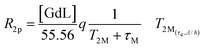 | (8) |
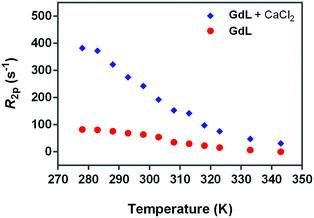 | ||
Fig. 5
17O-R2p values (normalized to 20 mM Gd3+) of GdL, measured at 600 MHz in the absence (red circles) or presence of calcium (blue diamonds). The ratio between Gd3+ and Ca2+ was 1.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. 1. | ||
Hence, the occurrence of very low 17O-R2p values (as measured for GdL, Fig. 5) indicates the absence of the metal bound water molecule (q = 0). However, the paramagnetic contribution is not null due to the presence of small dipolar effects from outer- and second-sphere contributions.
On the other hand, for q > 0, the temperature dependence of 17O-R2p values reflects the balance between T2M and τM values, which show an opposite temperature dependence.
Fig. 5 (blue diamonds) indicates that the complexation of calcium causes a significant increase in the 17O water transverse relaxation rate, which is fully consistent with an increase in the hydration state of Gd3+ from 0 to 1. To verify this hypothesis, the NMRD profiles were analyzed with the relaxation model that includes the second-sphere and outer-sphere water protons for the calcium-free compounds, whereas for the samples where Ca2+ was added, the contribution from inner-sphere water protons was also considered (see below).
The values of the initial longitudinal relaxivities (i.e. in the absence of Ca2+, Table 1) for GdL and DCA0-2 show that there is a direct correlation between the relaxivity and the molecular size of the SCAs as previously reported in other studies.47,48 Furthermore, the value measured for GdL appears to be quite lower with respect to Gd(III) complexes with a similar size, but q = 1, thus confirming the qualitative result (q = 0) obtained from the analysis of the 17O data reported above. Since even the relaxivities of the dendrimer-based complexes are consistent with that of GdL (considering the differences in molecular size), it is reasonable to assume that also DCA0-2 species lack inner-sphere water molecules.
| Sample | r 1 (mM−1 s−1) |
|---|---|
| GdL | 3.9 |
| DCA0 | 5.1 |
| DCA1 | 6.7 |
| DCA2 | 7.3 |
Based on these observations, the NMRD profile of GdL (Fig. 6, red circles) was analyzed using a relaxation model lacking the contribution from inner-sphere water protons. However, as the relaxivity of the complex was significantly higher than the numbers reported for “pure” outer-sphere Gd3+ complexes (3.9 mM−1 s−1vs. 2.2–2.3 mM−1 s−1 at 20 MHz and 25 °C),49 the NMRD data were analyzed adding a contribution arising from the so-called “second-sphere” water protons. These are exchangeable protons relatively close to the metal center (typically within 5 Å), which intensively interact with polar moieties of the ligand.50 The obtained results supported previous observations that GdL and its analogues are indeed q = 0 complexes, with substantial contribution of the second-sphere water to the overall relaxivity value.
This contribution can be modeled using a set of equations very similar to those used for describing the inner-sphere contribution (see the Experimental section), with an average number of contributing water protons (q2sf), their average distance from Gd3+ (r2sf), and an overall correlation time (τ2sfC) that modulates the dipolar interaction and encloses the role of the rotation and exchange dynamics of the second sphere protons. As the same ditopic ligand was used to get the other three dendrimeric SCAs investigated in this work, an identical relaxation model was applied for the analysis of all the NMRD data.
Besides the three parameters that describe the second-sphere contribution, the fitting was carried out varying the parameters describing the electronic relaxation rate of the unpaired electrons of Gd3+ according to the Bloembergen–Morgan theory, such as the mean energy of the transient zero field splitting Δ2 and the corresponding time modulation τV. Conversely, the other two parameters defining the outer-sphere contribution according to Freed's model, i.e. the distance of maximum approach a and the relative diffusion constant D, were kept fixed to the typical values for this type of Gd3+ chelate, i.e. 3.8 Å and 2.24 cm2 s−1, respectively.
The quantitative analysis of the NMRD profiles according to the above-described relaxation model allowed the estimation of the relevant parameters controlling the relaxivity of the investigated systems (Table 2). The results obtained highlight the difference in the set of relaxation parameters between the monomeric complex GdL and the dendrimeric agent DCA0-2. This difference is mainly observed for the parameters determining the electronic relaxation rate, the number of second sphere protons, and their correlation times. On the other side, the main difference within the group of the three dendrimers relies on the number of the second-sphere protons, which progressively increases from G0 to G2.
| Parameter | GdL | DCA0 | DCA1 | DCA2 | ||||
|---|---|---|---|---|---|---|---|---|
| No Ca2+ | With Ca2+ | No Ca2+ | With Ca2+ | No Ca2+ | With Ca2+ | No Ca2+ | With Ca2+ | |
| Δ 2 × 1019 (s−2) | 1.05 ± 0.25 | 3.06 ± 0.01 | 0.64 ± 0.12 | 1.90 ± 0.01 | 0.65 ± 0.01 | 1.40 ± 0.01 | 0.65 ± 0.05 | 1.04 ± 0.01 |
| τ V (ps) | 42.7 ± 2.2 | 30.4 ± 0.2 | 56.5 ± 1.5 | 43.3 ± 0.1 | 56.3 ± 0.2 | 49.1 ± 0.1 | 56.3 ± 0.2 | 55.8 ± 0.3 |
| τ R (ns) | — | 0.15 ± 0.03 | — | 0.28 ± 0.01 | — | 0.39 ± 0.01 | — | 0.40 ± 0.10 |
| q 2sf | 1.5 ± 0.4 | 1.2 ± 0.3 | 1.9 ± 0.3 | 1.0 ± 0.01 | 2.4 ± 0.4 | 1.1 ± 0.1 | 2.6 ± 0.5 | 2.0 ± 0.4 |
| r 2sf (Å) | 4.6 ± 0.2 | 4.91 ± 0.2 | 4.6 ± 0.2 | 5.0 ± 0.1 | 4.8 ± 0.2 | 4.9 ± 0.1 | 4.9 ± 0.2 | 4.7 ± 0.2 |
| τ 2sfC (ns) | 0.65 ± 0.10 | 0.26 ± 0.16 | 0.97 ± 0.06 | 2.16 ± 0.01 | 0.96 ± 0.01 | 5.25 ± 0.02 | 0.90 ± 0.01 | 3.79 ± 0.13 |
To summarize, the coupling of the GdL monomer to PAMAM dendrimers to form calcium-sensitive paramagnetic dendrimer conjugates leads to a small (ca. 20%, from 190 ps to 230 ps) increase in the low-field limit (τS0) for the electronic relaxation time for the unpaired electrons of Gd3+.45 In addition, dendrimers display a longer second-sphere correlation time that is likely mainly responsible for the relaxivity hump characteristic of the DCA0-2 profiles. Likely, the elongation of τ2sfC originates from the slow down of the rotational motion of the complexes when they are part of the dendrimers.
However, the increase of relaxivity going from DCA0 to DCA2 does not seem attributable to τ2sfC that is almost unvaried along the series. Likely, the rotation of the chelates is only very weakly coupled to the tumbling motion of the dendrimeric core, and therefore, τ2sfC results are rather uncorrelated to the whole size of the system.
Hence, what appears to be mainly responsible for the relaxation enhancement within the dendrimeric series is the number of second-sphere water protons that increases from 1.9 to 2.6.
However, the Gd3+ chelates have the same structure and they are located at the terminal end of the dendrimer branches, thus making it difficult to find an explanation for the increase in q2sf values. One might speculate that the increase in the dendrimer generation (and consequently in the number of branches) may somehow affect the structure/dynamics of the water around the terminal end of the branches, thus leading to a little increase of the number of water protons in the second sphere of the paramagnetic ion.
Another observation that can be noted from the data presented in Table 1 and the NMRD profiles in Fig. 6 deals with the relaxivity jump among the investigated SCAs: r1 increases for 1.2 mM−1 s−1 (∼30%) between the monomer and DCA0, 1.6 mM−1 s−1 (∼30%) between DCA0 and DCA1, but only 0.6 mM−1 s−1 (∼10%) between DCA1 and DCA2. Interestingly, a similar result was reported in a previous study carried out by Bryant et al., where a plateau in relaxivity values was reached by G7 dendrimers and was maintained for G9 and G10 dendrimers.51 In principle, a reduced relaxivity enhancement upon increasing the size could be the consequence of a long residence lifetime of the inner-sphere water molecule, but if this hypothesis could explain the data cited above, it cannot be applied to this work due to the lack of inner-sphere water in the agents investigated here. As the relaxivity of the calcium-free SCAs examined in this work is primarily determined by q2sf, the observed changes within the series are nicely correlated with the number of second-sphere water protons reported in Table 2: the increase in q2sf is ∼27% from GdL to DCA0, ∼26% from DCA0 to DCA1, and ∼ 8% from DCA1 to DCA2.
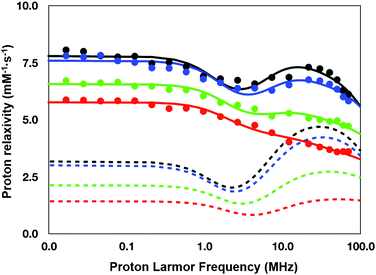
To understand the relaxation mechanisms associated with the calcium coordination of the investigated SCAs, the NMRD profiles at 25 °C for all the examined species after addition of CaCl2 were measured (Fig. 7) and integrated with the temperature-dependent experiments of water 17O-R2p performed with GdL (see above, Fig. 5, blue diamonds).
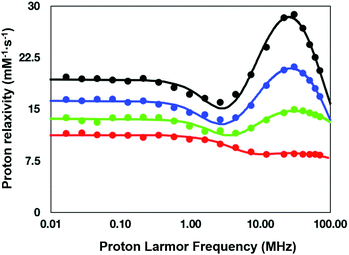 | ||
| Fig. 7 NMRD profiles (25 °C) for the calcium (II) adducts of the ditopic SCAs investigated in this work: GdL (red), DCA0 (green), DCA1 (blue), and DCA2 (black). | ||
As anticipated in the discussion of the 17O-water data shown in Fig. 5, the significant relaxation enhancement observed when calcium was added to GdL is attributable to a q = 0 → q = 1 hydration switch. Since the ditopic structure of the chelates in the dendrimers is equal to that of GdL, the NMRD data of the Ca2+-adducts were analyzed with the same relaxation model used for the calcium-free systems, but implemented with a model describing the contribution from inner-sphere water protons.
The NMRD data confirmed the significant relaxivity enhancement observed for all the Gd3+ complexes upon Ca2+ coordination over the entire magnetic field window examined.
Particularly clear is the increase of relaxivity in the low-to-intermediate field range, where r1 is mostly dependent on the rotational motion of the system, especially for the Gd3+ complexes having at least one inner-sphere water coordinated to the metal center. Actually, the relaxivity followed the order of the molecular size of the SCAs, i.e.GdL < DCA0 < DCA1 < DCA2. The good quality of the quantitative analysis of the profiles confirmed the goodness of the selected relaxation model, and, consequently, provided a support to the occurrence of the q = 0/q = 1 switch at the Gd3+ site triggered by the coordination of Ca2+ ions.
As expected, the correlation time associated with the rotational motion, τR, was found to be proportional to the overall size of the SCAs, with limit values of 80 ps for the Ca-GdL and 9.1 ns (i.e. two orders of magnitude larger) for Ca-DCA2. By considering that the 17O-R2p profile reported in Fig. 5 for the Ca2+ adduct is completely consistent with a short τM value and that the relaxivity of all the Ca2+ adducts examined in this work decreases from 25 °C to 37 °C (data not shown), the NMRD profiles of the Gd-complexes coordinated with Ca2+ have been analyzed fixing the τM value to 50 ns.
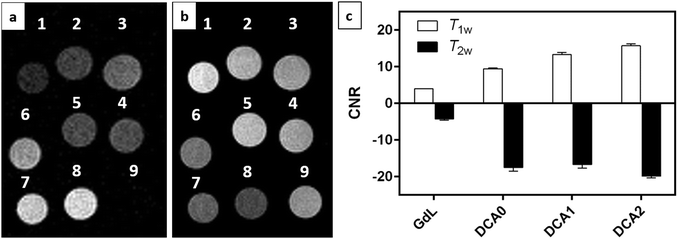
MRI on tube phantoms at low magnetic field
T 1w and T2w MR images were acquired at 1T with an Aspect M2 MRI System (Fig. 8a and b). To this end, GdL, DCA0, DCA1 and DCA2 were suspended in HEPES buffer at a Gd3+ concentration of 0.57 mM. The same amount of complexes was also separately incubated with CaCl2 (Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Gd 1.5
Gd 1.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and then suspended in HEPES buffer. T1 contrast observed by MRI matched the NMRD profile results, displaying increasing signals from GdL to DCA2, both in the absence and presence of calcium. Moreover, the difference in intensity of the T1w signal between the two states (without and with Ca2+) was clearly the highest for DCA2. This strong T1 contrast observed for the investigated dendrimeric systems after interaction with Ca2+ could be considered extremely promising for future in vitro and in vivo applications. Similarly, changes in the T2w contrast expectedly led to darkening of the recorded MR images (i.e. r2 relaxivity also increases along with the increase in r1).31,33 Hence, a T2 contrast enhancement was also observed for the dendrimer systems along with increasing generations upon addition of Ca2+. However, changes in T1w contrast completely followed the increase in the size of the investigated SCAs; on the other hand, the change in T2w contrast was pronounced between the GdL and already the first dendrimer conjugate DCA0, while the remaining dendrimer conjugates displayed similar properties and resulted in constant T2w contrast irrespective of the DCA0-2 size (Fig. 8c).
1) and then suspended in HEPES buffer. T1 contrast observed by MRI matched the NMRD profile results, displaying increasing signals from GdL to DCA2, both in the absence and presence of calcium. Moreover, the difference in intensity of the T1w signal between the two states (without and with Ca2+) was clearly the highest for DCA2. This strong T1 contrast observed for the investigated dendrimeric systems after interaction with Ca2+ could be considered extremely promising for future in vitro and in vivo applications. Similarly, changes in the T2w contrast expectedly led to darkening of the recorded MR images (i.e. r2 relaxivity also increases along with the increase in r1).31,33 Hence, a T2 contrast enhancement was also observed for the dendrimer systems along with increasing generations upon addition of Ca2+. However, changes in T1w contrast completely followed the increase in the size of the investigated SCAs; on the other hand, the change in T2w contrast was pronounced between the GdL and already the first dendrimer conjugate DCA0, while the remaining dendrimer conjugates displayed similar properties and resulted in constant T2w contrast irrespective of the DCA0-2 size (Fig. 8c).
Conclusions
In this work, we prepared a series of four SCAs with different sizes, consisting of a typical monomacrocylic, DO3A-derived SCA and a triplet of dendrimeric conjugates of different generation (G0–2) bearing the same monomeric SCA unit. We thoroughly investigated the effect of the molecular size on the relaxometric properties of these systems at low magnetic fields. Combined NMRD and 17O NMR studies indicated the existence of non-hydrated species with substantial contribution from second-sphere and outer-sphere water for these complexes. Relaxometric titrations in the presence of Ca2+ showed strong response of the investigated systems towards this cation. Moreover, the magnitude of enhancement in longitudinal relaxivity was strongly correlated with the size of complexes, with the biggest G2 dendrimer SCA conjugate exhibiting the strongest r1 response in the presence of Ca2+. The results reported in this study confirm once again the critical contribution of the rotational correlation time to the longitudinal relaxation effect of the paramagnetic species at low magnetic fields. Given the wide abundance of MRI scanners operating at these fields, the above investigated systems proved to be good candidates for potential utilization in appropriate functional MRI studies.List of abbreviations
| BAPTA | 1,2-Bis(o-aminophenoxy)ethane-N,N,N′,N′-tetraacetic acid |
| CAs | Contrast agents |
| CNR | Contrast to noise ratio |
| DCAs | Dendrimeric contrast agents |
| DCA0 | G0 dendrimeric contrast agent |
| DCA1 | G1 dendrimeric contrast agent |
| DCA2 | G2 dendrimeric contrast agent |
| EDTA | Ethylenediaminetetraacetic acid |
| EGTA | Ethylene glycol-bis(β-aminoethyl ether)-N,N,N′,N′-tetraacetic acid |
| FOV | Field of view |
| Gd-DOTA | Gd3(III)-1,4,7,10 tetraazacyclododecane-1,4,7,10-tetraacetic acid |
| GdL | Monomeric Gd3+ complex |
| HEPES | 4-(2-Hydroxyethyl)-1-piperazineethanesulfonic acid |
| is | Inner sphere |
| MRI | Magnetic resonance imaging |
| NAV | Number of averages |
| NMR | Nuclear magnetic resonance |
| NMRD | Nuclear magnetic relaxation dispersion |
| os | Outer sphere |
| PAMAM | Poly(amidoamine) |
| r 1 | Longitudinal relaxivity |
| SCAs | Smart contrast agents |
| SD | Standard deviation |
| SI | Signal intensity |
| ss | Second-coordination sphere |
| T 1w | T 1 weighted |
| T 2w | T 2 weighted |
| TE | Echo time |
| TR | Repetition time. |
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The financial support of the Max-Planck Society and the Turkish Ministry of Education (PhD fellowship to S. G.) is gratefully acknowledged. Open Access funding provided by the Max Planck Society.Notes and references
- A. Hengerer and J. Grimm, Molecular magnetic resonance imaging, Biomed. Imaging Intervention J., 2006, 2(2), e8 CrossRef CAS PubMed.
- D. Parrott, W. S. Fernando and A. F. Martins, Smart MRI Agents for Detecting Extracellular Events In Vivo: Progress and Challenges, Inorganics, 2019, 7, 18 CrossRef CAS.
- M. C. Heffern, L. M. Matosziuk and T. J. Meade, Lanthanide probes for bioresponsive imaging, Chem. Rev., 2014, 114(8), 4496–4539 CrossRef CAS PubMed.
- M. Querol and A. Bogdanov, Amplification strategies in MR imaging: Activation and accumulation of sensing contrast agents (SCAs), J. Magn. Reson. Imaging, 2006, 24, 971–982 CrossRef PubMed.
- C. Tu, E. A. Osborne and A. Y. Louie., Activatable T1 and T2 magnetic resonance imaging contrast agents, Ann. Biomed. Eng., 2011, 39(4), 1335–1348 CrossRef PubMed.
- L. M. D. Leon-Rodriguez, A. J. Lubag, C. R. Malloy, G. V. Martinez, R. J. Gillies and A. D. Sherry, Responsive MRI agents for sensing metabolism in vivo, Acc. Chem. Res., 2009, 42(7), 948–957 CrossRef PubMed.
- F. K. Kálmán, M. Woods, P. Caravan, P. Jurek, M. Spiller, G. Tircsó, R. Kiraly, E. Brücher and A. D. Sherry, Potentiometric and relaxometric properties of a gadolinium-based MRI contrast agent for sensing tissue pH, Inorg. Chem., 2007, 46(13), 5260–5270 CrossRef PubMed.
- K. Srivastava, G. Ferrauto, V. G. Young Jr, S. Aime and V. C. Pierre, Eight-Coordinate, Stable Fe(II) Complex as a Dual 19F and CEST Contrast Agent for Ratiometric pH Imaging, Inorg. Chem., 2017, 56(20), 12206–12213 CrossRef CAS PubMed.
- X. Guo and F. C. Szoka, Chemical approaches to triggerable lipid vesicles for drug and gene delivery, Acc. Chem. Res., 2003, 36(5), 335–341 CrossRef CAS PubMed.
- J. A. Ronald, J. W. Chen, Y. Chen, A. M. Hamilton, E. Rodriguez, F. Reynolds, R. A. Hegele, K. A. Rogers, M. Querol, A. Bogdanov, R. Weissleder and B. K. Rutt, Enzyme-sensitive magnetic resonance imaging targeting myeloperoxidase identifies active inflammation in experimental rabbit atherosclerotic plaques, Circulation, 2009, 120(7), 592–599 CrossRef CAS PubMed.
- G. Ferrauto, E. Di Gregorio, M. Ruzza, V. Catanzaro, S. Padovan and S. Aime, Angew. Chem., Int. Ed., 2017, 56, 12170 CrossRef CAS PubMed.
- C. V. Gringeri, V. Menchise, S. Rizzitelli, E. Cittadino, V. Catanzaro, G. Dati, L. Chaabane, G. Digilio and S. Aime, Novel Gd(III)-based probes for MR molecular imaging of matrix metalloproteinases, Contrast Media Mol. Imaging, 2012, 7, 175–184 CrossRef CAS PubMed.
- T. Jin, H. Mehrens, P. Wang and S. G. Kim, Chemical exchange-sensitive spin-lock MRI of glucose analog 3-O-methyl-d-glucose in normal and ischemic brain, J. Cereb. Blood Flow Metab., 2018, 38(5), 869–880 CrossRef CAS PubMed.
- X. Xu, N. N. Yadav and L. Knutsson, et al., Dynamic Glucose-Enhanced (DGE) MRI: Translation to Human Scanning and First Results in Glioma Patients, Tomography, 2015, 1(2), 105–114 CrossRef PubMed.
- S. Aime, D. Delli Castelli, F. Fedeli and E. Terreno, A paramagnetic MRI-CEST agent responsive to lactate concentration, J. Am. Chem. Soc., 2002, 124(32), 9364–9365 CrossRef CAS PubMed.
- G. Liu, Y. Li and M. D. Pagel, Design and characterization of a new irreversible responsive PARACEST MRI contrast agent that detects nitric oxide, Magn. Reson. Med., 2007, 58(6), 1249–1256 CrossRef CAS PubMed.
- V. H. Liu, C. C. Vassiliou, S. M. Imaad and M. J. Cima, Solid MRI contrast agents for long-term, quantitative in vivo oxygen sensing, Proc. Natl. Acad. Sci. U. S. A., 2014, 111(18), 6588–6593 CrossRef CAS PubMed.
- S. Guo, X. Xiao, X. Wang, Q. Luo, H. Zhu, H. Zhang, H. Li, Q. Gong and K. Luo, Reductive microenvironment responsive gadolinium-based polymers as potential safe MRI contrast agents, Biomater. Sci., 2019, 7(5), 1919–1932 RSC.
- K. Zhang, Y. Cheng, W. Ren, L. Sun, C. Liu, D. Wang, L. Guo, H. Xu and Y. Zhao, Coordination-Responsive Longitudinal Relaxation Tuning as a Versatile MRI Sensing Protocol for Malignancy Targets, Adv. Sci., 2018, 5(9), 1800021 CrossRef PubMed.
- E. L. Que and C. J. Chang, Responsive magnetic resonance imaging contrast agents as chemical sensors for metals in biology and medicine, Chem. Soc. Rev., 2010, 39(1), 51–60 RSC.
- K. Srivastava, G. Ferrauto, S. M. Harris, D. L. Longo, M. Botta, S. Aime and V. C. Pierre, Complete on/off responsive ParaCEST MRI contrast agents for copper and zinc, Dalton Trans., 2018, 47(33), 11346–11357 RSC.
- E. L. Que, E. Gianolio, S. L. Baker, A. P. Wong, S. Aime and C. J. Chang, Copper-responsive magnetic resonance imaging contrast agents, J. Am. Chem. Soc., 2009, 131(24), 8527–8536 CrossRef CAS PubMed.
- E. L. Que, E. Gianolio, S. L. Baker, S. Aime and C. J. Chang, A copper-activated magnetic resonance imaging contrast agent with improved turn-on relaxivity response and anion compatibility, Dalton Trans., 2010, 2, 469–476 RSC.
- M. V. Clavijo Jordan, S. T. Lo and S. Chen, et al., Zinc-sensitive MRI contrast agent detects differential release of Zn(II) ions from the healthy vs. malignant mouse prostate, Proc. Natl. Acad. Sci. U. S. A., 2016, 113(37), E5464–E5471 CrossRef CAS PubMed.
- J. Yu, A. F. Martins and C. Preihs, et al., Amplifying the sensitivity of zinc(II) responsive MRI contrast agents by altering water exchange rates, J. Am. Chem. Soc., 2015, 137(44), 14173–14179 CrossRef CAS PubMed.
- A. Barandov, B. B. Bartelle, C. G. Williamson, E. S. Loucks, S. J. Lippard and A. Jasanoff, Sensing intracellular calcium ions using a manganese-based MRI contrast agent, Nat. Commun., 2019, 10(1), 897 CrossRef PubMed.
- G. Angelovski, Heading toward Macromolecular and Nanosized Bioresponsive MRI Probes for Successful Functional Imaging, Acc. Chem. Res., 2017, 50(9), 2215–2224 CrossRef CAS PubMed.
- W. H. Li, S. E. Fraser, T. J. Meade. and A. Calcium-Sensitive, Magnetic Resonance Imaging Contrast Agent, J. Am. Chem. Soc., 1999, 121(6), 1413–1414 CrossRef CAS.
- G. Angelovski, P. Fouskova, I. Mamedov, S. Canals, E. Toth and N. K. Logothetis, Smart Magnetic Resonance Imaging Agents that Sense Extracellular Calcium Fluctuations, ChemBioChem, 2008, 9, 1729–1734 CrossRef CAS PubMed.
- T. Savić, G. Gambino, V. S. Bokharaie, H. R. Noori, N. K. Logothetis and G. Angelovski, Early detection and monitoring of cerebral ischemia using calcium-responsive MRI probes, Proc. Natl. Acad. Sci. U. S. A., 2019, 201908503, DOI:10.1073/pnas.1908503116.
- S. Gündüz, N. Nitta, S. Vibhute, S. Shibata, M. E. Mayer, N. K. Logothetis, I. Aoki and G. Angelovski, Dendrimeric calcium-responsive MRI contrast agents with slow in vivo diffusion, Chem. Commun., 2015, 51(14), 2782–2785 RSC.
- S. Gündüz, T. Savić, R. Pohmann, N. K. Logothetis, K. Scheffler and G. Angelovski, Ratiometric Method for Rapid Monitoring of Biological Processes Using Bioresponsive MRI Contrast Agents, ACS Sens., 2016, 1(5), 483–487 CrossRef PubMed.
- L. Connah and G. Angelovski, Synergy of Key Properties Promotes Dendrimer Conjugates as Prospective Ratiometric Bioresponsive Magnetic Resonance Imaging Probes, Biomacromolecules, 2018, 19(12), 4668–4676 CrossRef CAS PubMed.
- F. Garello, S. Vibhute, S. Gündüz, N. K. Logothetis, E. Terreno and G. Angelovski, Innovative Design of Ca-Sensitive Paramagnetic Liposomes Results in an Unprecedented Increase in Longitudinal Relaxivity, Biomacromolecules, 2016, 17(4), 1303–13011 CrossRef CAS PubMed.
- T. M. Powers, The Evans Method, JoVE Science Education Database. Inorganic Chemistry, JoVE, Cambridge, MA, 2019 Search PubMed.
- S. Aime, M. Botta and E. Terreno, Gd-based contrast agents for MRI, Adv. Inorg. Chem., 2005, 57, 173–237 CrossRef CAS.
- S. Langereis, A. Dirksen, T. M. Hackeng, M. H. P. van Genderena and E. W. Meijer, Dendrimers and magnetic resonance imaging, New J. Chem., 2007, 31, 1152–1160 RSC.
- R. G. Denkewalter, J. Kolc and W. G. Lukasavage, US Pat., 4289872, September 15, 1981.
- R. G. Denkewalter, J. Kolc and W. G. Lukasavage, US Pat., 4360646, November 23, 1982.
- R. G. Denkewalter, J. Kolc and W. G. Lukasavage, US Pat., 4410688, October 18, 1983.
- D. A. Tomalia, H. Baker, J. Dewald, M. Hall, G. Kallos, S. Martin, J. Roeck, J. Ryder and P. Smith, A New Class of Polymers: Starburst-Dendritic Macromolecules, Polym. J., 1985, 17, 117–132 CrossRef CAS.
- M. Labieniec-Watala and C. Watala, PAMAM dendrimers: destined for success or doomed to fail? Plain and modified PAMAM dendrimers in the context of biomedical applications, J. Pharm. Sci., 2015, 104(1), 2–14 CrossRef CAS PubMed.
- M. Longmire, P. L. Choyke and H. Kobayashi, Dendrimer-based contrast agents for molecular imaging, Curr. Top. Med. Chem., 2008, 8(14), 1180–1186 CrossRef CAS PubMed.
- H. Kobayashi and M. W. Brechbiel, Nano-sized MRI contrast agents with dendrimer cores, Adv. Drug Delivery Rev., 2005, 57(15), 2271–2286 CrossRef CAS PubMed.
- A. S. Merbach, L. Helm and É. Tóth, The Chemistry of Contrast Agents in Medical Magnetic Resonance Imaging, John Wiley and Sons, 2nd edn, 2013, DOI:10.1002/9781118503652.
- P. Kadjane, C. Platas-Iglesias, P. Boehm-Sturm, V. Truffault, G. E. Hagberg, M. Hoehn, N. K. Logothetis and G. Angelovski, Dual-frequency calcium-responsive MRI agents, Chemistry, 2014, 20(24), 7351–7362 CrossRef CAS PubMed.
- E. Toth, D. Pubanz, S. Vauthey, L. Helm and A. E. Merbach, The role of water exchange in attaining maximum relaxivities for dendrimeric MRI contrast agents, Chem. – Eur. J., 1996, 2, 1607–1615 CrossRef CAS.
- E. C. Wiener, F. P. Auteri, J. W. Chen, M. W. Brechbiel, O. A. Gansow, D. S. Schneider, R. L. Belford, R. B. Clarkson and P. C. Lauterbur, Molecular dynamics of ion-chelate complexes attached to dendrimers, J. Am. Chem. Soc., 1996, 118, 7774–7782 CrossRef CAS.
- L. Connah, V. Truffault, C. Platas-Iglesias and G. Angelovski, Investigations into the effects of linker length elongation on the behaviour of calcium-responsive MRI probes, Dalton Trans., 2019, 48(36), 13546–13554 RSC.
- M. Botta, Second coordination sphere water molecules and relaxivity of gadolinium(III) complexes: Implications for MRI contrast agents, Eur. J. Inorg. Chem., 2000, 399–407 CrossRef CAS.
- L. H. Bryant Jr, M. W. Brechbiel, C. Wu, J. W. Bulte, V. Herynek and J. A. Frank, Synthesis and relaxometry of high-generation (G = 5, 7, 9, and 10) PAMAM dendrimer-DOTA-gadolinium chelates, J. Magn. Reson. Imaging, 1999, 9(2), 348–352 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2020 |