Morphology of Cu clusters supported on reconstructed polar ZnO (0001) and (0001̄) surfaces

Abstract

Unbiased Monte Carlo procedures are applied to investigate the structure of Cu clusters of various sizes deposited over reconstructed polar ZnO surfaces. Four distinct reconstructed polar ZnO surfaces (two Zn terminated (0001) reconstructions and two O terminated (0001̄) reconstructions) were investigated, having previously been determined to be the most stable under typical conditions, as revealed by the grand canonical ensemble studies. Random sampling was performed considering ∼400 000 random initial structural configurations of Cu atoms over the ZnO surfaces, with each structure being optimised using interatomic potential techniques, and the most stable resultant structures being refined using a plane-wave DFT approach. The investigation reveals the key role of surface adatoms and vacancies arising from the reconstruction of the polar ZnO surface in determining the morphology of deposited Cu clusters. Strong Cu–Zn interactions play an essential role in Cu cluster growth, with reconstructed polar ZnO surfaces featuring sites with undercoordinated Zn surface atoms promoting highly localised three dimensional Cu cluster morphologies, whist reconstructions featuring undercoordinated O atoms tend to result in more planar Cu clusters, in order to maximise the favourable Cu–Zn interaction. This is the first study that evaluates the thermodynamically most stable Cu/ZnO structures using realistic reconstructed ZnO polar surfaces, and thus provides valuable insights into the factors affecting Cu cluster growth over ZnO surfaces, as well as model catalyst surfaces that can be utilised in future computational studies to explore catalytic activity for key processes such as CO₂ and CO hydrogenation to methanol.

---

Introduction

Cu/ZnO-based catalysts have long been used for a variety of industrially and environmentally important processes, including methanol synthesis,^1–10 methanol steam reforming,^11,12 and the water-gas shift reaction;^13,14 yet despite the extensive use of these catalysts, much remains to be fully understood in terms of the role of ZnO in facilitating catalytic activity and the effect of ZnO surface structure in determining Cu cluster growth. The dominant facets of wurzite ZnO are the non-polar (101̄0) and (112̄0) surfaces, and the polar (0001) and (0001̄) facets; clearly, the different surface structures presented by these four terminations will have consequences for Cu cluster growth. However, for the polar (0001) and (0001̄) surfaces, their complexity is further enhanced by their atomic reconstruction, which is essential for the stability of these polar surfaces. Atomic reconstruction in polar surfaces can significantly stabilise them to the extent that their stability is able to compete with non-polar surfaces.¹⁵ Moreover, it has been established that high levels of disorder in ZnO polar surfaces result in a significant configurational entropy contribution, enhancing stabilisation.¹⁶ Experimentally, studies have demonstrated that the polar ZnO surfaces are highly active in hydrogenation processes such as methanol synthesis.^17,18 In particular, ZnO polar surfaces have been shown to play a key role in the synthesis of methanol.

STM studies reported that different Cu cluster growth behaviours were observed for the Zn- and O-terminated surfaces.^19,20 Three-dimensional Cu cluster growth and surface pits with O-terminated edges, which have been suggested to act as Cu nucleation sites, were observed on the Zn-terminated surface.²⁰ In contrast, for the O-terminated surface, 2-D Cu clusters were observed, although a more detailed analysis was limited by the limitations of the STM on O-teminated surfaces.¹⁹ A wide variety of ZnO surface features are likely to be present between different samples, thus allowing adsorbed Cu clusters to show different morphologies.

Cu cluster growth over the non-polar ZnO (101̄0) surface has already been subject to rigorous computational investigation, with studies utilising an unbiased Monte Carlo exploration of the energy landscape for Cu clusters supported on ZnO (101̄0) surfaces using interatomic potentials (IP) techniques, to identify accurately global minimum energy structures, which were then subsequently optimised using a more accurate plane-wave DFT approach.²¹ The studies revealed significantly wetting of Cu clusters when adsorbed on ZnO (101̄0), with supported clusters having considerably different structures compared to the gas-phase Cu clusters. This result was attributed to a strong Cu–Zn interaction, in line with observations made in past experimental work. More recently, Cu cluster growth on ZnO (101̄0) surfaces was investigated using global optimisation techniques employing genetic algorithms in combination with high-dimensional neural network potentials;²² the results of this approach suggest that small Cu clusters tend to form 3-D clusters, in contrast to the previous studies. It was also reported that at the metal–oxide interface, facets resembling the low-index Cu(111) and Cu(110) surfaces emerge, which could be important in facilitating catalytic activity for CO₂ conversion to methanol. These computational studies reflects the utility of IP techniques coupled with an unbiased global optimisation approach as an effective screening method for exploring a vast array of surface structures, with a generally good agreement in terms of geometric structure and relative stability of competing stable minimum structures between IP and DFT optimised results, allowing for a rigorous investigation of surface structures.

In the light of the development of this new approach to computational exploration of surface structures, a similar method was used to rationalise reconstruction of the polar ZnO surface which has already been identified as an important phenomenon in surface stability.¹⁵ The studies examined different surface reconstructions by considering a range of different surface layer occupancies, transferring m Zn or O atoms from the Zn- or O-terminated surfaces, to the other side of the slab (O- or Zn-terminated surfaces, respectively), resulting in pairs of surfaces featuring surface vacancies on one side, and surface adatoms on the other. The studies revealed an optimal value m = 6, in order to minimise effectively the slab dipole moment with the (5 × 5) supercell used, and thus stabilise the polar ZnO surface. Applying the grand canonical ensemble method to determine the optimal surface occupancy revealed a drive towards full surface occupancy under typical conditions for both the Zn- and O-terminated reconstructed surfaces. Hence, it is expected that both surfaces consist of essentially full surface layer occupancy, with 6 Zn (O) vacancies or 6 O (Zn) adatoms for the Zn-terminated (O-terminated) surface, to eliminate the surface dipole within the (5 × 5) supercell used. These detailed computational investigations provide an ideal starting point for consideration of Cu cluster growth on realistic model reconstructed polar ZnO surfaces (Fig. 1).

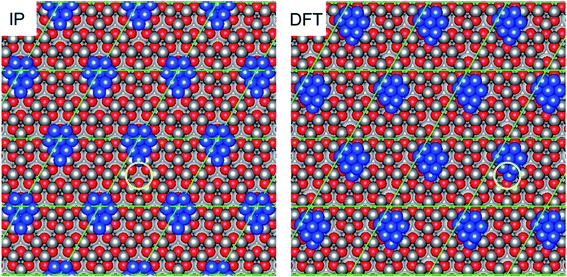
Fig. 1 The four different reconstructed ZnO surfaces considered in the present work, identified as representative surfaces by Mora-Fonz et al.¹⁵ The left panels (A and C) show the Zn-terminated surface, whilst the right panels (B and D) show the O-terminated surface. The top panels (A and B) depict reconstructions featuring O (Zn) adatoms atop a complete ZnO layer, whilst the bottom panels (C and D) show complete ZnO surface layers featuring Zn (O) vacancies. Grey spheres correspond to Zn atoms, whilst red spheres correspond to O atoms; atoms in the topmost layer are in bold colours whilst subsurface atoms are in faded colours. The blue circles and labels indicate the topmost surface features, either Zn or O adatoms or vacancies originating from the surface reconstruction. The graphics above show the extended periodic structure of the surface with the (5 × 5) surface supercells used in the calculations indicated by black lines.

The polar ZnO (0001) and (0001̄) facets have already been subject to computational investigation using hybrid QM/MM methods,^23–28 investigating the possible participation of the ZnO surfaces in CO₂ activation for methanol synthesis over the unreconstructed O-terminated surface²³ and model reconstructed surfaces for both the Zn- and O-terminated facets,²⁵ as well as for Cu cluster growth. The studies identify vacant O interstitial surface sites as being key to CO₂ hydrogenation activity over the O-terminated ZnO surface, whilst it is suggested that Cu cluster growth is dependent on the presence of oxidised Cu⁺ and Cu²⁺ to serve as anchors for cluster growth. Whilst these hybrid QM/MM studies provide many useful insights into the nature of the polar ZnO surface, the manner in which the reconstruction of the surface is modelled has its limitations, with surface vacancies introduced into the embedded cluster model not accounting for the density and distribution of surface vacancies.¹⁵ Hence, it is of interest to consider the nature of Cu cluster growth over these latest models for ZnO surface reconstruction.

In previous DFT studies investigating CO₂ activation over a model catalyst consisting of a Cu₈ cluster supported on a ZnO (0001̄) surface,²⁹ it was revealed that the structural flexibility of the Cu nanoparticle plays a key role in the extent of CO₂ activation. Additionally, experimental studies investigating the catalytic activity of Cu clusters on an Al₂O₃ support show that catalytic activity is correlated with Cu cluster size.³⁰ Experimental investigations of the CO₂ hydrogenation activity of ZnO nanorod-supported Cu clusters suggest that the surface morphology of the ZnO nanorods greatly influence Cu cluster growth and have a critical impact on CO₂ hydrogenation activity.³¹ Hence, it is of interest to determine precisely how reconstruction of the ZnO surface affects Cu cluster size morphology, and in turn, CO₂ adsorption and related catalytic activity.

In this work, the Cu/ZnO potential energy landscape was explored using IP MC techniques, from which low energy structures were refined with a DFT approach. Four distinct reconstructed ZnO surface structures were selected, representing O- (Zn-) rich Zn- (O-) terminated surfaces and O- (Zn-) poor O- (Zn-) terminated surfaces, as they were determined to be the most stable under typical conditions as revealed by the grand canonical ensemble studies performed previously.¹⁵ The role of surface features arising from reconstruction of the polar ZnO surface in determining the shape of Cu clusters is investigated. Moreover, we provide model Cu/ZnO catalyst structures for future studies investigating the mechanism for CO₂ hydrogenation to methanol.

Methods and computational details

This work uses a similar MC approach to that established by previous studies^15,21 for filtering low energy Cu/ZnO structures with interatomic potentials (IP) and a subsequent DFT refinement using a plane-wave DFT approach. Details of the potential energy exploration is given below.

Global optimisation of Cu/ZnO structures

We use the Knowledge-Led Master Code (KLMC)^32–34 to perform an unbiased Monte Carlo (MC) exploration of the energy landscape for Cu_n clusters (for n = 1–8, 24, 50) on four reconstructed polar ZnO (0001) and (0001̄) facets obtained by Mora-Fonz et al.¹⁵ These four surface structures were selected as they were determined to be the most stable under typical conditions as revealed by the grand canonical ensemble studies performed previously.¹⁵ The MC routine generated 10 000 initial random Cu_n/ZnO structures by swapping Cu atoms over a lattice mesh placed atop the ZnO surfaces. The ZnO slabs consisted of a 6-layer (5 × 5) supercell model, as described previously,¹⁵ whilst the Cu mesh consisted of 3-layer (7 × 7) Cu(111) slab, for a total of 147 possible Cu sites. The (7 × 7) Cu(111) slab was used as this afforded the best match to the ZnO slab dimensions based on the DFT optimised bulk Cu lattice parameter. The Cu mesh was placed 2.5 Å above the topmost atoms of the ZnO slab.

Interatomic potentials calculations

Optimisation of the KLMC-generated structures was performed using the Generalised Utility Lattice Programme (GULP),^35,36 applying a polarisable shell model potential to the ZnO oxygen atoms.³⁷ The Cu–ZnO potentials used were derived by Mora-Fonz et al.,²¹ with Buckingham and Morse potentials describing the Cu–O and Cu–Zn interactions, respectively, whilst Cu–Cu interactions were accounted for using many-body Gupta potentials.³⁸ All of the Cu atoms were fully relaxed, as were the top three ZnO layers. Following the established procedure for modelling the reconstructed ZnO surfaces,¹⁵ a 2D periodic surface model was used, with uniform charge compensation applied to the bottom of the slab to account for the charge mismatch inherent in the approach employed to model the ZnO surface reconstruction, and a mesh of 100 fixed point charges at a distance of 50 Å above and below the Cu/ZnO slab was included to eliminate the residual dipole moment. Structural optimisation within GULP was performed using the BGFS algorithm; the lowest five structures obtained were identified for each Cu_n cluster and their relative stabilities compared. Structures for the five lowest energy configurations are freely and publicly available via the SAINT database (https://saint.chem.ucl.ac.uk/).

Periodic ab initio calculations

To verify the KLMC-GULP approach, the five lowest energy Cu₈ structures were refined using DFT methods; the DFT optimised structures are also available via the SAINT database. Refinement of the IP-optimised structures was performed using plane-wave DFT as implemented in the Vienna Ab initio Simulation Package (VASP).^39,40 Interactions between core and valence electrons were described using the Projector Augmented Wave (PAW) pseudopotential approach.^41,42 The PBESol exchange correlation functional was used throughout,⁴³ as was a plane-wave cut-off energy of 450 eV, which was deemed to be sufficient to obtain accurate DFT optimised geometries. All calculations were performed using Γ-centred k-mesh of (1 × 1 × 1). As for the IP optimisations, all Cu atoms were allowed to relax, as were the top three ZnO layers, until the forces on the atoms were converged to within 0.01 eV Å⁻¹. As a 3D periodic model was used, a vacuum gap of 18 Å was introduced between the top ZnO layer of the slab and the bottom layer of the adjacent periodic image. For each of the ZnO slabs, Zn or O atoms were removed randomly from the bottom of the slab to eliminate any charge mismatch arising from the reconstruction (rather than applying a uniform charge compensation as was done for the IP calculations); likewise, the fixed-point charges used in the IP calculations to eliminate the residual surface dipole moment were replaced by a dipole correction as implemented in VASP.

Results

Relative stability of minimum energy IP structures and Cu cluster adsorption energies

Zn-rich O-terminated surface. The structures of the lowest Cu/ZnO(000-1) energy structures are shown in Table 1, whilst the corresponding relative energies for the five lowest energy structures for each Cu cluster size are presented in Table 2; higher energy structures can be found in the ESI (Table S1†). This reconstruction features a total of 6 Zn adatoms per (5 × 5) surface supercell (hence we will describe this surface as a “Zn-rich” O-terminated surface), which are important in Cu cluster growth. For up to 3 Cu atoms, we see that the structures are all very close in energy, with the 1^st and 5^th ranked structures being within less than ∼0.1 eV of each other. This result can be attributed to the fact that there is no significant variation in the structure of the Cu “cluster”, hence the different structures simply represent different adsorption sites on the reconstructed ZnO surface. Indeed, as can be seen from the graphics for the competing structures presented in the ESI (Table S1†), all the structures feature almost identical groups of Cu atoms adjacent to a surface Zn adatom, merely in a variety of different orientations.

Table 1 Graphics for lowest energy structures obtained for adsorbed Cu clusters of various sizes. See ESI for the remaining 4 candidate local minimum structures (Table S1). Blue spheres represent Cu, whilst red and grey spheres represent O and Zn, respectively. The top ZnO layer (i.e. involved in the reconstruction) atoms are highlighted with darker spheres, whilst the subsurface ZnO atoms are represented by faded spheres. Thin green lines indicate cell boundaries. IP-calculated adsorption energies with respect to bulk Cu are listed below the graphics for each lowest energy structure

No. Cu
1	2	3	4	5
Adsorption energy w.r.t. bulk Cu/eV
2.552	1.194	0.817	0.574	0.535
No. Cu
6	7	8	24	50
Adsorption energy w.r.t. bulk Cu/eV
0.494	0.441	0.391	0.219	0.102

---

Table 2 Relative energies (in eV) for the 5 lowest energy structures for adsorbed Cu clusters of various sizes. The tabulated values are calculated with respect to the global minimum energy structure. See ESI for corresponding structures (Table S1)

No. Cu
Rank	1	2	3	4	5	6	7	8	24	50
1	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
2	0.059	0.009	0.028	0.446	0.060	0.070	0.068	0.074	0.079	0.084
3	0.073	0.012	0.032	0.454	0.115	0.135	0.140	0.309	0.222	0.299
4	0.077	0.072	0.045	0.546	0.130	0.165	0.203	0.358	0.243	0.302
5	0.092	0.107	0.097	0.857	0.278	0.192	0.219	0.361	0.312	0.450

---

However, for n > 4, a greater variation is seen between the IP lowest minimum energy structure and the competing local minima, which is especially pronounced for the Cu₄ cluster, whose lowest minimum energy structure is found to be remarkably stable, by over 0.44 eV, compared to the second most stable local minimum. Additionally, a preference for 3-dimensional Cu cluster growth emerges; the top 3 most stable structures feature a highly coordinated tetrahedral Cu cluster, whereas the local minimum structures ranked 4^th and 5^th exhibit a planar Cu cluster geometry, with the Cu plane lying incommensurate with plane of the topmost complete ZnO surface layer, coordinating with a surface Zn adatom. The remarkable stability of the Cu₄ global minimum structure can be attributed to its optimal distance between the Cu cluster and adjacent Zn surface adatoms; in the global minimum energy structure, the Cu₄ tetrahedron is located equidistantly between Zn surface adatom nearest neighbours, hence maximising the favourable attractive interaction between Zn and Cu. For the other two local minima featuring Cu₄ tetrahedra, the Cu₄ cluster is adsorbed such than only one surface Zn adatom is well-coordinated with the Cu cluster.

For larger Cu clusters, the high stability of the Cu₄ lowest minimum energy structure is reflected in the fact that because the most stable local minimum energy structures are based around the Cu₄ global minimum energy structure, e.g. for the Cu₅ clusters, the 5 top-ranked local minima are identical apart from the positioning of the 5^th Cu atom, with each of the five clusters featuring the tetrahedral Cu₄ arrangement and adsorption site between two surface Zn adatoms as observed for the Cu₄ global minimum energy structure. Indeed, the global minimum structures up to Cu₈ represent sequential growth, with each subsequent structure being virtually identical apart from the additional Cu atom. We also note that the top two most stable structures for Cu₅, Cu₆, Cu₇ and Cu₈ clusters feature very similar Cu cluster geometries adsorbed on the same ZnO surface site, and differ only in their rotational orientation, as is evident in the IP-calculated relative energies, which show that 3^rd, 4^th and 5^th ranked structures are all much closer in terms of relative energy to each other, and are further in terms of relative energy from the 1^st and 2^nd ranked structures. This sequence is especially evident for the Cu₈ clusters, with the 1^st and 2^nd ranked structures being very close in relative stability (with 0.08 eV), whilst the 3^rd, 4^th and 5^th ranked structures are all considerably less stable (>0.22 eV difference in relative stability between 2^nd and 3^rd ranked structures) and close to each other in relative stability (within 0.06 eV).

These trends identified in the relative stability are present for the larger Cu₂₄ cluster, but less pronounced. It is notable that these much larger clusters tend to be positioned such that up to 4 surface Zn adatoms are occluded by the Cu cluster, rather than the Cu cluster being coordinated by only 2 Zn adatoms as seen for the Cu₄–Cu₈ global minimum structures. This behaviour can simply be attributed to the larger cluster being more effectively able to maximise its favourable attractive interactions with the Zn adatoms at this adsorption site. We also see that the Cu₂₄ cluster, whilst covering a significantly greater area of the ZnO surface, is not at an appreciably greater height than the smaller clusters; it can be seen in the side view presented in Fig. 2 that both the Cu₈ and Cu₂₄ global minimum supported Cu clusters consist of 2–3 Cu layers, with the topmost Cu atoms in the Cu₂₄ cluster lying no more than 4.17 Å above the topmost subsurface atoms (i.e. not the Zn surface adatom layer); the corresponding distance for the Cu₈ and Cu₁ global minima were 3.04 Å and 1.72 Å, respectively. It is also worth noting that for the Cu₂₄ global minimum structure, the topmost subsurface atoms were lattice Zn, whilst for the smaller Cu₈ cluster, the topmost subsurface atoms were lattice O, suggesting that the strong Cu/Zn interaction lifts the subsurface Zn above the subsurface O for the larger cluster. Additionally, comparing the top 5 most stable local minimum energy structures, whilst 4 of the 5 minima correspond to discrete, isolated Cu clusters, coalescence of the Cu clusters can be seen in the 4^th ranked structure. It is likely that this is at least in part an artefact of the limited size of the ZnO surface supercell that can be used, as identified in the previous studies on the ZnO reconstruction.¹⁵ Whilst the (5 × 5) supercell is largely sufficient to allow for near complete elimination of the slab dipole moment through surface reconstruction, it cannot be excluded that a larger supercell would enable a greater variety of structures to be sampled; such a possibility is, however, largely outside the realm of computational exploration using present methods and resources. Likewise, the size of the (5 × 5) supercell imposes a limit on the size of discrete Cu clusters that can be investigated in this study.

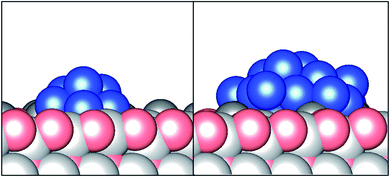Fig. 2 Side view of the global minimum energy structures for Cu₈ (left) and Cu₂₄ (right) clusters adsorbed on the reconstructed O-terminated ZnO surface featuring Zn adatoms.

For very high Cu loading (50 Cu per ZnO (5 × 5) supercell), the ZnO surface is saturated with Cu, achieving approximately 2 monolayer coverage. Nonetheless, the structures obtained in this study provide insights into the nature of the interaction of Cu with the ZnO polar surface. For all of the top ranked 5 local minima, there is no apparent Cu coverage in the hexagonal region – which represents the greatest expanse of the slab surface uninterrupted by surface Zn adatoms – of the reconstructed ZnO surface. This observation is consistent with the fact that the Cu–Zn interaction is attractive, as shown by the IP terms. It was also found that height of the topmost Cu₅₀ atom is slightly less than that of the Cu₂₄ cluster, relative to the topmost ZnO subsurface atoms. This observation would suggest that for a given number of Cu atoms, upward Cu cluster growth becomes less favourable than outward wetting of the Cu cluster, with the further addition of Cu resulting in spreading of the cluster to interact with additional nearby surface Zn adatoms.

The presence of Zn adatoms plays, therefore, a key role in Cu cluster growth. Moreover, this surface feature appears to support the growth of 3D Cu clusters, rather than flat, planar Cu arrays on the ZnO surface, with the Cu clustering around the Zn adatoms and the growth of Cu clusters being most favourable at surface sites that maximise contact between the Cu cluster and the Zn adatoms. Whilst an attractive interaction between Cu and Zn had been reported previously in experimental^19,20 studies and in computational studies of the non-polar surface using a similar methodology to the present work,²¹ previous work suggested planar Cu cluster formation, for both the non-polar ZnO surface and for O-terminated surfaces. The 3D cluster formation reported here provides further evidence that the features of the reconstructed polar ZnO surface determine adsorbed Cu cluster morphology.

Adsorption energies with respect to bulk Cu as calculated using the same many-body Cu–Cu potentials are also presented in Table 1, according to the equation E_ads = E_Cun/ZnO − E_ZnO − nE_Cu, where the adsorption energy is E_ads, n is the number of Cu atoms in the cluster, the energy for the Cu_n cluster adsorbed on the reconstructed ZnO surface is E_Cun/ZnO, E_ZnO is the total energy for the clean reconstructed ZnO surface, and E_Cu is the total bulk energy per Cu atom. We find that the Cu cluster adsorption becomes more exothermic for increasing numbers of Cu atoms present on the surface (Table 1), reflecting the stabilisation afforded by Cu–Cu interactions and the overall increased stability of larger clusters, in agreement with the previous computational studies of the non-polar ZnO surface.²¹ However, it can also be seen that the calculated adsorption energy remains endothermic with respect to bulk Cu across the whole range of Cu cluster sizes.

O-poor O-terminated surface. We now consider the (000-1) ZnO surface featuring 6 O vacancies in the surface layer (hence this surface is referred to as the “O-poor” O-terminated surface). The results are presented in Tables 3 and 4; likewise, graphics for the five lowest energy structures for each Cu cluster size can be found in the ESI (Table S2†).

Table 3 Graphics for lowest energy structures obtained for adsorbed Cu clusters of various sizes. See ESI for the remaining 4 candidate local minimum structures (Table S2). Blue spheres represent Cu, whilst red and grey spheres represent O and Zn, respectively. The top ZnO layer (i.e. involved in the reconstruction) atoms are highlighted with darker spheres, whilst the subsurface ZnO atoms are represented by faded spheres. Thin green lines indicate cell boundaries. IP-calculated adsorption energies with respect to bulk Cu are listed below the graphics for each lowest energy structure

No. Cu
1	2	3	4	5
Adsorption energy w.r.t. bulk Cu/eV
1.233	−0.139	−0.379	−0.357	−0.398
No. Cu
6	7	8	24	50
Adsorption energy w.r.t. bulk Cu/eV
−0.442	−0.404	−0.383	−0.164	−0.020

---

Table 4 Relative energies (in eV) for the 5 lowest energy structures for adsorbed Cu clusters of various sizes. The tabulated values are calculated with respect to the global minimum energy structure. See ESI for corresponding structures (Table S2)

No. Cu
Rank	1	2	3	4	5	6	7	8	24	50
1	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
2	0.037	0.212	0.536	0.110	0.072	0.306	0.299	0.206	0.724	0.853
3	0.047	0.296	0.624	0.259	0.220	0.521	0.584	0.257	1.754	1.004
4	0.387	0.389	0.826	0.543	0.398	0.668	0.662	0.340	1.782	1.229
5	0.749	0.559	0.874	0.607	0.466	0.721	0.664	0.372	1.812	1.351

---

In the three most stable Cu₁/ZnO structures, we see that there are two main surface pits which serve to accommodate the Cu clusters. The 4^th and 5^th ranked structures, on the other hand, feature the Cu atom in smaller O-vacancy sites. The top three structures are all close in energy, within 0.05 eV, whereas the 4^th and 5^th ranked structures are considerably less stable, at >0.38 eV less stable that the lowest minimum, which can be attributed to the higher number of Cu–Zn interactions.

For smaller Cu clusters, up to Cu₅, the lowest minimum structures feature a Cu cluster accommodated in the smaller of the two pits, whilst for Cu₆, Cu₇ and Cu₈ lowest minima, the Cu clusters are located in the largest surface indentation because of the limited surface pit size. Structures with the Cu atom in the larger surface pit are present amongst the top 5 ranked structures for all Cu cluster sizes (see ESI†). For larger n, however, Cu sits in both the smaller and larger surface pits with energy differences being within ∼0.3 eV. Cu clusters adsorbed in the smaller pit persist for Cu₇ but are considerably less stable (>0.55 eV less stable than the lowest minimum), and are completely absent from the top 5 ranked local minima for Cu₈.

For higher Cu loadings (Cu₂₄), the lowest minimum has two smaller separate clusters, consisting of a smaller, flatter Cu₉ cluster in the larger surface pit, and a larger, taller Cu₁₅ cluster in the smaller pit. The structure suggests that the larger (smaller) surface pit can accommodate up to 8 (5) Cu atoms; subsequent Cu cluster growth predominantly takes place atop Cu atoms in the smaller pit and is driven primarily by Cu–Cu interactions, since the undercoordinated Zn is no longer accessible to Cu and Cu–O interactions are repulsive. We also find that the other local minimum energy structures for Cu₂₄ show single, contiguous Cu clusters, spreading across the two surface pits that serve as nucleation sites for Cu cluster growth.

For very high Cu loading (Cu₅₀), as with the Zn-rich O-terminated reconstructed surface, we see that the ZnO surface is saturated with Cu, with a few islands present on the surface devoid of Cu growth. Comparing the local minimum energy structures for the Zn-rich and O-poor O-terminated surfaces, we see that the Cu₅₀ structures for the O-poor surface leaves a greater area of the ZnO surface exposed and free of Cu. We can attribute this behaviour to the initial Cu cluster growth being predominantly within the surface pits, and thus smaller clusters do not take up an appreciable proportion of the total slab surface area, since initial Cu cluster growth is essentially vertical; hence for very high Cu loading, where Cu cluster growth begins to spread beyond the confines of the surface pits, the area of the slab covered is less than that for the Zn-rich surface, for which smaller clusters are more spread out on the surface initially.

The IP adsorption energies with respect to bulk Cu are also presented in Table 3. The calculated adsorption energies, in contrast to the Zn-rich O-terminated surface, are generally exothermic, with only the system containing a single adsorbed Cu atoms being unstable with respect to the bulk. This is probably due to high energetic cost associated with separating a single atom, rather than a cluster of atoms, from the bulk structure. For smaller Cu clusters, there is a general trend of increasingly exothermic adsorption energies with respect to bulk Cu as the cluster size grows, although we note that there are maxima in adsorption energies for Cu₃ and Cu₆ clusters. It is notable that the Cu₃ cluster represents the largest Cu cluster size where the global minimum IP structure features the Cu cluster positioned within the smaller of the three O-vacancy surface pits; hence one can infer that the particular stability of the Cu₃ and Cu₆ clusters is related to the dimensions of the surface pits, which happen to be commensurate with the Cu clusters of these sizes to maximise attractive Cu–Cu and Cu–Zn interactions – with clusters consisting of greater numbers of Cu atoms being too large to accommodate optimally in these surface pits. This behaviour is further reflected in the considerably less exothermic adsorption energy relative to bulk Cu for the Cu₂₄ and Cu₅₀ systems, since clearly clusters of these sizes are far too large to fit within the O vacancy pits. Hence, the presence of these vacancy sites can be inferred as key to the stability of Cu clusters adsorbed on this particular surface reconstruction.

O-rich Zn-terminated surface. Turning now to the Zn-terminated surfaces, we will consider first the surface reconstruction featuring O adatoms distributed over the ZnO surface, (which we refer to as the “O-rich” Zn-terminated surface). The five lowest energy structures are presented in Table 5, with relative energies reported in Table 6; higher energy structures can be found in the ESI (Table S3†). Surface O adatoms form large hexagonal regions on the reconstructed surface (Fig. 3). For Cu₁, we note that the local minimum energy structures are all very close in terms of energy (all within 0.025 eV), reflecting the fact that the favoured 3-coordinate hollow site between three surface Zn atoms is very similar for the different structures, with the small variations in stability being attributable to the marginal repulsive effect of nearby surface O adatoms. For Cu₂ and Cu₃ clusters, the range of stability is greater across the top 5 ranked local minimum energy structures, with all being within ∼0.3 eV, as the larger Cu cluster size limits the number of distinct surface sites that afford minimal repulsive interactions between Cu and O atoms; however, the observed structures reveal that there are still many surface sites that can accommodate clusters of up to 3 Cu atoms. For larger clusters of 4 or 5 Cu atoms, the lowest minima feature planar Cu clusters in the large hexagonal region enclosed by surface O adatoms, although planar Cu clusters outside this region still appear amongst the top 5 ranked structures. This behaviour can be attributed to the hexagonally enclosed region representing the greatest uninterrupted expanse of exposed surface Zn uninterrupted by surface O adatoms; hence larger (i.e., more than 3 Cu atoms) are more easily accommodated within this region to maximise attractive Cu–Zn interactions. Notably, in contrast to the two reconstructions of the O-terminated surface already discussed, for this Zn-terminated surface, larger planar structures are favoured, whereas for the O-terminated surfaces, the lowest minima for Cu₄ and larger clusters are invariably 3D structures, although a mixture of planar and 3D structures are observed amongst the top 5 ranked structures for all of the reconstructed ZnO surfaces discussed so far. The preference for planar Cu cluster growth on the O-rich Zn-terminated surface can be attributed simply to the fact that the unreconstructed surface presents essentially a close-packed sheet of surface Zn which necessarily would result in planar Cu cluster growth to maximise Cu–Zn attractive interactions; in this particular reconstruction, the O adatoms merely serve to interrupt planar Cu cluster growth.

Table 5 Graphics for lowest energy structures obtained for adsorbed Cu clusters of various sizes. See ESI for the remaining 4 candidate local minimum structures (Table S3). Blue spheres represent Cu, whilst red and grey spheres represent O and Zn, respectively. The top ZnO layer (i.e. involved in the reconstruction) atoms are highlighted with darker spheres, whilst the subsurface ZnO atoms are represented by faded spheres

No. Cu
1	2	3	4	5
Adsorption energy w.r.t. bulk Cu/eV
1.710	0.414	0.084	−0.031	−0.057
No. Cu
6	7	8	24	50
Adsorption energy w.r.t. bulk Cu/eV
−0.065	−0.043	−0.040	−0.095	−0.086

---

Table 6 Relative energies (in eV) for the 5 lowest energy structures for adsorbed Cu clusters of various sizes. The tabulated values are calculated with respect to the global minimum energy structure. See ESI for corresponding structures (Table S3)

No. Cu
Rank	1	2	3	4	5	6	7	8	24	50
1	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
2	0.007	0.032	0.014	0.153	0.266	0.353	0.119	0.054	0.510	0.462
3	0.012	0.190	0.188	0.243	0.422	0.396	0.245	0.113	0.552	0.493
4	0.019	0.209	0.255	0.323	0.426	0.452	0.285	0.132	0.552	0.496
5	0.027	0.222	0.295	0.442	0.452	0.462	0.336	0.201	0.673	0.533

---

Fig. 3 Graphic illustrating the “hexagonal surface region” defined by surface O adatoms on the reconstructed Zn-terminated ZnO surface; the region is defined by the yellow lines.

For intermediate Cu cluster sizes (Cu₆ and Cu₇), the larger cluster size limits the number of surface sites that avoid repulsive Cu–O interactions, with the structures featuring Cu clusters within the large hexagonal region being more stable. Examining the top 5 ranked local minimum structures for Cu₆, the effects of the attractive Cu–Zn interaction, and repulsive Cu–O interaction, are especially pronounced; the global minimum energy structure, featuring a planar monolayer Cu₆ cluster within the hexagonal region, is considerably more stable that the 2^nd ranked structure (0.35 eV), which is also located within the hexagonal region, but rather adopts a 3D structure featuring a plane of 5 Cu atoms in contact with the ZnO surface and a 6^th Cu atom located atop this Cu₅ cluster. Hence, the difference in stability between the two structures can be largely attributed to the more strongly attractive Cu–Zn interaction over the comparatively weaker Cu–Cu interaction. Comparing the global minimum energy structure for the Cu₆ cluster, with the 5^th ranked local minimum, illustrates well the impact of the repulsive interactions between Cu and O; whilst the structure of the Cu clusters are identical, consisting of two rows of 3 Cu atoms in a close-packed arrangement, the lowest minimum energy structure is more stable by 0.46 eV. Measuring the shortest distance between Cu and adatoms O reveals that in the global minimum structure, Cu atoms are separated from surface O adatoms by at least 3.1 Å; however, for the 5^th ranked local minimum structure, the minimum separation is only 3.0 Å. Simply put, for Cu clusters consisting of at least 6 Cu atoms, the most stable planar configuration of Cu atoms is too large to be comfortably accommodated in the surface regions outside the hexagonal region defined by the surface O adatoms; hence the hexagonal region is the favoured site for adsorption of intermediate size planar Cu clusters.

For Cu₈ clusters, a change in behaviour is observed as 3D Cu cluster structures begin to emerge as the most favourable configuration, with the global minimum structure featuring a Cu₇ planar cluster resembling that of the 4^th ranked local minimum structure for Cu₇ clusters, with an additional Cu atom on top. Moreover, the global minimum energy structure is located outside the hexagonal region which was previously identified as being a favourable site for adsorption of smaller planar Cu clusters, whilst the remaining top candidate local minimum energy structures all feature 2D planar structures only, with the 2^nd, 3^rd and 4^th ranked structures being located within the hexagonal region. Additionally, the range of stabilities for the minimum energy structures is smaller than that obtained for smaller Cu₆ and Cu₇ clusters, with all structures being within 0.2 eV; only the local minima obtained for a single Cu atom are closer in energy than this. This result strongly suggests that the favourable hexagonal region can only comfortably accommodate up to 7 Cu atoms in a planar arrangement, hence for larger clusters consisting of at least 8 Cu atoms, there is a degree of competition between larger planar clusters, which maximise the attractive Cu–Zn interaction, although at the expense of increasing repulsive interactions between Cu and O adatoms, or alternatively the formation of 3D clusters, which avoid such repulsive interactions to a greater extent, but sacrifice attractive interactions between Cu and Zn in favour of the attractive Cu–Cu interactions between the first and second layers of the 3D structure.

For larger Cu₂₄ systems, we immediately note that the global minimum structure almost totally covers the ZnO surface outside the large hexagonal regions previously identified as being the ideal adsorption sites for intermediate sized Cu clusters. The remaining 4 top ranked local minimum energy structures are substantially similar, in all cases with the large hexagonal region devoid of Cu atoms, with only small variations in the connectivity between Cu-covered areas on the remainder of the surface. These results suggest that for larger amounts of Cu deposited on the surface, which cannot possibly be accommodated in the distinctive hexagonal region, the remainder of the Zn-terminated surface, outside the hexagonal region, is favoured for Cu adsorption, since it allows for improved Cu–Cu interactions. Hence, it is evident that the relative importance of the three different kinds of interactions present (attractive Cu–Zn, attractive Cu–Cu, and repulsive Cu–O) changes depending on the extent of surface loading of Cu.

For very high Cu loading (Cu₅₀), almost total coverage of the ZnO surface is observed, both within and outside the hexagonal region, with the surface being essentially saturated with Cu at this point, in common with the O-terminated surfaces already discussed; the main difference is the higher proportion of the ZnO surface covered by Cu for the Zn-terminated surface, which can be attributed simply to the fact that the Zn-terminated surface necessarily contains more Zn atoms which are evenly spread across the surface, rather than Cu atoms being initially concentrated at either Zn adatom or O vacancy sites, as was observed for the two O-terminated surfaces.

The IP-calculated adsorption energies for Cu clusters on this surface are also presented in Table 5. For the O-rich Zn-terminated surface, Cu clusters consisting of 4 or more Cu atoms are adsorbed exothermically. For the smaller clusters (up to Cu₈), there is a maximum in exothermicity of adsorption for Cu₅, as larger clusters are less easily accommodated within the favoured hexagonal surface region defined by the O adatoms, without incurring repulsive interactions between Cu and surface O. For high numbers of adsorbed Cu atoms (i.e. the Cu₂₄ and Cu₅₀ systems), the adsorption energy with respect to bulk Cu is even more exothermic, probably due to the extensive attractive Cu–Cu interactions which make these systems more stable with respect to bulk Cu. We also find that the adsorption energies with respect to bulk Cu are less exothermic compared to those for the O-poor O-terminated surface, which can be rationalised by considering the stronger Cu–Zn attractive interaction for the highly undercoordinated Zn atoms present in the surface pits resulting from O vacancies.

Zn-poor Zn-terminated surface. The fourth reconstructed ZnO surface is the Zn-terminated surface featuring Zn vacancies (hence we will refer to this as the “Zn-poor” Zn-terminated surface), leaving pits in the surface layer containing under-coordinated O atoms; the remainder of the surface substantially resembles the unreconstructed Zn-terminated surface, consisting of interconnected small Zn₃ triangular surface platforms, intermediate sized Zn₄ platforms, and a larger hexagonal Zn₇ surface platform (Fig. 4). The global optimisation studies show that these flat Zn-terminated surface platforms are the favoured adsorption sites for small Cu clusters, as summarised in Tables 7 and 8; graphics for the five lowest energy structures for each Cu cluster size can be found in the ESI (Table S4†). For a single Cu atom, all of the top ranked local minimum structures feature Cu adsorbed in a 3-coordinate hollow site defined by surface Zn. Two types of 3-coordinate Zn sites are present on the surface, either with or without the added Cu eclipsing a O atom below; the sites without Cu eclipsing O were found to be more stable, attributable to a minimisation of repulsive Cu–O interactions. The three most stable minima consisted of structures in which the Cu atom is accommodated in such a site in each of the three different surface platforms identified, with the global minimum energy structure featuring the Cu atoms adsorbed on a triangular site. This finding can be attributed to the fact that the triangular site is bound by three Zn surface vacancy pits, resulting in a stronger interaction between the undercoordinated O atoms defining the edge of the surface pits, and the three Zn atoms forming the 3-coordinate adsorption site, which in turn induces a stronger interaction between the Zn and Cu. Similarly, the 2^nd and 3^rd ranked structures consist of Cu adsorbed in the non-eclipsed site of the parallelogrammical and hexagonal surface platforms, respectively.

Fig. 4 Graphic illustrating the different surface adsorption sites on the reconstructed Zn-poor Zn-terminated surface (i.e. featuring Zn vacancies). The yellow lines define the three different surface platforms consisting of either 3, 4 or 7 surface Zn atoms. Within each of these surface platforms, two types of 3-coordinate Zn adsorption site exist, with the adsorbed Cu atom either eclipsing a surface O atom (indicated by green circles) or not (indicated by blue circles).

Table 7 Graphics for lowest energy structures obtained for adsorbed Cu clusters of various sizes. See ESI for the remaining 4 candidate local minimum structures (Table S4). Blue spheres represent Cu, whilst red and grey spheres represent O and Zn, respectively. The top ZnO layer (i.e. involved in the reconstruction) atoms are highlighted with darker spheres, whilst the subsurface ZnO atoms are represented by faded spheres. Thin green lines indicate cell boundaries. IP-calculated adsorption energies with respect to bulk Cu are listed below the graphics for each lowest energy structure

No. Cu
1	2	3	4	5
Adsorption energy w.r.t. bulk Cu/eV
1.873	0.760	0.424	0.303	0.227
No. Cu
6	7	8	24	50
Adsorption energy w.r.t. bulk Cu/eV
0.187	0.160	0.185	0.136	0.052

---

Table 8 Relative energies (in eV) for the 5 lowest energy structures for adsorbed Cu clusters of various sizes. The tabulated values are calculated with respect to the global minimum energy structure. See ESI for corresponding structures (Table S4)

No. Cu
Rank	1	2	3	4	5	6	7	8	24	50
1	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
2	0.003	0.070	0.091	0.357	0.329	0.174	0.078	0.048	0.036	0.057
3	0.121	0.144	0.184	0.397	0.497	0.433	0.362	0.107	0.219	0.079
4	0.349	0.375	0.466	0.418	0.501	0.450	0.447	0.128	0.247	0.182
5	0.362	0.382	0.569	0.535	0.824	0.656	0.511	0.368	0.600	0.194

---

For two Cu atoms, the triangular site is too small to accommodate both Cu atoms comfortably, hence this site only appears as the 5^th ranked local minimum; on the other hand, the intermediate parallelogrammical surface platform is the Cu₂ adsorption site for both the global minimum and 4^th ranked structure, whilst two distinct Cu₂ structures are observed on the larger hexagonal platform in the 2^nd and 3^rd ranked structures. As we move to larger Cu₃ and Cu₄ clusters, the triangular adsorption site no longer appears in any of the top 5 ranked local minimum structures, with the hexagonal site becoming predominant for larger clusters, owing to its larger size, although for both Cu₃ and Cu₄, structures featuring Cu adsorbed on the parallelogrammical sites persist amongst the local minima. Notably, there is a conspicuous absence of 3D clusters for Cu₄, in contrast with both the O-terminated reconstructed surfaces, and also the O-rich Zn-terminated surface; although for the latter, the global minimum structure did indeed feature a planar arrangement of adsorbed Cu. For Cu₅ clusters on the present reconstructed surface, 3D clusters begin to emerge, appearing as the 2^nd and 5^th ranked local minimum structures, but planar Cu configurations dominate. The results suggest that whilst planar Cu cluster formation is favourable due to the maximised interaction with the flat Zn-terminated surface platforms (similar to that observed for the Zn-terminated surface decorated with O-adatoms), once the Zn-terminated surface platforms are sufficiently covered by monolayer Cu, 3D Cu cluster formation begins to appear; that planar cluster formation is favoured until the boundaries of the Zn-terminated surface platforms are reached is reflected further by the fact that of the top 5 ranked local minimum structures for Cu₅ clusters, all are located atop the large hexagonal platform, with the smaller triangular and parallelogrammical Zn-terminated platforms being too small to accommodate Cu clusters of this size. The tendency towards planar Cu cluster formation persists for Cu₆, although the relative energies presented in Table 8 show that 3D Cu cluster formation is more competitive compared to that for Cu₅; for both Cu₅ and Cu₆, the global minimum structure features a planar Cu cluster, whilst the second ranked local minimum structure shows a 3D Cu cluster geometry; however for Cu₆, the 1^st and 2^nd ranked structures are closer in energy by ∼0.15 eV compared to that for Cu₅. This trend continues for Cu₇ and Cu₈, with the planar cluster geometry remaining evident in the global minimum, but for increasing amounts of Cu, the alternative 3D Cu cluster geometry becomes increasingly competitive, with the 1^st and 2^nd ranked structures for Cu₈ being separated by only 0.05 eV.

For larger Cu₂₄ clusters, the emergence of 3D Cu clusters is clearly evident, as expected for such a high Cu loading. The global minimum structure and the 2^nd ranked local minimum structure both show discreet Cu clusters, whilst the remaining structures show coalescence of the Cu clusters, forming bars of Cu across the periodically repeated surface; however we see that the discreet Cu₂₄ clusters are more stable, with the 2^nd ranked structure being within only 0.03 eV of the global minimum, whilst the 3^rd ranked structure, which exhibits coalescence of the Cu clusters is 0.22 eV less stable than the global minimum. In all of the top ranked structures, we find that the Cu clusters form as a result of the cluster spreading beyond the confines of the distinct flat ZnO surface platforms identified, with clusters on the large hexagonal and intermediate parallelogrammical platforms merging together. Whilst the large size of the Cu₂₄ cluster means that some O vacancy surface pits are covered by the Cu cluster, we still find that the boundaries of the flat surface platforms largely define the boundaries of the Cu cluster. For the very high Cu loading in the Cu₅₀ system, the surface is essentially saturated with Cu, in common with the other three reconstructed surfaces investigated. For each of the top 5 ranked structures, the regions of the surface not covered by Cu correspond to the Zn-vacancy sites; however it is notable that the global minimum structure shows a greater degree of Cu wetting, with only two Zn surface vacancies being left exposed, compared to the remaining 4 local minima in which three surface Zn surface vacancies remain visible and are not subducted beneath the Cu layer. This observation suggests that for high Cu surface concentrations, Cu–Cu interactions become relatively more important in determining cluster morphology, with any repulsive Cu–O interactions arising from coverage of the Zn surface vacancies being compensated by the favourable Cu–Cu interactions.

The IP adsorption energies for the Cu clusters on this surface with respect to bulk Cu are also presented in Table 7. The general trend in adsorption energies resembles that of the Zn-rich O-terminated surface, with adsorption being endothermic across the full range of Cu cluster sizes, but becoming less so for larger Cu clusters, which can be attributed to the greater number of attractive Cu–Cu interactions for larger Cu clusters. The exception to this trend is the Cu₇ cluster, which is the least endothermically adsorbed of all of the smaller Cu clusters up to Cu₈, which is adsorbed slightly more endothermically, which can simply be attributed to the limited size of the hexagonal Zn-terminated surface platform that serves as the favoured adsorption site; the larger Cu₈ cluster spills over the boundaries of this site, thus incurring a repulsive Cu–O interaction as the additional Cu is forced closer to the undercoordinated O associated with the Zn vacancy.

DFT refinement of IP structures

Having obtained structures for the five lowest energy IP structures for each of the surface reconstructions and a variety of Cu cluster sizes from the global optimisation studies, DFT refinement of these structures is required to verify the validity of the global optimisation approach, and to allow for a more detailed analysis. For this purpose, the Cu₈ clusters for each of the four surface reconstructions were subject to DFT refinement. In alignment with previous studies,^15,21 it was found that, in general, the morphology of the IP optimised structures is retained by the DFT optimisation and that the lowest minimum IP structure is also found to be the most stable local minimum after DFT refinement, therefore confirming that the potentials used in this study for the exploration of the potential energy surface are suitable for these types of systems. A full discussion is provided in the ESI.† Nonetheless, there are a few important instances where the DFT refined systems deviate from the IP structures and relative stability ordering of lowest energy minima, which we will discuss here.

For both of the O-terminated surfaces, and for the Zn-poor Zn-terminated surface, good agreement between the IP and DFT optimised structures and ordering of relative stability of low energy structures is obtained. However, for the O-rich Zn-terminated surface, DFT refinement results in a significant deviation in terms of both Cu cluster structure, and relative stability (Table 9). Perhaps the two most striking structural features evident post-refinement are the close proximity of Cu and surface O adatoms, and the considerable displacement of these surface O adatoms with respect to their positions in the IP optimised structures; during IP optimisation, these atoms largely remain unperturbed from their positions on the clean IP optimised surfaces. These differences can be rationalised by considering that the highly undercoordinated surface O adatoms are likely to be considerably less reduced compared to their bulk and subsurface counterparts, owing to having fewer Zn neighbours. Not only would this factor reduce the repulsive interaction between Cu and O implied by the potentials used (i.e. both species being comparatively electron rich), but also open the possibility for electron transfer from Cu to O (that is to say, partial Cu oxidation), which clearly cannot be accounted for explicitly using the IP unlike the DFT approach. In tandem, these two conclusions support the observed changes upon DFT refinement, which suggest a stronger and more attractive interaction between the surface O adatoms and the Cu cluster atoms.

Table 9 Structure and relative stability for the top 5 ranked low energy IP structures for Cu₈ clusters adsorbed on the reconstructed O-rich Zn-terminated ZnO surface, before and after DFT refinement

IP rank
1	2	3	4	5
IP relative energy/eV
0.000	0.054	0.113	0.132	0.201
DFT rank
4	2	5	3	1
DFT relative energy/eV
2.086	1.063	2.453	1.183	0.000

---

To examine the extent of charge transfer between Cu and surface O adatoms, Bader charge analysis was performed for the lowest energy DFT-optimised structure (corresponding to the 5^th ranked IP structure). The calculated Bader charges show a moderate decrease in electronic charge compared to bulk Cu for all except two of the Cu atoms, with Δβ ranging from −0.17e to −0.28e, averaging −0.23e. The remaining two Cu atoms showed negligible changes in the Bader charges with respect to bulk Cu, with Δβ = −0.00017 and Δβ = +0.003. As illustrated in Fig. 5, the two Cu atoms with least significant Δβ are the only two Cu atoms coordinated only by other Cu atoms, and not coordinated with any surface O adatoms, strongly suggesting that charge transfer from coordinating Cu atoms via surface O adatoms plays a key role in stabilisation of the adsorbed Cu cluster.

Fig. 5 Graphic depicting the lowest energy DFT-optimised structure for a Cu₈ cluster adsorbed on the O-rich Zn-terminated reconstructed polar ZnO surface. The values superimposed on the Cu atoms correspond to Δβ, the difference in the calculated Bader charge for that Cu atom relative to bulk Cu.

The higher mobility of the surface O adatoms (which may be attributed both to a weaker O–Zn interaction and stronger Cu–O interaction for these surface O adatoms compared to that assumed by the IP approach) appears to play an important role in the re-ordering of the lowest energy structures after DFT optimisation. For the IP optimised Cu₈ clusters, the surface O adatoms present a barrier to the favoured planar Cu cluster growth across the flat Zn-terminated surface observed for smaller Cu clusters, hence the IP global minimum features a 3D Cu cluster (consisting of a highly coordinated Cu₇ planar base, with an additional Cu atom on top), whilst the remaining 4 lowest energy structures all feature flat Cu₈ clusters that compromise Cu–Cu coordination in order to minimise close contact with the O surface adatoms. However, upon DFT refinement, no such condition appears to be present, hence the DFT global minimum (which was obtained from refinement of the 5^th lowest energy IP structure) features a distinctive planar Cu cluster with a minimal perimeter (maximising Cu–Cu coordination), with the surface O adatoms positions at the corners of the flat Cu cluster (i.e. interacting with the least coordinated Cu atoms). By contrast, the IP global minimum structure is only the 4^th lowest energy DFT structure (whilst retaining its 3D morphology), with only the 3^rd lowest energy IP structure being found to be less stable upon DFT refinement, which can be attributed to the low Cu–Cu coordination evident in the initial IP structure, which is preserved upon DFT optimisation.

Clearly, in this case, the IP global optimisation approach cannot be used alone to approximate DFT global minimum energy structures. However, the present results illustrate the limitations of the approach and provide key insights that will be invaluable in the tailoring of the interatomic potentials to meet the needs of more complex systems.

Another interesting observation pertains to the O-poor Zn terminated surface. Whilst the overall trend in stability is reproduced, with the lowest energy IP structure being found to also be the lowest energy DFT structure, the DFT-refined lowest minimum structure is considerably more stable than the other low-energy DFT-refined structures compared to the IP relative energies. The enhanced stability of the DFT global minimum structure compared to its IP counterpart can be linked to the lesser degree of O reduction for the O atoms that define the Zn surface vacancy pit. Whilst the highly coordinated planar Cu₈ structure is largely retained after DFT optimisation of the IP global minimum, we see that the position of the cluster has shifted such that the least coordinated Cu atom (having only 2 Cu neighbours) is located within the Zn vacancy pit, implying a degree of Cu oxidation from interaction with the O atoms within the surface pit that lack a full complement of Zn neighbours (Fig. 6). To test this, Bader charge analysis was performed; we find that the Cu atom located within the Zn vacancy surface pit is significantly more oxidised than the remaining 7 Cu atoms in the cluster, with a Bader charge increase of Δβ = −0.57e, with respect to a single isolated neutral Cu atom. By comparison, for the remaining 7 Cu atoms, Δβ ranges from −0.21e to +0.06e, averaging Δβ = −0.09e, consistent with essentially unoxidized Cu⁰, with this small deviation being attributable to the charge delocalisation owing to the metallic character of Cu. The Δβ calculated for the Cu atom located within the Zn vacancy site is consistent with previous studies which determined the Bader charges for Cu and O in bulk Cu₂O, determining Δβ = −0.53e using the PBE GGA functional.⁴⁴ Hence, there is strong evidence that in the present system, the Cu atom which is located within the Zn surface vacancy site after DFT refinement corresponds to a Cu⁺ cation, in line with previous DFT studies which suggest that oxidising Cu atoms within surface Zn vacancy sites can serve as anchor sites for Cu cluster growth.²⁶ This finding is consistent with our rationalisation of the more drastic changes observed for DFT refinement of the Cu clusters on top of the O-rich Zn-terminated surface. For the other DFT refined structures, no such migration of the Cu cluster to accommodate one Cu atom in a Zn vacancy site is observed, which is reflected in the gap in stability between the global minimum and all 4 of the remaining DFT optimised structures. Nonetheless, in all of the other structures, it is still the case that after DFT refinement, the Cu clusters adopt slightly more planar clusters; whilst none of the cluster geometries deviate significantly from their IP optimised positions atop the large hexagonal surface ZnO platform, the DFT optimised structures show Cu atoms much closer to the edges of the hexagonal platform, decreasing the distance between the Cu atoms at the edge of the cluster and the undercoordinated O atoms defining the edges of the Zn vacancy pits. This result further suggests that the interaction between Cu and undercoordinated surface O is perhaps not as repulsive as that described using IP methods, agreeing with the rationalisation for the impact of DFT refinement on the O-rich Zn-terminated surface.

Fig. 6 Graphics depicting the lowest energy IP structure (left) and the DFT-refined lowest energy structure (right) for a Cu₈ cluster adsorbed on a Zn-poor Zn-terminated surface (i.e. featuring Zn vacancies). Note the shift of the Cu₈ cluster such that one of the Cu atoms is located within the Zn vacancy in the DFT-refined structure (indicated with yellow circles). Thin green lines indicate cell boundaries.

For comparison, Bader charge analysis was also performed on the lowest energy DFT optimised Cu₈ configuration for the remaining two surfaces. Whilst we do not observe the same extent of Cu oxidation observed for the Cu atom located within the Zn vacancy of the Zn-poor Zn-terminated surface, a similar trend is noted whereby more significant charge transfer from Cu atoms is observed for Cu atoms which are more highly coordinated with surface O atoms.

For the O-poor O-terminated surface, the most stable DFT structure consists of the Cu₈ located largely within the surface pits arising from the O vacancies, with most of the Cu atoms lying below the topmost ZnO layer. Bader charge analysis reveals that whilst the topmost three Cu atoms are not significantly oxidised (average Δβ = −0.04e), the 5 Cu atoms located mostly below the topmost ZnO layer were significantly more so (average Δβ = −0.28e). For the topmost ZnO layer, whilst the Bader analysis showed little deviation between the electron count for surface O atoms and that of O atoms in the ZnO bulk, some of the surface Zn atoms were considerably reduced compared to Zn atoms in bulk ZnO (average Δβ = +0.31e for the 3 most reduced Zn atoms). This suggests that stabilisation of the Cu cluster involves some degree of charge transfer from Cu to surface Zn atoms which are necessarily undercoordinated owing to the missing surface O atoms arising from the vacancy. Whilst the electron count values are insufficient to suggest full oxidation of Cu by surface Zn, the observations are consistent with delocalisation of electron density between the adsorbed Cu and the less oxidised undercoordinated Zn atoms which are thus more metal-like.

For the Zn-rich O-terminated surface, we see a very similar trend, with three of the eight adsorbed Cu atoms having small Δβ (average +0.02e), and the remaining five being moderately oxidised (average Δβ = −0.27e). Again, the three relatively unperturbed Cu atoms are located in the topmost layer of the 3D Cu cluster observed on this surface, and thus have no direct contact with the surface ZnO atoms, thus more closely resembling bulk Cu. Conversely, for the surface Zn adatoms, whilst four of the six present have relatively small Δβ values relative to Zn atoms in bulk ZnO (average Δβ = +0.08e), the remaining two surface Zn atoms show a marked increase in electronic charge (average Δβ = +0.60e). These two surface Zn adatoms are those directly adjacent to the adsorbed 3D Cu cluster, strongly suggesting that undercoordinated surface Zn adatoms are able to stabilise the Cu cluster by accepting electrons from Cu.

Overall, the Bader charge analyses show that there is indeed an electronic component to the stabilisation of adsorbed Cu clusters, and that the surface features arising from reconstruction of the polar ZnO surfaces, namely O and Zn adatoms and vacancies, are of importance in mediating this stabilisation mechanism.

Discussion

Structure of Cu clusters adsorbed on reconstructed polar ZnO surfaces

The global optimisation studies show very clearly that the Cu cluster morphology is closely linked to the different surface sites presented by different ZnO surface reconstructions. In general, we find that, at least for smaller Cu clusters, planar growth is favoured on the Zn-terminated surface, whilst 3D cluster growth is favoured for the O-terminated surfaces. This difference can be attributed to the highly attractive Cu–Zn interaction modelled by the IP method used; in the absence of any surface reconstruction, the Zn-terminated surface presents a flat plane of surface Zn atoms, hence Cu clusters form by spreading evenly over this surface to maximise the attractive Cu–Zn interaction, with the surface features arising from the reconstruction (Zn vacancies and O adatoms) merely serving to impede complete Cu monolayer formation due to the repulsive Cu–O interactions. On the other hand, the unreconstructed O-terminated surface conversely presents as a flat plane of O atoms which is not conducive to Cu cluster growth; however the surface features arising from reconstruction (O vacancies and Zn adatoms) provide undercoordinated Zn atoms at the surface which can serve as a nucleation site for 3D Cu cluster growth.

Whilst the observed Cu cluster morphology determined in the present work appears to contradict previous experimental STM studies, which reported 3D Cu cluster growth on the Zn-terminated surfaces,¹⁹ and 2D planar Cu cluster growth on the O-terminated surface,²⁰ the rationalisation for the observed cluster morphologies in these works and the present work has, in fact, the same basis, and the apparent contradiction arises from the difference in cluster size. Dulub et al. rationalise the 3D Cu cluster growth over the reconstructed Zn-terminated surface as being the result of a high kinetic barrier to extensive planar Cu cluster growth resulting from repulsive interactions between Cu and undercoordinated surface O at surface ZnO terrace edges and Zn vacancy pits, implying then that Cu cluster growth is indeed 2D planar up until the point at which the Cu monolayer becomes larger enough to reach the barriers imposed by the undercoordinated surface O atoms, at which point subsequent Cu cluster growth results in the 3D clusters observed experimentally.¹⁹ This argument is entirely consistent with the observed patterns of Cu cluster growth on the Zn-terminated surface obtained from the global optimisation studies performed in the present work; for both the O-adatom and Zn-vacancy reconstructions, planar Cu growth does indeed occur for smaller numbers of Cu atoms, and as can be seen for the larger Cu₈, Cu₂ and Cu₅₀ systems, 3D Cu cluster growth does indeed take place instead of continued planar cluster growth once the Cu cluster meets the boundaries imposed by the undercoordinated surface O atoms. This effect is particularly noticeable for the Zn-poor Zn terminated surface; Cu cluster growth is almost exclusively planar up to and including the Cu₈ system, whilst the Cu₂₄ cluster shows distinct 3D growth, and the boundaries of the Cu₂₄ are observed to be consistent with that defined by the edges of the surface Zn vacancy pits which consist of undercoordinated O atoms. Hence, the apparent contradiction between the present work and previous experimental studies is merely a consequence of the inability of experimental studies to observe Cu cluster growth at a level of sequential atomic growth of small clusters, and conversely the limitation imposed by ZnO surface cell size in the present work that prohibits the modelling of very large Cu clusters confined to ZnO surface terraces, as observed in the experimental studies. Taken in tandem, however, the present work and the previous STM studies provide a detailed illumination of the factors controlling Cu cluster growth on the reconstructed Zn-terminated polar (0001) surface. Hence, upon closer inspection, there is in fact no true contradiction between the previous STM studies and the present work, since the Cu cluster sizes investigated are of vastly different orders of magnitude. The rationalisation for the observed Cu cluster morphologies put forward in the present work confirm those suggested by the previous experimental studies, illustrating how these factors can affect the structures of small and large adsorbed Cu clusters in different ways.

The findings of the present work concerning Cu cluster morphology over the O-terminated reconstructed polar ZnO surface are more difficult to reconcile with those of the experimental STM studies, owing to the various technical challenges inherently associated with the O-terminated polar ZnO surface.^19,20 Whilst the experimental studies concluded that planar Cu cluster growth takes place on the O-terminated surface, a maximum Cu cluster height of ∼4.7 Å was observed, which is consistent with Cu clusters consisting of more than one layer of adsorbed Cu, and corresponds well with the 3D Cu clusters on the O-terminated surface obtained in the present work, such as the Cu₂₄ cluster adsorbed on the reconstructed O-terminated surface featuring Zn adatoms, for which the topmost Cu atoms were positioned at 4.17 Å above the topmost complete ZnO surface layer and consisted of 2–3 layers of Cu atoms. Moreover, it was observed for this system that the strong Cu–Zn interaction between the cluster and the surface resulted in the surface Zn atoms being lifted above their equilibrium positions on the clean surface, hence with respect to the clean O-terminated surface, the height of the topmost Cu atoms would be even greater than 4.17 Å, bringing the computationally determined cluster height closer to the experimentally reported value. It is possible, then, that the apparent contradiction between the Cu cluster height and supposed planar Cu cluster growth observed in the experimental STM studies could essentially be a result of saturation of the O-terminated surface with Cu, resulting in a coalescence of discrete Cu clusters (cf. the Cu₅₀ systems), which might present experimentally as a flat surface consisting of 2 or 3 layers of adsorbed Cu. In any case, whilst the comparison between the STM studies and the computational results in the present work may be less complete for the O-terminated surface than for the Zn-terminated surface, the rationalisation for the 3D Cu cluster growth on the O-terminated surfaces in the present work is simply a consequence of the well-established attractive Cu–Zn interaction, and the presence of surface sites featuring undercoordinated Zn (i.e. Zn adatoms or O vacancies) which were found to be the favoured sites for Cu cluster growth, as opposed to Cu atoms spreading over the surface to maximise Cu–Zn interactions as observed for the Zn-terminated surfaces, thus promoting 3D Cu cluster growth. Once again, it can be seen that the conclusions drawn from our studies are consistent with those obtained from previous experimental studies; hence, no true contradiction between the present work and these previous studies exist, with any apparent discrepancies linked to the vastly different Cu cluster sizes being modelled here, compared with those being observed in STM studies.

Adsorption of Cu clusters

The IP calculated adsorption energies for the global minimum structures with respect to bulk Cu show that Cu clusters of the same size are more strongly adsorbed on the O-poor O-terminated surface, and on the O-rich Zn-terminated surface, compared to the remaining other two reconstructed surfaces. In both cases, this behaviour can be attributed to these reconstructions affording undercoordinated Zn environments that maximise the opportunity for attractive Cu–Zn interactions upon adsorption of the Cu cluster. However, whilst the Cu cluster adsorption energies with respect to bulk Cu were found to be endothermic for the Zn-rich O-terminated and Zn-poor Zn-terminated surfaces, this finding can be attributed to the high energetic cost of cleaving small Cu clusters from bulk, hence we might expect small, isolated Cu nanoclusters to interact strongly and exothermically with the reconstructed polar ZnO surfaces discussed in the present work. As we might expect that, under real conditions, reconstructed surfaces will feature a mixture of surface sites resembling the various Zn and O adatom and vacancy sites explored in the present work, we can expect that Cu cluster growth might take place at any of these sites.

Validation of IP approach

The interatomic potentials used in the present work have already been demonstrated to be highly successful in obtaining low-energy structures for Cu clusters adsorbed on the non-polar ZnO surface, and are an effective means of screening potential structures in a computationally expedient manner. However, the reconstructed polar ZnO surface explored in the present work shows surface features that consist of undercoordinated Zn and O atoms that deviate considerably from typical surface and bulk Zn and O coordination environments present in the non-polar ZnO surface that was used as a model for fitting the Cu–ZnO potentials. Hence, it is of interest to assess the extent to which these potentials successfully identify global and local minima which are reproduced upon DFT refinement. Overall, the results show that in most cases, these potentials perform very well, with the global minimum energy IP structure for a Cu₈ cluster being retained upon DFT optimisation for three of the four surface reconstructions investigated. Furthermore, in those cases, the general trend in stability for the remaining top 4 local minima was broadly reproduced, with only minor changes in stability ordering being observed. The O-rich Zn-terminated surface was the only surface reconstruction for which the IP approach failed to identify a global minimum energy structure or retain any reasonable agreement in terms of stability ordering of the local minimum energy structures upon DFT refinement. This problem can be attributed to the highly exothermic electron affinity of O, resulting in stronger Cu–O attractive interactions than that supposed by the IP approach, owing to partial oxidation of Cu by undercoordinated surface O adatoms, which is also reflected in the significant displacement of the surface O adatoms from their positions on the clean surface, since any energetic cost associated with this process is compensated by exothermic electron transfer from Cu to O adatoms. Furthermore, it is noted that the IP approach utilised Cu/ZnO potentials fitted to DFT calculations performed for small Cu clusters approaching relaxed, unreconstructed, non-polar ZnO (101̄0) and (112̄0) surfaces, and thus were not fitted to systems that have significantly undercoordinated surface O atoms, which are present in some of the reconstructed surfaces discussed in the present work. Hence, given that potentials used do not account for undercoordinated surface O atoms, which can be understood to be less reduced than typical surface O atoms that have more Zn neighbours, it is worth considering that perhaps an IP approach including potentials for Cu⁺ and Cu²⁺ would perform far better in identifying global minima which are reproduced upon DFT refinement, if there is indeed a more significant extent of Cu oxidation taking place in this system. Whilst deriving new potentials for Cu⁺ and Cu²⁺ is outside the scope of the present work, an IP approach considering different Cu oxidation states would additionally be of interest to afford comparison with previous computational QM/MM studies which found oxidised Cu to play a key role in Cu cluster growth by functioning as an anchor site, in particular at surface Zn vacancy sites.^26,28

Conclusions

The IP global optimisation approach employed in the present work is largely successful in identifying low-energy structures for Cu cluster growth upon different O- and Zn-terminated reconstructed polar ZnO surfaces, as largely verified by the DFT refinement. Only the O-rich Zn-terminated reconstructed surface posed a significant challenge, which we conclude is a result of electron transfer, namely from adsorbed Cu to undercoordinated surface O adatoms which are not fully reduced, which is not well-accounted for by the IP model applied. Hence, future studies will consider applying a similar methodology including potentials for Cu⁺ and Cu²⁺, in order to be able to conduct a more effective screening of potential Cu cluster adsorption geometries. Nonetheless, for all four of the reconstructed surfaces investigated, IP and DFT structures largely agreed upon typical Cu cluster morphologies, with planar Cu cluster growth being favoured for Zn-terminated reconstructions, whilst 3D Cu cluster growth was observed for the O-terminated reconstructed surfaces. Whilst at first sight these findings do not appear to agree with previous experimental STM studies, upon closer examination it is clear that the discrepancies are probably a consequence of the differences in the size of the clusters modelled in the current study compared with those investigated in the experimental work. Moreover, the rationalisation for the observed behaviour, namely that a strong Cu–Zn attractive interaction and Cu–O repulsive interactions are responsible for the observed Cu cluster morphology, is consistent with the rationalisations proposed for previous experimental studies. Hence, the results obtained in the present work corroborate the previous STM experimental studies and illustrate how surface features of the reconstructed polar ZnO surfaces can affect the morphology of adsorbed Cu clusters of different sizes. The IP-calculated Cu cluster adsorption energies show that Cu clusters adsorbed on the O-poor O-terminated surface, and the O-rich Zn-terminated surface, are especially stable, with highly exothermic adsorption energies, although for Cu clusters adsorbed on all four ZnO reconstructed surfaces investigated, the attractive interaction between Cu and the ZnO surface means that all of the investigated Cu cluster morphologies are potentially feasible.

The present work represents a detailed and thorough investigation of the growth and morphology of Cu clusters over reconstructed polar ZnO surfaces, providing additional evidence for the efficacy of the IP global optimisation approach used in this work and in related previous computational studies, and revealing new insights into the structure of Cu clusters on ZnO surfaces that is complementary to existing experimental studies. Furthermore, the Cu/ZnO structures obtained in the present work are an ideal starting point for future computational investigations exploring key processes, such as CO₂ adsorption and activation, and subsequent catalytic hydrogenation processes, providing model catalysts that exhibit interesting surface features, especially at the Cu/Zn interface, that could play an important role in the behaviour of the industrial Cu/ZnO catalyst used for methanol synthesis. We intend that this comprehensive and exhaustive computational study will provide valuable insights into the role of support surface structure in determining metal nanoparticle growth, and thus continue the drive towards a more complete and accurate model for complex multi-component catalyst materials.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported through the Global Challenges Research Fund (GCRF) through Science & Technology Facilities Council (STFC), grant number ST/R002754/1: Synchrotron Techniques for African Research and Technology (START). Additionally, the authors acknowledge the support of the Supercomputing Wales project, which is part-funded by the European Regional Development Fund (ERDF) via Welsh Government, STFC Scientific Computing Department's SCARF cluster, and the UK National Supercomputing Service ARCHER (accessed via membership of the Materials Chemistry Consortium which is funded by EPSRC (EP/L000202)), for the provision of computational resources. The UK Catalysis Hub is thanked for resources and support provided via membership of the UK Catalysis Hub Consortium and funded by EPSRC (Grants EP/R026815/1).

References

1. K. C. Waugh, Catal. Lett., 2012, 142, 1153–1166.
2. G. C. Chinchen, P. J. Denny, D. G. Parker, M. S. Spencer and D. A. Whan, Appl. Catal., 1987, 30, 333–338.
3. G. C. Chinchen, P. J. Denny, J. R. Jennings, M. S. Spencer and K. C. Waugh, Appl. Catal., 1988, 36, 1–65.
4. M. Bowker, R. A. Hadden, H. Houghton, J. N. K. Hyland and K. C. Waugh, J. Catal., 1988, 109, 263–273.
5. D. Waller, D. Stirling, F. S. Stone and M. S. Spencer, Faraday Discuss. Chem. Soc., 1989, 87, 107–120.
6. M. M. Günter, T. Ressler, R. E. Jentoft and B. Bems, J. Catal., 2001, 203, 133–149.
7. B. L. Kniep, T. Ressler, A. Rabis, F. Girgsdies, M. Baenitz, F. Steglich and R. Schlögl, Angew. Chem., Int. Ed., 2004, 43, 112–115.
8. T. Ressler, B. L. Kniep, I. Kasatkin and R. Schlögl, Angew. Chem., Int. Ed., 2005, 44, 4704–4707.
9. M. Behrens, F. Studt, I. Kasatkin, S. Kuhl, M. Havecker, F. Abild-Pedersen, S. Zander, F. Girgsdies, P. Kurr, B.-L. Kniep, M. Tovar, R. W. Fischer, J. K. Norskov and R. Schlogl, Science, 2012, 336, 893–897.
10. M. Behrens, I. Kasatkin, S. Kühl and G. Weinberg, Chem. Mater., 2010, 22, 386–397.
11. J. P. Breen and J. R. H. Ross, Catal. Today, 1999, 51, 521–533.
12. G. C. Shen, S. I. Fujita, S. Matsumoto and N. Takezawa, J. Mol. Catal. A: Chem., 1997, 124, 123–136.
13. F. Studt, M. Behrens and F. Abild-Pedersen, Catal. Lett., 2014, 144, 1973–1977.
14. M. S. Spencer, Top. Catal., 1999, 8, 259–266.
15. D. Mora-Fonz, T. Lazauskas, M. R. Farrow, C. R. A. Catlow, S. M. Woodley and A. A. Sokol, Chem. Mater., 2017, 29, 5306–5320.
16. M. Capdevila-Cortada and N. López, Nat. Mater., 2017, 16, 328–334.
17. M. Bowker, H. Houghton, K. C. Waugh, T. Giddings and M. Green, J. Catal., 1983, 84, 252–255.
18. M. Grunze, W. Hirschwald and D. Hofmann, J. Cryst. Growth, 1981, 52, 241–249.
19. L. V. Koplitz, O. Dulub and U. Diebold, J. Phys. Chem. B, 2003, 107, 10583–10590.
20. O. Dulub, M. Batzill and U. Diebold, Top. Catal., 2005, 36, 65–76.
21. D. Mora-Fonz, T. Lazauskas, S. M. Woodley, S. T. Bromley, C. R. A. Catlow and A. A. Sokol, J. Phys. Chem. C, 2017, 121, 16831–16844.
22. M. L. Paleico and J. Behler, J. Chem. Phys., 2020, 153(5), 054704.
23. S. A. French, A. A. Sokol, S. T. Bromley, C. R. A. Catlow, S. C. Rogers, F. King and P. Sherwood, Angew. Chem., 2001, 113, 4569–4572.
24. C. R. A. Catlow, S. A. French, A. A. Sokol, M. Alfredsson and S. T. Bromley, Faraday Discuss., 2003, 124, 185–203.
25. S. A. French, A. A. Sokol, S. T. Bromley, C. R. A. Catlow and P. Sherwood, Top. Catal., 2003, 24, 161–172.
26. S. T. Bromley, S. A. French, A. A. Sokol, C. R. A. Catlow and P. Sherwood, J. Phys. Chem. B, 2003, 107, 7045–7057.
27. C. R. A. Catlow, S. A. French, A. A. Sokol and J. M. Thomas, Philos. Trans. R. Soc., A, 2005, 363, 913–936.
28. S. A. French, A. A. Sokol, C. R. A. Catlow and P. Sherwood, J. Phys. Chem. C, 2008, 112, 7420–7430.
29. L. Martínez-Suárez, J. Frenzel and D. Marx, Phys. Chem. Chem. Phys., 2014, 16, 26119–26136.
30. B. Yang, C. Liu, A. Halder, E. C. Tyo, A. B. F. Martinson, S. Seifert, P. Zapol, L. A. Curtiss and S. Vajda, J. Phys. Chem. C, 2017, 121, 10406–10412.
31. G. Shi, Q. Chen, Q. Zhang, W. Cai, Z. Li, S. Zhai, H. Yu, F. Tan and Y. Wang, J. Saudi Chem. Soc., 2020, 24, 42–51.
32. S. M. Woodley, J. Phys. Chem. C, 2013, 117, 24003–24014.
33. M. R. Farrow, Y. Chow and S. M. Woodley, Phys. Chem. Chem. Phys., 2014, 16, 21119–21134.
34. T. Lazauskas, A. A. Sokol and S. M. Woodley, Nanoscale, 2017, 9, 3850–3864.
35. J. D. Gale, J. Chem. Soc., Faraday Trans., 1997, 93, 629–637.
36. J. D. Gale and A. L. Rohl, Mol. Simul., 2003, 29, 291–341.
37. L. Whitmore, A. A. Sokol and C. R. A. Catlow, Surf. Sci., 2002, 498, 135–146.
38. F. Cleri and V. Rosato, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 22–33.
39. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(6), 11169–11186.
40. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
41. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
42. G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
43. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 1–4.
44. R. Laskowski, P. Blaha and K. Schwarz, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 075102.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ta08351h

---