Vanadium oxynitrides as stable catalysts for electrochemical reduction of nitrogen to ammonia: the role of oxygen

Abstract

Electrochemical reduction of nitrogen to ammonia can potentially replace the existing centralized fossil fuel-based Haber–Bosch process with small, decentralized units relying on electrical energy from renewable sources, thus supporting a sustainable food and energy infrastructure. Recent activities in the development of transition metal nitride electrocatalysts for this reaction have shown promise, but oxynitrides remain unexplored. We have performed a rigorous computational study of the highly promising vanadium oxynitride (VON) to establish for the first time the nitrogen reduction pathway in oxynitrides and the role of the mixed anions that can lead to improved stability of the active surface-states, activity, and selectivity over hydrogen evolution. The electrocatalytic properties are best enhanced at low oxygen content (12.5%) due to optimal balance between consecutive protonation preference at N-sites over V-sites, low onset potential (0.4 V-RHE), and facile N₂ adsorption at N-vacancy sites, while a higher oxygen containing VON (31.25%) shows the lowest N₂ adsorption/dissociation barrier (∼0.3 eV) on the anion vacancy and can also be a potential N₂RR catalyst with a higher NH₃ turn over frequency, albeit with a lower stability and higher overpotential (0.6 V-RHE) compared to x = 12.5%. The critical N-vacancy active sites are protected from self-annihilation by the mixed-valency anions, large kinetic barriers, and site blocking by O*/OH*/H* due to highly favorable N₂ absorption.

---

Introduction

Activation of dinitrogen from the atmosphere to produce ammonia via biological and industrial processes sustains life on Earth as we know it. Ammonia is an essential chemical feedstock for the synthesis of nitrogen-based fertilizers that enables farmers to feed billions more people than our planet could otherwise not support.^1,2 Ammonia is also a building block for manufacturing other synthetic chemicals, medicaments, dyes, explosives, and resins. Liquid NH₃ contains 17.6 wt% hydrogen, is easy to transport and store – thus, it can be a carbon-free energy carrier as well.^3,4 Ammonia is the world's most-produced chemical at 170 million metric tons per year. Although nitrogen is an abundant raw material for ammonia production, the large bond energy (940.95 kJ mol⁻¹) of the N≡N bond makes N₂ reduction reaction (N₂RR) extremely difficult. Industrial-scale NH₃ production relies on the Haber–Bosch process,⁵ where the H₂ feedstock is normally produced from fossil fuels, and each metric ton of NH₃ produced will emit ∼1.9 metric tons of CO₂. Also, high-temperature (620–820 K) and high-pressure (150–350 atm) production conditions necessitates capital-intensive centralized production, while the consumption is distributed quite uniformly over all populated areas on Earth. Less developed regions are dependent on inefficient and expensive supply from centralized sources and thus pose a risk to equitable growth. Small-scale devices that produce ammonia onsite could alleviate some of these problems by producing fertilizer on-demand at the point of usage.⁶ However, such devices would require a much simpler and near-ambient condition process. An electrochemical route to NH₃ production from N₂, H₂O, and renewable energy sources can revolutionize a green NH₃ production industry by cutting down fossil fuel consumption and reducing the carbon footprint of agricultural activities.⁷ It can provide decentralization of the process and thus reduce the waste and transportation-related impacts as well. Electrochemical N₂RR works well with the intermittency of renewable energy sources like wind and solar power, as ammonia can be produced and stored⁸ when excess renewable electricity is generated over user demands.

Given the impact of discovering highly active and stable electrocatalysts for ammonia production, the field has seen intense research activity across the world.^9–17 Platinum group metal catalysts are often used as catalysts because of their stability in acidic environments, but they generally have low faradaic efficiencies (FE < 0.1%) for N₂RR. This is attributed to the scaling relation between various surface adsorbed intermediates in the N₂RR and the competing hydrogen evolution reaction (HER), which is always favored across different metals.¹⁸ As an alternative to noble metal catalysts, non-precious metal catalysts and metal-free carbon catalysts have been explored broadly as N₂RR electro-catalysts. Among them, transition metal nitrides (TMN) has been proposed as being both active and highly conductive.^19–25 Nitrides have a potential advantage of being able to form ammonia by a Mars–van Krevelen (MvK) mechanism, in which a surface N atom is reduced to NH₃ and the surface vacancy thus created is repopulated with N₂. This is followed by the removal of the extra N-atom as ammonia through consecutive protonation. Hence, the catalyst surface is regenerated rather than adsorbing N₂ directly to the catalyst surface. It has been observed experimentally that the best yield rate and faradic efficiencies are obtained for transition metal oxynitrides (TMON) compared to pure nitride catalysts.^22,26–28 Existing theoretical work^21,29,30 has focused on the N₂RR mechanism on nitride surfaces, and have not studied the atomistic mechanism, thermodynamic limitations on oxynitrides in details. For example, vanadium nitride, which has been investigated theoretically,²⁹ does not display good long term stability^31–33 in the N₂RR electrochemical environment as nitrogen and vanadium leach into typical electrolyte solutions, thus limiting its application in ammonia electro-synthesis through N₂RR. In fact, some experiments indicate that pure nitrides might actually be just decomposing towards ammonia evolution,^32,34 and recent spectroscopic characterization identifies that pure vanadium nitride is inactive for N₂RR,^22,34 while oxynitride variety shows good activity.^22,26 It is hypothesized that only the surface N sites adjacent to a surface O show activity for the N₂RR.³³ The most recent studies on other TMONs^26–28 further strengthen the necessity of oxygen/nitrogen co-existence for favorable N₂RR activity and stability.

A detailed understanding of the structural details, stability, N₂RR mechanism and the thermodynamic pathway is lacking for TMON N₂RR catalysts. Such fundamental insights are critical for further development and optimization of TMON electro-catalysts for N₂RR. Here, we have performed a rigorous study of the structural aspects of bulk and surface VON to identify the beneficial chemical properties towards nitrogen reduction over pure vanadium nitride. We also establish the impact of oxygen in stabilizing and keeping the catalytic site and surface active.

Results

VON bulk structure

The structure of VON has been resolved with multiple experimental techniques to be stable cubic rock-salt phase (for VO_xN_1−x with nitrogen-rich compositions, x < 0.5).^35–37 The nitrogen-rich composition of the cubic VO_xN_1−x can be explained from the fact that the pure vanadium nitride (VN) exists in a cubic rock-salt structure, where pure vanadium oxide does not have a stable cubic phase. The most stable vanadium oxide is V₂O₅ with an orthorhombic crystal structure. Therefore, the reported stable rock-salt phase of VO_xN_1−x is compositionally closer to vanadium nitride than vanadium oxide. However, the most stable (and active) composition of VO_xN_1−x is not yet well defined. To determine the crystal structure and thermodynamically favorable composition, we have calculated the mixing enthalpy of rock-salt VN and VO phases. Based on a 32 atom supercell, all possible 1610 unique symmetry inequivalent VON structural configurations were simulated considering ferromagnetic and antiferromagnetic spin ordering. Based on these total energy calculations, low energy structures were identified for the full range of O/N ratio. The resultant convex hull with varying O-concentration (x%) is demonstrated in Fig. 1a using VO rock-salt as a reference. If pure V₂O₅ is used as a reference for vanadium oxide (Fig. S1†), the calculated cubic phases are higher in energy, but the rock-salt structures have been shown experimentally to be metastable for limited-to-moderate oxygen content, possibly due to large ion/vacancy migration barrier and related surface stabilization as discussed below. Experimental evidence also suggests N/O ratio > 1 in the ternary phase diagram of V, N, and O.³⁵

Fig. 1 (a) The mixing energy of VN and VO phases and (b) distorted polyhedral in VON compared to pure VN and pure VO (V: golden yellow, O: red and N: blue).

We find a non-uniform distribution of N and O in the crystal structure of the minimum energy configurations for different N/O compositions (Fig. S2†) along the convex hull. There is a sharp disparity in the chemical interaction of O and N with V in VON. The charge density analysis shows that the degree of covalency for the N–V bond is more pronounced than the V–O bond (Fig. S3†). This disparity between O and N anions also results in distorted polyhedral around V cations (Fig. 1b). Table S1† contains the lattice parameters and the cell volume of the lowest energy configurations of VO_xN_1−x with different N/O ratios. The combined effect of the difference in the chemical nature of V–O and V–N bonds and non-uniform distribution of N/O breaks the crystal symmetry in VO_xN_1−x, although structure remains close to cubic rock-salt.

VON surface composition and stability

We studied (100) surfaces of the lowest energy configurations from the convex hull with different N/O compositions (O < 50%). The cleaving of bonds makes the surface atoms chemically different from the bulk, and the stability of the surface depends on the surface composition and atomic ordering. Both VO and VN are known to display non-stoichiometry mainly due to the presence of a significant amount of V-vacancies^38–40 along with anion vacancies. It is important to note that the formation and stabilization of anion surface vacancies are not detrimental, but the opposite in this case, as they are the active sites for N₂ adsorption and continuation of the N₂RR by MvK mechanism. The V-vacancy formation, on the other hand, can cause structural instability and inactivity of the catalytic surface. Eqn (1), represents the V-vacancy (*^V-vac) formation along with metallic vanadium (V_metal) from the surface metal site (*^V).

*^V → *^V-vac + V_metal (1)

O on the nitride surface is reported to be unstable under N₂RR conditions. Any O on the nitride surface is reduced and removed as water long before the system attends the N₂RR onset potential.²⁹ Hence, in the working condition of N₂RR, O will mostly be in the bulk while the surface will contain N and V atoms of the VON. Therefore in the N₂RR study of VON, we focused on these surfaces. Fig. 2 shows the relative stability regarding the V-vacancy formation energy of stoichiometric surfaces for the N-rich composition (x = 0% to x = 43.75%) on the convex hull. The top layer of these surfaces consists of N and V atoms, while the O atoms populate the subsurface layers (Fig. S4†). The stability of the V atoms on the surface increase with an increasing amount of O concentration in the system and reaches a peak at x = 18.75% and is followed by a decreasing trend. For O concentrations x = 6.25% to x = 37.5%, the surface V-atom display enhanced stability compared to pure VN (x = 0). It confirms the positive influence of oxygen on the stability of the catalytic surface.

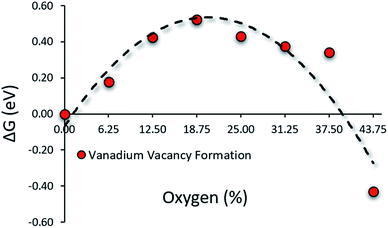Fig. 2 Presence of oxygen in low concentrations enhances surface stability by hindering vanadium leaching from the surface.

Catalysis on VON surface

Reduction of N₂ to NH₃ occurs on the cathode surface, and the overall electrochemical reaction is:

N_2(g) + 6(H⁺ + e⁻) → 2NH_3(g) (2)

The corresponding anode reaction that acts as a proton source is:

3H_2(g) ↔ 6(H⁺ + e⁻) (3)

The main challenge in N₂RR selectivity is the competition with hydrogen evolution reaction, which often have lower overpotential than N₂RR.

Selectivity over HER

In a MvK mechanism, a surface N (*^N) gets protonated thrice to release one molecule of NH₃ leaving an N-vacancy (*^N-vac) on the site (eqn (4)–(7)).

*^N + 6(H⁺ + e⁻) → *^NH + 5(H⁺ + e⁻) (4)

*^NH + 5(H⁺ + e⁻) → *^N2H + 4(H⁺ + e⁻) (5)

*^N2H + 4(H⁺ + e⁻) → *^N3H + 3(H⁺ + e⁻) (6)

*^N3H + 3(H⁺ + e⁻) → *^N-vac + NH_3(g)↑ + 3(H⁺ + e⁻) (7)

A competing hydrogen transfer step is hydrogenation of the V-site (*^V) instead of the N-site (eqn (8)). It is important to note that the hydrogen will not be protonic, but hydridic, as discussed below.

*^V + (H⁺ + e⁻) → *^VH (8)

H* on protonated N and H* on V has a very different chemical nature. H* on protonated N takes a positive oxidation character, while H* on V takes a negative oxidation character (hydride ion). Table S2† contains the Bader charges calculated for different H. The bond length of N–H is ∼1.0 Å, and V–H is ∼1.70 Å (Fig. 3). In the case of V, the hydride ion can react with a proton from water (eqn (9)) or H from neighboring protonated N site (eqn (10)) to evolve hydrogen. The existence of H* with anionic and cationic character in the neighboring sites is unstable and reacts spontaneously with each other to form H₂ (Fig. S5†). The possible mechanism of HER from a protonated V-site is schematically represented in Fig. 3a.

*^VH + (H⁺ + e⁻) → *^V + H_2(g)↑ (9)

*^VH + *^NH → *^V + *^N + H_2(g)↑ (10)

Fig. 3 (a) Mechanism of HER from protonic and hydride hydrogen, (b) relative energy of –NH over –VH, and (c) energetically strong preference of –NH₂ formation over –NH–VH. (d) Linear correlation between the free energy of fist protonation and N-vacancy format.

Fig. 3b, shows the energy comparison of the VON surface with protonated N and hydrogenated V sites. We found that on the VON surface, protonation of N-site is strongly preferred over V, especially for a lower concentration of O. With increasing O-concentration, the energy difference between these two protonation paths decreases. In Fig. 3c, we have compared formation energy after second hydrogen transfer, one at the N and V sites respectively, or both at the N site. This plot clearly shows the strong thermodynamic drive towards the formation of a consecutive protonation at N-site rather than the formation of protonated one N-site along with one V-site, which leads to HER. The results presented in Fig. 3b and c together has declined the possibility of HER and confirmed selectivity of the VON surface for N₂RR.

According to the MvK mechanism, the N-site that started getting protonated will eventually form one molecule of NH_3, leaving a surface N-vacancy in its place. A linear correlation is observed between the free energy of the first protonation (*^NH) and N-vacancy formation (*^N-vac) on the VON surface with O concentration 0 to 37.5% (Fig. 3d).

The solvent plays an important role on the stability and activity of the VON electrocatalysts and while the applied computational hydrogen electrode (CHE) approach (ref) does not allow for studying the effect of varying pH directly and an explicit treatment of the solvent dynamics, e.g. with AiMD⁴¹ on the work function of the interface states at a given pH⁴² is beyond this type of DFT-based screening study, it is worth noting that increasing pH has recently been shown experimentally to suppress the parasitic hydrogen evolution reaction (HER) as the shift in proton donation form hydronium to water leads to larger barriers and suppressed HER kinetics.⁴³ As N₂RR on VON is not limited by the proton transfer, this could lead to improved selectivity and a detailed computational analysis of the most promising VON compositions should thus be performed subsequently at varying pH conditions.

Regarding an assessment of the stability of the VON catalysts under operating conditions, we present a comprehensive analysis of the thermodynamic aspects and kinetic processes relevant for the catalyst decomposition as a function of potential (in the absence of an explicit solvent). These findings align with our previous analysis of transition metal oxynitride nanoclusters⁴⁴ and experimental findings that the stability of vanadium oxynitride catalyst in reducing electrochemical environment has been shown experimentally to be better than Pt/C,^45,46 as discussed in more detail in the following sections.

N₂RR activity by MvK mechanism on VON

In the MvK mechanism, the N-vacancy formation due to the creation of one molecule of NH₃ from the surface N (eqn (4)–(7)) is followed by the absorption of one N₂ molecule at the vacant site. N₂ adsorption on the vacancy site can happen in two ways: associative and dissociative mechanism. In an associative MvK, the N–N bond remains intact during the adsorption process and starts dissociating only after the protonation of the topmost N of the adsorbed N₂. Eqn (11)–(15) describes the associative MvK, in which gaseous N₂ bound to the vacancy is represented as (*^N-vacN₂). The protonation of the topmost N atom of the vacancy bound N₂ leads to the formation of NH_3(g) and a regenerated catalytic surface (*^N-vacN) which is equivalent to (*^N).

*^N-vac + N_2(g) + 3(H⁺ + e⁻) → *^N-vacN₂ + 3(H⁺ + e⁻) (11)

*^N-vacN₂ + 3(H⁺ + e⁻) → *^N-vacNNH + 2(H⁺ + e⁻) (12)

*^N-vacNNH + 2(H⁺ + e⁻) → *^N-vacNNH₂ + (H⁺ + e⁻) (13)

*^N-vacNNH₂ + (H⁺ + e⁻) → *^N-vacNNH₃ (14)

*^N-vacNNH₃ → *^N-vacN + NH_3(g)↑ = *^N + NH_3(g)↑ (15)

In a dissociative MvK, the N–N bond dissociates directly during the adsorption process, and one of the N atoms then fills up the vacancy site while the second N atom bonds with the neighboring V ion of the vacancy site. Eqn (16)–(20) demonstrate the dissociative MvK. Here, after dissociation of N_2(g), the N replenishing the vacancy site and the N binding to the neighboring metal site is denoted as (*^N-vacN) and (*^VN), respectively.

*^N-vac + N_2(g) + 3(H⁺ + e⁻) → *^N-vacN + *^VN + 3(H⁺ + e⁻) (16)

*^VN + 3(H⁺ + e⁻) → *^VNH + 2(H⁺ + e⁻) (17)

*^VNH + 2(H⁺ + e⁻) → *^VNH₂ + (H⁺ + e⁻) (18)

*^VNH₂ + (H⁺ + e⁻) → *^VNH₃ (19)

*^VNH₃ → *^V + NH_3(g)↑ (20)

Here, we calculate the free energy of all chemical and electrochemical steps considering zero-point energy correction (ΔE_ZPE) and the change in entropy (ΔS) for the adsorbate and the gaseous molecules. Eqn (21) shows the free energy estimation, where the DFT reaction energy is (ΔE).

ΔG = ΔE + ΔE_ZPE − TΔS (21)

The free energy path of NH₃ formation on the VON surface according to associative MvK and dissociative MvK is presented in Fig. 4a. The result shows that the associative MvK path is energetically more demanding than the dissociative MvK. The free energy path is calculated at 0 V on the reversible hydrogen electrode (RHE) scale, and the largest positive step determines the reducing potential required. Strong bonding between V and N lowers the energy of the absorbed N₂ following dissociation of the N–N bonds (Fig. 4b). Our results match with the previous studies on vanadium nitride, which show that (100) facet of the rock-salt mono-nitrides preferred dissociative N₂ adsorption compared to the associative adsorption.²⁹ Our calculations show that the N–N dissociation barrier is in fact substantially larger on VN than previously found using a smaller supercell (∼0.3 eV)⁴⁷ and on the order of ∼1 eV, while the barrier on the oxygen-rich VON surface is substantially lower, e.g., barriers ≤ 0.5 eV, for x = 31.25% and 37.5% as shown in Fig. S6.† The path on the oxygen-rich VON surfaces has a transition state where N₂ is adsorbed on the surface V-site (near the N-vacancy) before dissociation (Fig. S7†). While the N₂ adsorption is preferred at x = 12.5% and 0.4 eV stronger than on VN, the activation energy is still almost as high (∼1 eV). The thermodynamic and kinetic barriers for the adsorption and dissociation reaches the lowest values of ∼0.3 eV for x = 31.25%, as shown in Fig. S8.† It is important to note that these barriers may potentially limit the catalytic turn over frequency, in particular at high overpotentials. Fig. 5a presents the free energy path of N₂RR on the VON surface with an O-concentration of 12.5%. The free energy paths for VON with 0 to 37.5% O content are presented in the supplementary Fig. S6a to S6g.† The highest electrochemical step in these paths is typically related to the first protonation of the surface N (*^NH), except for the VON surface with x = 6.25% (Fig. S9b†) and 18.78% (Fig. S9d†), where the second protonation step (*^N2H) is the highest electrochemical step. Fig. 5b shows the onset potential (vs. RHE) required for N₂RR for different VON surfaces. Increasing the O contents in the VON slab increases the onset potential insignificantly. The lowset onset potential is found for the slab with an O concentration range from 0% to 12.5%, which is only ∼0.4 V. N₂ adsorption on the vacancy site is a non-electrochemical step (eqn 17), and if the step is endothermic, the energy needs to be provided by the surrounding environment. Therefore, it is desirable to have exothermic N₂-adsorption. Fig. 5c demonstrates the free energy of N₂-adsorption on the VON surfaces with varied O-concentrations. The plot shows that for pure VN (x = 0%), the free energy required for the N₂-adsorption is 0.6 eV and endothermic in nature. Increasing O-concentration in the VON slab improves the situation, and the free energy of N₂-adsorption decreases. For VON slabs with x = 12.5, 31.25 and 37.5%, N₂-adsorption on the vacancy site is exothermic and hence expected to be a spontaneous process (Fig. 5c). The N₂-adsorption energy depends explicitly on the surface coverage of N vacancies. Here, the energetics are calculated with 12.5% surface coverage of N vacancies(Fig. 5a and S9†). We observed that by increasing the surface coverage of N vacancies from 12.5% to 25%, the N₂-adsorption energy decreases by 0.7 eV(Fig. S10†) on the VN surface. Based on these results, we can conclude that the VON surface with an x = 12.5% composition, is expected to be the best catalyst for N₂RR considering both activity and selectivity over HER, as well as spontaneous absorption of N₂ at the vacancy site.

Fig. 4 (a) Free energy path of dissociative and associative MvK. (b) N–N dissociation energy of N₂ adsorbed at the N-vacancy site on the VON surface.

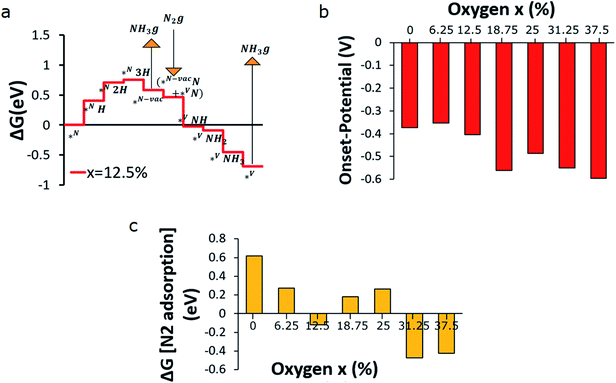Fig. 5 (a) free energy path of N₂RR (at x = 12.5%), (b) onset potentials, (c) N₂ adsorption free energy on the N-vacant site at different oxygen concentrations (x).

It is important to note that although oxygen is not explicitly present in the top layer of the catalyst surface, it indirectly affects the vanadium and nitrogen electronic states and manipulates the binding free energy of the adsorbates. This effect can be understood from the d-band theory of adsorption energies. Variations in the d-orbitals due to the hybridization of the d-states of the surface V atoms with the nitrogen and the oxygen atoms leads to a modification in the adsorbate interactions, i.e. a ligand effect (ref) due to the hybridized electronic states arising from a mixture of p-orbitals from N and O interacting with the adsorbate states. The presence of oxygen changes the oxidation state, occupancy, position, and bandwidth of the d-orbitals of the vanadium. We quantify these effects with d band center shift of the VON surface compared to pure VN. Our results show that the surface d-band center shifts significantly towards the Fermi level in VON compared to pure VN. The presence of oxygen also changes the p-orbitals of the anions, and in the case of the VON surface, the p-band center also moves towards the Fermi level compare to the pure VN. However, the p-bands are much deeper in energy level than the d-bands. Which means that any shift in the d-band center will have a more substantial effect on the adsorbate binding energy than the change in the p-band center. We correlate these with the observed changes in adsorbate binding energy to explain the basis for ligand effect origination from a mixed anion system.

Shielding of N-vacancy site against poisoning

According to the MvK mechanism, the N-vacancy formed by protonation of surface N-site to NH₃, needs to be replenished by a gaseous N₂ molecule (eqn 17) to complete the N₂RR cycle. For this, N-vacancies must be sufficiently stable on the surface and not get poisoned by other species like OH* or a water molecule. Further, there is also the possibility of this vacancy site to migrate towards bulk and self-annihilate.

Self-annihilation

The bulk of the VON slab contains both N and O anions. Nitrogen vacancy created during the initial stages of the MvK mechanism can get self-annihilated by migration of N or O atoms from the subsurface layers. Fig. 6a and b displays the thermodynamic and kinetic barriers for a sub-surface N-ion and O-ion to migrate on the vacancy site. The thermodynamic barrier for the N-migration from sub-surface to surface vacancy site is positive but low (average ∼0.5 eV) for all the O compositions. In the case of sub-surface O, the migration is thermodynamically downhill, but the kinetic barriers are insurmountable (1.2–2.8 eV) for both types of migration and expected to keep vacancies kinetically stable on the surface.

Fig. 6 Self-annihilation of the N-vacancy site on the surface by: (a) migration of N atom from the sub-surface and (b) migration of O atom from the subsurface.

Poisoning with O*/OH*/H*

Multiple species compete with N₂ for being adsorbed at the nitrogen-vacancy side. In an aqueous electrolyte system under reducing conditions, H*, O*, OH*, and water molecules can block the reaction site preventing catalytic activity. The calculated binding free energy trend confirms that adsorption of N₂ is significantly preferred over O*/OH*/H* adsorption at the nitrogen-vacancy site (Fig. 7a). This supports the continual reaction cycle for ammonia production via the dissociative MvK mechanism. Our detailed mechanistic analysis points out that the catalyst surface layer should consist of V and N atoms, while O atoms stay in the subsurface layer, supporting the catalyst activity through electronic interaction and stabilization of non-stoichiometry. The calculated potential for removal of oxygen atoms from the top layer via protonation and water formation is much more positive than the reducing potential required for N₂RR (Fig. 7b). Thus any O*/OH* species that might populate the top layer would get removed very fast at the operating potential.

Fig. 7 (a) N₂ is preferentially adsorbed at the vacancy site over O*/OH*/H* for x < 25% oxygen content. (b) O from the top layer is removed as water at much before the VON surface reaches N₂RR potential.

While DFT+U⁴⁸ or higher level methods like hybrid functionals such as HSE06 (ref. 49) in general provide a better description of basic properties of transition metal oxides,⁵⁰ it is important to note that during the electrochemical reactions investigated here, the oxidation state of the surface vanadium atoms in VON will vary dynamically depending on the adsorbed reaction intermediate as well as the anionic configuration and relative concentration of the O/N neighbors and the resulting d-orbital occupancy. As no single U_eff value is able to capture this variation across all oxygen concentrations and reaction intermediates investigated here, and the choice of U_eff-value (or similarly the alpha-value for HSE calculations) will be directly reflected in the calculated overpotential,⁵⁰ we are relying on standard GGA-level calculations for the computational screening study and comparisons performed here. Recent DFT+U and hybrid functional level investigations of vanadium-oxide based structures have documented these difficulties in the treatment of vanadium in different oxidation states^51–54

Conclusion

TMONs are one of the most promising classes of inorganic transition metal compound electrocatalysts for nitrogen reduction to ammonia using renewable electricity at near-ambient conditions. The challenges of pure transition metal nitrides are overcome in this class of materials due to chemical interaction originating from anion substitution and stabilization of the active surface defect sites. We address the lack of knowledge of the structural details like anion ordering, surface (defect) stability, and structure as well as to unearth the hitherto unknown mechanism by which TMONs are far superior electrocatalysts in terms of selectivity, stability, and activity towards electrocatalytic nitrogen reduction.

We conclude that oxygen content leads to a kinetically stable cubic rock salt structure and surfaces that suppress leaching and other structural transformation hampering the catalytic activity, while a high oxygen concentration is detrimental to both stability and catalytic activity. The most catalytically active surfaces contain only nitrogen and vanadium due to the thermodynamic stability as well as the removal of surface oxygen by reduction to water. VON surfaces with low oxygen content (x ≤ 12.5%) show remarkable selectivity over HER due to a thermodynamic preference for repetitive protonation at the nitrogen site over the vanadium site leading to ammonia release. The onset potential for 12.5% O containing VON is only ∼0.4 V, while keeping the surface facile for N₂ absorption at the nitrogen-vacancy site, unlike other low oxygen-containing compositions and pure VN. The anion-vacancy sites are critical for continued ammonia production and remain shielded from lattice ion-based self-annihilation due to large kinetic barriers for anion migration. Also, the surface is protected against O*/OH*/H* poisoning due to the thermodynamic preference for N₂ absorption and fast electrochemical removal of surface oxygen at potentials relevant for N₂RR. Given the lower activation energy for dissociative N₂ chemisorption, higher oxygen containing VON (x = 31.25%) is also a potential candidate for N₂RR catalysis, with the lowest thermodynamic and kinetic barrier for N₂ adsorption and dissociation, suggesting a better turn over frequency of NH₃ formation, albeit with a lower stability and higher overpotential (0.6 V-RHE) compared to x = 12.5%. Our study establishes a fundamental understanding of the catalytic behavior of VON for ammonia electro-synthesis. Along with the explanation of why the oxynitride phase can sustain catalytic activity and other beneficial effects of oxygen substitution. Finally, it also identifies the optimal N/O ratio in VON for further investigation and experimental validation.

Computational details

Density functional theory-based simulations were performed with plane wave basis set and projector-augmented wave based implementation in VASP⁵⁵ package. Revised Perdew–Burke–Ernzerhof (RPBE)⁵⁶ with Pade Approximation is used as an exchange correlation functional. The wave functions are expanded in plane waves with an energy cutoff of 500 eV for bulk and 350 eV for surface simulations. The first Brillouin zone is sampled with 4 × 2 × 2, 7 × 5 × 2, and 2 × 2 × 1 Monkhorst–Pack k-point mesh for the 32 atom VON supercell (1 × 2 × 2), V₂O₅ unit cell and VON surfaces respectively.

We have used the site occupancy disorder method⁵⁷ to create 1610 symmetry inequivalent structures of VNO in a 1 × 2 × 2 supercell with 16 V and 16 O/N atoms followed by geometry optimization using VASP for all of them. Both ferromagnetic and antiferromagnetic ordering was considered. The mixing energy of each structure was estimated for the 32 atom (V₁₆N_(x−16)O_x) structures following equation

E_mix(V₁₆N_x−16O_x) = E(V₁₆N_x−16O_x) − xE(VO) − (x − 16)E(VN)

The energy of pure VO and VN is calculated using DFT simulations of the cubic bulk crystal structure divided by the number of vanadium atoms in the unit cell. The low energy structures at different O/N ratios are used for constructing the surfaces and studying the bulk properties.

In the periodic repeating unit cell used for surface simulation, 18 Å of vacuum is used in the z-direction to minimize any interaction under periodic boundary conditions. The bottom two layers are fixed during atomic relaxations, and top two layers were optimized including any adsorbate until forces on each free atom are lower than 0.003 eV Å⁻¹. Gaussian smearing of 10 meV is used for the electronic states. The lattice parameters are optimized for bulk calculations and are provided in Table S1.† For surface calculations, lattice parameters are kept fixed.

To estimate the change in free energy under an applied potential for protonation steps, the free energies are calculated using the computational hydrogen electrode (CHE) model.⁵⁸ It is a simple linear model that approximates free energy change to the applied potential for an elementary electrochemical reaction step. The free energies of molecules are calculated within the ideal gas approximation. Phonon modes for adsorbates that are used for evaluation of zero-point energy and entropy (Table S3†) are done by performing small-displacement energy/force calculations in all three directions of all adsorbate atoms. References for water, ammonia, hydrogen, and nitrogen molecules are used for adsorption free energy calculations. We use the nudged-elastic band method⁵⁹ as implemented in VASP with a tolerance of 0.03 eV Å⁻¹. All computation was managed, processed, and visualized within the atomic simulation environment (ASE).⁶⁰

Conflicts of interest

No conflicts of interest.

Acknowledgements

The authors wish to acknowledge support from the Velux Foundations through the research center V-Sustain (grant 9455) and the European project ARENHA (#862482)

References

1. V. Smil, Nature, 1999, 400, 415.
2. J. W. Erisman, M. A. Sutton, J. Galloway, Z. Klimont and W. Winiwarter, Nat. Geosci., 2008, 1, 636–639.
3. R. Lan, J. T. S. Irvine and S. Tao, Int. J. Hydrogen Energy, 2012, 37, 1482–1494.
4. A. Klerke, C. H. Christensen, J. K. Nørskov and T. Vegge, J. Mater. Chem., 2008, 18, 2304–2310.
5. L. Wang, M. Xia, H. Wang, K. Huang, C. Qian, C. T. Maravelias and G. A. Ozin, Joule, 2018, 2, 1055–1074.
6. M. Jewess and R. H. Crabtree, ACS Sustainable Chem. Eng., 2016, 4, 5855–5858.
7. J. G. Chen, R. M. Crooks, L. C. Seefeldt, K. L. Bren, R. M. Bullock, M. Y. Darensbourg, P. L. Holland, B. Hoffman, M. J. Janik, A. K. Jones, M. G. Kanatzidis, P. King, K. M. Lancaster, S. V. Lymar, P. Pfromm, W. F. Schneider and R. R. Schrock, Science, 2018, 360(6391).
8. T. Vegge, R. Z. Sørensen, A. Klerke, J. S. Hummelshøj, T. Johannessen, J. K. Nørskov and C. H. Christensen, in Solid-State Hydrogen Storage, ed. G. Walker, Woodhead Publishing, 2008, pp. 533–564.
9. S. L. Foster, S. I. P. Bakovic, R. D. Duda, S. Maheshwari, R. D. Milton, S. D. Minteer, M. J. Janik, J. N. Renner and L. F. Greenlee, Nat. Catal., 2018, 1, 490–500.
10. S. D. Minteer, P. Christopher and S. Linic, ACS Energy Lett., 2019, 4, 163–166.
11. M. A. Shipman and M. D. Symes, Catal. Today, 2017, 286, 57–68.
12. C. Guo, J. Ran, A. Vasileff and S.-Z. Qiao, Energy Environ. Sci., 2018, 11, 45–56.
13. V. Rosca, M. Duca, M. T. de Groot and M. T. M. Koper, Chem. Rev., 2009, 109, 2209–2244.
14. E. Skúlason, T. Bligaard, S. Gudmundsdóttir, F. Studt, J. Rossmeisl, F. Abild-Pedersen, T. Vegge, H. Jónsson and J. K. Nørskov, Phys. Chem. Chem. Phys., 2011, 14, 1235–1245.
15. J. G. Howalt, T. Bligaard, J. Rossmeisl and T. Vegge, Phys. Chem. Chem. Phys., 2013, 15, 7785–7795.
16. J. G. Howalt and T. Vegge, Beilstein J. Nanotechnol., 2014, 5, 111–120.
17. S. Z. Andersen, V. Čolić, S. Yang, J. A. Schwalbe, A. C. Nielander, J. M. McEnaney, K. Enemark-Rasmussen, J. G. Baker, A. R. Singh, B. A. Rohr, M. J. Statt, S. J. Blair, S. Mezzavilla, J. Kibsgaard, P. C. K. Vesborg, M. Cargnello, S. F. Bent, T. F. Jaramillo, I. E. L. Stephens, J. K. Nørskov and I. Chorkendorff, Nature, 2019, 570, 504–508.
18. J. H. Montoya, C. Tsai, A. Vojvodic and J. K. Nørskov, ChemSusChem, 2015, 8, 2180–2186.
19. X. Zhang, R.-M. Kong, H. Du, L. Xia and F. Qu, Chem. Commun., 2018, 54, 5323–5325.
20. S. Chen, S. Perathoner, C. Ampelli, C. Mebrahtu, D. Su and G. Centi, Angew. Chem., 2017, 129, 2743–2747.
21. Q. Li, L. He, C. Sun and X. Zhang, J. Phys. Chem. C, 2017, 121, 27563–27568.
22. X. Yang, J. Nash, J. Anibal, M. Dunwell, S. Kattel, E. Stavitski, K. Attenkofer, J. G. Chen, Y. Yan and B. Xu, J. Am. Chem. Soc., 2018, 140, 13387–13391.
23. L. Zhang, X. Ji, X. Ren, Y. Luo, X. Shi, A. M. Asiri, B. Zheng and X. Sun, ACS Sustainable Chem. Eng., 2018, 6, 9550–9554.
24. J. G. Howalt and T. Vegge, Phys. Chem. Chem. Phys., 2013, 15, 20957–20965.
25. T.-N. Ye, S.-W. Park, Y. Lu, J. Li, M. Sasase, M. Kitano and H. Hosono, J. Am. Chem. Soc., 2020, 142, 14374–14383.
26. B. Chang, L. Deng, S. Wang, D. Shi, Z. Ai, H. Jiang, Y. Shao, L. Zhang, J. Shen, Y. Wu and X. Hao, J. Mater. Chem. A, 2020, 8, 91–96.
27. Y. Yao, Q. Feng, S. Zhu, J. Li, Y. Yao, Y. Wang, Q. Wang, M. Gu, H. Wang, H. Li, X. Yuan and M. Shao, Small Methods, 2019, 3, 1800324.
28. S. Kang, J. Wang, S. Zhang, C. Zhao, G. Wang, W. Cai and H. Zhang, Electrochem. Commun., 2019, 100, 90–95.
29. Y. Abghoui, A. L. Garden, J. G. Howalt, T. Vegge and E. Skúlason, ACS Catal., 2016, 6, 635–646.
30. Y. Abghoui and E. Skúlasson, Procedia Comput. Sci., 2015, 51, 1897–1906.
31. R. Manjunatha, A. Karajić, H. Teller, K. Nicoara and A. Schechter, ChemCatChem, 2020, 12, 438–443.
32. B. Hu, M. Hu, L. Seefeldt and T. L. Liu, ACS Energy Lett., 2019, 4, 1053–1054.
33. X. Yang, J. Nash, J. Anibal, M. Dunwell, S. Kattel, E. Stavitski, K. Attenkofer, J. G. Chen, Y. Yan and B. Xu, J. Am. Chem. Soc., 2018, 140, 13387–13391.
34. H.-L. Du, T. R. Gengenbach, R. Hodgetts, D. R. MacFarlane and A. N. Simonov, ACS Sustainable Chem. Eng., 2019, 7, 6839–6850.
35. B. Wang, B. C. Chakoumakos, B. C. Sales and J. B. Bates, J. Solid State Chem., 1996, 122, 376–383.
36. E. F. de Souza, C. A. Chagas, T. C. Ramalho, V. Teixeira da Silva, D. L. M. Aguiar, R. S. Gil and R. B. de Alencastro, J. Phys. Chem. C, 2013, 117, 25659–25668.
37. I. P. Parkin and G. S. Elwin, J. Mater. Chem., 2001, 11, 3120–3124.
38. P. Rodríguez, J. L. Brito, A. Albornoz, M. Labadí, C. Pfaff, S. Marrero, D. Moronta and P. Betancourt, Catal. Commun., 2004, 5, 79–82.
39. S. Surnev, M. G. Ramsey and F. P. Netzer, Prog. Surf. Sci., 2003, 73, 117–165.
40. P. S. Bell and M. H. Lewis, Phys. Status Solidi A, 1971, 7, 431–439.
41. H. H. Kristoffersen, T. Vegge and H. A. Hansen, Chem. Sci., 2018, 9, 6912–6921.
42. M. H. Hansen, A. Nilsson and J. Rossmeisl, Phys. Chem. Chem. Phys., 2017, 19, 23505–23514.
43. P. S. Lamoureux, A. R. Singh and K. Chan, ACS Catal, 2019, 9, 6194–6620.
44. J. G. Howalt and T. Vegge, Beilstein J. Nanotechnol., 2014, 5, 111–120.
45. X. Yang, J. Nash, J. Anibal, M. Dunwell, S. Kattel, E. Stavitski, K. Attenkofer, J. G. Chen, Y. Yan and B. Xu, J. Am. Chem. Soc., 2018, 140, 13387–13391.
46. K. Huang, K. Bi, Y. K. Lu, R. Zhang, J. Liu, W. J. Wang, H. L. Tang, Y. G. Wang and M. Lei, Sci. Rep., 2015, 5, 17385.
47. Y. Abghoui, A. L. Garden, J. G. Howalt, T. Vegge and E. Skúlason, ACS Catal., 2016, 6, 635–646.
48. M. Cococcioni and S. de Gironcoli, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035105.
49. A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106.
50. V. Tripkovic, H. A. Hansen, J. M. Garcia-Lastra and T. Vegge, J. Phys. Chem. C, 2018, 122, 1135–1147.
51. B. Stahl and T. Bredow, J. Comput. Chem., 2020, 41, 258–265.
52. K. Bhola, J. J. Varghese, L. Dapeng, Y. Liu and S. H. Mushrif, J. Phys. Chem. C, 2017, 121, 21343–21353.
53. M. Huang and S. Fabris, J. Phys. Chem. C, 2008, 112, 8643–8648.
54. R. Schira and C. Latouche, New J. Chem., 2020, 44, 11602–11607.
55. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
56. B. Hammer, L. B. Hansen and J. K. Nørskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413–7421.
57. R. Grau-Crespo, S. Hamad, C. R. A. Catlow and N. H. de Leeuw, J. Phys.: Condens. Matter, 2007, 19, 256201.
58. J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, J. Phys. Chem. B, 2004, 108, 17886–17892.
59. G. Mills, H. Jónsson and G. K. Schenter, Surf. Sci., 1995, 324, 305–337.
60. A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dulak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter, 2017, 29, 273002.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ta08313e

---