Role of particle size and surface functionalisation on the flexibility behaviour of switchable metal–organic framework DUT-8(Ni)

Abstract

Flexible MOF nanoparticles, i.e. MOF nanoparticles that change their structure upon external stimuli such as guest uptake, are promising for numerous applications including advanced gas adsorption, drug delivery and sensory devices. However, the properties of MOFs are typically characterised based on the bulk material with no consideration of how the particle size and external surface influences their performance. This combined computational and experimental contribution investigates the influence of the particle size and surface functionalisation on the flexibility of DUT-8(Ni) (Ni₂(2,6-ndc)₂ dabco, ndc = naphthalene dicarboxylate, dabco = 1,4-diazabicyclo[2.2.2]octane, DUT = Dresden University of Technology). DUT-8 nanoparticles remain rigid in their open pore form while microparticles, synthesised under slightly different conditions, undergo gate opening upon nitrogen adsorption suggesting that the particle size has an important role to play in the flexibility of DUT-8. While the adsorption environment at the surface capped with modulators smaller than the 2,6-ndc ligand is very different compared to the bulk of the crystal with considerably weaker guest–framework interaction, simulations reveal that the nanoparticles should close. We conclude that the size of the nanoparticles is not the major contributor for keeping DUT-8 nanoparticles open but that it is more likely that defects or nucleation barriers dominate. Moreover, our work reveals for the first time that functionalising the external surface of nanoparticles with different modulators or capping groups offers the opportunity to manipulate the gate opening/closing pressure. This principle is generally applicable and could be exploited to tune the gate opening/closing pressure for the application of interest.

---

Introduction

Metal–organic frameworks (MOFs) consist of metal nodes connected by organic ligands forming porous crystalline materials. They have record internal surface areas (up to ∼7800 m² g⁻¹),¹ high porosities,² and their properties can be systematically tailored by using different building units.³ These properties have resulted in extensive research towards the application of MOFs in gas separation,⁴ storage,⁵ and catalysis.⁶

Some MOFs also exhibit framework flexibility due to their weak intramolecular bonding (for instance, π–π bonds, and hydrogen bonds). Framework flexibility is an exciting property whereby the crystal switches between stable structures upon exposure to external stimuli such as guest molecules, electromagnetic radiation, or changes in temperature or pressure.⁷ Some MOFs are more flexible than others, and so the phase transition can cause marginal or major changes in the structure. ZIF-8 (zeolitic imidazole framework), for example, is a relatively rigid structure that shows a reversible rotation of its 2-methyl-imidazole linkers during the phase transition. This modest structural change results in a relatively small step in the adsorption isotherm.⁸ On the other hand, MOFs such as MIL-53 and DUT-8 show transitions between open and closed pore structures associated with larger volume changes, which results in a large change in the porosity and consequently pronounced steps and hysteresis in the adsorption isotherms.^9,10

Framework flexibility can have severe consequences for the use of MOFs in practical applications. For instance, finely tuned pore sizes and window diameters are used to exclude larger molecules in molecular sieving applications, which is forfeited if the pores can change shape.⁷ On the other hand, framework flexibility also opens up new applications for MOFs, such as their use in sensory devices,^11,12 advanced gas separations¹³ or as carriers for drug delivery.^7,14 In sensing devices, the well-defined topologies and highly porous nature of MOFs means they offer enhanced sensitivity and selectivity towards the analyte.¹⁵ Contact with the analyte typically induces a phase transition that can be detected by changes in the MOF's optical properties¹⁶ or conformational changes of a reporter molecule.¹⁷ As carriers for drug delivery, flexible MOFs will adapt to optimize their geometric and energetic properties, so the guest–host interaction energies can be tailored to retain the drug and decrease its rate of release.¹⁸ Finally, due to differences in gate-opening pressures, flexible MOFs offer the ability to separate gases with similar physiochemical properties at near ambient conditions.¹⁹

In many of these applications, it is preferable to use MOF nanoparticles. Whilst nanoparticles exhibit the physiochemical properties of typical microparticles, their properties are also largely governed by the external surface, which can be functionalized to improve the particle stability and incorporation into the system of interest. For example, in gas separation applications, the incorporation of smaller MOF nanoparticles into mixed-matrix membranes increases the MOF-polymer contact area. This reduces voids between the two materials, hence the structure retains its selectivity.²⁰

It is clear from the previous examples that flexible MOF nanoparticles have a huge potential in many applications. However, MOFs are normally characterized based on the typical micrometre-sized particles, the properties of which are governed by the “bulk” crystal (i.e. the repeating unit cell) and surprisingly few studies have addressed the influence of particle size and the external surface on the properties of flexible MOFs. For several gating and breathing MOFs, particle-size dependent flexibility was observed, including MIL-53(Al),²¹ DUT-49,²² DUT-98 ²³ and interpenetrated pillared layer MOFs such as Cu₂(bdc)₂(bpy) (bdc = 1,4-benzenedicarboxylate, bpy = 4,4′-bipyridine).²⁴ In a detailed experimental and simulation study Zhang et al. shed light on why the gate-opening pressure of ZIF-8 increases with decreasing particle size.²⁵ From theory, it is well known that the pressure of the phase transition depends on: (a) the free energy of the empty framework, (b) the external work imposed on the system, and (c) the guest–host interaction energy.²⁶ In the case of ZIF-8, it was proposed that weaker adsorption energies at the external surface are the underlying cause for the crystal-size dependence on gate-opening.²⁵

Another MOF for which particle size dependence on phase transition has been observed is the pillared layer MOF DUT-8(Ni) which consists of Ni₂ paddle wheel units that are each coordinated by four 2,6-ndc (2,6-naphthalenedicarboxylate) anions, forming 2-D square nets. The 3-D structure arises from the axial coordination of Ni metal sites to dabco molecules (1,4-diazabicyclo[2.2.2]octane), connecting the neighbouring nets.¹⁰ DUT-8 is unusual as it can be obtained as a flexible material when synthesised as micrometre-sized crystals or as a rigid material when synthesized as at submicron size (<500 nm).^27–29

Using a mixture of DMF, MeOH, and a defined dabco concentration during the synthesis results in micrometre-sized crystals in the open pore form (op). Immediately upon the removal of solvent, DUT-8(Ni) microparticles undergo a phase transition from the open pore (op) to the closed pore (cp) form. During the physisorption of N₂ at 77 K, CO₂ at 195 K, n-butane at 273 K, ethane at 185 K or ethylene at 169 K, desolvated DUT-8(Ni) microparticles switch back to the op form, if a certain adsorptive pressure is reached which depends on the guest molecule.³⁰ In high-pressure physisorption experiments at 298 K, the “gate opening” can only be induced by CO₂ and n-butane but not nitrogen,¹⁰ and methane will not lead to gate opening for pressures up to 6 MPa at 300 K.³¹ This transition between a closed and open pore structure leads to a large change in pore volume and hence a large, abrupt step in the corresponding adsorption isotherm.¹⁰ Moreover, it was shown that repeated adsorption/desorption in this system leads to the changes in flexibility and adsorption behaviour, manifested in the slope of the adsorption isotherms.³²

However, if DUT-8(Ni) is synthesized using a somewhat modified preparation method in pure DMF with an excess of dabco, this results in the fast deprotonation of H₂(2,6-ndc) ligands and rapid nucleation. This gives rise to DUT-8(Ni) nanoparticles (50–500 nm in size) that remain rigid in their open pore (presumably metastable) phase after solvent removal and gas physisorption.^27,28 Synthesis of DUT-8(Ni) in a microreactor (which allows precise tailoring of the particle size) confirmed that small particles remain rigid.²⁷ A comparable behaviour is observed for DUT-8(Co) demonstrating the stiffening effect for smaller particles.²⁹ On first sight, these differences between the flexible, microsized DUT-8 particles and the rigid nanoparticles indicate that the particle size plays a role in determining whether DUT-8 is flexible or not.

It was recently found that the open pore form of the larger microcrystals of DUT-8(Ni) exists in two conformational isomers, A and B.³³ However, these isomers only represent two limiting, ordered instances of a much larger configurational landscape.³⁴ As shown in Fig. 1, conformer A describes the isomer in which all four 2,6-ndc ligands around a Ni₂ unit point in the same direction. In conformer B, two pairs of adjacent 2,6-ndc ligands point in opposite directions around the metal node. X-ray diffraction experiments show that the “as-made” (i.e. solvent containing) larger op microparticles are either conformer B, or a disordered structure containing both conformers A and B. For example, a disordered phase, containing both conformers Aop and Bop, is initially observed after synthesis in DMF and methanol.²⁹ Desolvation of the microparticles transforms the “as-made” structure into conformer Bcp. During gas adsorption, the pores in the microparticles open forming a gas@Bop conformer, where the structures differ slightly depending on the accommodated guest molecules.^30,33 In contrast, the exact conformation of the smaller, rigid (op) nanoparticles is still challenging to resolve due to peak broadening and hence limited information from X-ray diffraction analysis. However, electron diffraction demonstrates disordered superstructures to persist on the nanodomain level.²⁹

Fig. 1 Structures of conformers (a) Aop, (b) Bop, and (c) Bcp.^30,35 Colour scheme: red = oxygen, grey = carbon, white = hydrogen, blue = nitrogen, green = nickel.

Recent computational work has shown that the phase transition Aop → Acp is energetically unfavourable and that the phase transition from open to closed pore form has to go through Bop → Bcp.³³ While these results show unequivocally that the closed pore form must be Bcp, we cannot deduce that the rigid nanoparticles consist of Aop and therefore that the rigidity is caused by the conformer as there is preliminary experimental evidence that Aop can convert into Bop.²⁹ The different conformers of DUT-8(Ni) are therefore unlikely to be the origin of the different flexibility behaviour resulting from the different synthesis pathways.

The different synthesis pathways, however, result in very different crystallization conditions. Supersaturation in the synthesis of the rigid nanoparticles leads to rapid nucleation and small crystals while the higher solubility during the synthesis of the flexible microparticles leads to slower crystallization and larger crystals.²⁸ Using continuous wave electron paramagnetic resonance (EPR) spectroscopy studies, Mendt et al. showed that the rigid nanoparticles contain considerably more defects in the form of missing 2,6-ndc²⁻ and dabco linkers and defective paddle wheel units with only one Ni²⁺ ion.³⁶

Despite being generally accepted that defects play an important role in determining the flexibility behaviour it remains unclear what role the external surface plays in terms of providing a different adsorption environment compared to the bulk of the particle as well as potentially acting as a platform to tailor gate opening/closing using different capping groups. In this paper, we use a combination of experiments, density functional theory (DFT) and grand-canonical Monte Carlo (GCMC) simulations to study the size-dependent uptake and phase transition witnessed during N₂ adsorption in DUT-8(Ni) and investigate the effect of different surface groups.

Methods

Computational methods

Structural Models. For DUT-(Ni) two different conformers, A and B, can be considered as the limiting cases depending on the orientation of the 2,6-ndc²⁻ linkers.³³ For both conformer A and B, the open and closed pore DUT-8(Ni) microparticles were modelled as the bulk unit cell duplicated in periodic boundary conditions to mimic the bulk behaviour. To understand how adsorption varies across the nanoparticles, the optimized conformer B (op and cp) bulk unit cells were extended and cleaved to form (001) and (110) surfaces. These faces have high BFDH (Bravais Friedel Donnay Harker) morphological indices (full BFDH morphologies are given in the ESI, Section S1†)^37,38 and are also observed experimentally. To ensure a fair comparison between the different phases, each slab type was cut to have the same number of atoms in the open and closed pore structure. This resulted in 2-D infinite slabs of length 40–70 Å (surface to surface). A vacuum gap of 20 Å was implemented either side of the external surface to prevent overlapping surface energies and to mimic adsorption in a nanoparticle surrounded by the “bulk” gas phase. During the surface creation coordination bonds were cleaved as opposed to covalent bonds which would be less energetically favourable. Uncoordinated nickel atoms on the surface were then saturated with surface groups rationalised from the synthesis solution – (001) surfaces were saturated with protonated dabco or DMF molecules, whereas (110) surfaces were saturated with monoprotonated 2,6-ndc or formic acid groups (see the ESI, Section S2† for more information). The terminations were used to determine their influence on adsorption, and whether differences in strain and dispersion on the surface contribute to phase transition pressure of DUT-8 particles. Note that when we talk about external surface in the remainder of the paper, we refer to the slab models functionalised as described.

Ab initio cell and geometry optimizations. Prior to their use in GCMC simulations, all of the models were optimized in terms of their atomic positions and unit cell lengths using the Quickstep module in CP2K.^39–44 Quickstep uses a Gaussian and planewave (GPW) approach, in which Gaussian basis functions are centred on the atoms and the electron density is propagated with planewaves, resulting in efficient computation of the energy. Prior to optimization, appropriate values of the planewave cut-off and relative cut-off were determined based on the convergence of single-point static energy calculations. The cut-off and relative cut-off values used were 700 Ry and 50 Ry for the slabs, and 600 Ry and 50 Ry for the bulk. Non-classical exchange correlation terms were approximated using the PBE functional⁴⁵ with DFT-D3 dispersion corrections.^46,47 To reduce computational cost, the core electrons were modelled using pseudopotentials derived by Goedecker, Teter, and Hutter (GTH).^48,50,51 Quickstep solves the Kohn Sham matrix by representing the wavefunction as Gaussian type basis sets. Triple-zeta Gaussian type basis sets (TZV2P-MOLOPT) were used to describe all atoms with the exception of nickel which was described using double-zeta functions (DZVP-MOLOPT).⁴⁹ All structures were fully relaxed (both in terms of the atomic coordinates and unit cell parameters) using a BFGS optimizer. Tolerances for convergence were set to 0.003 and 0.0015 Bohr for the maximum and root-mean-square of atomic displacements, and 0.0004 and 0.0003 Bohr Ha⁻¹ for the maximum and root-mean-square of the atomic forces. During the minimizations, each bulk structure optimized to the same phase and conformer as the input (i.e. no gate-closing was observed). Hence, each phase and conformer are local minima on the DUT-8(Ni) energy landscape.

Grand-canonical Monte Carlo simulations. N₂ adsorption at 77 K was modelled using GCMC simulations as implemented in the multipurpose simulation code MuSiC⁵² using rigid frameworks. N₂–DUT-8(Ni) non-coulombic interactions were calculated using the Lennard-Jones (LJ) 12-6 potential, and N₂–DUT-8(Ni) coulombic interactions were calculated using Ewald summation.⁵³ N₂–N₂ coulombic and LJ interactions were calculated on-the-fly using the Wolf summation method⁵⁴ and the LJ 12-6 potential, respectively. A cut-off radius of 18 Å was used for all interactions which is large enough to ensure that the cut-off radius does not influence the results while using the truncated LJ 12-6 potential.⁵⁵ DUT-8(Ni) partial atomic charges were taken as the Mulliken charges from DFT minimized structures. LJ parameters for the framework were taken from the Dreiding force field,⁵⁶ with the exception of nickel, for which the parameters were taken from the Universal Force Field.⁵⁷ LJ parameters and partial atomic charges for the N₂ molecules were taken from the TraPPE force field which describes N₂ molecules as three spheres, with two nitrogen atoms (partial charges of −0.482e) separated at a distance of 0.55 Å from a dummy atom at the centre of mass which neutralizes the overall charge and has Lennard-Jones parameters of nil.⁵⁸ Microstates were generated using four GCMC moves: insertion, deletion, translation and rotation. 10 million iterations were used for each pressure point, and the first 40% of microstates were neglected to ensure the ensemble average is taken at equilibrium. Finally, to calculate the fugacity, the Peng Robinson equation of state was used.⁵⁹ In the slab models, there is early onset condensation in the confined space of the vacuum gap and therefore the size of the vacuum gap influences the adsorption isotherm when extracrystalline adsorption begins. A simple normalization (as described in the ESI, Section S3†) was used to correct for the influence of the vacuum gap, meaning the high-pressure region of the isotherm can be captured.

Phase-transition pressure prediction. The osmotic framework adsorbed solution theory (OFAST)²⁶ was used to determine the phase-transition pressure of DUT-8(Ni) microparticles and nanoparticles (see the ESI, Section S4† for details). The free energies of the empty frameworks were assumed to equal the internal energies calculated using ab initio optimizations on the bulk and slab models. Isotherms used to analyse the N₂ contributions to the osmotic potential were obtained using GCMC simulations.

Experimental methods

Microcrystals and nanoparticles were synthesised according to the published procedure.²⁸ After synthesis, the solvent in the pores was exchanged to dichloromethane in case of microcrystals and to ethanol in case of nanoparticles for three days. After solvent exchange, the microcrystals were evacuated first at 25 °C for 16 h and additionally at 120 °C for 4 h. The nanoparticles were desolvated at 150 °C in vacuum for 16 h. The activated samples were characterised by powder X-ray diffraction to ensure crystallinity and phase purity. PXRD patterns of both a freshly desolvated sample and the sample after seven nitrogen adsorption/desorption cycles at 77 K show phase-pure DUT-8(Ni) cp phase (Fig. S5, ESI†).

The cyclic nitrogen physisorption experiments on DUT-8(Ni) microcrystals at 77 K were performed on BELSORP-Max instrument (Microtrac BEL, Japan). Between the measurements the sample was evacuated for 2 h at 25 °C. Adsorption isotherms for DUT-8(Ni) nanoparticles were measured on Autosorb IQ gas sorption analyser (Quantachrome). Scanning electron microscopy (SEM) was performed with a HITACHI SU 8020 instrument.

Results and discussion

In order to contrast the N₂ adsorption behaviour for the micro- and nanoparticles, we first look at N₂ adsorption in the microparticles represented by infinite periodic structures in the GCMC simulations. Fig. 2 shows negligible difference between the simulated Aop and Bop isotherms, in which the pores saturate at a loading of ∼600 cm³ (STP) g⁻¹ at p/p₀ ≈ 0.0025.

Fig. 2 Simulated adsorption isotherms of N₂ in bulk conformers Aop and Bop, and the initial experimental N₂ adsorption isotherm at 77 K on a fresh sample of microparticles without cycling.

This maximum loading is similar to that observed experimentally in a fresh sample of DUT-8 (note that as previously reported,³² DUT-8 delaminates upon cycling which results in smaller domains, reduced maximum uptake, and an increase in the gate opening and closing pressures – see Section S6 in the ESI†). No adsorption is expected in Bcp as the maximum pore diameter (2.3 Å) is smaller than the collision diameter of N₂ (3.7 Å).

To illustrate the adsorption mechanism, Fig. 3 presents the Boltzmann distribution as a probability map for N₂ adsorption in the bulk conformer Bop at 77 K (note that the maps for Aop are nearly identical to those for Bop, see Fig. S8 in the ESI†). The most favourable adsorption site (site 1) is situated in the pore corners next to the Ni₂ unit, at which N₂ molecules experience overlapping interactions from adjacent 2,6-ndc²⁻ ligands, resulting in a relative adsorption probability of 1. There are weaker adsorption sites next to the dabco ligands (site 2) and next to the 2,6-ndc²⁻ ligands (site 3).

Fig. 3 Boltzmann probability distribution for N₂ at 77 K inside the bulk conformer Bop. The maximum probability (P = 1) corresponds to an adsorption energy of −6.7 kJ mol⁻¹. Showing (a) view down z-axis, and (b) view down x-axis.

At sites 2 and 3, N₂ molecules experience interactions from a high number of surrounding nitrogen and/or carbon atoms, resulting in relative adsorption probabilities of ∼0.1. Finally, there is a non-distinct, low probability region for adsorption elsewhere in the pores, as indicated by the dark blue regions on the maps. These adsorption sites are the same as those observed by Hoffmann et al. who simulated xenon adsorption in DUT-8(Ni).⁶⁰

To represent the nanoparticles and capture the effect of the external surface, infinite slab models were used in the simulations where nickel exposed at the external surface of the slabs were coordinated with functional groups based on the synthesis mixture: H(2,6-ndc)⁻, dabco, DMF or formate. Due to the expense of the simulations and the negligible difference between adsorption in Aop and Bop, only conformer B was studied. Indexing of the single crystal faces on a diffractometer (Fig. 4) shows the (110) and (001) faces dominate the shape of DUT-8(Ni), thus the slab surfaces were created along these indices.

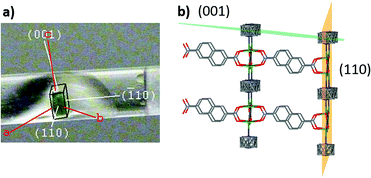Fig. 4 (a) Assignment of the crystal faces for DUT-8(Ni) conformer Bop, (b) planes in the DUT-8(Ni) conformer Bop crystal structure, corresponding to the surface termination of crystal faces.

Fig. 5 shows that there is very little difference in the simulated isotherms in the slab models capped with different surface groups. Compared to the bulk, the uptake and slope of the slab isotherms are lower at pressures p/p₀ < 0.25, because a lower density of framework atoms on the external surface reduces N₂–DUT-8 interaction energies. As the pressure exceeds p/p₀ = 0.25, the bulk isotherm levels off whilst the slab isotherms continue to rise due to extracrystalline adsorption.

Fig. 5 N₂ adsorption isotherms at 77 K inside the simulated Bop slabs and bulk, and the experimental isotherm in rigid DUT-8 nanoparticles. Slabs are capped with: dabco, dimethylformamide (DMF), formate (FA), or H(2,6-ndc⁻) (NDC).

This is also seen in the experimental isotherm for small, rigid DUT-8 particles (also shown for comparison). Extracrystalline adsorption is also responsible for the uptake observed in slabs of Bcp where the bulk pores, i.e. those not in direct contact with the surface and experiencing the same chemical environment as the period bulk unit cell, are too small to accommodate any N₂ molecules.

Probability maps for N₂ adsorption in the Bop slabs (Fig. 6) show that N₂ molecules occupy the same adsorption sites in the bulk pores of the slab, regardless of their position relative to the external surface. Hence, ignoring kinetic hindrance, the same amount will adsorb in all bulk pores regardless of their position in the particle. In contrast, adsorption sites on the external surface depend on the capping group. For Bop slabs capped with H(2,6-ndc⁻) or a dabco ligand, the same adsorption sites are present on the external surface as in the bulk, albeit, the interaction energies at the surface are weaker as half the groups that would contribute to the interaction energy are missing. Replacing the capping ligands with smaller capping groups (formate or DMF) further reduces the strength of interactions at the surface. These reduced interaction energies at the surface contribute to a shift in the gate-opening/closing pressures to higher values.

Fig. 6 Probability maps for N₂ adsorption at 77 K in the conformer Bop slab models: (a) 001 dabco, (b) 001 DMF, (c) 110 formate, and (d) 110 ndc.

In line with the results for the microcrystals, N₂ is too large to fit inside the bulk pores of Bcp slabs (Fig. 7 and 8). On the external surface however, there is a strong and very localised adsorption site next to the narrow corner of the pore (site 1). In contrast, the probability of N₂ adsorption in the wide pore corners (site 2) is lower because the 2,6-ndc²⁻ ligands are further spread. At site 1, N₂ interactions will overcome the dispersion interactions, likely acting as a driving force for gate-opening.

Fig. 7 Probability maps for N₂ adsorption at 77 K in the Bcp slabs. Viewing the surface pores of (a) 001 dabco, and (b) 001 DMF capped Bcp slabs facing into the structure. *1 and *2 mark the adsorption sites in the “narrow” and “wide” pore corners. Note that the diameter of the bulk pores of Bcp are too narrow to accommodate N₂ molecules.

Fig. 8 Magnified probability maps for N₂ adsorption at 77 K on one of the external surfaces of the conformer Bcp slabs, showing (a) 001 dabco, (b) 001 DMF, (c) 110 FA (formate), and (d) 110 ndc. (The slabs and probability distributions were generated in the same way as the Bop slabs shown in Fig. 6).

It is clear that weak N₂–DUT-8 interaction energies on the external surface increase the gate-opening/closing pressure in the flexible microparticles. However, this does not explain why the rigid DUT-8 nanoparticles, obtained by changing the synthesis conditions, favour the op form. To get more insight, the osmotic framework adsorbed solution theory (OFAST) was applied to predict the gate-closing pressure. OFAST states that when two structures (e.g. the op and cp structures) are in equilibrium, those structures have equal osmotic potentials.²⁶ The calculations are based on the system energy when N₂ molecules are present inside the pores, therefore they determine the gate-closing pressure. Gate-opening requires N₂ molecules to open the pores from the external surface inwards, therefore is dominated by kinetics. For the periodic, bulk structure representing the microparticles, OFAST predicts a gate-closing pressure of p/p₀ = 0.005 (0.5 kPa), which is within the experimentally observed range for gate-closing in DUT-8(Ni) microparticles ∼0.5–1 kPa (see ESI, Section S9† for details).

Fig. 9 shows the Bcp → Bop energy difference normalized with respect to the number of bulk unit cells (i.e. “complete” DUT-8 unit cells) in each slab which illustrates how capping groups influence the flexibility behaviour.

Fig. 9 Normalized Bcp → Bop energy differences inside the guest-free bulk and slab models.

As with the bulk, the internal energies show that each Bcp slab is more favourable than the corresponding solvent free Bop slab because of dispersion interactions between the ligands. If ligands are removed (i.e. by introducing an external surface), Bcp becomes relatively less favourable (i.e. the Bcp → Bop energy difference decreases). Similarly, if the size of ligands is reduced, reduced dispersion interactions decrease the Bcp → Bop energy difference.

In a thermally induced phase transition the change in volume Gibbs free energy (ΔG_V) is typically proportional to the latent heat of transformation (L)

where for undercooling ΔT = T_e − T with T_e being the equilibrium phase transition temperature.⁶¹ Hence, considering only the empty host, the reduced dispersion interactions decrease the energy difference and latent heat of the Bop → Bcp phase transition. As ΔG_V is the driving force for this phase transition, it is reasonable to obtain Bop nanoparticles as a metastable form upon desolvation.

Considering additionally host–guest interactions, this in turn means that overall, as the particle size decreases, weaker N₂–DUT-8 interaction energies on the external surface will increase the gate-opening/closing pressure as more N₂ molecules are needed to overcome the Bcp → Bop barrier. On the other-hand, weaker dispersion interactions on the surface reduce the energy difference between Bop and Bcp, reducing the gate-opening/closing pressure. To determine which of the two effects dominate the shift in gate-opening/closing pressure, OFAST was applied to the slab models. Fig. 10 shows that the gate-closing pressure, i.e. the pressure where the relative osmotic potential (Ω_Bop–Bcp) is equal to zero, varies depending on the surface group but is in the same order of magnitude as calculated for the periodic bulk material (p/p₀ = 0.005 (p = 0.5 kPa)). These results indicate that the influence of the surface is not a major contributing factor to why the nanoparticles are rigid and do not show gate closing for DUT-8(Ni).

Fig. 10 Relative osmotic potentials, Ω_Bop–Bcp in the slab models with different capping groups as function of pressure. The gate closing pressure can be found at Ω_Bop–Bcp = 0.

However, closer inspection of Fig. 9 and 10 reveals the complex interplay of two opposing effects: reduced N₂–DUT-8 interaction energies at the surface leading to an increase in the gate-transition pressure and reduced dispersion interactions between the capping groups, leading to a decrease in the gate-transition pressure which can be exploited to modify the gate closing pressure. Compared to the bulk (p/p₀ = 0.005; p = 0.5 kPa), the transition pressure is slightly reduced for the 001-DMF slab (p/p₀ = 0.003; p = 0.3 kPa). This slab has the smallest capping group, and hence the lowest Bcp → Bop energy barrier (Fig. 9). Since the other slabs have larger capping groups which result in larger dispersion interactions, the reduced N₂–framework interaction energies on the surface outweigh the decreased Bcp → Bop energy difference compared to the bulk. Hence relative to the bulk the gate-closing pressure increases up to p/p₀ = 0.05 (p = 5 kPa) for ndc (see Table S1 in the ESI† for the energy differences and the actual values of the gate closing pressures). Although our study focussed on DUT-8, the results are transferable to other MOF nanoparticles which will also exhibit a considerable reduction of the fluid–framework interaction energies at the surface compared to the bulk crystal combined with a complex interplay of the interactions capping groups unique for each combination of MOF, capping group and guest molecule. Overall, these results show that the targeted capping of flexible nanoparticles could in general provide a powerful handle to modify the gate closing pressure in a systematic way tailoring it for the application of interest.

Conclusions

We used a combination of experimental and simulation techniques to study N₂ adsorption in DUT-8(Ni). In particular we looked at the influence of the external surface on the gate opening/closing behaviour of DUT-8(Ni) comparing nanoparticles, which experimentally remain rigid in their op form, to microparticles, synthesized using slightly different conditions, which undergo N₂ induced gate-opening/closing. Cyclic adsorption of these flexible DUT-8 microparticles leads to their disintegration and mosaic structure formation leading to an increase in the gate-opening pressures. Simulations in slabs of DUT-8, to account for surface effects, reveal that on the surface, where paddle wheel units are capped with modulators substantially smaller than the 2,6-ndc ligands, the adsorption environment for guest molecules is very different with considerably weaker guest–framework interaction. This effect is, however, short-ranged and as soon as the nitrogen molecules encounter paddle wheel units with four coordinated linkers even in the pores exposed at the surface the adsorption environment is nearly identical to the bulk material. Calculations using the osmotic framework adsorbed solution theory (OFAST)²⁶ using slabs capped with different surface groups representing DUT-8(Ni) nanoparticles revealed that the nanoparticles should close. Therefore, we conclude that the size of the nanoparticles and the capping of the surface with surface group is not a major contributor to keeping DUT-8(Ni) nanoparticles open as observed experimentally and that it is more likely that defects and/or nucleation barriers dominate.³⁶ However, the reduced energy difference between the open and the closed form (E_Bop–Bcp) in nanoparticles reduces the driving force for the op → cp transition increasing the probability to obtain metastable op polymorphs as a result of a kinetically hindered nucleation. Moreover, our results reveal, for the first time, that surface groups capping nanoparticles offer the opportunity to manipulate the gate opening/closing pressure. For the four surface groups that we investigated, the complex interplay between guest-framework and framework interactions lead to a lower (0.3 kPa for DMF) or increased (5 kPa for ndc) gate closing pressure compared to the bulk (0.5 kPa). This principle is applicable beyond DUT-8 and could be exploited to tune the gate opening/closing pressure of MOF nanoparticles in general for the application of interest.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement no 648283 “GROWMOF”) and the DFG through the FOR2433 program. It made use of the Balena High Performance Computing (HPC) Service at the University of Bath. The authors acknowledge T. Gorelik for collecting TEM images.

References

1. I. M. Hönicke, I. Senkovska, V. Bon, I. A. Baburin, N. Bönisch, S. Raschke, J. D. Evans and S. Kaskel, Angew. Chem., Int. Ed., 2018, 57, 13780–13783.
2. H. Furukawa, N. Ko, Y. B. Go, N. Aratani, S. B. Choi, E. Choi, A. Ö. Yazaydin, R. Q. Snurr, M. O'Keeffe, J. Kim and O. M. Yaghi, Science, 2010, 329, 424–428.
3. J. L. C. Rowsell and O. M. Yaghi, Microporous Mesoporous Mater., 2004, 73, 3–14.
4. R.-B. Lin, S. Xiang, H. Xing, W. Zhou and B. Chen, Coord. Chem. Rev., 2019, 378, 87–103.
5. B. Li, H.-M. Wen, W. Zhou and B. Chen, J. Phys. Chem. Lett., 2014, 5, 3468–3479.
6. L. Ma and W. Lin, in Functional Metal-Organic Frameworks: Gas Storage, Separation and Catalysis, ed. M. Schröder, Springer Berlin Heidelberg, Berlin, Heidelberg, 2010, pp. 175–205,  DOI:10.1007/128_2009_20.
7. A. Schneemann, V. Bon, I. Schwedler, I. Senkovska, S. Kaskel and R. A. Fischer, Chem. Soc. Rev., 2014, 43, 6062–6096.
8. D. Fairen-Jimenez, S. A. Moggach, M. T. Wharmby, P. A. Wright, S. Parsons and T. Duren, J. Am. Chem. Soc., 2011, 133, 8900–8902.
9. S. Bourrelly, P. L. Llewellyn, C. Serre, F. Millange, T. Loiseau and G. Férey, J. Am. Chem. Soc., 2005, 127, 13519–13521.
10. N. Klein, C. Herzog, M. Sabo, I. Senkovska, J. Getzschmann, S. Paasch, M. R. Lohe, E. Brunner and S. Kaskel, Phys. Chem. Chem. Phys., 2010, 12, 11778–11784.
11. P. Freund, I. Senkovska and S. Kaskel, ACS Appl. Mater. Interfaces, 2017, 9, 43782–43789.
12. P. Freund, L. Mielewczyk, M. Rauche, I. Senkovska, S. Ehrling, E. Brunner and S. Kaskel, ACS Sustainable Chem. Eng., 2019, 7, 4012–4018.
13. L. Yang, X. Cui, Y. Zhang, Q. Yang and H. Xing, J. Mater. Chem. A, 2018, 6, 24452–24458.
14. W. Cai, J. Wang, C. Chu, W. Chen, C. Wu and G. Liu, Adv. Sci., 2019, 6, 1801526.
15. D. Liu, K. Lu, C. Poon and W. Lin, Inorg. Chem., 2014, 53, 1916–1924.
16. G. Mehlana and S. A. Bourne, CrystEngComm, 2017, 19, 4238–4259.
17. N. Yanai, K. Kitayama, Y. Hijikata, H. Sato, R. Matsuda, Y. Kubota, M. Takata, M. Mizuno, T. Uemura and S. Kitagawa, Nat. Mater., 2011, 10, 787–793.
18. P. Horcajada, C. Serre, G. Maurin, N. A. Ramsahye, F. Balas, M. Vallet-Regí, M. Sebban, F. Taulelle and G. Férey, J. Am. Chem. Soc., 2008, 130, 6774–6780.
19. L. Li, R. Krishna, Y. Wang, X. Wang, J. Yang and J. Li, Eur. J. Inorg. Chem., 2016, 4457–4462.
20. B. Ghalei, K. Sakurai, Y. Kinoshita, K. Wakimoto, A. P. Isfahani, Q. Song, K. Doitomi, S. Furukawa, H. Hirao, H. Kusuda, S. Kitagawa and E. Sivaniah, Nat. Energy, 2017, 2, 17086.
21. T. Kundu, M. Wahiduzzaman, B. B. Shah, G. Maurin and D. Zhao, Angew. Chem., Int. Ed., 2019, 58, 8073–8077.
22. S. Krause, V. Bon, I. Senkovska, D. M. Többens, D. Wallacher, R. S. Pillai, G. Maurin and S. Kaskel, Nat. Commun., 2018, 9, 1573.
23. S. Krause, V. Bon, H. Du, R. E. Dunin-Borkowski, U. Stoeck, I. Senkovska and S. Kaskel, Beilstein J. Nanotechnol., 2019, 10, 1737–1744.
24. Y. Sakata, S. Furukawa, M. Kondo, K. Hirai, N. Horike, Y. Takashima, H. Uehara, N. Louvain, M. Meilikhov, T. Tsuruoka, S. Isoda, W. Kosaka, O. Sakata and S. Kitagawa, Science, 2013, 339, 193–196.
25. C. Zhang, J. A. Gee, D. S. Sholl and R. P. Lively, J. Phys. Chem. C, 2014, 118, 20727–20733.
26. F.-X. Coudert, Phys. Chem. Chem. Phys., 2010, 12, 10904–10913.
27. H. Miura, V. Bon, I. Senkovska, S. Ehrling, S. Watanabe, M. Ohba and S. Kaskel, Dalton Trans., 2017, 46, 14002–14011.
28. N. Kavoosi, V. Bon, I. Senkovska, S. Krause, C. Atzori, F. Bonino, J. Pallmann, S. Paasch, E. Brunner and S. Kaskel, Dalton Trans., 2017, 46, 4685–4695.
29. S. Ehrling, I. Senkovska, V. Bon, J. D. Evans, P. Petkov, Y. Krupskaya, V. Kataev, T. Wulf, A. Krylov, A. Vtyurin, S. Krylova, S. Adichtchev, E. Slyusareva, M. S. Weiss, B. Büchner, T. Heine and S. Kaskel, J. Mater. Chem. A, 2019, 7, 21459–21475.
30. V. Bon, N. Klein, I. Senkovska, A. Heerwig, J. Getzschmann, D. Wallacher, I. Zizak, M. Brzhezinskaya, U. Mueller and S. Kaskel, Phys. Chem. Chem. Phys., 2015, 17, 17471–17479.
31. M. Sin, N. Kavoosi, M. Rauche, J. Pallmann, S. Paasch, I. Senkovska, S. Kaskel and E. Brunner, Langmuir, 2019, 35, 3162–3170.
32. V. Bon, N. Kavoosi, I. Senkovska and S. Kaskel, ACS Appl. Mater. Interfaces, 2015, 7, 22292–22300.
33. P. S. Petkov, V. Bon, C. L. Hobday, A. B. Kuc, P. Melix, S. Kaskel, T. Düren and T. Heine, Phys. Chem. Chem. Phys., 2019, 21, 674–680.
34. S. Ehrling, E. Reynolds, V. Bon, I. Senkovska, T. Gorelik, M. Rauche, M. Mendt, M. Weiss, A. Pöppl, E. Brunner, U. Kaiser, A. Goodwin and S. Kaskel, Adaptive Response of a Metal–organic Framework Through Reversible Disorder–disorder Transitions, ChemRxiv, 2020 DOI:10.26434/chemrxiv.12326165.v1.
35. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr. B, 2016, 72, 171–179.
36. M. Mendt, F. Gutt, N. Kavoosi, V. Bon, I. Senkovska, S. Kaskel and A. Pöppl, J. Phys. Chem. C, 2016, 120, 14246–14259.
37. C. E. Macrae, P. McCabe, E. Pidcock, G. Shields, R. Taylor, M. Towler and J. van de Streek, J. Chem. Inf. Model., 2006, 44, 2133–2144.
38. J. H. Donnay and D. Harker, Am. Mineral., 1937, 22, 446–467.
39. J. Hutter, M. Iannuzzi, F. Schiffmann and J. VandeVondele, Wiley interdisciplinary reviews, Comput. Mol. Biosci., 2014, 4, 25.
40. J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128.
41. U. Borštnik, J. VandeVondele, V. Weber and J. Hutter, Parallel Comput., 2014, 40, 47–58.
42. M. Frigo and S. G. Johnson, Proc. IEEE, 2005, 93, 216–231.
43. J. VandeVondele and J. Hutter, J. Chem. Phys., 2003, 118, 4365–4369.
44. G. Lippert, J. Hutter and M. Parrinello, Mol. Phys., 1997, 92, 477–488.
45. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
46. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
47. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
48. M. Krack, Theor. Chem. Acc., 2005, 114, 145–152.
49. J. VandeVondele and J. Hutter, J. Chem. Phys., 2007, 127, 114105.
50. C. Hartwigsen, S. Goedecker and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 3641–3662.
51. S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710.
52. A. Gupta, S. Chempath, M. J. Sanborn, L. A. Clark and R. Q. Snurr, Mol. Simul., 2003, 29, 29–46.
53. B. A. Wells and A. L. Chaffee, J. Chem. Theory Comput., 2015, 11, 3684–3695.
54. D. Wolf, P. Keblinski, S. R. Phillpot and J. Eggebrecht, J. Chem. Phys., 1999, 110, 8254–8282.
55. M. J. Lennox, M. Bound, A. Henley and E. Besley, Mol. Simul., 2017, 43, 828–837.
56. S. L. Mayo, B. D. Olafson and W. A. Goddard, J. Phys. Chem., 1990, 94, 8897–8909.
57. A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. Goddard and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035.
58. J. J. Potoff and J. I. Siepmann, AIChE J., 2001, 47, 1676–1682.
59. D.-Y. Peng and D. B. Robinson, Ind. Eng. Chem. Fundam., 1976, 15, 59–64.
60. H. C. Hoffmann, B. Assfour, F. Epperlein, N. Klein, S. Paasch, I. Senkovska, S. Kaskel, G. Seifert and E. Brunner, J. Am. Chem. Soc., 2011, 133, 8681–8690.
61. J. D. Evans, V. Bon, I. Senkovska, H.-C. Lee and S. Kaskel, Nat. Commun., 2020, 11, 2690.

---

Footnotes

† Electronic supplementary information (ESI) available: Details of the crystal morphology prediction, microparticle and nanoparticle models, isotherm normalisation, phase transition prediction, characterisation of DUT-8(Ni) samples by PXRD, cyclic adsorption experiments, probability maps, and energy differences between the slab models. See DOI: 10.1039/d0ta07775e

‡ Current address: EaStChem School of Chemistry and Centre for Science at Extreme Conditions, University of Edinburgh, David Brewster Road, Joseph Black Building, Edinburgh, EH9 3FJ, UK.

---