Superoxide formation in Li₂VO₂F cathode material – a combined computational and experimental investigation of anionic redox activity

Abstract

Anionic redox activity in Li-rich cathode materials is a topic of intense interest because it presents the potential to increase the energy density of Li-ion batteries. An in-depth understanding of the anionic redox activity such as lithiation/voltage levels in which peroxide and superoxide formations take place and the reversibility of the reactions are important. In this work, we present a combined computational and experimental analysis that probes the formation of anionic redox species during electrochemical cycling. We report the formation of peroxides and superoxides in Li₂VO₂F when charged up to a relatively low potential of 4.1 V for Li-rich cathode materials. The formation of superoxide is not entirely reversible upon discharge, which is closely linked to the vanadium dissolution and limited reversibility of the vanadium redox couple. This article provides new insights and fundamental understanding of anionic redox activities in disordered Li-rich materials.

---

1 Introduction

Increasing the energy density of lithium-ion batteries (LIBs) is a topic of keen interest as they are one of the most widely used technologies to store energy for portable applications.^1–3 Cathodes constitute a substantial part of LIBs in terms of volume, weight and cost^3,4 and thus, developing high energy density cathode materials is one of the areas of recent research focus. In particular, much development has been made to utilize LiTMO₂ (TM = transition metal) like LiCoO₂,^5–7 which forms a layered pattern in a rocksalt lattice in general (α-NaFeO₂ structure, S.G. R3̄m); alternating layers of Li and TM ions form along the (111) planes of cationic sublattice while O ions occupy anionic sublattice. Further efforts have been made to increase the performance of LiCoO₂ by partial substitution with other TM ions. The most notable examples are LiNi_0.8Co_0.15Al_0.05O₂ (ref. 8) and LiNi_xMn_yCo_1−x−yO₂ (0 ≤ x ≤ 1, 0 ≤ y ≤ 1, and 0 ≤ x + y ≤ 1).⁹ As the mixing of Li and TM sublattices is often linked to the capacity loss upon cycling,^8,10–12 a traditional approach would be to search among materials exhibiting well-ordered structures.⁴

Research focus on cathode materials for LIBs is currently going through a paradigm shift where the previously overlooked disordered rocksalt (DRS) materials are receiving an increasing level of interest. It was reported that Li-rich materials with a high Li-to-TM ratio allow the formation of percolating network with low energy barriers for Li diffusion, which leads to good transport properties while its structural integrity is retained.^4,13,14 Several Li-rich transition metal oxides with a DRS structure such as Li_1+xTi_2xFe_1−3xO₂ (0 ≤ x ≤ 0.333),¹⁴ Li_1.2Ni_1/3Ti_1/3Mo_2/5O₂,¹⁵ Li_1.2Ti_0.4Mn_0.4O₂,¹⁶ Li_1.3Nb_0.3Fe_0.4O₂ (ref. 17) and Li_1.3Nb_0.43Ni_0.27O₂ (ref. 17) have been studied, and their high reversible capacities showed a promising prospect of discovering new cathode material in much less explored domain. Li₂VO₂F is the first Li-rich DRS material where O was partially substituted by F.^18,19 The substitution increases the performance of the cathode such as discharge capacity and nominal voltage.²⁰

The charge compensation by non-cationic species upon Li extraction is referred to as an anionic redox, and it became a very important topic in the battery research community.^21–24 Controlling the anionic redox contribution has the potential to increase the energy density beyond the theoretical energy density based on the TM-capacity contribution.^21,25,26 The anionic redox activity is often driven by the oxidation of O²⁻, which is more likely to occur when they have Li-rich local environment; O²⁻ ions have a higher probability to participate in the redox reaction (e.g., forming peroxides and superoxides) when the nearby Li ions are extracted. However, the anionic redox process may not be fully reversible, particularly when a high degree of oxygen redox activity leads to oxygen loss.^15,16,27,28

Fluorination can be used as a strategy to suppress the anionic redox activity, which leads to irreversible oxygen gas formation.^27,29 It has also been found that the fluorination increases accessible capacity when sufficiently high concentration of fluorine is added.³⁰ In spite of high fluorine content, there have been some experimental observations which indicate the anionic redox activities of oxyfluorides such as Li₂Mn_2/3Nb_1/3O₂F, Li₂Mn_1/2Ti_1/2O₂F and Li₂MnO₂F^31–33 when they are charged up to 4.5 V or above. In this work, we focus on Li₂VO₂F material as a comprehensive electrochemical study showed promising results such as good initial capacity and rate capability.¹⁸ However, it suffers from poor cycling performance due, in part, to degradation processes occurring at the electrode–electrolyte interface during extended cycling.²⁸ We report a comprehensive computational and experimental investigation on the evolution of the anionic redox process in Li₂VO₂F under typical cycling conditions. The computational simulations suggest that the oxygen species evolve subsequently to peroxide and to superoxide when the cell is charged up to 4.1 V, a potential lower than the commonly used upper limit of 4.5 V to 4.8 V. The formation of superoxide is confirmed using electron paramagnetic resonance spectroscopy. The superoxide remains to be present in the material upon discharge, which suggests that the superoxide formation is not entirely reversible and can contribute to the capacity fading of the material upon cycling.

2 Methods

2.1 Density functional theory calculations

A total of 650 density functional theory (DFT) calculations were performed with the Vienna Ab initio Simulation Package (VASP)^34–37 using the projector augmented-wave (PAW) method.³⁸ Both ordered and disordered structures are calculated for Li_xVO₂F with x ranges from 0 to 2 in order to capture the structure–property relationship of the compound. The calculations were performed with supercells containing up to 74 atoms. The generalized gradient approximation as parametrized by Perdew, Burke and Ernzerhof³⁹ was used as the exchange-correlation functional. The plane-wave cutoff of 500 eV was used, and both the cell and atomic positions were fully relaxed such that all the forces are smaller than 0.02 eV Å⁻¹. A rotationally invariant Hubbard U correction^40,41 was applied to the d orbital of V with the U value of 3.25 eV. It is noted that applying U correction on V favors the oxidation of V, and the anionic oxidation observed in this work does not stem from the bias caused in the Hubbard U scheme. Integrations over the Brillouin zone were carried out using the Monkhorst–Pack scheme⁴² with a grid with a maximal interval of 0.04 Å⁻¹.

2.2 Cluster expansion model

A cluster expansion (CE) model was constructed using CLuster Expansion in Atomic Simulation Environment (CLEASE) software package.⁴³ The CE model assumes that Li_xVO₂F takes on a rocksalt lattice, and it is trained for Li_xVO₂F with x ranges from 0 to 2 using 650 DFT calculations. Up to four-body clusters were included in the model, and the maximum cluster diameter was set to 7.0 Å for two- and three-body clusters and to 4.5 Å for four-body clusters. regularization scheme was applied to avoid the overfitting of data. The optimal regularization parameter value was found by assessing the lowest Leave-One-Out Cross Validation (LOOCV) for the parameter values ranging from 10⁻⁷ to 10². The final CE model yielded the LOOCV score of 23.6 meV per atom.

2.3 Metropolis Monte Carlo simulations

A Metropolis Monte Carlo simulations were carried out to generate minimum-energy structures for the training of CE model and to generate an open-circuit voltage (OCV) plot. The minimum-energy structures were generated using Monte Carlo simulated annealing with supercells containing up to 74 atoms, and the DFT calculations were performed on the generated structures. The temperature was gradually lowered from 10 000 K to 1 K with 1000 sweeps at each temperature. A 9 × 9 × 9 supercell consisting of 1458 atoms was used for generating an open-circuit voltage plot. Semi-grand canonical MC simulations were carried out using various fixed chemical potential values. The temperature was gradually lowered from 10 000 K to 297 K, while the structures were first equilibrated with 100 sweeps, followed by 1000 additional sweeps for sampling. The chemical potential of Li_xVO₂F and the Li concentration at 297 K were used to compute the OCV, which is expressed aswhere μ_Li and e are chemical potential in eV per Li atom and an electron charge, respectively. For a battery consisting of Li_xVO₂F as a cathode and Li as an anode, the OCV can be calculated directly from the chemical potential of Li_xVO₂F as a function of x because e and μ^anode_Li are constant.

2.4 Li₂VO₂F sample preparation

The Li₂VO₂F active material was prepared following the mechanochemical ball milling synthesis under argon atmosphere in a sealed jar as described elsewhere.^18,19 All of the subsequent steps were performed in a glovebox under argon atmosphere with water and oxygen levels below 0.1 ppm. The precursors were V₂O₃ (Alfa Aesar, 99.7%), Li₂O (Alfa Aesar, 99.7%) and LiF (Alfa Aesar, 99.9%). An active material/carbon black composite (77.8% active material/22.2% carbon black) was prepared by ball milling Li₂VO₂F with carbon black (acetylene black, Alfa Aesar) at 300 rpm for 3 h (Fritsch Pulverisette 6, 80 mL Si₃N₄ jar and balls).

To produce Li₂VO₂F samples in different states of charge (SOC), Li₂VO₂F carbon black composite was pressed into pellets (7 mm diameter, 2 tons, 2 min) of around 30 mg in order to have enough material for analyses. Two-electrode Swagelok cells were assembled using these pellets as cathodes and lithium metal as anode, separated by Whatman glass fiber separators. LP30 (1 M LiPF₆ in 1 : 1 wt% ethylene carbonate (EC)/dimethyl carbonate (DMC), water content < 20 ppm, Sigma Aldrich, ≥99.9%) was used as electrolyte. Three pellets of different SOC were produced. One was kept at OCV for 24 h, the second was charged at a rate of C/100 to 4.1 V vs. Li/Li⁺ and allowed to rest for 24 h. The third was charged up to 4.1 V, subsequently discharged to 1.3 V vs. Li/Li⁺ at a rate of C/100 and allowed to rest for 24 h.

Li₂VO₂F electrodes were produced by coating a slurry consisting of 70 wt% active material, 20 wt% carbon black and 10 wt% polyvinylidene difluoride binder (PVdF) (Solvey 6050) as previously reported.¹⁹ The slurry was prepared by mixing the materials with N-methyl-2-pyrrolidone (NMP, Alfa Aesar, 99.5%). Subsequently, a film with 250 μm wet film thickness was coated on an aluminum foil and dried in vacuum for 12 h with a step-wise increasing temperature up to 120 °C.

2.5 Magic angle spinning nuclear magnetic resonance spectroscopy

^6,7Li and ⁵¹V Magic Angle Spinning Nuclear Magnetic Resonance (MAS NMR) spectra were measured on a 600 MHz Varian NMR system equipped with a 1.6 mm Varian T3 HXY MAS probe. Larmor frequencies for ⁶Li, ⁷Li and ⁵¹V nuclei were 88.22 MHz, 233.00 MHz and 157.60 MHz, respectively. The ⁶Li MAS NMR spectrum was better resolved than the ⁷Li MAS NMR spectrum. The spectrum was recorded at 32 kHz sample rotation frequency using single-pulse excitation; duration of the pulse was 3.2 μs, repetition delay was 120 s and number of scans was 1000. ⁵¹V MAS NMR spectra were recorded at sample rotation frequencies of 32 kHz and 38 kHz in order to identify the centerband and the spinning sidebands. The spectra were obtained through 240 scans of single-pulse excitations with a 0.7 μs pulse duration and 2 s repetition delay. Frequency axes of the ⁶Li and ⁵¹V MAS NMR spectra are reported relative to the signal of Li₂SiO₃ (0 ppm) and the signal of VOCl₃ (0 ppm), respectively. In case of ⁵¹V, NH₄VO₃ was used as a secondary reference (−571.4 ppm).

2.6 Magnetism and electron paramagnetic resonance

The static molar magnetic susceptibilities of the two materials (χ(T) = M(T)/H where H is the magnetic field and M is the magnetization) were measured between 5 and 300 K using a superconducting quantum interference device (SQUID) magnetometer (Quantum Design MPMS-XL-5). The zero field cooled χ values were obtained by cooling the sample in zero field down to 5 K and then heating them under the measuring field of μ₀H = 1 T. The raw data were corrected for the sample holder contribution and for the temperature-independent Larmor diamagnetism, as calculated using empirical Pascal's constants⁴⁴ to obtain the molar paramagnetic susceptibility χ^M.

X-band Electron Paramagnetic Resonance (EPR) (Larmor frequency ∼ 9.6 GHz) was performed in a continuous wave mode on a commercial Bruker E580 spectrometer using a Varian TEM104 dual-cavity resonator. The microwave power was set to 1 mW and the modulation field to 0.1 mT. The Easyspin simulation package⁴⁵ has been employed to fit the experimental spectra. Powder samples (typically around 10 mg) were sealed under a dynamic vacuum into standard EPR Suprasil quartz tubes (outer diameter 4 mm, Wilmad-Labglass).

2.7 Quantification of vanadium dissolution

The dissolution of V in Li₂VO₂F was studied by determining the residual content of V in electrodes after cycling by inductive couples plasma optical emission spectroscopy (ICP OES). Multiple cells were cycled at 25 °C with a C/5 rate in a potential range between 1.3 V and varying upper cut-off voltages of 3.7, 4.1 and 4.5 V vs. Li/Li⁺. The cells were disassembled after cycling and the cycled Li₂VO₂F electrodes were dissolved in aqua regia and immersed in 50 mL H₂O. The samples were sonicated in an ultrasonic bath and stored at room temperature for one week to completely dissolve V. The ICP OES measurements were carried out using standard calibration solutions.

3 Results

3.1 Atomistic simulation investigation

It has been experimentally confirmed that Li_xVO₂F has a DRS structure.^18–20,46 However, existing density functional theory (DFT) simulation results⁴⁷ suggest that the layered rocksalt-type structure similar to the layered transition metal oxides is energetically favored for Li₂VO₂F (i.e., Li_xVO₂F with x = 2). This discrepancy between the experimental and computational descriptions is bridged using Monte Carlo simulated annealing based on the cluster expansion (CE) model trained by DFT calculations.

The ground-state structure of Li₂VO₂F in a rocksalt lattice found from simulated annealing cooled down to 1 K is shown in Fig. 1. The structure has a layered rocksalt-type structure, which is very similar to a closely-related oxide compound, LiVO₂.^48,49 Although the layered structure being the most energetically stable Li₂VO₂F in a rocksalt lattice is consistent with the previous DFT simulation results,⁴⁷ it has higher energy compared to its decomposed product (i.e., LiVO₂ and LiF), suggesting that the layered rocksalt-type structure is metastable. The metastability of the layered Li₂VO₂F is consistent with the recent reports where the Li₂VO₂F operates in a metastable phase.^19,46

Fig. 1 Ground-state structure of Li₂VO₂F found from simulated annealing.

Further analyses are carried out to explore the link between the layered and DRS structures by comparing their relative energies at various lithiation levels; a constraint imposing the structure to remain layered is applied to one set of simulations while no such constraint is imposed on another. The two cases lead to the same layered structure, the structure shown in Fig. 1, for Li_xVO₂F when x = 2 as shown in Fig. 2. The minimum-energy structures found in the DRS become increasingly more stable relative to the layered counterparts upon delithiation. In other words, the layered phase becomes energetically more stable than the DRS phase only when x approaches 2. However, the only known method to synthesize Li₂VO₂F is high-energy ball milling that triggers the formation of dislocations and disordering of the structure,⁵⁰ which explains the lack of any experimental observation of the layered phase even when x = 2.

Fig. 2 Formation energies of Li_xVO₂F (0 ≤ x ≤ 2) obtained from simulated annealing at each composition x. Blue circles represent ground-state energies found when Monte Carlo simulations do not have layering constraints in the atom swaps while red triangles represent the case with the layering constraint.

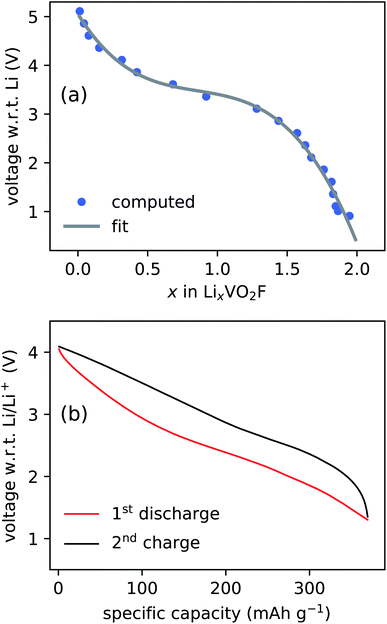
The CE model used to assess the relative stability of layered and DRS phases is employed to simulate the voltage profile. The simulated and experimentally measured voltage profiles are compared in Fig. 3. The two voltage plots show a good qualitative agreement, illustrating that the model is capable of predicting the electrochemical behavior of Li_xVO₂F. A minor discrepancy observed in the voltage range can be explained by the fact that the simulated voltage curve represents the thermodynamic limit (i.e., no kinetic effects are included in the model) and that the exact stoichiometry of Li_xVO₂F is not known during the experimental cycling.^18,46 The absence of the electrolyte contribution to the voltage profile, due to the limitations of the CE modeling approach, is another source of the discrepancy.

Fig. 3 Voltage profiles of Li_xVO₂F at room temperature obtained from (a) semi-grand canonical MC simulations and (b) electrochemical cycling (cycled between 1.3–4.1 V vs. Li/Li⁺ at a rate of C/20 in LP30 electrolyte).

The anionic redox activity progresses from peroxide (O₂²⁻) to superoxide (O₂⁻) and ultimately to molecular oxygen (O₂) as the number of localized holes is increased from 2 to 4.⁵¹ The minimum-energy structures are generated at varying lithiation levels based on the CE model, and the DFT calculations of the generated structures often result in the formation of oxygen redox species such as peroxide and superoxide as shown in Fig. 4. It is not straightforward to classify the anionic redox species based on DFT calculations, and a such a procedure is discussed in detail elsewhere.⁵¹ In short, a bond length, d_OO, magnetic moments of the constituting oxygen atom, μ_i, and Bader charge are used to determine the type of anionic redox species. The sum of the absolute values of the magnetic moments of each species, ∑|μ_i|, can be used to distinguish one species from the others (e.g., ∑|μ_i| ≤ 0.3 for peroxides and 0.3 ≤ ∑|μ_i| ≤ 1.4 for superoxides). In general, there is a strong correlation between the type of species and the bond length; peroxides have 1.40 Å < d_OO < 1.5 Å and superoxides have 1.25 Å < d_OO < 1.40 Å.

Fig. 4 Disordered structures of Li_0.78VO₂F containing (a) peroxide and (b) superoxide after DFT calculations.

The formation of peroxides is observed for Li_xVO₂F when x is as high as 1.4, indicating the anionic redox process starts at high lithiation levels. The superoxides, on the other hand, start to form when x is around 0.8. The cycling range shown in Fig. 3 indicate that the electrochemical cycling up to 4.1 V sufficiently delithiates the Li_xVO₂F to induce the formation of both peroxides and superoxides. The existence of peroxides has been experimentally observed when V is in +5 oxidation state for alkali fluoroperoxovanadates (e.g., K₂(VFO(O₂)₂)).⁵² A formation of oxygen molecule is expected at very high potential up to 4.5 V or 5.0 V as observed in similar oxyfluoride materials.^27,32 However, the focus of current work is on the formation of superoxides upon charging (delithation), and the oxygen gas formation is beyond its scope.

3.2 Diamagnetic behavior of pristine Li₂VO₂F

The redox activity involves exchange of electronic charges as Li is extracted/inserted, which alters the oxidation states and the magnetic moments of V and O. Consequently, understanding the magnetic property of Li₂VO₂F is critical in investigating its redox activities with electron paramagnetic resonance (EPR) spectroscopy to detect/observe the O redox activity. However, the magnetic behavior of Li₂VO₂F remains poorly understood and has been only briefly discussed.¹⁸ Here, we establish a baseline magnetic response of the pristine material before electrochemical cycling. The DRS structure of Li₂VO₂F implies that V³⁺ is octahedrally coordinated by O²⁻ and F⁻ with an electronic configuration of 3d²: t²_2ge⁰_g. However, experimental data indicate, based on the oxidation state of V, that the exact composition deviates slightly from the ideal stoichiometry.^18,19,28,46 The non-stoichiometry affects the valence state of vanadium, which should be possible to determine through a magnetic susceptibility measurements. The molar magnetic susceptibility multiplied with temperature, χ^MT, of Li₂VO₂F is investigated as a function of temperature and compared against other related V-based compounds (Fig. 5). Li₂VO₂F shows a diamagnetic response, and even the Curie-tail due to impurities is negligibly small.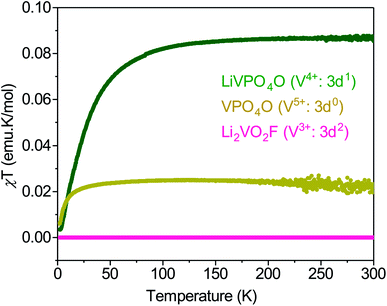

Fig. 5 Temperature dependence of the χ^MT for LiVPO₄O and VPO₄O within which vanadium valence state is V⁴⁺ and V⁵⁺, respectively. The data are compared with those obtained for Li₂VO₂F.

The diamagnetic behavior of Li₂VO₂F suggests that all the spins of vanadium in Li₂VO₂F are coupled despite the possible off-stoichiometry effects. To further shed light on the reasons for the unexpected diamagnetic behavior of Li₂VO₂F we conducted ⁵¹V and ⁶Li magic angle spinning nuclear magnetic resonance (MAS NMR) measurements to detect differences in the local environment of the selected elements. A ⁵¹V MAS NMR spectrum of pristine Li₂VO₂F sample is shown in Fig. 6. The spectrum exhibits a centerband at −546 ppm and a set of spinning sidebands. Such a spectrum is typical for quadrupolar vanadium nuclei in diamagnetic centers. This result is consistent with the observed magnetic susceptibility. If V centers were paramagnetic, ⁵¹V nuclei would become ‘NMR invisible’ due to their strong interaction with the unpaired electronic spins. Moreover, a similar diamagnetic behavior has been observed in the previous study of Li₂VO₂F.¹⁸

Fig. 6 ⁵¹V and ⁶Li MAS NMR spectra of Li₂VO₂F. The latter spectrum can be decomposed into three strongly overlapped contributions (grey lines).

The ⁶Li MAS NMR spectrum further confirms the diamagnetic behavior of the material. The spectrum is composed of at least three strongly overlapped contributions; an intense broad peak resonating at −8.5 ppm and two narrow peaks resonating at −1 ppm and −2 ppm. The broad peak arises from the nuclei in the disordered lattice of Li₂VO₂F; variations in the local environments lead to a distribution of chemical shifts and thus to the smearing of the NMR signal.¹⁸ The narrow peaks could stem from residual LiF and Li₂O, which could remain in the sample due to an incomplete synthesis.¹⁸

Although unexpected, the diamagnetic behavior of V³⁺ ions is not unique to Li₂VO₂F; a diamagnetic behavior has also been observed in the closely related LiVO₂ material.⁵³ In LiVO₂, one could expect the V³⁺ ions to be paramagnetic since they are 3d² ions in a quasi-octahedral environment. Their diamagnetic behavior has been attributed to either a strong Jahn–Teller distortion in the octahedra (which will lower the energy of one of the three t_2g orbitals)⁵⁴ or to the coupling of three V³⁺ ions.⁵⁵ The latter explanation was shown to be more plausible by core spectroscopy experiments.⁵⁴ In the case of Li₂VO₂F, a large energy splitting in the t_2g triplet is expected due to the fact that not all ligands of V ions are O²⁻ ions. The large energy splitting implies that the two d electrons of V³⁺ ions occupy the lowest t_2g orbital, which leads to its diamagnetic behavior.

3.3 Formation of superoxides

The anionic redox activity in Li₂VO₂F was already suspected in our previous study.²⁸ Here, we report EPR spectroscopy measurements of Li_xVO₂F samples in three different state of charges (SOC) in order to directly address the presence of the anionic redox activity (Fig. 7). Li₂VO₂F is typically cycled up to 4.1 V vs. Li/Li⁺.^18,19 The 4.1 V is lower than the typical upper limit used for cycling similar oxyfluoride materials, but it is still expected to be sufficiently high to induce the superoxide formation based on the DFT computation results.

Fig. 7 Voltage profile over time of the Li₂VO₂F carbon black active material pellets. Red circles indicate the SOC of the pellets used for the EPR measurements.

The room-temperature X-band EPR spectra of the Li_xVO₂F at three different SOCs are shown in Fig. 8a. The pristine Li₂VO₂F (black line in Fig. 8a) is EPR silent, confirming that the sample is diamagnetic as shown in the magnetic susceptibility and NMR studies. Charging (Li extraction) and discharging (Li reinsertion) processes of Li₂VO₂F have dramatic effects on the respective X-band EPR spectra. The EPR spectrum of the charged Li_xVO₂F (red line in Fig. 8a) consists of a sharp resonance at g ≈ 2.001 and additional broader satellite peaks that flank the center of the spectrum. The broader peaks can be assigned to the hyperfine interaction between the unpaired electron of the V⁴⁺ and the ⁵¹V nucleus. However, the paramagnetic V⁴⁺ alone cannot explain the sharp peak.

Fig. 8 (a) Comparison of the X-band EPR spectra of as-prepared Li₂VO₂F (black line), charged sample at 4.1 V (red line) and discharged sample at 1.3 V (blue line). (b) X-band EPR spectrum of charged Li_xVO₂F (red circles) measured at room temperature with a high signal-to-noise ratio reached by EPR signal averaging. The solid black line is a fit to a model of paramagnetic O₂⁻ and V⁴⁺ (3d¹).

Therefore, we fit the spectrum to two coexisting paramagnetic centers where the V⁴⁺ signal is broadened by the hyperfine interaction while the second sharp resonance is broadened by the g-factor anisotropy (Fig. 8b). The V⁴⁺ component is fit to g_xx = 1.978, g_yy = 1.940 and g_zz = 1.958 and with the components of the hyperfine coupling tensor to the ⁵¹V nucleus A_xx = 143.6 MHz, A_yy = 140.7 MHz, and A_zz = 443.8 MHz. While these values are characteristic of the V⁴⁺S = 1/2 center, they also suggest the rhombic distortion of the local vanadium coordination, which is in a qualitative agreement with the disordered nature of the sample. An unconstrained fit yields for the sharp resonance g_⊥ = 2.0094 and g_‖ = 2.0012, which are typical values for the superoxide.⁵⁶ The presence of superoxide EPR signal upon charging thus corroborates the predictions made based on DFT calculations.

The material shows a very broad and strong EPR signal when it is discharged to 1.3 V (blue line in Fig. 8a). The broad component has a nearly Lorentzian lineshape and is centered at g = 1.97, i.e., at the position expected for V⁴⁺. The broadness of the EPR spectrum and the peak-to-peak linewidth of ∼65 mT suggest that these V⁴⁺ centers strongly interact with each other. On top of the broad V⁴⁺ one can still notice traces of isolated superoxide and isolated V⁴⁺ centers, indicating the presence of the superoxide upon discharge. The presence of V⁴⁺ aligns well with previous reports on the limited reversibility of the vanadium redox couple.^19,28 However, the EPR measurements also indicate that the superoxide formation is also not entirely reversible, which may contribute to the capacity fading.

3.4 Proposed degradation mechanism

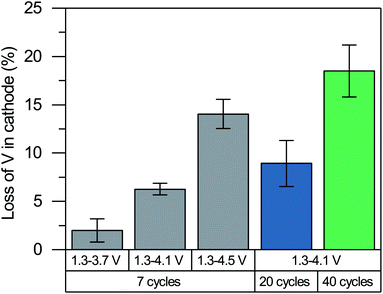
It may seem surprising that the superoxide ions formed upon charging remain to be present after the discharge, particularly because they are known to be unstable. Ideally, reinserting Li⁺ reduces vanadium and oxidized anions back to their initial oxidation states of +3 and −2, respectively. The residual superoxides after the discharge seem to violate the charge neutrality of cathode. Furthermore, our recent degradation study of Li₂VO₂F with extended cycling²⁸ has shown limited reversibility of the V³⁺/V⁵⁺ redox couple where vanadium no longer reaches the V³⁺ state. The partially irreversible redox (both vanadium and oxygen) can be explained by the loss of vanadium in the cathode.

The vanadium loss of the cathode is measured using inductive coupled plasma optical emission spectroscopy (ICP OES) after 7, 20 and 40 cycles in the discharged state as it is difficult to accurately quantify the small amount of dissolved vanadium after the first cycle. It can be seen from Fig. 9 that a considerable amount of V is lost from the cathode. The extent of vanadium dissolution is roughly proportional to the upper potential limit used in the cycling, which indicates a correlation between the V loss and the anionic redox activity. The vanadium dissolution allows the V⁴⁺ ions and partially oxidized oxygen ions (e.g., O⁻ ions, peroxides and superoxides) to remain in the structure upon the reinsertion of Li⁺ based on the charge neutrality. The formation of anionic redox species and its reversibility are closely linked to the vanadium dissolution, although their causalities remain unclear (i.e., whether the vanadium dissolution leads to the formation of anionic redox species and reduce its reversibility, or vice versa). We note that a lack of causality is also possible as they may occur simultaneously to stabilize each other due to their opposite contribution to the net charge.

Fig. 9 Loss of V in Li₂VO₂F cathodes cycled for 7 cycles with varying upper cut-off voltages (from 1.3 to 3.7, 4.1 and 4.5 V vs. Li/Li⁺, grey) and cycled from 1.3 to 4.1 V vs. Li/Li⁺ for 20 (blue) and 40 (green) cycles.

The limited redox reversibility and the loss of V ions are expected to be some of the primary contributors to the performance degradation of Li₂VO₂F. We hypothesize that the vacancies created by the loss of V ions facilitate the formation of the percolating network in the subsequent charging cycles when the Li vacancies are created upon delithiation. The percolating network formed by the V and Li vacancies makes it more likely for the residual and newly formed peroxides and superoxides to diffuse and leave the material (i.e., oxygen loss). The missing oxygen in the cathode, in turn, promotes further V-ion dissolution. In other words, we postulate that the V-ion dissolution and limited redox reversibility cause a runaway process where the loss of vanadium and oxygen triggers the loss of another, further deteriorating the material. Our proposed degradation process aligns well with the continued vanadium dissolution up to the 40 cycles we tested and with the results reported by Cambaz et al.⁵⁷ that suppressing vanadium dissolution by using concentrated electrolyte improves cycling stability.

4 Conclusions

A comprehensive computational and experimental analysis of the anionic redox activities in Li₂VO₂F is presented. We elucidate the structural properties of Li₂VO₂F using MC simulations based on the CE model trained using DFT calculations. Both the DRS and layered-rocksalt phases of Li₂VO₂F are found to be metastable with respect to its decomposed product (i.e., LiVO₂ and LiF), which explains the absence of successful synthesis approaches besides the high-energy ball milling that forces the material to be in the metastable phase by introducing dislocations and disorder. Furthermore, we established a correlation between the lithiation level and the anionic redox activity via simulated voltage profile and DFT calculation results. The model predicts the formation of peroxides and superoxides when the material is charged up to 4.1 V, which is lower than the values typically used for cycling similar oxyfluorides. Although the high fluorine content suppresses the oxygen redox activity, superoxides are detected in our EPR measurements for the charged sample, confirming the superoxide formation as predicted by the model. Moreover, the superoxide formation is not completely reversible, which is linked to the limited reversibility of the V³⁺/V⁵⁺ redox couple and dissolution of vanadium. We propose a possible degradation mechanism where vanadium dissolution and limited redox reversibility cause a runaway process that leads to further losses of vanadium and oxygen.

Our study underlines the importance of gaining deeper insights into the anionic redox activities of Li-rich materials for designing a new cathode material for future LIBs. Promoting the reversible anionic redox contributions while suppressing the irreversible reactions is vital in designing a cathode material with high energy density and good cycling performance. The combined computational/experimental approach presented here can be applied to predict and verify the anionic redox activities in other Li-rich materials to accelerate the discovery of materials with high energy density and good cycling performance.

Author contributions

J. H. C., C. B. and J. M. G. L. planned the project. J. H. C. conducted the computational analysis with help of T. V. and J. M. G. L. C. B. synthesized the materials, performed the electrochemical measurements and conducted the dissolution study. D. A. conducted the EPR and magnetism experiments. G. M. conducted the NMR experiments. The manuscript was written by J. H. C. and C. B. with the help of J.-M. A. M., D. A. and G. M. The manuscript was revised with the help of all authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This project has received funding from the European Union's Horizon 2020 research and innovation program (FET-OPEN project “LiRichFCC”) under grant agreement No. 711792. HIU is part of the platform CELEST (Center for Electrochemical Storage Ulm-Karlsruhe).

Notes and references

1. M. Armand and J.-M. Tarascon, Nature, 2008, 451, 652–657.
2. J. B. Goodenough and K.-S. Park, J. Am. Chem. Soc., 2013, 135, 1167–1176.
3. M. S. Whittingham, Chem. Rev., 2004, 104, 4271–4301.
4. J. Lee, A. Urban, X. Li, D. Su, G. Hautier and G. Ceder, Science, 2014, 343, 519–522.
5. K. Mizushima, P. Jones, P. Wiseman and J. Goodenough, Mater. Res. Bull., 1980, 15, 783–789.
6. J. N. Reimers and J. R. Dahn, J. Electrochem. Soc., 1992, 139, 2091–2097.
7. W.-D. Yang, C.-Y. Hsieh, H.-J. Chuang and Y.-S. Chen, Ceram. Int., 2010, 36, 135–140.
8. Y. Makimura, T. Sasaki, T. Nonaka, Y. F. Nishimura, T. Uyama, C. Okuda, Y. Itou and Y. Takeuchi, J. Mater. Chem. A, 2016, 4, 8350–8358.
9. N. Yabuuchi and T. Ohzuku, J. Power Sources, 2003, 119–121, 171–174.
10. X. Zhang, W. J. Jiang, A. Mauger, Qilu, F. Gendron and C. M. Julien, J. Power Sources, 2010, 195, 1292–1301.
11. R. Hausbrand, G. Cherkashinin, H. Ehrenberg, M. Gröting, K. Albe, C. Hess and W. Jaegermann, Mater. Sci. Eng., B, 2015, 192, 3–25.
12. Y. Xia, J. Zheng, C. Wang and M. Gu, Nano Energy, 2018, 49, 434–452.
13. A. Urban, J. Lee and G. Ceder, Adv. Energy Mater., 2014, 4, 1400478.
14. S. L. Glazier, J. Li, J. Zhou, T. Bond and J. R. Dahn, Chem. Mater., 2015, 27, 7751–7756.
15. J. Lee, D.-H. Seo, M. Balasubramanian, N. Twu, X. Li and G. Ceder, Energy Environ. Sci., 2015, 8, 3255–3265.
16. N. Yabuuchi, M. Nakayama, M. Takeuchi, S. Komaba, Y. Hashimoto, T. Mukai, H. Shiiba, K. Sato, Y. Kobayashi, A. Nakao, M. Yonemura, K. Yamanaka, K. Mitsuhara and T. Ohta, Nat. Commun., 2016, 7, 1–10.
17. N. Kitamura, Y. Araki, N. Ishida and Y. Idemoto, Phys. Status Solidi B, 2020, 2000112.
18. R. Chen, S. Ren, M. Knapp, D. Wang, R. Witter, M. Fichtner and H. Hahn, Adv. Energy Mater., 2015, 5, 1401814.
19. C. Baur, I. Källquist, J. Chable, J. H. Chang, R. E. Johnsen, F. Ruiz-Zepeda, J.-M. Ateba Mba, A. J. Naylor, J. M. Garcia-Lastra, T. Vegge, F. Klein, A. R. Schür, P. Norby, K. Edström, M. Hahlin and M. Fichtner, J. Mater. Chem. A, 2019, 7, 21244–21253.
20. R. Chen, S. Ren, M. Yavuz, A. A. Guda, V. Shapovalov, R. Witter, M. Fichtner and H. Hahn, Phys. Chem. Chem. Phys., 2015, 17, 17288–17295.
21. D.-H. Seo, J. Lee, A. Urban, R. Malik, S. Kang and G. Ceder, Nat. Chem., 2016, 8, 692–697.
22. M. Sathiya, G. Rousse, K. Ramesha, C. P. Laisa, H. Vezin, M. T. Sougrati, M. L. Doublet, D. Foix, D. Gonbeau, W. Walker, A. S. Prakash, M. Ben Hassine, L. Dupont and J. M. Tarascon, Nat. Mater., 2013, 12, 827–835.
23. M. Saubanère, E. McCalla, J. M. Tarascon and M. L. Doublet, Energy Environ. Sci., 2016, 9, 984–991.
24. K. Luo, M. R. Roberts, R. Hao, N. Guerrini, D. M. Pickup, Y.-S. Liu, K. Edström, J. Guo, A. V. Chadwick, L. C. Duda and P. G. Bruce, Nat. Chem., 2016, 8, 684–691.
25. N. Yabuuchi, M. Nakayama, M. Takeuchi, S. Komaba, Y. Hashimoto, T. Mukai, H. Shiiba, K. Sato, Y. Kobayashi, A. Nakao, M. Yonemura, K. Yamanaka, K. Mitsuhara and T. Ohta, Nat. Commun., 2016, 7, 13814.
26. M. A. Cambaz, B. P. Vinayan, H. Geßwein, A. Schiele, A. Sarapulova, T. Diemant, A. Mazilkin, T. Brezesinski, R. J. Behm, H. Ehrenberg and M. Fichtner, Chem. Mater., 2019, 31, 4330–4340.
27. J. Lee, J. K. Papp, R. J. Clément, S. Sallis, D.-H. Kwon, T. Shi, W. Yang, B. D. McCloskey and G. Ceder, Nat. Commun., 2017, 8, 981.
28. I. Källquist, A. J. Naylor, C. Baur, J. Chable, J. Kullgren, M. Fichtner, K. Edström, D. Brandell and M. Hahlin, Chem. Mater., 2019, 31, 6084–6096.
29. R. J. Clément, Z. Lun and G. Ceder, Energy Environ. Sci., 2020, 13, 345–373.
30. B. Ouyang, N. Artrith, Z. Lun, Z. Jadidi, D. A. Kitchaev, H. Ji, A. Urban and G. Ceder, Adv. Energy Mater., 2020, 10, 1903240.
31. N. Yabuuchi, Chem. Rec., 2019, 19, 690–707.
32. J. Lee, D. A. Kitchaev, D.-H. Kwon, C.-W. Lee, J. K. Papp, Y.-S. Liu, Z. Lun, R. J. Clément, T. Shi, B. D. McCloskey, J. Guo, M. Balasubramanian and G. Ceder, Nature, 2018, 556, 185–190.
33. R. A. House, L. Jin, U. Maitra, K. Tsuruta, J. W. Somerville, D. P. Förstermann, F. Massel, L. Duda, M. R. Roberts and P. G. Bruce, Energy Environ. Sci., 2018, 11, 926–932.
34. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
35. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269.
36. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
37. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
38. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
39. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
40. V. I. Anisimov, J. Zaanen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 943–954.
41. M. Cococcioni and S. de Gironcoli, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035105.
42. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
43. J. H. Chang, D. Kleiven, M. Melander, J. Akola, J. M. Garcia-Lastra and T. Vegge, J. Phys.: Condens. Matter, 2019, 31, 325901.
44. G. A. Bain and J. F. Berry, J. Chem. Educ., 2008, 85, 532.
45. S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55.
46. X. Wang, Y. Huang, D. Ji, F. Omenya, K. Karki, S. Sallis, L. F. J. Piper, K. M. Wiaderek, K. W. Chapman, N. A. Chernova and M. S. Whittingham, J. Electrochem. Soc., 2017, 164, A1552–A1558.
47. A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002.
48. C. Baur, J. Chable, F. Klein, V. S. K. Chakravadhanula and M. Fichtner, ChemElectroChem, 2018, 5, 1484–1490.
49. J. Chable, C. Baur, J. H. Chang, S. Wenzel, J. M. García-Lastra and T. Vegge, J. Phys. Chem. C, 2020, 124, 2229–2237.
50. P. G. McCormick and F. H. Froes, JOM, 1998, 50, 61–65.
51. A. Tygesen, J. H. Chang, T. Vegge and J. M. García-Lastra, npj Comput. Mater., 2020, 6, 65.
52. R. Stomberg, Acta Chem. Scand., Ser. A, 1984, 38, 223–228.
53. T. A. Hewston and B. L. Chamberland, J. Solid State Chem., 1986, 65, 100–110.
54. H. Pen, L. Tjeng, E. Pellegrin, F. de Groot, G. Sawatzky and M. van Veenendaal, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 15500–15505.
55. J. Goodenough, Magnetism and the chemical bond, Interscience Publishers, 1963.
56. M. Sathiya, J. B. Leriche, E. Salager, D. Gourier, J. M. Tarascon and H. Vezin, Nat. Commun., 2015, 6, 1–7.
57. M. A. Cambaz, B. P. Vinayan, S. A. Pervez, R. E. Johnsen, H. Geßwein, A. A. Guda, Y. V. Rusalev, M. K. Kinyanjui, U. Kaiser and M. Fichtner, Chem. Mater., 2019, 31, 7941–7950.

---