The relationship between oxide-ion conductivity and cation vacancy order in the hybrid hexagonal perovskite Ba₃VWO_8.5

Abstract

Significant oxide ionic conductivity has recently been reported in cation-deficient hexagonal perovskite Ba₃M′M′′O_8.5 derivatives (M′ = Nb; M′′ = Mo, W), with disordered hybrid 9R-palmierite average structures. Here, we present a study of the crystal structure and electrical properties of the related compound Ba₃VWO_8.5. Electrical characterization demonstrates that Ba₃VWO_8.5 is also an oxide ion conductor with a bulk conductivity of 2.0 × 10⁻³ S cm⁻¹ in air at 900 °C, thus revealing that it is possible to obtain oxide ion conducting Ba₃M′M′′O_8.5 materials with a variety of different M′M′′ combinations. Whilst Ba₃NbMoO_8.5 and Ba₃NbWO_8.5 present a random distribution of cationic vacancies, X-ray and neutron diffraction experiments demonstrate that the cationic vacancies are ordered on the M2 sites in Ba₃VWO_8.5, resulting in a structure where M1O_x palmierite-like layers are separated by empty octahedral cavities. Bond-valence site energy (BVSE) analysis on the different phases reveals that ordering of the cationic vacancies hinders long-range oxygen diffusivity parallel to the c-axis in Ba₃VWO_8.5 explaining the reduced ionic conductivity of this compound. These results suggest that, together with the dominant 2-dimensional conduction pathway along the palmierite-like layers, additional diffusion routes parallel to the c-axis provide a relevant contribution to the conductivity of these Ba₃M′M′′O_8.5 systems by creation of a complex 3-dimensional ionic percolation network, the topology of which depends on the particular arrangement of cation and anion vacancies.

---

Introduction

Solid oxide fuel cells (SOFCs) are electrochemical devices able to generate electricity from renewable energy sources, with high efficiency and low emissions of pollutants.^1–3 However, oxide ion transport in most commercially available solid electrolytes is enabled only at high working temperatures (>700 °C), thus making the commercialization of SOFCs particularly challenging.^2,4,5 The high operating temperature reduces the components' durability, results in slow start up times and the necessitation of expensive materials for seals and interconnects.^1,4 In order to overcome these issues, it is desirable to develop novel electrolyte materials with significant oxide ion conductivity at intermediate temperatures (300–600 °C). Ionic conduction in solid oxides is strongly related to the crystal structure, and as a result the discovery and characterization of novel oxide ion conductors in various structural families has attained significant attention from researchers.⁶ Several fast oxide ion conductors have been reported in systems such as fluorite-type structures,^7–9 silicon and germanium apatites,¹⁰ rare earth molybdates (La₂Mo₂O₉, LAMOX materials),¹¹ Bi₄V₂O₁₁-derived oxides (BIMEVOX),¹² and compounds containing GaO₄ tetrahedral moieties.^13,14 High oxide ion conductivity has also been observed in different cubic and layered perovskite systems.^15–18 The perovskite ABO₃ structure is generally composed by a framework of corner-sharing BO₆ octahedral units, in which the A cations occupy the interstitial voids. When there is a large difference in size between the constituent cations, some of the B octahedra share faces to release the strain caused by the size mismatch between the cations, resulting in the formation of hexagonal polytypes.¹⁹ Mixed combinations of corner-sharing and face-sharing octahedra can give rise to a variety of hexagonal perovskite derivatives able to accommodate cationic and anionic vacancies.^19,20 Recently, we have reported the first hexagonal perovskite derivative with significant oxide ion conductivity, Ba₃NbMoO_8.5.²¹ Ba₃NbMoO_8.5 exhibits bulk oxide ion conductivity of 2.2 × 10⁻³ S cm⁻¹ at 600 °C, competitive with other electrolyte materials, and the conductivity is predominantly ionic in a wide pO₂ range. Ba₃NbMoO_8.5 is a cation-deficient hexagonal perovskite derivative with an average structure composed of a hybrid of the 9R perovskite and palmierite units.²¹ Variable coordination M1O_x polyhedral units are generated within the palmierite-like layers due to considerable positional oxygen disorder. Average octahedral and tetrahedral units arise from partial occupation of two crystallographic oxygen positions (O2 and O3),^21,22 with the existence of 5-fold geometries on the local-scale.^23,24 The random distribution of intrinsic oxygen vacancies and available oxygen sites results in a continuous 2-dimensional ionic diffusion pathway for oxide migration along the palmierite-like layers.²⁵ The cationic vacancies are disordered on two mutually exclusive metal sites (M1 and M2), leading to the formation of complex disordered stacking configurations of M1O_x and M2O₆ polyhedral units.^23,26 Substantial oxide ion conductivity has been discovered in other compounds of the Ba₃M′M′′O_8.5 (M′ = Nb; M′′ = Mo, W) family.^26–30 In particular, members of the Ba₃Nb_1−xV_xMoO_8.5 series present enhanced ionic conductivity, with the x = 0.1 composition showing a bulk conductivity of ∼0.01 S cm⁻¹ at 600 °C, one order of magnitude higher than the conductivity of Ba₃NbMoO_8.5.²⁶ Furthermore, Ba₃NbWO_8.5 exhibits similar conductivity to Ba₃NbMoO_8.5 at 600 °C and greater stability in a reducing 5% H₂/N₂ atmosphere.²⁷ High oxide ion and proton conductivity has also been reported in Ba₇Nb₄MoO₂₀, a hexagonal derivative with an average crystal structure composed of a disordered arrangement of 12R hexagonal perovskite and palmierite-like layers, similar to Ba₃NbMoO_8.5.³¹ The structures of these cation-deficient hexagonal perovskite derivatives are versatile and able to accommodate various transition metal cations, potentially enabling ionic conduction in different disordered layered systems.

In this study, we present the crystal structure and electrical properties of the hexagonal perovskite derivative Ba₃VWO_8.5. This phase has been synthesized previously, but the conductivity has not been measured, nor the structure characterized by neutron diffraction.³² Impedance spectroscopy measurements reveal that Ba₃VWO_8.5 is also an oxide ion conductor at high and intermediate oxygen partial pressures, with a bulk conductivity of 2.0 × 10⁻³ S cm⁻¹ at 900 °C. Hence, it is possible to synthesise hexagonal perovskite oxide ion conductors without the elements of Mo and Nb, opening up further opportunities for discovering novel oxide and/or proton conductors in the hexagonal perovskite family. While all the Ba₃M′M′′O_8.5 phases reported so far are isostructural with Ba₃NbMoO_8.5, in Ba₃VWO_8.5 the cationic vacancies are ordered on the M2 sites, thus resulting in a structure where M1O_x palmierite-like layers are separated by empty octahedral cavities. Bond-valence site energy (BVSE) analysis on the average structure confirms the presence of diffusion pathways along the palmierite-like layers but demonstrates the absence of long-range oxygen mobility parallel to the c-axis. The relationship between the electrical properties and BVSE calculations on Ba₃NbMoO_8.5, Ba₃NbWO_8.5 and Ba₃VWO_8.5 suggests that additional pathways parallel to the c-axis may provide a relevant contribution to the conductivity of these systems, highlighting the importance of both cation disorder and the chemistry of the M′M′′ cations in defining the ionic conducting properties of Ba₃M′M′′O_8.5 derivatives.

Experimental

Ba₃VWO_8.5 was prepared by the solid-state reaction of stoichiometric quantities of Ba(NO₃)₂ (99.999%, Aldrich), WO₃ (99.9%, Aldrich) and V₂O₅ (≥99.6%, Aldrich). The starting materials were ground, pressed into a pellet and then calcined in air at 900 °C for 10 hours. The pellet was subsequently ground, re-pelletized and sintered at 1060 °C for 24 hours in air with a heating rate of 5 °C min⁻¹ and then cooled down to room temperature with a cooling rate of 5 °C min⁻¹. The last sintering step was repeated multiple times until a phase pure sample was obtained. The synthesis of Ba₃VWO_8.5 is very sensitive to sintering temperature and a phase pure material is only obtained over a very narrow temperature range (1060 °C ± 10 °C). This could be a result of Ba volatilisation. Impurities of BaWO₄ form above this temperature.

Powder X-ray diffraction (XRD) data were collected with a PANalytical Empyrean Powder diffractometer with Cu Kα₁ radiation at room temperature. Data were acquired in the range 10° ≤ 2θ ≤ 110°, with a step size of 0.013°. Time-of-flight neutron powder diffraction experiments were performed at room temperature on the Polaris diffractometer³³ at the ISIS pulsed neutron source (Rutherford Appleton Laboratory). A sample of 5 g of Ba₃VWO_8.5 was loaded into an 8 mm diameter cylindrical vanadium can and data were recorded for a total of 350 μA h proton charge to the ISIS target, corresponding to ∼2 hours exposure in the neutron beam. Rietveld analysis was performed using the GSAS/EXPGUI package.³⁴ The background was fitted by the Chebyschev polynomial function and the peak shapes were modelled using profile function 3, which is a convolution of a pseudo-Voigt function with two back-to-back exponentials.

For the impedance spectroscopy measurements, a pellet of ∼10 mm diameter and ∼1.5 mm thickness was prepared using a sample of Ba₃VWO_8.5 sintered at 1060 °C for 48 hours to achieve 90% of the theoretical density. Platinum electrodes were painted on both sides of the pellet using Pt paste (Metalor 6082). Impedance measurements were acquired in the frequency range 0.1 Hz to 1.0 MHz with a Solartron 1260 impedance analyser with an applied alternating voltage of 0.1 V. Data were recorded upon cooling from 900 °C to 350 °C in a sealed tube furnace under a flow of dry air, oxygen, nitrogen and 5% H₂/N₂ gas mixture. Dry gaseous atmospheres were obtained by flowing the employed gas through a column of a commercial desiccant (Drierite) (pH₂O < 10⁻⁴ atm). Impedance data were measured every ∼15 °C allowing 2 hours equilibration time at each temperature. The recorded impedance data were corrected using the geometrical factor and analysed with the ZView software (Scribner Associates, Inc.)

Bond-valence site energy (BVSE) calculations were performed with the softBV program,^35,36 using the structural models from Rietveld refinement as input. Details about the softBV approach and the type of force-field employed for the BVS analysis can be found elsewhere.^35,36 Bond-valence site energy landscapes for the interaction of a test O²⁻ ion were calculated for a dense grid of points with a resolution of 0.1 Å. Diffusion pathways were identified with regions of low bond-valence site energy by direct visualization of the connectivity of the isosurfaces and by examination of the calculated pathway segments. BVSE models of migration barriers were plotted from the calculated energy profiles of the pathway segments.

Analysis of minimum bonding ellipsoids using the PIEFACE software was employed to evaluate the effect of doping on the relaxation of the average metal coordination polyhedra.³⁷ The polyhedral distortion was quantified by the standard deviation, σ(R), of the three principal ellipsoids' radii (R_x, R_y, R_z).

Results and discussion

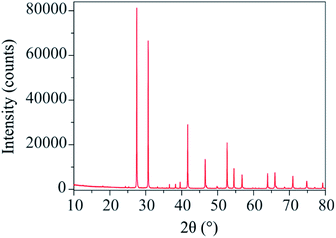
The X-ray diffraction pattern of Ba₃VWO_8.5 (Fig. 1) shows that there are no impurities in the as prepared sample and that the peaks could be indexed in the space group R3̄m H, as previously reported for Ba₃NbMoO_8.5.²¹

Fig. 1 X-ray diffraction pattern of Ba₃VWO_8.5 which can be indexed by the R3̄m H space group.

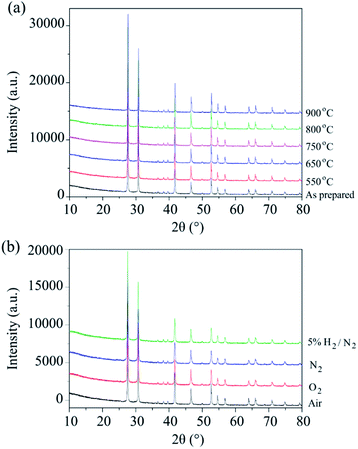
The phase stability of Ba₃VWO_8.5 was investigated by annealing the sample in air at selected temperatures between 550 °C and 900 °C for 24 hours. There is no evidence of Bragg reflections from impurity phases after annealing, as shown in the X-ray diffraction data in Fig. 2a. This indicates that Ba₃VWO_8.5 is stable in air between 500 to 900 °C. This contrasts with Ba₃NbMoO_8.5, which is not stable between 650–1000 °C, with the formation of BaMoO₄ and Ba₇Nb₄MoO₂₀ impurities above 650 °C.²¹ The Ba₃VWO_8.5 sample was also annealed at 900 °C for 24 hours under the flow of a range of different gases (O₂, N₂, 5% H₂/N₂). The XRD data demonstrate that the Ba₃VWO_8.5 phase is stable in both oxidizing and reducing environments (Fig. 2b).

Fig. 2 (a) XRD patterns of Ba₃VWO_8.5 recorded after a 24 hour anneal in air at selected temperatures. (b) XRD patterns of Ba₃VWO_8.5 recorded after 24 hours annealing at 900 °C under different flowing gases (air, O₂, N₂, 5% H₂/N₂).

AC impedance spectroscopy was used to investigate the ionic conductivity of Ba₃VWO_8.5. Typical complex impedance plane (Z*) plots are displayed in Fig. 3a and b. The bulk (C ∼7–12 pF cm⁻¹) and grain boundary responses (C ∼30–40 pF cm⁻¹) have very similar time constants and overlap in the high-intermediate frequency regime (Fig. 3a), resulting in a broad and depressed grain arc.

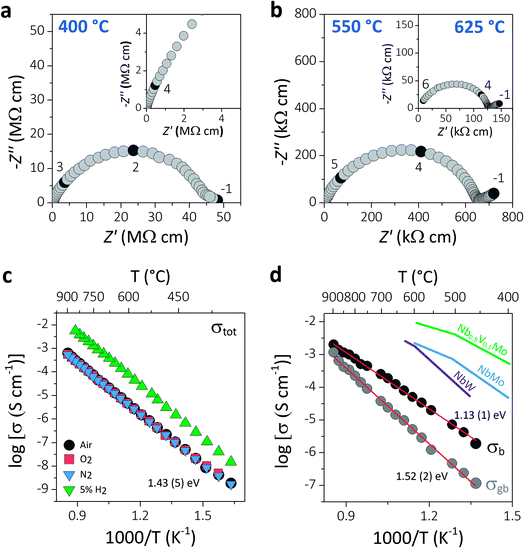Fig. 3 (a and b) Typical complex impedance plots recorded in oxygen at 400 °C, 550 °C, and 625 °C. The inset in (a) shows a magnification of the high frequency region. The numbers and corresponding filled symbols indicate selected frequency decades. (c) Arrhenius plot of the total conductivity of Ba₃VWO_8.5 recorded in a range of different dry atmospheres (air, O₂, N₂, 5% H₂/N₂), with the reported activation energy in dry air. (d) Arrhenius plots of the bulk and grain boundary conductivity of Ba₃VWO_8.5; red lines show the linear fit to the data with the corresponding activation energies. The bulk conductivities of Ba₃NbMoO_8.5 (NbMo, ref. 21), Ba₃NbWO_8.5 (NbW, ref. 27) and Ba₃Nb_0.9V_0.1MoO_8.5 (Nb_0.9V_0.1Mo, ref. 26) are reported for comparison.

A low-slope electrode signal is observed at low frequencies above 450 °C (Fig. 3b). This feature indicates finite length diffusion typical of a Warburg electrode response and is evidence of ionic conduction in a material with partially blocking electrodes.³⁸ The electrode response becomes less resistive upon increasing the oxygen partial pressure, consistent with oxygen ion diffusion. Total resistivity (R_b + R_gb) values were obtained from the high frequency intercept of the grain boundary semicircle on the real axis at all temperatures. The total conductivity values of Ba₃VWO_8.5 recorded in a range of different atmospheres are presented in the Arrhenius plot in Fig. 3c. Ba₃VWO_8.5 exhibits a total conductivity of 6.2 × 10⁻⁴ S cm⁻¹ in air at 900 °C, with an activation energy of 1.43 (5) eV. There is no change in the conductivity values recorded in air, O₂ and N₂, revealing that the total conductivity of Ba₃VWO_8.5 is independent of oxygen partial pressure at high pO₂ (see ESI Fig. S1†), so that pure oxide ion conduction is observed at high pO₂. There is an increase in the conductivity in 5% H₂/N₂, which reveals that Ba₃VWO_8.5 exhibits an electronic component in the more reducing atmosphere. This is analogous to Ba₃NbMoO_8.5, where concentration cell experiments revealed a minor electronic component,²¹ but is in stark contrast to Ba₃WNbO_8.5 and Ba₃Nb_0.9V_0.1MoO_8.5, for which impedance spectroscopy measurements under 5% H₂/N₂ revealed a negligible electronic conductivity contribution.^26,27

Equivalent circuit analysis was used to extract the individual bulk (R_b) and grain boundary resistivity values (R_gb). An equivalent circuit constituted by a series combination of a resistor (R) in parallel with a constant phase element (CPE) was employed to model the bulk and grain boundary impedance responses of the data collected in dry air (see ESI Fig. S2†). Representative equivalent circuit fits of the complex impedance data at 500 °C and 700 °C are shown in ESI Fig. S3.† The Arrhenius plot in Fig. 3d shows the bulk conductivity of Ba₃VWO_8.5 compared with the bulk conductivities of Ba₃NbMoO_8.5, Ba₃NbWO_8.5 and B₃Nb_0.9V_0.1MoO_8.5. The bulk conductivity of Ba₃VWO_8.5 is 5.0 × 10⁻⁵ S cm⁻¹ at 600 °C, two orders of magnitude lower than the bulk conductivity of Ba₃NbMoO_8.5 (2.2 × 10⁻³ S cm⁻¹) and Ba₃NbWO_8.5 (1.8 × 10⁻³ S cm⁻¹) and three orders of magnitude lower than the conductivity of the V-doped B₃Nb_0.9V_0.1MoO_8.5 composition (1.0 × 10⁻² S cm⁻¹). The grain boundaries of Ba₃VWO_8.5 present reduced conductivity (5.3 × 10⁻⁶ S cm⁻¹ at 600 °C) and considerably higher activation energy (1.52 (2) eV) than for ionic transport in the bulk domain (1.13 (1) eV). The grain boundaries clearly constitute the most resistive part, dominating the total resistivity of the material, as reported also for other Ba₃M′M′′O_8.5 derivatives.^21,27 Materials containing barium that are sintered at high temperature can have a different chemical composition of the grain boundaries resulting in a higher grain boundary resistivity due to the presence of blocking effects, as in the case of Ba₃Nb_0.8W_1.2O_8.6.²⁸ This is generally caused by barium volatilisation and/or segregation of secondary phases in the grain boundary region and is a common problem in various Ba-containing oxide ion and proton conductors.^39–42 Further sintering studies will be required in order to reduce the grain boundary resistivity of Ba₃M′M′′O_8.5 derivatives and further exploit their high bulk conductivity.

Time-of-flight (TOF) neutron powder diffraction data⁴³ were recorded on the Polaris diffractometer in order to determine the crystal structure of Ba₃VWO_8.5 and to obtain accurate oxygen occupancies. Ba₃VWO_8.5 was previously reported to crystallize with a 9R hexagonal polytype structure with stacking sequence (hhc)₃, in which trimers of face-sharing (V/W)O₆ octahedra are connected via corner sharing.³² This model, which contains purely octahedral coordination of the metals, resulted in a poor Rietveld fit. The hybrid 9R perovskite – palmierite average structure previously reported for Ba₃M′M′′O_8.5 (ref. 20, 21 and 27) was therefore employed as a starting model for Ba₃VWO_8.5. In this model, the oxygen atoms occupy three different sites. The oxygen atom at Wyckoff position 18h (O1) is common to both the 9R and palmierite structures. The 9R perovskite structure also has an oxygen atom at Wyckoff position 9e (O2), whereas the palmierite structure has an oxygen atom at 6c (O3). The hybrid average structural model contains oxygen on all three sites. The intrinsic oxygen vacancies are randomly distributed along the pseudo-cubic BaO_2.5 layers, resulting in partial occupation of the average O2 and O3 crystallographic sites, and in the formation of mixed average tetrahedral and octahedral metal coordination units within the palmierite-like layers. Large positional oxygen disorder along the O2–O3 layers leads to local disruption of the crystallographic oxygen site configurations and generates 4-, 5-, and 6-fold coordination geometries on the local scale.^23,24 The barium atoms occupy the 6c and 3a Wyckoff positions (Ba1 and Ba2 respectively), while the transition metal cations are at Wyckoff position 6c (M1) and at Wyckoff position 3b (M2).^21,27 Refinement of the fractional occupancy of the transition metals in Ba₃VWO_8.5 from neutron diffraction data is difficult because vanadium has a low scattering cross section for neutrons.⁴⁴ For this reason, we first performed Rietveld refinement of the structural model from high-resolution X-ray diffraction data in order to determine the fractional occupancies of tungsten and vanadium within the crystal structure of Ba₃VWO_8.5.

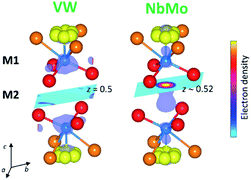
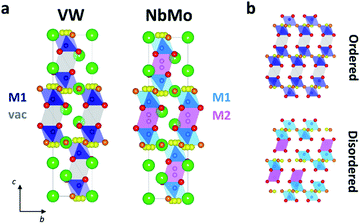
In the reported hybrid structural model of Ba₃M′M′′O_8.5, the transition metals and the cationic vacancies are distributed in a disordered pattern over the M1 and M2 sites.^21,27 In contrast, unconstrained refinement of the W and V site occupancies in Ba₃VWO_8.5 reveals that the M1 site is fully occupied, while the M2 site is empty. Examination of X-ray difference Fourier maps shows no evidence of significant missing scattering density on or in proximity of the (0,0,0.5) M2 site (VW in Fig. 4). For comparison, an X-ray difference Fourier map calculated on Ba₃NbMoO_8.5 by setting the occupancy of M2 to zero clearly reveals un-modelled electron density located at 6c (0,0,∼0.52) (NbMo in Fig. 4), above and below the nominal 3b position, in agreement with previous reports of splitting of the M2 site.^23,26

Fig. 4 Volumetric data obtained from the X-ray difference Fourier analysis on the refined structures of Ba₃VWO_8.5 (VW) and Ba₃NbMoO_8.5 (NbMo). The difference Fourier map for Ba₃VWO_8.5 shows no evidence of electron density on or in proximity of the 3b (0,0,0.5) M2 site. In contrast the map for Ba₃NbMoO_8.5, calculated by setting the occupancy of M2 to zero, clearly indicates missing electron density located for the most part at the 6c (0,0,∼0.52) site. Sections represent slices of the volumetric Fourier data seen along the [001] direction at z = 0.5 (VW) and at z ∼0.52 (NbMo). The metal cations are represented by the blue spheres, while the oxygen atoms are in red (O1), orange (O2) and yellow (O3).

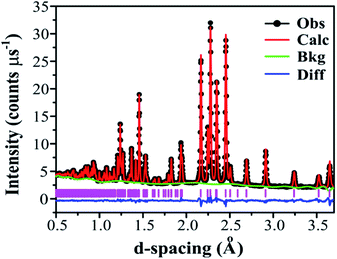
Adopting the vacant M2 model for Ba₃VWO_8.5 resulted in a significant improvement of the goodness of fit parameters, which were reduced from χ² = 5.34, R_wp = 8.87% to χ² = 2.93, R_wp = 5.55%, and in a good match between the observed and calculated X-ray diffraction histograms (see ESI Fig. S4 and Table S1†). The V and W occupancies obtained from the high-resolution X-ray diffraction data were then fixed in the refinement of the Ba₃VWO_8.5 structure from neutron diffraction data. Refining the oxygen site occupancies from the collected neutron diffraction data gave an overall oxygen stoichiometry of 8.5; O1 is fully occupied, while the O2 and O3 crystallographic positions are partially occupied. The fractional occupancies of the Ba atoms refined to within ±1% of full occupancy and were fixed at 1.0. Refinement of the atomic displacement parameters, U, for all atoms was performed anisotropically. The oxygen atom O3 exhibits large anisotropic thermal displacement parameters U₁₁ = U₂₂ = 0.0706 (6) Ų, giving evidence of disorder at the O3 apical site of the M1O₄ pseudo-tetrahedron, on the ab plane. Therefore, the general position 36i was assigned to O3 instead of the ideal 6c position in the palmierite structure, in order to account for the disorder of the oxygen atoms within the M1O_x polyhedra on the 3-fold axis. The splitting of this site has previously been reported also for Ba₃NbMoO_8.5.²¹ The O3 atom was subsequently modelled by using a single isotropic U_iso factor. An excellent Rietveld fit to this model was obtained (space group R3̄m H; a = b = 5.82254 (6) Å, c = 21.1327 (2) Å, V = 620.45 (2) ų; χ² = 4.397, R_p = 2.12% and R_wp = 1.53%; Fig. 5, Table 1).

Fig. 5 Fitted neutron diffraction histogram for Ba₃VWO_8.5 at ambient temperature. The TOF neutron diffraction data from the 90° bank detector of the Polaris diffractometer is shown. Black dots indicate the observed data, the red line the Rietveld fit, the blue line indicates the difference between the observed and the calculated patterns, the green line the background function, and the pink vertical bars the reflection positions.

Table 1 Refined atomic parameters from the Rietveld fit to the R3̄m H model from powder neutron diffraction data^a

Atom	Site	x	y	z	Fraction	U 11 = U22	U 33	U 12
a Data were refined in space group R3̄m H with χ^2 = 4.397, Rp = 2.12%, Rwp = 1.53%; refined unit cell parameters; a = b = 5.82254(6) Å, c = 21.1327(2) Å, V = 620.45 (2) Å^3. Uij (in Å^2) represent atomic displacement parameters; U13 and U23 are zero. The M1 site is composed of 50% V and 50% W.
Ba1	3a	0	0	0	1	0.0140 (2)	0.0064 (3)	0.00703 (8)
Ba2	6c	0	0	0.20693 (4)	1	0.0111 (2)	0.0148 (3)	0.00559 (8)
M1	6c	0	0	0.39415 (7)	1	0.0097 (4)	0.0137 (7)	0.00480 (2)
O1	18h	0.17269 (4)	0.82730 (4)	0.10188 (2)	1	0.0149 (1)	0.0136 (2)	0.0115 (2)
O2	9e	0.5	0	0	0.361 (1)	0.0446 (6)	0.0305 (9)	0.0279 (3)
O3	36i	0.0526 (4)	0.0103 (9)	0.32659 (6)	0.118 (1)	0.0212 (6)	—	—

---

Significant differences exist between the average structures of Ba₃VWO_8.5 and Ba₃M′M′′O_8.5. The average structure of Ba₃VWO_8.5 is composed of M1O_x polyhedral units spaced by empty octahedral cavities (Fig. 6a, VW), as a consequence of ordering of the cationic vacancies on the M2 sites. In contrast the average structure of Ba₃NbMoO_8.5 is formed by hybrid trimer stacks of face-sharing polyhedral units (Fig. 6a, NbMo) in which the cationic vacancies are disordered on two metal sites M1 and M2 which, due to the short separation between the positions, are mutually exclusive and cannot be occupied simultaneously. The random distribution of cation vacancies leads to the formation of local complex disordered stacking M1-vac-M1, M1-M2-vac, or vac-M2-M1 configurations, resulting in a random arrangement of face-sharing or separated M1O_x and M2O₆ polyhedral units (Fig. 6b, bottom).^23,26 Instead, the ordered distribution of cationic vacancies in Ba₃VWO_8.5 results in an ordered stacking of palmierite-like layers separated by empty octahedral sites (Fig. 6b, top). The average structure of Ba₃VWO_8.5 exhibits oxygen disorder similar to Ba₃M′M′′O_8.5, with competitive occupation of the two average crystallographic O2/O3 sites leading to the formation of average M1(O1₃O3) tetrahedral units and average M1(O1₃O2₃) octahedral units. It is expected that the occurrence of neighbouring tetrahedral and octahedral units, in conjunction with the large positional oxygen disorder, results in disruption of the local oxygen configuration and in the formation of local intermediate 5-fold geometries as reported for Ba₃NbMoO_8.5.^23,24

Fig. 6 (a) Average crystal structure of Ba₃VWO_8.5 (VW) and Ba₃NbMoO_8.5 (NbMo). The green spheres are the Ba atoms, while the oxygen atoms are represented by red (O1), orange (O2) and yellow (O3) spheres. Blue and light blue polyhedra represent the average M1O_x units created by partial occupation of O2 and O3. The grey polyhedra in VW represents the empty octahedral cavities. M2O₆ octahedra are represented in magenta in NbMo. (b) Representation of the ordered stacking of palmierite-like layers and cation vacancies in Ba₃VWO_8.5 (top), and of a possible disordered arrangement of face-sharing and isolated polyhedral units in Ba₃NbMoO_8.5 (bottom). O3 is represented at 6c for simplicity.

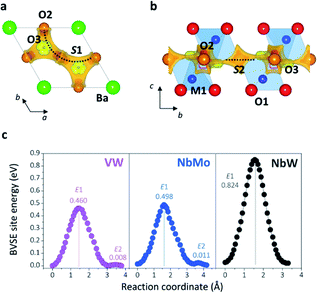
Bond-valence site energy (BVSE) calculations were employed to analyse the migration pathway and energy landscape of the oxide ion conduction in the average crystal structure of Ba₃VWO_8.5. Bond-valence based methods have been shown to reproduce well the ionic conduction pathway in several ionic conductors^17,45–50 and have successfully been employed for the screening and discovery of new oxide ion conducting materials.^51–54 Despite being not as accurate, BVSE barriers generally show a good agreement with results from density functional theory (DFT) calculations.³⁵ Therefore, BVSE analysis can provide useful general indicators on the energetics of ionic migration of inherently complex crystal structures, at a fraction of the computational cost, and the results can be used as a proxy, in relative terms, for more detailed studies.^35,47 This approach has recently been employed to further understand the conduction mechanism and relative energetics of migration in V-doped Ba₃NbMoO_8.5.²⁶ BVSE calculations on Ba₃VWO_8.5 were performed with the softBV program. Bond-valence site energy landscapes describing connecting local minima, saddle points and relative energy barriers for the interaction of a probe oxide ion were calculated from the refined structural model. Two-dimensional O2–O3 conduction pathways (on the ab plane) corresponding with the lowest bond-valence site energy barriers (<0.5 eV) are evidenced along the palmierite-like layers (Fig. 7a, b), in accordance with previous reports.^23,25,26 The oxygen migration along the palmierite-like layers occurs through two saddle points. The saddle point S1 is associated with oxide ion exchange along the connected distribution of partially occupied oxygen positions (Fig. 7a). The saddle point S2 is perpendicular to the undulating distribution of crystallographic oxygen sites (Fig. 7b); its relative energy barrier (E2) can be associated with the energy necessary for the relaxation of the oxygen atoms during migration, and is linked to the average distortion of the M1O_x polyhedral units, σ(R).²⁶ In Ba₃M′M′′O_8.5, the average metal polyhedra are distorted due to the out-of-centre displacement resulting from the second-order Jahn–Teller distortion induced by the d⁰ cations.^21,23,55 The magnitude of this average distortion depends on the nature and combination of the M′M′′ cations.^20,28,30,56 Ba₃VWO_8.5 presents σ(R) similar to Ba₃NbMoO_8.5 (∼0.0753 Å and ∼0.0759 Å respectively), and the two systems shows analogous E2 energy barriers (Fig. 7c). The relative energy barrier E1 is influenced by the populations of the average O2/O3 sites, and its height decreases when the fractional occupancy of O3 increases,²⁶ since a larger number of lower coordination geometries provides more favourable and dynamic environments for oxygen transfer.^13,14,57Fig. 7c shows that Ba₃VWO_8.5 and Ba₃NbMoO_8.5 have comparable relative BVSE energy barriers for the 2-dimensional ionic conduction along the palmierite-like layers, which are considerably smaller than the barrier for Ba₃NbWO_8.5. However, the bulk conductivity of Ba₃VWO_8.5 is significantly lower than the bulk conductivity of both Ba₃NbMoO_8.5 and Ba₃NbWO_8.5 (see Fig. 3d). Therefore, it would seem that other factors are influencing the ionic transport in these systems.

Fig. 7 BVSE map of Ba₃VWO_8.5 showing the 2-dimensional ionic conduction pathway along the palmierite-like layer as seen down the c-axis (a) and a-axis (b). Isosurface levels are drawn at < 0.5 eV (over the global minimum). The dotted lines represent the saddle points as identified by the softBV software. (c) BVSE models of migration barriers along the palmierite-like layers for Ba₃VWO_8.5 (VW), Ba₃NbMoO_8.5 (NbMo), and Ba₃NbWO_8.5 (NbW). Relative bond-valence energy barriers are reported in eV. Note that the minimum site energies have relative values.

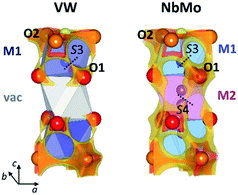
The softBV approach reveals all the possible path segments that exist for a given structure,³⁶ therefore further examination and comparison of the BVSE maps and pathways besides the 2-dimensional lowest energy pathway for Ba₃VWO_8.5, Ba₃NbMoO_8.5 and Ba₃NbWO_8.5 can be particularly informative. The BVSE maps calculated for the average structures of Ba₃NbMoO_8.5 and Ba₃NbWO_8.5 demonstrate sizeable connectivity between adjacent O1–O2 and O1–O1 positions (Fig. 8, right, and ESI Fig. S5†), implying oxygen motion along the edges of the M1O_x and M2O1₆ polyhedra, similar to the migration mechanism in cubic ABO₃ perovskites.⁵⁸ The O1–O2 and O1–O1 pathway segments in Ba₃NbMoO_8.5 have relative BVSE energy barriers of 0.675 eV and 1.257 eV respectively, and of 1.058 eV and 1.491 eV in Ba₃NbWO_8.5. The BVSE map of Ba₃VWO_8.5, while showing O1–O2 exchange (with a relative energy barrier of 0.780 eV), does not present any O1–O1 connectivity along the edges of the (vac)O1₆ pseudo-octahedron (Fig. 8, left). In a previous study, a bond-valence energy landscape (BVEL) map calculated on a refined structure of Ba₃NbMoO_8.5 from single crystal X-ray diffraction data, modified to contain an ordered M1-vac-M1 stacking configuration, showed connectivity parallel to the c-axis via the O1 sites and the vacant M2 polyhedra.²³ It was also proposed that occupation of the M2 site reduces the ease of oxide ion exchange between the O1 layers and the BaO_2.5 layers. We performed a similar BVS analysis with softBV on an average Ba₃NbMoO_8.5 structural model with the M2 site occupancy set to zero. While the calculated BVSE map evidenced sizeable connectivity between O1–O1 sites (Fig. S6 in ESI†), in agreement with the previous single crystal study,²³ further examination of the specific pathway segments identified by softBV reveals that this connectivity does not correspond to a viable diffusion pathway. The BVS density within the empty M2 octahedral site is the result of the presence of calculated interstitial energy minimum sites and the associated exchange between these sites and O1. There are no such interstitial oxygen present at the vacant M2 site in Ba₃VWO_8.5 which would result in unrealistic O–O separations (<2 Å). Hence the calculated BVS density is chemically infeasible.

Fig. 8 Bond-valence site energy maps calculated for Ba₃VWO_8.5 (VW) and Ba₃NbMoO_8.5 (NbMo). The cation vacancy (vac) in VW is represented by the grey octahedron. The dotted lines represent the saddle points at the median of the O1–O2 (S3) and O1–O1 (S4) distances, with bottlenecks constituted by triangles formed by two Ba cations and one M cation, as identified by the softBV software. Darker colours indicate the lower isosurface levels (<0.5 eV over the global minimum), while the lighter colours are for the highest isosurface levels (between 0.7 eV and 1.4 eV over the global minimum).

The presence of connectivity between oxygen sites is certainly a prerequisite for the evaluation of a possible conduction pathway. However, its likelihood as a migration route needs to be rigorously assessed by examination of both the relative energy barrier and the characteristics of the connectivity within the specific pathway segment, to ensure that the pathway is physically viable.^36,59

Amongst all the possible pathway segments calculated from BVSE analysis of the average structure, the 2-dimensional O2–O3 pathway along the palmierite-like layer presents the lowest relative BVS energy barrier and is most likely the dominant route contributing to the overall conduction. However, the presence of a continuous connectivity network formed by O1–O2 and O1–O1 pathway segments with accessible relative energy barriers implies long-range diffusion parallel to the c-axis, so that the ionic conductivity in the hybrid structure of Ba₃M′M′′O_8.5 (M′ = Nb; M′′ = Mo, W) is 3-dimensional.²³ The disorder in the cation sub-lattice, together with the inherent ability of the cation defects to rearrange themselves in the hybrid structure,^22,24 allow for the formation of a complex and dynamic 3-dimensional ionic percolation network, the topology of which will depend on the average temperature- and time-dependent distribution of cationic and anionic vacancies. In contrast, ordering of the cationic vacancies on the M2 sites in Ba₃VWO_8.5 disrupts the 3-dimensional conduction/percolation network by hindering any long-range oxygen diffusion (O1–O2 + O1–O1) parallel to the c-axis^59,60 so that the conductivity mechanism is two-dimensional. The reduction in dimensionality results in a dramatic reduction in the bulk conductivity (see Arrhenius plot in Fig. 3d). Cation ordering in pyrochlore Gd₂(Ti, Zr)₂O₇ systems has been reported to have a similar negative impact on the conductivity and mobility of the oxygen vacancies, with an analogous reduction in the dimensionality of oxide ion conduction.^61,62 We note that the different chemical characteristics of the M′M′′ cations may also influence the ionic conductivity. If we examine the average M1–O2 and M1–O3 bond lengths, we notice that these are considerably shorter in Ba₃VWO_8.5: respectively 2.1160 (9) Å and 1.455 (2) Å, compared to 2.2065 (8) Å and 1.766 (4) Å in Ba₃NbMoO_8.5.²¹ These short distances are typical of V⁵⁺O_x polyhedra containing vanadyl bonds⁶³ and may act as a trap for the mobile oxygen atoms along the palmierite-like layers, further reducing the oxide ionic conductivity. Such trapping of the mobile oxide ions due to local structural relaxation/distortion has previously been postulated also for Ba₃Nb_1−xV_xMoO_8.5.²⁶

Conclusions

In summary, we have reported the successful synthesis of a new oxide ion conductor Ba₃VWO_8.5. Similar to Ba₃M′M′′O_8.5 (M′ = Nb; M′′ = Mo, W), the average crystal structure of Ba₃VWO_8.5 contains palmierite-like layers with considerable positional oxygen disorder leading to the formation of average mixed coordination M1O_x polyhedral units. However, the cationic vacancies are ordered on the M2 sites in Ba₃VWO_8.5, thus resulting in an ordered stacking of palmierite-like layers separated by empty octahedral cavities. Electrical characterization reveals that Ba₃VWO_8.5 is an oxide ion conductor at high pO₂. However, the bulk conductivity of this compound is substantially lower than the conductivities of other members of the Ba₃M′M′′O_8.5 family. BVSE analysis on the average structure of Ba₃VWO_8.5 reveals that the lowest-energy ionic conduction pathway is along the 2-dimensional palmierite-like layers, in agreement with previous studies on Ba₃M′M′′O_8.5 (M′ = Nb; M′′ = Mo, W), implying cooperative oxide ion transport via exchange between the partially occupied average oxygen sites within the BaO_2.5 layers. The BVSE analysis also shows the absence of any long-range oxygen connectivity parallel to the c-axis, in contrast with what has been reported for Ba₃NbMoO_8.5 and Ba₃NbWO_8.5 These results suggest that, although the 2-dimensional conduction pathway along the palmierite-like layers is the predominant diffusion route, long-range ionic migration parallel to the c-axis also provides a relevant contribution to the conductivity of Ba₃M′M′′O_8.5 systems, thus resulting in a complex 3-dimensional ionic percolation network.²³ Ordering of the cation vacancies on the M2 sites most likely disrupts such a network in Ba₃VWO_8.5, so that the reduction in conductivity can be ascribed to the reduction in the dimensionality of ionic diffusion. These findings highlight how the chemical characteristics of the M′M′′ couple and the presence of disorder in the cationic sub-lattice can have a profound influence on the ionic conducting properties of Ba₃M′M′′O_8.5 derivatives. Various reports have demonstrated how the presence of disorder and the particular distribution of cations and defects in the cation sub-lattice can affect the conductivity of different oxide ion conductors, and how these generally depend on the composition and chemistry of the cations.^61–67 These findings highlight the importance of the oxygen and cation vacancy disorder in defining the ionic conducting properties of Ba₃M′M′′O_8.5 hexagonal perovskite derivatives. The results also demonstrate that it is possible to obtain oxide ion conducting Ba₃M′M′′O_8.5 with a range of different cations and synthesis of novel phases with different combinations of M′M′′ are warranted.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank the UK Science and Technology Facilities Council (STFC) for provision of Xpress Access neutron beamtime at ISIS. This research was supported by the Leverhulme trust (RPG-2017-351) and the Commonwealth Scholarship Commission for provision of a split-site studentship for AG.

References

1. A. J. Jacobson, Chem. Mater., 2009, 22, 660.
2. E. D. Wachsman and K. T. Lee, Science, 2011, 334, 935.
3. T. A. Adams, J. Nease, D. Tucker and P. I. Barton, Ind. Eng. Chem. Res., 2012, 52, 3089.
4. D. J. L. Brett, A. Atkinson, N. P. Brandon and S. J. Skinner, Chem. Soc. Rev., 2008, 37, 1568.
5. Z. Gao, L. V. Mogni, E. C. Miller, J. G. Railsback and S. A. Barnett, Energy Environ. Sci., 2016, 9, 1602.
6. L. Malavasi, C. A. J. Fisher and M. S. Islam, Chem. Soc. Rev., 2010, 39, 4370.
7. C. R. A. Catlow, Solid State Ionics, 1984, 12, 67.
8. X. Kuang, J. L. Payne, M. R. Johnson and I. R. Evans, Angew. Chem., Int. Ed., 2012, 51, 690.
9. C. E. Mohn, S. Stølen, S. T. Norberg and S. Hull, Phys. Rev. Lett., 2009, 102, 155502.
10. E. Kendrick, M. S. Islam and P. R. Slater, J. Mater. Chem., 2007, 17, 3104.
11. P. Lacorre, F. Goutenoire, O. Bohnke, R. Retoux and Y. Laligant, Nature, 2000, 404, 856.
12. F. Abraham, M. Debreuille-Gresse, G. Mairesse and G. Nowogrocki, Solid State Ionics, 1988, 28, 529.
13. E. Kendrick, J. Kendrick, K. S. Knight, M. S. Islam and P. R. Slater, Nat. Mater., 2007, 6, 871.
14. X. Kuang, M. A. Green, H. Niu, P. Zajdel, C. Dickinson, J. B. Claridge, L. Jantsky and M. J. Rosseinsky, Nat. Mater., 2008, 7, 498.
15. T. Ishihara, H. Matsuda and Y. Takita, J. Am. Chem. Soc., 1994, 116, 3801.
16. M. Li, M. J. Pietrowski, R. A. De Souza, H. Zhang, I. M. Reaney, S. N. Cook, J. A. Kilner and D. C. Sinclair, Nat. Mater., 2014, 13, 31.
17. K. Fujii, Y. Esaki, K. Omoto, M. Yashima, A. Hoshikawa, T. Ishigaki and J. R. Hester, Chem. Mater., 2014, 26, 2488.
18. J. B. Goodenough, J. E. Ruiz-Diaz and Y. S. Zhen, Solid State Ionics, 1990, 44, 21.
19. J. Darriet and M. A. Subramanian, J. Mater. Chem., 1995, 5, 543.
20. S. Fop, K. S. McCombie, E. J. Wildman, J. M. S. Skakle and A. C. Mclaughlin, Chem. Commun., 2019, 55, 2127.
21. S. Fop, J. M. S. Skakle, A. C. McLaughlin, P. A. Connor, J. T. S. Irvine, R. I. Smith and E. J. Wildman, J. Am. Chem. Soc., 2016, 138, 16764.
22. S. Fop, E. J. Wildman, J. T. S. Irvine, P. A. Connor, J. M. S. Skakle, C. Ritter and A. C. Mclaughlin, Chem. Mater., 2017, 29, 4146.
23. J. E. Auckett, K. L. Milton and I. R. Evans, Chem. Mater., 2019, 31, 1715.
24. M. S. Chambers, K. S. McCombie, J. E. Auckett, A. C. McLaughlin, J. T. S. Irvine, P. A. Chater, J. S. O. Evans and I. R. Evans, J. Mater. Chem. A, 2019, 7, 25503.
25. M. Yashima, T. Tsujiguchi, K. Fujii, E. Niwa, S. Nishioka, J. R. Hester and K. Maeda, J. Mater. Chem. A, 2019, 7, 13910.
26. S. Fop, K. S. McCombie, R. I. Smith and A. C. Mclaughlin, Chem. Mater., 2020, 32, 4724.
27. K. S. McCombie, E. J. Wildman, S. Fop, R. I. Smith, J. M. S. Skakle and A. C. Mclaughlin, J. Mater. Chem. A, 2018, 6, 5290.
28. K. S. McCombie, E. J. Wildman, C. Ritter, R. I. Smith, J. M. S. Skakle and A. C. Mclaughlin, Inorg. Chem., 2018, 57, 11942.
29. A. Bernasconi, C. Tealdi and L. Malavasi, Inorg. Chem., 2018, 57, 6746.
30. S. Fop, E. J. Wildman, J. M. S. Skakle, C. Ritter and A. C. Mclaughlin, Inorg. Chem., 2017, 56, 10505.
31. S. Fop, K. S. McCombie, E. J. Wildman, J. M. S. Skakle, J. T. S. Irvine, P. A. Connor, C. Savaniu, C. Ritter and A. C. Mclaughlin, Nat. Mater., 2020, 19, 752.
32. B. Mössner and S. Kemmler-Sack, J. Less-Common Met., 1985, 114, 333.
33. R. I. Smith, S. Hull, M. G. Tucker, H. Y. Playford, D. J. McPhail, S. P. Waller and S. T. Norberg, Rev. Sci. Instrum., 2019, 90, 115101,  DOI:10.1063/1.5099568.
34. B. H. Toby, J. Appl. Crystallogr., 2001, 34, 210.
35. H. Chen, L. L. Wong and S. Adams, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2019, 75, 18.
36. H. Chen and S. Adams, IUCrJ, 2017, 4, 614.
37. J. Cumby and J. P. Attfield, Nat. Commun., 2017, 8, 14235.
38. J. T. S. Irvine, D. C. Sinclair and A. R. West, Adv. Mater., 1990, 2, 132.
39. H. Kim, S. Kim, K. Lee, H. Lee and K. Lee, J. Power Sources, 2014, 267, 723.
40. G. B. Zhang and D. M. Smyth, Solid State Ionics, 1995, 82, 161.
41. Y. Yamazaki, R. Hernandez-Sanchez and S. M. Haile, J. Mater. Chem., 2010, 20, 8158.
42. S. Wang, F. Zhao, L. Zhang and F. Chen, Solid State Ionics, 2012, 213, 29.
43. A. C. Mclaughlin, STFC ISIS Neutron and Muon Source, 2019, https://doi.org/10.5286/ISIS.E.RB1890374-1.
44. V. F. Sears, Neutron News, 1992, 3, 29.
45. X. Yang, S. Liu, F. Lu, J. Xu and X. Kuang, J. Phys. Chem. C, 2016, 120, 6416.
46. W. Uno, K. Fujii, E. Niwa, S. Torii, P. Miao, T. Kamiyama and M. Yashima, J. Ceram. Soc. Jpn., 2018, 126, 341.
47. M. L. Tate, C. A. Fuller, M. Avdeev, H. E. A. Brand, G. J. McIntyre and I. Radosavljevic Evans, Dalton Trans., 2017, 46, 12494.
48. M. Duchardt, S. Neuberger, U. Ruschewitz, T. Krauskopf, W. G. Zeier, J. Schmedt auf der Günne, S. Adams, B. Roling and S. Dehnen, Chem. Mater., 2018, 30, 4134.
49. L. Zhou, A. Assoud, A. Shyamsunder, A. Huq, Q. Zhang, P. Hartmann, J. Kulisch and L. F. Nazar, Chem. Mater., 2019, 31, 7801.
50. K. Park, K. Kaup, A. Assoud, Q. Zhang, X. Wu and L. F. Nazar, ACS Energy Lett., 2020, 5, 533.
51. R. Inoue, K. Fujii, M. Shiraiwa, E. Niwa and M. Yashima, Dalton Trans., 2018, 47, 7515.
52. Y. Yasui, E. Niwa, M. Matsui, K. Fujii and M. Yashima, Inorg. Chem., 2019, 58, 9460.
53. E. Niwa and M. Yashima, ACS Appl. Energy Mater., 2018, 1, 4009.
54. W. Zhang, K. Fujii, E. Niwa, M. Hagihala, T. Kamiyama and M. Yashima, Nat. Commun., 2020, 11, 1224.
55. M. Kunz and I. D. Brown, J. Solid State Chem., 1995, 115, 395.
56. K. M. Ok, P. S. Halasyamani, D. Casanova, M. Llunell, P. Alemany and S. Alvarez, Chem. Mater., 2006, 18, 3176.
57. X. Yang, A. J. Fernández-Carrión, J. Wang, F. Porcher, F. Fayon, M. Allix and X. Kuang, Nat. Commun., 2018, 9, 4484.
58. M. Cherry, M. S. Islam and C. R. A. Catlow, J. Solid State Chem., 1995, 118, 125.
59. S. Adams, Solid State Ionics, 2000, 136–137, 1351.
60. S. Adams, Solid State Ionics, 2006, 177, 1625.
61. B. P. Uberuaga, R. Perriot and G. Pilania, Phys. Chem. Chem. Phys., 2019, 21, 5956.
62. R. Perriot, B. P. Uberuaga, R. J. Zamora, D. Perez and A. F. Voter, Nat. Commun., 2017, 8, 618.
63. M. Schindler, F. C. Hawthorne and W. H. Baur, Chem. Mater., 2000, 12, 1248.
64. B. P. Uberuaga and R. Perriot, Phys. Chem. Chem. Phys., 2015, 17, 24215.
65. B. P. Uberuaga and G. Pilania, Chem. Mater., 2015, 27, 5020.
66. P. K. Moon and H. L. Tuller, Solid State Ionics, 1988, 28–30, 470.
67. H. L. Tuller, J. Phys. Chem. Solids, 1994, 55, 1393.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ta05581f

---