Thermoelectric properties of n-type half-Heusler NbCoSn with heavy-element Pt substitution

Abstract

Half-Heusler compounds with a valence electron count of 18, including ZrNiSn, ZrCoSb, and NbFeSb, are good thermoelectric materials owing to favorable electronic structures. Previous computational studies had predicted a high electrical power factor in another half-Heusler compound NbCoSn, but it has not been extensively investigated experimentally. Herein, the synthesis, structural characterization, and thermoelectric properties of the heavy-element Pt-substituted NbCoSn compounds are reported. Pt is found to be an effective substitute enabling the optimization of electrical power factor and simultaneously leading to a strong point defect scattering of phonons and the suppression of lattice thermal conductivity. Post-annealing significantly improves the carrier mobility, which is ascribed to the decreased grain boundary scattering of electrons. As a result, a maximum power factor of ∼3.4 mW m⁻¹ K⁻² is obtained at 600 K. In conjunction with the reduced lattice thermal conductivity, a maximum figure of merit zT of ∼0.6 is achieved at 773 K for the post-annealed NbCo_0.95Pt_0.05Sn, an increase of 100% compared to that of NbCoSn. This work highlights the important roles that the dopant element and microstructure play in the thermoelectric properties of half-Heusler compounds.

---

Introduction

Thermoelectric materials allow the direct conversion of heat into electrical energy. Thermoelectric devices are suitable for various applications owing to a lack of mobile parts, quiet operation, good reliability, endurance, and flexible implementation.^1,2 Therefore, they have been used for temperature control, power generation, and refrigeration.^3–5 The conversion efficiency of a thermoelectric material is determined by its figure of merit, zT, which is calculated from the transport properties, i.e., zT = α²σT/(κ_e + κ_L), where α is the Seebeck coefficient, σ is the electrical conductivity, T is the absolute temperature, and κ_e and κ_L are the electronic and lattice components of thermal conductivity, respectively. Among the strategies employed to improve the thermoelectric performance of a material, the optimization of carrier concentration (n), usually through chemical doping or defect manipulation, could be the first and foremost one.² With this strategy, a large enhancement of zT can be achieved if the initial n of a material deviates significantly from its optimal one. Moreover, band engineering⁶ and hierarchical phonon scattering⁷ are important approaches that can be implemented to further improve the thermoelectric performance.^8,9 For thermoelectric power generation devices, thermally stable, low-cost, and non-toxic materials are highly desirable.^8,10 Fulfilling these requirements, half-Heusler alloys with a valence electron count (VEC) of 18 exhibit good thermoelectric properties at high temperatures^11,12 and have thus attracted considerable attention for power generation applications.^13,14 Besides carrier concentration optimization, many different strategies have been employed to improve the thermoelectric performance of the half-Heusler alloys, e.g., point defect scattering,¹⁵ nanostructuring,¹⁶ phase separation,¹⁷ band engineering,¹⁸ and plastic deformation.¹⁹ Consequently, several half-Heusler systems, including (Ti,Zr,Hf)NiSn,^17,20,21 (Ti,Zr,Hf)CoSb,^22–24 and (V,Nb,Ta)FeSb,^19,25,26 have been found to exhibit good zT values of above unity. Half-Heusler alloys with a nominal VEC of 19 have also attracted significant attention, where the intrinsic vacancies play a key role in determining the thermoelectric properties.²⁷

NbCoSn is another half-Heusler alloy with a VEC of 18. The prediction of a large power factor (α²σ) in both n-type and p-type NbCoSn indicates its potential thermoelectric application.^28,29 Particularly, for the p-type NbCoSn, the calculated α²σ is the largest among all studied half-Heusler alloys,²⁸ which might originate from the high band degeneracy in the valence band edge.³⁰ However, the preparation of a heavily hole-doped NbCoSn is experimentally challenging, and good thermoelectric performance has not been reported to date. Ti, Mo, and Hf were initially described as weak p-type acceptors for NbCoSn by Kawaharada et al.^31,32 Later, Ferluccio et al.³³ reported Zr- and Ti-doped NbCoSn with a positive Seebeck coefficient. Sc was also used as an acceptor for NbCoSn by Yan et al.³⁴ However, the low electrical conductivities in these p-type NbCoSn samples suggested that the electrical power factors were not yet optimal, preventing the attainment of the predicted high performance. The interstitial Co, predicted to be the most stable intrinsic defect in NbCoSn by Bhattacharya and Madsen,²⁹ was thought to be the possible ‘killer-defect’, hindering the realization of heavily hole-doped NbCoSn. Excess Co was found in the synthesized NbCoSn samples, despite being designed to have the nominal composition.^34,35 A similar phenomenon was also observed in the ZrNiSn system, in which excess Ni significantly changes the electronic structure and transport properties.^36,37 Therefore, further experimental understanding of the intrinsic defect in NbCoSn is necessary to optimize its p-type thermoelectric properties.

Meanwhile, n-type doping has been successfully achieved using Sb as a dopant.^31,33,38 The alloys of NbCo_1+xSn were prepared by optical floating zone method.³⁹ Among these, NbCo_1.05Sn showed the highest phase-purity and thermoelectric performance. He et al.⁴⁰ reported an 80% enhancement of the power factor by improving the samples' phase purity, resulting in a maximum zT of 0.6 at 973 K in Sb-doped NbCoSn. Additionally, a material comprising the half-Heusler NbCoSn mixed with the full-Heusler NbCo₂Sn was studied, and the antisite disorder was found to be suppressed by annealing.⁴¹ Generally, half-Heusler alloys require a high content of chemical doping to realize the optimal electrical power factor. Thus, the dopants could also generate significant suppression on phonon transport.¹³ A dopant element, which has large mass and radius differences with the host element, could enhance point defect scattering of phonons, thereby suppressing the lattice thermal conductivity.

In this study, we have prepared heavy-element Pt-substituted NbCo_1−xPt_xSn (x = 0.00–0.15) samples using arc-melting and high-energy mechanical alloying, followed by a spark plasma sintering (SPS) process. After obtaining the sintered pellets, several samples are further annealed. Laboratory and synchrotron X-ray diffraction (XRD) measurements show that the obtained samples possess pure half-Heusler phase with negligible secondary phases. Heavy-element Pt substitution leads to the simultaneously improved power factor and suppressed lattice thermal conductivity. Post-annealing is effective in decreasing the grain boundary scattering of carriers and leads to high mobility in the annealed samples. As a result, a maximum zT of ∼0.6 is obtained at 773 K for the post-annealed NbCo_0.95Pt_0.05Sn, which is the highest value for this system at this temperature.⁴⁰

Experimental

In the first set of the experiments, stoichiometric amounts of Nb slug (99.95%, Alfa Aesar), Co slug (99.95%, Alfa Aesar), Sn shot (99.999%, Alfa Aesar), and Pt shot (99.9%) with compositions of NbCo_1−xPt_xSn (x = 0.00, 0.03, 0.06, 0.09, 0.12, and 0.15) were weighed and loaded in a water-cooled Cu crucible of the arc-melter to prepare 4.5 g of each sample. Each pellet was melted three times under an inert Ar atmosphere to guarantee homogenization. To remove the residual impurities, the samples were annealed at 1073 K for seven days inside vacuum-sealed quartz ampoules using Ta foil to minimise the oxidation. Subsequently, the samples were ground using a ball-milling machine (Pulverisette 7, Fritsch), after which the resulting powders were compacted under inert conditions using SPS. The powders were placed in a 10 mm cylindrical graphite die and a uniaxial pressure of 80 MPa was applied while heating rapidly to 1223 K and then kept for 5 min. Then, the sintered pellets were used for the characterization of structural and transport properties. In the second set of experiments, two additional NbCo_1−xPt_xSn samples were prepared with x = 0.05 and 0.1. To improve the phase purity, these two samples were additionally annealed for seven days at 1073 K after the SPS process.

XRD was performed at room temperature using an image-plate Huber G670 Guinier camera equipped with a Ge(111) monochromator and employing Co K_α1 radiation. Synchrotron XRD (SXRD) patterns were collected with an incident beam of 28 keV energy (λ = 0.4427 Å), in the high angular resolution mode (MAD set-up) on the MSPD-diffractometer at the ALBA synchrotron in Barcelona, Spain. The ground samples were analysed using quartz capillaries with 0.25 mm radius. Rietveld refinements of XRD and SXRD patterns were performed using FullProf program.^42,43 A pseudo-Voigt function was employed for analyzing the shapes of the diffraction peaks. There were no excluded regions in the refinements. The final refinement of the synchrotron data was performed using parameters such as scale factor, set of background points, zero-point shift, pseudo-Voigt shape, and isotropic thermal displacement parameters of Nb, Co/Pt, and Sn.

Microstructural analysis of the samples was performed using scanning electron microscopy (SEM, Zeiss Merlin scanning electron microscope, Carl Zeiss AG, Oberkochen, Germany) in the backscattered mode, at an accelerating voltage of 30 kV and a beam current of 2 nA.

High-temperature measurements of the Seebeck coefficient and electrical resistivity were performed using an ULVAC-RICO ZEM-3 equipment. The thermal conductivity was calculated using the equation, κ = C_pDρ, where C_p is the specific heat, D is the thermal diffusivity, and ρ is the sample density, employing thermal diffusivity values (Fig. S1, ESI†) measured by a LASER Flash (LFA 457, Netzsch). C_p (Fig. S2, ESI†) is calculated using the formula, C_p = C_ph,H + C_D, where C_ph,H and C_D are the contributions of the harmonic phonons and lattice dilation, respectively, which can be calculated by employing the sound velocity, thermal expansion coefficient, and density (Table S1†).²⁴

The Hall effect measurements were performed in sample rods in a four-probe configuration using the resistivity option of the physical property measurement system (PPMS, Quantum Design). The measurements were symmetrized to eliminate the magnetoresistance contribution, and the carrier concentration was calculated using the formula, R_H = −1/en_H, where R_H is the Hall coefficient, e is the free electron charge, and n_H is the Hall carrier concentration.

Band structure calculations were performed using density functional theory (DFT) as implemented in the Vienna ab initio simulation package (VASP) code.^44–46 The generalized-gradient approximation (GGA) for the exchange–correlation functional is used. The cut-off energy is set to be 500 eV for expanding the wave functions into plane-wave basis. In the calculation, the Brillouin zone (BZ) is sampled in the k space within Monkhorst–Pack scheme.⁴⁷ On the basis of the equilibrium structure, the k mesh used is 12 × 12 × 12, and spin orbital coupling (SOC) is included in our calculation.

Results and discussion

The laboratory XRD patterns of the two sets of NbCo_1−xPt_xSn (x = 0.00–0.15) samples are shown in Fig. 1a. The main phase is consistent with the cubic MgAgAs-type half-Heusler structure, and tiny impurity peaks are hardly observed in the range of binary phases (Nb₃Sn, Co₇Nb₆) typically reported for this compound.⁴¹ Although the impurity peaks are more noticeable for the samples with high Pt contents, the peak intensities are very low to enable precise identification of these secondary phases using the laboratory XRD analysis. Moreover, despite further annealing of the samples with x = 0.05 and x = 0.10 in the second set of experiments for seven days at 1073 K, no marked difference in the phase purity is observed compared to that of the other samples from the first set of experiments. To perform a more detailed analysis of the structure and phase purity, high-resolution SXRD experiments were carried out for samples with x = 0.00 and x = 0.05 from the first and second sets of experiments, respectively. The crystalline structure corresponds to the F4̄3m space group, with Nb atoms located at 4a (0,0,0), Co/Pt at 4c (1/4,1/4,1/4), and Sn at 4b (1/2,1/2,1/2) Wyckoff positions. The refinements yield good agreement factors (Table S2, ESI†), while the isotropic displacement parameters are slightly higher than those described by neutron diffraction due to the effects of radiation absorption.^33,41 The accurate calculation of the occupation factors to analyze the defects as off-stoichiometry or antisite defects is not possible owing to the highly symmetric positions of the atoms and the absorption effects. The full Heusler phase is not detected, and very weak intensity peaks are observed in the 9–11° range corresponding to an extremely low volume fraction of the secondary impurity phases (Fig. 1b and c). Overall, the high-resolution SXRD measurements also suggest no marked differences in the phase purity for the samples with x = 0.00 and x = 0.05, despite the higher Pt content and post-annealing of the latter.

Fig. 1 (a) Indexed laboratory XRD patterns of NbCo_1−xPt_xSn (x = 0.00–0.15). Rietveld refinement of synchrotron XRD patterns using λ = 0.4427 Å at room temperature with experimental (red crosses), calculated (black line), difference (blue line), and Bragg reflections (green segments) of NbCoSn (b) and the post-annealed NbCo_0.95Pt_0.05Sn (c), displaying an almost complete absence of impurities in the inset (magnified image) in the typical 2θ range. (d) Lattice parameters for NbCo_1−xPt_xSn (x = 0.00, 0.03, 0.06, 0.09, 0.12, and 0.15) represented by empty blue circles, and post-annealed NbCo_1−xPt_xSn (x = 0.05, 0.10) represented by filled blue circles. Blue dashed line is a guide for the eye. Carrier concentration is represented by red empty and filled circles. The red dashed line denotes the carrier concentration calculated assuming one added electron per Pt atom.

Lattice parameters (Fig. 1d) were determined using Rietveld refinements of the XRD patterns in the F4̄3m space group, displaying an excellent match with the literature data.³³ The lattice parameter increases almost linearly with increasing Pt content, which indicates the efficiency of Pt as a donor for NbCoSn. Carrier concentration measurements allow the assessment of the effectiveness of Pt substitution in terms of the electron transfer to the half-Heusler structure. Fig. 1d shows that the carrier concentration follows an approximately linear behaviour with increasing Pt content. Using a simple assumption of one added electron per Pt atom, the estimated carrier concentrations (red dashed line in Fig. 1d) are consistent with the experimental values. The calculated carrier concentration is 9.42 × 10²⁰ cm⁻³ for x = 0.05, which is close to the experimental value. The results indicate that Pt is a highly effective dopant for this system.

The temperature-dependence of the electrical conductivity σ for NbCo_1−xPt_xSn (x = 0.00–0.15) samples is shown in Fig. 2a. An increasing trend is observed for the pristine NbCoSn sample, indicating a semiconducting behaviour. After substituting with Pt, the σ shows a noticeable increase in the complete temperature range, with a decreasing trend at temperatures above 500 K, suggesting a degenerate semiconductor behaviour. Interestingly, the sample with x = 0.05, which was post-annealed, shows a higher σ compared to that of the sample with x = 0.06, despite the higher carrier concentration of the latter. A similar phenomenon is also observed for another post-annealed sample with x = 0.10, whose σ value at room temperature is higher than that of the sample with x = 0.12. Thereafter, the carrier mobilities of the samples were calculated (Fig. 2b). Overall, the two post-annealed samples with x = 0.05 and x = 0.10 have higher carrier mobilities than those of the others, suggesting an annealing-induced change in the microstructure. Therefore, the backscattered electron imaging was performed for samples with x = 0.05 and x = 0.06, as shown in Fig. 2c and d, respectively. This analysis shows that the sample with x = 0.05, with post-annealing after SPS, has a grain size of a few micrometres, which is almost ten times larger than that of the sample with x = 0.06. Grain boundary scattering has recently been found to hinder the mobilities and conductivities (particularly near room temperature) of Mg₃Sb₂,⁴⁸ half-Heusler Nb_1−xTi_xFeSb⁴⁹ and (Zr,Hf)CoSb,⁵⁰ and elemental Te.^51,52 Herein, an increase in the grain size in post-annealed samples can support their high electrical conductivities and carrier mobilities. The confirmation of the influence of grain boundary processes will be the focus of a separate study.

Fig. 2 (a) Temperature dependence of the electrical conductivity of NbCo_1−xPt_xSn (x = 0.00–0.15). (b) Carrier mobility as a function of the Pt content, where the dashed blue line is a guide for the eye. Backscattered electron images of (c) NbCo_0.94Pt_0.06Sn and (d) the post-annealed NbCo_0.95Pt_0.05Sn.

The temperature dependence of the Seebeck coefficient (Fig. 3a) of Pt-substituted NbCoSn shows an approximately linear increase with rising temperature, which is a typical behaviour of a degenerate semiconductor, as expected from the Mott equation.^2,53 The absolute Seebeck coefficient increases in the complete temperature range with no observable contribution from bipolar conduction. In contrast, the pristine NbCoSn shows an increase in the absolute Seebeck coefficient up to 600 K, when a small bump is observed. Similar data have been previously reported for the pristine compound.^33,39 As expected according to the Pisarenko relationship,⁹ the absolute Seebeck coefficient decreases with an increase of Pt content due to the increased electron concentration.

Fig. 3 (a) Temperature dependence of Seebeck coefficient for NbCo_1−xPt_xSn (x = 0.00–0.15). (b) Pisarenko plot at room temperature for several n-type half-Heusler compounds including NbCoSn,⁴⁰ (Zr,Hf)CoSb,^24,50,54 and (Zr,Hf)NiSn.^20,55 (c) Temperature dependence of power factor for NbCo_1−xPt_xSn (x = 0.00–0.15). (d) Power factor as a function of Pt content at 300 K () and 765 K (), respectively. Red and blue dashed lines are a guide for the eye describing the overall trend.

A Pisarenko plot using the single parabolic band model²⁴ (Fig. 3b) was used to better assess the electrical properties of n-type NbCoSn. The density of states (DOS) effective mass m* is linked to the single-valley effective mass via the expression, , where N_v is the number of degenerate valleys.⁹ A m* of 6.5 m_e is derived for the Pt-substituted NbCoSn samples. Notably, this m* value is close to that of the n-type (Zr,Hf)CoSb,^24,50,54 but more than two times higher than that of n-type (Zr,Hf)NiSn.^20,55

The variation in calculated power factor is shown in Fig. 3c. It follows an increasing trend with an increase in temperature because of the increase in the absolute Seebeck coefficient up to 600–700 K and then saturates at high temperatures. Pt-substituted NbCoSn samples exhibit noticeably higher power factors than that of the undoped NbCoSn, suggesting the optimization of electrical properties. The Pt content dependence of the power factor at 300 and 765 K is shown in Fig. 3d. The second set of samples with x = 0.05 and x = 0.10, which have larger grain sizes, show overall higher power factors than those of the first set of samples. This is attributed to the decreased grain scattering and thus improved carrier mobility. Electrical conductivity and Seebeck coefficient of Pt-substituted NbCoSn samples show clear trends resulting from the carrier concentration evolution, but this is not the case for the power factor, which displays a non-monotonous change with increasing Pt content. A maximum power factor of ∼3.4 mW m⁻¹ K⁻² is obtained at 600 K for the post-annealed sample with x = 0.05, which is comparable to that of NbCoSn_0.9Sb_0.1 at 900 K.⁴⁰

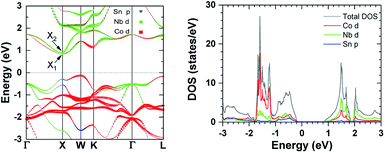
Complementary to the above electrical transport analysis, the calculated band structure and DOS are shown in Fig. 4. As previously reported by He et al.,⁴⁰ at the conduction band bottom (CBB), there are two bands (denoted as X₁ and X₂) which converge at the X point. Considering the symmetry of the X point in the Brillouin zone, a high N_v of 6 is found for the CBB of NbCoSn. In contrast, for (Zr,Hf)NiSn^30,37 and (Zr,Hf)CoSb,²⁴ there is only one band at the CBB, giving a smaller N_v of 3. Therefore, different from n-type (Zr,Hf)CoSb, the similar m* (Fig. 3b) of NbCoSn should also have a contribution from its larger N_v, indicating a smaller . Moreover, Fig. 4 shows also the orbital weighted contribution of each element to the band structure and DOS. The electronic states in the CBB are dominated by the Nb-d orbitals, with additional contribution from the d orbitals of Co. In contrast, the valence band top is dominated by the d orbitals of Co, with additional contributions from both the d orbitals of Nb and the p orbitals of Sn.

Fig. 4 The contribution of each atom in the calculated (left panel) band structure and (right panel) density of states (DOS) of NbCoSn with SOC. In the band structure, the orbital weighted contribution of each element is represented by the size of the symbol. The Fermi level is set to zero energy.

The change in the total thermal conductivity κ of NbCo_1−xPt_xSn with temperature is shown in Fig. 5a. A decrease in the κ value of Pt-substituted samples is observed near room temperature. To further understand this behaviour, κ_e and κ_L were calculated using the equations, κ_e = LσT and κ_L = κ − κ_e, where L is the Lorenz number (Fig. S3a, ESI†), which was calculated using the single parabolic band model.²⁴ As shown in Fig. 5b, a notable decrease in κ_L is observed upon Pt substitution and a maximum reduction of 45% is obtained for x = 0.15, indicating that heavy element substitution is effective in enhancing the phonon scattering by introducing strong mass and strain field fluctuations.¹³Fig. 5c shows a monotonic reduction of κ_L as a function of Pt content, regardless of the grain size distribution of the samples, suggesting that point defect scattering dominates the phonon transport.

Fig. 5 Temperature evolution of (a) total thermal conductivity and (b) lattice thermal conductivity. (c) Variation of κ, κ_e, and κ_L with an increase in Pt content at room temperature. (d) Figure of merit zT for NbCo_1−xPt_xSn (x = 0.00–0.15) as a function of temperature. zT for the optimized NbCoSn_0.9Sb_0.1 is also shown (dashed line).⁴⁰

Table S3† displays the disorder scattering parameters, which were calculated as described in the ESI.† The slight differences between experimental Γ_exp and mass fluctuation Γ_M parameter indicate that large mass difference between Co and Pt atoms dominates the reduction in the κ_L. This description agrees with the monotonic evolution of κ_L upon Pt substitution, as the governing mass fluctuation scattering mechanism would depend directly on the amount of Pt in NbCo_1−xPt_xSn. Moreover, in spite of the increased grain size of x = 0.05 and x = 0.10 samples, κ_L shows no deviation from this trend. This could be explained as grain boundary scattering acting on a different length scale within the grain size range observed in these samples. At a high Pt content, κ_L shows values down to 4.0–3.2 W m⁻¹ K⁻¹ for x = 0.10–0.15, lower than those previously reported for this system, typically in the range of 5–10 W m⁻¹ K⁻¹ at room temperature.^33,40,41 In addition, an increase in κ_e (Fig. S3b†) is observed with increasing Pt content due to the evolution of the electrical conductivity. Compared to Sb doping,⁴⁰ Pt substitution is more effective at suppressing the κ_L of NbCoSn, thereby contributing to the decrease in κ. These values are comparable and even lower than those obtained for the NbCoSn–NbCoSb solid-solutions, in which the disorder and Nb vacancies have a strong impact on the phonon conduction.³³

Owing to the simultaneously decreased κ_L and improved power factor, Pt substitution is effective in improving the figure of merit zT of NbCoSn (Fig. 5d). A 100% increase in the peak zT is observed for NbCo_0.95Pt_0.05Sn, compared to that for NbCoSn, leading to a maximum value of ∼0.6 at 773 K. This value is similar to that of Sb-doped NbCoSn system but occurs at a lower temperature. Furthermore, the almost linear temperature dependence of zT in all the studied NbCo_1−xPt_xSn samples suggests that a higher peak zT can be achieved at higher temperatures. Post-annealing to eliminate the negative effect of grain boundary on carrier transport should also be helpful for improving the zT of the other n-type NbCoSn system.

Conclusions

In summary, heavy-element Pt-substituted NbCoSn alloys are successfully prepared via arc-melting and high-energy mechanical alloying followed by SPS. The structure and thermoelectric properties are systematically characterized. Pt is found to be effective in simultaneously tuning the electrical and thermal transport properties, thereby resulting in enhanced thermoelectric performance. Post-annealing is effective in decreasing the grain boundary scattering of carriers and thus contributes to a high carrier mobility. A maximum power factor of ∼3.4 mW m⁻¹ K⁻² is obtained at 600 K. Furthermore, the lattice thermal conductivity is significantly decreased due to the enhanced point defect scattering of phonons, and a direct relationship between the substitution content and this reduction is observed. A peak zT of 0.6 at 773 K is obtained for the post-annealed NbCo_0.95Pt_0.05Sn, which is comparable to the highest reported value for this half Heusler alloy⁴⁰ and can be further improved at high temperatures. This work highlights the importance of the selection of doping elements and microstructure in improving the thermoelectric properties of half-Heusler compounds.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Projektnummer (392228380), the ERC Advanced Grant No. 742068 “TOPMAT”, and the National Natural Science Foundation of China (no. 51761135127). F. Serrano acknowledges financial support by the Spanish Ministry of Economy and Competitivity through grant MAT2017-84496-R and the European Union's Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement No 839821. Dr T. Luo is grateful for the financial support from the Alexander von Humboldt Stiftung. We thank ALBA synchrotron (Barcelona, Spain) for providing the SXRD beam time. A. W. and W. X. acknowledge the financial support from Deutsche Forschungsgemeinschaft (Project No. BA 4171/4-1).

Notes and references

1. D. M. Rowe, Renewable Energy, 1999, 16, 1251–1256.
2. G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105–114.
3. B. Russ, A. Glaudell, J. J. Urban, M. L. Chabinyc and R. A. Segalman, Nat. Rev. Mater., 2016, 1, 16050.
4. R. He, G. Schierning and K. Nielsch, Adv. Mater. Technol., 2018, 3, 1700256.
5. T. R. Barnhart, M. Ranalli and M. Adldinger, US Patent and Trademark Office, Washington, DC, No. 9,447,994, 2016.
6. Y. Pei, X. Shi, A. LaLonde, H. Wang, L. Chen and G. J. Snyder, Nature, 2011, 473, 66–69.
7. K. Biswas, J. He, I. D. Blum, C.-I. Wu, T. P. Hogan, D. N. Seidman, V. P. Dravid and M. G. Kanatzidis, Nature, 2012, 489, 414–418.
8. J. He and T. M. Tritt, Science, 2017, 357, eaak9997.
9. T. Zhu, Y. Liu, C. Fu, J. P. Heremans, G. J. Snyder and X. Zhao, Adv. Mater., 2017, 29, 1605884.
10. M. Rull-Bravo, A. Moure, J. F. Fernández and M. Martín-González, RSC Adv., 2015, 5, 41653–41667.
11. T. Graf, C. Felser and S. S. P. Parkin, Prog. Solid State Chem., 2011, 39, 1–50.
12. T. Zhu, C. Fu, H. Xie, Y. Liu and X. Zhao, Adv. Energy Mater., 2015, 5, 1500588.
13. C. Fu, S. Bai, Y. Liu, Y. Tang, L. Chen, X. Zhao and T. Zhu, Nat. Commun., 2015, 6, 8144.
14. Y. Xing, R. Liu, J. Liao, Q. Zhang, X. Xia, C. Wang, H. Huang, J. Chu, M. Gu and T. Zhu, Energy Environ. Sci., 2019, 12, 3390–3399.
15. J. Yang, G. P. Meisner and L. Chen, Appl. Phys. Lett., 2004, 85, 1140–1142.
16. W. Xie, A. Weidenkaff, X. Tang, Q. Zhang, J. Poon and T. M. Tritt, Nanomaterials, 2012, 2, 379–412.
17. M. Schwall and B. Balke, Phys. Chem. Chem. Phys., 2013, 15, 1868–1872.
18. C. Fu, T. Zhu, Y. Liu, H. Xie and X. Zhao, Energy Environ. Sci., 2015, 8, 216–220.
19. G. Rogl, S. Ghosh, L. Wang, J. Bursik, A. Grytsiv, M. Kerber, E. Bauer, R. C. Mallik, X.-Q. Chen and M. Zehetbauer, Acta Mater., 2020, 183, 285–300.
20. Y. Liu, H. Xie, C. Fu, G. J. Snyder, X. Zhao and T. Zhu, J. Mater. Chem. A, 2015, 3, 22716–22722.
21. G. Rogl, P. Sauerschnig, Z. Rykavets, V. V. Romaka, P. Heinrich, B. Hinterleitner, A. Grytsiv, E. Bauer and P. Rogl, Acta Mater., 2017, 131, 336–348.
22. X. Yan, W. Liu, H. Wang, S. Chen, J. Shiomi, K. Esfarjani, H. Wang, D. Wang, G. Chen and Z. Ren, Energy Environ. Sci., 2012, 5, 7543–7548.
23. E. Rausch, B. Balke, S. Ouardi and C. Felser, Phys. Chem. Chem. Phys., 2014, 16, 25258–25262.
24. Y. Liu, C. Fu, K. Xia, J. Yu, X. Zhao, H. Pan, C. Felser and T. Zhu, Adv. Mater., 2018, 30, 1800881.
25. J. Yu, C. Fu, Y. Liu, K. Xia, U. Aydemir, T. C. Chasapis, G. J. Snyder, X. Zhao and T. Zhu, Adv. Energy Mater., 2018, 8, 1701313.
26. H. Zhu, J. Mao, Y. Li, J. Sun, Y. Wang, Q. Zhu, G. Li, Q. Song, J. Zhou, Y. Fu, R. He, T. Tong, Z. Liu, W. Ren, L. You, Z. Wang, J. Luo, A. Sotnikov, J. Bao, K. Nielsch, G. Chen, D. J. Singh and Z. Ren, Nat. Commun., 2019, 10, 270.
27. K. Xia, Y. Liu, S. Anand, G. J. Snyder, J. Xin, J. Yu, X. Zhao and T. Zhu, Adv. Funct. Mater., 2018, 28, 1705845.
28. J. Yang, H. Li, T. Wu, W. Zhang, L. Chen and J. Yang, Adv. Funct. Mater., 2008, 18, 2880–2888.
29. S. Bhattacharya and G. K. H. Madsen, J. Mater. Chem. C, 2016, 4, 11261–11268.
30. M. T. Dylla, A. Dunn, A. Jain and G. J. Snyder, Research, 2020, 2020, 6375171.
31. Y. Kawaharada, K. Kurosaki, H. Muta, M. Uno and S. Yamanaka, J. Alloys Compd., 2004, 377, 312–315.
32. Y. Kawaharada, K. Kurosaki, H. Muta, M. Uno and S. Yamanaka, J. Alloys Compd., 2004, 384, 303–307.
33. D. A. Ferluccio, R. I. Smith, J. Buckman and J. W. G. Bos, Phys. Chem. Chem. Phys., 2018, 20, 3979–3987.
34. R. Yan, W. Xie, B. Balke, G. Chen and A. Weidenkaff, Sci. Technol. Adv. Mater., 2020, 21, 122–130.
35. S. Li, H. Zhu, J. Mao, Z. Feng, X. Li, C. Chen, F. Cao, X. Liu, D. J. Singh and Z. Ren, ACS Appl. Mater. Interfaces, 2019, 11, 41321–41329.
36. W. G. Zeier, J. Schmitt, G. Hautier, U. Aydemir, Z. M. Gibbs, C. Felser and G. J. Snyder, Nat. Rev. Mater., 2016, 1, 16032.
37. C. Fu, M. Yao, X. Chen, L. Z. Maulana, X. Li, J. Yang, K. Imasato, F. Zhu, G. Li and G. Auffermann, Adv. Sci., 2020, 7, 1902409.
38. Y. Ono, S. Inayama, H. Adachi and T. Kajitani, in 2006 25th International Conference on Thermoelectrics, 2006, pp. 124–127.
39. Y. Kimura, Y. Tamura and T. Kita, Appl. Phys. Lett., 2008, 92, 2–5.
40. R. He, L. Huang, Y. Wang, G. Samsonidze, B. Kozinsky, Q. Zhang and Z. Ren, APL Mater., 2016, 4, 104804.
41. M. L. C. Buffon, G. Laurita, N. Verma, L. Lamontagne, L. Ghadbeigi, D. L. Lloyd, T. D. Sparks, T. M. Pollock and R. Seshadri, J. Appl. Phys., 2016, 120, 075104.
42. H. M. Rietveld, J. Appl. Crystallogr., 1969, 2, 65–71.
43. J. Rodríguez-Carvajal, Phys. B, 1993, 192, 55–69.
44. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558.
45. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
46. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
47. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188.
48. K. Imasato, C. Fu, Y. Pan, M. Wood, J. J. Kuo, C. Felser and G. J. Snyder, Adv. Mater., 2020, 32, 1908218.
49. R. He, D. Kraemer, J. Mao, L. Zeng, Q. Jie, Y. Lan, C. Li, J. Shuai, H. S. Kim and Y. Liu, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 13576–13581.
50. Q. Qiu, Y. Liu, K. Xia, T. Fang, J. Yu, X. Zhao and T. Zhu, Adv. Energy Mater., 2019, 9, 1803447.
51. Y. Wu, Q. Zhang, F. Liu, T. Fang, T. Zhu and X. Zhao, Adv. Electron. Mater., 2020, 6, 2000038.
52. Y. Wu, F. Liu, Q. Zhang, T. Zhu, K. Xia and X. B. Zhao, J. Mater. Chem. A, 2020, 8, 8455–8461.
53. X. Lu, W. Yao, G. Wang, X. Zhou, D. Morelli, Y. Zhang, H. Chi, S. Hui and C. Uher, J. Mater. Chem. A, 2016, 4, 17096–17103.
54. R. He, H. Zhu, J. Sun, J. Mao, H. Reith, S. Chen, G. Schierning, K. Nielsch and Z. Ren, Mater. Today Phys., 2017, 1, 24–30.
55. H. Xie, H. Wang, Y. Pei, C. Fu, X. Liu, G. J. Snyder, X. Zhao and T. Zhu, Adv. Funct. Mater., 2013, 23, 5123–5130.

---

Footnote

† Electronic supplementary information (ESI) available: Calculated heat capacity, coefficient of linear thermal expan-sion, electronic contribution to thermal conductivity, structural parameters of Rietveld refinement of SXRD patterns. See DOI: 10.1039/d0ta04644b

---