Substitutional doping of hybrid organic–inorganic perovskite crystals for thermoelectrics

Abstract

Hybrid organic–inorganic perovskites have generated considerable research interest in the field of optoelectronic devices. However, there have been significantly fewer reports of their thermoelectric properties despite some promising early results. In this article, we investigate the thermoelectric properties of bismuth-doped CH₃NH₃PbBr₃ (MAPbBr₃) single crystals. The high-quality Bi-doped crystals were synthesized by inverse temperature crystallization and it was found that Bi substitutes onto the B-site of the ABX₃ perovskite lattice of MAPbBr₃ crystals with very little distortion of the crystal structure. Bi doping does not significantly alter the thermal conductivity but dramatically enhances the electrical conductivity of MAPbBr₃, increasing the charge carrier density by more than three orders of magnitude. We obtained a negative Seebeck coefficient of −378 μV K⁻¹ for 15% (x = 0.15) Bi-doped MAPb_(1−x)Bi_xBr₃ confirming n-type doping and also measured the figure of merit, ZT. This work highlights routes towards controlled substitutional doping of halide perovskites to optimise them for thermoelectric applications.

---

Introduction

Global energy use is increasing significantly with population growth and demand for power-hungry technologies. Currently fossil fuels are still the main source of energy, but they release harmful emissions that are causing global temperatures to rise. The demand for eco-friendly and alternative energy technologies is hence becoming ever more urgent. For grid scale renewable energy generation, solar, wind and hydroelectric power are highly suitable, but there is also the possibility of harvesting energy locally to power smaller devices. One such example is for wireless sensor networks which typically rely on batteries. Battery replacement is often one of largest costs of running these networks,¹ and it therefore makes sense to for these networks and other off-grid technologies to harvest energy locally using photovoltaic, piezoelectric,² triboelectric³ or thermoelectric devices.¹ Thermal energy in the form of temperature gradients is a ubiquitous energy resource making it a focus of much research in the field of energy harvesting. Thermoelectric generators (TEGs) can recover waste heat and directly convert it into electricity via the Seebeck effect in a quiet and highly reliable way as they do not use moving parts.^4,5 Yet thermoelectric technology is not in widespread use, in part due to the relatively low efficiencies of current devices in the low temperature region as well as brittleness, toxicity and scarcity of the constituent materials. The development of new materials for low temperature thermoelectric energy harvesting is a key requirement to deploy the technology.

The energy conversion efficiency of thermoelectric devices is determined in part by the device design and in part by the dimensionless figure of merit, ZT, of the active materials, where ZT = σS²T/κ, and σ, S, T and κ are the electrical conductivity, Seebeck coefficient, absolute temperature and thermal conductivity, respectively. A high efficiency TEG requires the active materials to have a high ZT, which means combining a high power factor (PF = σS²) with low κ. Currently, the highest reported ZT for a bulk thermoelectric material is 2.6 ± 0.3 at 923 K for SnSe crystals.⁶ However, there are few thermoelectric materials made from abundant elements, that operate at low temperatures with a high ZT. The most commonly used thermoelectric materials in refrigeration are bismuth telluride (Bi₂Te₃) alloys, since they have high ZT near ambient temperature.⁷ However, these inorganic materials contain toxic and rare elements or have a costly synthesis process, which means a high payback requirement. Organic thermoelectric materials have been suggested as alternatives^8,9 alongside carbon materials¹⁰ and composites of the two.^11,12 These materials have demonstrated decent power factors^9,11 and offer scalable processing by printing and other techniques, though ZT values are still well below unity.

Hybrid organic–inorganic perovskites (HOIPs) are highly promising materials for photovoltaic devices due to their long carrier lifetimes, high absorption coefficients, high and balanced hole and electron mobility, low exciton energy and solution processiblity.^13–15 Over the past decade, solution-processed HOIP solar cells have recorded remarkable progress with their stability increasing along with their power conversion efficiency – from 3.8% in 2009 to a certified efficiency of 25.2% in 2019.^16–18 Recently, HOIPs have been considered as possible thermoelectric materials due to their ultra-low thermal conductivity,^19–24 high charge mobility^25,26 and high Seebeck coefficients.^19,27,28 However, HOIPs typically have a very low carrier concentration resulting in a low electrical conductivity.^29,30 This makes it difficult for them to achieve a high ZT. Nonetheless, ab initio calculations suggest that HOIPs could have a high value of ZT between 1 and 2 when their carrier concentration reaches ∼10¹⁸ cm⁻³.³¹ Such carrier concentrations have been achieved in inorganic tin-halide perovskites, with several groups, including ourselves,³² reporting ZT > 0.1.^22,33 This is achieved by a self-doping mechanism that occurs through the oxidation of Sn²⁺ to Sn⁴⁺,^32,34 and is therefore not applicable to the more stable families of lead and bismuth halide perovskites. Mettan et al. increased the ZT of MAPbI₃ by more than two orders of magnitude by photodoping,¹⁹ whilst Baran and co-workers tuned the stoichiometry of the material to improve electrical conductivity and achieve n-type and p-type MAPbI₃ thin films with high Seebeck coefficients, but still in a highly resistive regime.²⁸ Nonetheless, there remains a poor understanding of doping mechanisms for optimising ZT in halide perovskites, including a lack of study of substitutional doping.

In this paper, we explore the thermoelectric properties of MAPbBr₃ single crystals that are doped by substitution of Bi for Pb on B-sites in the perovskite ABX₃ crystal structure. We show an electrical conductivity enhancement of >3 orders of magnitude with increasing Bi concentration, whilst the thermal transport properties remain unaffected. Structural characterization shows that Bi atoms are incorporated into the perovskite lattice without significant distortions or phase separation. The carrier concentration was increased by more than 3 orders of magnitude by Bi-incorporation in the crystal, and the Seebeck coefficient of the most heavily doped MABi_xPb_(1−x)Br₃ crystal was negative, confirming n-type doping, with a value 378 μV K⁻¹ at room temperature. The thermal conductivity remained low, giving hope that, despite a modest ZT value, that there remains plenty of scope to further increase the figure of merit of this class of materials.

Experimental methods

Materials

Lead bromide (≥98%), bismuth bromide (≥98%) and dimethyl formamide (DMF, anhydrous, 99.8%) were purchased from Sigma-Aldrich. Methylammonium bromide (98%) was purchased from Ossia Ltd. All salts and solvents were used as received without any further purification.

Growth of Bi-doped CH₃NH₃PbBr₃ crystals

Inverse temperature crystallization (ITC) was used to grow single crystals:³⁵ 1 M solutions containing PbBr₂ and CH₃NH₃Br or BiBr₃ and CH₃NH₃Br were prepared separately in DMF at room temperature. Both solutions were filtered using a PTFE filter with 0.22 μm pore size and then their filtrates were mixed together to give the desired Bi³⁺ concentration (0%, 1.0%, 5.0%, 10% and 15.0% atomic% with respect to Pb²⁺). Three millilitres of the mixture was then transferred to a vial that was kept in an oil bath undisturbed at 85 °C. The crystallization process continued for about 6 hours, at which point the crystals were removed from the solution and placed on filter paper on top of a hotplate at 100 °C to dry. All procedures were carried out under a fume hood in ambient conditions, and the synthesised crystals were up to ∼6 mm in diameter. The level of doping expressed here refers to the percentage of bismuth in the crystal growth solution.

Hall measurements

Hall effect measurements were performed using a Model 8404 AC/DC Hall Effect Measurement System (Lake Shore Cryotronics, Inc) with an AC magnetic field of 1.19 T. The resistivity was measured using the van der Pauw geometry with the same system. The sample dimensions were typically 6 mm × 6 mm × 2 mm. Contacts were formed by depositing 300 nm thick silver contacts on all four corners of the sample via thermal evaporation. Copper wires were then attached to the silver contact pads with silver paste to form an ohmic contact. The contact configuration and experimental apparatus are depicted in Fig. S5 (ESI†). During the measurement, the sample was kept in ambient atmosphere at room temperature and in complete darkness.

Thermal conductivity

The thermal conductivity, κ, was calculated from κ = DC_pρ, where the thermal diffusivity (D) was measured from 20 °C to 80 °C using the laser flash method with a Netzsch LFA457. C_p is the specific heat capacity and ρ is the density. For the thermal diffusivity measurements, high-quality pristine, 1%, 5%, 10% and 15% Bi-doped MAPbBr₃ single crystals were cut and polished into cuboids of ∼6 mm × 6 mm × 1 mm. A graphite coating was sprayed evenly on two sides of these samples to avoid transmission and reflection of the incident laser pulse to the detector. Thermal diffusivity was measured along the short (∼1 mm) crystal dimension. The raw data were analysed using a Cowan model with pulse correction. The specific heat capacity measurements were performed using differential scanning calorimetry (DSC 25, TA Instruments) from 20 °C to 80 °C. The density was determined using Archimedes' principle to measure the volume of a known mass of material.

X-ray photoelectron spectroscopy (XPS)

XPS measurements were performed on a freshly cleaved crystal surface with a Thermo Scientific™ Nexsa™ Surface Analysis System, using an electron flood gun to avoid sample charging. All XPS spectra were recorded and processed using the Thermo Avantage software.

X-ray diffraction (XRD)

Specular XRD measurements were performed on a D5000 X-ray Powder Diffractometer (Siemens) over a 2θ range of 5°–70° using Cu-Kα radiation and a Ni-filter.

High resolution X-ray diffraction (HRXD) measurements were performed on a Smartlab diffractometer (Rigaku) equipped with a Cu rotating anode. High angular resolution was obtained by combining a Ge (220) ×4 monochromator and a Ge (220) ×2 analyzer. With this set-up, specular scans (theta/2 theta scans) and (002) Rocking Curves (theta scan around the (00l) reflection) were collected.

Seebeck coefficient

The Seebeck coefficient was measured using an SB1000 Seebeck Measurement System with integrated K20 Programmable Temperature Controller (MMR Technologies Inc.), in the temperature range 293 K to 353 K under a vacuum of 10⁻⁵ mbar in complete darkness. A Bi-doped MAPbBr₃ single crystal was cut with dimension 1 mm × 1 mm × 5 mm. The reference sample and crystal sample were mounted onto the sample holder using silver paste, as schematized in Fig. S4 (ESI†).

Results and discussion

The retrograde (inverse temperature) solubility of methylammonium lead bromide perovskites is most significant in DMF, for which the solubility at the temperature used for crystallisation (85 °C) is ∼40% of the room temperature solubility.³⁶ The pristine and Bi-doped MABi_xPb_(1−x)Br₃ single crystals were synthesized by heating the precursor solution to 85 °C for about 6 hours, as shown in Fig. 1(a). High quality intrinsic and Bi-doped MAPbBr₃ single crystals were obtained by this method with typical dimensions of 6 × 6 × 2 mm (Fig. 1(b)). The crystals are readily distinguished by their color, from orange for the undoped crystal to almost black for the 15% Bi-doped crystal.

Fig. 1 Crystal growth process, photograph and structure. (a) Graphical illustration of crystallization process by ITC. (b) Picture of pristine and Bi-doped MAPbBr₃ single crystal.

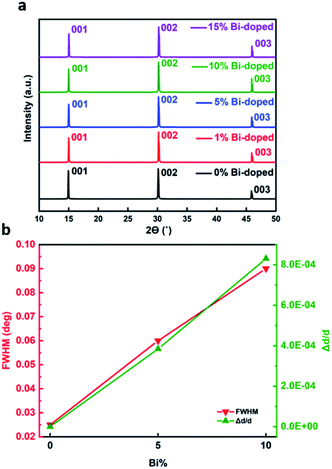
Fig. 2(a) shows the XRD pattern of a pristine MAPbBr₃ crystal and Bi-doped MAPbBr₃ single crystals with different doping concentrations. The invariance of XRD patterns indicates the structure of the Bi-doped crystals is very similar to the pristine crystal and no new peaks formed with bismuth incorporation. Even the 15% Bi-doped MAPbBr₃ crystal maintains the cubic perovskite structure. This is a strong indication that no secondary phase of methylammonium bismuth bromide is formed, and that there is no crystalline residual metal halide salt.

Fig. 2 XRD patterns of pristine and Bi-doped MAPbBr₃ single crystals. (a) Powder XRD patterns of un-doped and Bi-doped MAPbBr₃ single crystals. (b) The full width at half maximum (FWHM) of the rocking curve around the (002) reflection and the increase in d-spacing of the (003) 2θ diffraction peak for 0%, 5% and 10% Bi-doped MAPbBr₃ single crystals from high-resolution XRD spectra.

However, the introduction of Bi does cause small distortions of the pristine crystalline structure which can be determined by HRXD measurements. In particular, both the position and width of the diffracted peaks are affected by the presence of Bi. Fig. 2(b) (green line) shows the small average increase in d-spacing, which is proportional to the doping level. The detection of this small shift was enabled by our high resolution HRXRD obtained using a Ge (220) ×4 monochromator which gives a resolution of 0.003°, allowing very small d-spacing variation to be resolved which cannot be resolved by conventional XRD.³⁷ The full width at half maximum (FWHM, Fig. 2(b)) of the rocking curves recorded around the (002) diffraction peak (red line in Fig. 2(b)) increases with increasing doping level, although it remains very low: going from 0.025° for pristine MAPbBr₃ crystal to 0.09° for the 10% Bi-doped MAPbBr₃ crystal (Fig. S1†). This indicates that a small but detectable degree of disorder is introduced into the MAPbBr₃ crystal due to a slightly shorter average Bi–Br bond length (2.87 Å)³⁸ than the Pb–Br bond length (2.97 Å).³⁹ The small increase in lattice parameter and the induced disorder could be caused by crystal imperfections and structural defects arising from the bismuth substitution, either point defects (such as interstitials or vacancies) or extended defects (such as dislocations or stacking faults). XPS survey spectra of freshly cleaved internal surfaces of the MABi_xPb_(1−x)Br₃ crystals indicate that the degree of Bi-doping in the synthesized crystals was approximately the same as in the feedstock, making this a remarkably small lattice distortion for a high degree of doping.

Fig. 3(a) and (b) show Bi 4f and Pb 4f doublet peaks respectively obtained by XPS of MAPbBr₃ single crystals with different Bi doping concentrations. An increasing intensity of the Bi 4f peak is observed when the % Bi/Pb in the feed solution is increased during crystal growth with the Bi/Pb ratio in the crystal approximately matching the ratio in the feed solution. Two different chemical states of Bi were observed for the most heavily Bi-doped crystals by tracking the 4f_7/2 peak: Bi(0) at ∼156.5 eV, and Bi(III) at ∼159 eV.⁴⁰ The formation of a small amount of bismuth metal can be ascribed to the electron beam irradiation. Pb metal peaks were observed (at ∼141.2 eV and 136.3 eV) in pristine and lower Bi-doped crystals. According to McGettrick and co-workers, the appearance of a Pb(0) peak in XPS spectra of MAPbI₃ is caused by the interaction of the electron beam with the sample, and that the mechanism for this is the degradation of MAPbI₃ to PbI₂ in the low pressure XPS chamber, and subsequently of PbI₂ to Pb(0) during XPS measurement.⁴¹ However, there are no clear Pb(0) peaks for the higher Bi-doped crystals. We hypothesize that Bi-doping of MAPbBr₃ crystals improves stability slowing down degradation during X-ray exposure. This agrees with the observation of increased stability of MAPbI₃ thin films after Bi³⁺ doping reported by Xu and Hu.⁴²

Fig. 3 X-ray photoelectron spectroscopy (XPS) spectra of (a) Bi 4f and (b) Pb 4f in freshly cleaved MAPbBr₃ single crystals with different Bi doping concentrations.

The thermal conductivity was measured as a function of Bi-doping using the laser flash method (Fig. 4). The thermal diffusivity (D, Fig. S3(a)†) of Bi-doped MAPbBr₃ single crystals is between 0.31 and 0.34 mm² s⁻¹ at 20 °C, decreasing with increasing temperature to between 0.30 and 0.33 mm² s⁻¹ at 80 °C. Meanwhile, the heat capacity (C_p, Fig. S3(b)†) increases over the same temperature range, and is comparable to values published elsewhere.⁴³ Our measurements of thermal conductivity of undoped MAPbBr₃ single crystals fall comfortably in the ultra-low regime (0.33 ± 0.04 W m⁻¹ K⁻¹, calculated by κ = DC_pρ) and is in agreement with previous reports (0.44 ± 0.08 W m⁻¹ K⁻¹ (ref. 23) and 0.37 ± 0.04 W m⁻¹ K⁻¹ (ref. 24)), giving us confidence in the results. We might have expected that the Bi point defects would further reduce the thermal conductivity, but our results clearly indicate that this is not the case with the thermal conductivity remaining unchanged upon doping. We attribute this, in part, to the combination of the already ultra-low lattice thermal conductivity with the relatively small lattice distortion introduced by the Bi substitutions.

Fig. 4 Temperature-dependent thermal conductivity κ of pristine and Bi-doped MAPbBr₃ single crystals.

Thermoelectric properties

Van der Pauw and Hall effect measurements were used to investigate the transport properties. Fig. 5(a) shows electrical conductivity and charge carrier concentration of MABi_xPb_(1−x)Br₃ single crystals as a function of Bi-doping. With increasing bismuth concentration in the crystal, the electrical conductivity increases sharply from 1.5 × 10⁻⁸ S cm⁻¹ for non-doped crystals to 1.5 × 10⁻⁴ S cm⁻¹ for 15% Bi-doped MAPbBr₃, a difference of 4 orders of magnitude. This result is in line with earlier reports that bismuth doping can greatly improve the electrical conductivity of MAPbBr₃.⁴⁴ Shi³⁰ and Abdelhady⁴⁴ obtained a hole carrier concentration in undoped MAPbBr₃ crystals of 6 × 10⁹ to 5 ×10¹⁰ cm⁻³ by DC hall measurement. We performed an AC Hall measurements in the van der Pauw configuration using 300 nm thick evaporated silver as contact pads that were connected to the system with copper wires (Fig. S5, ESI†). AC Hall measurements have the advantage of being able to more accurately measure low mobility and high resistance materials, as the AC magnetic field can be used to effectively reduce noise and misalignment voltage effects. In this way we got an ohmic contact to the sample and found that our undoped crystals were p-type with a hole concentration of 1.19 × 10¹¹ cm⁻³, marginally higher than the earlier reports. After bismuth doping, electrons become the dominant charge carrier with a concentration of 5 × 10¹⁴ cm⁻³ in 15% Bi-doped MAPbBr₃ crystals, an increase of more than 3 orders of magnitude. The extracted Hall mobilities (Table S2†) show that the charge carrier mobility reduces above 10% Bi-doping, pointing to this as the reason for the plateau in electrical conductivity at high doping levels.

Fig. 5 Electrical properties and Seebeck coefficient of pristine and Bi-doped MAPbBr₃ single crystals. (a) Electrical conductivity and number of charge carriers of Bi-doped MAPbBr₃ single crystals (error bars of electrical conductivity is too small (<1%) to view). (b) Temperature-dependent Seebeck coefficient of 15% Bi-doped MAPbBr₃ single crystals.

The temperature dependent (293 K–353 K) Seebeck coefficient of a 15% Bi-doped MAPbBr₃ crystal is shown in Fig. 5(b). The negative sign of the Seebeck coefficient confirms that electrons are the majority charge carriers, in agreement with the Hall measurement. Its value is −378 ± 25 μV K⁻¹ at room temperature (293 K) and does not change significantly over the temperature range studied.

Conclusions

In conclusion, we have used substitutional doping of Bi on the B-site of an ABX₃ hybrid organic–inorganic perovskite single crystal to increase electrical conductivity and studied its effect on thermoelectric properties. Our results show that bismuth atoms can substitute on Pb-sites to remarkably high concentrations with only slight distortion of the lattice. Meanwhile, the introduction of Bi dramatically increases the free carrier concentrations and electrical conductivity by 3–4 orders of magnitude. As is well-known for this class of materials, the thermal conductivity is ultralow but we found it to be surprisingly unaffected by the large density of point defects introduced by the Bi-doping, a result which, in part, we assign to the limited lattice distortion introduced by these defects. The Seebeck coefficient of 15% Bi-doped MAPbBr₃ (−378 ± 25 μV K⁻¹) confirmed that the Bi-doping produced n-type doping, although the thermoelectric figure of merit, ZT, was low at 1.8 × 10⁻⁶ (at 293 K). The low ZT value is therefore the result of low doping efficiency, which this study indicates is ∼10⁻⁵%, rather than the degree of Bi-incorporation (which can be close to 15% of the B-sites). The reason for this low doping efficiency may be ionic compensation of point defects,⁴⁵ in addition to an electronic structure that is tolerant of defects caused by bonding orbitals at the conduction band minimum as well as anti-bonding orbitals at the valence band maximum.⁴⁶ This work has therefore introduced the role of substitutional doping in the development of halide perovskites as thermoelectric materials and highlights that the key area for future research effort is the doping efficiency. Overcoming this hurdle may allow hybrid organic–inorganic halide perovskites to achieve the ZT values > 1, that have been predicted by theory.³¹ This may be possible through substitutional doping on the B-site or X-site and using elements other than bismuth.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financed under OF's Royal Society University Research Fellowship, UF140372, and a Royal Society International Exchanges Scheme grant (IE161598) held by O. F. and S. M. W. T. and T. L. are funded by the China Scholarship Council. S. R. is funded by the Engineering and Physical Sciences Research Council (UK) under the Centre for Doctoral Training in Plastic Electronics (EP/L016702/1).

References

1. D. Narducci, JPhys Energy, 2019, 1, 024001.
2. J. Briscoe and S. Dunn, Nano Energy, 2015, 14, 15–29.
3. D. A. Barkas, C. S. Psomopoulos, P. Papageorgas, K. Kalkanis, D. Piromalis and A. Mouratidis, Energy Procedia, 2019, 157, 999–1010.
4. L. E. Bell, Science, 2008, 321, 1457.
5. T. M. Tritt, Annu. Rev. Mater. Res., 2011, 41, 433–448.
6. L.-D. Zhao, S.-H. Lo, Y. Zhang, H. Sun, G. Tan, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Nature, 2014, 508, 373–377.
7. I. T. Witting, T. C. Chasapis, F. Ricci, M. Peters, N. A. Heinz, G. Hautier and G. J. Snyder, Adv. Electron. Mater., 2019, 5, 1800904.
8. Q. Zhang, Y. Sun, W. Xu and D. Zhu, Adv. Mater., 2014, 26, 6829–6851.
9. V. Vijayakumar, Y. Zhong, V. Untilova, M. Bahri, L. Herrmann, L. Biniek, N. Leclerc and M. Brinkmann, Adv. Energy Mater., 2019, 9, 1900266.
10. A. D. Avery, B. H. Zhou, J. Lee, E.-S. Lee, E. M. Miller, R. Ihly, D. Wesenberg, K. S. Mistry, S. L. Guillot, B. L. Zink, Y.-H. Kim, J. L. Blackburn and A. J. Ferguson, Nat. Energy, 2016, 1, 16033.
11. C. Cho, S. Qin, K. Choi and J. C. Grunlan, ACS Appl. Polym. Mater., 2019, 1, 1942–1947.
12. A. J. Paleo, E. M. F. Vieira, K. Wan, O. Bondarchuk, M. F. Cerqueira, L. M. Goncalves, E. Bilotti, P. Alpuim and A. M. Rocha, Carbon, 2019, 150, 408–416.
13. G. Xing, N. Mathews, S. Sun, S. S. Lim, Y. M. Lam, M. Grätzel, S. Mhaisalkar and T. C. Sum, Science, 2013, 342, 344–347.
14. M. A. Green, A. Ho-Baillie and H. J. Snaith, Nat. Photonics, 2014, 8, 506.
15. J. M. Ball and A. Petrozza, Nat. Energy, 2016, 1, 16149.
16. NREL Best Research-Cell Efficiency, https://www.nrel.gov/pv/assets/pdfs/best-research-cell-efficiencies.20190923.pdf, accessed 10/10/ 2019.
17. A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, J. Am. Chem. Soc., 2009, 131, 6050–6051.
18. J.-P. Correa-Baena, A. Abate, M. Saliba, W. Tress, T. Jesper Jacobsson, M. Grätzel and A. Hagfeldt, Energy Environ. Sci., 2017, 10, 710–727.
19. X. Mettan, R. Pisoni, P. Matus, A. Pisoni, J. Jaćimović, B. Náfrádi, M. Spina, D. Pavuna, L. Forró and E. Horváth, J. Phys. Chem. C, 2015, 119, 11506–11510.
20. T. Hata, G. Giorgi and K. Yamashita, Nano Lett., 2016, 16, 2749–2753.
21. R. Heiderhoff, T. Haeger, N. Pourdavoud, T. Hu, M. Al-Khafaji, A. Mayer, Y. Chen, H.-C. Scheer and T. Riedl, J. Phys. Chem. C, 2017, 121, 28306–28311.
22. W. Lee, H. Li, A. B. Wong, D. Zhang, M. Lai, Y. Yu, Q. Kong, E. Lin, J. J. Urban, J. C. Grossman and P. Yang, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 8693–8697.
23. C. Ge, M. Hu, P. Wu, Q. Tan, Z. Chen, Y. Wang, J. Shi and J. Feng, J. Phys. Chem. C, 2018, 122, 15973–15978.
24. T. Liu, S.-Y. Yue, S. Ratnasingham, T. Degousée, P. Varsini, J. Briscoe, M. A. McLachlan, M. Hu and O. Fenwick, ACS Appl. Mater. Interfaces, 2019, 11, 47507–47515.
25. C. C. Stoumpos, C. D. Malliakas and M. G. Kanatzidis, Inorg. Chem., 2013, 52, 9019–9038.
26. L. M. Herz, ACS Energy Lett., 2017, 2, 1539–1548.
27. T. Ye, X. Wang, X. Li, A. Q. Yan, S. Ramakrishna and J. Xu, J. Mater. Chem. C, 2017, 5, 1255–1260.
28. M. A. Haque, M. I. Nugraha, S. H. K. Paleti and D. Baran, J. Phys. Chem. C, 2019, 123, 14928–14933.
29. Y. Liu, Z. Yang, D. Cui, X. Ren, J. Sun, X. Liu, J. Zhang, Q. Wei, H. Fan, F. Yu, X. Zhang, C. Zhao and S. F. Liu, Adv. Mater., 2015, 27, 5176–5183.
30. D. Shi, V. Adinolfi, R. Comin, M. Yuan, E. Alarousu, A. Buin, Y. Chen, S. Hoogland, A. Rothenberger, K. Katsiev, Y. Losovyj, X. Zhang, P. A. Dowben, O. F. Mohammed, E. H. Sargent and O. M. Bakr, Science, 2015, 347, 519.
31. Y. He and G. Galli, Chem. Mater., 2014, 26, 5394–5400.
32. S. Saini, A. K. Baranwal, T. Yabuki, S. Hayase and K. Miyazaki, MRS Adv., 2019, 4, 1719–1725.
33. T. Liu, X. Zhao, J. Li, Z. Liu, F. Liscio, S. Milita, B. C. Schroeder and O. Fenwick, Nat. Commun., 2019, 10, 5750.
34. Y. Takahashi, H. Hasegawa, Y. Takahashi and T. Inabe, J. Solid State Chem., 2013, 205, 39–43.
35. M. I. Saidaminov, A. L. Abdelhady, B. Murali, E. Alarousu, V. M. Burlakov, W. Peng, I. Dursun, L. Wang, Y. He, G. Maculan, A. Goriely, T. Wu, O. F. Mohammed and O. M. Bakr, Nat. Commun., 2015, 6, 7586.
36. M. I. Saidaminov, A. L. Abdelhady, G. Maculan and O. M. Bakr, Chem. Commun., 2015, 51, 17658–17661.
37. P. K. Nayak, M. Sendner, B. Wenger, Z. Wang, K. Sharma, A. J. Ramadan, R. Lovrinčić, A. Pucci, P. K. Madhu and H. J. Snaith, J. Am. Chem. Soc., 2018, 140, 574–577.
38. W. Bi, N. Leblanc, N. Mercier, P. Auban-Senzier and C. Pasquier, Chem. Mater., 2009, 21, 4099–4101.
39. Y. Rakita, S. R. Cohen, N. K. Kedem, G. Hodes and D. Cahen, MRS Commun., 2015, 5, 623–629.
40. A. Y. Teterin, Y. A. Teterin, K. I. Maslakov, V. G. Yarzhemskiĭ, S. E. Sverchkov, B. I. Denker, B. I. Galagan, L. D. Iskhakova, L. I. Bulatov, V. V. Dvoĭrin, V. M. Mashinskiĭ, A. A. Umnikov, A. N. Gur’yanov, V. I. Nefedov and E. M. Dianov, Dokl. Phys., 2008, 53, 566–570.
41. J. D. McGettrick, K. Hooper, A. Pockett, J. Baker, J. Troughton, M. Carnie and T. Watson, Mater. Lett., 2019, 251, 98–101.
42. Y. Xiong, L. Xu, P. Wu, L. Sun, G. Xie and B. Hu, Adv. Funct. Mater., 2019, 29, 1900615.
43. N. Onoda-Yamamuro, T. Matsuo and H. Suga, J. Phys. Chem. Solids, 1990, 51, 1383–1395.
44. A. L. Abdelhady, M. I. Saidaminov, B. Murali, V. Adinolfi, O. Voznyy, K. Katsiev, E. Alarousu, R. Comin, I. Dursun, L. Sinatra, E. H. Sargent, O. F. Mohammed and O. M. Bakr, J. Phys. Chem. Lett., 2016, 7, 295–301.
45. A. Walsh, D. O. Scanlon, S. Chen, X. G. Gong and S.-H. Wei, Angew. Chem., Int. Ed., 2015, 54, 1791–1794.
46. R. E. Brandt, V. Stevanović, D. S. Ginley and T. Buonassisi, MRS Commun., 2015, 5, 265–275.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ta03648j

---