Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Reversible densification in nano-Li2MnO3 cation disordered rock-salt Li-ion battery cathodes†
Maria
Diaz-Lopez
 *ab,
Philip A.
Chater
*ab,
Philip A.
Chater
 b,
Yves
Joly
c,
Olivier
Proux
b,
Yves
Joly
c,
Olivier
Proux
 c,
Jean-Louis
Hazemann
c,
Jean-Louis
Hazemann
 c,
Pierre
Bordet
c and
Valerie
Pralong
c,
Pierre
Bordet
c and
Valerie
Pralong
 d
d
aISIS Facility, STFC Rutherford Appleton Laboratory, Didcot, OX11 0QX, UK. E-mail: maria.diaz-lopez@stfc.ac.uk
bDiamond Light Source Ltd, Diamond House, Harwell Science and Innovation Campus, Didcot OX11 0DE, UK
cGrenoble Alpes Univ., CNRS, Inst. Neel, 38000 Grenoble, France
dNormandie Univ., Ensicaen, Unicaen, CNRS, Crismat, 14000 Caen, France
First published on 22nd May 2020
Abstract
The full structure of nano-Li2MnO3 with superior reversible capacities of 290 mA h g−1 for over 10 cycles was investigated by neutron and X-ray total scattering, which demonstrate that contrary to previous claims, a phase transformation occurs during synthesis forming a disordered cubic MnO-type rock-salt with nanodomains of Li/Mn layering of ∼1 nm. A comprehensive study of the structural and charge evolution combining in operando X-ray total scattering with advanced spectroscopic methods at the Mn K-edge such as High Energy Resolved Fluorescence Detected XANES, EXAFS and Emission Spectroscopies including main and valence-to-core transitions, point to a lattice densification with an effective loss of Li2O, with the subsequent electrochemical activation of Li2O as the main responsible mechanism for the exchanged capacity. Interestingly, and unlike previous studies, no capacity losses could be associated to the material's densification.
Introduction
The increasing demand for higher energy density batteries continues to foster research on cathode materials with superior capacities to the current state-of-the-art ranging from 140 (in LiCoO2)1 to 200 mA h g−1 (in LiNi0.8Mn0.1Co0.1O2).2 Significant improvement of the cathode specific capacity has been realized in Li-rich layered oxides xLi2MnO3 (1 − x)LiMO2,3 where M is a 3d transition metal (TM), offering extra capacities beyond the limit of conventional TM redox reactions. These composites deliver capacities as high as 250 mA h g−1 (ref. 4) when charged to a high potential (∼4.5 V vs. Li/Li+) that activates charge compensation mechanisms alternative to unfavourable TM redox reaction involving Mn4+oct/Mn5+oct in the over-lithiated Li2MnO3 component.Several studies have focused on the performance of Li2MnO3 (ref. 5) to better understand this extra capacity which has been partly attributed to H+ for Li+ substitution6–8 and more notably to oxygen redox reactions.9,10 Anionic redox reactions in Li2MnO3 are accompanied by the irreversible evolution of O2− at the particle surface into gaseous O2 and superoxide radicals (O2˙−). Part of the O2 released is removed from the cell triggering structural reorganization, such as phase segregation (gradual transformation to spinel with cycling)11,12 or particle densification with diffusion of transition metal ions from surface to bulk where they occupy vacancies created by Li removal.13 Highly reactive O2˙− radicals can react with the carbonate solvent to form Li2CO3 and Li2O decomposition products.14 As a result, while exhibiting excellent initial capacities, Li-rich layered cathodes suffer from voltage fade and poor rate capabilities. In spite of significant efforts directed to avoid the irreversible evolution of O2− and capacity fade in Li2MnO3 and xLi2MnO3 (1 − x)LiMO2 composites15 through material processing and coating,16 this remains an issue to be resolved prior to wider application of these systems.
Interestingly, unfavourable O2 evolution is overcome in isostructural compounds to Li2MnO3 with 4d (Li2RuO3 (ref. 17)) and 5d (Li2IrO3 (ref. 18)) TMs, where reversible anionic redox is hypothesized to be stabilized by the formation of ‘peroxo-like’ 2.5 Å O–O dimers. Reversible oxygen redox have also been proposed for Li2−xIr1−ySnyO3 based on peroxide 1.4 Å O–O dimers bridging Ir and Sn cations, which are closer to the range of bond lengths of typical peroxide species.19
Within the last few years, superior capacities (200–350 mA h g−1) have been observed in Li-rich cubic cation disordered rock-salts owing to the low energetic percolation of lithium diffusion paths associated with a high Li![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TM ratio. This emerging new family of cathode materials show no obvious structural changes involving complex phase transformations that could eventually lead to particle cracking and battery failure upon extensive cycling. These promising features have motivated extensive work on these materials and several Li-rich disordered rock-salts have been reported,20–22 where the highest capacities have been observed in Li1.3Nb0.3Mn0.4O2 (ref. 23) (250 mA h g−1), Li1.2Ti0.4Mn0.4O2 (ref. 24) (300 mA h g−1) and Li4Mn2O5 (ref. 25) (350 mA h g−1). The versatility of these phases provides further scope to explore multivalent TMs, anionic redox and mixed (O2−/F−) systems which may lead to improved performance.
TM ratio. This emerging new family of cathode materials show no obvious structural changes involving complex phase transformations that could eventually lead to particle cracking and battery failure upon extensive cycling. These promising features have motivated extensive work on these materials and several Li-rich disordered rock-salts have been reported,20–22 where the highest capacities have been observed in Li1.3Nb0.3Mn0.4O2 (ref. 23) (250 mA h g−1), Li1.2Ti0.4Mn0.4O2 (ref. 24) (300 mA h g−1) and Li4Mn2O5 (ref. 25) (350 mA h g−1). The versatility of these phases provides further scope to explore multivalent TMs, anionic redox and mixed (O2−/F−) systems which may lead to improved performance.
In a previous work, we reported the reduction of the particle size in the range of 10 nm (ref. 26) in layered Li2MnO3 (space group C2/m) by high-energy milling with no change of the space group symmetry. Nanostructured Li2MnO3 (hereafter referred to as nano-Li2MnO3) features improved capacity (290 mA h g−1) and reduced fading (200 mA h g−1 retained after over ten cycles)26 over its micro-structured counterpart which displays a 50% capacity drop over the first five cycles.27 Upon cycling, a phase transformation into a cubic disordered MnO-type rock-salt was determined by ex situ electron diffraction of electrosynthesized Li0.5MnO3 charged to 4.5 V, although no plateau characteristic of a phase transformation could be identified in the electrochemical curve.
In the present study, average and local structural studies involving combined neutron and X-ray total scattering demonstrate that, contrary to previous claims,26 a phase transformation occurs during the nanostructuring of Li2MnO3, forming a disordered cubic MnO-type rock-salt structure analogous to that of Li4Mn2O5, but with nanodomains of Li/Mn layering with a size of ∼1 nm. The structure and charge evolution of nano-Li2MnO3 during battery cycling was characterized by a combination of techniques performed in operando, including X-ray total scattering and advanced X-ray spectroscopic methods performed at the Mn K-edge, such as High Energy Resolved Fluorescence Detected near-edge X-ray Absorption (HERFD-XANES), Extended X-ray Absorption Fine Structure (EXAFS) and X-ray Emission Spectroscopies (XES) including main (kβ1,3 and kβ′) and valence-to-core or V2C (kβ2,5 and kβ′′) transitions; this is the first time these XES techniques have been reported for batteries under in operando conditions.
X-ray total scattering, HERFD-XANES and EXAFS reveal a solid-solution-type response, where the reversible cycling between charged and discharged states is allowed by the breathing of a cubic Mn-framework, in discordance with a phase transformation from C2/m to Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m from previous studies.26 Note also that the structural evolution of nano-Li2MnO3 during cycling significantly differs to that of layered Li2MnO3 in a crystalline state, which contracts along the c-lattice parameter upon delithiation. The analysis of diffraction data in reciprocal space show a large structural reversibility of nano-Li2MnO3 with a constant structural coherence length of Li/Mn layering nanodomains. In the real space, no distribution of O–O interatomic distances was observed that could be ascribed to the recently reported peroxo-like distances proclaimed in other high capacity cathodes, such as in layered Li2MnO3-type structures like (Li/Na)2RuO3 (ref. 28 and 29) and Li2IrO3,18 Li3IrO4 (ref. 30) and 3D structures like β-Li2IrO3.31
m from previous studies.26 Note also that the structural evolution of nano-Li2MnO3 during cycling significantly differs to that of layered Li2MnO3 in a crystalline state, which contracts along the c-lattice parameter upon delithiation. The analysis of diffraction data in reciprocal space show a large structural reversibility of nano-Li2MnO3 with a constant structural coherence length of Li/Mn layering nanodomains. In the real space, no distribution of O–O interatomic distances was observed that could be ascribed to the recently reported peroxo-like distances proclaimed in other high capacity cathodes, such as in layered Li2MnO3-type structures like (Li/Na)2RuO3 (ref. 28 and 29) and Li2IrO3,18 Li3IrO4 (ref. 30) and 3D structures like β-Li2IrO3.31
The determination of the charge compensation mechanism in nano-Li2MnO3 was possible by the joint analysis of HERFD-XANES and XES data. We characterized the changes of the oxidation state of Mn following the evolution of the kβ1,3 transition, and utilized for the first time V2C transitions to probe plausible charge compensation mechanisms involving oxygen, like bulk anionic redox or hydroxyl –OH group formation. While soft X-rays are typically used to probe the K-edges of light atoms, these are only sensitive to surface effects given their short penetration depth. Unlike soft-XAS, the V2C spectra measured with hard X-rays (∼6.5 keV) are able to probe the bulk material. Moreover, this technique only detects oxygen bound to manganese, and there is no contamination to the recorded signal from oxygen present in other components of the battery, like the electrolyte. The analysis of the data was aided by ab initio simulations of HERFD-XANES and V2C signals using proposed structural models based on different charge compensation mechanisms, and their confrontation with the measured spectra. Our data and simulations of spectroscopy signals point to a densification mechanism with an effective loss of electrochemically active Li2O, which produces electrons and is the main responsible for the exchanged capacity for nano-Li2MnO3. The oxygen evolved from the Li2O electrochemical activation could in turn be stabilized in peroxide species at the cathode surface, or by the trapping of O2 molecules in vacancy clusters originated during Li-extraction. Interestingly, and unlike previous studies, very small capacity losses (0–3% over the first 10 cycles)26 could be associated with the material's densification.
Results
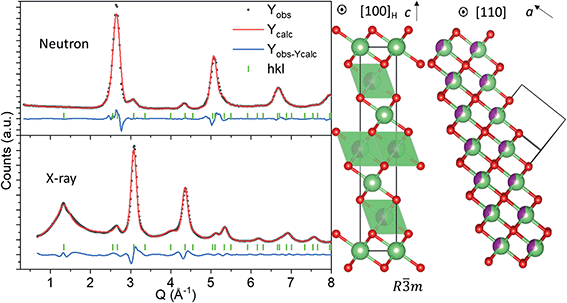
Structural description of pristine nano-Li2MnO3
The atomic structure of nano-Li2MnO3 was investigated by joint analysis of neutron and X-ray total scattering data to analyse both short- and long-range ordering. Rietveld refinement was used to determine how well reported crystallographic models matched to the observed average structure. The well-known Li2MnO3 layered model (space group C2/m) failed to produce a satisfactory fit to the observed data (Rwp > 10%, see Fig. S1†), which disproves previous work26 and indicates that a structural transformation occurs during the mechanochemical synthesis of nano-Li2MnO3 by the ball milling of microstructured Li2MnO3. A model based on a rock-salt MnO-type structure (space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) with modified occupancy values to include Li on the Mn site produced a good fit to the neutron data, but several broad reflections in the X-ray diffraction pattern could not be indexed with the cubic Fm
m) with modified occupancy values to include Li on the Mn site produced a good fit to the neutron data, but several broad reflections in the X-ray diffraction pattern could not be indexed with the cubic Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group (Fig. S1†). These reflections were attributed to the formation of a short-range ordered superstructure formed from ordering alternating layers of Li and Mn cations into alternating (111) planes in the rock-salt structure, as previously reported in LixNi2−xO2.32 The chemical ordering of Li and Mn is described by the rhombohedral space group R
m space group (Fig. S1†). These reflections were attributed to the formation of a short-range ordered superstructure formed from ordering alternating layers of Li and Mn cations into alternating (111) planes in the rock-salt structure, as previously reported in LixNi2−xO2.32 The chemical ordering of Li and Mn is described by the rhombohedral space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, as shown in Fig. 1.
m, as shown in Fig. 1.
The rhombohedral model in Fig. 1 enables the simultaneous description of both cubic Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m reflections from the rock salt structure, and the R
m reflections from the rock salt structure, and the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m short-range ordered supercell peaks from cation ordering.32 In the hexagonal unit cell description, reflections deriving from the cubic structure have Miller indices with even values of l (hkleven), whereas hexagonal reflections that are forbidden in the cubic unit cell, but arise due to nanodomains of Li and Mn layering, exhibit odd values of l (hklodd). Both sets of broad and sharper reflections were fitted using a single structural model, where the hkl-dependent peak broadening was modelled to evaluate the crystallite size of the cubic and hexagonal sublattices. The sample size was calculated using the double-Voigt approach33 to estimate the volume-weighted column height separated into Lhex and Lcub components for hklodd and hkleven reflections, respectively. The refined value of Lhex of 1.2(6) nm accounts for the volume weighted length of chemical coherence of the layered hexagonal ordering, and Lcub = 3.8(4) nm represents the total volume weighted crystallite size of the nanostructured material, which is independent of the layered ordering. This refinement approach allowed us to quantify the extent of Li and Mn layering as approximately equal to the length of the c lattice parameter of the R
m short-range ordered supercell peaks from cation ordering.32 In the hexagonal unit cell description, reflections deriving from the cubic structure have Miller indices with even values of l (hkleven), whereas hexagonal reflections that are forbidden in the cubic unit cell, but arise due to nanodomains of Li and Mn layering, exhibit odd values of l (hklodd). Both sets of broad and sharper reflections were fitted using a single structural model, where the hkl-dependent peak broadening was modelled to evaluate the crystallite size of the cubic and hexagonal sublattices. The sample size was calculated using the double-Voigt approach33 to estimate the volume-weighted column height separated into Lhex and Lcub components for hklodd and hkleven reflections, respectively. The refined value of Lhex of 1.2(6) nm accounts for the volume weighted length of chemical coherence of the layered hexagonal ordering, and Lcub = 3.8(4) nm represents the total volume weighted crystallite size of the nanostructured material, which is independent of the layered ordering. This refinement approach allowed us to quantify the extent of Li and Mn layering as approximately equal to the length of the c lattice parameter of the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m model (chex = 14.14157(6) Å) in Fig. 1, and is therefore a very short-range phenomena. It is important to note that the growth of this short-range layered ordering may occur along any of the [111] rock-salt directions, with coherent cubic domains between them. This structural difference between nano-Li2MnO3 and its microstructured counterpart may be in part responsible for the increased capacity and reversibility in this material, as opposed to nanostructuring alone.
m model (chex = 14.14157(6) Å) in Fig. 1, and is therefore a very short-range phenomena. It is important to note that the growth of this short-range layered ordering may occur along any of the [111] rock-salt directions, with coherent cubic domains between them. This structural difference between nano-Li2MnO3 and its microstructured counterpart may be in part responsible for the increased capacity and reversibility in this material, as opposed to nanostructuring alone.
Details of the short-range structure can be revealed by studying the pair distribution function (PDF) data. Simulation of the short r-range of the PDF (r < 10 Å) using the refined average model produced a large mismatch to the observed data in Fig. S2,† indicating a high degree of local atomic rearrangement in this material. The study of the local structure in cation disordered rock-salts is particularly challenging due to the overlap of all cation–cation, oxygen–oxygen partial PDFs and is beyond the scope of this work; a future study will focus on structural modelling via fitting of EXAFS, X-ray and neutron total scattering data by Reverse Monte Carlo methods using a modified version of the RMCProfile software,34 allowing the refinement of multiple Bragg data and where the new hkl-dependent peak shape functions formerly introduced have been implemented. In the present study, the evolution of the local structure of nano-Li2MnO3 during cycling was interpreted by the curve fitting and PDF simulations using small clusters of LiO6 and MnO6 polyhedra and is introduced in the following section.
Bulk structural evolution during battery cycling
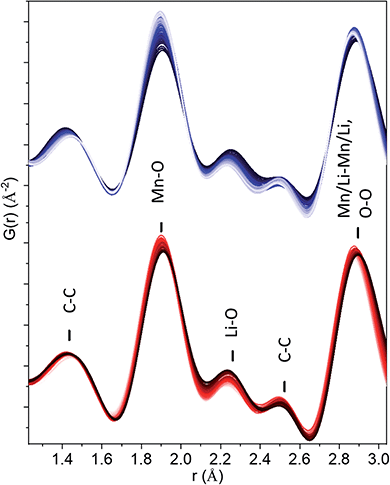
Rietveld refinement of total scattering data collected during cycling (Fig. 2) showed a continuous evolution of the lattice parameters that mirrors the shape of the electrochemical curve, indicative of solid solution behaviour. The cell parameter of the cubic sublattice, acubic, contracted from 4.0741(2) to 4.054(2) Å with the extraction of ∼1.5 Li during the first charge to 4.5 V, and re-expanded to 4.101(2) Å during the discharge to 2 V. The solid solution response, contradicting previous claims,26 is in congruent with the absence of characteristic plateaus in the electrochemical curve associated with phase transformations, and further supports our finding that the structure of pristine nano-Li2MnO3 corresponds to that of a cation disordered rock-salt structure with nanodomains of Li/Mn layering. The isotropic breathing of nano-Li2MnO3 is characteristic of cation disordered rock-salts, and is markedly different to the micro-structured compound where the contraction of the cell occurs predominantly along the stacking direction.35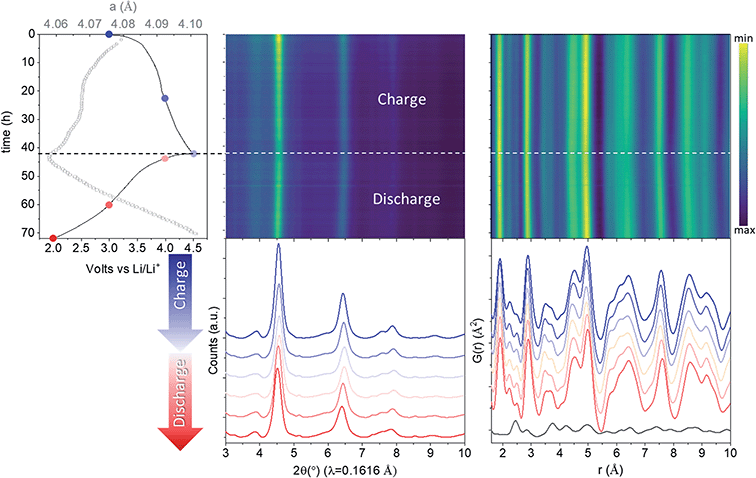 | ||
| Fig. 2 In operando nano-Li2MnO3 evolution with cycling characterized by X-ray total scattering. From left to right: electrochemical performance (solid line) overlaid with lattice parameters from a sequential Rietveld refinement (grey empty circles with error bars), reciprocal and real space (PDF) total scattering data. The PDF of carbon black additive to aid electronic conductivity of the electrode is provided at the bottom of the figure. See Fig. S3† for the evolution of all refined parameters and fits. Charge data is given in blue (from dark to light) and discharge in red (from light to dark). | ||
The evolution of all refined parameters with cycling is given in Fig. S3.† The correlation length for the cubic sublattice, Lcub = 3.3(2) nm, remained constant during cell charge/discharge. No significant differences in the profile of hklodd reflections were observed; however a large overlap between the most intense hklodd 003 reflection and the cell backgrounds (see diffraction data from PFA cell and carbon black additive in Fig. S3†) meant that the correlation length for the hexagonal sublattice Lhex could not be accurately refined and was fixed to the value obtained the joint neutron and X-ray refinement of pristine nano-Li2MnO3 (Lhex = 1.2 nm). The absence of major structural- or microstructural-rearrangements combined with good structural reversibility are both highly desirable features for cycling reversibility and capacity retention of cathode materials.
The evolution of the average structure in nano-Li2MnO3 resembles that of the non-stoichiometric cation disordered rock-salt of composition Li4Mn2O5,25 in that in both compounds the extraction and insertion of lithium is accompanied by the breathing of the Mn cubic framework. The similarities between the evolution of the local and average structures in Li4Mn23+O5 and Li2Mn4+O3 are remarkable, given that different charge compensation mechanisms are expected in these cathode materials.
X-ray PDF data was used to extract the Mn–O distance during cycling (Fig. 2). Only very minor changes in the Mn–O distance were observed, evolving from 1.907(2) Å for pristine, 1.894(2) Å for charged and 1.908(2) Å for discharged phases, all of which are consistent with the expected r(Mn4+VI − O2−VI) of 1.93 Å.36 This constant Mn4+ oxidation state may be expected from ligand field theory considerations, where the splitting in energy of Mn5+ d-orbitals in an octahedral configuration is substantially larger than for tetrahedral. In absence of Mn redox, and alternative charge compensation mechanism must be found.
PDF data can also provide information on the local oxygen environment and so potential for anionic redox mechanisms involving oxygen were investigated. Reversible anionic redox have been attributed to the sharing of one electron hole between two oxygen atoms via formation of peroxo-like (O2)3− species in Li2RuO3 and Li2IrO3, which are isostructural with the crystalline phase of Li2MnO3 (space group C2/m). O–O dimers approximately 2.3–2.5 Å apart have been proposed based on Ru K-edge EXAFS,28 Bragg diffraction,31 and transmission electron microscopy (TEM). Unlike PDF analysis, these techniques are not direct probes of O–O distances. (i) EXAFS is a model dependent technique where interatomic distances appear shifted due to the scattering phase-shift, (ii) Bragg diffraction quantifies the distance between mean atomic positions d〈O〉–〈O〉 different to the actual distribution of interatomic distances d〈O–O〉, and (iii) projection limitations exist by TEM. Therefore, large uncertainties surround the estimated O–O distances in peroxo-like dimers. In the absence of Mn redox, we consider whether a charge compensation mechanism accounting for ∼1.5Li during charge may be solely attributed to anionic redox. Such a compensation mechanism would change the oxidation state of all oxygen anions from 2− to 1.5− to give Li0.5Mn4+O31.5−, where all the oxygen atoms could become dimerized following the charge compensation mechanisms hypothesized for Li2RuO3 and Li2IrO3. At such a high concentration of O–O dimers, their contribution to the total XPDF signal is not negligible. To demonstrate the impact of dimer formation, XPDF data was simulated for MnO6 containing three dimerized O–O pairs at 2.3 Å and 1.4 Å for peroxo-like and peroxo bridges19 respectively (Fig. S4†). The formation of ‘peroxo-like’ dimers significantly changes the O–O partials within MnO6 which in turn gives rise to the formation of new peaks with detectable/measurable intensities at the new O–O distances (at 2.3 and 1.4 Å in Fig. S4†), and also affects the width and intensity of the peak at ∼2.9 Å comprising overlapped cation–cation and O–O distances.
The 1.4–2.5 Å range in the observed in operando PDF data were carefully examined (Fig. 3) and the evolution of peak width and intensity were characterized by the fitting of five Gaussian functions (Fig. S5†). The superposition of PDFs for the peaks at ∼1.4 and 2.5 Å attributed to C–C distances from the carbon black additive, rules out the O–O evolution at these distances. The intensity of the Li–O peak at ∼2.3 Å decreases during charge and increases during discharge, as expected for the reversible extraction–reincorporation of lithium. No increase in the intensity of this peak at the 4–4.5 V range characteristic of anionic redox activity was observed that could be attributed to the formation of O–O dimers in significant concentrations. For the Mn–O peak at ∼1.9 Å, a decrease in width was observed upon charging, corresponding to a more ordered local structure, but the integrated intensity remained constant. The absence of peroxo-like or peroxo bridge distances is further supported by the constant refined width of the peak at ∼2.9 Å attributed to cation–cation and O–O distances overlapped in the rock-salt structure. As previously shown by our simulations, the O–O pairs contribute to 20% of the intensity of this peak, and dimer formation would entail a significant change of its width and intensity, which was not observed experimentally. It can be concluded that PDF data does not support anionic redox process stabilized by the formation of peroxo-like or peroxo bridges in nano-Li2MnO3.
Local structure around Mn during cycling
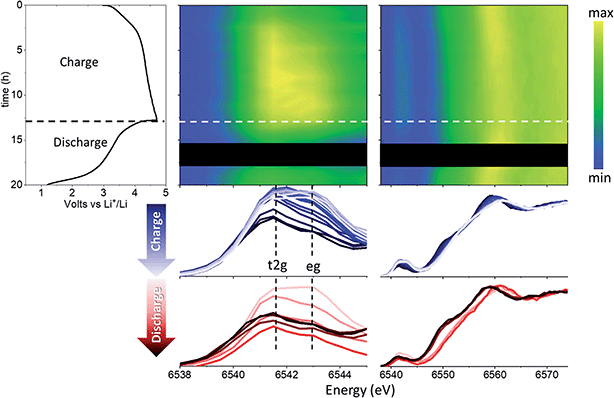
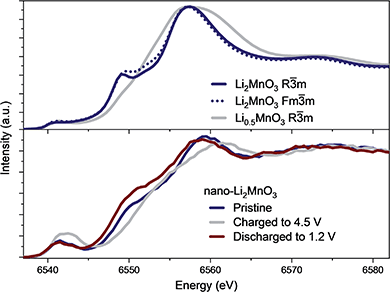
The evolution of the coordination environment around MnO6 in nano-Li2MnO3 was further characterized by in operando Mn K-edge HERFD-XANES, which is highly sensitive to structural changes around Mn cations. As established for known Mn standards,37 different coordination environments of 3d transition metals show very different pre-edges, and these features were used to characterize changes in the coordination number and centrosymmetricity of Mn in nano-Li2MnO3.The evolution of the HERFD-XANES data measured in operando during the first charge to 4.5 V and discharge to 1.2 V are shown in Fig. 4. The most significant change in the spectra correspond to the progressive fading of the shoulder at ∼6550 eV. First principle calculations were performed using the proposed R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structural model and an Fm
m structural model and an Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m models where suitable Li and Mn compositions were randomly distributed on the same site (Fig. 5); these calculations demonstrated that the intensity of the shoulder feature correlates with the amount of Li on the Mn lattice, as determined previously by first principle calculations on Li4Mn2O5.37 The absence of this shoulder simulated at a charged composition of Li0.5MnO3 is reflected in the observed data at 4.5 V and the reappearance of this feature at the same energy during discharge indicates a high reversibility, in agreement with in operando total scattering data. Note that the apparent shift of the edge to higher energy values during charge is not caused by an increased Mn oxidation state, but instead by the expansion of the spectra on the energy scale due to the contraction of the lattice in accordance with Natoli's rule, and in agreement with the smaller lattice parameter observed from Rietveld refinement.
m models where suitable Li and Mn compositions were randomly distributed on the same site (Fig. 5); these calculations demonstrated that the intensity of the shoulder feature correlates with the amount of Li on the Mn lattice, as determined previously by first principle calculations on Li4Mn2O5.37 The absence of this shoulder simulated at a charged composition of Li0.5MnO3 is reflected in the observed data at 4.5 V and the reappearance of this feature at the same energy during discharge indicates a high reversibility, in agreement with in operando total scattering data. Note that the apparent shift of the edge to higher energy values during charge is not caused by an increased Mn oxidation state, but instead by the expansion of the spectra on the energy scale due to the contraction of the lattice in accordance with Natoli's rule, and in agreement with the smaller lattice parameter observed from Rietveld refinement.
Significant changes of the pre-edge region of the XANES spectra are shown in Fig. 5. In the pristine material, two peaks can be distinguished at 6541 and 6543 eV, which are ∼2 eV apart as expected for the energy gap between the t2g and eg states of a regular octahedral environment. Upon charging, the overall intensity of the pre-edge increases, and the relative intensity between the two peaks gradually changes until they become approximately equal intensity in the charged state. Such an observation points to a reduction in centrosymmetricity of the Mn centres, which become more distorted/irregular during charge. This reduction is centrosymmetricity is completely reversible upon discharge. Since no meaningful differences were apparent between the calculated spectra using R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and Fm
m and Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m models from XANES simulations, only the Fm
m models from XANES simulations, only the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m model, which allowed more facile composition changes to be investigated, was retained for further spectroscopic analyses in the following sections.
m model, which allowed more facile composition changes to be investigated, was retained for further spectroscopic analyses in the following sections.
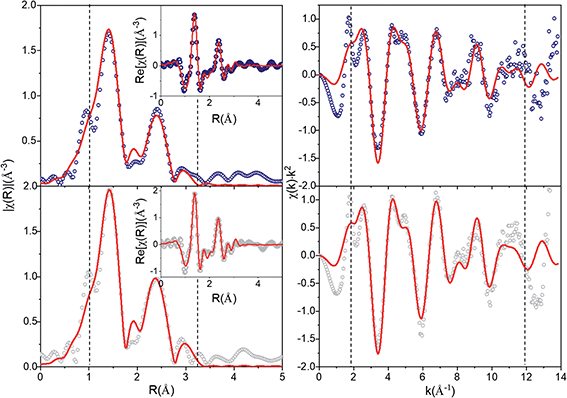
The evolution of the environment around manganese that could be responsible for the changes in the shape and intensity of the HERFD-XANES pre-edge were investigated ex situ using EXAFS collected at the start (pristine) and end of the first charge cycle (charged to 4.5 V). A comparison with in operando data collections is provided in Fig. S6,† showing an excellent agreement. Fig. S7† compares the χ(k) and Fourier transform (FT) χ(r) signals for the pristine and charged to 4.5 V compositions with a significant damping of the higher order shells (>3 Å) in χ(r), a common feature in nanostructured materials (e.g., Li4Mn2O5,37 α-MnO2 (ref. 38)) and attributed to a high degree of structural disorder.
The average structures from Rietveld refinements were used as starting configurations for the least-square fitting of EXAFS data, to quantitatively evaluate short-range order structural parameters. Three single scattering paths including O and Mn shells were refined, while Li shells were not included in the refinement due to the small scattering power of this atom. Interatomic distances (R) and mean square displacements (σ2) were refined for all paths. However, due to the high degree of correlation amongst path degeneracies (Ndegen) and σ2, Ndegen were fixed to known values, which produced a good fit to the data for pristine nano-Li2MnO3 (Rwp = 2.8%, Fig. 6). However, for charged nano-Li2MnO3, Ndegen were fixed to known values for Mn–O and Mn–O2 shells (see Table S1†), while those of Mn–Mn were allowed to vary. The interested reader is referred to Page S14† for a full discussion of the fitting parameters. The refinement of Mn–Mn path degeneracy was key for the obtainment of a good fit for the charged sample. The fit improved from Rwp = 4.6 to 2.9%, when the refined mean path degeneracy varied from 2 in the Rietveld model to 5 ± 2. This result could be correlated to the migration of Mn cations to the vacancies generated by the extraction of ∼1.5 Li per formula unit amounting to 50% of the cations in nano-Li2MnO3. Such an increase in the Mn–Mn path degeneracy will imply the occupation of 25% of the generated cation vacancies by Mn. Cation rearrangement and densification processes are not uncommon amongst positive electrode materials,39 and have been previously reported in other Li–Mn–O systems including crystalline Li2MnO3 (ref. 11) and Li4Mn2O5.37 However, unlike for the non-stoichiometric Li4Mn2O5 rock-salt, no oxygen vacancies are present in stoichiometric nano-Li2MnO3 with a fully occupied cation and oxygen sublattices, where cation densification would imply an effective extraction of Li2O from the material.
A comparison of the refined distances with those from the average model is given in Table S1.† For both samples, refined Mn–Mn and Mn–O distances match those of the average structure within errors, while there is a shortening of the average of Mn–O bond length that amounts to 92% of the expected value, and are in good agreement with Mn–O distances observed in the PDF and expected for these atoms in oxidation states Mn4+ and O2−. A shortening of the Mn–O bonds that could result from the change in the oxidation state of Mn and/or O was detected neither by XPDF nor by EXAFS.
In summary, the evolution of HERDF-XANES and total scattering data measured in operando demonstrated an excellent structural reversibility of the nano-Li2MnO3 cathode during the first (dis)charge cycle with a solid-solution type response allowed by the breathing of a cubic Mn-framework, in agreement with in operando total scattering data evolution. The evolution of the short r-range structure studied by EXAFS, and previously by XPDF, did not show a shortening of Mn–O bonds characteristic of peroxide species with smaller radii, or significant changes in the local structure associated to the formation of ‘peroxo-like’, or peroxo-bridge species during the stabilization of anionic redox processes, but pointed instead to the densification of the cation sublattice. During densification, the migration of Mn cations between two octahedral sites will involve the formation of intermediate stages with Mn in different coordination environments, which will in turn explain the increased pre-edge intensity in Fig. 5. The participating charge compensation mechanisms were studied in depth by X-ray emission spectroscopies, and are discussed in the following section.
Electronic structure evolution during cycling
Note that while the position of the absorption edge or “white line” is commonly used as an indication of the oxidation state, its shape is strongly influenced by structural effects leading to large inaccuracies. We have instead determine the oxidation state of Mn with greater precision from the position of the kβ1,3 transition, as explained in the following section.Redox processes were investigated through in operando XES by the combined interpretation of main (kβ′ and kβ1,3) and V2C (kβ′′ and kβ2,3) transitions (Fig. 7). The kβ emission of first row TMs can be explained as a two-step process represented by the schematic diagram in Fig. 7a. The different chemical selectivity of main kβ and V2C to manganese and oxygen respectively, makes XES a powerful tool to investigate the electrochemical activity of Li-rich cathode materials with capacities beyond those expected from TM redox. The use of hard X-rays in XES or Resonant Inelastic X-ray Scattering (RIXS) provides bulk structural information, unlike techniques employing soft X-rays (e.g., XPS, or light elements K-absorption edges) which are only sensitive to surface atoms and require high vacuum compatible sample environments. In addition, V2C combines both bulk sensitivity and selectivity to the detect exclusively the O bound to Mn in the active material; unlike RIXS, V2C measurements eliminate possible contamination of the spectroscopy signal with oxygen in other components of the battery, like the cell case or electrolyte. In operando XES data was collected using a conventional cell for XAS experiments equipped with a beryllium window.37 While advanced spectroscopic measurements including HERFD-XANES and XES have been previously applied to the in operando characterizations of catalysts,40 the present work constitutes the first in operando XES (main kβ and V2C transitions) study of Li-ion batteries.
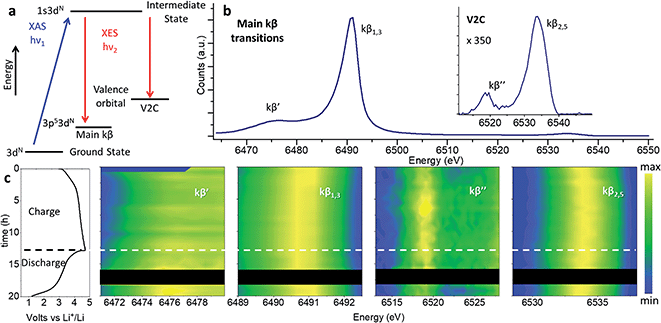 | ||
| Fig. 7 Nano-Li2MnO3 charge evolution with cycling characterized by in operando XES. (a) Two-step energy schematic of main kβ and V2C transitions. (b) Whole energy range spectra for pristine nano-Li2MnO3. (c) From left to right: electrochemical performance and contour plots of the magnified energy regions for kβ′, kβ1,3, kβ′′ and kβ2,5 transitions. Curve-fitted kβ′, kβ1,3, kβ′′ and kβ2,5 energies and integrated intensities are introduced in Fig. S10.† | ||
Previously we demonstrated the use of main kβ transitions are a more accurate indication of the Mn oxidation state than XANES 1s–4p energy transitions.37 The 3p orbitals lay deeper within the electronic shells, and as such are less dependent on structural effects than the 1s–4p transition probed at the Mn absorption K-edge. In main kβ XES, the number of unpaired 3d electrons can be indirectly inferred from magnitude of 3p–3d exchange interactions (proportional to the number of unpaired 3d electrons), given by the difference between kβ′ and kβ1,3 transitions. We use the comparison of the most intense kβ1,3 transition with those of Mn oxides with well-known oxidation states in Fig. S8 and S9† as a gauge of Mn oxidation state at different states of charge.
The main kβ spectra of pristine nano-Li2MnO3, as the HERFD-XANES discussed above and the V2C spectra below, are in good agreement with the MnO2 data with the same oxidation state of manganese. During charge, a shift of kβ1,3 transition towards lower energy values is observed that is fully reversed during discharge, in agreement with the good structural reversibility observed for the in operando total scattering and HERFD-XANES data. Note the subtle variation of kβ1,3 energy is the only difference between the spectra, and the integrated intensities for kβ′ and kβ1,3, and the kβ′ energy transition remain constant during battery cycling (see Fig. S10†). As well as the number of unpaired 3d electrons, the magnitude of the 3p–3d exchange interaction depends also on the spin state and the covalency/charge-transfer contribution effects which are expected to change when chemical environment around MnO6 centres is modified during cell (dis)charge. Due to the lower magnitude of the kβ1,3 shift, in comparison to the more significant differences observed when the oxidation state of Mn is varied across the different standards, this subtle energy variation was attributed to changes in the Mn–O covalency that accompany the slight shortening of Mn–O bonds during charge by ∼0.02 Å observed by PDF. Therefore, this analysis indicates manganese remains at a constant state of Mn4+, but changes of the Mn–O covalency occur during charge and discharge processes.
Mn–O interactions were further investigated by V2C spectroscopy (including lower kβ′′ and higher kβ2,5 energy transitions) which has a high sensitivity to the chemical environment around Mn centres. The energy separation between kβ′′ and kβ2,5 transitions is determined by the binding energy difference between ligand-s and -p orbitals, and their intensities reflect the degree of hybridization between ligand and TM p states.41 The lower energy kβ′′ transition, which originates from ligand s molecular orbitals to TM p states, is a valuable tool for ligand identification. The energy of this kβ′′ transition depends on the difference between the ligand-2s and TM-1s binding energies, and reflects the spatial overlap between ligand 2s and TM 4p/3d molecular orbitals. The kβ′′ intensity is affected by the TM-ligand distance and by the coordination number of the TM. Shorter distances (e.g. from higher bond order or deprotonation) result in increased kβ′′ intensity, with an approximate exponential dependence on distance.42 Thus, the evolution of the kβ′′ transition during cycling is able to detect changes in the charge density on the metal (Mn), ligand (O) protonation, and changes in the coordination environment of the ligand. The higher energy and more intense kβ2,5 originates from the transition of electrons in an occupied valence molecular orbital with mainly ligand-p and metal-p contributions (see Fig. S11†). The evolution of this signal during cycling signifies changes in the valence orbitals and TM-ligand chemical bond nature.
The evolution of kβ2,5 and kβ′′ transitions with electrochemical cycling of nano-LiMn2O3 are given in Fig. 7. Very small changes of the peak position and intensities were observed upon cycling, which were particularly small in comparison with the much larger changes between the spectra of standard compounds of Mn in different oxidation states. During charge, the kβ2,5 transition increased in energy by ∼0.5 eV with a concurrent increase of 5% in the integrated intensity; these changes was fully reversed during discharge. No significant change in the kβ′′ transition was identified by curve-fitting (Fig. S10†).
The V2C spectra were simulated using a 2 × 2 × 2 supercell of composition Li21Mn11O32 built from the expansion of the proposed average model from Rietveld where the lattice parameters have been refined with a high accuracy (acubic = 4.0741(2) Å), and Mn–O distances were relaxed to ∼1.9 Å to match the values proposed from XPDF and EXAFS analyses (Fig. S12†). These simulations reproduced the main V2C spectral features for pristine nano-Li2MnO3. Minor changes were observed in the V2C spectra during cycling, which we evaluate along with input from other observations in the following section.
Evaluating possible charge compensation mechanisms
The combination of observations from the above techniques allows for possible charge compensation mechanisms to be compared and appraised as an alternative to the unfavourable evolution of octahedrally coordinated manganese from Mn4+ to Mn5+/7+.43 Here we evaluate four proposed hypotheses of plausible charge compensation mechanisms in nano-Li2MnO3: (i) lattice densification, (ii) formation of hydroxyl groups (–OH), (iii) trapping of positively charged hydronium molecules (H3O+), and (iv) anionic redox.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mn ratio of 1
Mn ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
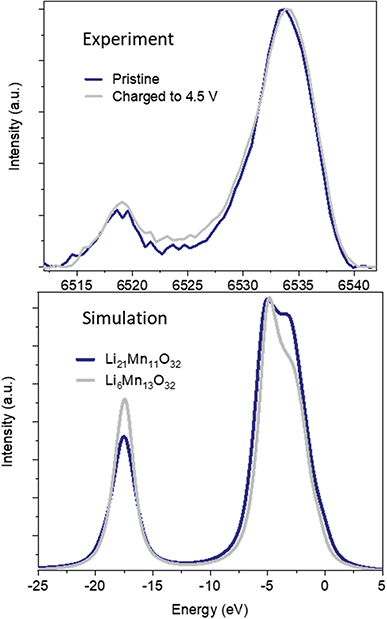
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 based on the ratio proposed by electrochemistry and ICP analyses. The V2C simulation of such model (Li5Mn10O32), with ∼50% cation vacancies is given in Fig. S12.† Additionally, 23% of the cation vacancies were removed from Li5Mn10O32 in a second ‘densified’ model (Li6Mn13O32) matching the Mn–Mn path degeneracies suggested by EXAFS. Such a structural modification will imply the effective loss of 25% of oxygen in nano-Li2MnO3 with the effective extraction of Li2O following the reaction:
2 based on the ratio proposed by electrochemistry and ICP analyses. The V2C simulation of such model (Li5Mn10O32), with ∼50% cation vacancies is given in Fig. S12.† Additionally, 23% of the cation vacancies were removed from Li5Mn10O32 in a second ‘densified’ model (Li6Mn13O32) matching the Mn–Mn path degeneracies suggested by EXAFS. Such a structural modification will imply the effective loss of 25% of oxygen in nano-Li2MnO3 with the effective extraction of Li2O following the reaction:| Li2MnO3 → 0.75Li2/3□Mn4/3O3 + 0.75Li2O | (1) |
The comparison between V2C simulations of ‘undensified’ Li5Mn10O32 and densified Li6Mn13O32 in Fig. S12† shows a shift of the kβ′′ and kβ2,5 transitions to higher energies for the ‘undensified’ composition by approximately 0.5 and 1 eV. This trend is also observed for Mn standards, where kβ′′ and kβ2,5 transitions shift also by 0.5–1 eV to higher energies with the increased oxidation state of manganese, and is consistent with the higher oxidation state of Mn expected for the undensified model vs. the densified one. The different energy transitions between pristine and the undensified models are not experimentally observed and a much better agreement is obtained with the densified model based on EXAFS refined path degeneracies. Additionally, the lower intensity of the kβ′′ transition in the undensified model correlated to the lower number of Mn neighbours around oxygen in this model, is opposite to the experimental observation with a small 5% increase of the kβ′′ intensity.
The V2C spectral signature of trapped H3O+ molecule was evaluated by the simulation of V2C spectra from structural models for α-MnO2 reported in the literature with/without H3O+ in Fig. S14.† These simulations show a small increase in of the kβ′′ intensity, compatible with the 5% increase of the integrated intensity observed for this transition during cycling of nano-Li2MnO3. Similarly-sized one-dimensional tunnels to those present for α-MnO2 2 × 2 (0.46 × 0.46 nm2), with only a slightly smaller surface of 0.44 × 0.44 nm2, are formed as a result of the extraction of lithium in nano-Li2MnO3; the surface of these voids could be further enlarged by the displacement of Mn cations away from their average positions. The large concentration of voids in charged nano-Li2MnO3 generated from the extraction of lithium could potentially host H3O+ molecules originated from electrolyte decomposition, where trapped H3O+ molecules compensate part of the charge exchanged upon charging following the reaction in eqn (2).
| Li2MnO3 + xH3O+ → (H3O)xLi2−xMnO3 + xLi+ | (2) |
The participation of eqn (2) in the charge compensation of nano-Li2MnO3 (if any) is expected to be small, based on the reported concentration of these molecules previously reached in α-MnO2 with a H3O+ to Mn ratio of 0.15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. This amounts to only 10% of the 1.5 electrons per formula unit extracted over the course of the first charge. The corroboration and quantification of this charge compensation mechanism to the overall capacity could not be accurately determined by the techniques used in this work, and requires follow-up H-NMR studies.
1. This amounts to only 10% of the 1.5 electrons per formula unit extracted over the course of the first charge. The corroboration and quantification of this charge compensation mechanism to the overall capacity could not be accurately determined by the techniques used in this work, and requires follow-up H-NMR studies.
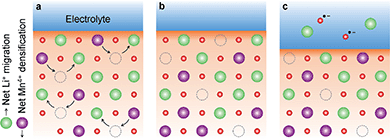
From the results above, the best agreement between proposed charge compensation mechanism and observed experimental data (XPDF, EXAFS and V2C) is given by the densified model, as shown in Fig. 8 (and Table S2†). The proposed densification of the Mn sublattice implies the loss of Li2O during the cathode charge, and has been previously reported in other cathode materials within the LiMnO system.54,55 However, unlike previous studies, the cation densification could not be linked to unfavourable anionic redox that result in the formation of evolving O2(g) or O˙− radicals that in turn react with the electrolyte to produce LiOH, Li2O2 or Li2CO3 secondary phases associated with capacity drop and structural instability. The absence of undesirable secondary phases in nano-Li2MnO3 could be the origin of the large structural reversibility and reversible charge capacity of over 290 mA h g−1.
Discussion
This comprehensive study utilising multiple techniques with different chemical and lenghtscale sensitivities have provided an unequivocal answer: no oxygen or manganese redox reactions in the bulk material or structural transitions are responsible for the charge compensation in nano-Li2MnO3. Instead, the observation of lattice densification points to the reversible extraction and reinsertion of Li2O in nano-Li2MnO3. The absence of a Li2O secondary phase in our data is indicative of the electrochemical activation of this compound as the main charge compensation mechanism responsible for the reversible capacity in nano-Li2MnO3 (see Fig. 9). This observation is in agreement with the recently reported ability of nanostructured Li–Mn–O disordered rock-salts to catalyse the electrochemical activation of Li2O in Li2O:Li–Mn–O nanocomposites56 with superior first charge capacities (>1100 mA h g−1) following the reactions: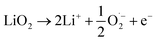 | (3) |
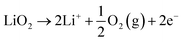 | (4) |
The reaction of highly reactive oxygen radicals formed in eqn (3) with the electrolyte at the electrode surface is known to generate C2O62− ions, and finally form57 Li2CO3 at the cathode surface, which causes serious problems in the cycling reversibility and repeatability as often reported for Li–O2 batteries.14,58 Here, the absence of Li2CO3 or other electrolyte decompositions products during cycling could be linked to the higher cycling reversibility of nano-Li2MnO3, where C2O62− ions could be stabilized at the surface of nano-Li2MnO3, acting as an oxygen reservoir during discharge.
The formation of molecular O2 in eqn (4) has been frequently associated with capacity losses and compositional changes on Li-rich cathode materials. Recently, House et al.59 have identified reversible bulk O-redox reactions forming molecular O2 inside Na0.75[Li0.25Mn0.75]O2 cathodes with a ribbon superstructure. During charge, the O2 molecules are trapped in the vacancy clusters formed as a results of the Li-extraction and have no mechanism of diffusing to the surface; and during discharge, the trapped O2 molecules may be cleaved, enabling reversible capacities.
Therefore, both (i) the stabilization of C2O62− ions at the surface of the nano-Li2MnO3 cathode; or (ii) the trapping of O2 molecules in vacancy clusters could be plausible charge compensation mechanisms responsible for the absence of significant formation of secondary phases at the cathode interface or electrolyte degradation during the first cycle. Further studies are needed to clarify the contribution of eqn (3) or (4), and charge compensations (i) or (ii) to the reversible electrochemical activation of Li2O.
Note the ability to reverse the Li2O formation reaction in nano-Li2MnO3 with such a large efficacy (∼97% of coulombic efficiency during the first cycle) is an unprecedented observation for Li2MnO3 or other Li-rich cathodes. Since Li2O is the ultimate discharged product of a Li–O cell or a hybrid Li-ion/Li–O2 cell,60 the possibility to reverse the formation of Li2O by the reversible oxidative decomposition of the electrolyte is a desirable feature previously explored in other lithium metal oxides. This is the case of Li5FeO4 (5Li2O·Fe2O3)60 and Li6MO4 (3Li2O·MO, M = Mn, Co)61 compounds with an antifluorite-type structure, CaFeO3,62 Ca1−xLaxFeO3−δ,63 Li(4−x)/3Ti(2−2x)/3FexO2, SrMO3−δ (M = Co, Fe),64 and Bi2Fe4O9 (ref. 65) electrodes when used in aprotic lithium or sodium cells.
Our results showed that, contrary to the general assumption that extra capacities of cation-disordered rock salts are mediated by bulk anionic redox reactions, nano-Li2MnO3 acts as an activator to catalyse the reversible formation of electrochemically active Li2O. The use of full structural (and not just average structural) probes, as well as bulk probes of anionic redox sensitive to only the oxygen bounds to Mn, avoids issues of surface sensitivity of XPS and soft-XAS, which are also sensitive to any other oxygen containing phases like the electrolyte. Based on the success of these techniques to characterize in operando and with excellent time resolution and data quality these bulk structural phenomena, the introduced methods should be used to revisit the characterisation of other high capacity cathodes with bulk anionic redox process have been based on TEM, TM K-edge EXAFS, average structure, XPS or DFT calculations, to find conclusive evidence of such reactions.
We further explore the similarities between nano-Li2MnO3 and other nanostructured Li–Mn–O cathodes, namely Li4Mn2O5. In operando Bragg data of the Li4Mn2O5 cathode charged to 4.5 V revealed the appearance of broad reflections unindexed by the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group (see Fig. S16†) that were attributed to unidentified impurities in previous work.66 The comparison between Fig. 1 and S16† indicates the origin of the diffuse reflections in charged Li4Mn2O5 could be instead linked to the formation of a short-range ordered superstructure during cycling. In addition, previous studies of Li4Mn2O5 combining main kβ transitions, XANES and EXAFS showed Mn3+ irreversibly oxidizes to Mn4+ during the first charge.37 Therefore, Li4Mn2O5 could be transformed into a ‘nano-Li2MnO3 like' material (i.e., with nanodomains of Li/Mn layering and Mn4+) that cycles reversibly between charged and discharged states with a constant oxidation state of Mn4+ and charge compensation could be allowed by the reversible formation of Li2O. Even though Li-rich cation disordered rock-salts are generally associated with the absence of structural transformation during cycling, the chemical ordering observed during charging of Li4Mn2O5 warrants further investigations into the chemical ordering of other cation disordered rock-salts showing diffuse nature peaks in their pristine state like Li1.25Nb0.25Mn0.5O2,67,68 Li1.2Ti0.4Mn0.4O2,24,69 or Li1.2Mn0.4Zr0.4O2.69
m space group (see Fig. S16†) that were attributed to unidentified impurities in previous work.66 The comparison between Fig. 1 and S16† indicates the origin of the diffuse reflections in charged Li4Mn2O5 could be instead linked to the formation of a short-range ordered superstructure during cycling. In addition, previous studies of Li4Mn2O5 combining main kβ transitions, XANES and EXAFS showed Mn3+ irreversibly oxidizes to Mn4+ during the first charge.37 Therefore, Li4Mn2O5 could be transformed into a ‘nano-Li2MnO3 like' material (i.e., with nanodomains of Li/Mn layering and Mn4+) that cycles reversibly between charged and discharged states with a constant oxidation state of Mn4+ and charge compensation could be allowed by the reversible formation of Li2O. Even though Li-rich cation disordered rock-salts are generally associated with the absence of structural transformation during cycling, the chemical ordering observed during charging of Li4Mn2O5 warrants further investigations into the chemical ordering of other cation disordered rock-salts showing diffuse nature peaks in their pristine state like Li1.25Nb0.25Mn0.5O2,67,68 Li1.2Ti0.4Mn0.4O2,24,69 or Li1.2Mn0.4Zr0.4O2.69
Conclusion
This work has determined the true average structure of nano-Li2MnO3 as a cubic superstructure with short-range layered ordering in space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. This ordering has been observed in similar systems, such as LixNi2−xO2,32 or charged Li4−xMn2O5 compositions.66 With respect to previous reports, we have determined there is no unfavourable phase transformations during cycling, in agreement with the absence of the characteristic plateau originated from phase transitions in the electrochemical curve. The large reversible capacity in nano-Li2MnO3 is consistent with the high structural reversibility from total scattering and XAS studies carried out under in operando conditions. The combination of total scattering, absorption and emission spectroscopy has ruled out O2−/O−, O2−/O1.5−, Mn4+/Mn5+/7+ (ref. 43) redox or oxygen protonation reactions as suitable mechanisms of charge compensation, and provides a clear evidence of the densification of the Mn-sublattice. The main charge compensation responsible for the extraordinary capacity reversibility in nano-Li2MnO3 is the electrochemical activation of Li2O, with the subsequent stabilization of oxygen radicals at the cathode surface and/or trapping of O2 molecules within the vacancy clusters. The cathode nanostructuration permits reversible reactions with Li2O in a controlled manner with high cycling and structural reversibility. Unlike for microstructured cathodes, where compositional changes or decomposition products such as Li2CO3 or Li2O2 have been ascribed to capacity fading and battery performance deterioration. Other charge compensations mechanisms, with a minor contribution to the overall charge exchanged like the substitution of H3O+ for Li+ should be further investigated by H-NMR.
m. This ordering has been observed in similar systems, such as LixNi2−xO2,32 or charged Li4−xMn2O5 compositions.66 With respect to previous reports, we have determined there is no unfavourable phase transformations during cycling, in agreement with the absence of the characteristic plateau originated from phase transitions in the electrochemical curve. The large reversible capacity in nano-Li2MnO3 is consistent with the high structural reversibility from total scattering and XAS studies carried out under in operando conditions. The combination of total scattering, absorption and emission spectroscopy has ruled out O2−/O−, O2−/O1.5−, Mn4+/Mn5+/7+ (ref. 43) redox or oxygen protonation reactions as suitable mechanisms of charge compensation, and provides a clear evidence of the densification of the Mn-sublattice. The main charge compensation responsible for the extraordinary capacity reversibility in nano-Li2MnO3 is the electrochemical activation of Li2O, with the subsequent stabilization of oxygen radicals at the cathode surface and/or trapping of O2 molecules within the vacancy clusters. The cathode nanostructuration permits reversible reactions with Li2O in a controlled manner with high cycling and structural reversibility. Unlike for microstructured cathodes, where compositional changes or decomposition products such as Li2CO3 or Li2O2 have been ascribed to capacity fading and battery performance deterioration. Other charge compensations mechanisms, with a minor contribution to the overall charge exchanged like the substitution of H3O+ for Li+ should be further investigated by H-NMR.
The full understanding of the charge compensation in nano-Li2MnO3 was possible thanks to hard X-rays techniques in XES that provide bulk structural information in operando; techniques employing soft X-rays (e.g. XPS, or light elements K-absorption edges) may not provide such rich information due to their surface-sensitivity and the requirement for high vacuum environments which may compromise the observed electrochemistry.70–73
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge Jean Justine at CRISMAT for technical assistance, Dr James M. Ablet and Dr Jean Pascal Rueff for support during beamtime at GALAXIES-Soleil, Dr Henry Fischer for support during beamtime at D4c-ILL and Diamond Light Source for beamtime under proposals EE20893 and EE20094.References
- K. Ozawa, Solid State Ionics, 1994, 69, 212 CrossRef CAS.
- H. Noh, S. Youn, C. Seung and Y. Sun, J. Power Sources, 2013, 233, 2 CrossRef.
- H. Yu and H. Zhou, J. Phys. Chem. Lett., 2013, 4, 1268 CrossRef CAS PubMed.
- C. S. Johnson, N. Li, C. Lefief and M. M. Thackeray, Electrochem. Commun., 2007, 9, 787 CrossRef CAS.
- A. R. Armstrong, A. D. Robertson and P. G. Bruce, J. Power Sources, 2005, 146, 275 CrossRef CAS.
- A. D. Robertson and P. G. Bruce, Chem. Commun., 2002, 2790 RSC.
- R. Benedek, M. M. Thackeray and A. Van De Walle, Chem. Mater., 2008, 5485 CrossRef CAS.
- A. D. Robertson and P. G. Bruce, Chem. Mater., 2003, 1984 CrossRef CAS.
- R. Xiao, H. Li and L. Chen, Chem. Mater., 2012, 24, 4242 CrossRef CAS.
- H. Chen and M. S. Islam, Chem. Mater., 2016, 28, 6656 CrossRef CAS.
- D. Y. W. Yu, K. Yanagida, Y. Kato and H. Nakamura, J. Electrochem. Soc., 2009, 156, A417 CrossRef CAS.
- K. Shimoda, M. Oishi, T. Matsunaga, M. Murakami, K. Yamanaka, H. Arai, Y. Ukyo, Y. Uchimoto, T. Ohta, E. Matsubara and Z. Ogumi, J. Mater. Chem. A, 2017, 5, 6695 RSC.
- A. R. Armstrong, M. Holzapfel, P. Novák, C. S. Johnson, S. H. Kang, M. M. Thackeray and P. G. Bruce, J. Am. Chem. Soc., 2006, 128, 8694 CrossRef CAS PubMed.
- S. A. Freunberger, Y. Chen, Z. Peng, J. M. Gri, L. J. Hardwick, P. Nov and P. G. Bruce, J. Am. Chem. Soc., 2011, 133, 8040 CrossRef CAS PubMed.
- J.-K. Noh, S. Kim, H. Kim, W. Choi, W. Chang, D. Byun, B.-W. Cho and K. Yoon, Sci. Rep., 2014, 2, 1 Search PubMed.
- S. Zhao, B. Sun, K. Yan, J. Zhang, C. Wang and G. Wang, ACS Appl. Mater. Interfaces, 2018, 10, 33260 CrossRef CAS PubMed.
- D. Mori, H. Kobayashi, T. Okumura, H. Nitani, M. Ogawa and Y. Inaguma, Solid State Ionics, 2016, 285, 66 CrossRef CAS.
- E. McCalla, A. M. Abakumov, M. Saubanère, D. Foix, E. J. Berg, G. Rousse, M.-L. Doublet, D. Gonbeau, P. Novák, G. Van Tendeloo, R. Dominko and J.-M. Tarascon, Science, 2015, 350, 1516 CrossRef CAS PubMed.
- J. Hong, W. E. Gent, P. Xiao, K. Lim, D. Seo, J. Wu, P. M. Csernica, C. J. Takacs, D. Nordlund, C. Sun, K. H. Stone, D. Passarello, W. Yang, D. Prendergast, G. Ceder, M. F. Toney and W. C. Chueh, Nat. Mater., 2019, 18, 256 CrossRef CAS PubMed.
- R. Chen, S. Ren, M. Yavuz, A. A. Guda, V. Shapovalov, R. Witter and H. Hahn, Phys. Chem. Chem. Phys., 2015, 17, 17288 RSC.
- N. Takeda, S. Hoshino, L. Xie, S. Chen, I. Ikeuchi, R. Natsui, K. Nakura and N. Yabuuchi, J. Power Sources, 2017, 367, 122 CrossRef CAS.
- J. Lee, D. A. Kitchaev, D. Kwon, C. Lee, J. K. Papp, Y. Liu and Z. Lun, Nature, 2018, 556, 185 CrossRef CAS PubMed.
- N. Yabuuchi, M. Takeuchi, M. Nakayama, H. Shiiba, M. Ogawa, K. Nakayama, T. Ohta, D. Endo, T. Ozaki, T. Inamasu, K. Sato and S. Komaba, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 7650 CrossRef CAS PubMed.
- B. Huang, R. Wang, Y. Gong, B. He and H. Wang, Front. Chem., 2019, 7, 1 CrossRef PubMed.
- M. Freire, N. V. Kosova, C. Jordy, D. Chateigner, O. I. Lebedev, A. Maignan and V. Pralong, Nat. Mater., 2015, 15, 1 Search PubMed.
- M. Freire, O. I. Lebedev, A. Maignan, C. Jordy and V. Pralong, J. Mater. Chem. A, 2017, 21898 RSC.
- M. Oishi, K. Yamanaka, I. Watanabe, K. Shimoda, T. Matsunaga, H. Arai, Y. Ukyo, Y. Uchimoto, Z. Ogumi and T. Ohta, J. Mater. Chem. A, 2016, 4, 9293 RSC.
- G. Assat, A. Iadecola, C. Delacourt, R. Dedryvère and J. M. Tarascon, Chem. Mater., 2017, 29, 9714 CrossRef CAS.
- A. J. Perez, D. Batuk, M. Saubanère, G. Rousse, D. Foix, E. Mccalla, E. J. Berg, R. Dugas, K. H. W. Van Den Bos, M. Doublet, D. Gonbeau, A. M. Abakumov, G. Van Tendeloo and J. Tarascon, Chem. Mater., 2016, 10, 8278 CrossRef.
- A. J. Perez, Q. Jacquet, D. Batuk, A. Iadecola, M. Saubanère, G. Rousse, D. Larcher, H. Vezin and M. Doublet, Nat. Energy, 2020, 2, 954 CrossRef.
- P. E. Pearce, A. J. Perez, G. Rousse, M. Saubanère, D. Batuk, D. Foix, E. McCalla, A. M. Abakumov, G. Van Tendeloo, M. L. Doublet and J. M. Tarascon, Nat. Mater., 2017, 16, 580 CrossRef CAS PubMed.
- P. T. Barton, Y. D. Premchand, P. A. Chater, R. Seshadri and M. J. Rosseinsky, Chem.–Eur. J., 2013, 14521 CrossRef CAS PubMed.
- D. Balzar, N. Audebrand, M. R. Daymond, A. Fitch, A. Hewat, J. I. Langford, A. Le Bail, D. Louer, O. Masson, C. N. McCowan, N. C. Popa, P. W. Stephens and B. H. Toby, J. Appl. Crystallogr., 2004, 37, 911 CrossRef CAS.
- M. G. Tucker, D. A. Keen, M. T. Dove, A. L. Goodwin and Q. Hui, J. Phys.: Condens. Matter, 2007, 19, 335218 CrossRef PubMed.
- S. F. Amalraj, L. Burlaka, C. M. Julien, A. Mauger, D. Kovacheva, M. Talianker, B. Markovsky and D. Aurbach, Electrochim. Acta, 2014, 123, 395 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., 1976, 32, 751 CrossRef.
- M. Diaz-lopez, Y. Joly, M. Freire, C. Colin, O. Proux, V. Pralong and P. Bordet, J. Phys. Chem. C, 2018, 122, 29586 CrossRef CAS.
- S. Kobayashi, I. R. M. Kottegoda, Y. Uchimoto and M. Wakihara, J. Mater. Chem., 2004, 1, 1843 RSC.
- N. Tran, L. Croguennec, M. Mènètrier, F. Weill, P. Biensan, C. Jordy and C. Delmas, Chem. Mater., 2008, 20, 4815 CrossRef CAS.
- B. M. Weckhuysen, Chem. Soc. Rev., 2010, 39, 4754 RSC.
- G. E. Cutsail, N. L. Gagnon, A. D. Spaeth, W. B. Tolman and S. Debeer, Angew. Chem., Int. Ed., 2019, 2, 9114 CrossRef PubMed.
- U. Bergmann, C. R. Horne, T. J. Collins, J. M. Workman and S. P. Cramer, Chem. Phys. Lett., 1999, 302, 119 CrossRef CAS.
- M. D. Radin, J. Vinckeviciute, R. Seshadri and A. Van Der Ven, Nat. Energy, 2019, 4, 639–646 CrossRef CAS.
- A. I. Palos, M. Anne and P. Strobel, J. Solid State Chem., 2001, 117, 108 CrossRef.
- C. M. Fang and G. A. De Wijs, Chem. Mater., 2006, 18, 1169 CrossRef CAS.
- B. Ammundsen, D. J. Jones, J. Rozie, L. Agre, H. Berg, R. Tellgren and J. O. Thomas, Chem. Mater., 1998, 10, 1680 CrossRef CAS.
- N. Lee, T. Petrenko, U. Bergmann, F. Neese and S. Debeer, J. Am. Chem. Soc., 2010, 132, 9715 CrossRef CAS PubMed.
- B. Lassalle-kaiser, T. T. B. Iii, V. Krewald, J. Kern, M. A. Beckwith, M. U. Delgado-jaime, H. Schroeder, R. Alonso-mori, D. Nordlund, T. Weng, D. Sokaras, F. Neese, U. Bergmann, V. K. Yachandra, S. Debeer, V. L. Pecoraro and J. Yano, Inorg. Chem., 2013, 52, 12915 CrossRef CAS PubMed.
- L. M. Housel, L. Wang, A. Abraham, J. Huang, G. D. Renderos, C. D. Quilty, A. B. Brady, A. C. Marschilok, K. J. Takeuchi and E. S. Takeuchi, Acc. Chem. Res., 2018, 51, 575 CrossRef CAS PubMed.
- M. H. Rossouw, D. C. Liles and M. M. Thackeray, Mater. Res. Bull., 1992, 27, 221 CrossRef CAS.
- N. Kijima, Ã. T. Ikeda, K. Oikawa, F. Izumi and Y. Yoshimura, J. Solid State Chem., 2004, 177, 1258 CrossRef CAS.
- Y. Pushkar, X. Long, P. Glatzel, G. W. Brudvig, G. C. Dismukes, T. J. Collins, V. K. Yachandra, J. Yano and U. Bergmann, Angew. Chem., Int. Ed., 2010, 49, 800 CrossRef CAS PubMed.
- J. A. Rees, V. Martin-diaconescu, J. A. Kovacs and S. Debeer, Inorg. Chem., 2015, 54, 6410 CrossRef CAS PubMed.
- M. M. Thackeray, S.-H. Kang, C. S. Johnson, J. T. Vaughey, R. Benedek and S. A. Hackney, J. Mater. Chem., 2007, 17, 3112 RSC.
- S. Hy, F. Felix, J. Rick, W. Su and B. J. Hwang, J. Am. Chem. Soc., 2014, 999–1007 CrossRef CAS PubMed.
- M. Diaz-Lopez, P. A. Chater, P. Bordet, M. Freire, C. Jordy, O. I. Lebedev and V. Pralong, Adv. Energy Mater., 2020, 10, 1902788 CrossRef CAS.
- J. Hong, H. Lim, M. Lee, S. Kim, H. Kim, S. Oh, G. Chung and K. Kang, Chem. Mater., 2012, 24, 2692 CrossRef CAS.
- M. M. O. Thotiyl, S. A. Freunberger, Z. Peng and P. G. Bruce, J. Am. Chem. Soc., 2013, 135, 494 CrossRef PubMed.
- R. A. House, U. Maitra, M. A. Pérez-osorio, J. G. Lozano, L. Jin, J. W. Somerville, L. C. Duda, A. Nag, A. Walters, K. Zhou, M. R. Roberts and P. G. Bruce, Nature, 2020, 577, 502 CrossRef CAS PubMed.
- M. M. Thackeray, M. K. Y. Chan, L. Trahey, S. Kirklin and C. Wolverton, J. Phys. Chem. Lett., 2013, 4, 3607 CrossRef CAS.
- Y. Lim, D. Kim, J. Lim, J. Kim, J. Yu, Y. Kim, D. Byun, M. Cho, K. Cho and M. Park, J. Mater. Chem. A, 2015, 3, 12377 RSC.
- M. Hibino, R. Harimoto, Y. Ogasawara, R. Kido, A. Sugahara, T. Kudo, E. Tochigi, N. Shibata, Y. Ikuhara and N. Mizuno, J. Am. Chem. Soc., 2014, 136, 488 CrossRef CAS PubMed.
- M. Hibino, T. Kimura, Y. Suga, T. Kudo and N. Mizuno, Sci. Rep., 2012, 2, 601 CrossRef PubMed.
- Y. Ogasawara, M. Hibino, T. Kudo and N. Mizuno, J. Electrochem. Soc., 2014, 161, 792 CrossRef.
- M. Liu, C. Lin, Y. Gu, T. Yang, Z. Gong, G. Yin, X. Gao, X. Zhou and W. Wen, J. Phys. Chem. C, 2019, 118, 14711 CrossRef.
- M. Freire, M. Diaz-Lopez, P. Bordet, C. V. Colin, O. I. Lebedev, N. V. Kosova, C. Jordy, D. Chateigner, A. L. Chuvilin, A. Maignan and V. Pralong, J. Mater. Chem. A, 2018, 6, 5156 RSC.
- R. Wang, X. Li, L. Liu, J. Lee, D. Seo, S. Bo, A. Urban and G. Ceder, Electrochem. Commun., 2015, 60, 70 CrossRef CAS.
- M. A. Jones, P. J. Reeves, I. D. Seymour, M. J. Cliffe, S. E. Dutton and C. P. Grey, Chem. Commun., 2019, 55, 9027 RSC.
- H. Ji, A. Urban, D. A. Kitchaev, D. Kwon, N. Artrith, C. Ophus, W. Huang, Z. Cai, T. Shi, J. C. Kim, H. Kim and G. Ceder, Nat. Commun., 2019, 10, 592 CrossRef CAS PubMed.
- Y.-C. Lu, E. J. Crumlin, G. M. Veith, J. R. Harding, E. Mutoro, L. Baggetto, N. J. Dudney, L. Zhi and Y. Shao-Horn, Sci. Rep., 2012, 2, 7015 Search PubMed.
- E. J. Crumlin, H. Bluhm and Z. Liu, J. Electron Spectrosc. Relat. Phenom., 2013, 190, 84 CrossRef CAS.
- N. J. Dudney, Z. Liu and Y. Shao-horn, J. Phys. Chem. C, 2013, 117, 25948 CrossRef.
- J. Maibach, C. Xu, S. K. Eriksson, J. Åhlund, T. Gustafsson, H. Siegbahn, H. Rensmo, K. Edström and M. Hahlin, Rev. Sci. Instrum., 2015, 86, 044101 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ta03372c |
| This journal is © The Royal Society of Chemistry 2020 |