Open Access Article
Open Access ArticleThe favourable thermodynamic properties of Fe-doped CaMnO3 for thermochemical heat storage†
Emanuela
Mastronardo
 *ab,
Xin
Qian
*ab,
Xin
Qian
 b,
Juan M.
Coronado
b,
Juan M.
Coronado
 a and
Sossina M.
Haile
b
a and
Sossina M.
Haile
b
aInstitute of Catalysis and Petrochemistry, Spanish National Research Council (CSIC), C/ Marie Curie, 2. E-28049, Madrid, Spain. E-mail: e.mastronardo@csic.es
bMaterials Science and Engineering, Northwestern University, 2220 Campus Drive Cook Hall, 60208 Evanston, IL, USA
First published on 10th April 2020
Abstract
The CaMnO3 oxide can reversibly release oxygen over a relatively wide range of temperatures and oxygen partial pressures (pO2) and is thus a promising candidate for thermochemical heat storage in Concentrated Solar Power (CSP) plants. Moreover, it is composed of earth-abundant, inexpensive and non-toxic elements and exhibits a high-energy storage density, which are desirable characteristics for decreasing the deployment costs of the system. However, it undergoes decomposition at pO2 ≤ 0.008 atm and temperature ≥ 1100 °C. Here the possibility of overcoming this limitation and extending the operating temperature range by B-site doping with Fe (CaFexMn1−xO3−δ0) is explored. Two doping levels are investigated, x = 0.1 and 0.3. The enthalpy of reduction was determined from a measurement of continuous equilibrium non-stoichiometry curves (δ, T) at several pO2, enabling an evaluation of the heat storage capacity with high accuracy over widely ranging oxygen non-stoichiometry. Introduction of 0.1 Fe (CaFe0.1Mn0.9O3−δ0) prevented CaMnO3 decomposition up to 1200 °C at pO2 = 0.008 atm, thus widening the operating temperature range and the oxygen reduction extent. The increase in the accessible nonstoichiometry translates into an increase in the heat storage capacity (QM (kJ molABO3−1)) from ∼272 kJ kgABO3−1 in CaMnO3 to ∼344 kJ kgABO3−1 in CaFe0.1Mn0.9O3−δ0. While even larger changes in oxygen content were accessible in CaFe0.3Mn0.7O3−δ0, the oxidation state changes are accompanied by a lower enthalpy of reduction, resulting in a diminished heat storage capacity of ∼221 kJ kgABO3−1.
Introduction
Solar energy, being effectively limitless, is an attractive source of energy that can be converted into electricity by means of different technologies such as Concentrating Solar Power (CSP) plants.1,2 For their future development, CSP plants need to be coupled with a storage system due to the intermittency and the diurnal nature of the solar light that prevent its continuous use during off-sun time. Finding an inexpensive, efficient means of storing energy produced by CSP plants would be a milestone for the fast growing renewable energy sector.3 For this purpose, Thermal Storage (TS) systems can directly store solar energy produced by the CSP plant during on-sun operation mode as heat and reuse it on demand during off-sun operation mode.4,5 Such technology offers the notable advantages of being less expensive and simpler to implement than battery technology, more commonly applied in Photovoltaic (PV) plants.6,7Among the existing TS technologies, ThermoChemical Storage (TCS) is one of the most promising. It is based on the exploitation of the reaction heat of a reversible chemical reaction:8
| A + ΔHr ⇌ B + C | (1) |
The thermochemical heat storage capacity associated with such a reaction is directly proportional to the reaction enthalpy. During the charging step, carried out at high temperature, thermal energy is used to dissociate a chemical reactant (A), into products (B) and (C). This reaction is endothermic. During the release or discharge step, carried out at low temperature, the products of the endothermic reaction (B and C) are mixed together and react to form the initial reactant (A). This reaction is exothermic and releases heat. Hence, heat is stored in the form of chemical bonds in addition to sensible heat, and released when required.
The TCS system can have higher energy density and longer-term storage duration than other thermal energy storage technologies. A variety of reaction approaches can be used, spanning from gas–gas9 and liquid–gas10 to solid–gas reactions.11,12 Interest has recently grown in metal oxide reduction/oxidation (redox) pairs due to their reversibility, higher temperature of operation than molten salts, and absence of gas products that would otherwise require separation and/or storage. Metal oxides, such as Co3O4/CoO,13,14 Mn2O3/Mn3O4,15,16 CuO/Cu2O,17 have been widely investigated due to their high energy storage density and their ability to accumulate heat in a temperature range close to that at which CSP receivers operate. However, some of these materials display low cyclability due to sintering, which leads to a decrease of the reaction rates with increasing numbers of cycles.18,19 In some systems, particularly the Co3O4/CoO system, cost is also a concern. An additional limitation is that their reduction occurs below the ideal operating temperature of many Air Brayton turbines (1200 °C). Limiting the operational temperature of the system to accommodate the properties of the metal oxides decreases the maximum efficiency of the plant.20 Furthermore, these redox reactions, and all reactions of the type in eqn (1), are discrete and stoichiometric. Consequently, thermochemical heat can only be stored at the specific temperature of the reaction. Heat supplied at lower temperatures, because, for the example, the threshold is not reached by the CSP receiver, is not stored. Similarly, heat supplied at higher temperatures, once the entirety of the material has undergone transformation, is wasted. Additionally, the transformation temperature may be undesirably close to the sintering and/or sublimation temperatures of the material, causing the observed poor cyclability.
Increasing the heat storage temperature as well as the expanse of the temperature storage window can potentially improve the efficiency and economic competitiveness of CSP plants. Recently, perovskites have drawn attention as promising candidates for TCS systems that can potentially meet these temperature demands.21,22 Perovskites, represented by the prototype CaTiO3, are generically indicated as ABO3, with a wide range of A and B cation species that can be accommodated in the structure. The distinctive feature of this class of materials is that they can exhibit a continuous oxygen release/uptake over a broad temperature range through the creation and destruction of oxygen vacancies within the bulk of the crystalline structure. The endothermic charging reaction for a nonstoichoimetric perovskite is given as:
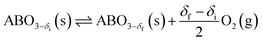 | (2) |
As shown schematically in Fig. 1, the heat stored upon cycling between the charge and discharge temperatures comprises not only the chemical heat due to reaction (2) and associated change in δ between δi and δf, but also a certain amount of sensible heat. The amount of chemical heat stored per mole of material, or chemical heat storage capacity, is given as
 | (3) |
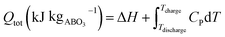 | (4) |
In perovskites, cations can be easily replaced by similar elements, thus the thermochemical behaviour of the material can potentially be tuned through the doping mechanism. Encouraging but preliminary results of a few perovskites as thermochemical heat storage material are reported in literature. LaxSr1−xCoyM1−yO3−δ (M = Mn, Fe) compositions, with 0.1 ≤ x ≤ 0.9 and 0.1 ≤ y ≤ 0.9, have been investigated by Babiniec and co-workers,21 among which La0.3Sr0.7Co0.8Mn0.2O3 showed a calculated heat storage capacity of ∼250 kJ kgABO3−1. The attention has shifted towards more cost-effective and earth-abundant compositions. In particular, CaMnO3 (CM) has been proposed as a TCS material.22,23 However, at temperatures above 900 °C and pO2 ≤ 0.004 atm CaMnO3 decomposes into the spinel (CaMn2O4) and Ruddlesden–Popper (Ca2MnO4) phases. Because reoxidation of these decomposition products is slow,22,24 the operating temperature range is limited. A- and B-site doping are hypothesized to stabilize the perovskite structure, thus allowing heat storage at higher temperatures. Ti and Al, being cations that are difficult to reduce, have been suggested as dopants for CaMnO3 in order to increase the average M–O bond strength and thus the reduction enthalpy.23 The reaction enthalpies of Ti- and Al-doped CaMnO3 (with dopant content of 0.2) have been estimated to be 390 and 370 kJ kgABO3−1 at 1250 °C and pO2 = 0.001 atm, respectively.23 According to the thermodynamic limit (i.e. the calculated δmax achievable at a certain pO2 and temperature according to the point-defect model) the reaction enthalpy of CaMnO3 doped on the A-site with Sr (Ca0.95Sr0.05MnO3) could theoretically be as large as 555 kJ kgABO3−1 at 1000 °C and 10−4 bar.22 However, the evaluated experimental heat storage capacity at the same conditions (1000 °C and 10−4 bar) has been estimated to be about ∼275 kJ kgABO3−1, 20% lower than the thermodynamic limit.22,25
In this study, Fe-doped CaMnO3 (Ca(Mn1−xFex)O3−δ, x = 0, 0.1 and 0.3) oxides are investigated as candidate TCS materials. Prior studies focused on chemical looping combustion have shown that Fe, as well as several other B-site dopants, enhance the phase stability of the material.26,27 Fe is particularly attractive amongst candidate dopants because it is earth-abundant, inexpensive, and non-toxic. The dopant amount (x) has been ranged between 0–0.3 because, according to literature studies, higher dopant concentration induces the formation of a secondary phase, the Ruddlesden–Popper structured Ca2(Mn,Fe)O4 phase,26 thus compromising the purity of the sample. We carry out here a comprehensive thermodynamic study of these compositions under temperatures and oxygen partial pressures of relevance to thermochemical heat storage. The thermodynamic data, not previously available in the literature, enable evaluation of the heat storage under arbitrary cycling conditions.
Materials and methods
Synthesis and chemical and crystallographic characterization
CaMnO3 and Ca(Mn1−xFex)O3 materials with x = 0.1, 0.3, hereafter CM, CMF91 and CMF73, respectively, were prepared according to a modified Pechini method.28 Briefly, stoichiometric amounts of the nitrate salt precursors, Ca(NO3)2 4H2O (Sigma-Aldrich, 99.0% purity), Mn(NO3)2·4H2O (Sigma-Aldrich, ≥97.0% purity), and Fe(NO3)3·9H2O (Sigma-Aldrich, ≥98% purity) were dissolved in distilled water. Citric acid (CA) was added in the solution in a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio of CA
1 molar ratio of CA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Metal, and the mixture was stirred at 70 °C for 3 h, ethylene glycol (EG) was then added in a 3
Metal, and the mixture was stirred at 70 °C for 3 h, ethylene glycol (EG) was then added in a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio of CA
2 ratio of CA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EG and stirred again at 90 °C for 45 minutes, at which point a gel was obtained. The gel was dried at 200 °C for 12 h, transforming into a brittle char, which was then ground and subsequently calcined at 1100 °C for 24 h under static air. Cylindrical porous monoliths were prepared for subsequent characterization by moistening ∼500 mg of the calcined powder with isopropyl alcohol and pressing it into a cylindrical alumina die (internal diameter 10 mm). After the evaporation of the alcohol under ambient temperature and removal from the die, the monolith was sintered at 1200 °C for 3 h under static air. The resulting porosities where 76, 61 and 58%, respectively, for CM, CMF91 and CMF73, with features sizes at the tens of micrometers length-scale (see Fig. A.2 Appendix A.2†), indicating the suitability of the samples for thermogravimetric analysis due to easy gas access to the entirety of the material.
EG and stirred again at 90 °C for 45 minutes, at which point a gel was obtained. The gel was dried at 200 °C for 12 h, transforming into a brittle char, which was then ground and subsequently calcined at 1100 °C for 24 h under static air. Cylindrical porous monoliths were prepared for subsequent characterization by moistening ∼500 mg of the calcined powder with isopropyl alcohol and pressing it into a cylindrical alumina die (internal diameter 10 mm). After the evaporation of the alcohol under ambient temperature and removal from the die, the monolith was sintered at 1200 °C for 3 h under static air. The resulting porosities where 76, 61 and 58%, respectively, for CM, CMF91 and CMF73, with features sizes at the tens of micrometers length-scale (see Fig. A.2 Appendix A.2†), indicating the suitability of the samples for thermogravimetric analysis due to easy gas access to the entirety of the material.
Chemical analysis was performed by inductively coupled plasma-optical emission spectrometry (ICP-OES, iCAP7000 ThermoFisher Scientific in axial configuration) for the simultaneous detection of Ca, Mn, and Fe. Samples were dissolved by digestion in a solution of HNO3 and H2O2 for 12 h at 60 °C. Morphological studies were performed by scanning electron microscopy (SEM, Hitachi SU8030). Additional chemical analysis was performed along with the morphological studies by energy dispersive X-ray spectroscopy (EDX, Oxford AZtec X-max 80 SDD) at an acceleration voltage of 20 kV. X-ray diffraction (XRD) studies were carried out to evaluate phase behavior (Rigaku Ultima IV, Cu Kα, 40 V, 44 mA, 0.05°/s scan rate), using powders obtained by grinding the sintered porous monoliths. Data were collected in situ at temperatures between ambient and 1100 °C in 50–100 °C increments (HTK 1200 heating chamber) under 30 ml min−1 of N2 (pO2 ∼ 10−3 atm). After each heating interval (10 °C min−1) the sample was equilibrated for 20 min before collecting the diffraction pattern. Diffraction data were also collected upon completion of selected thermal analysis experiments. Phase formation and evolution were analyzed using whole pattern fitting (or the Pawley method) as implemented in the commercial software package Materials Data by Jade, Inc. Lattice parameters were evaluated by Rietveld refinement using the GSAS-II Crystallography Data Analysis Software.29
Thermal analysis
Thermogravimetric analysis (TGA), in which mass was measured as a function of temperature at selected gas atmospheres, was performed using a simultaneous thermal analyzer (STA449 F5 Jupiter Netzsch) coupled with an inline pO2 sensor (MicroPoas, Setnag) for measuring the oxygen partial pressure of the TGA exhaust gas. In order to record a detectable mass change upon oxygen loss or uptake, large samples, 200–500 mg in mass, were employed (porous cylindrical monoliths as described above). In some cases, the differential scanning calorimetry (DSC) signal was recorded in conjunction with the mass measurement, a configuration which required the use of small samples (50–80 mg). Measurements were made up to temperatures of 1200 °C. For attaining equilibrium data for thermodynamic analysis, a heating rate of 5 °C min−1 was employed, and each experiment was initiated with a 1 h hold at the initiation of the experiment under pO2 = 0.18 atm to remove surface sorbed species. Data were recorded at six different pO2 values: 0.18, 0.09, 0.07, 0.04, 0.02, 0.008 atm, achieved by mixing dry synthetic air and Ar. The total gas flow rate was fixed at 250 ml min−1. The equality of mass values obtained on heating and on cooling was used to establish that equilibrium behavior had been measured. This was further confirmed by the observation that the oxygen sensor recorded only small variations of pO2 value over the course of the experiment, with the exception of phase change events. Simultaneous DSC-TGA measurements were performed at larger heating rates (10 °C min−1) and at oxygen partial pressures of 0.18 and 5.1 × 10−4 atm, corresponding to the most oxidizing and most reducing conditions considered. The faster ramp rate enabled detection of the DSC signal with good resolution.The change in oxygen non-stoichiometry (Δδ (molO molABO3−1)) from the initial (as-prepared) condition was computed according to:
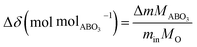 | (5) |
Thermodynamic evaluation
Non-stoichiometry profiles, δ(T), obtained from the thermogravimetry experiments were used to determine the thermodynamic parameters (enthalpy and entropy) characterizing the reduction reaction, inverse of eqn (2), according to the van't Hoff approach.31 In the limit of an infinitesimal extent of reduction, δi → δf and the chemical activities of ABO3−δi and ABO3−δf become equal.The equilibrium constant for the infinitesimal reduction reaction is thus
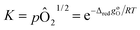 | (6) |
 | (7) |
From the slopes and intercepts of plots of ln(pO2) vs. 1/T for each δ, the molar enthalpy (ΔredhøO (kJ molO−1)) and entropy (ΔredsøO (J molO−1 K−1)) of reduction per mole of oxygen can be extracted, respectively, as functions of δ. The resulting enthalpy function is then used to compute the chemical heat storage capacity by eqn (3), for a given change in oxygen non-stoichiometry.
Results and discussion
Materials synthesis and chemical analysis
Chemical and structural characteristics of the as-prepared materials, specifically, the results of ICP-OES chemical analysis, the lattice parameters, the orthorhombicity (defined below), and the oxygen nonstoichiometry (δ0), are provide in Table 1, with the complete reduction profiles and their analysis for the determination of δ0, presented in the ESI (Fig. A.1 Appendix A.1†). The measured cation compositions were all well within 1 at% of the target Mn/Ca (nMn/nCa) and Fe/Mn (nFe/nMn) values, with all elements readily detected by EDX analysis, Fig. A.3 Appendix A.2.† Furthermore, as revealed by the EDX composition mapping, Fig. 2, the cations are uniformly distributed across the CMF91 and CMF73 materials. The initial oxygen non-stoichiometries (δ0) were found to be 0.0017, 0.043, and 0.1538, respectively, for CM, CMF91, and CMF73. In the Fe-bearing compositions δ0 are very close to the values of 0.05 and 0.15, respectively, that would occur if all of the Fe were in the +3 oxidation state and charge compensated by the generation of oxygen vacancies.| Lattice parameters | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Composition | Code | n Mn/nCa (mol mol−1) | n Fe/nCa (mol mol−1) | δ 0 | a (Å) | b (Å) | c (Å) | V cell (Å3) | O (%) |
| CaMnO3−δ | CM | 1.0065 (13) | 0 | 0.0017 (4) | 5.2785 (4) | 7.4564 (5) | 5.2664 (2) | 207.27 (4) | 0.0766 (15) |
| CaMn0.9Fe0.1O3−δ | CMF91 | 0.9070 (1) | 0.1004 (1) | 0.0430 (2) | 5.2906 (5) | 7.4737 (4) | 5.2804 (7) | 208.79 (6) | 0.0677 (10) |
| CaMn0.7Fe0.3O3−δ | CMF73 | 0.6985 (4) | 0.3004 (8) | 0.1538 (2) | 5.3093 (8) | 7.5102 (5) | 5.3054 (9) | 211.54 (8) | 0.0377 (27) |
At ambient temperature, all synthesized compounds exhibit an orthorhombic (Pnma) CaMnO3 structure (PDF 04-007-8030), Fig. A.5a Appendix A.3,† with Fe fully dissolved into the CaMnO3 structure up to 30 at%. A slight broadening of the peaks with increasing Fe concentration reflects the incorporation of the dopant into the structure Fig. A.5b Appendix A.3.†
Relative to the cubic perovskite architype, the orthorhombic phase displays superstructure peaks with general indices k = odd, or h + l = odd (with h, k, and l referred to the orthorhombic lattice).32 The diffraction data reveal that as the Fe content increases, the intensities of the superstructure reflections decrease, indicating a decrease in the extent of the orthorhombic distortion. The extent of the distortion is also reflected in the relative magnitudes of the unit cell parameters, permitting a quantitative definition of the orthorhombicity according to:33
 | (8) |
![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif) = (abc/√2)1/3. By this metric also, Table 1, the orthorhombicity of the structure decreases as the dopant amount increases (Fig. 3).34 Moreover, the cell parameters increase slightly in response to the Fe doping, suggesting the Fe3+ adopts a high spin electron configuration (with a larger effective radius than the low spin configuration). The reasons for the increase in average symmetry with increasing Fe content is not immediately obvious, but may be connected to the increase in cell volume. As is well documented in the literature and discussed in detail below, CaMnO3 undergoes successive transitions to higher symmetry phases on heating, in conjunction with volume expansion. Expansion resulting from incorporation of Fe may mimic this effect. Alternatively, the presence of a substantial number of randomly distributed point defects may favor greater global symmetry.
= (abc/√2)1/3. By this metric also, Table 1, the orthorhombicity of the structure decreases as the dopant amount increases (Fig. 3).34 Moreover, the cell parameters increase slightly in response to the Fe doping, suggesting the Fe3+ adopts a high spin electron configuration (with a larger effective radius than the low spin configuration). The reasons for the increase in average symmetry with increasing Fe content is not immediately obvious, but may be connected to the increase in cell volume. As is well documented in the literature and discussed in detail below, CaMnO3 undergoes successive transitions to higher symmetry phases on heating, in conjunction with volume expansion. Expansion resulting from incorporation of Fe may mimic this effect. Alternatively, the presence of a substantial number of randomly distributed point defects may favor greater global symmetry.
Thermal stability and phase evolution
Shown in Fig. 4 and 5 are simultaneous thermal analysis profiles for the CM and CMF materials performed at a relatively high ramp rate (10 °C min−1) under the most oxidizing and most reducing conditions considered in this study, pO2 = 0.18 and 5.1 × 10−4 atm, respectively. The results under both conditions immediately reveal that with increasing Fe content mass loss increases. Under pO2 = 0.18 atm and up to a temperature of 1100 °C (Fig. 4) the mass loss is essentially reversible for all compositions, with thermal events recorded by DSC that coincide with changes in the slope of the mass loss, i.e., with peaks in the differential mass loss curves (Fig. A.6 Appendix A.4†). The reversibility of the high-temperature mass loss indicates phase stability under these relatively oxidizing conditions, which as shown below, extends up to 1200 °C.The thermal events of the undoped composition, with DSC peaks at 894 and 913 °C (pO2 = 0.18, Fig. 4) are known to reflect orthorhombic to tetragonal and tetragonal to cubic phase transitions, respectively.35 No hysteresis is observed for these transitions, with the reverse transformations occurring at exactly the same temperatures as the forward reactions. The majority of the mass loss (on heating) in the CM composition occurs after transformation to these higher symmetry phases. Introduction of Fe into CM shifts the phase transition temperatures downwards significantly, while also causing the two transitions to merge into a single step. The doping also results in mass loss at temperatures below the transformation events. As concluded on the basis of in situ high-temperature diffraction studies shown below, the Fe-doped materials undergo a direct transition from the orthorhombic to the cubic phase; no tetragonal phase is observed. This transition is furthermore hysteric upon Fe doping. In CMF91 the hysteresis is relatively small, with forward and reverse events occurring at temperatures that differ by 9 °C, whereas in CMF73 the hysteresis is significant, amounting to almost 40 °C. Post TGA diffraction analysis revealed that the CMF73 completely reverted to the orthorhombic phase (Fig. A.9 Appendix A.7†). The trivial amount of mass loss that is not recovered on cooling in the low temperature region, Fig. 4a, is attributed to incomplete recovery of the oxygen content in the orthorhombic phase relative to the initial state.
Comparison of Fig. 4 and 5 reveals that decreasing the oxygen partial pressure causes the transition temperatures to shift downwards and the total mass loss at high temperature to increase (for a given oxide composition). In the case of CM, along with this shift, the two formerly distinct thermal events merge into a single, relatively broad response, indicating a vanishingly small window of stability of the tetragonal phase under low pO2. Similar results have been reported previously.35 The thermal events for all compositions again coincide with peaks in the differential TG profiles (Fig. A.6 Appendix A.4†). In the low pO2 condition, these events now also coincide with spikes in the oxygen signal. Such a response was not detectable over the relatively high pO2 background of the experiments represented in Fig. 4. The clear release of oxygen at low pO2 suggests a discontinuity in oxygen content across the phase boundaries. Thus, the thermal responses that occur at these transitions (summarized in Table A4.1 Appendix A.4†) reflect not only the enthalpy associated with a change in structure, but also the heat necessary to liberate oxygen as required to accommodate the phase change.
A noticeable feature of the measurements at pO2 = 5.1 × 10−4 atm (Fig. 5) is the complete irreversibility of the mass loss for all compositions. This behavior is attributed to decomposition into CaMn2O4 (spinel) and Ca2MnO4 (Ruddelsden-Popper, or RP) phases, with Mn reduced to the 3+ and 2+ oxidation states, respectively, where the reverse reaction is known to be extremely sluggish.22,36 Furthermore, all the compositions underwent continuous mass loss during a brief isothermal hold at 1000 °C, whereas no mass loss was observed at 1100 °C and pO2 = 0.18 atm (Fig. 4). This result implies that the 10 °C min−1 heating rate was too rapid to allow the samples to remain in equilibrium during heating. Accordingly, the thermal stability and reversibility were next evaluated under less aggressive conditions.
Shown in Fig. 6 are thermogravimetric profiles for the CM and CMF materials performed at a slow ramp rate (5 °C min−1) under the most reducing conditions employed for thermodynamic evaluation (pO2 = 0.008 atm) up to a temperature of 1200 °C. Under these conditions the behaviors of the three materials are distinct. Similar to the case under pO2 = 5.1 × 10−4 atm the undoped material undergoes a sharp change in the rate of mass loss at high temperature, here ∼830 °C, which is accompanied by a sharp increase in the pO2 level, and can be associated again with the orthorhombic to cubic transition. At around 1100 °C, the rate of mass loss decreases, suggesting a kinetically retarded process, which is again ascribed to decomposition into spinel and RP phases. This process remains incomplete after holding the sample at 1200 °C for 1 h and reduction even continues into the initial stages of cooling. Further cooling, results in only partial re-oxidation. XRD analysis of the sample after the TGA experiment (Fig. A.9 Appendix A.7†) revealed the presence of small impurity peaks, readily assigned to the spinel and RP phases. Thus, it is evident that both the forward decomposition and reverse perovskite formation reactions are sluggish, and the undoped composition is stable only to about 1100 °C even under these less reducing conditions.
In the case of the Fe-doped samples, the mass loss profiles (Fig. 6) on heating again look very similar to those obtained under pO2 = 5.1 × 10−4 atm (Fig. 5). Oxygen release initiates at lower temperatures than in CM, and sharp changes in the rate of mass loss are accompanied by sharp peaks in the oxygen concentration of the gas phase. The events are again taken to correspond to the orthorhombic to cubic transition. In contrast to the behavior under pO2 = 5.1 × 10−4 atm, here (pO2 = 0.008 atm) the high-temperature mass loss is fully recovered (similar to the case under pO2 = 0.18 atm). Furthermore, during the 1200 °C isothermal hold, no mass loss was detected for either CMF91 or CMF73, indicating that the heating/cooling rate of 5 °C min−1 is sufficiently slow to capture equilibrium behavior throughout almost the entire experiment. The stability at 1200 °C sharply contrasts the behavior of CM, which underwent a partially irreversible, high-temperature mass loss at this temperature. The high Fe composition sample CMF73 is however distinct from CMF91 in that the low temperature mass loss, which occurs in a relatively sharp step at ∼386 °C on heating, is only partially recovered, Fig. 6. Post-experiment diffraction data, Fig. A 9 Appendix A.7,† revealed the CMF73 product to be a mixture of the orthorhombic and cubic phases (68 and 32 phase %, respectively). In general, recovery of the mass loss associated with the orthorhombic to cubic transition was sluggish in CMF73 and increasingly incomplete with decreasing pO2 (compare Fig. 4 and 6). Accordingly, subsequent thermodynamic analysis was limited to temperatures of 400 °C and above (i.e., the cubic phase of CMF73), which in any case, meets the objectives of this study for high temperature heat storage.
The in situ diffraction data (collected under inert atmosphere, pO2 ∼ 10−3 atm), Fig. 7, reveal phase transformation behavior that is consistent with the TGA and ex situ XRD results. Specifically, upon heating, each of the compositions transforms from the as-prepared orthorhombic phase to a cubic phase, with a transformation temperature that decreases with increasing Fe content. Absence of the tetragonal phase from the CM patterns is expected on the basis of the low oxygen partial pressures of these diffraction studies, which are carried out at more reducing conditions than any of the thermal analysis experiments. Additionally, for the undoped composition the incipient formation at 1100 °C of the spinel and RP phases is evident, whereas the CMF91 and CMF73 compositions do not undergo any such decomposition, in further agreement with the thermal analysis and ex situ diffraction studies.
The temperature dependent cell parameters, obtained by Rietveld refinement and shown in Fig. 8 (as well as in Tables of §A.5 Appendix A†), reveal that the thermal expansion in these materials is somewhat anisotropic. The results for CM generally agree with a similar study of this material carried out under air rather than inert atmosphere.32,37 Upon transformation to the cubic phase, the apparent thermal expansion of all three materials noticeably increases. This likely results from a contribution of chemical expansion upon reduction to the overall expansion behavior. The apparently high thermal expansion coefficient of CMF73, the largest amongst the three materials, may also reflect such chemical expansion effects, as this material also displays the largest change in nonstoichiometry with temperature amongst the three (Fig. 6a).
 | ||
| Fig. 8 Evolution of the lattice parameters as a function temperature under inert atmosphere (30 ml min−1 N2, pO2 ∼ 0.01 atm) of (a) CM, (b) CMF91, and (c) CMF73. | ||
Thermodynamic data extraction and phase behavior
With the stability ranges of the CM and CMF materials determined and a heating/cooling rate of 5 °C min−1 established as suitable for the measurement of equilibrium behavior, oxygen non-stoichiometry (δ) profiles were obtained from the thermogravimetric analysis (recorded at pO2 = 0.18, 0.09, 0.07, 0.04, 0.02, 0.008 atm, up to a temperature of 1100 °C for CM and 1200 °C for CMF). The results are presented in Fig. 9. Consistent with the conclusion that the measurement conditions were suitable for evaluating equilibrium behavior, it is evident that at any given pO2, the heating and cooling curves almost perfectly overlap. Moreover, the oxygen sensor recorded negligible variations of pO2 over the course of the experiment, with the exception of phase change events (Fig. A 7 Appendix A.6†). In the case of CMF73, complete reoxidation at temperatures below 400 °C was not captured (as discussed already in the context of Fig. 4 and 6), and the thermodynamic analysis was performed only in the range 400–1200 °C.Because the crystallographic phase changes involve discrete changes in mass, is possible to extract the temperatures at which the phase transitions occur from the derivative of the δ(T) curves, (dδ/dT), as illustrated in examples of the behavior of the undoped composition presented in Fig. A.12 Appendix A.10.† The dδ/dT profile collected under pO2 = 0.18 atm (5 °C min−1) (Fig. A.12 Appendix A.10†) coincides rather closely with the DSC profile collected for this material under the same pO2 (10 °C min−1), Fig. 4b, indicating the validity of the method for evaluating the phase boundaries. Combining the phase boundary information across all measurement conditions enabled construction of pO2-T phase stability diagrams and schematic phase diagrams for the CM and CMF91 materials (Fig. 10). CMF73 adopts the cubic phase over the entirety of the conditions considered (T ≥ 400 °C), for which reason no diagrams are shown for this composition. The stability diagrams clearly reveal that the high temperature and low oxygen partial pressure conditions favor the cubic phase, whereas the orthorhombic phase is favored at low temperatures and high oxygen partial pressures. The peaks in the DSC and dδ/dT profiles have breadths (∼15 to ∼50 °C) that correspond to the widths of the two-phase regions. The disappearance of the tetragonal phase at low pO2 from the stability diagram of CM and at all measured pO2 from the stability diagram of CMF91 is captured in the proposed schematic phase diagrams. The presentation of the results in these phase and stability diagrams emphasizes the role of oxygen nonstoichiometry in the realization of the cubic phase. Because thermodynamics dictates that high entropy phases are favoured at high temperature, the transformation of CM and CMF to the cubic variant on heating implies that the cubic phase must have high entropy relative to the lower symmetry distortions. As this transformation occurs at any (fixed) value of nonstoichiometry and is moreover favoured as non-stoichiometry increases, we propose that the cubic phase may be entropy stabilized by supporting a greater number of energetically equivalent configurations than do the lower symmetry variants. As noted, the Fe dopant creates oxygen vacancies at a level implying all Fe is in the 3+ valence state. These vacancies may be responsible for the expansion of the stability range of the cubic phase with respect to T and pO2. On the other hand, the stability range of the orthorhombic rather than cubic phase is expanded with respect to T and δ. The fundamental origins of this behavior are as yet unknown.
Turning to the thermodynamics of the reduction behavior, iso-δ plots of the undoped material are presented in Arrhenius form in Fig. 11, with analogous figures presented for CMF91 and CMF73 in Fig. A.10 Appendix A.8.† Given the continuous nature of the δ(T) profiles, it was possible to extract the temperature and pO2 corresponding to any δ accessed in the measurements. Thus, a set of six (pO2, T) pairs are available for each arbitrarily selected δ within the measurement range and single phase region. The summary in Fig. 11 emphasizes the result presented schematically in Fig. 10c that the phase boundaries do not occur at fixed δ but rather at δ values that vary with and are determined by T and pO2. The positions of the phase boundaries are reported in Table A8.1 Appendix A.8.†
The extracted molar enthalpy of oxidation ΔhO (kJ molO−1) for each of the three compositions is plotted as a function of oxygen nonstoichiometry in Fig. 12a. Here the nonstoichiometry of relevance is the excess, δexcess, beyond that due to the presence of Fe3+, where specifically δexcess = δmeas − δdopant, and the δdopant values are taken to be 0, 0,05 and 0.15, respectively, for CM, CMF91 and CMF73. The apparently fixed 3+ oxidation state of Fe over the range of conditions considered here prompts the presentation the results in this manner. For completeness, the extracted molar entropy (ΔsO (J molO−1 K−1)) is reported as ESI (Fig. A 11 Appendix A.9†). In the low δ orthorhombic phases, the enthalpies of CM and CMF91 are quite different from one another, and in the case of CMF91 the enthalpy shows a strong dependence of δ. For δexcess ≥ 0.08, within the cubic regime, the enthalpies of CM and CMF91 are similar to one another and also relatively constant with δ, displaying values of 167 ± 5 and 182 ± 6 kJ molO−1, respectively. In CMF73, which again, was only evaluated in the cubic phase, the enthalpy is strongly dependent on δ, and it approaches an almost constant value of 161 ± 4 kJ molO−1 when δexcess ≥ 0.15. The measured enthalpy for CM is in good agreement with literature data, reported as 172.05 and 217.22 kJ molO−1, respectively, in the cubic and orthorhombic regimes.38
The heat storage capacity per unit mass of perovskite (QM (kJ kgABO3−1)), determined according to the eqn (3), is presented in Fig. 12b as a function of δf (a), where the δi values are fixed at 0.01, 0.05, and 0.18, respectively, for CM, CMF91 and CMF73. For the first two materials, these values are just higher than the as-synthesized δ0 values, whereas for CMF73, 0.18 corresponds to the minimum δ value at which the enthalpy (in the cubic phase) could be estimated. In principle, the heat of the orthorhombic to cubic phase change contributes to the heat storage capacity of CM and CMF91, and the occurrence of this transition is responsible for gaps in the data for these two compositions in Fig. 12a. Rather than risk overestimating the phase change contribution to the heat storage, which will depend on the specific conditions of the thermal cycling, this contribution was ignored and the integration required by eqn (3) was performed by assuming a straight line connection between the orthorhombic and cubic phases in the enthalpy curves. The analysis reveals that for a given change in δ from their respective δi, CM and CMF91 have comparable heat storage capacities, significantly higher than that of CMF73. Because CMF91 can undergo a larger reduction extent than CM (due to its greater thermal stability), it presents the highest maximum heat storage capacity amongst the three compositions, 344.3 ± 0.6 kJ kgABO3−1 (or 460.4 ± 0.8 kW h m−3) as compared to 272.5 ± 1.1 (or 364.9 ± 0.8 kW h m−3) and 221.5 ± 4.7 kJ kgABO3−1 (or 296.9 ± 6.3 kW h m−3), respectively, for CM and CMF73.
Operationally, one controls the temperature and gas conditions of the heat storage process rather than directly the δf adopted by a material. Accordingly, in Fig. 13 is shown the heat storage capacity of the three materials as a function of temperature at selected specified, fixed pO2 (with the complete set of results presented in Fig. A 13 Appendix A.11†) The calculation again follows eqn (3), but now with δf = δ (T, pO2 = pO2fixed), and the same oxygen partial pressure on cooling as on heating. Presented in this manner, the superior heat storage capacity of CMF91 is readily appreciated to result from the stability of the material to higher temperature than CM under moderately reducing conditions (pO2 = 0.008 atm). Additionally, the CMF91 composition enables a small amount of chemical heat storage in the low temperature orthorhombic phase because the enthalpy of oxidation is small enough to enable reduction. In contrast, CM has a high enthalpy in this phase (Fig. 12a) and little change in the oxygen content below the transition temperature. As temperature increases, the CM composition accesses the heat storage capacity of its orthorhombic phase and thereafter the two materials behave similarly. Ultimately, the key benefit of introduction of Fe is in the increased thermal stability. The more heavily Fe doped composition CMF73 is also stable to higher temperature than CM under moderately reducing conditions, but due to the overall smaller oxidation reaction enthalpy, the total heat storage is diminished.
Estimation of the technologically relevant total heat storage capacity (eqn (4)) requires knowledge of the specific heat capacity, Cp. For CM the value of this property, as reported in the literature, is about 0.8 kJ kg−1 K−1 (ref. 36, 39 and 40) and it is reasonable to assume that Fe doping will not change this substantially. Assuming, due to the high thermal stability of CMF91 (Fig. 9b), operation over a wide temperature window between 400 and 1200 °C (ΔT = 800 °C), the total heat storage capacity for this material is ∼984 kJ kgABO3−1. This is considerably larger than the storage capacity of undoped CM (∼832 kJ kgABO3−1) which would be operated only up to 1100 °C (Fig. 9a). In addition, despite having the same thermal stability (Fig. 9c) and hence temperature storage window, CMF91 has a larger total heat storage capacity than that of CMF73 (∼861 kJ kgABO3−1). The relative contributions to the heat storage of the three materials are summarized in Fig. 13c. In comparison to the most promising stoichiometric redox systems reported in literature to date (i.e. Co3O4/CoO, Mn2O3/Mn3O4 redox pairs),15,41 the temperature for storing heat in CMF91 is higher and the window for temperature storage is broader. Furthermore, CMF91 is composed of earth-abundant elements which implies a large decrease in material cost relative to the Co3O4/CoO system. In comparison to other doped CaMnO3 compositions evaluated for TCS (i.e. Al-, Ti-, Sr-doped),22,23,25 CMF91 enables operation at higher temperature and more moderate pO2 for a comparable level of heat storage. These are attractive features as the higher temperature of storage can boost the efficiency of the thermodynamic cycles and hence of the CSP plant,23,42 whereas the functionality under moderate (rather than low) pO2 can keep reactor operating costs low and also contribute to overall increased energy efficiency.
Cyclability of CMF91
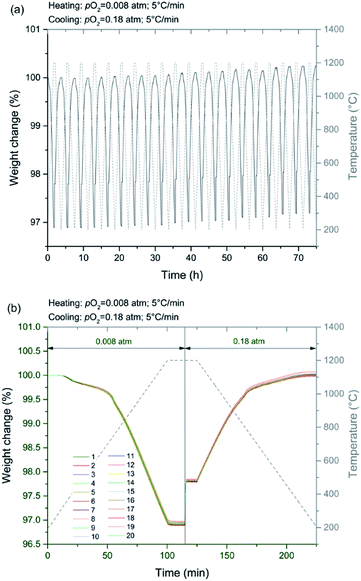
In light of its favorable thermodynamic properties, CMF91 emerges as an attractive candidate for heat storage at CSP plants. Accordingly, it was further investigated in terms of cyclability over multiple reduction/re-oxidation reactions. The mass profiles collected from a sample ∼400 mg in mass over 20 cycles are plotted in Fig. 14, where reduction was carried out upon heating at 5 °C min−1 to 1200 °C under pO2 = 0.008 atm and subsequent oxidation upon cooling, also at 5 °C min−1, to 200 °C under pO2 = 0.18 atm. With the exception of a small overall drift, the overlap in data between cycles is high. Thus, CMF91 appears suitable for long life-time heat storage even under demanding cycling conditions.Conclusions
In this study, CaFexMn1−xO3 oxides, formed of earth-abundant, inexpensive, non-toxic elements, have been investigated as possible high temperature heat storage materials for concentrated solar power plants. Two doping levels have been considered, x = 0.1 and 0.3. Undoped CaMnO3 does not undergo appreciable reduction below ∼700 °C, at which it exists in the orthorhombic form, and it suffers from a largely irreversible decomposition reaction above 1100 °C when pO2 < 0.008 atm. Doping with Fe shifts the orthorhombic to cubic transition to lower temperature and enables oxygen release at temperatures as low as 400 °C. The stabilization of the cubic phase is tentatively attributed to the generation of oxygen vacancies as a result of the incorporation of Fe in the 3+ valence state. The doping further stabilizes the perovskite phase to temperatures as high as 1200 °C under all oxygen partials studied. These features contribute to an increase in the reversible reduction/oxidation extent. In the case of the more lightly doped composition (CMF91) the enthalpy of oxidation is only slightly changed relative to CaMnO3 (CM) as a result of Fe doping, and thus the wider range of accessible δ results in an increase in the chemical heat storage. In the more heavily doped material (CMF73) the enthalpy of reduction is substantially lower than in the other two systems. Consequently, despite similarity in the thermal stability and maximum extent of reduction, CMF73 offers a lower heat storage capacity than CMF91. The thermodynamic behavior moreover suggests that Fe retains the 3+ oxidation state across much of the oxygen nonstoichiometry range explored, a surprising result. The implication is that even redox inactive elements may be advantageous dopants as long as they enhance overall thermal stability. Under technologically relevant conditions, specifically operating over a temperature window of 400 to 1200 °C and under an oxygen partial pressure of 8 × 10−3 atm, CMF91 offers a total heat storage capacity of ∼984 kJ kgABO3−1, of which ∼344 kJ kgABO3−1 is due chemical heat storage. These attractive characteristics are complemented by good stability over multiple oxidation/reduction cycles. In sum, CMF91 appears ideally suited for heat storage applications. Its properties warrant further evaluation in large scale reactor systems.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project has received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No 746167. Support of the US Department of Energy, Office of Energy Efficiency and Renewable Energy, Award DE-EE0008089.0000, is also acknowledged. We acknowledge the support with the publication fee by the CSIC Open Access Publication Support Initiative through its Unit of Information Resources for Research (URICI).References
- C. Prieto, P. Cooper, A. I. Fernández and L. F. Cabeza, Renewable Sustainable Energy Rev., 2016, 60, 909–929 CrossRef CAS.
- M. Liu, N. H. Steven Tay, S. Bell, M. Belusko, R. Jacob, G. Will, W. Saman and F. Bruno, Renewable Sustainable Energy Rev., 2016, 53, 1411–1432 CrossRef CAS.
- D. Salas, E. Tapachès, N. Mazet and D. Aussel, Energy Convers. Manage., 2018, 174, 932–954 CrossRef.
- S. Kuravi, J. Trahan, D. Y. Goswami, M. M. Rahman and E. K. Stefanakos, Prog. Energy Combust. Sci., 2013, 39, 285–319 CrossRef.
- A. J. Carrillo, J. Gonza, M. Romero and J. M. Coronado, Chem. Rev., 2019, 119, 4777–4816 CrossRef CAS PubMed.
- A. J. De Jong, L. Van Vliet, C. Hoegaerts, M. Roelands and R. Cuypers, Energy Procedia, 2016, 91, 128–137 CrossRef CAS.
- M. Aneke and M. Wang, Appl. Energy, 2016, 179, 350–377 CrossRef.
- C. Milone, Y. Kato and E. Mastronardo, in Recent Advancements in Materials and Systems for Thermal Energy Storage, A. Frazzica and L. F. Cabeza, Springer, Switzerland, 2019, 1, pp. 15–32 Search PubMed.
- C. Chen, Y. Li, M. Zhou, S. Zhou and W. Jin, Sol. Energy, 2018, 176, 220–229 CrossRef CAS.
- C. Chen, L. Zhao, M. Kong and A. S. Lavine, Sol. Energy, 2018, 176, 256–266 CrossRef CAS.
- P. Pardo, A. Deydier, Z. Anxionnaz-Minvielle, S. Rougé, M. Cabassud and P. Cognet, Renewable Sustainable Energy Rev., 2014, 32, 591–610 CrossRef CAS.
- T. Dalgleish, J. M. G. Williams, A.-M. J. Golden, N. Perkins, L. F. Barrett, P. J. Barnard, C. Au Yeung, V. Murphy, R. Elward, K. Tchanturia and E. Watkins, J. Exp. Psychol. Gen., 2007, 136, 23–42 Search PubMed.
- G. Karagiannakis, C. Pagkoura, E. Halevas, P. Baltzopoulou and A. G. Konstandopoulos, Sol. Energy, 2016, 133, 394–407 CrossRef CAS.
- C. Agrafiotis, M. Roeb, M. Schmücker and C. Sattler, Sol. Energy, 2015, 114, 440–458 CrossRef CAS.
- A. J. Carrillo, D. P. Serrano, P. Pizarro and J. M. Coronado, J. Energy Storage, 2016, 5, 169–176 CrossRef.
- M. Wokon, T. Block, S. Nicolai, M. Linder and M. Schmücker, Sol. Energy, 2017, 153, 471–485 CrossRef CAS.
- E. Alonso, C. Pérez-Rábago, J. Licurgo, E. Fuentealba and C. A. Estrada, Sol. Energy, 2015, 115, 297–305 CrossRef CAS.
- C. Agrafiotis, M. Roeb, M. Schmücker and C. Sattler, Sol. Energy, 2014, 102, 189–211 CrossRef CAS.
- A. J. Carrillo, D. P. Serrano, P. Pizarro and J. M. Coronado, J. Mater. Chem. A, 2014, 2, 19435–19443 RSC.
- C. S. Turchi, J. Stekli and P. C. Bueno, Concentrating solar power, Elsevier Ltd, 2017 Search PubMed.
- S. M. Babiniec, E. N. Coker, J. E. Miller and A. Ambrosini, Sol. Energy, 2015, 118, 451–459 CrossRef CAS.
- L. Imponenti, K. J. Albrecht, J. W. Wands, M. D. Sanders and G. S. Jackson, Sol. Energy, 2017, 151, 1–13 CrossRef CAS.
- S. M. Babiniec, E. N. Coker, J. E. Miller and A. Ambrosini, Int. J. Energy Res., 2015, 40, 280–284 CrossRef.
- B. Bulfin, J. Vieten, D. E. Starr, A. Azarpira, C. Zachäus, M. Hävecker, K. Skorupska, M. Schmücker, M. Roeb and C. Sattler, J. Mater. Chem. A, 2017, 5, 7912–7919 RSC.
- L. Imponenti, K. J. Albrecht, R. Kharait, M. D. Sanders and G. S. Jackson, Appl. Energy, 2018, 230, 1–18 CrossRef CAS.
- N. Galinsky, M. Sendi, L. Bowers and F. Li, Appl. Energy, 2016, 174, 80–87 CrossRef CAS.
- M. Arjmand, A. Hedayati, A. M. Azad, H. Leion, M. Rydén and T. Mattisson, Energy and Fuels, 2013, 27, 4097–4107 CrossRef CAS.
- D. Sastre, A. J. Carrillo, D. P. Serrano, P. Pizarro and J. M. Coronado, Top. Catal., 2017, 60, 1108–1118 CrossRef CAS.
- B. H. Toby and R. B. Von Dreele, J. Appl. Crystallogr., 2013, 46, 544–549 CrossRef CAS.
- D. N. Mueller, R. A. De Souza, H. I. Yoo and M. Martin, Chem. Mater., 2012, 24, 269–274 CrossRef CAS.
- Y. Hao, C. K. Yang and S. M. Haile, Chem. Mater., 2014, 26, 6073–6082 CrossRef CAS.
- Q. Zhou and B. J. Kennedy, J. Phys. Chem. Solids, 2006, 67, 1595–1598 CrossRef CAS.
- P. Thiel, S. Populoh, S. Yoon and A. Weidenkaff, J. Solid State Chem., 2015, 229, 62–67 CrossRef CAS.
- A. D. Neetika, I. Dhiman, A. K. Nigam, A. K. Yadav, D. Bhattacharyya and S. S. Meena, J. Appl. Phys., 2012, 112, 123913–123916 CrossRef.
- E. I. Leonidova, I. A. Leonidov, M. V Patrakeev and V. L. Kozhevnikov, J. Solid State Electrochem., 2011, 15, 1071–1075 CrossRef CAS.
- E. Bakken, T. Norby and S. Stølen, Solid State Ionics, 2005, 176, 217–223 CrossRef CAS.
- W. Paszkowicz, J. Piętosa, S. M. Woodley, P. A. Dłużewski, M. Kozłowski and C. Martin, Powder Diffr., 2010, 25, 46–59 CrossRef CAS.
- E. I. Goldyreva, I. A. Leonidov, M. V Patrakeev and V. L. Kozhevnikov, J. Solid State Electrochem., 2013, 17, 3185–3190 CrossRef CAS.
- E. Bakken, T. Norby and S. Stølen, J. Mater. Chem., 2002, 12, 317–323 RSC.
- K. J. Albrecht, G. S. Jackson and R. J. Braun, Appl. Energy, 2016, 165, 285–296 CrossRef CAS.
- C. Agrafiotis, T. Block, M. Senholdt, S. Tescari, M. Roeb and C. Sattler, Sol. Energy, 2017, 149, 227–244 CrossRef CAS.
- J. E. Miller, A. Ambrosini, S. M. Babiniec, E. N. Coker, C. K. Ho, H. Al-ansary, S. M. Jeter, P. G. Loutzenhiser, N. G. Johnson and E. B. Stechel, in Proceedings of the ASME 2016 10th International Conference on Energy Sustainability, Charlotte, North Carolina, USA. June 26–30, 2016, pp. 1–8 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ta02031a |
| This journal is © The Royal Society of Chemistry 2020 |