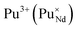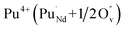Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Insights into the fabrication and structure of plutonium pyrochlores†
S.
Finkeldei
 *ab,
M. C.
Stennett
*ab,
M. C.
Stennett
 *c,
P. M.
Kowalski
*c,
P. M.
Kowalski
 ad,
Y.
Ji
ad,
Y.
Ji
 ad,
E.
de Visser-Týnová
e,
N. C.
Hyatt
ad,
E.
de Visser-Týnová
e,
N. C.
Hyatt
 c,
D.
Bosbach
c,
D.
Bosbach
 a and
F.
Brandt
a and
F.
Brandt
 a
a
aForschungszentrum Jülich, Institute of Energy and Climate Research – IEK-6, Nuclear Waste Management and Reactor Safety, 52425 Juelich, Germany. E-mail: sfinkeld@uci.edu
bOak Ridge National Laboratory, Oak Ridge, TN, USA
cUniversity of Sheffield, Department of Materials Science and Engineering, S1 3JD, UK. E-mail: m.c.stennett@sheffield.ac.uk
dJARA High Performance Computing, Schinkelstrasse 2, 52062 Aachen, Germany
eNuclear Research and Consultancy Group (NRG), Research & Innovation, 1755 LE Petten, The Netherlands
First published on 20th January 2020
Abstract
Rare earth zirconates, such as Nd2Zr2O7, crystallise with the pyrochlore structure and are a group of materials which have been suggested as potential nuclear waste forms for actinide immobilisation. In this work, a new hydroxide co-precipitation route is presented to investigate the incorporation of Pu into Nd2Zr2O7. The plutonium content was varied between 5 and 10 mol% and the structural uptake and Pu oxidation state were probed by X-ray diffraction (XRD), scanning electron microscopy (SEM), and X-ray absorption spectroscopy (XAS). The experimental findings were complemented by DFT ab initio calculations. For all the incorporation mechanisms studied PuO2 was used as the reference reactant state to allow for a direct comparison between the possible Pu uptake scenarios. Analysis of the experimental data suggests that Pu(IV) cations substitute for Nd(III) cations leading to structural distortion of the pyrochlore A-sites. The computed solution energies and bond-distances corroborate the experimental findings and indicate that the excess charge is balanced via the introduction of oxygen at formerly vacant sites.
1. Introduction
Due to their unique properties the class of oxides with the pyrochlore crystal structure have been studied for many different applications. These include thermal barrier coatings,1 solid-oxide fuel cells,2 and nuclear waste forms for the immobilisation of radionuclides.3 They are of particular interest for the immobilisation of actinides such as plutonium due to their high chemical flexibility, high tolerance to radiation damage, and high aqueous durability.4–6 In addition to being a key phase in SYNROC multiphase ceramics,6 pyrochlores have also been studied as single phase waste forms to immobilise actinide rich waste-streams such as separated plutonium from spent nuclear fuel reprocessing.7 The pyrochlore crystal structure is a superstructure of the fluorite structure and its general formula can be described as A2B2X6Y. Most commonly pyrochlores are of the (3+, 4+) type with rare earth-elements favouring the A-site and 3d, 4d, or 5d transition metals favouring the B-site.8 (2+, 5+) type pyrochlores can also form but have not been widely studied for application as waste-forms. If the origin of the cubic (Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) structure is chosen to coincide with the B-site, the A cations occupy the 16d, the B cations the 16c, and the oxygen anions on the X and Y sites the 48f and 8b Wyckoff positions, respectively. In contrast to simple fluorite structured compounds such as ZrO2, pyrochlores contain combinations of aliovalent cations and the charge compensation required to maintain electrical neutrality occurs via the introduction of oxygen vacancies. Pyrochlore structured compounds are missing one eighth of the anions and the resulting oxygen vacancy is localised at the 8a Wyckoff position. The pyrochlore structure can be viewed as being ordered with respect to the fluorite structure. The A-site cations sit in the center of a scalenohedron and are coordinated to six X anions and two Y anions where the cation–anion bond length is slightly shorter. The B-site cations are coordinated solely to six X anions which form a trigonal antiprism around the site. The oxygen deviation parameter x is an indicator of the distortion of the coordination polyhedra surrounding the A and B cations. If x equals 0.375 the A site cations are surrounded by anions arranged as a regular cube and the ideal fluorite structure is observed. For x = 0.3125 the B site anion arrangement is regular octahedral which corresponds to the ideal pyrochlore crystal structure.4,9 The pyrochlore structure has been shown to be flexible and will accommodate cations with a variety of ionic radii at the A- and B-sites. Pyrochlores of mixed cationic occupancy can also be formed and these are referred to as non-stoichiometric pyrochlores.10,11
m) structure is chosen to coincide with the B-site, the A cations occupy the 16d, the B cations the 16c, and the oxygen anions on the X and Y sites the 48f and 8b Wyckoff positions, respectively. In contrast to simple fluorite structured compounds such as ZrO2, pyrochlores contain combinations of aliovalent cations and the charge compensation required to maintain electrical neutrality occurs via the introduction of oxygen vacancies. Pyrochlore structured compounds are missing one eighth of the anions and the resulting oxygen vacancy is localised at the 8a Wyckoff position. The pyrochlore structure can be viewed as being ordered with respect to the fluorite structure. The A-site cations sit in the center of a scalenohedron and are coordinated to six X anions and two Y anions where the cation–anion bond length is slightly shorter. The B-site cations are coordinated solely to six X anions which form a trigonal antiprism around the site. The oxygen deviation parameter x is an indicator of the distortion of the coordination polyhedra surrounding the A and B cations. If x equals 0.375 the A site cations are surrounded by anions arranged as a regular cube and the ideal fluorite structure is observed. For x = 0.3125 the B site anion arrangement is regular octahedral which corresponds to the ideal pyrochlore crystal structure.4,9 The pyrochlore structure has been shown to be flexible and will accommodate cations with a variety of ionic radii at the A- and B-sites. Pyrochlores of mixed cationic occupancy can also be formed and these are referred to as non-stoichiometric pyrochlores.10,11
Due to the dismantling of nuclear weapon programmes, many countries have large volumes of separated plutonium12 which may ultimately require immobilisation in a ceramic wasteform. We focus in this study on zirconate pyrochlores because they are known to retain their crystalline structure when subjected to radiation damage; self-irradiation in zirconate pyrochlores leads to the formation of a defective fluorite structure whereas titanate pyrochlore analogues readily amorphise.13 Moreover, ZrO2-based pyrochlores show high aqueous durability14,15 which is another important property for nuclear waste forms. In order to benefit from the inherent advantages of such a crystalline waste form, structural uptake of the radionuclide has to be ensured. Previous studies have probed the uptake of curium at ppm levels on the A site of a zirconate pyrochlore16 however, to investigate the ability of pyrochlore to serve as potential wasteform for actinides it is important to synthesize materials where the actinide is a major component. Icenhower et al. performed dissolution experiments on titanate pyrochlores containing about 12 wt% PuO2,5 Nästren et al.17 synthesised Nd1.8An0.2Zr2O7 (where An = Pu, Am, Np, Th, U) pyrochlores by a liquid infiltration method into porous ceramic beads, and Gregg et al.18 used a modified alkoxide nitrate route to fabricate lanthanum zirconate pyrochlores. To the best of our knowledge, this is the first time a hydroxide co-precipitation route, for the formation of Pu-pyrochlores, has been reported in the literature. A wet-chemical co-precipitation route was adapted with the aim of ensuring homogeneous incorporation of Pu within the pyrochlore crystal structure. Samples doped with 5 and 10 mol% Pu were fabricated and the structural uptake was probed by complimentary experimental techniques (XRD, SEM, and XAS) supported by ab initio structural calculations. The data presented here provides new insights into the preferred mechanism of incorporation of Pu within the pyrochlore crystal structure.
Pyrochlore compounds have been extensively investigated by computational methods.10,19–34 Radiation induced effects such as damage cascade formation,21–23 amorphization,30 the energetics of defects formation,19,24–29,34 and order/disorder transitions10,20–23,34,35 have been studied, and the results used to support the interpretation of experimental results. Cleave et al.31 and Williford & Weber32 investigated the incorporation of Pu into a range of rare earth pyrochlore compounds. On the basis of computed solution energies they predicted the incorporation of Pu(III) onto the Nd-site in Nd2Zr2O7 as the most energetically preferable mechanism. We have directly tested this prediction in our studies. Recently, Perriot et al.33 have considered the behaviour of Pu(III) and Pu(IV) across pyrochlore-defect fluorite structural interfaces and predicted the preferential segregation of Pu(IV) into the disordered phase. It should be noted that all these studies were performed using a force-field approach with Buckingham-type interaction potentials between atoms. Li et al.34,36 have shown that, although such a force-field based approach often results in reasonable predictions, it can produce defect formation energies that are significantly different from those calculated from ab initio methods. Recently, Finkeldei et al.10 have shown that the formation enthalpies and structure of NdxZr1−xO2−0.5x pyrochlores can be accurately simulated by density functional theory (DFT)-based ab initio methods. Here we use the same approach to support the reported experimental results with the computation of Pu solution energies in Nd2Zr2O7 pyrochlore.
2. Experimental section
2.1 Fabrication of plutonium pyrochlore ceramics
The synthesis work described below was carried out in dedicated glovebox lines designed for the handling of alpha-emitting radioisotopes such as plutonium. All samples were prepared by a wet chemical precipitation or co-precipitation approach to obtain highly homogeneous ceramic powders. Aqueous standard solutions of 0.3 mol L−1 were prepared from ZrOCl2·8H2O and Nd(NO3)3·6H2O dissolved in de-ionised water. The concentrations of the solutions were checked by inductively coupled plasma optical emission spectrometry (ICP-OES). The precipitation of the hydroxides took place in a glovebox line with an air atmosphere, whereas the thermal treatment was carried out in a furnace in a glovebox line with an argon atmosphere. The Pu precursor used was plutonium nitrate (239Pu) which had been previously characterised by thermal analysis. The weight loss observed occurred in two steps which is in agreement with the reported thermal decomposition of Pu(NO3)4·xH2O (x = 3, 5) to PuO2, via a plutonylnitrate intermediate.37,38 The nitrate was found to be X-ray amorphous and on the basis of the former analysis assumed to have a stoichiometry of Pu(NO3)4·5H2O.39 Precautions such as acidification of the solutions and direct processing were taken to avoid the formation of a plutonium polymer.Slight modifications of the Pu-pyrochlore fabrication process led to two different synthesis procedures which are hereafter referred to as synthesis route 1 and synthesis route 2. To obtain highly homogeneous materials, the synthesis of 239Pu-pyrochlore was carried out by a co-precipitation route which was developed by the authors.40 A stoichiometric Nd2Zr2O7 pyrochlore was synthesised at the same time to serve as a reference. To synthesise 4 mmol Nd2Zr2O7, 8 mmol of aqueous Nd(NO3)3 and ZrOCl2 solutions (diluted to a concentration of 0.1 mol L−1) were mixed and transferred (1–3 drops per s) into 100 mL of conc. NH4OH solution to co-precipitate the hydroxides. The precipitate was separated from the supernatant by centrifuging (4000 rpm, 10 min) and the supernatant was subsequently checked for complete precipitation. Six washing steps were performed on the precipitate, each using 250 mL of deionised water, until the washing water was free of chloride and nitrate. The absence of chlorine and nitrates was confirmed using dipsticks (Macherey-Nagel). The precipitate was transferred into the inert gas glovebox line and dried at 60 °C. After grinding, a calcination step was performed at 600 °C for 2 h with a heating and cooling rate of 4.8 °C min−1. After a second grinding step two pellets were pressed in a 6 mm die at 707 MPa. The pellets were sintered under reducing atmosphere (Ar-5% H2) at 1450 °C for 10 h. A heating and cooling rate of 200 °C h−1 was used. One of the pellets was subsequently crushed for analysis by XRD.
| Sample | Targeted chemical formula | Synthesis route | n(Nd) (mmol) | n(Pu) (mmol) | n(Zr) (mmol) |
|---|---|---|---|---|---|
| SF-70 | Nd2Zr2O7 | 1 | 8 | — | 8 |
| SF-74-P1 | Nd1.8Pu0.2Zr2O7 | 1 | 2.39 | 0.265 | 2.65 |
| SF-74-P2 | Nd1.8Pu0.2Zr2O7 | 1 | |||
| SF-77-P1 | Nd1.9Pu0.1Zr2O7 | 2 | 1.28 | 0.0675 | 1.35 |
| SF-77-P2 | Nd1.9Pu0.1Zr2O7 | 2 |
| Sample | Mass (mg) | Calcination heating rate (°C h−1) | Sintering dwell time (h) | Sintering heating rate (°C h−1) |
|---|---|---|---|---|
| SF-74-P1 | 348.6 | 200 (h and c) | 25 | 200 (h and c) |
| SF-74-P2 | 302.7 | 200 (h and c) | 80 | 100 (h)/200 (c) |
| SF-77-P1 | 80.9 | 100 (h)/200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (c) (c) |
80 | 100 (h)/200 (c) |
| 5* | 100 (h)/200 (c) | |||
| SF-77-P2 | 179.6 | 100 (h)/200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (c) (c) |
80 | 100 (h)/200 (c) |
2.2 Characterisation
The equipment used for the characterisation of the pyrochlores is specified below.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 057 eV) and the Zr K (17
057 eV) and the Zr K (17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 998 eV) edges. The following scanning intervals were used (energy values relative to E0): −170 eV to −30 eV (step size 5 eV, 2 second integration time), −30 eV to 30 eV (step size 0.5 eV, 2 second integration time), and 30 eV to 12.5k (step size 0.035k, 0.5k integration time). Several scans were taken for each sample and summed to improve the signal-to-noise ratio. Energy calibration of the monochromator was performed by collecting spectra from a Zr metal foil; the edge position of the foil (measured at the first inflection in the derivative of the absorption) was aligned to the expected value of 17
998 eV) edges. The following scanning intervals were used (energy values relative to E0): −170 eV to −30 eV (step size 5 eV, 2 second integration time), −30 eV to 30 eV (step size 0.5 eV, 2 second integration time), and 30 eV to 12.5k (step size 0.035k, 0.5k integration time). Several scans were taken for each sample and summed to improve the signal-to-noise ratio. Energy calibration of the monochromator was performed by collecting spectra from a Zr metal foil; the edge position of the foil (measured at the first inflection in the derivative of the absorption) was aligned to the expected value of 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 998 eV. Due to the overlap of the Pu and Zr absorption edges data was collected in fluorescence mode on sintered pellet samples contained in a double ultra-high-molecular-weight polyethylene (UHMWPE) containment. The INE beamline is a bending magnet beamline which provides an operating X-ray energy range between 2.1 and 25 keV. The optical setup comprises a Ge(422) double crystal monochromator and Rh coated silicon mirrors to focus the beam down to a 500 μm by 500 μm spot. The incident X-ray intensity was measured using a gas filled ionisation chamber and the emitted fluorescence X-ray photons intensity was measured using a 4 element silicon drift detector (Vortex, SII NanoTechnology). For collection of the Zr Kα1 fluorescence photons (15
998 eV. Due to the overlap of the Pu and Zr absorption edges data was collected in fluorescence mode on sintered pellet samples contained in a double ultra-high-molecular-weight polyethylene (UHMWPE) containment. The INE beamline is a bending magnet beamline which provides an operating X-ray energy range between 2.1 and 25 keV. The optical setup comprises a Ge(422) double crystal monochromator and Rh coated silicon mirrors to focus the beam down to a 500 μm by 500 μm spot. The incident X-ray intensity was measured using a gas filled ionisation chamber and the emitted fluorescence X-ray photons intensity was measured using a 4 element silicon drift detector (Vortex, SII NanoTechnology). For collection of the Zr Kα1 fluorescence photons (15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 775 eV) the detector was windowed over a range of 15
775 eV) the detector was windowed over a range of 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200–16
200–16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 eV. For collection of the Pu Lα1 fluorescent photons (14
300 eV. For collection of the Pu Lα1 fluorescent photons (14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 288 eV) the detector was windowed over a narrow range between 14
288 eV) the detector was windowed over a narrow range between 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 050 and 14
050 and 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 eV. The narrow range was required to remove any interference from the Zr Kα photons which were contributing a large signal in this energy region due to the high relative concentration of Zr, in relation to Pu, in the samples. No spectra were recorded at a Nd LIII edge (7126 eV) due to the high attenuation of low energy X-rays by the sample and the holder.
400 eV. The narrow range was required to remove any interference from the Zr Kα photons which were contributing a large signal in this energy region due to the high relative concentration of Zr, in relation to Pu, in the samples. No spectra were recorded at a Nd LIII edge (7126 eV) due to the high attenuation of low energy X-rays by the sample and the holder.
XAS data on Nd2Zr2O7 and the Zr reference standards were collected at the Zr K edge on beamline X23A2 of the now decommissioned National Synchrotron Light Source (NSLS) at the Brookhaven National Laboratory (BNL). The following scanning intervals were used (energy values relative to E0); −200 eV to −20 eV (step size 1 eV, 1 second integration time), −20 eV to 30 eV (step size 0.3 eV, 1 second integration time), and 30 eV to 15k (step size 0.05k, 0.5k integration time). Energy calibration of the monochromator was performed by collecting spectra from a Zr metal foil; the edge position of the foil (measured at the first inflection in the derivative of the absorption) was aligned to the expected value of 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 998 eV. Data were acquired in transmission mode using finely ground powder specimens dispersed in polyethylene glycol (PEG) to give a thickness of one absorption length. X23A2 consisted of an unfocused bending magnet beamline (4.9 to 32 keV) with an optics setup incorporating a Si(311) monochromator with a fixed exit Golovchenko–Cowan design, and a single bounce flat Rh-coated harmonic rejection mirror. Slits were employed to reduce the beam size to 7 mm in the vertical and 0.5 mm in the horizontal. The incident and transmitted X-ray intensities were measured using gas filled ionisation chambers.
998 eV. Data were acquired in transmission mode using finely ground powder specimens dispersed in polyethylene glycol (PEG) to give a thickness of one absorption length. X23A2 consisted of an unfocused bending magnet beamline (4.9 to 32 keV) with an optics setup incorporating a Si(311) monochromator with a fixed exit Golovchenko–Cowan design, and a single bounce flat Rh-coated harmonic rejection mirror. Slits were employed to reduce the beam size to 7 mm in the vertical and 0.5 mm in the horizontal. The incident and transmitted X-ray intensities were measured using gas filled ionisation chambers.
All raw data was processed using the Athena software and EXAFS analysis was performed using FEFF6 and the Artemis program.43 The Zr k-edge data was corrected for self-absorption using the Troger algorithm.44 The Pu LIII edge data was not corrected as self-absorption is not a concern when working in the dilute limit.45
 | (1) |
2.3 Molecular simulation
The atomistic modelling studies of Pu incorporation into the Nd2Zr2O7 pyrochlore structure were performed using the density functional theory (DFT)-based Quantum-ESPRESSO simulation package.48 In order to make reliable predictions of the energetics of Pu incorporation the PBE exchange–correlation functional was applied.49 This methodology has previously been successfully employed in studies of actinide containing systems50,51 and NdxZr1−xO2−0.5x pyrochlores-type compounds, including Nd2Zr2O7.10,34 As in these previous studies, the PBEsol functional52 was used to obtain better geometries of selected atomic configurations. The core electrons of the constituent atoms were modelled with ultrasoft pseudopotentials53 and the 6s2 6p6 6d2 7s2 electrons (plus 5f electrons in DFT + U calculations) of the Pu atoms were computed explicitly. Based on previous experience in computing f elements-bearing systems, 50 Ryd was selected as the plane-wave energy cut-off.51 Pu has strongly correlated 5f electrons therefore the correlation effects were computed using the DFT + U approach as a correction to the regular DFT calculations. This approach has previously been successfully applied to simulate NdxZr1−xO2−0.5x pyrochlore-type systems10 however, because the computed correlation effects for Nd atoms in Nd2Zr2O7 are negligibly small,10 the focus in this study was on the correlation effects associated with the Pu atoms only. The Hubbard U parameter values for Pu(III) and Pu(IV) applied in this study were 2.0 eV and 2.7 eV, respectively. These representative values were taken from Beridze et al.51 and were derived from a series of Pu-bearing compounds using the linear response method.54Following our methodology from previous studies,10,34,36 the Nd2Zr2O7 pyrochlore structure was represented by an 88 atoms cubic supercell and calculations were performed on the 2 × 2 × 2 Methfessel–Paxton k-point grids.55 The solution energies of the Pu atoms was computed assuming the following reactions:
Incorporation of Pu(III) on the Nd (A) site:
 | (2) |
Incorporation of Pu(III) on the Zr (B) site:
 | (3) |
Incorporation of Pu(IV) on the Zr (B) site:
 | (4) |
Incorporation of two Pu(IV) on the Nd (A) site with subsequent introduction of an oxygen atom on an oxygen vacancy site:
 | (5) |
Incorporation of three Pu(IV) on the Nd (A) site with subsequent introduction of one Nd vacancy:
 | (6) |
Incorporation of Pu(III) on the Nd (A) or Zr (B) site via the reduction of Pu(IV):
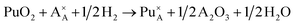 | (7) |
 | (8) |
In all the above reactions the reference reactant state chosen for Pu was PuO2. Reactions (2), (3), (7) and (8) would only be relevant under reducing synthesis conditions such as those used during this study. The rationale behind using the same Pu reference state for all reactions was to allow direct comparison of the resulting reaction enthalpies. This approach differs from previous reported modelling studies,31–33 in which Pu2O3 has been used as the reference for reactions involving incorporation of Pu(III). Because different pseudopotentials were applied for Pu(III) and Pu(IV) when performing DFT calculations with 5f electrons included in the pseudopotential core, we used Pu2O3 as the reference for reactions leading to the formation of Pu(III). However, because PuO2 was used as the reference reactant in all of the above mentioned reactions, the standard enthalpy difference between Pu2O3 and PuO2 of 232 kJ mol−1 (ref. 56) was added to the relevant reaction enthalpies computed with Pu2O3. To obtain solution energies for reaction (7) and (8) the standard formation enthalpy of water gas (−241.8 kJ mol−1 = −1.25 eV) was added to the solution energies of reactions (2) and (3), respectively. In order to find the most energetically favourable Pu incorporation mechanism, allowed by the 88 atoms supercell, Pu incorporation configurations were calculated.
3. Results and discussion
3.1 Synthesis routes and X-ray diffraction (XRD)
Synthesis route 1 involved precipitation of the plutonium hydroxide prior to Nd- and Zr-hydroxide formation; this allows the two steps to be studied separately. However, to allow for a co-precipitation of all three hydroxides and the formation of a homogeneous precursor at the molecular level, the metal salt solutions of plutonium, neodymium and zirconium were mixed prior to precipitation, in synthesis route 2. The Nd- and Zr-metal salt solution was acidified and the concentration of the Pu-solution was reduced to c(Pu) = 0.01 mol L−1. All thermal treatments were carried out under reducing conditions with the intention to reduce Pu(IV) to Pu(III), which should occupy the A-site in pyrochlore.The presence of a Pu(IV) species was reported by Toth et al.57 for 0.05 mol L−1 Pu(NO3)4 in 0.11 M HNO3. Disproportionation reactions led to the presence of additional Pu species so the Pu(NO3)4 was always freshly dissolved in 1 M HNO3 prior to being used. Calculations of the thermodynamic equilibrium Pu species were carried out with GEMS using the NAGRA-PSI database,58 according to the experimental conditions of synthesis route 1 in the presence of 1 kg water. The calculations indicated aqueous plutonyl PuO22+ to be the predominant species. It should be noted however, that the GEMS calculations can only predict the thermodynamic equilibrium and no kinetic effects of the reaction are taken into account. Clark et al.59 reported Pu(IV) to be unstable if it comes into contact with oxygen but the rate for this reaction was found to be negligible. The presence of Pu(VI) has also been described by Glazyrin et al.60 in 1–5 M HNO3 at 90 °C. In the present study the presence of Pu(VI) was not expected as the solutions were always freshly prepared prior to each synthesis and directly consumed. The disproportionation reaction of Pu(IV) in acidic solutions is given below:
| 3Pu4+ + 2H2O ↔ 2Pu3+ + PuO22+ + 4H+ | (9) |
The fourth order dependence of the disproportionation on [H+] makes this reaction highly unlikely to occur. Under strongly acidic conditions59 there was no experimental observation for the disproportionation reaction having taken place. Therefore, the dissolution of Pu(NO3)4 in 1 M HNO3 at room temperature is assumed to result in a Pu(IV) solution. In addition, sintering of the resulting powders takes place under reducing conditions which makes the oxidation state in the solution less critical for the final product.
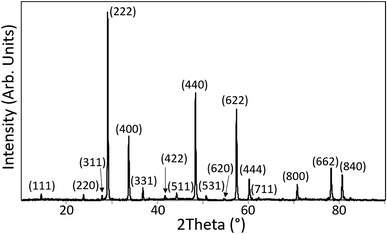
For both synthesis routes all thermal treatments were carried out under reducing atmosphere to promote the reduction of Pu(IV) to Pu(III) and inhibit the formation of PuO2 as a discrete phase. For synthesis route 2 the sintering duration was extended to 80 h, because the kinetics of the reduction of Pu(IV) to Pu(III) and the incorporation mechanism of Pu into the pyrochlore structure are not well understood. Two Nd2(Zr1.9Pu0.1)O7 pellets were pressed and sintered for 80 h to reduce the plutonium to Pu(III). One of the pellets was ground and the powder characterised by XRD. The XRD patterns obtained for the pure Nd2Zr2O7 compound and 5 and 10 mol% Pu doped compounds contained reflections which could all be attributed to a pyrochlore structured phase. Fig. 1 shows the pattern acquired from Nd1.9Pu0.1Zr2O7 which is representative of all the samples. The powder was subsequently pressed and re-sintering to be used for SEM characterisation.
Previous studies in the literature concerning the fabrication of plutonium pyrochlores lack a thorough analysis of both the structural incorporation and the oxidation state of Pu. Kulkarni et al.61 prepared a Pu2Zr2O7 pyrochlore via a solid state route under helium atmosphere. They ascribed an observed weight loss between 1000–1400 °C to the reduction of Pu(IV) to Pu(III) driven by oxidation of graphite present in the system. They observed a linear decrease of the lattice parameter in the series (PuxLa1−x)2Zr2O7 (where x = 0.0–1.0) with an increase in Pu content. This is consistent with a reduction in the average size of the A-site cation, because both Pu(IV) and Pu(III) have a smaller ionic radius in eightfold coordination than La(III). Although the authors stated that a weight gain could be observed when the samples were re-oxidised no direct measurement of the Pu oxidation state was provided. Burakov et al.7 reported the fabrication of Pu-238 doped titanate pyrochlores via a modified solid state route. A plutonium nitrate solution was added to a mixture of inactive oxide precursors and subsequently calcined and sintered in air. No specific details were provided in the publication but it is assumed that denitration of the plutonium nitrate occurred yielding PuO2, prior to a further solid state reaction resulting in the formation of the target phase. There was no characterisation of the plutonium oxidation state or structural environment and based on the analysis provided it is unclear as to whether the samples were homogenous.
3.2 Scanning electron microscopy (SEM) and energy dispersive X-ray spectroscopy (EDX)
The Nd1.9Pu0.1Zr2O7 pellet prepared via synthesis route 2, was further characterised by SEM and EDX. Fig. 2(a) shows a secondary electron (SE) image of the pellet surface; the areas where EDX spot measurements were made are marked. The elemental distribution was probed by mapping the surface of the pellet. The maps are shown in Fig. 2(c–e) and they indicate a homogeneous distribution of Pu, Zr, and Nd. The surface imperfection, visible on the right side of the pellet in Fig. 2(a), is either an artefact of the sintering process or material deposited during the surface coating process. It was not possible to prepare the surface of the sample using metallographic techniques prior to the analysis but there was no indication that this region was chemically dissimilar to the rest of the pellet. | ||
| Fig. 2 (a) SE image of the coated pellet (synthesis route 2) where the numbers indicate the regions where EDX measurements were made; (b) overview of the pellet for elemental EDX mapping; (c) Pu distribution; (d) Zr distribution; (e) Nd distribution. In total 20 frames were collected for the EDX mappings. Adapted from ref. 40. | ||
EDX measurements of the composition, at the four spots of interest in Fig. 2(a) indicated a mean Pu content of 5.4 at%, and that the Pu was distributed homogeneously at locations 1, 2 and 3 within the limit of sensitivity for the technique. The measurement at location 4 was taken from an agglomeration of ceramic grains, with a diameter of about 40 μm, located in the cavity shown Fig. 3(d). The plutonium content at this location was 7.8 at% which is approximately one and a half times higher than the value measured at locations 1, 2, and 3. The microstructure of the four locations were subsequently characterised in more detail. Fig. 3(a–c) show location 1 at three different magnifications. The microstructure is composed of primary grains between 1–5 μm in diameter as seen in Fig. 3(c). The pellet surface appears porous and is covered with small grains. This may be caused by the grinding of the pellet and the relatively short sintering time of 5 h after the repressing step. The difference in the brightness of the smaller grains, with respect to the larger ones, is related to non-uniformities in the conductive surface coating.
 | ||
| Fig. 3 (a–c) SE images of location 1 taken at different magnifications; (d) magnification of location 4. Taken from ref. 40. | ||
There is no indication of any gross differences in chemical composition, or the presence of any secondary phases in the sample, which is consistent with the XRD analysis and confirms that a single phase Pu-pyrochlore has been formed.
The wet-chemical synthesis routes, used in this work, could plausibly result in three possible scenarios for the charge and position of plutonium within the pyrochlore crystal lattice:
(1) The synthesis conditions will promote reduction of Pu(IV) in the starting precursor and formation of a pyrochlore with Pu(III) on the A-site. Nästren et al.17 reported the formation of a single phase Pu-doped neodymium pyrochlore, containing Pu(III), under reduction conditions (Ar/H2). It was not indicated whether the Pu was added in the tri- or tetra-valent state so it is unclear as to whether the processing environment had driven the reduction from Pu(IV) to Pu(III) or simply stabilised the Pu(III) already present. This processing route led to Pu(III) being accommodated in eightfold coordination at the A-site in the pyrochlore structure with no charge compensation required. Gregg et al. reported the synthesis of La1.9Pu0.1Zr2O7via a modified alkoxide route using PuO2 dissolved in nitric acid and observed the formation of a near single phase pyrochlore with Pu(III) present at the A-site.18
(2) The kinetics of the pyrochlore crystallisation process may be faster than the reduction of the Pu in the precursor from Pu(IV) to Pu(III). This could lead to the formation of the pyrochlore with Pu(IV) occupying the A-site. It is also plausible that Pu(IV) could be incorporated onto the B-site however this would require substitution of Zr onto the A-site which seems unlikely based on the relative ionic size difference between Nd(III) and Zr(IV) in eightfold coordination.
(3) The synthesis conditions are inadequate to reduce Pu(IV) to Pu(III) during the thermal treatment. In this case Pu(IV) could occupy either the A-site or the B-site. Mixed occupancy of both sites is also possible.
To resolve these questions EXAFS and XANES measurements were carried out at the ANKA-INE beamline. Complimentary atomistic simulation studies were also performed.
3.3 XAS
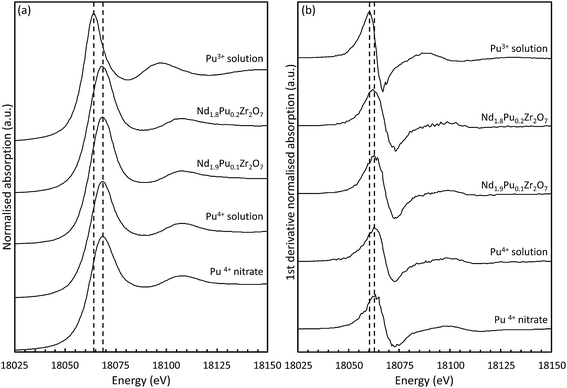 | ||
| Fig. 4 (a) Normalised absorption spectra of the pyrochlore samples compared to the two liquid plutonium standards and the original Pu(NO3)4 starting material;42 (b) first derivative of the Pu LIII absorption edge for the samples and standards. | ||
| Compound | Edge energy (eV) | Peak energy (eV) | Valence state |
|---|---|---|---|
| Pu(III) 1 M HClO4; [Pu] 30 mM | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 060.2 060.2 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 064.1 064.1 |
3 |
| Pu(NO3)4 precursor | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 063.4 063.4 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 068.6 068.6 |
4 |
| Pu(IV) 1 M HClO4; [Pu] 30 mM | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 065.1 065.1 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 068.9 068.9 |
4 |
| Pu(IV) 1 M HClO4; [Pu] 4 mM | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 063.9 063.9 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 068.9 068.9 |
4 |
| Nd1.9Pu0.1Zr2O7 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 063.4 063.4 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 068.7 068.7 |
3.98 |
| Nd1.8Pu0.2Zr2O7 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 062.8 062.8 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 068.4 068.4 |
3.92 |
The absorption edge energy is primarily determined by the charge of the central Pu atom although the exact position, and shape, will be modified by the degree of electron transfer to the surrounding ligands. In the case of the lower valence actinides (Act) there is a monotonic increase in the energy of the absorption edge with valence however a discontinuity arises between Act(IV) and Act(V) which is related to the formation of trans-dioxo species.63,64 For the case of Pu aquo-complexes (prepared in 1 M HClO4) clear differences in the shape of the near-edge spectra for the dioxo-containing species were reported.65 Multiple scattering (MS) events along the dioxo-species give rise to a feature at approximately 15 eV above the white line which has also been well documented in U and Np compounds.66,67 The absence of this feature in our data indicates that no short Pu–O bonds are being formed and excludes the presence of dioxo-species in these samples. The shape of the edge is sensitive to both the local coordination environment and the electronegativity of the connecting ligands. The features in the Act L3 XANES are therefore determined, to some extent, by the photoelectron scattering paths and not simply by the occupancy of the 6d electronic orbitals.62 It is therefore necessary to select appropriate standards and the correct methodology for assigning valence; comparison of data from a range of aquo-, aquochloro-, aquonitrato-, and carbonato-complexes indicated that the shift in the inflection point on the absorption edge is far more sensitive to changes to the extended chemical environment than the valence of the central Pu cation.62 These changes can influence the interpretation of unknown compounds; asymmetry in the white line will influence the determination of the edge energy, from the first inflection point on the absorption edge, and care should be exercised to allow unambiguous assignment of the valence state. Soldatov et al. demonstrated this effect in tertiary U oxides.68 As can be seen in Table 3 there is a wide spread in the edge energy position for the Pu(IV) standards but the peak energies are more tightly clustered. It was therefore decided to determine the oxidation state of the samples from the peak energy. An average peak energy was calculated for the Pu(IV) standards and a linear change in peak position with oxidation state was assumed. The results presented here for the standards are in good agreement with those published previously.18,65 The tabulated values for the sample oxidation states were then determined by interpolation; the results indicate that for both pyrochlore samples the majority of the Pu is the tetravalent oxidation state, which is unexpected given that the samples were fired under reducing conditions. The isostructural Pu2Zr2O7 and Am2Zr2O7 compounds are known to form when heated under a hydrogen (4% in Ar) atmosphere at 1500 °C (10–20 hours dwell time).69 Shoup et al.70 described the synthesis of monoclinic Pu2Ti2O7 by solid state reaction under the same atmosphere. PuO2 was used as a starting material and TiN was used as a titanium source. The combination of the reducing agent (TiN), a reducing atmosphere, and long heating times resulted in the Pu being stabilised in the Pu(III) oxidation state. Gregg et al. reported an almost complete reduction of the plutonium in (La1.9Pu0.1)Zr2O7 when synthesised under hydrogen (N2–3.5% H2) at 1450 °C (24 hours dwell time).18 Similar results were also reported by Naestren at low dopant concentration although they used a significantly higher sintering temperature (1650 °C) and a metal furnace.17 Although our findings differ from previously published results it is worth considering the fact that differences in Pu content, processing conditions, and heat treatment parameters will have an effect on the final Pu oxidation state. It should also be noted that the experimental results are consistent with the results of the molecular modelling (Section 3.4). These suggest that the most energetically favourable mechanism is for the Pu to be incorporated as Pu(IV) on the Nd(III) site with the introduction of oxygen atoms into oxygen vacancy sites.
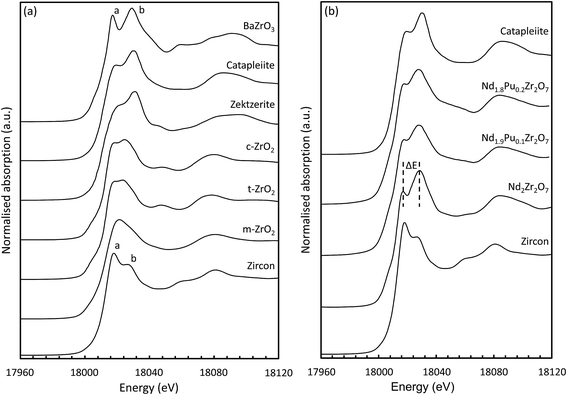 | ||
| Fig. 5 (a) Zirconium k-edge XANES spectra for standard compounds; (b) selected standards overlaid with the data from the pyrochlore samples. | ||
Inspection of the K-edge XANES region of the spectra from these materials shows marked differences in the shape and relative intensity of the individual components of the doublet (indicated by a and b in Fig. 5(a)) on the absorption edge.72 The octahedrally coordinated Zr standard (ZrSiO4) is characterised by a larger intensity component on the low energy side of the doublet whilst for the six-fold coordinated standard (BaZrO3) the component on the high energy side is more intense. These two features appear at approx. 6 and 15 eV above the position of the edge (E0) and can be used as a qualitative diagnostic for the average coordination environment of the Zr. When Zr is situated in a highly centro-symmetric environment then the splitting between the two features is far more pronounced; this can be seen clearly in the data obtained from the BaZrO3 sample. Lee et al. observed that the splitting (ΔE) increased with increasing crystal symmetry in Gd2Zr2O7 samples prepared by the Pechini method and processed at different temperatures.80 Samples processed at lower temperatures adopted a more disordered structure and had a smaller ΔE. Similar trends were shown by Li et al.77 in their study on different zirconia polytypes, indicating that the k-edge absorption spectra provide a useful tool for studying order/disorder. Changes in the relative intensity of the two features also indicate a change in the local Zr structural environment. In the yttria doped zirconia system a slight increase in the relative intensity of a in conjunction with a small shift in b to lower energy was characteristic of an increase in the average Zr–O coordination number.81
Data acquired at the Zr k-edge for the pyrochlore samples (Nd2−xPuxZr2O7; where x = 0.0, 0.1, and 0.2) are shown in Fig. 5(b) together with the reference spectra from catapleiite and zircon. All three spectra show a marked similarity to catapleiite indicating that the Zr is six-fold coordinated. This result is consistent with the expected crystal structure for Nd2Zr2O7,82 and the X-ray diffraction results presented in Section 3.1. Semi-quantitative inspection of the spectra shows that the splitting between the two features is reduced for the Pu doped samples suggesting that the local Zr environment is being distorted by the introduction of Pu cations on the A-site in the pyrochlore structure. This is not unexpected given the 13.3% difference in ionic radii, between eight-fold coordinated Nd(III) (IR = 1.109 Å) and Pu(IV) (IR = 0.962 Å).83 A small contraction in the average size of the A-site alongside an increase in the local structural distortion would be anticipated when Nd is replaced with smaller Pu cations. Changes in the relative intensity of the a and b features are also observed with increasing Pu content consistent with the introduction of Pu(IV) on the Nd(III) site and subsequent charge balance by the filling of oxygen vacancies associated with the Zr.
The local structural environment around the Pu atoms was investigated by quantitative analysis of the EXAFS region of the Pu LIII-edge data. In order to refine the contact distances, between the central absorbing Pu atoms and the nearest neighbour coordination shells, a structural model was required. The structure of rare earth zirconate pyrochlores are well reported in the literature; in this study the structure of Nd2Zr2O7 refined by Harvey et al.82 was used as the starting model. The Pu was targeted for incorporation on the A-site of the pyrochlore structure which is characterised as having eight nearest neighbours; six longer A–O48f bonds and two shorter A–O8b bonds. As a first approximation, a structural model containing two scattering paths was used to represent the two different A–O bond lengths. The degeneracies of the paths were weighted accordingly and a mean square displacement parameter σ2(O1) was used to model the thermal vibrations of the nearest neighbour oxygens. The amplitude reduction factor (S02) and the shift in the edge energy (ΔE0) were also allowed to vary. It should be noted at this stage the fitted k and R ranges were restrained to only model the signal in the FT k3χ(k) at approx. 1.8 Å (uncorrected for phase shift). This model gave a fit to the data which was deemed unacceptable due to the large refined value of ΔE0 and negative mean square displacement parameters. This result suggests that the Pu first shell environment is significantly distorted from that of the classic pyrochlore A-site structural motif. The degeneracies of the two Pu–O1 paths were then inverted to give six short Pu–O1s paths and two longer Pu–O1l paths. This approach yielded a reasonable fit with sensible values for the S02, ΔE0, and the mean square displacement parameters. In order to confirm the robustness of the model the electron reduction factor S02 was fixed at the value refined previously, and the degeneracy of the two Pu–O1 paths were allowed to vary. This method returned a fit where the degeneracies converging towards six for the short Pu–O1s path and two for the longer Pu–O1l path. For completeness, an attempt to fit a single oxygen shell around the Pu was made. Fitting a structural environment like Zr in Nd2Zr2O7 failed returning an unacceptably large S02 and a negative mean square displacement parameter. Efforts to fit a single environment with eight nearest neighbour oxygen atoms were also unsuccessful, indicating that the environment around the Pu atoms is significantly distorted.
In order to satisfactorily fit the spectral features at higher radial distance, additional scattering paths were added to the model. This took into account the Pu–Nd, Pu–Zr1, Pu–O2, Pu–O3, Pu–Zr2, and Pu–O4 scattering paths; where applicable an appropriately weighted scattering path was chosen to model all like atom pairs at similar distances. Fractional occupancy of plutonium was incorporated by inclusion of a Pu–Pu scattering path. The available scattering paths are generated by the FEFF algorithm which uses ab initio theory to calculate multiple scattering paths based on a given structural model.84 The structural model used is taken from a crystallographic input file often referred to as a CIF.85 In order to allow FEFF to generate the additional Pu–Pu scattering path the CIF was modified by changing one of the six second shell neighbours from a Nd atom to a Pu atom. This change alone would result in a fractional occupancy of 0.167 formula units Pu on the A-site. In order to correctly model the fractional occupancy, the contribution (amplitude) of the resulting Pu–Pu scattering path was multiplied by a factor of x/(1/6) and the Pu–Nd scattering paths were multiplied by a factor of (1−x)/(5/6), where x is the fraction of Pu atoms on the A-site.
This produced a model which afforded a good fit (R-factor = 2%) to the main features in both the k3χ(k) waveform and the FT k3χ(k) spectral envelope out to a k of 11 Å−1 and an R of 5.5 Å, respectively. The fits to both data sets are shown in Fig. 6 and the refined model parameters are shown in Table 4. The data were modelled with thirteen independent variables: two variables related to the overall EXAFS scattering process (S02 and E0) and eleven variables related to nine independent single scattering path lengths and associated mean squared displacement parameters. The average nearest neighbour Pu–O bond lengths were determined to be 2.35 Å ± 0.03 for Nd1.9Pu0.1Zr2O7, and 2.33 Å ± 0.03 for Nd1.8Pu0.2Zr2O7. These values are smaller than the weighted mean Nd–O bond length (2.52 Å) from the crystal structure published by Harvey et al.82 although this is sensible given that the ionic radius of Pu(IV) in eight-fold coordination (0.962 Å) is smaller than that of Nd(III) (1.109 Å).83 Independent validation of the refined path lengths can be performed using the bond valence sum approach.46 The bond valence sums determined from the refined EXAFS models were 3.9 ± 0.1 valence units (v.u.) for Nd1.9Pu0.1Zr2O7, and 4.0 ± 0.1 v.u. for Nd1.8Pu0.2Zr2O7. Both differ by less than 5% from the formal Pu valence of 4 v.u.
 | ||
| Fig. 6 (a) k3 weighted Pu LIII-edge EXAFS for the pyrochlore samples; (b) the Fourier transform of the EXAFS in R space. | ||
| Nd1.9Pu0.1Zr2O7 | Nd1.8Pu0.2Zr2O7 | |||
|---|---|---|---|---|
| ± | ± | |||
| E 0(eV) | 5.5 | 0.9 | 3.25 | 1.1 |
| R(Pu–O1s) (Å) | 2.29 | 0.01 | 2.27 | 0.02 |
| N(Pu–O1s) | 6 | — | 6 | — |
| R(Pu–O1l) (Å) | 2.52 | 0.03 | 2.51 | 0.03 |
| N(Pu–O1l) | 2 | — | 2 | — |
| Avg. R(O1) | 2.35 | 0.03 | 2.33 | 0.03 |
| Total N(O1) | 8 | — | 8 | — |
| σ 2(O1) (Å2) | 0.008 | 0.002 | 0.008 | 0.002 |
| R(Pu–Pu) (Å) | 3.76 | 0.04 | 3.85 | 0.20 |
| N(Pu–Pu) | 0.3 | — | 0.6 | — |
| σ 2(Pu) (Å2) | 0.012 | 0.004 | 0.050 | 0.080 |
| R(Pu–Nd) (Å) | 3.76 | 0.04 | 3.85 | 0.20 |
| N(Pu–Nd) | 5.7 | — | 5.4 | — |
| σ 2(Nd) (Å2) | 0.012 | 0.004 | 0.050 | 0.080 |
| R(Pu–Zr1) (Å) | 3.67 | 0.03 | 3.63 | 0.03 |
| N(Pu–Zr1) | 6 | — | 6 | — |
| σ 2(Zr1) (Å2) | 0.010 | 0.001 | 0.010 | 0.002 |
| R(Pu–O2) (Å) | 4.06 | 0.06 | 3.99 | 0.04 |
| N(Pu–O2) | 12 | — | 12 | — |
| σ 2(O2) (Å2) | 0.008 | 0.002 | 0.008 | 0.002 |
| R(Pu–O3) (Å) | 4.32 | 0.05 | 4.73 | 0.07 |
| N(Pu–O3) | 6 | — | 6 | — |
| σ 2(O3) (Å2) | 0.008 | 0.002 | 0.008 | 0.002 |
| R(Pu–Zr2) (Å) | 5.25 | 0.03 | 5.23 | 0.06 |
| N(Pu–Zr2) | 6 | — | 6 | — |
| σ 2(Zr2) (Å2) | 0.010 | 0.001 | 0.010 | 0.002 |
| R (Pu–O4) (Å) | 5.55 | 0.05 | 5.59 | 0.07 |
| N(Pu–O4) | 12 | — | 12 | — |
| σ 2(O4) (Å2) | 0.008 | 0.002 | 0.008 | 0.002 |
| R-factor | 0.02 | — | 0.05 | — |
| BVS (v.u.) | 3.9 | 0.1 | 4.0 | 0.1 |
 | ||
| Fig. 7 (a) k3 weighted Zr k-edge EXAFS for the pyrochlore samples; (b) the Fourier transform of the EXAFS in R space. | ||
| Nd2Zr2O7 | Nd1.9Pu0.1Zr2O7 | Nd1.8Pu0.2Zr2O7 | ||||
|---|---|---|---|---|---|---|
| ± | ± | ± | ||||
| E 0 (eV) | −4.2 | 1.8 | −3.7 | 1.4 | −2.3 | 1.7 |
| R(Zr–O1) (Å) | 2.10 | 0.02 | 2.09 | 0.02 | 2.10 | 0.02 |
| N(Zr–O1) | 6 | — | 6 | — | 6 | — |
| σ 2(O1) (Å2) | 0.004 | 0.002 | 0.004 | 0.003 | 0.005 | 0.004 |
| R(Zr–Nd) (Å) | 3.79 | 0.04 | 3.80 | 0.03 | 3.83 | 0.05 |
| N(Zr–Nd) | 6 | — | 5.7 | — | 5.4 | — |
| σ 2(Nd) (Å2) | 0.007 | 0.007 | 0.005 | 0.009 | 0.006 | 0.010 |
| R(Zr–Pu) (Å) | — | — | 3.81 | 0.03 | 3.83 | 0.05 |
| N(Zr–Pu) | — | — | 0.3 | — | 0.6 | — |
| σ 2(Pu) (Å2) | — | — | 0.005 | 0.009 | 0.006 | 0.010 |
| R(Zr–Zr) (Å) | 3.80 | 0.03 | 3.81 | 0.03 | 3.84 | 0.03 |
| N(Zr–Zr) | 6 | — | 6 | — | 6 | — |
| σ 2(Zr) (Å2) | 0.004 | 0.003 | 0.003 | 0.005 | 0.004 | 0.006 |
| R(Zr–O2) (Å) | 4.09 | 0.09 | 4.17 | 0.14 | 4.25 | 0.20 |
| N(Zr–O2) | 6 | — | 6 | — | 6 | — |
| σ 2(O2) (Å2) | 0.004 | 0.002 | 0.004 | 0.003 | 0.004 | 0.004 |
| R-factor | 0.03 | — | 0.06 | — | 0.09 | — |
| BVS (v.u.) | 3.9 | 0.1 | 4.0 | 0.1 | 4.0 | 0.1 |
The same approach was used to fit the EXAFS data from the Pu doped samples. In order to incorporate fractional occupancy of Pu on the A-site, and therefore a contribution from a Zr–Pu scattering path, the model was modified. In order to allow FEFF to generate the additional Zr–Pu scattering path the CIF was modified by changing one of the six second shell neighbours from a Nd atom to a Pu atom. This change alone would result in a fractional occupancy of 0.167 formula units Pu on the A-site. In order to correctly model the fractional occupancy, the contribution (amplitude) of the resulting Zr–Pu scattering path was multiplied by a factor of x/(1/6) and the Zr–Nd scattering paths were multiplied by a factor of (1−x)/(5/6), where x is the fraction of Pu atoms on the A-site. The (Nd2−xPux)Zr2O7 (x = 0.1 and 0.2) data sets were fitted using this modified model with the results shown in Fig. 7 and Table 5. The modified model provided acceptable fits to the EXAFS data with the Zr–O1 paths length determined to be 2.09 Å ± 0.02 and 2.10 Å ± 0.02, for the x = 0.05 and 0.10 samples, respectively. This yielded bond valence sums of 3.9 ± 0.1 v.u. and 4.0 ± 0.1 v.u. which were in good agreement with the crystallography. Although the small increases in the Zr–O1 path length is not significant in view of the magnitude of the associated errors, an increase would be expected if the extra oxygen atoms associated with charge balancing the alio-valent substitution of Nd(III) for Pu(IV) were associated with the Zr atoms. Attempts to introduce a contribution from this additional oxygen atom did not significantly improve the quality of the fit. This was not unexpected given that the content of Pu dopant is ten times lower than that of the Zr atoms. Any impact of the extra oxygen on the average Zr–O1 distance would be very small and difficult to detect due to the low occupancy of the vacancy site. The slight increase in the Zr–Nd and Zr–Zr path lengths are not significant given the magnitude of the associated errors. The large increase in the Zr–O2 path length, and the associated errors is consistent with an increase in the overall disorder around the zirconium atoms, as indicated by the analysis of the XANES region.
The immobilisation of Pu(IV) at the eightfold coordinated A site is in contradiction with Pauling's rule, but follows the behaviour described by Verwey and Heilmann.86,87 Verwey and Heilmann found that the cation with the highest charge adopted the structural site with the highest coordination number in spinels. Based on this, Pu(IV) would be expected to occupy the eightfold coordinated A site in a pyrochlore.
3.4 Molecular modelling
The calculated solution energies of Pu into the Nd2Zr2O7 pyrochlore crystal structure, for the reactions given in eqn (2)–(8), are reported in Table 6. The results determined using the force-field method approach of Cleave et al.31 and Perriot et al.,33 are also reported for comparison. Both these studies used the same force-field parameters.| Reaction | Site | Valence | ΔHsoln (eV) DFT (DFT + U) | ΔHsoln (eV)31 |
|---|---|---|---|---|
| 2 | Nd | Pu(III) | 2.37 (−0.03) | 2.28 |
| 3 |

|
Pu(III) | 3.02 (+0.05) | >2.28 |
| 4 | Zr | Pu(IV) | 1.33 (+0.11) | 0.97 |
| 5 |

|
Pu(IV) | 1.00 (−0.06) | >0.97 |
| 6 |

|
Pu(IV) | 3.83 (−0.06) | >0.97 |
| 7 | Nd | Pu(III) | 1.12 (−0.03) | |
| 8 |
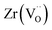
|
Pu(III) | 1.77 (+0.05) |
The results presented in Table 6 show that the force-field-based solution energies are slightly smaller than the ab initio results derived in this work, and that the 5f electrons correlation effects are rather small (c.a. 0.1 eV). The results suggest that Pu should be preferentially incorporated on the Nd site as Pu(IV) with an additional oxygen per two Pu atoms occupying an oxygen vacancy (reaction (5)). This prediction of Pu(IV) is in agreement with the analysis of the XAS data. Note that Cleave et al.,31 Perriot et al.,33 and Williford & Weber32 used Pu2O3 as the reference reactant state for Pu, which resulted in a small Pu(III) incorporation energy (−0.12 eV) when Pu(III) occupied the Nd site. The computed DFT energy is −0.01 eV. The approach presented here takes the oxidation step from Pu2O3 to PuO2 (where ΔHsoln = 2.4 eV)56 or the reduction process from Pu(IV) to Pu(III) in the pyrochlore structure, into account.
In order to gain more confidence about the rather surprising inverted bond distances of Pu–O from the EXAFS measurements, these bond distances were computationally derived. The computed Pu–O, Pu–Nd, Pu–Zr and Pu–Pu bond distances for the different structural configurations and oxidation states of Pu in pyrochlore, are reported in Table 7.
It is important to notice that the calculated Pu–O bond lengths are characterised by a set of short (c.a. 2.3 Å) and long (c.a. 2.5 Å) bonds for the A site. Pu(IV) incorporated on the Zr site has six short bonds, all of the same length, while Pu(IV) incorporated on the Nd site has three short and five long bonds; the configuration consists of two neighbouring Pu atoms and an oxygen atom in an associated vacancy  . A similar distribution is computed for the case of Pu incorporation on the A site with the formation of an Nd vacancy
. A similar distribution is computed for the case of Pu incorporation on the A site with the formation of an Nd vacancy 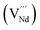 to ensure charge neutrality. Incorporation of Pu(III) on the Nd site results in two short and six long bonds. The EXAFS measurements indicate the incorporation of Pu on the Nd site, but with six short (Pu–O1s) bonds and two longer (Pu–O1l) bonds. The calculated bond distances for the scenarios where Pu(IV) occupies the A site are very close to those obtained from experiment. From the calculated solution energies (Table 6) it is energetically highly unfavourable to incorporate Pu(IV) at the A site with charge balance via Nd vacancy formation. In fact, the calculated solution energies indicate that Pu(IV) will favourably occupy the A site with charge balance occurring via the introduction of oxygen into a former oxygen vacancy. The unexpected results from the EXAFS measurements could indicate a mixture of Pu(IV) on the Nd and Zr sites with approximately equal proportions, which would statistically result in c.a 69% of the bonds being of the shorter length (c.a. 2.3 Å). This scenario was investigated by modifying the existing EXAFS fitting model to incorporate 50% of the Pu(IV) atoms on each available cation site. Unfortunately, it was not possible to obtain a reliable fit as the model now required more independently refinable variables than could be supported by the information content of the data (Nyquist theorem). This does not definitely preclude this model, however various parameters had to be fixed and the resulting fit yielded large S02 and E0 values in conjunction with negative mean square displacement parameters.
to ensure charge neutrality. Incorporation of Pu(III) on the Nd site results in two short and six long bonds. The EXAFS measurements indicate the incorporation of Pu on the Nd site, but with six short (Pu–O1s) bonds and two longer (Pu–O1l) bonds. The calculated bond distances for the scenarios where Pu(IV) occupies the A site are very close to those obtained from experiment. From the calculated solution energies (Table 6) it is energetically highly unfavourable to incorporate Pu(IV) at the A site with charge balance via Nd vacancy formation. In fact, the calculated solution energies indicate that Pu(IV) will favourably occupy the A site with charge balance occurring via the introduction of oxygen into a former oxygen vacancy. The unexpected results from the EXAFS measurements could indicate a mixture of Pu(IV) on the Nd and Zr sites with approximately equal proportions, which would statistically result in c.a 69% of the bonds being of the shorter length (c.a. 2.3 Å). This scenario was investigated by modifying the existing EXAFS fitting model to incorporate 50% of the Pu(IV) atoms on each available cation site. Unfortunately, it was not possible to obtain a reliable fit as the model now required more independently refinable variables than could be supported by the information content of the data (Nyquist theorem). This does not definitely preclude this model, however various parameters had to be fixed and the resulting fit yielded large S02 and E0 values in conjunction with negative mean square displacement parameters.
4. Conclusions
In this paper the fabrication of Pu doped neodymium zirconate pyrochlores via a newly developed co-precipitation route is reported. The co-precipitation approach allowed a homogeneous precursor to be formed which facilitates the uniform distribution of Pu at the molecular level. This precursor was subsequently utilised to synthesis single phase materials in the Nd2−xPuxZr2O7 system. Analysis of the XAS data determined the Pu to be incorporated as Pu(IV) on the A-site in the pyrochlore structure. These experimental findings were supported by atomistic simulations which indicate that the lowest solution energy for formation is achieved, when Pu(IV) is substituted on the A-site in the pyrochlore structure, and oxygen atoms are introduced at vacancy sites to charge balance. Further analysis showed that the local coordination environment of the Pu(IV) consists of six short and two long Pu–O bonds, which differs from the A site coordination environment in rare earth zirconate pyrochlores. The incorporation of Pu(IV) on the A-site results in significant distortion of the A-site local geometry; this observation is consistent with the smaller ionic radius of Pu(IV), in comparison to Nd(III), and the difference in ionic charge and corresponding crystal field energies. BVS calculations corroborated the calculated bond distances and oxidation state assignment. Analysis by XRD confirmed that the long range structure of the samples was consistent with the pyrochlore structure and confirmed the uptake of Pu(IV) into the structure. The use of precursors generated by novel co-precipitation routes, such as the one reported here, offers the potential for fabrication of samples with an improved degree of chemical homogeneity on a smaller length scales than those produced by more conventional solid state routes.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors wish to acknowledge the following people: Jessica Bruin, Frodo Klaassen and Paul van den Idsert for assistance with fabricating the Pu doped ceramics at NRG (Petten, NL); Marika Vespa, Jörg Rothe, Kathy Dardenne, Tonya Vitova, and Christian Marquardt for assistance with the sample transportation and support at the INE beamline at ANKA; Tonya Vitova for providing the Pu-reference spectra;42 Konstantin Rozov for assistance with the GEMS calculations; Tobias Reich and Samer Amayri for providing the design of the sample holder which made the XAS measurements possible; Kurt Sickafus for enlightening discussions. This work was, in part, performed at the synchrotron light source ANKA, which we would like to acknowledge for provision of instrumentation and beamtime. This work was, in part, performed in the MIDAS facility at the University of Sheffield, for which the financial support of the Department of Energy and Climate Change (UK) is gratefully acknowledged. Use of the National Synchrotron Light Source, Brookhaven National Laboratory, was supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Contract No. DE-AC02-98CH10886. This work was supported, in part, by the UK Engineering & Physical Science Research Council under grants EP/S01019X/1, EP/N017870/1, and EP/R511754/1. The computational resources were provided by the Excellence Initiative of the German federal and state governments and the Jülich-Aachen Research Alliance - High Performance Computing. We thank the JARA-HPC awarding body for time on the RWTH Aachen and FZJ computing clusters awarded through JARA-HPC Partition. Parts of this manuscript are indicated as having already been published in the dissertation of S. Finkeldei entitled “Pyrochlore as nuclear waste form: actinide uptake and chemical stability” 2015.References
- R. Vaßen, M. O. Jarligo, T. Steinke, D. E. Mack and D. Stöver, Surf. Coat. Technol., 2010, 205(4), 38–942 CrossRef.
- S. T. Norberg, S. Hull, S. G. Eriksson, I. Ahmed, F. Kinyanjui and J. J. Biendicho, Chem. Mater., 2012, 24(22), 4294–4300 CrossRef CAS.
- G. R. Lumpkin, K. R. Whittle, S. Rios, K. L. Smith and N. J. Zaluzec, J. Phys.: Condens. Matter, 2004, 16(47), 8557–8570 CrossRef CAS.
- R. C. Ewing, W. J. Weber and J. Lian, J. Appl. Phys., 2004, 95(11), 5949–5971 CrossRef CAS.
- J. P. Icenhower, D. M. Strachan, M. M. Lindberg, E. A. Rodriguez, and J. L. Steele, Report PNNL-14252, 2003.
- G. R. Lumpkin, Elements, 2006, 2(6), 365–372 CrossRef CAS.
- B. Burakov, E. Anderson, M. Yagovkina, M. Zamdryanskaya and E. Nikolaeva, J. Nucl. Sci. Technol., 2002, 39(suppl. 3), 733–736 CrossRef.
- M. A. Subramanian, G. Aravamudan and G. V. S. Rao, Prog. Solid State Chem., 1983, 15(2), 55–143 CrossRef CAS.
- T. Hartmann, A. Alaniz, F. Poineau, P. F. Weck, J. A. Valdez, M. Tang, G. D. Jarvinen, K. R. Czerwinski and K. E. Sickafus, J. Nucl. Mater., 2011, 411(1–3), 60–71 CrossRef CAS.
- S. Finkeldei, P. Kegler, P. M. Kowalski, C. Schreinemachers, F. Brandt, A. A. Bukaemskiy, V. L. Vinograd, G. Beridze, A. Shelyug, A. Navrotsky and D. Bosbach, Acta Mater., 2017, 125, 166–176 CrossRef CAS.
- Y. Tabira and R. L. Withers, J. Solid State Chem., 1999, 148(2), 205–214 CrossRef CAS.
- R. C. Ewing, W. J. Weber and F. W. Clinard, Prog. Nucl. Energy, 1995, 29(2), 63–127 CrossRef CAS.
- J. Lian, J. Chen, L. M. Wang, R. C. Ewing, J. M. Farmer, L. A. Boatner and K. B. Helean, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68(13), 134107 CrossRef.
- S. Finkeldei, F. Brandt, K. Rozov, A. A. Bukaemskiy, S. Neumeier and D. Bosbach, Appl. Geochem., 2014, 49, 31–41 CrossRef CAS.
- S. Finkeldei, F. Brandt, A. A. Bukaemskiy, S. Neumeier, G. Modolo and D. Bosbach, Prog. Nucl. Energy, 2014, 72, 130–133 CrossRef CAS.
- K. Holliday, S. Finkeldei, S. Neumeier, C. Walther, D. Bosbach and T. Stumpf, J. Nucl. Mater., 2013, 433, 479–485 CrossRef CAS.
- C. Nästren, R. Jardin, J. Somers, M. Walter and B. Brendebach, J. Solid State Chem., 2009, 182(1), 1–7 CrossRef.
- D. J. Gregg, Y. J. Zhang, S. C. Middleburgh, S. D. Conradson, G. Triani, G. R. Lumpkin and E. R. Vance, J. Nucl. Mater., 2013, 443(1–3), 444–451 CrossRef CAS.
- K. E. Sickafus, L. Minervini, R. W. Grimes, J. A. Valdez, M. Ishimaru, F. Li, K. J. McClellan and T. Hartmann, Science, 2000, 289(5480), 748–751 CrossRef CAS PubMed.
- J. A. Purton and N. L. Allan, J. Mater. Chem., 2002, 12(10), 2923–2926 RSC.
- A. Chartier, C. Meis, J. P. Crocombette, L. R. Corrales and W. J. Weber, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67(17), 13 CrossRef.
- A. Chartier, C. Meis, J. P. Crocombette, W. J. Weber and L. R. Corrales, Phys. Rev. Lett., 2005, 94(2), 025505 CrossRef CAS PubMed.
- A. Chartier, G. Catillon and J. P. Crocombette, Phys. Rev. Lett., 2009, 102(15), 4 CrossRef PubMed.
- L. Minervini, R. W. Grimes and K. E. Sickafus, J. Am. Ceram. Soc., 2000, 83(8), 1873–1878 CrossRef CAS.
- F. X. Zhang, J. W. Wang, J. Lian, M. K. Lang, U. Becker and R. C. Ewing, Phys. Rev. Lett., 2008, 100(4), 4 CrossRef.
- W. R. Panero, L. Stixrude and R. C. Ewing, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70(5), 11 CrossRef.
- L. J. Chen, X. Su and Y. H. Li, First-Principles Study on Cation-Antisite Defects of Stannate and Titanate Pyrochlores, Open Access Library Journal, 2014, 1, e516 Search PubMed.
- Z. J. Chen, H. Y. Xiao, X. T. Zu and F. Gao, J. Appl. Phys., 2008, 104(9), 6 Search PubMed.
- N. Li, H. Y. Xiao, X. T. Zu, L. M. Wang, R. C. Ewing, J. Lian and F. Gao, J. Appl. Phys., 2007, 102(6), 6 Search PubMed.
- A. Chartier, C. Meis, W. J. Weber and L. R. Corrales, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65(13), 11 CrossRef.
- A. Cleave, R. W. Grimes and K. E. Sickafus, Philos. Mag., 2005, 85(9), 967–980 CrossRef CAS.
- R. E. Williford and W. J. Weber, J. Nucl. Mater., 2001, 299(2), 140–147 CrossRef CAS.
- R. Perriot, P. P. Dholabhai and B. P Uberuaga, Phys. Chem. Chem. Phys., 2016, 18(33), 22852–22863 RSC.
- Y. Li, P. M. Kowalski, G. Beridze, A. R. Birnie, S. Finkeldei and D. Bosbach, Scr. Mater., 2015, 107, 18–21 CrossRef CAS.
- B. P. Uberuaga and R. Perriot, Phys. Chem. Chem. Phys., 2015, 17(37), 24215–24223 RSC.
- Y. Li and P. M. Kowalski, J. Nucl. Mater., 2018, 505, 255–261 CrossRef CAS.
- J. L. Drummond and G. A. Welch, J. Chem. Soc., 1956, 2565–2566 CAS.
- G. H. Bryan, J. K. Thompson, H. H. Van Tuyl, C. L. Brown, and J. L. Ryan, Report BNWL-1941, UC-71, 1976.
- J. Bruin, personal communication, 2012.
- S. Finkeldei, Pyrochlore as nuclear waste form: actinide uptake and chemical stability, PhD thesis, Schriften des Forschungszentrums Jülich, Reihe Energie & Umwelt/Energy & Environment, Jülich, Band/Volume 276, 2015.
- J. Rothe, M. A. Denecke, K. Dardenne and T. Fanghanel, Radiochim. Acta, 2006, 94(9–11), 691–696 CAS.
- T. Vitova, I. Pidchenko, D. Fellhauer, P. S. Bagus, Y. Joly, T. Pruessmann, S. Bahl, E. Gonzalez-Robles, J. Rothe, M. Altmaier, M. A. Denecke and H. Geckeis, Nat. Commun., 2017, 8, 16053 CrossRef CAS PubMed.
- B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12(4), 537–541 CrossRef CAS PubMed.
- L. Tröger, D. Arvanitis, K. Baberschke, H. Michaelis, U. Grimm and E. Zschech, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46(6), 3283–3289 CrossRef PubMed.
- J. Goulon, C. Goulon-Ginet, R. Cortes and J. M. Dubois, J. Phys., 1982, 43(3), 539–548 CrossRef CAS.
- I. D. Brown and D. Altermatt, Acta Crystallogr., Sect. B: Struct. Sci., 1985, 41, 244–247 CrossRef.
- W. H. Zachariasen, J. Less Common. Met., 1978, 62(C), 1–7 CrossRef CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21(39), 19 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77(18), 3865–3868 CrossRef CAS PubMed.
- G. Beridze and P. M. Kowalski, J. Phys. Chem. A, 2014, 118(50), 11797–11810 CrossRef CAS PubMed.
- G. Beridze, A. Birnie, S. Koniski, Y. Q. Ji and P. M. Kowalski, Prog. Nucl. Energy, 2016, 92, 142–146 CrossRef CAS.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. L. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100(13), 4 CrossRef PubMed.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41(11), 7892–7895 CrossRef PubMed.
- M. Cococcioni and S. de Gironcoli, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71(3), 16 CrossRef.
- M. Methfessel and A. T. Paxton, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40(6), 3616–3621 CrossRef CAS PubMed.
- R. J. M. Konings, O. Benes, A. Kovacs, D. Manara, D. Sedmidubsky, L. Gorokhov, V. S. Iorish, V. Yungman, E. Shenyavskaya and E. Osina, J. Phys. Chem. Ref. Data, 2014, 43(1), 95 CrossRef.
- L. M. Toth, H. A. Friedman and M. M. Osborne, J. Inorg. Nucl. Chem., 1981, 43(11), 2929–2934 CrossRef CAS.
- W. Hummel, U. Berner, E. Curti, F. J. Pearson and T. Thoenen, Radiochim. Acta, 2002, 90(9–11), 805–813 CAS.
- D. L. Clark, S. S. Hecker, G. D. Jarvinen, and M. P. Neu, Plutonium, The Chemistry of the Actinide and Transactinide Elements, ed. L. R. Morss, N. M. Edelstein, and J. Fuger, Springer, Dordrecht, The Netherlands, 2010, pp. 813–1264 Search PubMed.
- S. A. Glazyrin, P. Y. Rodchenko and L. P. Sokhina, Radiokhimiya, 1989, 31(4), 48–52 CAS.
- N. K. Kulkarni, S. Sampath and V. Venugopal, J. Nucl. Mater., 2000, 281(2–3), 248–250 CrossRef CAS.
- S. D. Conradson, K. D. Abney, B. D. Begg, E. D. Brady, D. L. Clark, C. den Auwer, M. Ding, P. K. Dorhout, F. J. Espinosa-Faller, P. L. Gordon, R. G. Haire, N. J. Hess, R. F. Hess, D. W. Keogh, G. H. Lander, A. J. Lupinetti, L. A. Morales, M. P. Neu, P. D. Palmer, P. Paviet-Hartmann, S. D. Reilly, W. H. Runde, C. D. Tait, D. K. Veirs and F. Wastin, Inorg. Chem., 2004, 43(1), 116–131 CrossRef CAS PubMed.
- S. Bertram, G. Kaindl, J. Jové, M. Pagès and J. Gal, Phys. Rev. Lett., 1989, 63(24), 2680–2683 CrossRef CAS PubMed.
- M. Antonio, L. Soderholm, C. Williams, J. Blaudeau and B. Bursten, Radiochim. Acta, 2001, 89, 17–25 CAS.
- S. D. Conradson, I. Al Mahamid, D. L. Clark, N. J. Hess, E. A. Hudson, M. P. Neu, P. D. Palmer, W. H. Runde and C. Drew Tait, Polyhedron, 1998, 17(4), 599–602 CrossRef CAS.
- E. A. Hudson, J. J. Rehr and J. J. Bucher, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 13815 CrossRef CAS PubMed.
- M. A. Denecke, K. Dardenne and C. M. Marquardt, Talanta, 2005, 65, 1008–1014 CrossRef CAS PubMed.
- A. V. Soldatov, D. Lamoen, M. J. Konstantinović, S. Van den Berghe, A. C. Scheinost and M. Verwerft, J. Solid State Chem., 2007, 180(1), 54–61 CrossRef CAS.
- R. G. Haire, P. E. Raison and Z. Assefa, J. Nucl. Sci. Technol., 2002, 39(suppl. 3), 616–619 CrossRef.
- S. S. Shoup, C. E. Bamberger and R. G. Haire, J. Am. Ceram. Soc., 1996, 79(6), 1489–1493 CrossRef CAS.
- D. A. McKeown, I. S. Muller, A. C. Buechele and I. L. Pegg, J. Non-Cryst. Solids, 1999, 258(1), 98–109 CrossRef CAS.
- F. Farges, G. Brown and D. Velde, Am. Mineral., 1994, 79, 838–847 CAS.
- F. Farges, Geochim. Cosmochim. Acta, 1991, 55(11), 3303–3319 CrossRef CAS.
- G. Mountjoy, D. M. Pickup, R. Anderson, G. W. Wallidge, M. A. Holland, R. J. Newport and M. E. Smith, Phys. Chem. Chem. Phys., 2000, 2(10), 2455–2460 RSC.
- K. Robinson, G. V. Gibbs and P. H. Ribbe, Am. Mineral., 1971, 56(5–6), 782 CAS.
- D. K. Smith and H. W. Newkirk, Acta Crystallogr., 1965, 18(6), 983–991 CrossRef CAS.
- P. Li, I. W. Chen and J. E. Penner-Hahn, J. Am. Ceram. Soc., 1994, 77(1), 118–128 CrossRef CAS.
- S. Ghose and C. Wan, Am. Mineral., 1978, 63(3–4), 304–310 CAS.
- G. D. Ilyushin, A. A. Voronkov, V. V. Ilyukhin, N. N. Nevskij and N. V. Belov, Dokl. Akad. Nauk SSSR, 1981, 260(3), 623–627 CAS.
- Y.-H. Lee, J.-M. Chen, J.-F. Lee and H.-C. I. Kao, J. Chin. Chem. Soc., 2009, 56(3), 543–548 CrossRef CAS.
- P. Li, I. W. Chen and J. E. Penner-Hahn, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 48(14), 10063–10073 CrossRef PubMed.
- E. J. Harvey, K. R. Whittle, G. R. Lumpkin, R. I. Smith and S. A. T. Redfern, J. Solid State Chem., 2005, 178(3), 800–810 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- J. J. Rehr, J. J. Kas, M. P. Prange, A. P. Sorini, Y. Takimoto and F. Vila, C. R. Phys., 2009, 10(6), 548–559 CrossRef CAS.
- S. R. Hall, F. H. Allen and I. D. Brown, Acta Crystallogr., Sect. A: Found. Crystallogr., 1991, 47(6), 655–685 CrossRef.
- E. J. W. Verwey and E. L. Heilmann, J. Chem. Phys., 1947, 15(4), 174–180 CrossRef CAS.
- G. R. Lumpkin, M. Pruneda, S. Rios, K. L. Smith, K. Trachenko, K. R. Whittle and N. J. Zaluzec, J. Solid State Chem., 2007, 180(4), 1512–1518 CrossRef CAS.
- F. A. Kröger and H. J. Vink, Solid State Phys., 1956, 3, 307–435 Search PubMed.
Footnote |
| † This manuscript has been authored in part by UT-Battelle, LLC, under contract DE-AC05-00OR22725 with the US Department of Energy (DOE). The US government retains and the publisher, by accepting the article for publication, acknowledges that the US government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this manuscript, or allow others to do so, for US government purposes. DOE will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan (http://energy.gov/downloads/doe-public-access-plan). |
| This journal is © The Royal Society of Chemistry 2020 |