Elastic constants of biological filamentous colloids: estimation and implications on nematic and cholesteric tactoid morphologies

Abstract

Biological liquid crystals, originating from the self-assembly of biological filamentous colloids, such as cellulose and amyloid fibrils, show a complex lyotropic behaviour that is extremely difficult to predict and characterize. Here we analyse the liquid crystalline phases of amyloid fibrils, and sulfated and carboxylated cellulose nanocrystals and measure their Frank-Oseen elastic constants K₁, K₂ and K₃ by four different approaches. The first two approaches are based on the benchmark of the predictions of: (i) a scaling form and (ii) a variational form of the Frank-Oseen energy functional with the experimental critical volumes at order–order liquid crystalline transitions of the tactoids. The third and the fourth methods imply: (iii) the direct scaling equations of elastic constants and (iv) a molecular theory predicting the elastic constants from the experimentally accessible contour length distributions of the filamentous colloids. These three biological systems exhibit diverse liquid crystalline behaviour, governed by the distinct elastic constants characterizing each colloid. Differences and similarities among the three systems are highlighted and interpreted based on the present analysis, providing a general framework to study dispersed liquid crystalline systems.

---

Introduction

The spontaneous organization of rod-like particles into twisted nematic or cholesteric liquid crystals (CLCs) is present in different living systems¹ and has been exploited in materials science and biotechnology for decades.² In the area of CLCs, special attention has focused on biological rod-like colloids such as DNA,³ viruses,⁴ polypeptides,⁵ F-actin,⁶ collagen,⁷ cellulose nanocrystals⁸ and more recently, amyloid fibrils.⁹

When these filamentous colloids are dispersed at concentrations within the isotropic–nematic coexistence regime,^10,11 nematic droplets, named tactoids, nucleate and grow in the surrounding continuous isotropic phase.^12–17 The director field configuration and the shape assumed by these tactoids change with their increasing volume.⁹ It is a fascinating problem that has been the object of intense study in recent decades and still today carries forward some unclear aspects.^15,18,19

The shape and director field configurations are modeled using a free energy approach in which a tactoid of defined volume V is characterized by a bulk free energy defined by the Frank-Oseen free energy functional. The three main and independent bulk contributions are the splay, twist and bend, proportional to the elastic constants K₁, K₂ and K₃, respectively. To this, an anisotropic surface free energy must be added, defined by the Rapini and Papoular interfacial tension, dependent on the isotropic-nematic surface tension γ and a dimensionless anchoring strength ω. The total free energy can then be written as:

where n is the director of the nematic field, θ the angle between the surface normal and the nematic field, and q_∞ the cholesteric wave number, corresponding to the intrinsic twist. The above description omits the presence of a fourth term, K₂₄, called saddle-splay, which can be responsible in some cases of dramatic effects, such as chiral symmetry breaking in achiral systems.²⁰ In a previous study regarding the homogeneous to bipolar transition, it has been shown that K₂₄ can be included in the term K₁.²¹ Here, we extend this assumption to all the other cases for the lack of experimental evidence of saddle-splay-induced deformations, both in the droplet geometry and in confined capillary.²² The theoretical models presented here are proposed to predict only the three elasticities bend, splay and twist. The theoretical prediction of the saddle-splay remains challenging to date. The director field configuration can be predicted by minimizing the free energy described by eqn (1) for a given volume. The minima are not influenced by the absolute values of the different constants but they depend on the ratios The analysis of the morphology, the director field configurations and their transitions allow, in principle, to obtain information regarding the properties of the liquid crystalline phases^9,23–25 but the mathematical problem at hand is quite difficult to solve and theoretical models able to predict all the elastic constants based on the study of the configuration of the tactoids are still missing. Identifying these physical constants describing the free energy of the liquid crystalline phases is a crucial point in the development of CLC applications such as displays,²⁶ biomolecule detection,²⁷ grating²⁸ and more generally their self-assembly.^29–31

Multiple studies have focused on the theoretical estimation^32–35 of the elastic constants or on their experimental measurements; however, these works are mostly focused on only one single constant or on the ratio between them^36–39 and often rely on external stimuli such as electric or magnetic fields.^40–42 Due to the very sensitive conditions, experimental measurements of the elastic constants remain nontrivial and time consuming. Moreover, water-based biological CLCs such as cellulose nanocrystals (CNCs) and amyloid fibrils are weakly sensitive to electric and magnetic fields, and the measurement of the elastic constant for these systems is extremely elusive.^43–45

In this work, we shed light on the liquid crystalline behavior of three biological colloids: β-lactoglobulin amyloid fibrils (BLGs), sulfated cellulose nanocrystals (SCNCs) and carboxylated cellulose nanocrystals (CCNCs) and use four different ways to determine their relative Frank elastic constants K₁, K₂ and K₃. A first approach consists in extracting these elastic constants from the transition volumes of the tactoids from one configuration to the other, during their growth. The predictions of the constants use scaling forms of the Frank-Oseen energy functional of eqn (1). A second approach consists in a more accurate prediction using a variational method to describe the effect of the volume in the Frank-Oseen energy functional. To support the experimental finding, we estimate with a third approach the elastic constants from the contour length distribution of the rod-like filaments via computational molecular theory and lastly, we compute the elastic constants relying on existing scaling theories but including electrostatic effects.

By combining these results together, we show that these filamentous rod-like colloidal particles have different elastic constants, reflected by the distinctive liquid crystalline behavior of each class of colloid.

Variational theory

A theoretical model able to explain and predict different phase transitions has been developed⁴⁶ using the Frank-Oseen free energy. A twisting nematic field is parametrized by oblate spheroidal coordinates, with the pitch of cholesteric p, the foci of the coordinates β and the aspect ratio α of the ellipsoid as the variables. For discrete values of p, α and β, the free energy of eqn (1) is calculated, and the triplet of parameters that minimizes F, for a fixed volume V, is chosen. This process is repeated for different volumes resulting in the discontinuous black lines shown in Fig. 1E, 2D and 3D. A more detailed discussion can be found in the ESI,† of ref. 46.

Fig. 1 Amyloid fibrils: experiments and theory. Representative images of homogeneous (A), bipolar (B), uniaxial cholesteric (C) and radial cholesteric (D) droplets experimentally observed by LC PolScope imaging microscopy on the left and obtained by theoretical predictions by minimizing the free energy on the right. The plot in panel (E) shows the tactoid aspect ratio as a function of the volume. Three different transitions of the director field (highlighted by dashed lines) are observed experimentally by spontaneous increase of the volume: homogeneous to bipolar at 400 μm³, bipolar to uniaxial cholesteric at 10⁴ μm³ and uniaxial to radial cholesteric at 2 × 10⁶ μm³. The scale bar is equal to 25 μm in (A), (B) and (C) and to 100 μm in (D). The black lines refer to the variational theory using the fitting parameters, .

Fig. 2 Sulfated cellulose nanocrystals: experiments and theory. Representative images of homogeneous tactoid (A), uniaxial cholesteric tactoid with a single periodicity (B), and uniaxial cholesteric tactoid (C) containing several periodicities obtained by LC PolScope imaging microscopy on the left and relative theoretical predictions obtained by minimizing the free energy on the right. The plot in panel (D) shows the tactoid aspect ratio as a function of the volume. A single transition of the director field (highlighted by dashed lines) is observed by spontaneous increase of the volume: homogeneous to uniaxial cholesteric at 5000 μm³. The scale bar is equal to 20 μm in (A) and (B) and to 100 μm in (C). The black lines refer to the variational theory using the fitting parameters, .

Fig. 3 Carboxylated cellulose nanocrystals: experiments and theory. Representative images of homogeneous tactoid (A), radial nematic (B), and uniaxial cholesteric tactoid (C) realized by LC PolScope imaging microscopy on the left and relative theoretical predictions obtained by minimizing the free energy on the right. The scale bar is equal to 20 μm and applies to panels (A), (B) and (C). The plot in panel (D) shows the tactoid aspect ratio as a function of the volume. Two transitions of the director field (highlighted by dashed lines) are observed by spontaneous increase of the volume: homogeneous to radial nematic at 4 × 10³ μm³, and radial nematic to cholesteric at 3 × 10⁴ μm³. The black lines refer to the variational theory using the fitting parameters .

The values of ω and q_∞ come from the experimental values. The ratios are chosen as the best fits for the transition volumes observed experimentally between each phase. The value of comes from the transition into uniaxial cholesteric; while 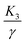is estimated from the transition into radial configurations. The errors in the estimates come from the uncertainties in the transition volumes. Since the splay energy is not directly influencing a particular geometry, this quantity has the greatest uncertainty. The ratio comes from tuning the homogenous to bipolar transition. This procedure and the comparison with the experimental data enable us to carefully tune each single constant of the free energy; the different classes of tactoids are then represented graphically based on the results of the minimization, using the extended Jones matrix to reproduce the PolScope results.⁴⁶

Amyloid fibril liquid crystalline phases

Amyloid fibrils are unfolded protein aggregates ubiquitous in nature and their formation in vivo has been deeply investigated due to their relation with pathological human disorders such as Parkinson's and Alzheimer's,⁴⁷ until the roles of functional amyloid were elucidated^48,49 and amyloid fibrils produced in vitro from non-pathological proteins were exploited as building blocks for advanced materials and biotechnologies thanks to their unique functionalities.^50–52 Amyloids obtained from β-lactoglobulin protein are semiflexible filaments, characterized by a diameter (D) of the order of 4 nm, a persistence length (L_p) of 2 μm and a contour length (L) of up to tens of microns.⁵³ Due to the high aspect ratio (L/D), dispersions of these amyloids undergo a nematic phase transition already at low concentrations⁵⁴ and form other phases, including a variety of cholesteric phase symmetries, which occur,^9,46 however, only when these fibrils are shortened below a contour length significantly lower than the persistence length.¹¹

In agreement with previous work,⁴⁶ amyloid-based tactoids show, at increasing volumes, four different equilibrium director field configurations, namely homogenous, bipolar, uniaxial and radial cholesteric and therefore undergo three director field transitions (see Fig. 1) and the critical volumes at which these transitions occur provide insights on the elastic properties of the crystalline phases. In particular, scaling laws for these transitions have already been proposed previously^9,46 and the homogeneous to bipolar phase transition,⁵⁵ observed at volumes of 4.95 ± 0.35 × 10² μm³, occurs when the droplet volume reaches the critical value of while the bipolar to uniaxial cholesteric phase transition, observed at 3.7 ± 2.7 × 10⁴ μm³, occurs when the droplet reaches a volume of Unfortunately, scaling arguments fail to predict the exact values of the critical volumes for the uniaxial to radial cholesteric transition, due to the fact that the latter configuration always exists with defects at the core of the droplets due to radial configuration with spherical confinement.⁴⁶ However, as we proposed previously,⁴⁶ the dimension of the core in the radial cholesteric droplets, which has been found in this case to be equal to ∼12 μm, is independent of the volume and its radius can be expressed as providing valuable information on the ratio In particular, by using the measured pitch p_∞ = 30 μm = 2π/q_∞ we have a first estimate of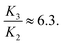

The variational theory⁴⁶ applied for this system, results in structures shown in Fig. 1 with The aspect ratio of homogenous tactoids is smaller than the observed one. This comes from the choice of using prolate ellipsoids in the theory, which have a lower aspect ratio compared to a spindle-like shape of the same volume. The bipolar regime appears at larger volumes compared to experimental data, while the transitions into uniaxial and radial cholesteric are correctly predicted.

Sulfated cellulose nanocrystal liquid crystalline phases

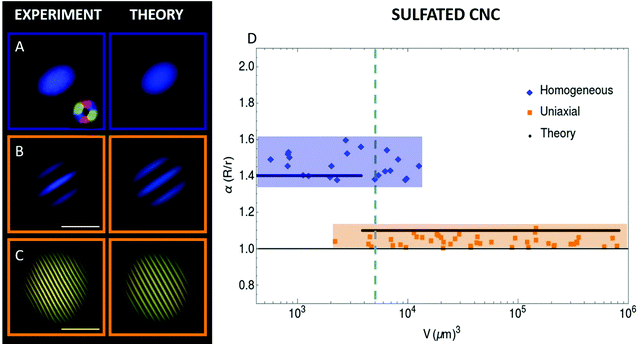
CNCs obtained by acid hydrolysis of wood or cotton are extremely versatile and sustainable biopolymers representing an ideal candidate for the development of nanomaterials with outstanding performance in strength,⁵⁶ energy storage⁵⁷ and insulation.⁵⁸ The ability of SCNCs to form cholesteric phases inspired several studies leading to a broad range of applications⁵⁹ but, although anisotropic phases of SCNCs have been discussed in several studies, the elastic properties of the anisotropic phase for this important system remain unclear.

As reported in a previous study,⁸ the tactoids formed by SCNC liquid crystals show only two main director field configurations: the homogeneous and the uniaxial cholesteric (see Fig. 2). In this system, the homogeneous tactoids have aspect ratios of around 1.5, the bipolar configuration is missing and the radial configuration is not achieved even for very large droplet sizes (see Fig. 2(C)), suggesting a higher bending constant compared to amyloids.

In this system, the droplets undergo only one transition, which is from homogeneous to uniaxial cholesteric configuration, experimentally observed at volumes of V = 8 ± 6 × 10³ μm³ (see Fig. 2). In this case, similarly to the bipolar to cholesteric transition, the transition happens when the energy of the homogeneous untwisted tactoid matches the energy of the anchoring term of the uniaxial cholesteric, γωα_homo⁻²V^2/3 + K₂(q_∞)²V ≈ γωα_uni⁻²V^2/3, suggesting that this transition happens at volumes 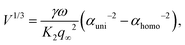considering that during this transition the aspect ratio discontinuously changes from 1.5 to ∼1 (see Fig. 2).

In SCNC, the radial cholesteric configuration has not been experimentally observed, and this configuration is expected to appear only at very large droplet volumes, larger than the inner diameter of the couvette used (200 μm). As expected, in some cases, few droplets with diameters similar to the couvette height start to bend (see the ESI†) suggesting that the transition may indeed happen at larger volumes; the contribution of the bend term becomes therefore important for droplets of diameter ∼200 μm, corresponding to spherical droplet volumes ≥10⁶ μm³ and so we expect the bend term to be in the order of Similar to the amyloid case, we can verify this result by analyzing the core of the droplets, which is assumed to be undergoing radial cholesteric configuration (see the ESI†), equal in this case to ∼20 μm, which together with the measured pitch, p_∞= 18 μm = 2π/q_∞ allows us to show that the ratio is In this case, the variational theory agrees with the experimental evidence and the best fit is found for ratios (see Fig. 2). The two morphologies are correctly predicted. The aspect ratio of the homogeneous is lower for the use of ellipsoids, and higher in the uniaxial cholesteric, since α = 1.1 is the lowest, non-unitary aspect ratio used.

Carboxylated cellulose nanocrystal liquid crystalline phases

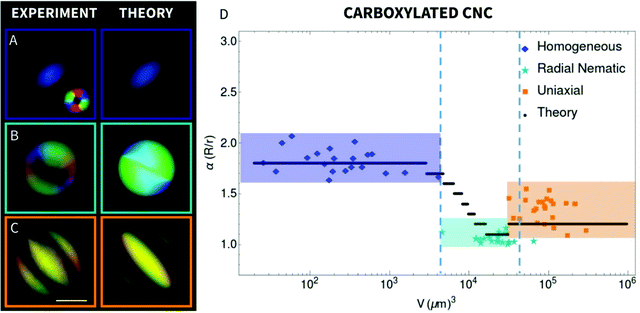
It has been shown that even small variations in the structure of identical mesogens might affect severely the anisotropic phase properties, from the inversion of chirality⁶⁰ to the depletion of the cholesteric phase.^4,11 Additionally, CNCs obtained by different acidic hydrolysis conditions are characterized by different properties.^61–63 The liquid crystalline behavior of CCNCs differs from that of the SCNCs and the chirality inversion from right-handed chiral rods to left-handed cholesteric phase has been recently discussed.⁶⁴

As already shown by Nyström et al.,⁶⁴ the liquid crystalline behavior of CCNCs is characterized by the formation of classes of tactoids, which are different from the previous systems. In particular, detailed PolScope analysis allowed discriminating three main director field configurations at increasing volumes: homogeneous, radial nematic and uniaxial cholesteric, see Fig. 3.

The transition volume from homogeneous to radial nematic is experimentally identified at 4.5 ± 0.5 × 10³ μm³, and is expected to take place when similar to the homogeneous to bipolar transition, since we can assume that the energy of a radial nematic droplet is the energy of a bipolar droplet with unitary aspect ratio. The second transition experienced by the tactoids in this system, the radial nematic to uniaxial cholesteric, is experimentally found for droplet volumes of 3.7 ± 2.7 × 10⁴ μm³ and, considering the aspect ratio equal to one in both configurations is expected to take place when K₂q_∞²V + K₃V^1/3 = γωV^2/3. However, also in the radial nematic configuration, a defect at the core of these droplets is always found due to spherical confinement with parallel anchoring, and thus the scaling might not be able to predict the exactly critical volume for this transition (see later for further discussion). For this reason, we can find a first estimation of K₂ assuming a homogeneous to uniaxial cholesteric transition that, similar to SCNC, is expected at and by setting this critical volume at 10⁴ μm³ and results in The variational theory applied for this system is shown in Fig. 3 using 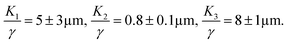In this case, homogenous, radial nematic and uniaxial cholesteric aspect ratios and transition volumes are correctly predicted. However, the variational theory shows a bipolar regime in between the homogenous and radial morphologies, with a pseudo-continuous decrease of the aspect ratio, which has not been found experimentally. This is due to the fact that the variational theory is unable to completely predict this structure that must include a defect at the core caused by the spherical confinement combined with planar anchoring.

Statistical analysis and contour length distribution of the colloids

In order to further understand the relationship between the mesogen properties, such as aspect ratio and length distribution of rods, and the observed liquid crystalline behavior governed by different elasticities, we first perform statistical analysis on AFM images (see Fig. 4A–C), and we then use the experimental distribution as a starting point for a molecular theoretical estimation of the elastic constants, described in the next section.

Fig. 4 Length distributions of the colloids studied and corresponding elastic constants. The first row shows representative AFM images and pictures of the samples under cross polarizers of BLGs (A), SCNCs (B) and CCNCs (C). The log-normal length distribution profiles extracted from AFM analysis are plotted for amyloid fibrils (D), SCNCs (E) and CCNCs (F). For amyloid fibrils (D) and SCNCs (E) the distribution was extracted from the isotropic (plotted in red) and from the nematic (plotted in green) phases, after the solution phase separated macroscopically. CCNCs never reached macroscopic phase separation and thus the distribution was extracted from the mixture of nematic and isotropic phases (plotted in blue). Scale bars in (A), (B) and (C) are equal to 400 nm. In panels (G), (H) and (I) the elastic constants predicted by the molecular theory are plotted as functions of the order parameter S for BLGs, SCNCs and CCNCs, respectively.

The length distribution of the rod-like molecules employed in this study is shown as log-normal distribution in Fig. 4. Additionally, in the case of amyloid fibrils and SCNCs, the distribution was extracted also from the isotropic and nematic phases separately, once the systems achieved macroscopic phase separation through sedimentation of the anisotropic particles (see Fig. 4 and the ESI,† for raw data distribution), allowing a more specific characterization of the composition of the anisotropic phase.

As expected theoretically^65,66 and as reported previously,^10,63 the fibril length distribution of the different phases clearly shows that the nematic phase is composed of more polydispersed fibril lengths than the isotropic counterpart (see Fig. 4(D) and (E)). Specifically, the nematic phase is composed of fibrils that are longer compared to the ones of the isotropic phase since, due to their higher aspect ratio, they undergo the isotropic–nematic transition earlier. In particular, the average length and height (corresponding to fibril diameter D) measured for amyloid fibrils are 〈L〉 =322 ± 134 nm and 〈D〉 =3.36 ± 0.78 nm in the isotropic phase (n = 417), while they are 〈L〉 =652 ± 400 nm and 〈D〉 =3.75 ± 0.83 nm in the nematic phase (n = 486), corresponding to aspect ratios (L/D) equal to 96 and 173 in the two phases, respectively. For SCNCs we found 〈L〉 =212 ± 115 nm in the isotropic (n = 429) and 〈L〉 =325 ± 168 nm in the nematic (n = 426) phase with a negligible difference in average height of 〈D〉 =4.60 ± 1.03 nm and 〈D〉 =4.58 ± 1.00 nm in the isotropic and nematic phase, corresponding to fibril aspect ratios equal to 46 and 71, respectively. In the case of CCNCs, the analysis of the compositions of rods in the two distinct phases was not possible since this system never reached macroscopic phase separation, probably due to the high viscosity of the solution or for smaller difference in concentration between the two phases and therefore an extremely slow sedimentation of tactoids. For CCNCs we therefore analyzed the mixture of the two phases (n = 400) finding 〈L〉 =464 ± 281 nm and 〈D〉 =3.76 ± 1.17 nm and corresponding to an aspect ratio of 123.

Moreover, for the amyloids, we measured a concentration of 1.9% for the isotropic and 2.8 wt% for the nematic phase, while for SCNCs we measured 2.3 wt% for the isotropic and 2.7 wt% for the nematic phase. The critical concentrations of the isotropic ϕ_I and nematic ϕ_N phases predicted using the classic Onsager theory, and considering the charges on the particles, can be estimated using 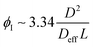and corresponding to 2.2 wt% and 2.9 wt% for BLGs and to 2.4 wt% and 3.3 wt% for SCNCs, in good agreement with the concentrations measured experimentally, considering the polydispersity of the systems^66,67 (see the length distribution data in the ESI,† and the discussion on the effective diameter below).

Under the experimental conditions reported, the dispersed rods are charged and the effect of electrostatic interactions on the diameter of the rods must be taken into account. The effective diameter proposed by Onsager is D_eff = D + k⁻¹(ln A + C + ln 2 − 1/2), where D is the diameter of the rod, k⁻¹ is the Debye length, C is Euler's constant (C = 0.577) and A, for a weakly charged rod in the anisotropic phase, is given by eqn (5.1) in ref. 32. Under the present conditions (see the ESI†), we found that the effective diameters for the three systems become 5.54, 15.7 and 20.0 nm for amyloids, SCNCs and CCNCs, respectively. This finding highlights the strong effect of electrostatic interactions, especially for the two cellulose systems, where the diameter of the fibrils increases drastically.

Molecular theory of elastic constants

The molecular theory of elastic constants provides an estimate of the elastic constants based on the molecular structure.^68,69 In ref. 35, the molecular theory is proposed, where the twist elastic constant K₂ and the chiral strength are calculated for a chiral coarse-grained model of BLGs as a function of the order parameter S for a given concentration. Within this approach, the free energy of a LC phase formed by a polydisperse mixture of fibrils is expressed as a functional of the contour length distribution of fibrils and of the generalized excluded volumes between the constituent particles. Here, we generalize the latter approach to also calculate the splay and bend elastic constants (for more details see the ESI†), where the BLGs, CCNCs and SCNCs are modelled as hard cylinders. Our modeling of the amyloid fibrils studied in the present work implies that chiral contributions to free-energy are neglected. We note that elastic constants are not expected to change significantly if one replaces hard cylinders with chiral particles of similar size such as the ones used in ref. 35 (see eqn (3) in the ESI†). We also neglect any attractive interaction between fibrils. For CCNC and SCNC fibrils the latter assumption seems rather plausible, since the fibrils are highly charged and charges are weakly screened, while for BLGs we can rule out any role played by attractive interactions since at pH 2 amyloid fibrils are positively charged and the electrostatic interactions are purely repulsive.^54,70

In the theoretical calculations, the diameter of the hard cylinders is assumed to be equal to the effective diameter previously discussed, in order to account for electrostatic repulsion between fibrils. We account for electrostatic effects only through an effective diameter of fibrils, thus neglecting the so-called twisting effect (see ref. 32 for more details on this) as well as possible counter-ion condensation effects. In a forthcoming publication we will study a model of fibrils where charges are explicitly considered to accurately evaluate their role played in the estimate of elastic constants.

The elastic constants predicted by this model are plotted as functions of the order parameters S in Fig. 4(G)–(I) for BLGs, SCNCs and CCNCs, respectively.

Elastic constants, surface tension and anchoring strength

Analytical expressions for the elastic constants of nematic solutions have been previously proposed.^33,42,65 The splay constant K₁ increases linearly with the contour length L of the aggregates as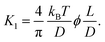 The twist constant K₂ is independent of the contour length of the aggregates, but it weakly depends on their persistence length L_p. In this case, we have The bend constant K₃ depends on the flexibility of the aggregates and is described by the persistence length of the particles as:⁴¹ Following this expression, we also deduce that K₃/K₁ = L_p/L and so, considering the hard rod behavior of these systems (L ≪ L_p), we expect for the three systems K₃ ≫ K₁. The persistence length values for the three systems are extracted from AFM measurements as discussed in the ESI,† and Fig. S5. By using the average rod length measured with AFM analysis, the effective diameter value calculated before, D_eff, together with the known volume fraction of the nematic phase in the coexistence region, it is possible to calculate the elastic constant values with these expressions. The values obtained from this theoretical approach are summarized in Tables 1–3. Although it is correct to replace the first diameter simply with an effective diameter³²D_eff, it should however be noted that, in these direct scaling equations, the last terms (or 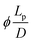) are invariants in the isotropic–nematic coexistence regime⁷¹ following the Onsager theory,⁸⁰ which implies their invariance in the regime of I + N coexistence. In order to allow such an invariance behavior when electrostatic interactions are accounted, another correction is also proposed where the diameter D in the last terms or is replaced by The values for the elastic constants obtained considering the last term as invariant and using this correction are also plotted in Fig. 5(A)–(C) as dark blue dots.

Table 1 Elastic constants for BLGs. Summary table of the elastic constants K₁, K₂ and K₃ estimated with different approaches for amyloid fibrils. Units are given in pN

BLGs	K 1 (pN)	K 2 (pN)	K 3 (pN)
Odijk (D^2/Deff)	5.1 ± 3.9	4 ± 0.8	15 ± 2
Tactoids	1.6 ± 1.1	0.3 ± 0.2	5 ± 3
Var. th.	2.0 ± 1.4	2.7 ± 0.7	8.5 ± 1.7
Mol. th. (S)	0.8 ± 0.1	0.26 ± 0.04	1.6 ± 0.1
Mol. th. (Lp/L)	0.4 ± 0.2	0.13 ± 0.07	1.1 ± 0.3

---

Table 2 Elastic constants for SCNCs. Summary table of the elastic constants K₁, K₂ and K₃ estimated with different approaches for sulfated cellulose nanocrystals. Units are given in pN

SCNCs	K 1 (pN)	K 2 (pN)	K 3 (pN)
Odijk (D^2/Deff)	1.4 ± 0.8	3.9 ± 0.3	15 ± 1
Tactoids	0.09 ± 0.04	0.02 ± 0.01	0.9 ± 0.4
Var. th.	2.6 ± 2.1	0.02 ± 0.01	2.3 ± 0.4
Mol. th. (S)	0.2 ± 0.1	0.07 ± 0.04	1.7 ± 0.7
Mol. th. (Lp/L)	0.2 ± 0.1	0.06 ± 0.04	1.4 ± 0.7

---

Table 3 Elastic constants for CCNCs. Summary table of the elastic constants K₁, K₂ and K₃ estimated with different approaches for carboxylated cellulose nanocrystals. Units are given in pN

CCNCs	K 1 (pN)	K 2 (pN)	K 3 (pN)
Odijk (D^2/Deff)	0.9 ± 0.6	0.7 ± 0.06	2.7 ± 0.2
Tactoids	0.7 ± 0.5	0.039 ± 0.004	2 ± 1
Var. th.	0.6 ± 0.4	0.10 ± 0.01	1.0 ± 0.1
Mol. th. (S)	0.10 ± 0.02	0.031 ± 0.008	0.20 ± 0.02
Mol. th. (Lp/L)	0.05 ± 0.03	0.017 ± 0.012	0.15 ± 0.05

---

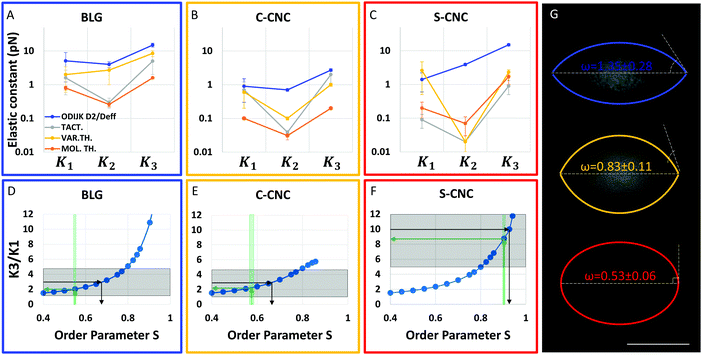Fig. 5 Elastic constants and anchoring strength for the three colloidal systems investigated. The elastic constants for BLGs, CCNCs and SCNCs are plotted in panels (A), (B) and (C), respectively. The elastic constants estimated from the theoretical scaling of Odijk are plotted as blue dots, from the tactoids director field transitions in grey dots, from the variational theory in yellow dots and the molecular theoretical prediction in orange dots. In panels (D), (E) and (F) the ratio K₃/K₁ obtained from the molecular theory are plotted as functions of the order parameter S values for BLGs, CCNCs, and SCNCs, respectively. The green arrows indicate the order parameters measured (see the ESI,† Fig. S7), and the corresponding K₃/K₁ values; the black arrows indicate the predicted order parameter S values, which are extracted by the imposed (experimentally accessible) L_p/L = K₃/K₁. Panel (G) contains examples of characteristic homogeneous tactoids, where the tip angle is shown, and the average anchoring value indicated, for BLGs in blue, CCNCs in yellow and SCNCs in red. The scale bar is equal to 10 μm.

The previously discussed molecular theory predicts the elastic behavior of the anisotropic phases from the rod length distribution and effective fibril diameter as function of the order parameter S and so, this variable is needed to predict the elastic constant values. The order parameters estimated in the three systems through the analysis of birefringence (see the ESI†) are equal to 0.55 ± 0.03, 0.58 ± 0.06 and 0.89 ± 0.03 for BLGs, CCNCs and SCNCs, respectively (green arrows in Fig. 5(D)–(F)). The high value of S for the SCNCs might be explained by the fact that these fibrils have the lowest values of L/L_p ratio among the three systems studied in the present work and it is known that the order parameter S increases on decreasing L/L_p for semiflexible polymers as discussed in ref. 72. Since the molecular theory gives elastic constants and their ratios, such as as functions of the order parameters, it is also possible to back-extract an estimated order parameter S, with the assumption K₃/K₁ = L_p/L and compare it with the one measured by birefringence. As shown by the black arrows in Fig. 5 panels (D)–(F), by fixing K₃/K₁ to L_p/L, we obtain order parameters equal to 0.67 ± 0.13, 0.67 ± 0.13 and 0.92 ± 0.12, for BLGs, CCNCs and SCNCs, respectively, in good agreement with the S values estimated with the birefringence method. The values of order parameter and of the ratio K₃/K₁ estimated are in the range expected for rod-like lyotropic liquid crystals and in agreement with previous experimental^18,55,73,74 and computational⁷⁵ works. The three elastic constants predicted by this molecular theory and corresponding to the order parameters estimated by the birefringence measurements are therefore plotted for the three systems in Fig. 5 (orange dots in panels (A)–(C)).

The interfacial tension of hard rod colloids in isotropic–nematic suspensions has been studied by various approaches, all leading to the universal law^76–79 The numerical prefactor b varies from 0.18 to 0.32⁸⁰ and is fixed here as 0.3 for the estimation of γ. Using the average length of the fibrils and the D_eff values estimated before we find interfacial tension values of 0.34 × 10⁻⁶ N m⁻¹ for BLGs, of 0.24 × 10⁻⁶ N m⁻¹ for SCNCs and 0.13 × 10⁻⁶ N m⁻¹ for CCNCs.

Following the Wulff model,²¹ the adimensional anchoring strength ω value can be estimated by analyzing the morphology of homogeneous tactoids, where indeed the twist bend and splay contributions are zero and the free energy is composed of the surface energy only; in the case of chiral systems, this approach neglects the energy contribution associated with the unrelaxed twist of the rods, however when the length scale of the volume is much smaller than the pitch of the cholesteric, the twist energy contribution can be disregarded. As a result, exclusively for homogeneous tactoids, tip angle θ and the aspect ratio α (with where R and r are the major and minor axes of the tactoid, respectively,) are a function of the anchoring only, where (ω = 1 + (tan θ))⁻² and ω = (α/2)² for ω > 1 and ω = α − 1 for ω ≤ 1. By measuring the tip angles in homogeneous tactoids, we obtained an average angle of 126 ± 6° for amyloids, 176 ± 6° for SCNCs and 156 ± 4° for CCNCs, corresponding to anchoring values of 1.26 ± 0.06 for amyloid, 1.00 ± 0.07 for SCNC and 1.04 ± 0.02 for CCNC. In agreement with a previous study, amyloids are characterized by the highest value of anchoring strength¹¹ and the homogeneous tactoids formed by this system have a more elongated shape and sharper tips when compared, for example, with the ones composed by CNCs (see Fig. 5(G)). At the same time, the homogeneous tactoids formed by CCNC show smaller tip angles and more prolate shapes compared with SCNC, suggesting that SCNC leads to an even weaker anchoring strength. The expression relating the anchoring to the tip angle lacks precision for tip angle values close to 180° and therefore, for a more precise measurement of the anchoring, we analyzed the aspect ratios of homogeneous tactoids of all three systems. Measuring the average aspect ratio of homogeneous tactoids in the three systems (see also the plots in Fig. 1–3) allowed estimating anchoring strength values of 1.35 ± 0.28, 0.53 ± 0.04 and 0.83 ± 0.10 for BLG, SCNC and CCNC, respectively, confirming the trends based on the tip angle estimation. Interestingly, in the sample of SCNC, characterized by the weaker anchoring, homogeneous tactoids appear to be prolate spheroids and not spindle-like as typically observed experimentally in hard-rod systems. The anchoring values measured are in the range predicted theoretically from several works on hard rods and worm-like chains⁷⁹ and smaller but in the same order of magnitude reported in the literature for carbon nanotubes.^24,81 Interestingly, when comparing the length of the mesogens with the anchoring strength measured, we observe that the anchoring is a function of the rod length also when comparing different systems, extending the validity of our previous study based only on amyloid fibrils of different lengths.¹¹

The values of surface tension γ and anchoring strength ω just calculated can now be used to compute the elastic constants from the scaling on the critical volumes at which the director field transitions are observed experimentally and from the variational theory discussed before (plotted in Fig. 5A–C as orange and grey dots, respectively).

For BLG in particular, using γ = 0.34 × 10⁻⁶ N m⁻¹ and ω = 1.35 and with the assumption 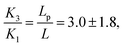we can compute K₃ and K₁, from the critical volume of the homogeneous to bipolar transition using and K₂ from the bipolar to uniaxial cholesteric transition using In particular, from these scaling arguments we obtain K₁ = 1.6 ± 1.1 pN K₂ = 0.3 ± 0.2 pN and K₃ = 5 ± 3 pN and from the variational theory K₁ = 2.0 ± 1.4 pN K₂ = 2.7 ± 0.7 pN and K₃= 8.5 ± 1.7 pN.

For SCNC, using γ = 0.24 × 10⁻⁶ N m⁻¹ and ω = 0.53, the twist elastic constant K₂ can also be readily computed from the critical volume observed experimentally for the homogeneous to uniaxial cholesteric transition using and it results in K₂ = 0.02 ± 0.01 pN. The elastic constant K₃, can be calculated in two different approaches, both based on the analysis of the droplets undergoing uniaxial to radial cholesteric transition; as discussed before, (I) the dimension of the core in radial cholesteric depends on the ratio in this case ≈48, allowing one to estimate K₃ = 0.96 ± 0.48 pN from K₂, but additionally, (II) the critical volume at which the bend term starts to dominate, in this case suggesting that allows one to compute that K₃ ≈ 12.7 pN. The elastic constant K₁ becomes available from the ratio K₃/K₁ = L_p/L ∼ 10 ± 5 for this system, resulting in 0.09 ± 0.04 pN ≤ K₁ ≤ 1.2 ± 0.6 pN. The two approaches for the estimation of K₃ result in values that differ by one order of magnitude, but we consider the first method to be more accurate and to have the best agreement with the variational theory that results in K₁ = 2.6 ± 2.1 pN, K₂ = 0.02 ± 0.01 pN and K₃= 2.3 ± 0.4 pN.

In the case of CCNC, with the values γ = 0.13 × 10⁻⁶ N m⁻¹ and ω = 0.83, using the assumption 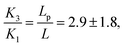we can extract K₃ and K₁ from the critical volume for the homogeneous to bipolar transition using and K₂ from the radial nematic to uniaxial cholesteric, using K₂q_∞²V + K₃V^1/3 = γωV^2/3, resulting in K₁ = 0.7 ± 0.5 pN K₂ = 0.03 ± 0.02 pN and K₃ = 2 ± 1 pN. Alternatively, K₂ can be computed by assuming the homogeneous to uniaxial cholesteric transition at intermediate volumes of 1.7 ± 1.3 × 10⁴ μm³ (see Fig. 1), expected when resulting in K₂ = 0.039 ± 0.004 pN, in good agreement with the scaling expression on the radial to uniaxial transition, suggesting that the defect energy cost in the radial nematic configuration is, in this case, almost negligible. The variational theory, for CCNC results in K₁ = 0.6 ± 0.4 pN K₂ = 0.10 ± 0.01 pN and K₃ = 1.0 ± 0.1 pN.

The large difference between SCNC (around 10) and CCNC (close to 1) in the ratio K₃/K₁ can be understood in terms of the difference between the nematic order parameter S values in these two systems. According to the molecular theory used in the present work, elastic constants depend on the effective stiffness of the semiflexible fibrils as quantified by the deflection length^11,33 (see the discussion on L₀ in the ESI†). As a consequence, even if two fibrils possess similar stiffness (L_p), their deflection length can vary a lot on changing α, thus inducing a large variation of K₃/K₁ according to the results of the molecular theory shown in panels D, E and F of Fig. 5.

Concerning the differences between the estimates of elastic constants obtained by the various approaches used in the present study, we note that the molecular theory overall underestimates the elastic constants when compared to the other methods, and this may depend on the simplified treatment of (i) bending fluctuations, which generally ease elastic deformations by inducing an effective reduced flexibility of the fibrils, and of (ii) electrostatic interactions, which play in these systems a significant role due to the largely unscreened charge of the fibrils. Indeed, (i) bending fluctuations enter the theoretical calculations through a deflection length, which is assumed to be inversely proportional to the degree of orientational order as quantified by the Onsager parameter α_N (see the ESI†) and (ii) electrostatic interactions are crudely accounted for through the effective diameters of fibrils.

The variational theory, on the other hand, seems to display a higher bending constant, probably due to the assumptions used for parametrizing the nematic field, while K₁ and K₂ are quite close to the scaling argument on the critical volumes, since both approaches use the critical volume of transition between classes for tactoids for estimating the constants. The variational theory results are extremely useful in predicting the transition volumes, ultimately needed for the estimation of the elastic constants. However, since the shape of the tactoids used for the calculations is ellipsoidal and does not consider the tip angle of spindle-like tactoids, the variational theory necessarily presents deviations in predicting the correct droplet aspect ratios, especially when the anchoring strength is high, resulting in elongated droplets with narrow tip angles. As an example, the BLG system is characterized by the highest anchoring and we observed homogeneous tactoids with an average aspect ratio α of 2.3 and bipolar tactoids with average α of 1.7, while the variational theory results in average α values of 2.1 and 1.9 for homogeneous and bipolar tactoids, respectively, corresponding to a difference of ∼10%. In uniaxial and radial cholesteric tactoids, where the tip angles are absent, we measured average α values of 1.2 and 1.0, for uniaxial and radial cholesteric, respectively, in good agreement with the variational theory predicting α value of 1.1 and 1.0. In SCNC, the system characterized by the lowest anchoring, the average α values measured in homogeneous and in uniaxial cholesteric tactoids are equal to 1.4 and to 1.05, respectively, and the variational theory can correctly predict their aspect ratios equal to 1.4 for homogeneous and 1.1, respectively.

Lastly, the Odijk scaling approach displays for cellulose a higher twist constant compared to other estimates, possibly because of the polydispersity of the fibrils, which is not taken into account in the scaling argument. For the three systems, we also notice that the twist is generally weaker than the other elasticities, while the ratio between bend and splay depends on the flexibility of the fibrils, as generally accepted. In fact, when the fibrils behave as rigid rods the bend elasticity is found to be much greater than the splay elasticity, especially compared to systems in which the fibrils behave as semiflexible wormlike chains, where the two contributions may become comparable. Granted that different systems are characterized by similar elastic constants (or the ratio between them), their liquid crystalline behavior might strongly vary due to differences in anchoring strength, which is found to decrease with fibril length. Therefore, it is ultimately the ratio between the elastic constants and the anchoring strength (also referred to as extrapolation length, i.e.), which plays a pivotal role in the configuration of the nematic field: an illustrative sample is offered by the SCNC system, where the very high extrapolation length compared to the other systems penalizes bending of the director, and thus a radial orientation of the nematic field, imposing absolutely straight cholesteric bands within a perfectly uniaxial chiral nematic field.

Additionally, omitting of the saddle-splay contribution might result in an additional error in the estimation based on the experimental analysis and the variational theory.

Conclusions

Cholesteric phases originating from biological filamentous colloids have attracted tremendous attention in recent decades, driving the development of several applications and nanomaterials. Although the estimation of the parameters governing the liquid crystalline behavior of these systems is demanded for the development of self-assembled materials and other applications, the characterization of the elastic properties of biological CLCs remains up to date nontrivial and challenging. In this paper, we describe the liquid crystalline behavior of amyloid fibrils, SCNCs and CCNCs, focusing on the characterization of anisotropic droplets (tactoids) spontaneously nucleating and growing at concentrations within the isotropic–nematic region. In particular, we estimate the surface tension, anchoring strength and the elastic constants K₁, K₂ and K₃ for the three chiral bio-colloids by describing the experimentally observed tactoid transitions with (i) scaling arguments and (ii) a variational theory based on the Frank-Oseen energy functional. The results obtained are supported by (iii) direct scaling equations on the elastic constants and (iv) by a molecular theory able to predict the elastic constants from the experimental contour length distribution.

The results show that the liquid crystalline structures originating from these chiral biological filaments with similar physical properties, present striking differences, reflected by distinct values of anchoring strength, elastic constants, and surface tension and provide a general framework to understand the morphologies in confined liquid crystalline systems.

Materials and methods

β-Lactoglobulin amyloid production

Six grams of purified β-lactoglobulin was dissolved in 300 mL of pH 2 milliQ water. The solution was centrifuged and the supernatant heated at 90 °C for 5 hours. During the heating process the solution was agitated with a magnetic stirrer. The solution was quenched on ice to stop the reaction and cooled fibril solution was homogenized using an immersion mixer for 1 minute, to mechanically induce shortening of the obtained amyloids. In order to remove unreacted protein and short peptides, the suspension was dialyzed with dialysis membrane (MWCO 100 kDa) for 5 days against pH 2 milliQ water with daily bath change. The solution was thereafter increased in concentration with reverse osmosis using a dialysis membrane (MWCO 6–8 kDa) against a pH 2, 5 wt% PEG (MW 35 kDa) solution.

Sulfated cellulose nanocrystal production

Freeze-dried SCNCs were obtained from FPInnovations. The powder was rehydrated in milliQ water at a concentration of 2.5 wt% and stored in a cold room (4 °C) over night. Then, the CNCs were dispersed by ultra-sonication (Hielscher UP200S, operated at 200 W, no interval, 40% amplitude, 7 mm probe, and cooled with ice water) for 2 min, followed by centrifugation for 20 min at 12 000 rcf. The dispersion was stored in a glass vial at room conditions until phase separation into an isotropic top phase and a cholesteric bottom phase occurred after several weeks.

Carboxylated cellulose nanocrystal production

The dispersion used in this work was produced following the procedure discussed in ref. 64. Carboxylated cellulose nanocrystals were extracted by heating 0.5 g L⁻¹ carboxylated cellulose fibrils at 105 °C and 2.5 M HCl. The resulting CCNCs, obtained by centrifugation (30 minutes at 12 000g), were dissolved in water, dialyzed against pH 4.6 milliQ water for 3 days and later concentrated using reverse osmosis against 10 wt% 35 kDa PEG solution.

Sample preparation and optical microscopy analysis

Rectangular cuvettes (VitroTubes, Vitrocom) of inner thickness 200 μm were filled with solutions at concentrations within the isotropic nematic coexistence regime using a pipet, and then the capillary tubes were immediately sealed with UV glues to avoid evaporation. The evolution of the liquid crystalline droplets for the three studied systems was recorded using an optical microscope combined with an LC-PolScope universal compensator, allowing one to analyze with high sensitivity and high resolution the spatial orientation of the director field in the anisotropic sample providing quantitative pixel-by-pixel information of local optical anisotropy.⁸² For this study, the cuvettes were analyzed during several days to carefully follow the evolution and growth of tactoids in the samples during equilibration.

Atomic force microscopy characterization

In order to perform AFM, the fibril samples were diluted in pH 2 Milli-Q water up to a final concentration of 0.01 wt%, and then 20 μL of solutions were deposited onto mica (freshly cleaved for BLG and APTES-coated for cellulose nanocrystals), incubated for 2 min, rinsed with Milli-Q water, and dried with compressed air flow. AFM experiments were performed in tapping mode at ambient conditions using a Multimode VIII scanning probe microscope (Bruker, USA). The height and contour and length distributions corresponding to amyloid fibrils and cellulose nanocrystals were extracted by tracing the fibrils on the images using the open-source code FiberApp.⁸³

Conflicts of interest

There are no conflict of interest to declare.

References

1. M. Mitov, Soft Matter, 2017, 13, 4176–4209.
2. S. J. Woltman, G. D. Jay and G. P. Crawford, Nat. Mater., 2007, 6, 929–938.
3. C. De Michele, G. Zanchetta, T. Bellini, E. Frezza and A. Ferrarini, ACS Macro Lett., 2016, 5, 208–212.
4. Z. Dogic and S. Fraden, Langmuir, 2000, 16, 7820–7824.
5. J. T. Kindt and W. M. Gelbart, J. Chem. Phys., 2001, 114, 1432–1439.
6. P. W. Oakes, J. Viamontes and J. X. Tang, Phys. Rev. E - Stat. Nonlinear, Soft Matter Phys., 2007, 75, 1–11.
7. R. Martin, J. Farjanel, D. Eichenberger, A. Colige, E. Kessler, D. J. S. Hulmes and M. M. Giraud-Guille, J. Mol. Biol., 2000, 301, 11–17.
8. P. X. Wang, W. Y. Hamad and M. J. MacLachlan, Nat. Commun., 2016, 7, 11515.
9. G. Nyström, M. Arcari and R. Mezzenga, Nat. Nanotechnol., 2018, 13, 330–336.
10. A. Hirai, O. Inui, F. Horii and M. Tsuji, Langmuir, 2009, 25, 497–502.
11. M. Bagnani, G. Nyström, C. De Michele and R. Mezzenga, ACS Nano, 2019, 13, 591–600.
12. P. W. Oakes, J. Viamontes and J. X. Tang, Growth of tactoidal droplets during the first-order isotropic to nematic phase transition of F-actin, Phys. Rev. E, 2007, 75(6), 061902.
13. K. L. Weirich, S. Banerjee, K. Dasbiswas, T. A. Witten, S. Vaikuntanathan and M. L. Gardel, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 2131–2136.
14. A. Modlinska, A. M. Alsayed and T. Gibaud, Sci. Rep., 2015, 5, 18–21.
15. S. A. Khadem and A. D. Rey, Front. Phys., 2019, 7, 88.
16. J. D. Bernal and I. Fankuchen, Nature, 1937, 139, 923–924.
17. Z. Dogic and S. Fraden, Philos. Trans. R. Soc. A Math. Phys. Eng. Sci., 2001, 359, 997–1015.
18. A. V. Kaznacheev, M. M. Bogdanov and A. S. Sonin, J. Exp. Theor. Phys., 2003, 97, 1159–1167.
19. E. G. Virga, Variational Theories for Liquid Crystals, 2018.
20. K. Nayani, R. Chang, J. Fu, P. W. Ellis, A. Fernandez-Nieves, J. O. Park and M. Srinivasarao, Nat. Commun., 2015, 6, 8067.
21. P. Prinsen and P. van der Schoot, Phys. Rev. E - Stat. Physics, Plasmas, Fluids, Relat. Interdiscip. Top., 2003, 68, 11.
22. S. A. Khadem, M. Bagnani, R. Mezzenga and A. D. Rey, Relaxation dynamics in bio-colloidal cholesteric liquid crystals confined to cylindrical geometry, Nat. Commun., 2020, 11, 4616.
23. J. H. Erdmann, S. Umer and J. W. Doane, Phys. Rev. Lett., 1990, 64, 1907–1910.
24. V. Jamali, N. Behabtu, B. Senyuk, J. A. Lee, I. I. Smalyukh, P. Van Der Schoot and M. Pasquali, Phys. Rev. E - Stat. Nonlinear, Soft Matter Phys., 2015, 91, 1–7.
25. J. Bajc and S. Zumer, Phys. Rev. E - Stat. Physics, Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 55, 2925–2937.
26. G. W. Gray and S. M. Kelly, J. Mater. Chem., 1999, 9, 2037–2050.
27. A. M. Lowe, B. H. Ozer, Y. Bai, P. J. Bertics and N. L. Abbott, ACS Appl. Mater. Interfaces, 2010, 2, 722–731.
28. R. L. Sutherland, V. P. Tondiglia, L. V. Natarajan, T. J. Bunning and W. W. Adams, Appl. Phys. Lett., 1994, 64, 1074–1076.
29. I. I. Smalyukh, S. Chernyshuk, B. I. Lev, A. B. Nych, U. Ognysta, V. G. Nazarenko and O. D. Lavrentovich, Ordered Droplet Structures at the Liquid Crystal Surface and Elastic-Capillary Colloidal Interactions, Phys. Rev. Lett., 2004, 93(11), 117801.
30. I. I. Smalyukh, O. D. Lavrentovich, A. N. Kuzmin, A. V. Kachynski and P. N. Prasad, Elasticity-Mediated Self-Organization and Colloidal Interactions of Solid Spheres with Tangential Anchoring in a Nematic Liquid Crystal, Phys. Rev. Lett., 2005, 95(15), 157801.
31. G. M. Koenig, J. J. De Pablo and N. L. Abbott, Langmuir, 2009, 25, 13318–13321.
32. G. J. Vroege and T. Odijk, J. Chem. Phys., 1987, 87, 4223–4232.
33. T. Odijk, Liq. Cryst., 1986, 1, 553–559.
34. T. Sato and A. Teramoto, Macromolecules, 1996, 29, 4107–4114.
35. E. Romani, A. Ferrarini and C. De Michele, Macromolecules, 2018, 51, 5409–5419.
36. A. Scharkowski, G. P. Crawford, S. Žumer and J. W. Doane, J. Appl. Phys., 1993, 73, 7280–7287.
37. A. A. Joshi, J. K. Whitmer, O. Guzmán, N. L. Abbott and J. J. De Pablo, Soft Matter, 2014, 10, 882–893.
38. R. D. Polak, G. P. Crawford, B. C. Kostival, J. W. Doane and S. Umer, Optical determination of the saddle-splay elastic constant K₂₄ in nematic liquid crystals, 1994, vol. 49.
39. S. Kralj and S. Žumer, Saddle-splay elasticity of nematic structures confined to a cylindrical capillary, 1995, vol. 51.
40. H. Gruler, T. J. Scheffer and G. Meier, Zeitschrift fur Naturforsch. - Sect. A J. Phys. Sci., 1972, 27, 966–976.
41. S. Zhou, Y. A. Nastishin, M. M. Omelchenko, L. Tortora, V. G. Nazarenko, O. P. Boiko, T. Ostapenko, T. Hu, C. C. Almasan, S. N. Sprunt, J. T. Gleeson and O. D. Lavrentovich, Phys. Rev. Lett., 2012, 109, 13–31.
42. S. Zhou, A. J. Cervenka and O. D. Lavrentovich, Phys. Rev. E - Stat. Nonlinear, Soft Matter Phys., 2014, 90, 42505.
43. P. X. Wang, W. Y. Hamad and M. J. MacLachlan, Chem, 2019, 5, 681–692.
44. S. Bolisetty, J. J. Vallooran, J. Adamcik and R. Mezzenga, ACS Nano, 2013, 7, 6146–6155.
45. B. Frka-Petesic, H. Radavidson, B. Jean and L. Heux, Dynamically Controlled Iridescence of Cholesteric Cellulose Nanocrystal Suspensions Using Electric Fields, Adv. Mater., 2017, 29(11), 1606208.
46. M. Bagnani, P. Azzari, S. Assenza and R. Mezzenga, Six-fold director field configuration in amyloid nematic and cholesteric phases, Sci. Rep., 2019, 9, 12654.
47. T. P. J. Knowles, M. Vendruscolo and C. M. Dobson, Nat. Rev. Mol. Cell Biol., 2014, 15, 384–396.
48. I. Cherny and E. Gazit, Angew. Chem., Int. Ed., 2008, 47, 4062–4069.
49. T. P. J. Knowles and R. Mezzenga, Adv. Mater., 2016, 28, 6546–6561.
50. S. Bolisetty and R. Mezzenga, Nat. Nanotechnol., 2016, 11, 365–371.
51. Y. Shen, L. Posavec, S. Bolisetty, F. M. Hilty, G. Nyström, J. Kohlbrecher, M. Hilbe, A. Rossi, J. Baumgartner, M. B. Zimmermann and R. Mezzenga, Nat. Nanotechnol., 2017, 12, 642–647.
52. G. Nyström, M. P. Fernández-Ronco, S. Bolisetty, M. Mazzotti and R. Mezzenga, Adv. Mater., 2016, 28, 472–478.
53. J. Adamcik, J. M. Jung, J. Flakowski, P. De Los Rios, G. Dietler and R. Mezzenga, Nat. Nanotechnol., 2010, 5, 423–428.
54. J. M. Jung and R. Mezzenga, Langmuir, 2010, 26, 504–514.
55. P. Prinsen and P. Van Der Schoot, Eur. Phys. J. E., 2004, 13, 35–41.
56. A. Dufresne, 9. Mechanical properties of nanocellulose-based nanocomposites, 2017.
57. M. Hamedi, E. Karabulut, A. Marais, A. Herland and G. Nyström, Angew. Chem., Int. Ed., 2013, 52, 12038–12042.
58. B. Wicklein, A. Kocjan, G. Salazar-Alvarez, F. Carosio, G. Camino, M. Antonietti and L. Bergström, Nat. Nanotechnol., 2015, 10, 277–283.
59. Y. Habibi, L. A. Lucia and O. J. Rojas, Chem. Rev., 2010, 110, 3479–3500.
60. E. Barry, D. Beller and Z. Dogic, Soft Matter, 2009, 5, 2563–2570.
61. S. Beck-Candanedo, M. Roman and D. G. Gray, Biomacromolecules, 2005, 6, 1048–1054.
62. I. Usov, G. Nyström, J. Adamcik, S. Handschin, C. Schütz, A. Fall, L. Bergström and R. Mezzenga, Nat. Commun., 2015, 6, 7564.
63. X. M. Dong, J. F. Revol and D. G. Gray, Cellulose, 1998, 5, 19–32.
64. G. Nyström, M. Arcari, J. Adamcik, I. Usov and R. Mezzenga, ACS Nano, 2018, 12, 5141–5148.
65. L. Onsager, Ann. N. Y. Acad. Sci., 1949, 51, 627–659.
66. H. H. Wensink and G. J. Vroege, J. Chem. Phys., 2003, 119, 6868–6882.
67. A. Speranza and P. Sollich, J. Chem. Phys., 2003, 118, 5213–5223.
68. M. M. C. Tortora and J. P. K. Doye, J. Chem. Phys., 2017, 146, 184504.
69. H. H. Wensink, Crystals, 2019, 9, 143.
70. P. Aymard, T. Nicolai, D. Durand and A. Clark, Macromolecules, 1999, 32, 2542–2552.
71. R. Mezzenga, J. M. Jung and J. Adamcik, Langmuir, 2010, 26, 10401–10405.
72. T. Odijk, Macromolecules, 1986, 19, 2313–2329.
73. A. Stroobants, H. N. W. Lekkerkerker and T. Odijk, Effect of Electrostatic Interaction on the Liquid Crystal Phase Transition in Solutions of Rodlike Polyelectrolytes, Oxford University Press, 1986, vol. 19.
74. R. B. Meyer, F. Lonberg, V. Taratuta, S. Fraden, S. D. Lee and A. J. Hurd, Measurements of the anisotropic viscous and elastic properties of lyotropic polymer nematics, 1985, vol. 79.
75. S. D. Lee and R. B. Meyer, J. Chem. Phys., 1986, 84, 3443–3448.
76. P. Van Der Schoot, J. Phys. Chem. B, 1999, 103, 8804–8808.
77. D. L. Koch and O. G. Harlen, Macromolecules, 1999, 32, 219–226.
78. Z. Y. Chen, Biaxial effect at an isotropic–nematic interface, 1993, vol. 47.
79. Y. Jiang and J. Z. Y. Chen, Macromolecules, 2010, 43, 10668–10678.
80. W. L. Chen, T. Sato and A. Teramoto, Measurement of the interfacial tension between coexisting isotropic and nematic phases of a lyotropic polymer liquid crystal, 1996, vol. 29.
81. N. Puech, E. Grelet, P. Poulin, C. Blanc and P. Van Der Schoot, Phys. Rev. E - Stat. Nonlinear, Soft Matter Phys., 2010, 82, 1–4.
82. M. Shribak and R. Oldenbourg, Appl. Opt., 2003, 42, 3009.
83. I. Usov and R. Mezzenga, Macromolecules, 2015, 48, 1269–1280.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm01886d

---