Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Variable pitch hydrodynamic electro-optic gratings utilising bent liquid crystal dimers†
R.
Morris
 ,
J. C.
Jones
,
J. C.
Jones
 and
M.
Nagaraj
and
M.
Nagaraj
 *
*
School of Physics and Astronomy, University of Leeds, Leeds LS2 9JT, UK. E-mail: m.nagaraj@leeds.ac.uk
First published on 7th October 2020
Abstract
Electrohydrodynamic instabilities (EHDI) in liquid crystals form uniform and continuously variable diffractive structures when subject to certain material and geometry determined conditions. A one-dimensional grating is one such diffractive structure, where the refractive index changes periodically in a direction parallel to the initial liquid crystal director. The period of this structure has been shown previously to vary continuously between the values of the cell gap and half-cell gap approximately, allowing continuous angular modulation of optical beams but with a limited angular range. In this work, the lower pitch limit is shown to also be governed in part by the ratio of the splay and bend elastic constants (k11/k33) of the liquid crystal. A host nematic liquid crystal with standard elastic constant ratios (k11/k33 < 1) is doped with odd-alkyl-spaced dimeric liquid crystal CB7CB, to create a liquid crystal mixture with a far higher elastic constant ratio (k11/k33 > 5) than for those previously used in literature EHDI studies. The EHDI gratings formed in this new mixture exhibit pitch lengths significantly below half-cell gap, allowing up to 50% wider angle continuous steering of light. This improves the potential for application in beamsteering and diffractive optical devices.
Introduction
Since the 1960s nematic liquid crystals (NLCs) have been used successfully as switchable optical materials in optoelectronic applications, including displays.1,2 The number of different applications of NLCs has expanded in recent decades to a wider variety of optical devices including spatial light modulators,3–8 lenses,9–11 diffraction gratings12–15 and beamsteering devices.4,16–18 An important goal has been to produce entirely arbitrary phase profiles for incident light when passed through the liquid crystal. Currently, liquid crystal on silicon (LCoS) spatial light modulators are used for such purposes.3–8,19–22 In LCoS devices, individual electrodes, driven by the silicon back-plane, reorient the NLC to induce the required optical phase profile. However, fringing fields and defects in the nematic director profile limit pixels to a minimum size of ∼5 μm.8,16 Given that many pixels are required to create all but the simplest optical features, and the fact that LCoS devices operate in reflection mode only (with much larger minimum pixel sizes for transmissive devices),5,16 developing alternative methodologies to create high-quality diffractive structures is desirable. In most NLC devices the electro-optic switching is achieved by utilising an external electric field, in order to rotate the average molecular orientation (n, the director), and hence the optic axis (Fréedericksz transition).23,24 The required electric field is mainly dictated by the dielectric anisotropy (Δε) and the elastic constants for splay (k11), twist (k22) and bend (k33),24–26 of the NLC. Optimisation of these material parameters is an essential part of ensuring good device performance.A less conventional method for creating diffractive optical structures in NLCs is by inducing viscous flow. Here, director reorientation is achieved by inducing a periodic material flow, which places a viscous torque on the director, causing it to reorient and form an optical grating.27,28 An example of such a process is the formation of electrically driven ion flow patterns created by electrohydrodynamic instability (EHDI).
In EHDIs the periodicity, described by pitch length (λC) of the induced optical grating, is typically dictated by the device spacing, d, the conductivity anisotropy (Δσ) and the dielectric anisotropy (Δε). The material elastic constants play a key role, as for the grating to form the systems elastic inertia must be overcome.28–30 In our previous work,31 it was argued that, for a given d, k11 and k33 influence the aspect ratio and the pitch length of the EHDI rolls, respectively. In this paper, the effect of changing the values of k11 and k33 of the NLC on the resulting EHDI is investigated by comparing different materials in several devices of different spacing. The variation in material elasticity is achieved by adding an odd-spaced dimer to the NLC. This increases k11/k33 to an atypical level, which is confirmed through the measurements of elastic constants. This results in shorter pitch EHDI gratings (<half-cell gap) than observed previously, thereby allowing wider angle continuous beamsteering steering.
Electro-hydro-dynamic instabilities
EHDIs have been the focus of extensive study since Williams first observed them in 1963. Such Williams domains are periodic structures that form when a relatively low-frequency voltage is applied across a layer of NLC.32,33 These periodic domains are formed by the reorientation of the NLC's optic axis, resulting in a periodic change of the refractive index for light polarised parallel to the axis of the grating vector. This change can be observed using both polarising optical microscopy (POM)32,34,35 and diffraction spectroscopy.15,27–29,36–38A basic understanding of the induced periodic domains was provided by Carr39 and Helfrich40 using a one-dimensional model based on periodic viscous flow and charge separation, leading to the standard model of EHDIs still used.27–30,34,36,41–45 This standard model is most straightforward for materials with negative dielectric (Δε < 0) and positive conductivity (Δσ > 0) anisotropies operating in a planar-aligned device, as shown schematically in Fig. 1a. Here, domain formation occurs once the applied voltage, V reaches a critical value, VC. This threshold is expected to vary with frequency in the manner shown in Fig. 1b, where two distinct regimes, ‘conduction’ and ‘dielectric’, are observed.27,28,41,44,46,47 In this work, we focus on the lower frequency conduction regime. In the conduction regime at VC, a one-dimensional phase contrast grating forms, with normal parallel to the initial director (Fig. 1c). Within this normal roll (NR) mode, the period (λC) decreases with increasing applied frequency.31,46
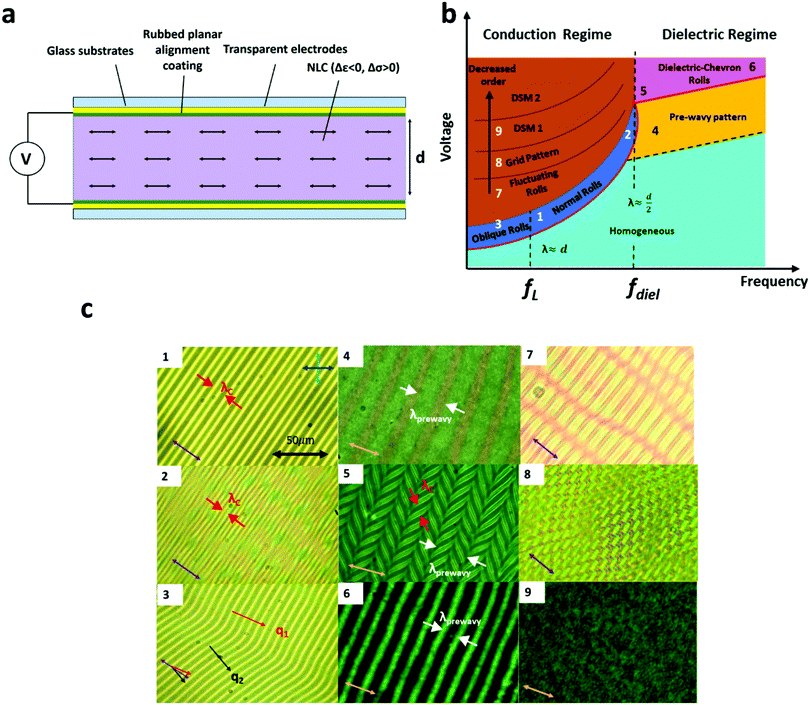 | ||
| Fig. 1 (a) Schematic representation of a device that can undergo EHDI. A thin layer of nematic liquid crystal with negative Δε and positive Δσ is placed between two glass plates separated by spacing d. The glass is coated with a transparent conductor, which allows a voltage V to be applied across the material, and an alignment layer, which gives the director (represented by double-headed arrows) an initial orientation. (b) Plot of the textures usually observed in standard EHDI as a mapping of voltage and frequency (see ref. 28). Here the threshold/critical voltage (VC) for onset of EHDI is shown as the red line below which the texture is homogenous. This behaviour of VC consists of the low frequency ‘conduction’ and high frequency ‘dielectric’ regimes. The focus of this work is the narrow region above VC in the conduction regime where well ordered normal rolls exist. (c) POM images of different regions shown in (b) between crossed polarisers where the scale bar in 1 applies to all figures. Here the rubbing direction is shown as either the pink or purple double headed arrow in the bottom left of each Fig. 1 and 2 shows the Normal Roll (NR) mode. 3 shows oblique rolls which occur at lower frequencies and have two wave vectors q1 and q2 oriented at ±θOb to the rubbing direction respectively. 4–6 show prewavy patterns. Here 5 shows a chevron texture, which is formed by the superposition of the NR and prewavy instabilities51,53 7–9 show the effect of increasing voltage within the conductive regime, where temporal and spatial disorder increases until the Dynamic Scattering Modes (DSM's 1 and 2) happen. DSMs are highly efficient optical scattering states. | ||
When VC is applied, the NR mode is induced by periodic hydrodynamic domains within the material (Fig. 2a). These domains are caused by ions moving to oppositely charge electrodes while the voltage oscillates. This has the dual effect of applying a viscous torque on the director29,48 and inducing a periodic charge separation in the material creating an in-plane electric field (shown as Eions in Fig. 2b). Both the hydrodynamic motion and the in-plane potential act to deviate the director inside the roll from its initial orientation. The resulting out-of-plane disruption of the director is resisted by the applied voltage across the device (due to negative Δε) and the material elasticity.28,29,39,40,45,49 This accounts for the threshold behaviour of VC, where for a given frequency, the combined deforming torques overcome the system inertia allowing the director within the rolls reorient when V > VC. At VC, this creates a NR mode phase modulating diffraction grating of the same period as the director modulation.15,37 The value of VC is seen to increase with applied frequency (Fig. 1a), as ions have shorter time periods to transit the cell.
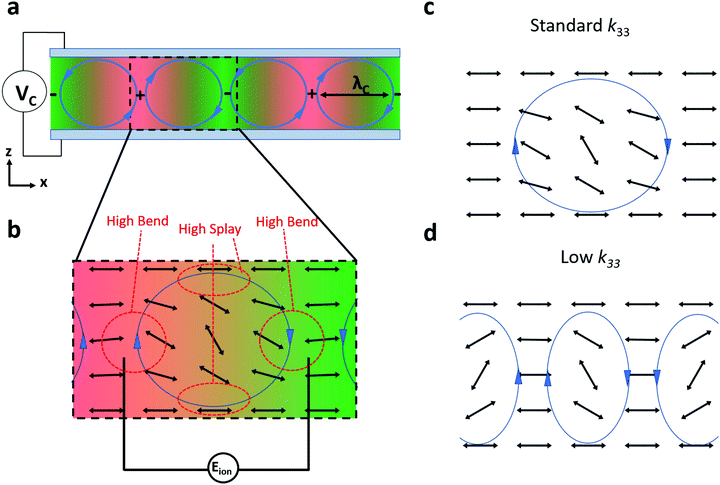 | ||
| Fig. 2 EHDI in the conduction regime, with a focus on the role of elastic constants in determining the grating size. (a) Schematic of typical roll formation in a device such as that shown in Fig. 1a when VC is applied. The hydrodynamic rolls are represented by the circles, with arrows showing the direction of flow. (b) Schematic of the director configuration within a roll, where the director rotates due to the combined effects of the viscous torque and periodic charge separation, represented by the electric field, Eions. (c) and (d) Schematics of the predicted effect of changing the bend elastic constant on the roll shape,31 where lower values allow the period of deformation to decrease creating a shorter pitch grating. | ||
At the onset of NR mode, the bend elastic constant, k33 is the dominant elasticity that must be overcome for the initial deviation of the director to occur.28,29 Meanwhile, the value of k11 becomes important at higher deviation. This is analogous to the Fréedericksz transition of a negative Δε material with the field applied parallel to the initial director. As mentioned previously, this suggests that a low k33 (and hence high ratio of k11/k33) should be advantageous for low pitch high contrast diffraction gratings: larger k11 implies any deformation will persist further in the z-direction, while a low k33 implies shorter pitch rolls (λC decreases).31
While maintaining the uniform NR mode, the range of pitches (λC) the rolls can exhibit is typically dictated by the device spacing, d. Here, the pitch only occupies values in the approximate range31,35,37,50–52
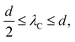 | (1) |
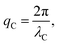 | (2) |
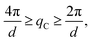 | (3) |
| 2q0 ≥ qC ≥ q0, | (4) |
EHDI in bent cores and dimers
In recent years, a wealth of novel mesogens have been synthesised, such as bent-core54–65 and bent dimeric63,66–80 compounds, which exhibit unusual viscoelasticity, flexoelectricity and phase behaviour. Studies have been carried out in driving bent-core LCs into a state of EHDI58,61,81–83 and there are a few similar reports on odd-spaced dimeric LCs.84–86 Both bent-core and dimeric LCs tend to exhibit significantly different EHDI behaviour (termed non-standard electroconvection) to those observed in conventional (calamitic) NLCs.87–89 These differences are attributed to the sizeable effect of flexoelectricity in the EHDI of these novel materials,41,83–85 where the standard Carr–Helfrich model assumes such effects are negligible.34,39,40 The EHDI of bent-core and dimeric LCs show different frequency dependencies of VC and optical textures, compared to calamitics, making a direct evaluation between standard and non-standard EHDI difficult. In instances where the conductivity is relatively low, low-frequency flexoelectric domains or non-standard rolls appear that are parallel to the director field, contrary to those of standard EHDI.90,91 Difficulties in comparisons are further compounded as both bent-core and bent dimeric LCs often have nematic phase at elevated temperatures and are usually difficult to align uniformly.Both bent-core and bent dimeric liquid crystals have been shown to exhibit unusual elastic constants when compared to calamitic NLCs. They exhibit values of k11/k33 that are significantly higher than unity,54,57,60,69,72,76,79,92 where standard calamitics typically exhibit k11/k33 between 0.6 and 0.8.93–95 It has also been shown that doping a standard calamitic liquid crystal with a bent-core or dimeric material can imbue the mixture with some similarly unusual elastic properties56,92,96–99 while still showing a nematic phase. For example, Parthasarathi et al.97 showed that binary mixtures of the bent dimer CB7CB with calamitic material 7OCB at certain temperatures exhibits k11/k33 > 5.
In order to understand the influence of elastic constants on the EHDI formation, our work uses a mixture of a bent dimer (CB7CB) and a standard calamitic NLC (MLC 2081). The permittivities of the resulting mixture were characterised to quantify the changes in dielectric and elastic properties. POM experiments were carried out on the mixture while it underwent EHDI to quantify VC and qC. It was hypothesised that if the outlined arguments of large k11/k33 are correct, this new mixture should exhibit larger values qC than those given in eqn (4). Such large values of qC are beneficial in the goal of achieving wider angle continuous beam steering.
Methods
Materials
Various mixtures of the NLC, MLC 2081, salt, tetra – butyl – ammonium – tetra – phenyl – borate (TBATPB, Fig. 3a) and bent dimer, 1,7-bis(4-cyanobiphenyl-4′-yl)heptane (CB7CB, Fig. 3b) were created. The naming format MMLC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CB7CB
CB7CB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TBATPB is used for convenience, where subscripts represent the weight fraction ratios of MLC 2081, CB7CB and TBATPB respectively. The choice and function of these various components is discussed in the following paragraphs.
TBATPB is used for convenience, where subscripts represent the weight fraction ratios of MLC 2081, CB7CB and TBATPB respectively. The choice and function of these various components is discussed in the following paragraphs.
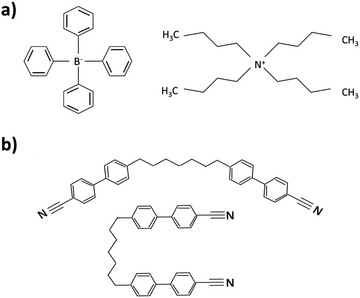 | ||
| Fig. 3 Chemical structure of (a) TBATPB and (b) CB7CB, shown in the dominant “banana” and “hairpin” conformations. | ||
MLC 2081 is a commercial NLC mixture provided by Merck Chemicals UK and was chosen as the host liquid crystal because it exhibits a wide nematic temperature range, a typical k11/k33 (0.7–0.8 at 25 °C), high negative dielectric anisotropy (Δε = −5.5 at 25 °C) and, importantly, a low inherent conductivity (σ⊥ < 10 nS m−1 at 25 °C) to enable conductivity to be controlled through the addition of dopants. The clearing temperature was measured to be 112 ± 2 °C, (using POM in a 10 μm spaced, planar-aligned glass cell on cooling at 0.5 °C min−1).
Due to its low conductivity and strongly negative Δε, MLC 2081 did not display a typical EHDI conduction regime at frequencies >1 Hz. To enhance it's conductivity, the ionic dopant TBATPB was added in concentrations of 0.5–1.0% (creating three mixtures M100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0
0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5/0.6/1.0). TBATPB was chosen as it (and other similar salts) has been shown previously to enhance conduction of LCs.31,56,100,101 Increase of TNI in mixtures were observed when measured over several months and application of high electric fields, potentially due to the breakdown of one of the lower clearing point components in the mixture caused by the addition of the ions. Hence, comparisons are made at the same reduced temperature (TNI − T) where TNI was checked at the time of each measurement.
0.5/0.6/1.0). TBATPB was chosen as it (and other similar salts) has been shown previously to enhance conduction of LCs.31,56,100,101 Increase of TNI in mixtures were observed when measured over several months and application of high electric fields, potentially due to the breakdown of one of the lower clearing point components in the mixture caused by the addition of the ions. Hence, comparisons are made at the same reduced temperature (TNI − T) where TNI was checked at the time of each measurement.
The bent dimeric dopant CB7CB (synthon chemicals) is one of a series of dimers that have received much interest in the past few years as it exhibits a novel nematic phase, called the twist-bend nematic, NTB.63,66–80 In addition to this, it has been shown that when the dimer is mixed with standard calamitics the resultant mixture can also show NTB phases, as well as exhibit distinctive changes in elastic constants.96–99 The transitions for the pure CB7CB were measured as Iso 116 °C N 102 °C NTB, in agreement with literature values.63,67,90 CB7CB has been shown to have a net positive Δε, due to the dominant effect of the longitudinal dipole moment of the “hairpin” conformer over the transverse dipole of the “banana” conformer (Fig. 3b).70,71 For the EHDI work the mixture composition 60% MLC 2081 and 40% CB7CB (M60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0) was chosen, since this was the composition with the highest concentration of CB7CB with the desired negative Δε over a wide nematic range (without the NTB phase). Compared to MLC 2081, M60
0) was chosen, since this was the composition with the highest concentration of CB7CB with the desired negative Δε over a wide nematic range (without the NTB phase). Compared to MLC 2081, M60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 showed only a slightly reduced TNI of 102 ± 2 °C and remained nematic until 20 °C. The similar nematic temperature range of the mixture components had the additional advantage that both T and TNI − T could be used for material comparisons. The materials were heated above TNI before any measurements were taken and typically all measurements of a particular type (optical or dielectric) were undertaken in a single cooling cycle. It was noted M60
0 showed only a slightly reduced TNI of 102 ± 2 °C and remained nematic until 20 °C. The similar nematic temperature range of the mixture components had the additional advantage that both T and TNI − T could be used for material comparisons. The materials were heated above TNI before any measurements were taken and typically all measurements of a particular type (optical or dielectric) were undertaken in a single cooling cycle. It was noted M60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 had sufficiently high conductivity to exhibit a EHDI conduction regime without the addition of TBATPB.
0 had sufficiently high conductivity to exhibit a EHDI conduction regime without the addition of TBATPB.
Dielectric studies
The dielectric and elastic properties of the materials were characterised as follows. The mixtures were filled into 10 μm spaced devices with bespoke guarded, circular electrodes for accurate permittivity measurements. We assume that there is no change to the elastic constants caused by the addition of TBATPB due to the low concentrations used. The polyimide SE1211 (Nissan Chemicals) was used to produce homeotropic (HT) alignment (pretilt ∼90°), whereas either SE2170 or SE130 (Nissan chemicals) were used for planar homogeneous (PH) alignment, both of which provide low pretilts (∼2°).102 Dielectric studies were performed using an Agilent E4980A LCR meter with coupled Linkam hotstage (TMS 95), to measure device capacitance and conductivity as functions of frequency, voltage and sample temperature. The signal was held at 50 kHz for a period of 60 s before each measurement, which was found to be sufficiently long for the capacitance to settle for all temperatures and voltages. This frequency was also found to be far from any relaxation processes and electrode effects. The measured capacitance Cm and conductance Gm values for the device includes the effect of the alignment layers. These were converted to measured permittivity components εm* using the 10 kHz empty cell capacitance, C0:103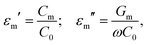 | (5) |
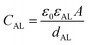 | (6) |
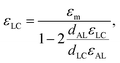 | (7) |
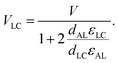 | (8) |
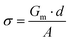 | (9) |
Devices
Several devices were used to assess the effects of elastic constants on NR diffraction gratings. These are listed in Table 1. Testing a range of devices allowed the effects of spacing, temperature, conductivity and permittivity on the VC and qC values of the NR mode be characterised. In all the devices where an NR mode was observed, the pitch qC was recorded using POM with a stage micrometre. Each frequency was set, and the applied voltage slowly increased from zero until the instability pattern was visible and the onset voltage VC was found. Within the NR regime, VC and qC were described by empirical fits:31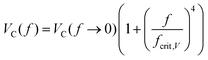 | (10) |
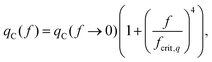 | (11) |
| Device | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| a Device 4 has a higher TNI due to the increase in TNI over time and application of field. All other devices were tested immediately on filling. | |||||||
| Material | M100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0 |
M100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0 |
M100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.6 0.6 |
M100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5 0.5 |
M100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.0 1.0 |
M60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0 |
M60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0 |
| Spacing | 10.6 ± 0.2 | 19.6 ± 0.2 | 10.0 ± 0.2 | 19.2 ± 0.3 | 19.1 ± 0.2 | 10.6 ± 0.4 | 18.9 ± 0.2 |
| Alignment layer | SE2170 | SE130 | SE130 | SE130 | SE130 | SE2170 | SE130 |
| NR EHDI | N | N | Y | Y | Y | Y | Y |
| T NI (°C) | 112 ± 2 | 112 ± 2 | 116 ± 2 | 129 ± 2a | 115 ± 2 | 102 ± 2 | 102 ± 2 |
The changes in grating pitch with frequency was confirmed through measurement of the diffraction angles as a function of frequency of the applied field. Results were taken using a HeNe 633 nm laser (Thorlabs) with the polarisation aligned parallel to the x-direction as shown in Fig. 2b, so that the incoming wavefronts experienced the periodic phase modulation. As in previous works,31,37,38m = 2 gave the highest intensity of the non-zero order diffraction peaks.
Results
Material characterisation
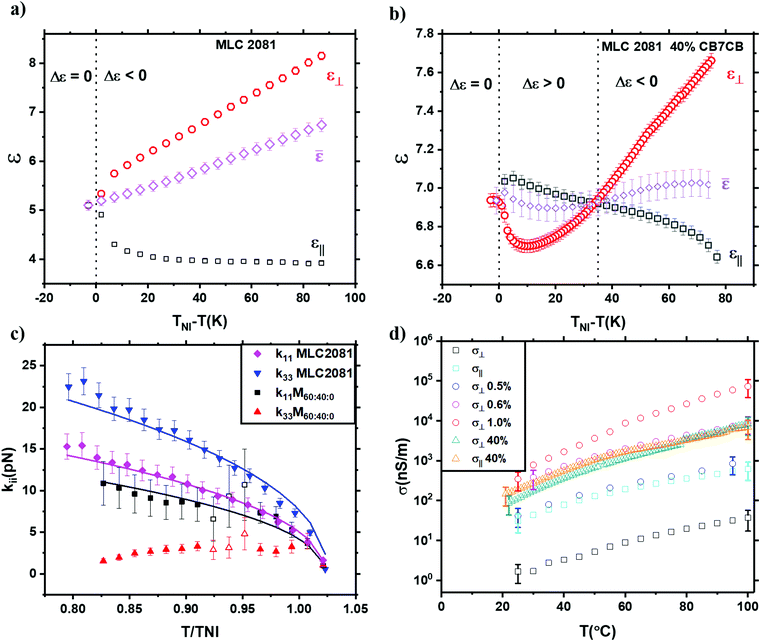
MLC 2081 was found to have a negative Δε from TNI (measured 112 ± 2 °C) to room temperature. The temperature dependence of the measured ε⊥, ε‖ and![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) is shown in Fig. 4a, where,
is shown in Fig. 4a, where,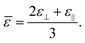 | (12) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0
0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5/0.6/1.0) had a slightly higher values of TNI in the range 115 ± 3 °C and did not have significantly different measured permittivity values.31
0.5/0.6/1.0) had a slightly higher values of TNI in the range 115 ± 3 °C and did not have significantly different measured permittivity values.31
The mixture of MLC 2081 and bent dimer CB7CB (M60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0) had a TNI = 102 ± 2 °C and Δε which changed sign from weakly positive between 102 °C and 63 °C, to weakly negative below 63 °C. This behaviour is due to the high gradient of permittivities versus temperature for the odd dimer mixture, due to the change in distribution of the conformational state from the positive Δε hairpin conformer to the negative Δε banana conformer.66,69,79,80,106 The values of ε⊥, ε‖ and εiso of M60
0) had a TNI = 102 ± 2 °C and Δε which changed sign from weakly positive between 102 °C and 63 °C, to weakly negative below 63 °C. This behaviour is due to the high gradient of permittivities versus temperature for the odd dimer mixture, due to the change in distribution of the conformational state from the positive Δε hairpin conformer to the negative Δε banana conformer.66,69,79,80,106 The values of ε⊥, ε‖ and εiso of M60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 are shown in Fig. 4b, where statistical errors from repeated measurements are used (found to be ±0.5% for ε⊥, ε‖, 1% for εiso). To confirm the changing sign of Δε, the homeotropic (HT) M60
0 are shown in Fig. 4b, where statistical errors from repeated measurements are used (found to be ±0.5% for ε⊥, ε‖, 1% for εiso). To confirm the changing sign of Δε, the homeotropic (HT) M60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 sample was cooled from TNI + 10 °C with a 30 V-(10 kHz) voltage continuously applied across the device. Above 63 °C, the sample remained dark since the electric field supported homeotropic alignment where the material has a positive Δε, while below this temperature a Schlieren texture was observed, due to the material undergoing a Fréedericksz transition.
0 sample was cooled from TNI + 10 °C with a 30 V-(10 kHz) voltage continuously applied across the device. Above 63 °C, the sample remained dark since the electric field supported homeotropic alignment where the material has a positive Δε, while below this temperature a Schlieren texture was observed, due to the material undergoing a Fréedericksz transition.
As MLC 2081 was negative throughout its nematic range, the elastic constants was obtained by fitting ε(V) in the HT device at a variety of temperatures. Due to the change in sign Δε for dimer mixture M60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 at a crossover temperature of 63 °C, a HT device was used to determine elastic constants below and a PH (planar homogeneous) device was used above this temperature, respectively (S1 includes examples of the fitted data). The values of the elastic constants obtained are shown in Fig. 4c, where errors are taken from the combined error in values of |Δε| and VC. Here, as Δε became very small closer to the crossover temperature of 63 °C, only a limited region of the entire Fréedericksz transition was studied. This resulted in a considerably higher experimental uncertainties around this region (shown as hollow symbols). In Fig. 4c, both k11 and k33 of MLC 2081 and k11 of M60
0 at a crossover temperature of 63 °C, a HT device was used to determine elastic constants below and a PH (planar homogeneous) device was used above this temperature, respectively (S1 includes examples of the fitted data). The values of the elastic constants obtained are shown in Fig. 4c, where errors are taken from the combined error in values of |Δε| and VC. Here, as Δε became very small closer to the crossover temperature of 63 °C, only a limited region of the entire Fréedericksz transition was studied. This resulted in a considerably higher experimental uncertainties around this region (shown as hollow symbols). In Fig. 4c, both k11 and k33 of MLC 2081 and k11 of M60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 are fitted to the square of the nematic order parameter estimated from the Maier–Saupe theory, calculated using:107
0 are fitted to the square of the nematic order parameter estimated from the Maier–Saupe theory, calculated using:107
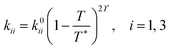 | (13) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 does not follow the Maier–Saupe relation (eqn (13)) and is found to have the opposite temperature dependence of decreasing magnitude with increasing order parameter. Similar behaviour has been observed in other bent dimeric compounds and their mixtures with calamitic materials previously.60,70,90 The origin of this is sometimes considered to be caused by stiffening of the alkyl spacer unit, which leads to the banana shaped conformer of the dimer molecules becoming favoured and hence dielectrically negative. Correspondingly, the banana-shaped conformer favours bend deformations thereby reducing k33.66
0 does not follow the Maier–Saupe relation (eqn (13)) and is found to have the opposite temperature dependence of decreasing magnitude with increasing order parameter. Similar behaviour has been observed in other bent dimeric compounds and their mixtures with calamitic materials previously.60,70,90 The origin of this is sometimes considered to be caused by stiffening of the alkyl spacer unit, which leads to the banana shaped conformer of the dimer molecules becoming favoured and hence dielectrically negative. Correspondingly, the banana-shaped conformer favours bend deformations thereby reducing k33.66
As discussed in earlier sections, for an NLC to adopt the NR mode of EHDI, sufficient ion flow is required to produce a torque that destabilises the uniformly aligned director.34,36,39,40Fig. 4d shows plots of σ as a function of temperature for pure MLC 2081 TBATPB and CB7CB doped samples (M100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0
0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) X materials and M60
X materials and M60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0). It is clear from the data that the addition of the salt TBATPB dramatically increases the σ values compared to pure MLC 2081 as intended, thereby enabling mixtures with similar conducitivies to be compared. As reported previously, the TBATPB appears to degrade HT alignment layer meaning values σ‖ were not possible to find accurately.31 It can be seen that in M60
0). It is clear from the data that the addition of the salt TBATPB dramatically increases the σ values compared to pure MLC 2081 as intended, thereby enabling mixtures with similar conducitivies to be compared. As reported previously, the TBATPB appears to degrade HT alignment layer meaning values σ‖ were not possible to find accurately.31 It can be seen that in M60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 the addition of CB7CB increased the conductivity of the mixture compared to pure MLC 2081, this conductivity was sufficient in M60
0 the addition of CB7CB increased the conductivity of the mixture compared to pure MLC 2081, this conductivity was sufficient in M60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 to undergo EHDI without the addition of TBATPB. It was also noted that above around 75 °C, the mixture M60
0 to undergo EHDI without the addition of TBATPB. It was also noted that above around 75 °C, the mixture M60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 changed sign Δσ from positive to negative. This behaviour is interesting and may be due to the same change in ratio of hairpin and banana conformer that leads to the change in sign Δε at 63 °C and the anomalous temperature dependence for k33 of the mixture.
0 changed sign Δσ from positive to negative. This behaviour is interesting and may be due to the same change in ratio of hairpin and banana conformer that leads to the change in sign Δε at 63 °C and the anomalous temperature dependence for k33 of the mixture.
EHDI characterisation
The NR mode EHDI behaviour of devices 3–7 was investigated in detail. The critical voltage and wave-vectors VC and qC were measured as functions of frequency for temperatures across the nematic range where Δε is negative. Although EHDI was observable in the dimer mixture M60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 while Δε was positive, the patterns were highly transient over time as found previously,106 due to the competition between Fréedericksz reorientation and the formation of EHDI rolls. In this case, the situation is further complicated by the crossover in Δσ.
0 while Δε was positive, the patterns were highly transient over time as found previously,106 due to the competition between Fréedericksz reorientation and the formation of EHDI rolls. In this case, the situation is further complicated by the crossover in Δσ.
In the NR mode, the values of VC and qC in all samples behaved in the manner described by eqn (10) and (11). Here at a given frequency, fdiel, the onset pattern (at VC) would change from the NR mode into the chevron pattern (see Fig. 1c). As has been previously observed this transition appears to consistently occur in standard calamitics at a frequency where λ = d/2,31,50–53 leading to the limits of continuous variation given in eqn (4). A possible reason for such behaviour could be a similar effect to that described by Penz and Ford,45 where due to a reduction in roll pitch a favourable hydrodynamic solution can be attained by partially overlaying two rolls above one another. Further work to confirm such a possibility within the structure of the standard model, is required.
Fig. 2d shows the hypothesis leading to this paper, where by creating a bent dimeric mixture with unusually low elastic constant k33 the rolls will become more ovular, allowing greater values qC than those given in eqn (4). To examine this, the devices were tested at several temperatures across their nematic range to observe the NR mode at a wide range of k11, k33 and their ratio. Fig. 5 shows an example comparison of VC and qC values for the NR mode in devices 4 and 7, which are filled with the ion-doped M100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0
0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5 and bent dimer doped M60
0.5 and bent dimer doped M60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 respectively. VC and qC are shown at several temperatures as functions of frequency while maintaining the NR state. These two devices were chosen for comparison because of the similar spacing (∼20 μm) and conductivity (∼100 nS m−1 at 30 °C) yet they display significantly different values of qC and VC. The lines in the figure represent best fits of the data points to eqn (10) and (11), respectively. As the temperature is increased, the divergences shift to higher fcrit values. This shift was observed previously and attributed to a higher number and mobility of the available charge carriers in the material at higher temperatures.31,56
0 respectively. VC and qC are shown at several temperatures as functions of frequency while maintaining the NR state. These two devices were chosen for comparison because of the similar spacing (∼20 μm) and conductivity (∼100 nS m−1 at 30 °C) yet they display significantly different values of qC and VC. The lines in the figure represent best fits of the data points to eqn (10) and (11), respectively. As the temperature is increased, the divergences shift to higher fcrit values. This shift was observed previously and attributed to a higher number and mobility of the available charge carriers in the material at higher temperatures.31,56
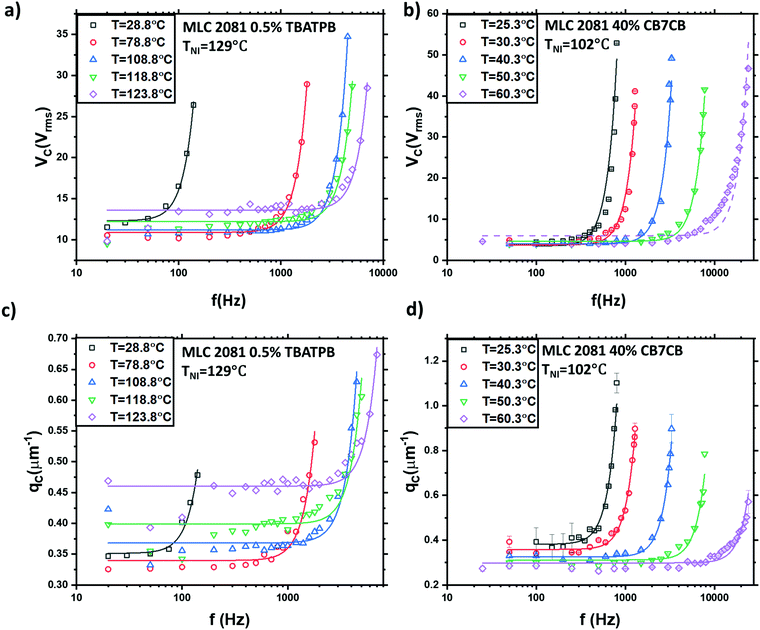 | ||
| Fig. 5 V C and qC curves for pure MLC 2081 (w/0.5% TBATPB) and the MLC 2081 with 40% CB7CB in ∼20 μm spaced devices (device 4 and 7 in Table 1). These only show values while the device maintained NR 1D diffractive structure. (a) and (b) show measured values of VC fitted with eqn (10), the dashed line in (b) indicates a poor fit, which only occurs in CB7CB doped sample when Δε is exceptionally small. (c) and (d) show the same but for qC values fitted with eqn (11). | ||
Comparing Fig. 5a, b and c, d, it is suggested that the manipulation of elastic constants caused by the addition of the CB7CB has led to significantly different values of VC and qC. From the examples given in Fig. 5 it can be seen that the dimer doped system has significantly lower VC values in the range 4 ± 2 V while the ion doped system is around 3 times this at 12 ± 2 V. Similarly the dimer doped mixture displays significantly larger maximum qC values as was predicted. This is considered in more detail in the Discussion section.
Effect of elastic constants on EHDI pitch
Fig. 6 shows the plots of the largest (qmax) and smallest (qmin) values observed for an NR grating in each of the devices in Table 1. The data demonstrate the causal link between the changes in elastic constants and the observed qC values. Here each quantity is normalised to q0 (= 2π/d) and the ratios plotted against the elastic constants and k11/k33. From these plots, it is clear that only the mixture including the bent dimer (M60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0) is outside the limits given in eqn (4), with new limits of approximately,
0) is outside the limits given in eqn (4), with new limits of approximately,| q0 × 75% ≤ qC ≤ 2q0 × 150%. | (14) |
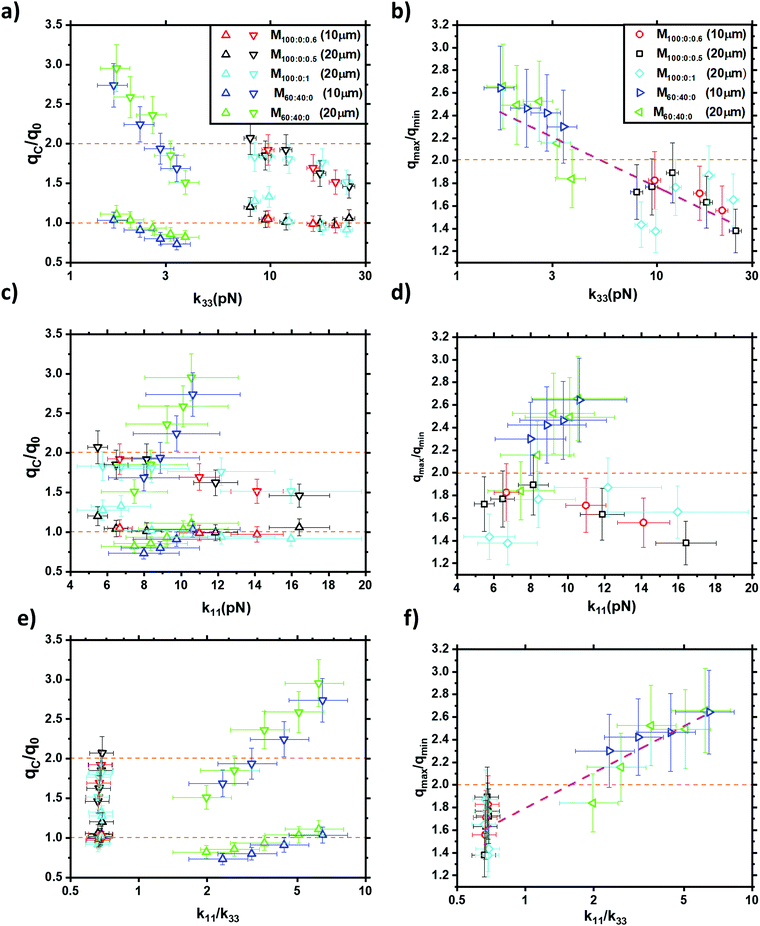 | ||
Fig. 6 Shows quantities related to qC as a function of elastic constants and their ratios. (a) Gives the key for all samples. The left side (a, c and e) plots show the maximum (downward triangles) and minimum (upward triangles) values of qC observed to form a uniform NR grating as the frequency was varied. The qC values are normalised by q0. The orange dotted lines represent the expected range of qC values according to eqn (4), where only the samples with CB7CB in are outside of them. The right side (b, d and f) shows the ratio of the qmax and the qmin. The horizontal orange dotted line shows only samples with CB7CB have a value of qmax/qmin greater than 2. In (b) and (f), the most continuous behaviour between the MLC 2081 and M60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 was observed; here, concatenated fits are used to guide the eye. 0 was observed; here, concatenated fits are used to guide the eye. | ||
 | ||
| Fig. 7 Plot comparing the steering angles of the dominant n = 2 diffraction order of devices undergoing EHDI in MLC 2081 with 1% TBATPB and MLC 2081 with 40% CB7CB (devices 5 and 7 in Table 1 respectively). Despite similar spacings, the device with CB7CB demonstrates considerably wider angle steering. | ||
Further, Fig. 6a and b show that lower k33 values tend to exhibit the most considerable disagreement with eqn (4), while higher values are always inside the limits. Fig. 6c and d, show how the qC ranges change with, k11, where the effect is less clear, possibly due to the changes in qC being dominated by k33. Fig. 6e and f, show this data as functions of k11/k33, which seems to indicate a trend of higher qC values and range as k11/k33 is increased as previously predicted.31
From each of these graphs, it is apparent that the concentration of TBATPB does not change values of qC displayed, provided there are sufficient ions for the system to undergo NR mode EHDI. Similarly, the device spacing does not change the limits of qC in either the CB7CB or the TBATPB doped MLC 2081, once the results are normalised by q0.
Discussion
So far, we focussed on the effect of varying material elastic constants to increase the values of qC and reduce VC. However, the results also show that the addition of CB7CB also change the material's dielectric and resistive properties (ε and σ in Fig. 4), in addition to probable changes in unmeasured viscosity. To establish that the effects mentioned are due to change in elastic constants, let us consider the likely effect of these other factors on the behaviour of VC and qC, separately.Behaviour of VC
Firstly to assess the observed changes in VC consider the model of Kramer and Pesch,44,47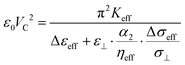 | (15) |
Although conductivity is included in eqn (15) it is unlikely that it is playing a dominant role in behaviour of VC for the dimer doped mixture. In the ion doping experiments (e.g. M100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0
0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5 and M100
0.5 and M100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0
0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 131) the conductivity values increase through nearly three orders of magnitude without a substantial change of low-frequency VC, while only a factor of three change is incurred in M60
131) the conductivity values increase through nearly three orders of magnitude without a substantial change of low-frequency VC, while only a factor of three change is incurred in M60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 (which has a intermediate conductivity of M100
0 (which has a intermediate conductivity of M100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0
0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5 and M100
0.5 and M100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0
0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). In contrast to conductivity, dielectric anisotropy is likely to play an important role in the reduction of VC. This is due to the lower value of |Δε| in M60
1). In contrast to conductivity, dielectric anisotropy is likely to play an important role in the reduction of VC. This is due to the lower value of |Δε| in M60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 reducing the stabilising torque imposed by the applied electric field on the director compared to that of MLC 2081 (reducing the negativity of the first term in the denominator of eqn (15)). Finally, although difficult to conclude about the effect of viscosity without a direct measurement, the addition of the dimer should increase the mixture viscosity and hence increase VC. This, in addition to the fact that samples were examined at a large range of temperatures with fairly small changes in VC indicates the role of the strongly temperature dependent viscosity, is small. These observations lead us to conclude that the reduction in VC is likely dominated by the dual effects of lowering the elastic term keff (mainly due to the reduction of k33) and reduction of the negative |Δε|.
0 reducing the stabilising torque imposed by the applied electric field on the director compared to that of MLC 2081 (reducing the negativity of the first term in the denominator of eqn (15)). Finally, although difficult to conclude about the effect of viscosity without a direct measurement, the addition of the dimer should increase the mixture viscosity and hence increase VC. This, in addition to the fact that samples were examined at a large range of temperatures with fairly small changes in VC indicates the role of the strongly temperature dependent viscosity, is small. These observations lead us to conclude that the reduction in VC is likely dominated by the dual effects of lowering the elastic term keff (mainly due to the reduction of k33) and reduction of the negative |Δε|.
Behaviour of qC
Similarly to the arguments for VC given above, it is unlikely that observed changes to qC range were caused by changing conductivity as this was not observed when examining different ion concentrations, with orders of magnitude variation in conductivity.31 Unlike the effect on VC, the reduction of minimum feature size defined by qC is not caused by changes to Δε. This has been shown in previous works,29,35 where it had been noted that a smaller |Δε| is likely to decrease qC values. This may allow qC for M60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 shown in Fig. 6 to go below the lower limits of eqn (4), but can not lead to rolls that surpass the upper limit. This supports the argument that the observed large qC values seen in the dimer doped mixtures are dominated by the changes to the elastic properties. Samples without dimer were tested at many temperatures and ionic dopant levels, covering a wide range of values of σ, ε and viscosity but none of them showed qC > 2q0.
0 shown in Fig. 6 to go below the lower limits of eqn (4), but can not lead to rolls that surpass the upper limit. This supports the argument that the observed large qC values seen in the dimer doped mixtures are dominated by the changes to the elastic properties. Samples without dimer were tested at many temperatures and ionic dopant levels, covering a wide range of values of σ, ε and viscosity but none of them showed qC > 2q0.
Role of flexoelectricity
Another potential material parameter that can influence the formation of EHDIs is the flexoelectric coefficients. CB7CB has been reported to have forty times higher flexoelastic coefficient values compared to standard calamitics108 so the mixture M60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 is likely also to have significantly increased flexoelectric coefficients (particularly e3). The EHDI analysis by Tavener et al.29 using the standard model does not include flexoelectric terms, and without such modelling methods, prediction of their effects on observed VC and qC values is difficult. However, it is unlikely that they are responsible for the observed change in the conduction regime, where such effects should be magnitudes smaller than the ionic effects.83–85,109,110 Flexoelectric rolls are observed in both bent-core and odd-dimer liquid crystals.111–113 However, it is unlikely the rolls investigated here are flexoelectric in origin since they depend strongly on sample conductivity,81 have the normal parallel to the director,82 and have a different frequency and voltage dependence of the onset behaviour.114–117 All mixtures studied here follow the predictions for the NR mode, indicating these flexoelectric terms are unlikely playing a significant role in the observed behaviour.58,61,81–83
0 is likely also to have significantly increased flexoelectric coefficients (particularly e3). The EHDI analysis by Tavener et al.29 using the standard model does not include flexoelectric terms, and without such modelling methods, prediction of their effects on observed VC and qC values is difficult. However, it is unlikely that they are responsible for the observed change in the conduction regime, where such effects should be magnitudes smaller than the ionic effects.83–85,109,110 Flexoelectric rolls are observed in both bent-core and odd-dimer liquid crystals.111–113 However, it is unlikely the rolls investigated here are flexoelectric in origin since they depend strongly on sample conductivity,81 have the normal parallel to the director,82 and have a different frequency and voltage dependence of the onset behaviour.114–117 All mixtures studied here follow the predictions for the NR mode, indicating these flexoelectric terms are unlikely playing a significant role in the observed behaviour.58,61,81–83
Conclusion
This paper demonstrates the influence of LC elastic constants on the pitch of the grating structures in nematic EHDIs. New nematic mixtures are designed by adding an odd-spaced bent dimeric nematic liquid crystal to a typical host calamitic NLC to deliberately change the elastic properties while maintaining negative Δε. EHDI are induced in a variety of mixtures and a systematic study of the influence of material properties on the grating formation is provided. In our previous work,31 it was predicted that a possible methodology of reducing λC values would be to create materials with significantly lower k33. The current work supports this hypothesis and demonstrates the ability of such low k33 values to increase qC values to higher than 2q0, which a standard calamitic NLC cannot usually achieve.This work acknowledges that, although the change in k33 is the principal candidate for the observed effects, there is also the possibility that changes in the material's viscosities, permittivities, conductivities or flexoelectric coefficients could also contribute to these changes. However, arguments are presented that suggest the change is dominated by the large reduction of k33 associated with the odd-spaced dimer.
Although LC systems undergoing EHDI have been considered unsuited in their ability to be applied to real-world devices compared to systems such as LCoS, this work demonstrates their ability to create well-ordered grating structures with sub 4 μm features, which are comparable to the limits of LCoS reflective devices, with the additional advantages of operating in transmissive mode and being continually variable. We demonstrate that as the frequency is increased, in a 10 μm spaced device, λ varies from 7 to 3.5 μm. This created a continuous angular variation from ∼9 to 21°, although reduction in efficiency at higher steering angles was observed.31 It should also be noted that the demonstrated technique of lowering k33 could also have application in other types of grating formation based on a hydrodynamic phenomenon, or in increasing the stability of structures that have a similar desired director conformation.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
EPSRC and Merck Chemicals UK funded this work with a CASE award under Dr Ben Snow as the industrial supervisor. JCJ thanks EPSRC Fellowship in Manufacturing (EP/S029214/1). The data associated with this paper can be found in https://doi.org/10.5518/859.References
- M. Schadt and W. Helfrich, Voltage-dependent optical activity of a twisted nematic liquid crystal, Appl. Phys. Lett., 1971, 18, 127–128, DOI:10.1063/1.1653593
.
- G. H. Heilmeier, L. A. Zanoni and L. A. Barton, Dynamic scattering in nematic liquid crystals, Appl. Phys. Lett., 1968, 13, 46–47, DOI:10.1063/1.1652453
.
- U. Efron, J. Grinberg, P. O. Braatz, M. J. Little, P. G. Reif and R. N. Schwartz, The silicon liquid-crystal light valve, J. Appl. Phys., 1985, 57, 1356–1368, DOI:10.1063/1.334487
.
- P. F. McManamon, T. A. Dorschner, D. L. Corkum, L. J. Friedman, D. S. Hobbs, M. Holz, S. Liberman, H. Q. Nguyen, D. P. Resler, R. C. Sharp and E. A. Watson, Optical phased array technology, Proc. IEEE, 1996, 84, 268–298, DOI:10.1109/5.482231
.
- P. F. McManamon, P. J. Bos, M. J. Escuti, J. Heikenfeld, S. Serati, H. Xie and E. A. Watson, A Review of Phased Array Steering for Narrow-Band Electrooptical Systems, Proc. IEEE, 2009, 97, 1078–1096, DOI:10.1109/JPROC.2009.2017218
.
- G. D. Love, Wave-front correction and production of Zernike modes with a liquid-crystal spatial light modulator, Appl. Opt., 1997, 36, 1517–1520, DOI:10.1364/ao.36.001517
.
- L. Hu, L. Xuan, Y. Liu, Z. Cao, D. Li and Q. Mu, Phase-only liquid crystal spatial light modulator for wavefront correction with high precision, Opt. Express, 2004, 12, 6403, DOI:10.1364/OPEX.12.006403
.
- Z. Zhang, Z. You and D. Chu, Fundamentals of phase-only liquid crystal on silicon (LCOS) devices, Light: Sci. Appl., 2014, 3, e213, DOI:10.1038/lsa.2014.94
.
- L. Susumu Sato, A. Sugiyama, R. Sato, S. Sato, L. Susumu Sato, A. Sugiyama, R. Sato and S. Sato, Liquid-crystal lens-cells with variable focal length, Jpn. J. Appl. Phys., 1979, 18, 1679–1684, DOI:10.1143/JJAP.18.1679
.
- S. Sato, Applications of Liquid Crystals to Variable-Focusing Lenses, Opt. Rev., 1999, 6, 471–485, DOI:10.1007/s10043-999-0471-z
.
- H.-C. Lin, M.-S. Chen and Y.-H. Lin, A Review of Electrically Tunable Focusing Liquid Crystal Lenses, Trans. Electr. Electron. Mater., 2011, 12, 234–240, DOI:10.4313/TEEM.2011.12.6.234
.
- R. G. Lindquist, T. M. Leslie, J. H. Kulick, G. P. Nordin, J. M. Jarem, S. T. Kowel and M. Friends, High-resolution liquid-crystal phase grating formed by fringing fields from interdigitated electrodes, Opt. Lett., 1994, 19, 670, DOI:10.1364/OL.19.000670
.
- J. Kim, C. Oh, S. Serati and M. J. Escuti, Wide-angle, nonmechanical beam steering with high throughput utilizing polarization gratings, Appl. Opt., 2011, 50, 2636, DOI:10.1364/AO.50.002636
.
- N. Mukohzaka, N. Yoshida, H. Toyoda, Y. Kobayashi and T. Hara, Diffraction efficiency analysis of a parallel-aligned nematic-liquid-crystal spatial light modulator, Appl. Opt., 1994, 33, 2804, DOI:10.1364/AO.33.002804
.
- R. A. Kashnow and J. E. Bigelow, Diffraction from a Liquid Crystal Phase Grating, Appl. Opt., 1973, 12, 2302, DOI:10.1364/AO.12.002302
.
- Z. He, F. Gou, R. Chen, K. Yin, T. Zhan and S.-T. Wu, Liquid Crystal Beam Steering Devices: Principles, Recent Advances, and Future Developments, Crystals, 2019, 9, 292, DOI:10.3390/cryst9060292
.
-
R. M. Matic, Blazed phase liquid crystal beam steering, in Laser Beam Propagation and Control, ed. H. Weichel and L. F. DeSandre, International Society for Optics and Photonics, Los Angeles, 1994, pp. 194–205 Search PubMed
.
- X. Wang, D. Wilson, R. Muller, P. Maker and D. Psaltis, Liquid-crystal blazed-grating beam deflector, Appl. Opt., 2000, 39, 6545, DOI:10.1364/AO.39.006545
.
-
J. Stockley and S. Serati, Advances in liquid crystal beam steering, in Free-Space Laser Communications IV, ed. J. C. Ricklin and D. G. Voelz, 2004, p. 32 Search PubMed
.
- X. Wang, B. Wang, J. Pouch, F. Miranda, M. Fisch, J. E. Anderson, V. Sergan and P. J. Bos, Liquid crystal on silicon(LCOS) wavefront corrector and beam steerer, Proc. SPIE, 2003, 5162, 139–146, DOI:10.1117/12.511504
.
- K. M. Johnson, D. J. McKnight and I. Underwood, Smart Spatial Light Modulators Using Liquid Crystals on Silicon, IEEE J. Quantum Electron., 1993, 29, 699–714, DOI:10.1109/3.199323
.
- D. J. McKnight, K. M. Johnson and R. A. Serati, 256 × 256 liquid-crystal-on-silicon spatial light modulator, Appl. Opt., 1994, 33, 2775, DOI:10.1364/AO.33.002775
.
- V. Fréedericksz and V. Zolina, Forces causing the orientation of an anisotropic liquid, Trans. Faraday Soc., 1933, 29, 919–930, 10.1039/TF9332900919
.
-
P. G. de Gennes and J. Prost, Static Distortions in Nematic Liquid Crystal, The Physics of Liquid Crystals, Oxford University Press, 1993, pp. 98–162 Search PubMed
.
- F. C. Frank, On the theory of liquid crystals, Discuss. Faraday Soc., 1958, 25, 19, 10.1039/df9582500019
.
- C. W. Oseen, The theory of liquid crystals, Trans. Faraday Soc., 1933, 29, 883, 10.1039/tf9332900883
.
-
P. G. de Gennes and J. Prost, Dynamical Properties of Nematics, in The Physics of Liquid Crystals, Oxford University Press, 1993, pp. 198–262 Search PubMed
.
- N. V. Madhusudana, Electroconvective instabilities in nematic liquid crystals, Phase Transitions, 1994, 50, 177–191, DOI:10.1080/01411599408200373
.
- S. J. Tavener, T. Mullin, G. I. Blake and K. A. Cliffe, Numerical bifurcation study of electrohydrodynamic convection in nematic liquid crystals, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63, 1–12, DOI:10.1103/PhysRevE.63.011708
.
- A. Buka, Pattern Formation in Liquid Crystals, Phys. Scr., 1989, 114–117, DOI:10.1088/0031-8949/1989/T25/019
.
- R. Morris, J. C. Jones and M. Nagaraj, Continuously variable diffraction gratings using electroconvection in liquid crystals for beam steering applications, J. Appl. Phys., 2019, 126, 224505, DOI:10.1063/1.5128205
.
- R. Williams, Domains in Liquid Crystals, J. Chem. Phys., 1963, 39, 384–388, DOI:10.1063/1.1734257
.
- R. Williams, Liquid crystals in an electric field, Nature, 1963, 199, 273–274, DOI:10.1038/199273a0
.
- E. Dubois-Violette, P. G. de Gennes and O. Parodi, Hydrodynamic instabilities of nematic liquid crystals under A. C. electric fields, J. Phys., 1971, 32, 305–317, DOI:10.1051/jphys:01971003204030500
.
-
A. Buka, N. Éber, W. Pesch and L. Kramer, Convective Patterns in Liquid Crystals Driven by an Electric Field, Advances in Sensing with Security Applications, Kluwer Academic Publishers, Dordrecht, 2005, pp. 55–82 Search PubMed
.
- Orsay Liquid Crystal Group, Hydrodynamic instabilities in nematic liquids under ac electric fields, Phys. Rev. Lett., 1970, 25, 1642–1643, DOI:10.1103/PhysRevLett.25.1642
.
- T. John, U. Behn and R. Stannarius, Laser diffraction by periodic dynamic patterns in anisotropic fluids, Eur. Phys. J. B, 2003, 35, 267–278, DOI:10.1140/epjb/e2003-00277-1
.
- C. Bohley, J. Heuer and R. Stannarius, Optical properties of electrohydrodynamic convection patterns: rigorous and approximate methods, J. Opt. Soc. Am. A, 2005, 22, 2818, DOI:10.1364/JOSAA.22.002818
.
- E. F. Carr, Influence of Electric Fields on the Molecular Alignment in the Liquid Crystal p -(Anisalamino)-phenyl Acetate, Mol. Cryst., 1969, 7, 253–268, DOI:10.1080/15421406908084876
.
- W. Helfrich, Conduction-Induced Alignment of Nematic Liquid Crystals: Basic Model and Stability Considerations, J. Chem. Phys., 1969, 51, 4092–4105, DOI:10.1063/1.1672632
.
-
L. Kramer and W. Pesch, Convection Instabilities in Nematic Liquid Crystals, Annual Review of Fluid Mechanics, 2006, pp. 515–539 Search PubMed
.
- E. Guyon and P. Pieranski, Convective instabilities in nematic liquid crystals, Physica, 1974, 73, 184–194, DOI:10.1016/0031-8914(74)90234-1
.
- E. Bodenschatz, W. Zimmermann and L. Kramer, On electrically driven pattern-forming instabilities in planar nematics On electrically driven pattern- forming instabilities in planar nematics, J. Phys., 1988, 49, 1875–1899, DOI:10.1051/jphys:0198800490110187500>
.
- A. Buka, N. Eber, W. Pesch and L. Kramer, Convective Patterns in Liquid Crystal Driven by Electric Field, Advances in sensing with security applications. NATO Science Series II: Mathematics, Physics and Chemistry, 2006, vol. 218, pp. 55–82, DOI:10.1007/1-4020-4355-4_02.
- P. A. Penz and G. W. Ford, Electromagnetic Hydrodynamics of Liquid Crystals, Phys. Rev. A: At., Mol., Opt. Phys., 1972, 6, 414–425, DOI:10.1103/PhysRevA.6.414
.
- E. Kochowska, S. Németh, G. Pelzl and Á. Buka, Electroconvection with and without the Carr-Helfrich effect in a series of nematic liquid crystals, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 011711, DOI:10.1103/PhysRevE.70.011711
.
-
L. Kramer and W. Pesch, Electrohydrodynamic Instabilities in Nematic Liquid Crystals, Pattern Formation in Liquid Crystals, 1996, pp. 221–255 Search PubMed
.
- E. Dubois-Violette, Theory of instabilities of nematics under A. C electric fields: Special effects near the cut off frequency, J. Phys., 1972, 33, 95–100, DOI:10.1051/jphys:0197200330109500
.
-
L. M. Blinov and V. G. Chigrinov, Electrooptic Effects in Liquid Crystal Materials, Springer New York, New York, NY, 1994 Search PubMed
.
- M. Scheuring, L. Kramer and J. Peinke, Formation of chevrons in the dielectric regime of electroconvection in nematic liquid crystals, Phys. Rev. E, 1998, 58, 2018–2026, DOI:10.1103/PhysRevE.58.2018
.
- N. Oikawa, Y. Hidaka and S. Kai, Formation of a defect lattice in electroconvection of nematics, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 6, DOI:10.1103/PhysRevE.70.066204
.
- H. Bohatsch and R. Stannarius, Frequency-induced structure transition of nematic electroconvection in twist cells, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 60, 5591–5599, DOI:10.1103/PhysRevE.60.5591
.
- J. H. Huh, Y. Hidaka, A. G. Rossberg and S. Kai, Pattern formation of chevrons in the conduction regime in homeotropically aligned liquid crystals, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 61, 2769–2776, DOI:10.1103/PhysRevE.61.2769
.
- S. Kaur, Elastic properties of bent-core nematic liquid crystals: the role of the bend angle, Liq. Cryst., 2016, 43, 2277–2284, DOI:10.1080/02678292.2016.1232442
.
- S. Kaur, J. Addis, C. Greco, A. Ferrarini, V. Görtz, J. W. Goodby and H. F. Gleeson, Understanding the distinctive elastic constants in an oxadiazole bent-core nematic liquid crystal, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 41703, DOI:10.1103/PhysRevE.86.041703
.
- S. Tanaka, H. Takezoe, N. Éber, K. Fodor-Csorba, A. Vajda and Á. Buka, Electroconvection in nematic mixtures of bent-core and calamitic molecules, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 021702, DOI:10.1103/PhysRevE.80.021702
.
- P. Sathyanarayana, M. Mathew, Q. Li, V. S. S. S. Sastry, B. Kundu, K. V. Le, H. Takezoe and S. Dhara, Splay bend elasticity of a bent-core nematic liquid crystal, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 010702, DOI:10.1103/PhysRevE.81.010702
.
- Y. Xiang, J. W. Goodby, V. Görtz and H. F. Gleeson, Revealing the uniaxial to biaxial nematic liquid crystal phase transition via distinctive electroconvection, Appl. Phys. Lett., 2009, 94, 193507, DOI:10.1063/1.3138867
.
- D. Shen, A. Pegenau, S. Diele, I. Wirth and C. Tschierske, Molecular Design of Nonchiral Bent-Core Liquid Crystals with Antiferroelectric Properties, J. Am. Chem. Soc., 2000, 122, 1593–1601, DOI:10.1021/ja993572w
.
- M. Majumdar, P. Salamon, A. Jákli, J. T. Gleeson and S. Sprunt, Elastic constants and orientational viscosities of a bent-core nematic liquid crystal, Phys. Rev. E, 2011, 83, 31701, DOI:10.1103/PhysRevE.83.031701
.
- A. Jákli, Liquid crystals of the twenty-first century – nematic phase of bent-core molecules, Liq. Cryst. Rev., 2013, 1, 65–82, DOI:10.1080/21680396.2013.803701
.
- G. Dantlgraber, A. Eremin, S. Diele, A. Hauser, H. Kresse, G. Pelzl and C. Tschierske, Chirality and Macroscopic Polar Order in a Ferroelectric Smectic Liquid-Crystalline Phase Formed by Achiral Polyphilic Bent-Core Molecules, Angew. Chem., Int. Ed., 2002, 41, 2408, DOI:10.1002/1521-3773(20020703)41:13<2408::AID-ANIE2408>3.0.CO;2-M
.
- I. Dozov, On the spontaneous symmetry breaking in the mesophases of achiral banana-shaped molecules, Europhys. Lett., 2001, 56, 247–253, DOI:10.1209/epl/i2001-00513-x
.
- C. Meyer, G. R. Luckhurst and I. Dozov, Flexoelectrically Driven Electroclinic Effect in the Twist-Bend Nematic Phase of Achiral Molecules with Bent Shapes, Phys. Rev. Lett., 2013, 111, 067801, DOI:10.1103/PhysRevLett.111.067801
.
- J. Etxebarria and M. Blanca Ros, Bent-core liquid crystals in the route to functional materials, J. Mater. Chem., 2008, 18, 2919, 10.1039/b803507e
.
- K. Adlem, M. Copič, G. R. Luckhurst, A. Mertelj, O. Parri, R. M. Richardson, B. D. Snow, B. A. Timimi, R. P. Tuffin and D. Wilkes, Chemically induced twist-bend nematic liquid crystals, liquid crystal dimers, and negative elastic constants, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 22503, DOI:10.1103/PhysRevE.88.022503
.
- V. P. Panov, M. Nagaraj, J. K. Vij, Y. P. Panarin, A. Kohlmeier, M. G. Tamba, R. A. Lewis and G. H. Mehl, Spontaneous Periodic Deformations in Nonchiral Planar-Aligned Bimesogens with a Nematic-Nematic Transition and a Negative Elastic Constant, Phys. Rev. Lett., 2010, 105, 167801, DOI:10.1103/PhysRevLett.105.167801
.
- G. Ungar, V. Percec and M. Zuber, Influence of molecular structure on the nematic-nematic transition in polyethers based on 1-(4-hydroxyphenyl)-2-(2-R-4-hydroxyphenyl)ethane where R = CH3 and Cl, and flexible spacers with an odd number of methylene units, Polym. Bull., 1994, 32, 325–330, DOI:10.1007/BF00308544
.
- M. Cestari, S. Diez-Berart, D. A. Dunmur, A. Ferrarini, M. R. De La Fuente, D. J. B. Jackson, D. O. Lopez, G. R. Luckhurst, M. A. Perez-Jubindo, R. M. Richardson, J. Salud, B. A. Timimi and H. Zimmermann, Phase behavior and properties of the liquid-crystal dimer 1,7-bis(4-cyanobiphenyl-4-yl) heptane: A twist-bend nematic liquid crystal, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 31704, DOI:10.1103/PhysRevE.84.031704
.
- N. Sebastián, B. Robles-Hernández, S. Diez-Berart, J. Salud, G. R. Luckhurst, D. A. Dunmur, D. O. López and M. R. de la Fuente, Distinctive dielectric properties of nematic liquid crystal dimers, Liq. Cryst., 2017, 44(1), 177–190, DOI:10.1080/02678292.2016.1218963
.
- K. L. Atkinson, S. M. Morris, F. Castles, M. M. Qasim, D. J. Gardiner and H. J. Coles, Flexoelectric and elastic coefficients of odd and even homologous bimesogens, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 012701, DOI:10.1103/PhysRevE.85.012701
.
- R. Balachandran, V. P. Panov, J. K. Vij, A. Kocot, M. G. Tamba, A. Kohlmeier and G. H. Mehl, Elastic properties of bimesogenic liquid crystals, Liq. Cryst., 2013, 40, 681–688, DOI:10.1080/02678292.2013.765973
.
- R. J. Mandle, M. P. Stevens and J. W. Goodby, Developments in liquid-crystalline dimers and oligomers, Liq. Cryst., 2017, 44, 2046–2059, DOI:10.1080/02678292.2017.1343500
.
- C. T. Imrie and P. A. Henderson, Liquid crystal dimers and higher oligomers: Between monomers and polymers, Chem. Soc. Rev., 2007, 36, 2096–2124, 10.1039/b714102e
.
- P. A. Henderson and C. T. Imrie, Methylene-linked liquid crystal dimers and the twist-bend nematic phase, Liq. Cryst., 2011, 38, 1407–1414, DOI:10.1080/02678292.2011.624368
.
- V. Borshch, Y.-K. Kim, J. Xiang, M. Gao, A. Jákli, V. P. Panov, J. K. Vij, C. T. Imrie, M. G. Tamba, G. H. Mehl and O. D. Lavrentovich, Nematic twist-bend phase with nanoscale modulation of molecular orientation, Nat. Commun., 2013, 4, 2635, DOI:10.1038/ncomms3635
.
- M. Cestari, E. Frezza, A. Ferrarini and G. R. Luckhurst, Crucial role of molecular curvature for the bend elastic and flexoelectric properties of liquid crystals: Mesogenic dimers as a case study, J. Mater. Chem., 2011, 21, 12303–12308, 10.1039/c1jm12233a
.
- D. A. Paterson, J. P. Abberley, W. T. Harrison, J. M. Storey and C. T. Imrie, Cyanobiphenyl-based liquid crystal dimers and the twist-bend nematic phase, Liq. Cryst., 2017, 44, 1–20, DOI:10.1080/02678292.2016.1274293
.
- G. Babakhanova, Z. Parsouzi, S. Paladugu, H. Wang, Y. A. Nastishin, S. V. Shiyanovskii, S. Sprunt and O. D. Lavrentovich, Elastic and viscous properties of the nematic dimer CB7CB, Phys. Rev. E, 2017, 96, 062704, DOI:10.1103/PhysRevE.96.062704
.
- Z. Zhang, V. P. Panov, M. Nagaraj, R. J. Mandle, J. W. Goodby, G. R. Luckhurst, J. C. Jones, H. F. Gleeson and R. Spectroscopy, Raman scattering studies of order parameters in liquid crystalline dimers exhibiting the nematic and twist-bend nematic phases, J. Mater. Chem. C, 2015, 3, 10007–10016, 10.1039/c5tc02174j
.
- D. Wiant, J. T. Gleeson, N. Éber, K. Fodor-Csorba, A. Jákli and T. Tóth-Katona, Nonstandard electroconvection in a bent-core nematic liquid crystal, Phys. Rev. E, 2005, 72, 041712, DOI:10.1103/PhysRevE.72.041712
.
- S. Kaur, A. Belaissaoui, J. W. Goodby, V. Görtz and H. F. Gleeson, Nonstandard electroconvection in a bent-core oxadiazole material, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 41704, DOI:10.1103/PhysRevE.83.041704
.
- P. Tadapatri, U. S. Hiremath, C. V. Yelamaggad and K. S. Krishnamurthy, Patterned electroconvective states in a bent-core nematic liquid crystal, J. Phys. Chem. B, 2010, 114, 10–21, DOI:10.1021/jp9058802
.
- M. Petrov, E. Keskinova, B. Katranchev and H. Naradikian, Electroconvection in dimeric nematic liquid crystals with short-range smectic C order: dynamical characteristics, Liq. Cryst., 2011, 38, 41–52, DOI:10.1080/02678292.2010.524944
.
- M. Petrov, B. Katranchev, E. Keskinova and H. Naradikian, The electroconvection in dimeric nematic liquid crystals, J. Optoelectron. Adv. Mater., 2007, 438–441 CAS
.
- K. S. Krishnamurthy, N. B. Palakurthy and C. V. Yelamaggad, Confined Electroconvective and Flexoelectric Instabilities Deep in the Freedericksz State of Nematic CB7CB, J. Phys. Chem. B, 2017, 121, 5447–5454, DOI:10.1021/acs.jpcb.7b03072
.
- A. Krekhov, W. Pesch, N. Éber, T. Tóth-Katona and Á. Buka, Nonstandard electroconvection and flexoelectricity in nematic liquid crystals, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 021705, DOI:10.1103/PhysRevE.77.021705
.
- T. Tóth-Katona, N. Éber and Á. Buka, Flexoelectricity in Electroconvection, Mol. Cryst. Liq. Cryst., 2009, 511, 11/[1481]–24/[1494], DOI:10.1080/15421400903048461
.
- W. Thom, W. Zimmermann and L. Kramer, The influence of the flexoelectric effect on the electrohydrodynamic instability in nematics, Liq. Cryst., 1989, 4, 309–316, DOI:10.1080/02678298908029184
.
- L. M. Blinov, Domain Instabilities in liquid crystals, J. Phys., Colloq., 1979, 40, C3-247–C3-258, DOI:10.1051/jphyscol:1979348
.
-
Á. Buka, T. Toth-Katona, N. Éber, K. Alexei and W. Pasch, The Role of Flexoelectricity in Pattern Formation, in Flexoelectricity in liquid crystals: Theory, experiments and applications, ed. Á. Buka and N. Éber, Imperial College Press, 2010, pp. 101–129 Search PubMed
.
- S. Srigengan, M. Nagaraj, A. Ferrarini, R. Mandle, S. J. Cowling, M. A. Osipov, G. Pająk, J. W. Goodby and H. F. Gleeson, Anomalously low twist and bend elastic constants in an oxadiazole-based bent-core nematic liquid crystal and its mixtures; contributions of spontaneous chirality and polarity, J. Mater. Chem. C, 2018, 6, 980–988, 10.1039/C7TC04664B
.
- E. P. Raynes, C. V. Brown and J. F. Strömer, Method for the measurement of the K22 nematic elastic constant, Appl. Phys. Lett., 2003, 82, 13–15, DOI:10.1063/1.1534942
.
- M. Cui and J. R. Kelly, Temperature Dependence of Visco-Elastic Properties of 5CB, Mol. Cryst. Liq. Cryst. Sci. Technol., Sect. A, 1999, 331, 49–57, DOI:10.1080/10587259908047499
.
- I. Haller, Elastic constants of the nematic liquid crystalline phase of p-methoxybenzylidene-p-n-butylaniline (MBBA), J. Chem. Phys., 1972, 57, 1400–1405, DOI:10.1063/1.1678416
.
- M. Cvetinov, D. Obadović, M. Stojanović, D. Lazar, A. Vajda, N. Éber, K. Fodor-Csorba and I. Ristić, Mesophase behaviour of binary mixtures of bent-core and calamitic compounds, Liq. Cryst., 2013, 40, 1512–1519, DOI:10.1080/02678292.2013.822938
.
- S. Parthasarathi, D. S. S. Rao, N. B. Palakurthy, C. V. Yelamaggad and S. Krishna Prasad, Binary System Exhibiting the Nematic to Twist-Bend Nematic Transition: Behavior of Permittivity and Elastic Constants, J. Phys. Chem. B, 2016, 120, 5056–5062, DOI:10.1021/acs.jpcb.6b03048
.
- N. Trbojevic, D. J. Read and M. Nagaraj, Dielectric properties of liquid crystalline dimer mixtures exhibiting the nematic and twist-bend nematic phases, Phys. Rev. E, 2017, 96, 52703, DOI:10.1103/PhysRevE.96.052703
.
- M. R. Tuchband, M. Shuai, K. A. Graber, D. Chen, L. Radzihovsky, A. Klittnick, L. Foley, A. Scarbrough, J. H. Porada, M. Moran, E. Korblova, D. M. Walba, M. A. Glaser, J. E. Maclennan and N. A. Clark, The twist-bend nematic phase of bent mesogenic dimer CB7CB and its mixtures, in APS March Meeting 2016, 2015.
- B. Zhang and H. Kitzerow, Pattern Formation in a Nematic Liquid Crystal Mixture with Negative Anisotropy of the Electric Conductivity—A Long-Known System with “Inverse” Light Scattering Revisited, J. Phys. Chem. B, 2016, 120, 6865–6871, DOI:10.1021/acs.jpcb.6b05080
.
- B. Allen and R. Daniel Louis, Method for increasing the conductivity of electrically resistive organic materials, 1975, https://patents.google.com/patent/US4033905A/en.
- Nissan Chemicals: Polyimide Data Sheet: Alignment Coatings for LCDs-SUNEVER Series-1.
-
I. S. Grant, S. Ian, W. R. Phillips and R. William, Electromagnetism, Wiley, 1975 Search PubMed
.
- M. G. Clark, E. P. Raynes, R. A. Smith and R. J. A. Tough, Measurement of the permittivity of nematic liquid crystals in magnetic and electric fields using extrapolation procedures, J. Phys. D: Appl. Phys., 1980, 13, 2151–2164, DOI:10.1088/0022-3727/13/11/025
.
- K. R. Welford and J. R. Sambles, Analysis of Electric Field Induced Deformations in a Nematic Liquid Crystal for any Applied Field, Mol. Cryst. Liq. Cryst., 1987, 147, 25–42, DOI:10.1080/00268948708084622
.
- C. Meyer, G. R. Luckhurst and I. Dozov, The temperature dependence of the heliconical tilt angle in the twist-bend nematic phase of the odd dimer CB7CB, J. Mater. Chem. C, 2015, 3, 318–328, 10.1039/C4TC01927J
.
- I. Haller, Thermodynamic and static properties of liquid crystals, Prog. Solid State Chem., 1975, 10, 103–118, DOI:10.1016/0079-6786(75)90008-4
.
- J. C. Jones, Comparison of the P2 and P4 order parameters between symmetric and asymetric liquid crystalline dimers with twist bend nematic phases. Special symposium: twist-bend nematics and beyond, University of Southampton, 2016, Unpublished.
- G. R. Luckhurst, C. Zannoni, P. L. Nordio and U. Segre, A molecular field theory for uniaxial nematic liquid crystals formed by non-cylindrically symmetric molecules, Mol. Phys., 1975, 30, 1345–1358, DOI:10.1080/00268977500102881
.
- B. Dressel and W. Pesch, Competition between electroconvection and Fréedericksz distortions in nematic liquid crystals with slightly positive dielectric anisotropy, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 031707, DOI:10.1103/PhysRevE.67.031707
.
- H. Wang, T. X. Wu, S. Gauza, J. R. Wu and S. Wu, A method to estimate the Leslie coefficients of liquid crystals based on MBBA data, Liq. Cryst., 2006, 33, 91–98, DOI:10.1080/02678290500446111
.
- A. Varanytsia and L.-C. Chien, Giant Flexoelectro-optic Effect with Liquid Crystal Dimer CB7CB, Sci. Rep., 2017, 7, 41333, DOI:10.1038/srep41333
.
- L. Kramer, E. Bodenschatz, W. Pesch, W. Thom and W. Zimmermann, Invited Lecture. New results on the electrohydrodynamic instability in nematics New results on the electrohydrodynamic instability in nematics, Liq. Cryst., 1989, 5, 699–715, DOI:10.1080/02678298908045420
.
- N. V. Madhusudana and V. A. Raghunathan, Influence of flexoelectricity on electrohydrodynamic instabilities in nematics, Liq. Cryst., 1989, 5, 1789–1812, DOI:10.1080/02678298908045689
.
- Y. Xiang, H. Z. Jing, Z. D. Zhang, W. J. Ye, M. Y. Xu, E. Wang, P. Salamon, N. Éber and Á. Buka, Tunable Optical Grating Based on the Flexoelectric Effect in a Bent-Core Nematic Liquid Crystal, Phys. Rev. Appl., 2017, 7, 064032, DOI:10.1103/PhysRevApplied.7.064032
.
- P. Tadapatri, K. S. Krishnamurthy and W. Weissflog, Patterned flexoelectric instability in a bent-core nematic liquid crystal, Soft Matter, 2012, 8, 1202–1214, 10.1039/c1sm06870a
.
- R. Balachandran, V. P. Panov, Y. P. Panarin, J. K. Vij, M. G. Tamba, G. H. Mehl and J. K. Song, Flexoelectric behavior of bimesogenic liquid crystals in the nematic phase-observation of a new self-assembly pattern at the twist-bend nematic and the nematic interface, J. Mater. Chem. C, 2014, 2, 8179–8184, 10.1039/c4tc01043d
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm01425g |
| This journal is © The Royal Society of Chemistry 2020 |