Defects and defect engineering in Soft Matter

Abstract

Soft matter covers a wide range of materials based on linear or branched polymers, gels and rubbers, amphiphilic (macro)molecules, colloids, and self-assembled structures. These materials have applications in various industries, all highly important for our daily life, and they control all biological functions; therefore, controlling and tailoring their properties is crucial. One way to approach this target is defect engineering, which aims to control defects in the material's structure, and/or to purposely add defects into it to trigger specific functions. While this approach has been a striking success story in crystalline inorganic hard matter, both for mechanical and electronic properties, and has also been applied to organic hard materials, defect engineering is rarely used in soft matter design. In this review, we present a survey on investigations on defects and/or defect engineering in nine classes of soft matter composed of liquid crystals, colloids, linear polymers with moderate degree of branching, hyperbranched polymers and dendrimers, conjugated polymers, polymeric networks, self-assembled amphiphiles and proteins, block copolymers and supramolecular polymers. This overview proposes a promising role of this approach for tuning the properties of soft matter.

---

Amir Jangizehi

Amir Jangizehi is a post-doctoral researcher in the group of Prof. Sebastian Seiffert at Johannes Gutenberg University Mainz. After obtaining his PhD in polymer science from Amirkabir University of Technology (Iran) in 2018, he spent one year as a post-doctoral researcher at Karlsruhe Institute of Technology working on microfluidic templating of charged microscopic hydrogels. His research is focused on the physical chemistry of supramolecular polymers and hydrogels, with a particular view to nanostructural complexity and connectivity defects.

Friederike Schmid

Friederike Schmid is a professor for theoretical physics at Johannes Gutenberg University Mainz. She studied physics in Heidelberg and Munich (LMU) and obtained her PhD (1991) and Habilitation in Theoretical Physics (1997) in Mainz. She was appointed professor at the University of Bielefeld in 2000, and in Mainz in 2009. External stays include postdoctoral research at the University of Washington (1992–1994). She obtained the “Gerhard Hess award” of the DFG in 1998 and the “Karl-Peter Grotemeyer” teaching award in 2003. She is currently senior editor of the ‘Journal of Physical Chemistry B’ and divisional associate Editor of ‘Physical Review Letters’.

Pol Besenius

Pol Besenius was born and raised in Luxemburg, and studied Chemistry in Vienna and Glasgow. He received his PhD from the University of Strathclyde (2008) und undertook postdoctoral studies at Eindhoven University of Technology, as Marie-Curie Fellow (2008–2011). He started his independent research group at the Organic Chemistry Institute in Münster, supported by a Liebig Fellowship in 2011, and moved to the Johannes Gutenberg University of Mainz in 2015 to take up a Professorship in Macromolecular Chemistry. In 2018, he was awarded an ERC Consolidator Grant, and since 2018 he is an Editor at the newly launched Thieme journal ‘Organic Materials’.

Kurt Kremer

Kurt Kremer is director and head of the theory department at Max Planck Institute for Polymer Research, Mainz. He obtained his PhD in 1983 at Cologne University and his Habilitation in 1988 at the University of Mainz. After that, he joined the solid state laboratory at KFA Juelich as senior scientific staff. His main research field is computational soft matter physics. He spent several extended visits as visiting professor/scientist at Exxon Research, UC Santa Barbara, University of Minnesota and New York University. He received several awards and recognitions and is member of the German National Academy of Science Leopoldina.

Sebastian Seiffert

Sebastian Seiffert is professor for physical chemistry of polymers at Johannes Gutenberg University Mainz since 2016. He obtained his PhD from Clausthal University of Technology (2007), was a postdoc at Harvard (2009–2010), and headed a junior research group at Helmholtz-Zentrum Berlin (2011–2014). His first faculty appointment was as associate professor for supramolecular polymer materials at Freie Universität Berlin (2014–2016). Sebastian's work was honored with the Reimund Stadler Award of the German Chemical Society (GDCh), an annual award by the Association of German University Professors in Chemistry (ADUC), and a young investigator award by the Polymer Networks Group (PNG).

---

1. Introduction

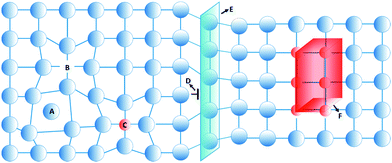
A perfect crystal is an idealization that does not exist in nature.¹ Instead, the structure of hard crystalline solids contains a considerable extent of irregularities and inhomogeneities, referred to as defects.² These defects strongly affect the physical and mechanical properties of hard crystalline solids. As an example, almost defect-free metallic single crystals have weaker mechanical properties than polycrystalline ones, since in the latter the interaction between defects and grain boundaries are strong.^3,4 Control over these defects and their associated nanostructural heterogeneity, known as defect engineering,^5–8 therefore is an approach that permits material properties to be tailored for functional devices such as semiconductors, paramagnets, thermoelectrics, and ferroelectrics.^9–13

In hard solids, defects are divided into four classes according to their dimension: point, line, planar, and volume defects,^14,15 as shown in Fig. 1. Zero-dimensional point defects are vacancies that are present in a significant concentration in all crystalline materials. This kind of defect is formed when an atom is missing at a position that ought to be filled in the crystal. Other types of point defects are the local imbalance of charges and the presence of solutes or impurities in the structure of the crystals. One-dimensional linear defects, or dislocations, are lines through the crystal along which crystallographic registry is lost. Two-dimensional defects can be considered as external surfaces, at which the solid terminates at a vapor or liquid, or as surfaces that separate grains or distinct phases within the solids, or yet alternatively as internal defects that disrupt a crystalline pattern over a surface within a crystal. Three-dimensional defects are aggregates of atoms or vacancies. A first type can be small particles that are introduced into the matrix by solid-state reactions, referred to as precipitates. A second type are dispersants with a grain size range of 1–100 μm, which are intentionally introduced into the microstructure.¹⁶ Voids and pores are another type of three-dimensional defect that forms by trapped gases or by accumulation of vacancies.

Fig. 1 Examples of defects in hard crystalline solids. (A) zero-dimensional point defects can be formed when an atom occupies an interstitial site where no atom would ordinarily appear, or (B) when an atom is missing at a position that ought to be filled. (C) The presence of foreign atoms is another type of point defect. (D) Edge dislocation is a one-dimensional defect that may form by insertion of an extra half plane of atoms in the crystal structure. (E) A stacking fault is an internal two-dimensional defect that disrupts the crystalline pattern. (F) A precipitate is a three-dimensional defect formed by aggregation of point defects.

Defects significantly affect the physical properties of solid crystals. The most well-known example is semiconducting silicon and germanium. Both are crystals with diamond structures. While pure silicon and germanium are intrinsic semiconductors, for creation of truly sophisticated materials, introduction of defects such as other atoms is necessary.¹⁵ Beyond the application area of semiconductors, diffusion within solid crystals relies on defects and can typically occur if a population of defects such as vacancies exists. In this case, atoms can jump from normal sites into neighboring vacancies.^1,15 A similar mechanism is valid for ionic conductivity.^17,18 For example, defects majorly control the electronic properties of Zn₂Sb₂ thermoelectric materials¹⁹ and the electrochemical properties of LiFePO₄ based materials.²⁰ Very generally, doping-type defects have found different applications in hard solids. For example, addition of titanium dioxide, TiO₂, into chromium oxide, Cr₂O₃, gives materials that are used in the sensing of reducing gases. Furthermore, the resistivity of doped transition-metal oxides such as NiO doped with Li₂O, Fe₂O₃ doped with TiO₂, and Mn₃O₄ doped with NiO, generally decreases exponentially with temperature. This makes these materials suitable for temperature measurement and sensing.¹⁵ Defects can also impart colored to transparent solids if they interact with white light. For example, while cerium(IV)oxide is transparent, its defective structure, which is made by mixing with praseodymium, displays a red/orange coloration, indicating light absorption in the blue/green region.¹⁸ In addition to such physical properties, also the mechanical properties of hard solids are influenced by defects. It has been shown that the elastic modulus of cerium(IV)oxide samples is a function of the oxygen vacancy concentration.^21–23 Also, the yield strength and subsequent plastic deformation of solid crystals is controlled by dislocation defects. Furthermore, three dimensional defects such as precipitates or dispersants change the strength of structural alloys.¹

In addition to their extreme and vast importance in inorganic materials, defects are also noteworthy in organic materials. For instance, controlled adjustment of the properties of metal–organic frameworks, MOFs, by defect engineering is an example.^24–26 In these materials, metal ions and/or clusters of metal ions are linked together by oligotopic organic molecules, thereby forming a hybrid material.²⁷ Defects in the internal structure of such MOFs can originate from partially missing metal nodes or linkers and from local breakage of the framework regularity.^26,28 Clustering of these linker or node vacancies generates mesopores, which may significantly influence the physical and mechanical properties of MOFs. This introduces the possibility of developing MOFs by defect engineering.²⁹ An example of such developing is to use MOFs as catalytic substrates. In this application, the targeted defects are mostly coordinative mismatches between the linker and metal ions, which results in Brønsted or Lewis acid sites, respectively. The catalytic activity of MOFs is directly related to the number of such defects.²⁴ For zinc terephthalate, as an example, linker vacancies partly occupied by OH groups catalyze the alkylation of biphenyl with tert-butyl chloride with 100% para-selectivity.^28,30 Acidic defects of MOFs can also serve as active catalysts for the condensation of benzaldehyde and ethyl cyanoacetate.³¹ Furthermore, the hydroxymethylation of 2-methylfuran, transesterification of vegetable oils with several aliphatic alcohols, cyclization of citronella to isopulegols, and Diels–Alder reactions between 1,3-cyclohexadiene and several dienophiles are other examples of defect-induced catalytic activity in MOFs.^32–34 For gas adsorption applications, the density of coordinatively unsaturated sites as well as the pore size distribution and specific surface area can be controlled by defect engineering. As an example, in MOFs made by [In(COO)₄] units linked through biphenyl-3,3′,5,5′,-tetra(phenyl-4-carboxylate) linkers, fragmentation and defects allow the desolvated phase to achieve a high specific surface area and pore volume.³⁵ A similar increase of porosity and capacity of CO₂ adsorption associated to that by engineering of linker vacancies are also reported for other types of MOFs.^26,36,37 Moreover, the uptake of H₂ and CH₄ can be tuned by metal node vacancies and other defects such as ZnO species in the nanopores and lattice interpenetration.^38,39 The modulation of electronic and magnetic properties of MOFs is another aspect of defect engineering in these materials. In this context, for example, change of the emission lifetime in [Ru(2,2′-bipyridine)₃]²⁺,⁴⁰ and modification of the electronic band structure in copper/1,3,5-benzenetricarboxylic acid-based MOFs have been reported.⁴¹ Moreover, vacancy-induced ferromagnetism in a series of copper based MOFs was discussed by Feng and coworkers.⁴²

Defect engineering has also been reported in pure organic materials such as carbon nanotubes and graphene sheets. These defects can be generated in carbon nanostructures by electron and ion irradiation.⁴³ That way, pentagon-heptagon-heptagon-pentagon defects are formed by C–C bond rotation.⁴⁴ These so called 5–7 pair defects act as nucleation cores of dislocations in the planar hexagonal network of the graphene layer.⁴⁵ These defects can migrate along a nanotube wall, which is responsible for the plastic deformation of carbon nanotubes.⁴⁶ The 5–7 defects can also be utilized for modifying the electronic properties of graphene sheets and carbon nanotubes. Beyond such pure-carbon materials engineering, joining a semiconducting nanotube to a metallic one through the use of a 5–7 pair can be the basis of a nanodiode for the design of nanoelectronics.⁴⁷ In another area of application, similar to the defect dependency of MOFs’ gas adsorption, Mercuri and coworkers showed that the adsorption and uptake of oxidizing gas in carbon nanotubes are likely to occur by interaction of the gas molecules and defective sites such as vacancies within the hexagonal networks of the nanotubes.⁴⁸ Considering the sensitivity of electronic and transport properties of nanotubes to the adsorption of gases such as NO₂ and NH₃,⁴⁹ defect engineering in nanotubes can therefore be used to design gas sensors. In addition to carbon nanotubes and graphene sheets, nanodiamonds can be considered as another example to highlight the importance of defects in pure organic materials. Nanodiamonds or diamond nanocrystals consist of crystalline balls of a few thousands of carbon atoms, which also have some nitrogen, oxygen, and hydrogen atoms.⁵⁰ The nitrogen atoms in nanodiamonds produce a variety of defects, among them negatively-charged nitrogen vacancies (NV) can be considered as point defects.⁵¹ These defects can be utilized as sensors for various relevant quantities like electrical, magnetic, or optical characteristics. Accordingly, nanodiamonds have found many applications in sensing, imaging, drug delivery, and tissue engineering.^52,53 NV defects in nanodiamonds are highly sensitive electrometers, which can be used to detect the electrical field even of a single electron at a distance of 150 nm.^54,55 Moreover, NV centers in nanodiamonds can be utilized for nano-scale thermometry based on the coherent manipulation of the electronic spin associated with the NV centers. With that, the local thermal environment on length scales as short as 200 nanometers can be measured. As another example, nanodiamonds can be utilized as biological sensors due to the influence of ferritin metalloproteins on the spin properties of single NV clusters, which originates from the capability of nanodiamonds to adsorb proteins on their NV sites via electrostatic interactions.⁵⁶

All the above examples of inorganic and organic materials are hard solids. A complementary class of materials is soft matter, as systematically introduced by de Gennes in his Nobel lecture.⁵⁷ This class of materials occupies a middle ground between the ideal fluid state and the ideal solid state,⁵⁸ based on three cornerstones. First, the size of the building blocks of soft matter is in the mesoscopic scale between 1–1000 nm, with polyatomic rather than just single or few-atomic constituents.⁵⁹ Second, due to that large size of the building blocks, their relaxation times are about 1–1000 ms. Third, the binding or interaction energy of the building blocks of soft matter is in the order of just singles to tens of RT (3–150 kJ mol⁻¹), which is considerably smaller than that of hard solid crystals. Typical energy densities, which to a first approximation determine the elastic constants, can be orders of magnitude smaller. Therefore, in contrast to hard solids, entropy and energy are equally important. As a consequence, soft matter can be easily perturbed even by just moderate external mechanical, thermal, or electrical agitation, whereupon it responds considerably, for example, by profound structural rearrangement that either persists or is followed by subsequent relaxation upon removal of the load and spans common experimental timescales. As a result, soft matter exhibits a rich structural (phase) behavior, with the ability to arrange, disarrange, and re-arrange in multiple ways in a rich free-energy landscape, thereby exhibiting a variety of mechanics, from elastic snap to viscous creep, as well as a variety of further properties, like optical or dielectric features. In addition, unlike atoms and molecules in hard solids, soft matter is often characterized by a distribution of sizes known as polydispersity.⁶⁰ Polymers, colloids, and amphiphiles are the prime examples of soft-matter building blocks,⁶¹ forming assembled structures such as (nano)composites, micelles, liquid-crystalline mesophases, and complex aggregates. Also, hybrids of these classical examples, such as microgels, block-copolymers, Janus particles, and also DNA, fd viruses, and proteins are examples of soft-matter building blocks, as all shown in Fig. 2. These materials have applications in a wide range of products that are important in diverse areas of human life, such as packaging, foams, adhesives, detergents, cosmetics, paints, rubbers, electronic boards and devices, foods, drugs, vascular prostheses, or implants. Therefore, understanding and controlling their properties is a key area in materials science. A question that now arises in this context is whether structural defects such as those in classical hard solids also exist in soft matter, and if their impact on the material properties, such as their viscoelasticity or phase behavior etc., is as severe.

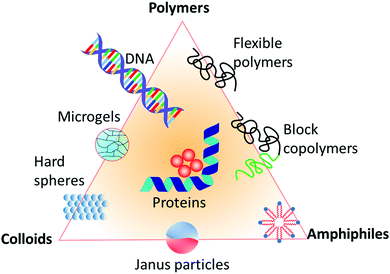Fig. 2 Different types of building blocks for soft matter systems, represented in a triangle diagram.

Different types of defects on the molecular-scale, such as branching, irregularities, loops, crosslinking, dimerization, or missing arms, have at least been studied to some extent for polymers, which are one representative of soft matter.^62–64 However, no systematic use for rational materials engineering has been made from that, and so it can be stated that “while the study of defect physics in crystalline inorganic solids is well-developed, a similar sophistication is currently lacking for ordered polymers”.⁶⁵ Today, even 25 years after this notion, this question is still not well-answered to scientists, as stated by Müllen,⁶⁶ who believes that one reason for this shortcoming is the goal of organic chemists to target discrete molecules and their aiming to precisely correlate their structures and properties. Müllen also mentioned that this correlation is weaker for macromolecules because of their unknown deviation from the perfect structure.⁶⁶ Regards to this shortcoming, the main question is what roles molecular defects play in soft matter, and how the achievement of so-far inaccessible properties could be possible by defect engineering.^66,67 The situation is different for structural defects in ordered materials such as liquid crystals or block copolymer mesostructures, which have been studied quite intensely both by theory and experiments.⁶⁸ However, the relation between the molecular structure (possibly including molecular defects) and structural defects is not yet fully understood.

The target of this review is to highlight these questions by giving an overview over numerous papers in which defects in soft matter and/or the (intentional) change of soft matter's properties by defect engineering have been discussed. We discuss defects in nine classes of materials based on liquid crystals, colloids, linear polymers with moderate degree of branching, hyperbranched polymers and dendrimers, conjugated polymers, polymeric networks, self-assembled amphiphiles and proteins, block copolymers and supramolecular polymers. The review is organized as follows: we start in Section 2 with liquid crystals, a state of matter that actually pioneered the perception of soft matter.⁶⁹ Many liquid-crystalline materials of practical use and relevance are actually still small-molecule based, and therewith still closely related to classical molecular matter, but their main distinction is the existence of anisotropic fluid phases with at least long-range orientational order of the building blocks. Section 3 describes defects in colloids with a focus on 2D colloidal crystals. Colloids are a further step away from classical matter, which shows both liquid and solid states. The latter has crystalline or glassy morphologies, but the main difference to classical hard matter is the larger size of their building blocks.⁷⁰ This large size causes the dynamics of these building blocks to be slow. As a result of both, they are good to observe (e.g., by microscopy), and therefore, colloidal systems are excellent models for atomic/molecular matter. Section 4 is about defects in polymers. The original notion of polymers was actually that of colloids; in fact, the word “colloid” derives from the Greek word for glue (κóλλα, colla), inspired by the sticky appearance of many natural polymers. In 1920, exactly 100 years ago, however, Staudinger reported about the macromolecular nature and chain structure of polymers;^71,72 in the following, polymer science separated itself as an own new field from colloid science. Section 5 describes defects in amphiphiles, which is the third prime class of soft matter shown in the triangle in Fig. 2. The word “amphiphile” derives from two Greek words that mean “both sides” (α′μφí, amphi) and “love, friend” (φíλoς, phylos), and refers to materials with two parts, a polar head, which likes water (hydrophile), and a non-polar tail, which likes oil (lipophile). These materials can self-assemble into a wide variety of structures such as biological membranes. With that, the focus has arced from physics (the home field of colloids) over chemistry (the home field of polymers) to biology (the home field of amphiphilic assemblies such as membranes), and therewith, from matter to life. As a further sub-section, defects in the self-assembly of block copolymers, which is a hybrid class of soft matter possessing both properties of polymers and amphiphiles, are discussed in this section. Finally, Section 6 presents our conclusion.

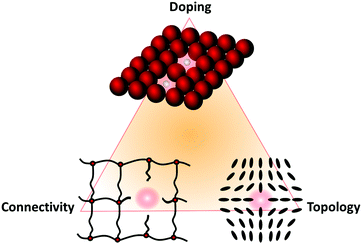
From what will be discussed in these diverse sections, we can condense the following general definition and classification scheme of defects in soft matter. Very generally, based on the three criteria to delimit soft matter (large building blocks, weak interaction energies, and long relaxation times), it is no surprise that soft matter has a rich variety of structures, each corresponding to a (local) minimum in the free-energy landscape. These structures, which are characterized by a suitable set of representative collective variables, are usually not regular but amorphous, but yet they can be assessed quantitatively by tools like correlation functions. Let one of these structures (and therewith one of the minima in the free-energy landscape) be a given reference state. A defect is now either a local structural perturbation that corresponds to a metastable minimum in the same free-energy landscape (which is reversible), or a local chemical modification that leads to a new free-energy landscape (which is irreversible). Both entails new properties. The three main types of defects in soft matter are

1. Doping defects: local replacement of an atomic, molecular, or colloidal building block.

2. Connectivity defects: a system with connectivity can be conceived as a set of vertices and connecting bonds. (Mathematically, this is a graph.) A reference state is built up by design principles that determine its structure, e.g., the degree of connectivity and the functionality of each connecting point. A defect in such a system is a local deviation from these principles.

3. Topological defects: Localized perturbation of the building blocks’ arrangement that cannot be transformed into a homogeneous structure by simple continuous rearrangement without creating a new discontinuity (somewhere else) in the system. In contrast to doping and connectivity defects, topological defects do not involve chemical modifications of the material at the molecular level.

Again, mixed forms of these three basic types of defects are also possible, so that a triangular scheme can be constructed again, as shown in Fig. 3.

Fig. 3 Classification of different types of defects in soft matter.

For some scientists, depending on their field and community, at a first glance, a connectivity defect might appear synonym to a topological defect. Note, however, that topological defects are a consequence of breaking symmetry in ordered systems, which does actually not require any chemical modification at the molecular level. By contrast, the formation of connectivity defects requires such kind of molecular modification. In polymeric networks, for example, a connectivity defect forms when a network junction misses at least one of its chemical bonds with other junctions.

The following sections will show how these types of defects decisively influence the properties of soft matter in its diverse variants, and how intentioned engineering of these defects has promising prospects.

2. Liquid crystals

Liquid crystals, LCs, are mesophases: they possess some typical properties of liquids, such as fluidity, and some typical properties of solid crystals, such as optical birefringence.^69,73 The liquid-crystalline state of matter can be small-molecule, particulate, or polymer-based, displaying orientational or even positional long-range order of the building blocks in one or more spatial directions.⁷⁴

LCs are commonly classified as thermotropic and lyotropic. Thermotropic LCs are made of pure organic crystalline molecules that form stable liquid crystals in a certain temperature interval; these molecules are either elongated linear (such as 4-n-octyl-4′-cyanobiphenyl) or plate-like flat (such as hexapentoxytriphenylene). One character common to all these thermotropic LC molecules is the coexistence of a rigid central part (usually benzene) and flexible exterior parts.⁷⁴ This is also valid for liquid-crystalline polymers, LCPs. In a main-chain structure, rigid liquid-crystalline units are separated by flexible hydrocarbon chains, and in a certain temperature range, these rigid units develop the orientational and sometimes positional order. In side-chain LCPs, by contrast, the rigid liquid-crystalline units are attached to a flexible polymer backbone by short flexible hydrocarbon linkers.^75,76

Lyotropic LCs are made of anisometric nanoscale building blocks in a fluid medium. Most typically, micelles formed from amphiphilic molecules with one polar head and one non-polar tail in water and/or oil (such as lecithin, sodium laurate, and sodium decylsulphate) can form lyotropic LCs.⁷⁴ For this class of LCs, the most important control parameter is the concentration rather than temperature or pressure.⁷³ In addition to these molecular-based LCs, rigid nanometer-sized rods in solution (like tobacco mosaic virus, TMV) or semi-rigid polymers in solution (like xanthan or DNA) show LC phases, too.

2.1 Liquid crystalline mesophases

The main characteristics of liquid crystals is their capacity to form mesophases that are intermediate between fully disordered fluids and crystals. Depending on the arrangement of the building blocks in a mesophase and its symmetry, LC structures are mainly divided into nematic, smectic, and columnar mesophases.^69,77 In a nematic mesophase, the building blocks possess a long-range orientational order with their long axes aligned along a preferred direction, but there is no long-range order in the positions of their centers of mass. The preferred direction, which is called director, may vary throughout the medium.^73,78,79 The director and the building-block arrangement in a nematic mesophase are illustrated in Fig. 4A. The name nematic derives from the Greek word for thread (ν[small eta, Greek, circumflex]μα, nema), since in a polarizing microscope, there are often many dark lines visible in thick film sample.⁷⁶ A sub-type of the nematic phase is the cholesteric mesophase,⁷³ in which the director varies throughout the medium in a regular fashion (Fig. 4F). Its distribution is precisely equivalent if the director rotates in a helical fashion around an axis perpendicular to it.⁷⁹ The distance along the helix over which the director rotates by 360° is called pitch. When this characteristic length is equal to the wavelength of light, the material shows interesting optical properties such as polarization of incident light and selective light reflection.⁸⁰

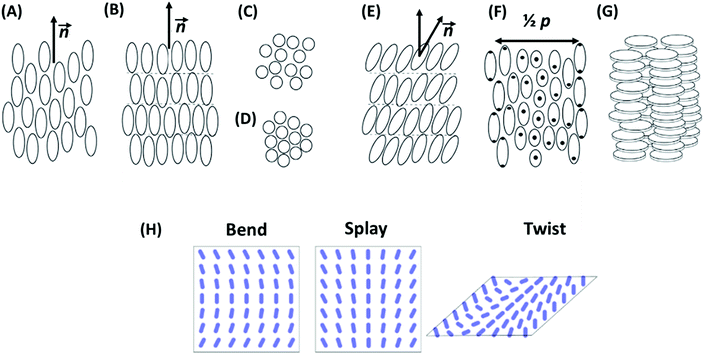Fig. 4 Building-block arrangement in liquid crystal mesophases. (A) Nematic LC: building blocks possess a long-range orientational order of their long axes without long-range positional order of their centers of mass. The average direction of the long axis is called director, n. (B) Smectic mesophases: building blocks are arranged in layers and exhibit 1D long-range translational orders in their positions in addition to the orientational ordering. (C) Smectic A: building blocks are aligned perpendicular to the layers, with 2D fluid-like intralayer short-range order. (D) Smectic B: hexatic order within the layers. (E) Smectic C: the preferred building-block axis is not perpendicular to the layers. (F) Cholesteric mesophase: the distribution of the director is precisely equivalent if the director rotates in helical fashion around an axis perpendicular to the director. p denotes the pitch of the cholesteric. (G) Columnar mesophase: building blocks assemble into cylindrical structures. The schemes are reprinted from ref. 73; copyright 2018 Elsevier. (H) Elastic modes in nematic LCs, showing long-wavelength perturbations of the director orientation. They differ in the relative orientations of director, n, wave vector, k, and director rotation axis, I. In the bend mode, n and k are parallel, in the twist mode, k and I are parallel, and in the splay mode, all three are perpendicular to each other.

In smectic mesophases, building blocks are arranged in layers and exhibit some correlations in their positions in addition to that layered ordering.⁸¹ The layers can slide freely over one another (Fig. 4B). Depending on the building-block order in the layers, different types of smectics exist. In smectic A, building blocks are aligned perpendicular to the layers, without long-range crystalline ordering (Fig. 4C). In smectic B, there is a hexagonal crystalline order within the layers (Fig. 4D). In smectic C, the preferred building-block axis is not perpendicular to the layers; therefore, this phase has biaxial symmetry (Fig. 4E). The name smectic derives from the Greek word for cleansing (σμηκτικóς, smēktikós), since the mechanical properties of these phases reminded early researches of soap systems.⁷⁶

Another type of liquid crystals is the class of columnar mesophases.^82,83 As obvious by its name, in this phase, the building blocks assemble into cylindrical structures (Fig. 4G). LCs in this phase are sometimes also called discotic liquid crystals, since columnar structures are often composed of stacked flat-shape discotic molecules, such as triphenylene.^84,85

2.2 Elasticity and surface anchoring

One striking property of liquid crystal mesophases is the existence of elastic deformations and long-range elastic interactions. From the point of view of statistical mechanics, such interactions are bound to emerge in systems with a long-range order characterized by a continuous symmetry.^86,87 For example, in liquid crystals, one can globally rotate the mesostructures without changing the free energy. As a result, long wavelength orientational perturbations become possible which have low free energy cost and dominate the interactions between defects at large distances. The three basic elastic modes in nematic liquid crystals (bend, splay, and twist) are illustrated in Fig. 4H. Such a mode with wave vector k and deformation amplitude u_k is associated with a free energy penalty per volume (the elastic energy) Δf (u_k) = Kk² |u_k|², where K is the Frank elastic constant of the mode (unit N). This form is imposed by the requirements that the elastic energy must vanish for deformations with infinite wavelength (k ≈ 0) and that the free energy may not depend on the sign of the wave vector (k or (−k)) nor that of u_k. Higher order contributions that are proportional to k⁴ or |u_k|⁴ are also present, but can be neglected compared to the quadratic terms at small k and for weak deformations.

The elastic perturbation field created by defects can be described by a superposition of elementary perturbations u_k. The deformation fields of two defects also superimpose each other, they can screen of amplify each other. Since the total free energy depends on |u_k|², this induces long-range effective interactions, which are very similar to electrostatic interactions.⁶⁹ For example, point like defects at a distance r experience Coulomb-like forces that decay as 1/r², and two parallel line defects confined by a slab of thickness d repel or attract each other with a force proportional to d/r, corresponding to a Coulomb force in two dimensions.⁶⁹

One important consequence of this elastic behavior is that interactions of liquid crystals with surfaces can influence their structure deep in the bulk. Surfaces typically have an orienting effect on liquid crystals, usually referred to as surface anchoring. The two most prominent types of surface anchoring in nematic liquid crystals are homeotropic anchoring, where the surface interaction favors a director orientation perpendicular to the surface, and planar anchoring, where the preferred orientation is parallel. In the latter case, in technological applications such as LC displays, surfaces are often prepared such that they favor a certain in-plane direction. The anchoring strength is typically characterized by the so-called anchoring energy parameter, W (unit J m⁻²), which depends on the chemical composition of the surface and on the surface morphology. The ratio K/W (unit N/J m⁻² = m) is called extrapolation length, ξ_e, and is typically between 50 nm and 10 μm.⁸⁸

2.3 Defects in liquid crystals

In many liquid-crystalline phases, there are different types of common defects. As an example, in a nematic mesophase, the continuous orientational symmetry is often broken. As mentioned before, the word nematic originates from its pattern (visible dark line) under a microscope. These lines are defects in the orientational order.^89–91 The theory of defects is therefore widely discussed in liquid-crystalline matter,^{74,89,92–96} and defects in liquid crystals are considered extensively from both academic and practical points of view.^68,77 Defects in liquid crystals typically belong to the class of topological defects.⁹⁷ In fact, one of the most precise existing and established formal definitions for defects in soft matter is the one for a liquid-crystalline “non-uniform molecular alignment that cannot be transformed into a uniform alignment without creating other defects”, laid down in IUPACS purple book.⁹⁸ LC-related defects are also relevant in technology. In optics, for example, defects usually play a detrimental role, such that defect walls in twist nematic cells or disclination in cholesteric cells are used in dye microlasers. More recently, defect structures have also found applications in three-dimensional photonic liquid crystals, bistable displays, and smart memory cards.⁸⁹

As mentioned before, defects are important features in liquid crystals, and have therefore been widely discussed in many liquid crystal papers and textbooks. What is presented in this subsection is just a short summary mostly from papers of Kleman on defects in liquid crystals,^74,92,93,99 and textbooks edited by Blinov⁸⁹ as well as Collings and Hird.⁷⁶

2.3.1 Nematic phases. The most prominent defects in nematic liquid crystals are the disclinations, which are topological line defects. Examples are shown in Fig. 5A, in which disclination lines are shown by red lines (bottom) or red circles (top: the line is perpendicular to the plane of the figure). Disclinations are characterized by their disclination strength of winding number m. A vector which traverses a full counter-clockwise loop around the disclination and changes its direction according to the director field, would rotate by an angle Δφ = m × 2π after finishing the loop. If m = ±1/2, then the director rotates by π for one full loop around the disclination. If the rotation axis is parallel to the disclination line, the defect is called wedge defect. If it is perpendicular, it is called twist defect. Most defects in liquid crystals are wedge defects with winding number m = ±1/2 or m = ±1.

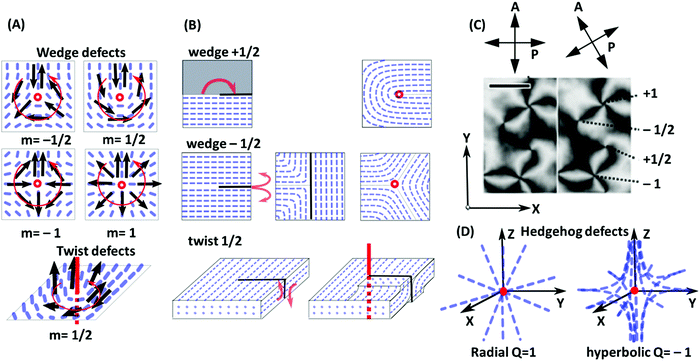Fig. 5 (A) Examples of line defects (disclinations) in nematic liquid crystals. In the wedge defect case, the disclination line is perpendicular to the plane of the figure (red circle). In the twist defect case, it is shown as thick red line. To determine the winding number or defect strength m, one considers a virtual vector (black arrows) which surrounds the disclination in counter-clockwise direction along a closed loop (thin red line), while always aligning with the local director field. In total, the vector then rotates by the angle m = 2π. (B) Corresponding Volterra processes; see the main text for explanation. (C) Nematic texture under a polarized-light microscope with crossed polarizers showing four types of wedge defects with defect strengths m = ±1/2 and m = ±1. The director is always in the plane of the figure and is oriented in the P or A direction in the dark regions. Since it rotates by m = 2π on a loop surrounding the defect (see A), 4m dark bands emerge from defects with strength m. (D) Illustration of hedgehog defects. Here the defect core is a point. For radial defects, the director points towards the core. For hyperbolic defects, the director field has a hyperbole shape and uniaxial symmetry in one direction (here: z direction). Panel C is adapted from ref. 100; copyright 2017 Nature Research.

A popular way to characterize line defects is the Volterra process (Fig. 5B). First, the Volterra knife is applied, i.e., a cut is made along a half-plane starting at the dislocation line. In wedge defects with m > 0, a wedge of angle m × 2π is then removed and the material is contracted to fill the void. In wedge defects with m < 0, a corresponding wedge of material is inserted. To this end, the Volterra cut is separated into two lips with the opening angle m × 2π, the new wedge of material is inserted between the lips, and the structure is relaxed. The procedure to create twist defects is similar. After applying the Volterra knife, the two lips are twisted by the angle m × 2π, and finally relaxed. Nematic defects can be visualized in a polarized light microscope using crossed polarizers. A wedge defect with strength ±1/2 is identified by the appearance of two dark bands under a microscope. A wedge defect with strength ±1 leads to the formation of a four-bands pattern (Fig. 5C).¹⁰⁰

In addition to the linear defects, nematic phases may contain point defects that are called hedgehogs (Fig. 5D). They can be constructed as rings of wedge disclination lines with strength m = ±1/2 and radius zero and carry a topological charge Q = 2m = ±1.¹⁰¹ At a certain temperature, hedgehogs are observed in spherical drops of nematics floating in an isotropic liquid, induced by competing surface anchoring conditions at the isotropic-nematic interface.

Defects induce a considerable amount of distortion (splay or twist and bend) in the surrounding director field (see Fig. 5A and D). The free energy penalty for defect formation has two contributions, the core energy and the elastic energy of director deformations. Note that the distortion fields of defects with opposite winding number or charge tend to compensate each other. This induces long-range attractive interactions between them. The attractive interaction between defects with opposite signs may lead to annihilation, which can be detected by tracking the distance between defect pairs over time.¹⁰²

2.3.2 Cholesteric phases. In the planar cholesteric texture observed along the helical z-axis, line defects are more complex than corresponding disclinations in the nematic phase. Understanding the appearance of these defects is possible by considering again the Volterra process. The same Volterra transformations illustrated in Fig. 5B are also possible for cholesteric phases.

2.3.3 Smectic A phases. Different types of defects are formed in a Smectic A phase due to the layered structure. Steps containing π-disclinations are formed during the preparation of a smectic at the edge of a drop on a surfactant-covered glass (Fig. 6A). In the smectic A, an additional smectic layer is incorporated between two other layers, and a dislocation is formed (Fig. 6B). Dislocation defects can also be described by a Volterra process similar to that used to create wedge disclinations. Instead of removing or adding a wedge, one removes a slab of fixed thickness. The most striking features of smectic textures are focal-conics, which are domains related to pairs of conjugate conics.^89,103 In a focal-conic pair, as shown in Fig. 6C, the structure is formed by two cones with a common ellipse base having apices at A and C and foci at O and O′. The hyperbola B–B′ passes through focus O. The focus of the hyperbola C coincides with the apex of the ellipse.^89,103,104 In such a domain, smectic layers with constant thickness form surfaces called Dupin cyclides. These are parallel tori. A complete torus divides into two regions with a disclination in between, one of negative Gaussian curvature and one of positive curvature.¹⁰³ Focal conic domains commonly assemble in large-scale clusters. These clusters form different textures such as flower texture or quasi-hexagonal tiling, observable under a polarized optical microscope (Fig. 6D).¹⁰⁵

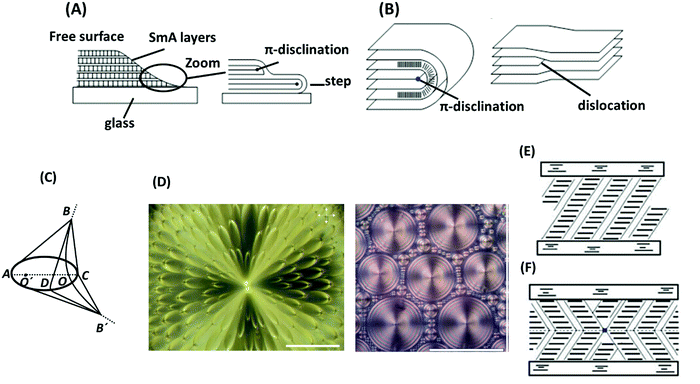Fig. 6 (A) Steps at the edge of a drop of a smectic A phase containing a π-disclination line. (B) Comparison of π-disclination and edge dislocation in a smectic A phase. (C) Focal-conic defect structure in a smectic A phase. (D) Examples of focal-conic textures under a polarized-light microscope: flower texture (left) and hexagonal texture (right). The scale bars represent 100 μm. (E) Uniform structure of a smectic C phase. (F) Structure with chevrons and a disclination between them. The schemes are adapted from ref. 89; copyright 2010, Springer. Panel D is adopted from ref. 105; copyright 2009 Multidisciplinary Digital Publishing Institute.

2.3.4 Smectic C phases. In a smectic C phase, different types of defects such as disclinations with strength of ±1, π-disclination, and focal conics domains including polygonal and fan-shaped textures are observed. In addition, instead of regular structures (Fig. 6E), so-called chevron patterns form upon cooling from the smectic A phase. When a smectic A to smectic C phase transition occurs, an increasing molecular tilt angle results in a corresponding decrease of the smectic layer thickness. The mismatch between the layer thickness values at the surfaces and within the bulk leads to formation of chevron structures, in which a layer kink or localized bend must form.^106–109 In such a pattern, the left and right chevrons are separated by a zigzag form disclination line (Fig. 6F).⁸⁹

2.4 Defect engineering in liquid crystals

Generally, defects in LCs have high elastic cost and appear as an uncontrollable and unstable feature in the bulk. One aspect of defect engineering in LCs is their stabilization, which is possible by geometrical frustration, e.g., if LCs are confined in geometries that are incompatible with the orientational symmetry.⁹⁰ The stabilization of defects by geometrical frustration can be achieved, among other, by incorporating LCs into cavities, porous materials, and microfluidic devices with strongly anchoring surfaces. As an example, in a spherical cavity with strong homeotropic anchoring, a point defect with m = +1 (Fig. 7A) or a loop of disclination line with m = +1/2 (Fig. 7B) are formed depending on the size of the cavity and the strength of elastic interactions.⁹⁰ In addition, confinement of LCs in specific geometries may induce new properties. As an example, it has been shown that confinement of achiral LCs can lead to reflection-symmetry breaking, and with that formation of chiral configurations.¹¹⁰ As an example, if a nematic liquid crystal is placed in a cylindrical capillary, a frustration is imposed between the uniform director field of an undeformed nematic liquid crystal and the radial director field by the boundary conditions. This frustration induces different types of configuration, exhibiting mirror planes and thus being achiral. This mirror symmetry can be broken to minimize the elastic energy induced by frustration, which leads to the formation of chiral configurations such as twisted escaped radial (TER) and twisted planar polar (TPP) ones. Giesselmann and coworkers investigated this idea experimentally by using dislike micelles as achiral lytropic nematic liquid crystal, confined in a glass capillary.¹¹¹ The liquid crystal orients normal to the capillary walls (homeotropically alignment). After cooling from the isotropic phase, the authors observed a TER configuration. This configuration further slowly relaxes over several weeks into the corresponding nonchiral configuration. Moreover, cooling from the isotropic phase under application of a magnetic field along the capillary axis induces another type of chiral configuration, which in the absence of a magnetic field transforms into a chiral configuration. The results show that inducing chirality on achiral liquid crystals using geometrical frustration is a general phenomenon in nematic liquid crystals.¹¹¹ Nikoubashman, Milchev, and coworkers observed novel nematic defect patterns when confining densely packed stiff polymers to spherical cavities of comparable size.¹¹² The authors demonstrated that at intermediate polymer densities, the ordering of polymer chains is the nematic type with bipolar defects. At the largest density in this work (0.7), however, the surface layer develops tennis ball-like textures. The authors point out that such patchiness provided by the topological defects on the sphere surface can find important applications for nanoparticles as building blocks for colloidal self-assembly.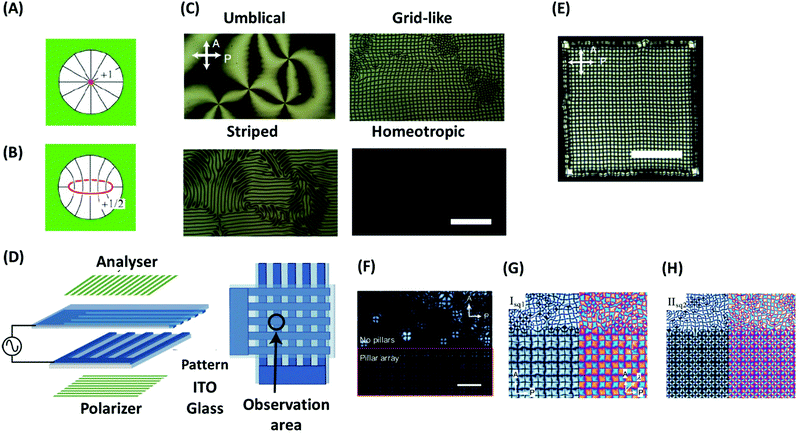

Fig. 7 (A and B) Defect structures of a nematic LC in a spherical cavity: (A) radial hedgehog and (B) disclination ring. (C) Four types of textures of defects of a nematic LC under an electrical field (scale bar, 100 μm). (D) Schematic illustration of a sample cell with patterned ITO electrodes for inducing a single domain of the grid-like texture. (E) Spreading of the grid-like texture over the whole square region of the overlapped electrodes and formation of about 1000 packed defects with a regular spacing (scale bar, 200 μm). (F–H) Pattern formation of a nematic LC under an electric field in the presence and without micropillars: (F) 220 Hz (14.4 V), (G) 350 Hz (15 V), (H) 190 Hz (25 V). The scale bar represent 100 μm. Panels A and B are reprinted from ref. 90; copyright 2018 Royal Society of Chemistry. Panels (C–E), and (F–H) are adopted from ref. 121 and 122, respectively. Copyright 2016 and 2019, Nature Research and Wiley-VCH, respectively.

2.4.1 Defect engineering in LCs with AC fields. Another aspect of defect engineering in LCs is controlling their pattern to form regular arrays. Such controlled patterns have a high potential in polymer templating,¹¹³ colloidal self-assembly,¹¹⁴ and designing innovative applications such as optical vortex generation,¹¹⁵ metasurfaces,¹¹⁶ bistable devices,¹¹⁷ and optical diffraction gradients.^118–120 In a seminal work, Orihara and coworkers introduced a method to control the director field of defects in nematic LCs without preparing a pre-patterned mask through the standard reorientation of the director supported by an AC voltage, V.¹²¹ They showed that doping with a small amount of an ionic compound promotes formation and stabilization of a large number of defects in a square arrangement without annihilation as the applied voltage can be greatly affected by the ionic groups. They utilized sandwich cells, consisting of two parallel glass plates coated with indium-tin-oxide (ITO), filled with a nematic LC and doped with an ionic compound. The ITO glasses were spin coated with a high-resistive, amorphous-fluorinated polymer dissolved in a fluorinated solvent to induce the homeotropic anchoring. For an AC voltage of V = V₀ × cos(2πft), the results showed that at least four typical textures of nematic LC can be formed by variation of frequency f and amplitude V₀ (Fig. 7C). The applied voltage increases upon increase of the frequency of the electric field. In addition, this parameter influences the minimum voltage required to observe a change of nematic textures under a polarized microscope. At high frequency, a texture well-known as umbilical is formed, consisting of randomly located defects with topological charges (defect strength) of ±1. By decreasing the frequency, a striped pattern forms. Additional decrease of the frequency induces orthogonal stripes that form a grid texture. At very low frequency, a texture of homeotropic alignment is created, which is not optically anisotropic and therefore observed as a dark field under a polarized microscope. At that low-frequency region, the applied voltage is approximated by V ∼ [2(σ_LC/σ_s)(l_s/d) + 1]V_LC, where V is the voltage, σ_LC the electrical conductivity, d the thickness of the nematic liquid crystals, and σ_s and l_s the corresponding terms for the alignment layer. Therefore, in this region, doping of the mesophase with an ionic compound, which affects the electrical conductivity, can have significant influence on the nematic textures. To create self-organized single domains in the grid texture, Orihara and coworkers utilized a top-down approach. In this method, two glass substrates with stripe-patterned ITO electrodes (with typically several hundreds of microns) were placed such that the ITO stripes cross (Fig. 7D), and then an AC voltage was applied to the square regions of the overlap of the ITO stripes. With that, uniform arrangements of defects are formed along the edges of the square region. By growing these defects, the grid texture spreads over the whole square region of the overlapped electrodes and finally about 1000 defects are packed with a regular spacing (Fig. 7E).

The arrays formed by this approach are sufficiently regular to make a well-defined 2D diffraction pattern. However, there are some shortcomings to use this system as a diffraction grating such as stability of the pattern regularity upon on-and-off of the field or change of the frequency and voltage. To overcome some of these shortcomings, Serra and coworkers have recently introduced a method for dynamic control of the defect periodicity by micropillars.¹²² The micropillars are strong attractors for defects that having radial alignment (topological charge of +1) due to the perpendicular anchoring of the nematic director. The concept of using micropillars to control the location of LC defects has already been confirmed for Saturn ring¹²³ or smectic focal conics defects.¹²⁴ Kim and Serra showed that by using micropillars, the radial defects form an ordered pattern everywhere, which is controlled by the position of the micropillar (Fig. 7F). By increasing the voltage above a threshold, the LC orientation arises randomly in the area outside the pillar array. By changing f and V₀ from 370 Hz (15 V) to 190 Hz (25 V), defect spacing reduces, but the ordering remains short range if the electrode surfaces have no pillars (Fig. 7G and H). Kim and Serra also illustrated that by use of a mixture of nematic LCs to adjust the refractive index, the electro-optic performance of the grating system can be further improved.

2.4.2 Defect engineering in curved LC films. Another level of defect engineering in LCs is possible in thin LC layers if the mesophases are frustrated due to curvature.¹²⁵ This is the case, e.g., when spherical colloid particles are coated with a thin layer of a nematic LC with planar anchoring.¹²⁶ According to the hairy ball theorem, a tangential director field in a closed spherical shell must contain at least one defect. In practice, one usually observes several defects, which form in order to relieve the elastic stress induced by the curvature.¹²⁷ Lopez-Leon, Fernandez-Nieves and coworkers illustrated that defects in such a shell have three different configurations: linear, trigonal, and tetrahedral. The linear configuration consists of two defects with m = 1 (Fig. 8A). The trigonal configuration consists of two defects with m = 1/2 and one defect with m = 1 (Fig. 8B). The tetrahedral configuration consists of four defects with m = 1/2 (Fig. 8C). Each configuration has specific number and orientation of defects, which can be engineered by variation of the shell thickness.¹²⁶ Lopez-Leon and coworkers also showed that the tetrahedral defect geometry can be changed to a great circle of the sphere by closing the temperature to the nematic–smectic phase transition temperature.¹²⁸ In another work, Lopez-Leon and coworkers investigated the potential of such defect engineering in cholesteric LCs.¹²⁹ They showed that the LC shells have two different defect configurations: bivalent and monovalent. The bivalent configuration possesses two highly structured defects, which are composed of smaller disclination rings that pile up through the shell (Fig. 8D). The monovalent configuration consists of a radial defect, which is composed of two distinct disclinations, winding around each other in a double-helix fashion (Fig. 8E). The number and position of defects can be controlled by the ratio of the shell thickness to the particle diameter as well as by the ratio of the pitch to the particle diameter. The angular distance between two defects at the outermost surface of the shell can be tuned by variation of the ratio of the shell thickness to the particle diameter. Above a critical value, the bivalent configuration cannot be formed anymore. This value is controlled by the ratio of the pitch to the particle diameter. In addition, the transition between two configurations is possible and can be controlled by the shell thickness. Similar to their previous works, Lopez-Leon and coworkers prepared core–shell particles by a glass capillary microfluidic device and varied the shell thickness systematically by change of the difference of the osmotic pressure between the core and the continuous phase. The authors showed that by increasing the ratio of the shell thickness to the particle diameter, the two defects (of bivalent configuration) get progressively closer. At a certain critical angular distance, which depends itself on the shell thickness, the two defects jump together toward the center of the shell and assemble to form a single defect. As another example, Lagerwall and coworkers studied defects and their alignment in a series of LC shells that surrounded spherical droplets. The droplets were dispersed in an incompatible liquid as a continuous phase.¹³⁰ The authors demonstrated that by variation of the surfactant in both the inner droplets and the continuous phase, the kind of alignment of the liquid crystal shells at the inner and outer interface (planar or homotropic) can be controlled. In this system, a nematic-smectic A transition makes a series of compelling textural developments with a regular array of focal conic defects. In addition, by variation of the shell thickness, the number of defects and periodicity of the generated pattern can be controlled.¹³⁰

Fig. 8 (A–C) Configuration of defects in a thin layer of a nematic LC coated on spherical colloidal particles: (A) linear, (B) trigonal, (C) tetrahedral. (D and E) Configuration of defects in a thin layer of cholesteric LC coated on spherical particles: (D) Bivalent, and (E) monovalent. The scale bars represent 20 μm. Panels (A–C) and (G and H) are reprinted from ref. 126 and 129, respectively. Copyright 2011 and 2016, Nature Research and National of Academy of Sciences of the United States of America, respectively.

2.4.3 Defect engineering in systems of colloids and liquid crystals. If a molecular nematic liquid crystal serves as a host medium in a colloidal suspension, the interaction between the colloids and the nematic fluid gives rise to a series of unusual phenomena. The effect of the colloids on the surrounding LC fluid depends on the extrapolation length, ξ_e, which is the ratio of the dominant Frank elastic constant K and the anchoring energy W as explained above. If the diameter of the colloidal particles is much smaller than this ratio, the effect of the boundary conditions is negligible, and particles induce no defects into the system. At that condition, the director alignment in the vicinity of the particles is similar to the far-field uniform alignment of the LC director. In contrast, when the diameter of the particles is much larger than ξ_e, the director around the particles is distorted. Colloids with strong homeotropic surface anchoring act as radial point defects (radial hedgehogs) with topological charge Q = 1. To compensate for the corresponding elastic deformation, one of two types of defects may form depending on the size of the particle:^88,131,132 A satellite point defect with topological charge Q = −1 (a hyperbolic hedgehog defect) (Fig. 9A) if the colloid is large, or a Saturn-ring defect, i.e., a wedge disclination ring with a strength of −1/2 (Fig. 9B) if the colloid is smaller.^73,133,134 The interaction of defects with opposite sign leads to defect-particle pairs with dipolar or quadrupolar symmetry, respectively. Such stable defects significantly influence the flow properties due to their elastic interaction with solid surfaces.

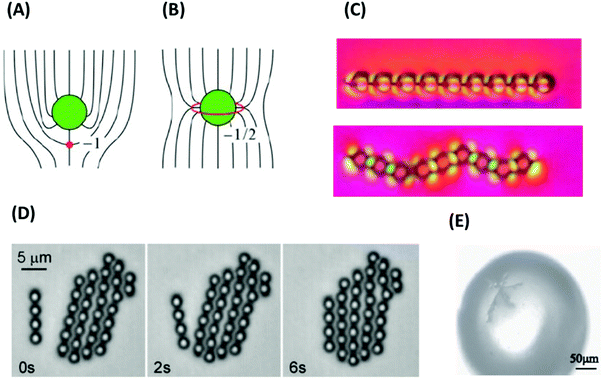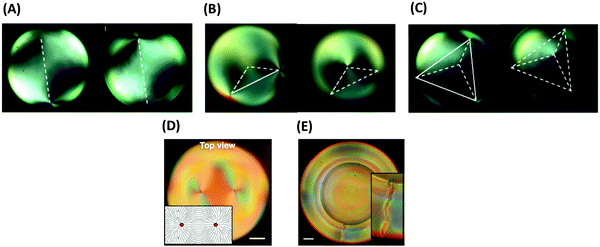
Fig. 9 (A and B) Defect structures of a nematic LC around a spherical particles: (A) hyperbolic hedgehogs and (B) Saturn rings (disclination lines). (C) Self-assembly of colloidal particles in LCs. A straight chain forms when point defects (boojums) exist at the surface of the LC. A zigzag chain forms when defects are of Saturn-ring type. The scale bar represents 50 μm. (D) Attraction of assembled colloidal chains forms 2D structures. (E) Star-like pattern of colloidal chains around a boojums defect in a nematic LC. Panels (A and B), and (C and D) are reprinted from ref. 90 and 139, respectively. Copyright 2018 and 2008 Royal Society of Chemistry. Panel E is adopted from ref. 141; copyright 2014, Elsevier.

The shape of colloidal particles has a significant influence on defect formation as well. Colloidal particles in the form of thin foils, with two lateral dimensions larger than ξ_e and one dimension smaller than ξ_e, generally induce no additional defect in LC continuous phases. By changing the shape of such particles, patterning of defects (like colloidal particles in nematic LC) is possible, but their properties are different from both microparticles larger than ξ_e with strong boundary conditions or nanoparticles smaller than ξ_e with effectively weak surface anchoring.^88,135 As an example, platelet colloids with odd and even numbers of edge faces exhibit well-defined alignment and elastic deformations of the LC vector with dipolar or quadrupolar symmetry, respectively. The dipolar structure of platelets with odd numbers of edge faces does not give rise to point or line defects in the bulk of a LC continuous phase, but only causes defects at the interface of the particles and the LC continuous phase.¹³⁶

The defects also influence the arrangements of colloids.^137,138 The elastic interaction between the particle-defect complexes stabilize chain-like aggregates. The shape of the assembly depends on the type of the defects, satellite point defect or Saturn-rings (see Fig. 9C).¹³⁹ When colloidal particles are confined into a homogenous layer of a nematic LC between two glass plates, self-assembled colloidal chains can attract each other to form 2D structures (Fig. 9D).^139,140 Gharbi and coworkers investigated the self-assembly of colloidal particles in two different systems. In one system, the colloids were placed at a flat air/nematic interface. In the second system, the colloids were confined at the surface of bipolar nematic droplets dispersed in a water phase.¹⁴¹ Using microscopy and optical tweezers, for the first system the authors suggested strong attachment of the colloidal particles into disclination defects at the bulk of the LC, which leads to self-assembly of the colloids and formation line-type structure. The authors also observed that the interaction between the particles and the nematic phase is stronger for a thinner layer of the LC. In the second system, the colloidal particles assemble into linear chains along longitude lines connecting the North and South poles of the nematic droplets, where surface-bound point defects (boojums defects) are located. By growing these chains over time, they form star patterns around the boojums (Fig. 9E). By heating the nematic phase to convert it to an isotropic liquid, the star patterns disappear as well.¹⁴¹ In addition to linear and 2D assembly, colloidal particles can be assembled in three dimensions using defects of LCs.^142,143 Musevic and coworkers studied and controlled colloidal particles in a nematic phase. They considered that each particle is accompanied by a topological point defect, which forms a topological dipole. They used laser tweezers to control the spatial and temporal positioning of these topological defects, and with that, the assembly of 3D nematic colloidal crystals.¹⁴²

We end this section by noting that LCs have many applications in industry, among them displays might be the best-known application. In addition, LCs have found different non-display applications such as light shutters, scanners for printers, temperature and electric field mapping, spatial light modulators, imaging systems, or optical signal processing applications. In addition, LCs have been considered in pharmacy and medicine. Examples are lipid lyotropic liquid crystalline mesophases as drug delivery materials, or cubic and inverse hexagonal phases as imaging agent in magnetic resonance imaging (MRI). Display and non-display applications of LCs have been extensively highlighted and reviewed.^144–149 One of the key points in developing current and potential applications of LCs is their topology including how their nanoscopic domains are organized.¹⁴⁵ In this sense, defects should be considered as a prime factor of influence. Generally, for display applications, defects should be removed; however, intrinsically deformed orientational order of defects can in fact create optoelectric and elastic effects, facilitating various applications such as templating for colloidal assembly,^88,150 or microlens arrays and photomasks.^151,152 Another example is the cholesteric blue phase, in which regularly aligned disclination lines with a cubic symmetry are utilized in displays because of a fast response.¹⁵³ Recently, Abbott and coworkers reviewed examples of specific advances in the intersection between LC science and other fields of soft matter involving surfactants, polymers, and colloids.¹⁵⁴ As shown in this perspective, in the intersection of LCs and surfactant science, topological defects in LCs are utilized to selectively trigger the self-assembly of amphiphiles under conditions where the amphiphiles are singly dispersed in the bulk of LCs. In the intersection of LC and polymer science, topological defects are used for the templating synthesis of polymeric micro and nano particles. The authors have mentioned areas of future research that have the potential to provide fundamental and practical advances in the design of LC-based soft matter systems. One of these areas is the selective assembly of amphiphiles within defects, in a sense of understanding the effect of defect strength or architectures of amphiphiles on the self-assembly in topological defects. The self-assembly of peptide amphiphiles, for example, has many applications ranging from controlled gene and drug release to 3D cell culture and tissue engineering.¹⁵⁵

3. Colloids

Colloids are a class of materials that have at least two components, one dispersed in a second. At least one component of the dispersed phase should have a size in the range of 1 nm–1 μm in at least one of its geometrical dimensions.¹⁵⁶ This very general definition covers a wide range of materials and applications, such as cosmetics, foams, adhesives, emulsions, inks, paints, or food stuff. The term colloid originates from the Greek word “κóλλα” (cola), which means glue. Colloids can be classified according to the state of the phases or according to their stability.^157,158 What is presented in this section is about a specific category of colloids with the definition of solid or liquids particles, each about a few tens or hundreds of nanometers in size, dispersed in a fluid and kept suspended by thermal fluctuations.

Colloid materials are of specific interest for fundamental reasons in the field of physical chemistry and also for practical reasons in many technical applications. Synthetic colloids that have dispersed phase with a well-defined size distribution are a model for understanding phase transitions.¹⁵⁹ These colloids can form crystals and other phases of matter seen also in atomic and molecular scales. The advantage of colloids, though, is the ability of direct observation of phase transitions under optical microscope, due to the comparably large size and slow motion of the particles. Even relatively small colloids with sizes below the optical resolution limit can be investigated by scanning electron microscopy or transmission electron microscopy.^160,161 In addition, the ability of colloids to form phases that are ordered on the scale of visible-light wavelengths entails optical properties, which renders these colloidal materials suitable for applications in photonics.¹⁵⁹

3.1 Defects in colloids

As mentioned above, colloidal particles dispersed in a solvent can self-assemble into ordered crystalline structures; as such, they may contain the various stereotype defects encountered in crystals. For example, two-dimensional colloidal crystals on a flat surface mostly arrange as a six-fold coordinated triangular lattice.¹⁶² Important point defects are the 5-fold or 7-fold coordinated disclinations, which are characterized by their topological or disclination charge, q, where q = 6 − c, and c is the coordination number (5 for a five-fold defect and 7 for a 7-fold defect), and the dislocations, which can be described as a pair of tightly bound disclinations with charges q = ±1 (Fig. 10A).¹⁶³ The disclination charge of such pairs is zero, and therefore they do not change the total disclination charge of a colloidal system. Such point defects can be created by manipulating individual particles with optical tweezers.^164–166 Removing one or two colloids from a perfect triangular lattice results in a mono or di-vacancy and to a topological arrangement of five-fold and seven-fold disclination defects around the cores of the mono and divacancies. Such defects have significant influence on the physical and mechanical properties of materials. One example is the mediation of stress relaxation in crystalline solids by formation and diffusion of topological defects. As revealed by experiment and simulation, when a single particle in a two-dimensional soft colloidal crystal is activated by optical tweezing, new five- or seven-fold defects form in the lattice, which creates additional relaxation mechanisms.¹⁶⁷ Structure, energetics, and dynamics of these defects have been studied by experiments and simulations.^168–170 Geometrical frustration is another driving force to induce defects in colloidal crystal structures.¹⁷¹ A flat triangular lattice cannot wrap on the curved surface of a sphere. Formation of such a wrapped lattice therefore requires topological defects.¹²⁷ According to the Euler theory, the total disclination charge of any triangulation of the sphere must be 12.¹⁷² Bausch and coworkers studied the structure of two-dimensional packing of colloidal particles on the surface of spherical water droplets.¹⁶² Their colloidal system consisted of self-assembled, 1 μm sized crosslinked polystyrene beads adsorbed on the surface of spherical water droplets, suspended in a toluene–chlorobenzene mixture. They found that while the total disclination charge is 12, the number of defects is more than 12. The excess defects consisted of pairs of five-fold and seven-fold disclination aligned in chains (Fig. 10B). To analyze this observation, Bausch and coworkers developed an elastic model showing that a single isolated five-fold disclination causes a large local elastic strain, resulting in a large elastic energy penalty. To avoid that, the crystal creates chains of defects, which gradually reduce the strain.¹⁶² Irvine and coworkers argued that for general curved surfaces, curvature stress in two dimensional colloidal surfaces can be relaxed by lines of dislocations (i.e., topologically uncharged disclination lines), so-called pleats.¹⁷³ Curvature is also expected to have a strong effect on defect formation and coarsening.¹⁷⁴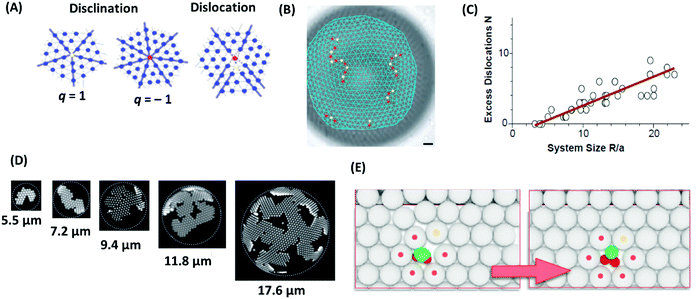

Fig. 10 (A) Schematic sketch of selected defects in 2D colloidal crystals: 5-fold and 7-fold disclination with charge −1 and +1, respectively, and dislocation. (B) Light microscope image of a water droplet coated with polystyrene particles and associated triangulation. The radius of the water droplet is 43.9 μm, and the mean particle spacing is 3.1 μm. Disclinations with charges of +1 and −1 are illustrated by red and yellow color, respectively. The scale bar represents 5 μm. (C) Number of excess dislocations in the colloidal system of panel (B) as a function of the system size, quantified as the ratio of the droplet radius to the mean particle spacing. (D) Confocal micrographs of crystals grown for a few hours on droplets with various curvatures. The radii of the curvature are presented below the micrographs. Dotted circles show the droplet surface. (E) Incorporation of shape-shifting building blocks into a self-assembled colloidal architecture in a two-dimensional hexagonal lattice (white spheres). The colloidal crystal is doped with a small amount of reconfigurable colloids, which act as substitutional impurities. At the center of the lattice, this substitutional impurity is shown. The green color shows oil, and the red color shows the colloidal substrate. This impurity creates strain in the lattice (left scheme). The strain disappears by time when the substitutional particle changes its morphology (right scheme). Panels (B, C) and D are adopted from ref. 162 and 175, respectively. Copyright 2003 and 2014, American Association for the Advancement of Science. Panel E are reprinted from ref. 180; copyright 2016 Nature Research.

In another work, Meng and coworkers studied the structure of rigid 2D colloidal crystals growing on the inside walls of highly curved spherical water droplets.¹⁷⁵ The colloidal system consisted of an aqueous dispersion of 1 μm sized polystyrene particles and 80 nm sized poly(N-isopropylacrylamide) hydrogel particles. This aqueous phase was emulsified in silicone oil. The presence of the poly(N-isopropylacrylamide) particles induces depletion attractions between the polystyrene spheres, which confine them to the droplet interface and force them to adopt the curvature of the droplet as they grow. Grown 2D crystals on flat surfaces (droplets with very large radius, larger than 2 mm in that work) are commonly compact. However, crystals that are grown on a spherical surface are composed of thin, single-crystal segments that wrap around the surface. These segments are called ribbons, and their widths are much smaller than their lengths (Fig. 10D). In droplets with higher surface coverage, the ribbons join together to form branched patterns with voids and gaps between them as defects. Beyond a critical crystal size, further growing of these ribbons is limited due to elastic instability. While this limitation can be tackled by incorporating topological defects, Manoharan and coworkers illustrated that in their system, due to the short-range attraction, formation of such defects costs energy and is therefore impossible.¹⁷⁵

3.2 Defect engineering in colloidal systems

For the self-assembly of colloidal particles into crystals, different ways of defect engineering are possible. As shown before in the discussion about the work of Bausch and coworkers, when colloids are frustrated on spherical surfaces, chain-aligned excess defects consisting of pairs of five-fold and seven-fold dislocations are formed.¹⁶² One possibility of engineering such defects is controlling their number. As illustrated in the work of Bausch and coworkers, the number of these excess defects can be controlled by the ratio of the droplet radius to the mean particle spacing (Fig. 10C). When this ratio is smaller than ∼4, the number of defects is fix (= 12). Above this critical value, excess defects are formed, and in a good approximation, their number has a linear relationship with the mentioned ratio. Another area of defect engineering can be considered for the branched patterns of joined ribbons in the self-assembly of colloidal particles on a curved surface via depletion attraction. These patterns can be changed by variation of the radius of the sphere surfaces, e.g. by the radius of water droplets as in the systems described by Manoharan and coworkers (see Fig. 10D).¹⁷⁵

The self-assembly of colloidal particles can also be controlled through the use of patchy particles.¹⁷⁶ Patchy particles are surface-patterned particles with a controlled number of favored interaction areas, which are symmetry-breaking zones with chemical (sticky patches) or topographic (such as dimples) discontinuities.^177,178 Due to the specific shape of these particles and due to the asymmetric interactions patterned on them, the interactions between these particles are selective and directional, resulting in assembled structures with substantially fewer defects than in those formed from conventional particles.¹⁷⁹ The self-assembly of patchy particles may lead to the formation of reconfigurable materials, which are able to erasing the inherent defect occurrence during the colloidal assembly process. As an example, Sacanna and coworkers described a new approach based on dewetting forces.¹⁸⁰ They showed that solid particles encapsulated in oil droplets can be dewetted by chemically reducing the oil phase affinity towards the colloidal substrate, which leads to new colloidal morphologies. Such system has the ability of erasing defects due to the dynamic changing of the particle morphologies, as illustrated in Fig. 10E.

In the case of formation of an ordered surface pattern by colloidal particles via drop-deposition on a substrate, defect engineering can be achieved by control of the wettability of the substrate. This parameter has a significant influence on solvent evaporation, which controls the order and quality of the surface. Lyutakov and coworkers studied the influence of surface modification of Au substrates via hydrophilic or hydrophobic substituents on the size and quality of a closed-packed polystyrene single domain.¹⁸¹ Their results illustrated that substrates with hydrophilic 4-carboxyphenyl modified surfaces show dislocation-like defects. By contrast, Schottky-like defects caused by missing of polystyrene spheres are dominant on substrates with 4-sulfophenyl functional groups, which have higher hydrophilicity than 4-carboxyphenyl groups. Modification of the Au substrate with hydrophobic functional groups disrupts the order of polystyrene microsphere arrays, which leads to strong deviations from a closely packed arrangement.¹⁸¹

4. Polymers

A polymer is “a molecule of high relative molecular mass, the structure of which essentially comprises the multiple repetition of units derived, actually or conceptually, from molecules of low relative molecular mass”.⁹⁸ This perception was recognized by Staudinger in 1920.^71,72 Before this time, polymeric materials had been considered as micelle-type aggregates, since their solutions exhibit properties like those of polydisperse, colloidal dispersions. Staudinger was later awarded the Nobel prize in 1953 for his prolonged efforts in this field.¹⁸² In the past 100 years, polymers have gained such broad relevance that the 20th century might rightfully be termed the plastic-age, and today, polymers and polymer-based materials play a role in almost every branch our daily lifes, and a wide range of this type of soft matter, including plastics, rubbers, fibers, adhesives, and more, are produced in mass amounts for different industries such as packaging, film, textile, membrane, coating, automotive, and electronic enterprises. Polymers are classified in several ways like their synthesis method, chemical structure, or architecture. Regards to the latter, polymers can be generally divided into linear, branched, and crosslinked chains.

4.1 Linear polymers with controlled moderate degrees of branching

The requirement for materials with tailored properties is the central driving force in the preparative polymer sciences.¹⁸³ One of the critical molecular parameters connected to properties and functionalities is the polymer main-chain architecture, such that manipulation of that architecture enables manipulation of the properties without alteration of the actual chemical composition.^184–187 For a linear macromolecule, such a basic structural variation can be modulated by introducing branches to the chain backbone, which can be done with different density as well as different length and distribution of the branches. The resulting versatile potential for structure and property variation has been a strong driving force to extensive investigation of branched polymers during the last two decades.

Today, branching is a general term for a huge class of polymer structures. As an example, comb polymers are a class of branched macromolecules consisting of a linear backbone with a low grafting density of branch chains. Another example is brush polymers, which have a comb-like structure, too, but with a significantly higher grafting density of branches.¹⁸⁸ In semi-crystalline polymers, branching has significant influence on the structure of crystallites. By increasing the branch content in polyethylene, for example, the unit cell parameters (a and b) and the associated unit cell basal area (ab) increase.¹⁸⁹ Branched polymers show completely different physical properties in comparison to linear polymers having the same molar mass. For example, in semi-crystalline polymers, branched polymers have lower degrees of crystallinity and lower melting points than their linear counterparts.¹⁹⁰ In addition, branching has a significant influence on the glass transition temperature. Mülhaupt and coworkers synthesized a series of branched polyethylenes via metallocene-based copolymerization of ethylene and propylene, or 1-buten, or 1-octen, which gives different extent of branching.¹⁹¹ Investigation of the thermal properties of these polymers illustrated that the glass transition temperature generally decreases upon increase of the number of branches per chain and/or the length of the branches. A similar trend was also reported by Huang, Yan and coworkers based on their experimental and theoretical work.¹⁹²

An attractive approach to make well-defined branched polymers is transition-metal catalyzed polymerization in which the metal-alkyl complexes define the location where a monomer can be added to propagating chains.¹⁹³ In contrast to many of the methods for the synthesis of polymers with controllable architecture, polymerization using transition metals does not include multi-step organic synthesis and does not require specially designed monomers. By this method, polymers with a different range of branching densities, from linear to highly branched (vide infra), can be synthesized. Another advantage is that this approach is widely utilized to control branching in polyolefines like polyethylene, which is produced in amounts of millions tons per year for broad applications such as fibers, plastics, and elastomers.^193–195 In a seminal work, Guan and coworkers introduced chain-walking polymerization concepts to control the branching of polyethylenes by utilizing Pd-diimine catalysts.¹⁹³ In the chain-growth step, the metal center walks randomly along the polymer chain, and hence, addition of the monomer to the growing chain occurs randomly instead of at the chain end only. In this mechanism, the degree of branching is controlled by the ratio of the chain walking rate to the chain propagation rate, which is tunable by the polymerization conditions such as pressure and temperature.^193,195 The chain-walking polymerization method has been widely used to adjust the thermal, rheological, and mechanical properties of polymers, specifically for macromolecules formed from α-olefin monomers.^196–199 In addition, Alamo and coworkers showed that chain-walking polymerization can be utilized to synthesize isotactic polypropylene with regional defects caused by irregularity in distribution or density of methyl groups along polymer chains.²⁰⁰ They illustrated that at comparable defect density, polypropylenes with such chain-walking defects have lower melting points and much lower degrees of crystallinity than isotactic polypropylenes with regional defects induced by copolymerization with other 1-alkene comonomers.²⁰⁰

Beyond structural variation of linear polymers through introduction of moderately branched content into their microstructure by controlled-architecture polymerization, the properties of these polymers can be engineered and modified by methods like blending and functionalization. In a specific viewpoint, such modification methods can be categorized as defect engineering via the incorporation of dopant defects into polymers. These property-adjusting methods have been extensively studied and reviewed for different types of polymers.^201–205 For this reason, a deeper discussion of this topic is excluded from this paper, and only two examples are presented to highlight the potential of these methods for modification of polymer properties. Kumaraswamy and coworkers modified the shrinkage of high density polyethylene melts upon cooling induced by crystallization via the addition of ∼0.4% dimethyl dibenzylidene sorbitol and ∼10% of linear low density polyethylene.²⁰⁶ With this modification, the warpage of high density polyethylene in a three-dimensional printing process is significantly minimized. This approach was even applicable for recycled polymers that were processed at least one time before use in the 3D printing process. Lele and coworkers modified the poor melt elasticity of telechelic poly(L-lactic acid) by conversion of hydroxyl end groups into ionic groups.²⁰⁷ The resulting ionomer demonstrated a significant increase in the melt elasticity compared to the precursor polymer due to the coulomb interactions of its ionic groups.

4.2 Dendritic polymers

The next level of polymeric structural complexity beyond the bottom of linear chains with little or medium extent of branching are dendritic polymers; these are a prime example of a scientific breakthrough in the synthesis of sophisticated macromolecules.^208–210 From a structural viewpoint, dendritic polymers can be classified in two major groups: monodisperse and regular frameworks such as dendrimers and dendrons, and polydisperse and irregular frameworks such as hyperbranched polymers (HBPs), dendrigrafts, dendritic-linear hybrids, and dendronized polymers (Fig. 11).^211–213 The latter are bottlebrush polymers with repeatedly branched dendron side chains, as defined by Schlüter.²¹³ Upon increase of the dendron generation, the densely packed side chains lead to an increase of the shape-persistence and cross-section of the polymers. Due to the high grafting density of dendronized polymers, dendron-generation and molecular-weight dependent rheological measurements revealed unusually long thermal equilibration times in the molten state, as shown by Vlassopoulos and coworkers.²¹⁴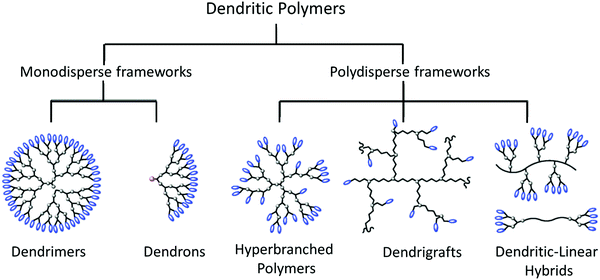

Fig. 11 Schematic classification of dendritic polymers. Adapted from ref. 212; copyright 2012 Royal Society of Chemistry.

The following section has a main focus on the larger classes of dendrimers and hyperbranched polymers. Dendrimers are perfect regularly branched macromolecules whose name originates from the Greek words δε′νδρoν (dendrons), meaning tree, and με′ρoς (meros) meaning part.²¹¹ Hyperbranched polymers (HBPs) are mimics of dendrimers, resembling their dendritic structures but with the presence of statistically distributed structural defects.²¹⁵ At a given molar mass, in comparison to linear macromolecules, dendritic polymers are generally more soluble,²¹⁶ and their solution viscosity is lower.^217–219 Very generally, the intrinsic viscosity and radius of gyration of dendritic polymers are reduced by increase of the molecular compactness,^220,221 which depends on the synthesis conditions.^{193,222–224} These materials are almost exclusively amorphous and have lower glass transition temperatures than their linear counterparts.^216,225 Due to these special physical properties as well as due to their unique three-dimensional tree-like topologies and multivalent functionalities, this class of soft matter is found to have exciting potential in cutting edge-applications such as sensing, light-harvesting, surface engineering, enzyme-like catalysis, and targeted delivery.^226–234

4.2.1 Defects and defect engineering in hyperbranched polymers and dendrimers. A dendrimer consists of two types of structural units: terminal units on the globular surface and dendritic units inside the specimen. By contrast, a hyperbranched polymer has three types of structural units: dendritic units, linear units, and terminal units. The terminal units are always located at the termini, but the dendritic and the linear units are randomly distributed within the macromolecular framework and may form structural defects there.^235,236

While dendrimers have a unique size and symmetric structure without any structural defects, the tedious stepwise procedure for synthesizing dendrimers often results in expensive products with limited availability, and therefore, in a restricted use for large-scale industrial applications. In contrast, hyperbranched polymers are often easy to synthesize in a large-scale single-step synthetic process and are therefore considered as attractive alternatives to dendrimers in the field of materials engineering.^{210,237–239} The main limitation for actually reaching this target is their uncontrolled statistical growth during polymerization, which results in structural defects, and with that, in uncontrolled variation of their properties.²¹¹ The main solution to address this limitation is to aim for engineering of these defects. Even more: the actual key to preparing a HBP that possesses effective cost as well as controlled properties is to engineer its structural defects.

4.2.1.1 Defect engineering in HBPs by control of the degree of branching. Defect engineering in HBPs is accessible by developing synthesis methods to set the degree of branching (DB),²⁴⁰ on a desired value, ideally such to becoming able to vary the DB between 0% (linear chain) and 100% (dendrimers). The most common synthetic route to hyperbranched polymers involves a one-pot procedure in which AB_x monomers are condensed.^241–243 HBPs can also be synthesized by self-condensing of vinyl monomers (AB*) containing an initiating moiety (B*) in addition to their double bond^244,245 or by multibranching ring-opening polymerization for monomers such as glycidol containing one epoxide and one hydroxyl group.

Generally, the degree of branching in HBPs can be controlled by the conversion of the polymerization reaction. Yan and Müller have shown that the DB of HBPs prepared by both condensation of AB₂ monomers and self-condensing of AB* monomers increases by propagation of the polymerization and increasing the conversion.²⁴⁶ In addition, when AB* is utilized with another vinyl monomer to synthesize a HBP, the ratio of the two monomeric species is a key parameter to control the degree of branching.²⁴⁷ One approach to increase the DB is changing the functionality, x, in AB_x monomers.^248,249 For example, comparison of hyperbranched poly(ether ketone)s formed by AB₂, AB₃, and AB₄ monomers with the same subunits revealed higher DB, 72%, for the polymer obtained from AB₄ monomer compared to the polymer obtained from AB₂ monomer.^250,251 A similar effect has been reported by Kakimoto and coworkers for hyperbranched aromatic polyamides.²⁴⁹ Another approach to control the DB in HBPs is the variation of the ratio of the rate constant of the linear unit, k_L, to the rate constant of the terminal unit, k_T.^252,253 Frey and coworkers proposed a relationship between this ratio and the DB for AB_x monomers. They showed that a degree of branching of 80% can be achieved if k_L/ k_T = 5.²⁵⁴ To synthesize compounds with DB = 100%, different approaches have been reported that depend on the monomer type. As an example, Maier and coworkers applied a cycloaddition of azine and diisocyanate to synthesize hyperbranched polymers with 100% DB using the reversible formation of an unstable azomethinimine.²⁵⁵ In another work, Smet and coworkers utilized an acidic-catalyst for the condensation of an isatin-based AB₂-type monomer with a highly reactive phenoxy group²⁵⁶ or monomers containing acenaphthenequinone units²⁵⁷ to synthesize hyperbranched polymers with 100% DB. Such acidic-catalysis is also efficient for fluorenone compounds.²⁵⁸ In addition, Bo and coworkers synthesized hyperbranched polymers with 100% DB using palladium, Pd, based catalysts and an AB₂ monomer containing one aromatic boronic pinacol ester and two aromatic bromo atoms linked by an alkyl chain spacer.²⁵⁹ Moreover, Ramakrishnan and Chatterjee showed that an AB₂ monomer carrying a dimethylacetal unit and a thiol group undergoes a rapid self-condensation in the melt under acid-catalysis, which yields a hyperbranched polydithioacetal with no linear defects.²³¹ In an opposite direction, 100% linear polymers can also be synthesized from AB₂ monomers. Zolotukhin and coworkers showed that linear poly(phenylene ether) with a high molar mass is prepared by polycondensation of 2,2,2-trifluoroacetophenone with 4,4′-diphenoxybenzophenone in an acidic medium.²⁶⁰ They found that the reason for formation of the linear topology is a significant faster kinetics of the first reaction between 2,2,2-trifluoroacetophenone and the phenoxy units than that of the second one between the generated mono-substituted product with one more phenoxy unit.²⁶¹ On top of these examples, it has been shown that for the AB₂ monomer of 1-[4-(4-phenoxyphenoxy)phenyl]ethanone, the degree of branching can be systematically changed between 0 and 100% using acidic catalysts by variation of the [monomer]/[acid] ratio in chloroform from 0 to 1.²⁶²

Defect engineering in hyperbranched polymers via control of the DB is not only developed for AB_x monomers, but it is also investigated for polyolefines such as polyethylene. One of the advantages of polyolefines is their commercial availability in contrast to many other multifunctional AB_x monomers. There are several strategies that give rise to some typical branched polyethylenes with unique branch-on-branch structures such as high temperature and high pressure radical polymerization for the production of low density polyethylene²⁶³ or the synthesis of linear low density polyethylene by metallocene-catalyzed coordination polymerization.²⁶⁴ The synthesis of hyperbranched polyethylenes with controlled degrees of branching has in fact been extensively developed by the introduction of the chain-walking polymerization, as discussed above.¹⁹³ Ye and coworkers further modified this approach to avoid the necessity of changing the polymerization condition to achieve tuning of the polymer branching.^265,266 For this target, they utilized chain-walking blocking sites such as ring structures in combination with a chain-walking catalyst. These blocking sites restrict the walking of the metal center along the chain, and therefore increase the level of chain linearization.

4.2.2. Application of defect engineering in HBPs. Due to their numerous binding sites, amphiphilic HBPs have prospect for application as hosts to carry small molecule guests.^{250,251,267–271} Haag and coworkers have shown that the loading capability of dyes within HBPs is highly controlled by their DB and maximized when the DB is in the range of 0.45 and 0.55.^268,272 Along a similar line, for application in gene therapy, Yan and coworkers have shown that the efficiency of DNA transfection of cationic HBPs is significantly improved by increase of the DB between 0.04 and 0.44. They attributed this observation to the more compact structure of HBPs with higher DB, which leads to a greater availability of primary and tertiary amino groups.²⁷³ The morphology of amphiphilic HBPs is also controlled by their DB. For example, Yan, Zhou and coworkers studied a series of hydrophilic poly(ethylene oxide) arms grafted onto the surface of a hydrophobic poly(3-ethyl-3-(hydroxymethyl)-oxetane) core. They illustrated that when the core is a HBP with a high DB, the morphology of the graft macromolecule is that of a core–shell star copolymer. If the core has no branching, by contrast, the morphology turns into that of a comb-like copolymer. When the core has a medium DB, the morphology is between that of a star and comb-like.²⁷⁴

In view of industrial applications, HBPs are used as modifiers for the processing of polymers.¹⁹⁰ In an example, Shaked and coworkers studied the nanomodification of poly(hydroxyl butyrate) with commercialized hyperbranched polyesters with different DB. They illustrated that the viscosity and flow properties, crystallinity, glass transition temperature, melting temperature, and mechanical properties of the modified polymers, which are important regards to their processing and/or final application, are controlled by the DB and the content of the HBPs modifiers.²⁷⁵

4.3 Conjugated polymers

Conjugation is generally defined as the alternation of single and multiple bonds along a chain of carbon (or hetero) atoms.^276,277 A conjugated polymer is the extreme of that: it is a (usually carbon-based) semi-crystalline or amorphous macromolecule through which valence π electrons are delocalized.²⁷⁸ Due to the electronic and optical properties of this class of macromolecules, they have many potential applications such as those in light emitting devices, nonlinear optical devices, photovoltaic devices, and plastic field-effect transistors.^278–284 The discovery and development of conductive conjugated polymers was recognized by the award of the Nobel prize for chemistry in 2000 to Heeger, MacDiarmid, and Shirakawa.²⁸⁵ The goal of development of organic opto-electronic devices is thereby not to attain or exceed the level of performance of silicon technologies,²⁷⁹ but instead, it aims at fabrication of optoelectronic devices with features such as synthetic variability, low temperature-plastic processing, mechanical flexibility, and low-cost production, which is challenging to achieve with silicon.^286–288 Soluble polymer semiconducting materials, for example, can be readily processed and easily printed, which removes the conventional requirement for photolithography for patterning. This is a key advantage for large scale processing of printed electronics.²⁸²

4.3.1 Defects in conjugated polymers. There are different types of structural defects in the microstructure of conjugated polymers (Fig. 12). These defects can be conformational kinks created by changes in the relative orientation of organic rings and/or the overall backbone induced by the thermal environment.²⁸⁹ Another type of defects in conjugated polymers is chemical defects that can be caused due to post-synthesis photopolymerization, the general synthesis process, or missing hydrogens on aliphatic pendant groups and/or the existence of impurities.^290–292 In the synthesis of poly(phenylenevinylene) with carbon–carbon double bonds along the backbone, for example, there are some sp³-hybridized centers in the chain, which interrupts the π-conjugation.²⁹³ In addition to these defects, distortion of sp²-hybridized carbons along the backbone of conjugated polymers from their equilibrium planar trigonal geometry may cause charge defects.²⁹⁴ Similar to non-conjugated polymers formed by asymmetric monomers, conjugated polymers like poly(3-hexyl thiophene-2,5-diyl), P3HT, contain regio-defects defined as the percentage of head-to-head or tail-to-tail conformations rather than preferred head-to-tail conformation.²⁹⁵ Conjugated polymers may also have morphological defects including misaligned crystalline grains (crystallite) and grain boundaries (interface of crystalline/amorphous phase) or macroscopic inhomogeneities due to aggregation.^296,297 These types of defects are commonly formed when a conjugated polymer is prepared by solution-based techniques where formation of crystalline domains or alignment and aggregation of polymer chains, all potentially subject to the foresaid defects, occur by evaporation of solvents.²⁹⁸

Fig. 12 Examples of defects in π-conjugated polymers: (A) Z double bond as a conformational defect (kink), (B) sp³-hybridized center as a chemical defect, (C) charged defects. Panels (A, B) and C are reprinted from ref. 302 and 294, respectively. Copyright 2006 and 2009, American Institute of Physics, and Royal Society of Chemistry, respectively.

Defects can change the conformation and crystalline structure of semi-crystalline conjugated polymers. In poly(2-methoxy-5-(2-ethylhexyloxy)-1,4-phenylenevinylene), MEH-PPV, charge defects induce a highly ordered, cylindrical collapsed conformation, which is a deviation from ideal toroid or rod structures.²⁹⁹ This highly ordered cylindrical conformation is a critical factor for the properties of MEH-PPV such as highly efficient intramolecular energy transfer and significant local optical anisotropy in thin films. Luscombe and coworkers have investigated the effect of regio-defects on the crystallinity and crystalline structure of P3HT nanowires.²⁹⁵ Decreasing regio-defects from 10% to 1% increases π–π stacking from ∼5 nm to ∼25 nm. Despite this drastic increase in crystalline order, there is no increase in the width of the crystal lamellae, since defects can be incorporated into the crystalline structure. Above 10%, regio-defects are excluded from the crystalline domain due to the onset of too many backbone torsions, which prevents successful folding of the polymer chains and close-packing with other chains. The incorporation of defects into the amorphous phase could in turn decrease the crystal lamellae thickness.

Generally, defects play an important role in the electronic and optical properties of conjugated polymers.^300,301 Conformational kinks and chemical defects, for example, can induce excited-state localization in addition to the strong electron–phonon coupling of conjugated polymers.³⁰² These defects break the conjugation along the polymer backbone, which confines the electronic excitation over small subunits acting as chromophores.³⁰² Such defects therefore cause optical anisotropy in conjugated polymers such as poly(p-phenylene vinylene). Rossky and coworkers have successfully predicted this anisotropy via Monte Carlo simulation by considering 5% of tetrahedral defects along the polymer backbone. These defects included Z double bonds and sp³-carbons.³⁰³ As another example, hydrated molecular oxygen complexes that act as impurities can trap electron transport in conjugated polymers like poly(phenylene vinylene).^304,305 This effect, which is known as trap-limited conduction, significantly reduces electron mobility.³⁰⁶ In addition to hydrated oxygen complexes, an unintentional presence of oxygen atoms inside conjugated polymers like P3HT may result in covalent bonding between oxygen and carbon or sulfur atoms. These chemical defects decrease the charge-carrier mobility, and with that, solar cell efficiencies.³⁰⁷ Such chemical defects may further induce deformation (kinks) along the polymer backbone.³⁰⁸ For instance, COH-CO defects deform the thiophene ring in P3HT, as the OH group pulls the bound carbon atom away from the ring plane, inserting a 34° kink along the polymer backbone. Such defects almost quench the conductivity of the polymer.³⁰⁸ In photo-luminescent conjugated polymers, defects may induce extra emission bands. In addition, point contacts between chains introduced by structural kinks along the backbone may create aggregation, which further induces extra emission band(s) in these materials.³⁰⁹

In study of the photoemission and inverse photoemission spectra of P3HT, Caruso and coworkers observed a weak photoemission feature at a binding energy of −1.7 eV, which could not be assigned to a molecular orbital. They attributed this feature to some sort of gap state, possibly a defect state. They theoretically illustrate that in the absence of such a defect state, P3HT is not very p-type, but its electronic structure is more characteristic of a n-type insulator. They also showed that the photoemission at −1.7 eV binding energy, is induced by a chemical or structural defect that is not related to the relative backbone orientation. These defects are heterogeneous and impart p-type character to the polymer.²⁹¹ In another work, Gregg showed that electrostatic fluctuations caused by charged defects significantly change the electrical properties of semi-conducting π-conjugated polymers. This change directly scales with the density of these defects. In some π-conjugated polymers with an intermediate density of such charged defects (10¹⁶–10¹⁹ cm⁻³), the properties are influenced by the charged defects but not wholly controlled by them. Based on these results, Gregg assumed that the largest fraction of available un-doped π-conjugated polymers are in fact strongly doped by their defects. While the typical values of conductivity for π-conjugated polymers are 10⁻⁸–10⁻⁵ S cm⁻¹,³¹⁰ these values are significantly higher than expected for defect-free materials, suggesting that the conductivity is dominated by defects.²⁹⁴ Another electrical property that is important in organic photovoltaic materials is the exciton diffusion length, L_ex, which determines the fraction of light absorbed close to a heterojunction interface to contribute to the photocurrent. L_ex is expected to be small in the presence of chemical defects.³¹¹ In π-conjugated polymers, L_ex is usually less than 10 nm, probably due to their charge defect density of 10¹⁸ cm⁻³ resulting in an average of about one charge per 10 nm.^312,313L_ex, however, is much longer for materials with lower charge defect density.^312,314

4.3.2 Defect engineering in conjugated polymers. As mentioned above, defects in conjugated polymers influence their photoelectrical properties, like intrinsic carrier density of organic semiconductors, which further inhibits transport of both excitons and charge carriers. This transport hindering leads to photochemical instabilities and complicates reproducibility and comparison to theory.²⁹⁴ While charged defects may act as dopants (see Section 4.3.3), and therefore have beneficial effects, they are poorly controlled, such that adjustment of the semiconducting properties by them is an inefficient way. One approach to overcome this limitation is defect engineering via chemical treatment of polymers.^314,315 Liang, Gregg and coworkers have shown that reacting P3HT with lithium aluminum hydride (LAH) or dimethyl sulfate (Me₂SO₄) makes substantial improvements in chemical stability and electrical properties due to a decrease of charge defect density.^312,314 Me₂SO₄ and LAH have low reactivity and cannot modify P3HT, but they may react at defect sites, e.g., where sp²-hybridized carbon is distorted from its equilibrium position (Fig. 12C). By the reaction with Me₂SO₄ and LAH, these charge defects convert to electro-inactive sp³ carbons. The density of reactant sites is very low (less than one thiopene unit in 10⁴–10⁵), and therefore, the treatment does not change the material chemically, but nevertheless, the optoelectronic properties significantly change. In summary, the treatment of P3HT with both chemicals increases the hole carrier mobilities, conductivity, and exciton diffusion length, and oppositely decreases the defect density. It should be noted that the impacts of Me₂SO₄ and LAH treatment on these properties are substantially different due to their different modification mechanism.^312,314 In a further study, the same researchers showed that the optoelectronic properties of P3HT can be adjusted via treatment with both Me₂SO₄ and LAH.³¹⁵ In opposite to their previous work, in which one chemical reagent ideally reacted with defects of one polarity and left the opposite polarity defects, in this further study, they investigated the effect of covalent modification of both defect sites. Their results showed that the sequence of treatments with nucleophilic and electrophilic chemicals impacts the final properties.³¹⁵

Morphological defects and aggregates in conjugated polymers can be controlled via controlling the processing of these polymers.^316,317 As mentioned before, one of the main advantages of conjugated polymers is the possibility of their processing (commonly making a thin film) by solution-based techniques. In this regard, controlling thin film morphology and related defects during printing or coating processes is critical due to its influence on device performance.

The aggregation of conjugated polymers like P3HT via π–π stacking can be controlled by using a mixture of polar and nonpolar solvents in an ultra-sonication assisted self-assembly process.³¹⁸ The amount of these aggregates can be controlled by the sonication time.³¹⁹ Such a synergistic combination of ultrasonic process and nonsolvent addition may enhance charge transport in the polymer thin film due to the decrease of grain boundaries, which increases efficient charge hopping between transport sites.³²⁰ Improvement of the carrier mobility in P3HT has been obtained by exposing polymer solutions to low intensity, limited-duration UV irradiation. This observation has been explained by a conformational change of the P3HT chains from aromatic to quinoid-like, which facilitates supramolecular self-assembly of the polymer into a low-defect, nanofibrillar morphology.³²¹ In conjugated polymers like MEH-PPV where inhomogeneities build-up by the aggregation of polymer chains and have a negative effect on the properties, addition of a small amount of a polar solvent such as methanol into the polymer solution (in a nonpolar solvent) prevents aggregation during the solution-based process.³²² In addition, morphological defects in conjugated polymers can be also controlled by changing the processing method. A thin film of alkyl-substituted thienylenevinylene and phthalimide-based copolymers that is processed by the wire-bar-coating method reveals a twofold enhancement in charge carrier mobility compared to a sample prepared by spin coating.³²³ In another example, processing of a solution of P3HT containing P3HT nanowires by solution shearing techniques significantly enhances charge carrier mobility of the obtained film up to 50 times compared to a sample prepared by spin-coating pristine method.^324,325

4.3.3 Doped π-conjugated polymers. Dopants are defects that are purposely introduced.²⁹⁴ In organic light-emitting diodes (OLEDs), where semiconducting organic layers are sandwiched between two electrodes and holes are injected by the anode, the injection of holes can be improved by utilizing doped π-conjugated polymer layers. By increasing the doping level, barriers against the hole injection can be continuously reduced, which decreases the operating voltage and improves the light output and efficiency.³²⁶ This concept can be utilized for tuning and structuring OLEDs for display applications. OLED displays are commercialized today in competition to liquid crystal displays. Both display technologies share quite similar perspectives. Liquid crystal displays commonly have lower cost, long lifetimes and good performance in resolution density and peak brightness. On the other hand, OLED displays possess high black states, panel flexibility and quick response times.³²⁷ Doping of conjugated polymers with low-ionization energy compounds that are enable to transfer charge to the unoccupied states of polymers (n-type dopant) can be utilized to reduce the density of defects that trap the electron transport. This strategy has been utilized by Boer and coworkers for MEH-PPV by doping this polymer with decamethylcobaltocene.³⁰⁴ Their results demonstrated that by increasing the doping concentration up to 0.05 wt%, a strong increase in the electron current over several orders of magnitude is obtained. For the 0.05 wt% of dopants, a quadratic dependence of the electron current density on voltage was observed, which was attributed to the filling of all electron traps (a trap-free structure).³⁰⁴ The same research group showed that doping conjugative polymers like MHE-PPV by acceptor dopants (p-type; such as tetra-fluoro-tetracyanoquinodimethane) can increase the current-voltage characteristics (current density versus characteristic voltage conductivity) by 1–3 orders of magnitude. In addition, the threshold voltage is controllable by adjustment of the doping concentration.³²² In another work, the authors demonstrated that doping P3HT with this p-type dopant strongly decreases the barrier against hole injection into P3HT at its interface with Ag.³²⁸

As another example, Xu, Huang, and coworkers designed a series of red-emitting conjugated polymers based on classical two-photon absorption units (bis(diphenylaminostyryl)benzene), electron units (fluorene), and small amounts of electron-deficient units (dithienylbenzothiadizole) as dopants along the polymer backbone. They showed that the introduction of these dopant units into the polymer backbone forms a donor–π–acceptor–π–donor structure, which facilitates charge transfer between the donor moieties and π systems and enhances the two-photon absorption cross section. In addition, polymers containing dopants had a significant higher red emission quantum yield than corresponding undoped polymers.³²⁹ In other work, Cooper and coworkers utilized small amounts of comonomer dopants to vary the photophysical properties of conjugated polymers. They illustrated that the optical band gap and the emission of conjugated polyphenylene networks can be tuned by inclusion of a small amount (0.1–5 mol%) of benzothiadiazole (BT), bisthiophenebenzothiadiazole (TBT) or perylenediimide as chromophores. As an example of their results, the networks doped with BT are insoluble green powders with an optical gap in the range of 2.59 eV (0.1 mol% of BT) and 2.41 eV (5 mol% of BT), whereas the networks doped with TBT are pale to deep red color powders with a band gap from 2.0 eV (0.1 mol% of TBT) to 1.95 eV (5 mol% of TBT).³³⁰

4.4 Polymer networks

Polymer networks are 3D structures composed of (macro)molecular building blocks connected by covalent or physical bonds named crosslinks.³³¹ In a structural view, polymer networks are composed of strands, which are flexible polymer chains, and junctions, which are nodes connecting three or more strands. The latter can be flexible short molecules or rigid linkers. In analogy to linear polymers, hence, polymer networks can be formed when molecules with functionality greater than three are involved, either solely or as part of a mixture with molecules of functionality two. This type of soft matter can be generally divided into four classes, including thermosets, elastomers, supramolecular networks, and gels.^332,333

Thermosets are composed of (macro)molecular building blocks that are crosslinked by covalent bonds, where the glass transition temperature of the network strands is higher than ambient temperature. These materials are rigid, insoluble (but yet swellable), and non-processable after formation. Formaldehyde and epoxy resins are examples of such thermoset networks. Elastomers such as vulcanized natural rubber have almost similar microstructures as thermosets, but in contrast to these, they consist of strands that have a glass transition temperature lower than ambient temperature. Elastomers are therefore generally soft, but insoluble and thus still hardly processable after formation. Thermoplastic elastomers are a specific class of elastomers that have no permanent crosslinks and therefore are soluble and processable at certain conditions, typically at high temperatures. One example is microphase separated block copolymers where the separated domains act as non-covalent crosslinks.³³⁴ Supramolecular networks are formed from (macro)molecular building blocks that are crosslinked through physical interactions such as hydrogen bonds or ionic interactions. By application of appropriate stimuli such as changes in temperature, pH, or oxidation states, the physical crosslinks can be dissociated, and the polymer network thereby transitions to a soluble and processable material.^335–337 Generally, the term “supramolecular networks” is assigned to a network in which functional groups with the ability of physical binding are rationally incorporated, e.g., by functionalization of (macro)molecular building blocks with such functional groups at the side or the ends of covalently jointed chains. In view of the properties of supramolecular networks, mainly their solubility and processability at specific conditions, one may think to also categorize linear or branched polymers as a type of supramolecular polymer network, wherein physical chain entanglements act as temporary network junctions; however, such a naming is uncommon, but instead, entanglement networks are more commonly named physical networks. The fourth class of polymer networks, gels, are covalent or supramolecular networks swollen in liquid media such as water or organic solvents. Such swelling occurs when a polymer network is exposed to a solvent with a sufficient affinity that could actually dissolve the (macro)molecular strands if the network junctions were not existent. As a result of that affinity, the solvent diffuses into the network microstructure and swells the network, but due to the permanent chain connectivity, complete dissolution is impossible. The focus of this section is on gels and elastomers. Supramolecular networks are discussed in Section 5 due to their ability for self-assembly. Thermosets are not discussed in this paper.

Their marked elasticity, permeability, and swellability make polymer networks important materials in view of academic studies as well as for industrial applications such as adhesives, cosmetics, adsorbers, membranes, rubber products, coating materials, or food packaging. In addition, multiple developments in the polymer network sciences have introduced further advanced applications, like those in drug delivery,³³⁸ tissue engineering,³³⁹ soft actuation,³⁴⁰ gas storage,³⁴¹ catalysis,³⁴² and electronics.³⁴³

There are three main synthesis approaches to create polymer networks: chain-growth polymerization, step-growth polymerization, and vulcanization. The first method is based on the addition of monomers onto a growing polymer chain. Through the use of monomers with more than one functionality (e.g., monomers with two unsaturated bonds), a polymer network is formed. The ratio of the multi-functional to the one-functional monomers defines the overall cross-linking density. In step-growth polymerization, by contrast, monomers react with each other first to form dimers. In the next step, these dimers react with each other to form tetramers, and so forth, until further such reactions lead to polymer chains. If monomers with functionality greater than two are used, the process leads to branched polymers, and further reaction between these branched polymers can form polymer networks. One example of a step-growth process to form a network is a mechanism known as end-linking.^344–346 In this mechanism, the chain ends of bifunctional monomers (A₂) are linked to those of other multi-functional monomers (B_f) in a reaction between functional groups of A and B. Historically, end-linking has been the first approach to control the network structure for preparation of model networks.^347–352 Polymer networks can also be prepared by vulcanization, which is a kind of polymer-analogous crosslinking process between polymer chains through the formation of bonds between functional groups along the polymer backbone. The classical textbook example is the sulfur-based vulcanization of natural rubber by crosslinking of alkene side groups along polyisoprene chains with elementary sulfur in presence of vulcanization agents.

4.4.1 Defects in polymer networks. The mechanical and further macroscopic properties of polymer networks are controlled not only specifically by their chemical specificity, but also universally by their topology. The latter in fact mainly determines the most relevant network properties such as their versatile elasticity, permeability, and swellability; it is characterized by features on different length scales, as illustrated in Fig. 13A:^{333,353–355}

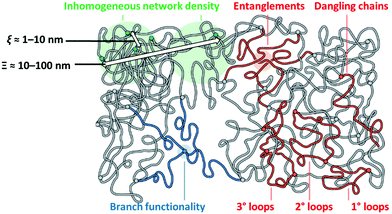Fig. 13 Features of polymer network topology on different length scale: 10–100 nm (green), 1–10 nm (red), and <1 nm (blue), and comparison of the length scale of two types of network structural parameters. ξ: strand length between two junctions on a scale of 1–10 nm. Ξ: spatial variation of the density of strands/junctions in swollen gels on a length scale of 10–100 nm. The sketch is adapted from ref. 333; copyright 2020 Wiley-VCH.

(i) <1 nm: branches along the network-strand backbones

(ii) 1–10 nm: connectivity defects on the network-mesh scale, such as dangling strands, loops of various order, and physical entanglements

(iii) 10–100 nm: spatial inhomogeneity of the junction and network-strand density

In view of the latter, note that Okay further delimited the term “inhomogeneity”, referring to “fluctuation of the crosslink density in space” from the term “heterogeneity”, referring to “the existence of phase-separated domains in polymer gels”.³⁵⁶ This view is in line with an earlier perspective by Dušek and Prins, who denoted “heterogeneous” gels to be formed by microsyneresis during their gelation.³⁵⁷ With that, hence, a potential fourth level of polymer-network structural complexity might be added to the list above, encompassing sponge-like gels penetrated by nano- to millimeter-sized pores.³⁵⁸ The most relevant and frequent of the above features in usual polymer networks, however, are connectivity and topological defects including spatial inhomogeneity (iii in the list) and local defects (ii in the list). Therefore, understanding these irregularities in polymer networks and their engineering is a key to rationally design these materials.

Local misconnectivities in polymer networks actually have a precise existing definition laid down in IUPAC's purple⁹⁸ and even gold book,²⁷⁷ which classifies network defects as “elastically ineffective chains in a polymer network”. Dangling chains occur when a reactive group from the network precursors remains unreacted after network formation. First order loops form when both ends of a strand are attached to the same junction. Second order loops form when two strands are connected to the same two junctions. Similarly, third order loops form when three strands are connected to the same three junctions.

On top of these local features, network meshsize non-uniformity and nanostructural spatial inhomogeneity in the form of a non-uniform distribution of crosslinks and strands in a network are the prime kind of network irregularity on larger scales. The latter nanostructural inhomogeneity is particularly exacerbated (in average by a factor of 10) if networks are swollen in a solvent post their gelation.³⁵⁹ This is because the local swelling degree depends on the local crosslinking density, and is therefore higher for local loosely crosslinked domains than for local densely crosslinked domains, thereby further pronouncing that variation. The difference in the local swelling degree therefore creates additional, significant fluctuations in the spatial density of strands and network junctions on scales of 10–100 nm (Fig. 13).³⁵³ As illustrated by Shibayama, Sakai, and coworkers, local defects (mostly dangling chains and loops) also significantly affect the spatial inhomogeneities in swollen networks, so there is a cross-coupling of these seemingly length scale-separated kinds of structural complexity.³⁶⁰

The most common experimental techniques to probe and quantify network spatial inhomogeneities on scales far beyond 10 nm are static and dynamic light, X-ray, and neutron scattering.³⁶¹ However, these methods are not applicable to characterize local topological features such as dangling chains and loops as well as the network mesh size distribution. To cover that range as well, multiple-quantum nuclear magnetic resonance (MQ NMR) spectroscopy³⁶² or network disassembly spectroscopy (NDS)³⁶³ can be utilized.

4.4.2 Control of local defects in polymer networks.
4.4.2.1 Engineering of dangling chains. Unreacted functionalities in a polymer network can be controlled by the reaction stoichiometry or by the presence of monofunctional network precursors during the network percolation process. With this concept, Appel and coworkers used an A₄-(B₃,B₁) monomer system, based on thiol–ene chemistry.³⁶⁴ In their work, A₄ and B₃/B₁ had alkene and thiol end groups, respectively. With these building blocks, different samples with different molar ratios of B₁ to B₃, but with a constant total concentration of functional thiol and alkene groups, were prepared and probed, showing that by change of the ratio of mono-to three functional monomers, which means variation of the dangling strand fraction, the mechanical and further physical properties of these networks such as the shear modulus, swelling capacity, and glass transition temperature can be highly controlled. As an example, by increasing the ratio of B₁/B₃ monomers from 0 to 0.5, which results in an increasing portion of dangling chains, the plateau modulus of the networks decreases by the order of 4000%. Another strategy to control (which often means to minimize) the content of unreacted functional groups and dangling chains is the use of very efficient and selective click chemistry such as copper(I)-catalyzed azide–alkyne cycloaddition or azide–alkyne Huisgen cycloaddition reactions to achieve the network precursor interconnection.^365–367
4.4.2.2 Engineering of loops. Loop defects are chemically and spectroscopically similar to other types of network structures. Therefore, their detection is challenging. Different theoretical and experimental methods have been developed to estimate the density of such defects in network structures, such as mass spectroscopy,³⁶⁸ theoretical modeling of the linear step-growth polymerization with a spanning-tree model,³⁶⁹ rheometry in conjunction with an elasticity model,^370,371 and MQ-NMR.^366,372,373

In a series of papers, Johnson, Olsen, and coworkers introduced novel methods to quantify local network defects, specifically primary and higher-order loops.^{363,374–380} In addition to such defect quantification, their results indirectly give valuable information about the possibility of engineering of these defects. In an end-linked network consisting of A₂ and B_f monomers, the fraction of primary loops can be measured if one of the network precursors contains cleavable groups such that cleavage yields distinct, identifiable products. In a seminal work, Zhou, Johnson, and coworkers utilized an asymmetric bifunctional degradable monomer (norborene-telechelich polyethylene glycol (PEG) oligomer containing one single ester group) that cleaves along the backbone to generate products with distinct masses: low and high.³⁶³ By reaction of this monomer with a B₃ unit (tris-tetrazine), a network is formed with network junctions that can be classified according to the strand length (Fig. 14A). By network disassembly via cleavage of the degradable monomer under basic conditions, soluble products with unique masses are formed for each junction type, which can be analyzed by liquid chromatography, mass spectroscopy, and gel permeation chromatography. This method has been further developed by the use of A₂ monomers with partially isotopically labeled chains (isotopic labeling network disassembly spectroscopy), thereby becoming able to measure the primary loops and dangling chains (Fig. 14B).³⁷⁴ With the use of these techniques, Johnson and coworkers illustrated that the fraction of 1° loops can be controlled by variation of the A₂ concentration.³⁶³ In addition, they found that the kinetics of gel formation is a key parameter to control the fraction of primary loops and dangling chains (Fig. 14C).³⁷⁴ Their results also showed that the fraction of triply reacted junctions that contain primary loops (n_λ3) is approximately constant throughout the gelation process, which means that loops form at triply reacted junctions with equal likelihood both before and after the gel point. In contrast, the fraction of doubly reacted junctions that contain a primary loop and a dangling chain (n_λ2) gradually decreases with the reaction time until bifunctional junctions cannot be detected. In addition, the fraction of all network junctions that possess a triply reacted primary loop (n_T3) and the fraction of all network junctions that are cyclic molecules (n_T2) can be controlled by the kinetics of the gelation reaction. At early time points, the summation of these two fractions increases rapidly. At later time points, this value continues to increase, though more slowly. Later on, Johnson and coworkers further developed the NDS method to quantify the primary loops in a tetra-functional click gel formed from an A₂–B₄ monomer system via copper catalyzed azide–alkyne cycloaddition.³⁷⁵ The authors showed that this method is also applicable to symmetric nonuniform polymer chains that differ by one methylene unit without requiring isotopic labels. Their results illustrated that the monomer architecture is another parameter that defines the effect of network defects on the network properties. In contrast to A₂–B₃ networks, the gel point in gels from tetrafunctional precursors is not dominated by primary loops. Instead, higher-order cyclic defects significantly preclude the gel points in these materials. The authors concluded that A₂–B₃ networks are inherently less sensitive than A₂–B₄ networks to higher-order cyclic defects.

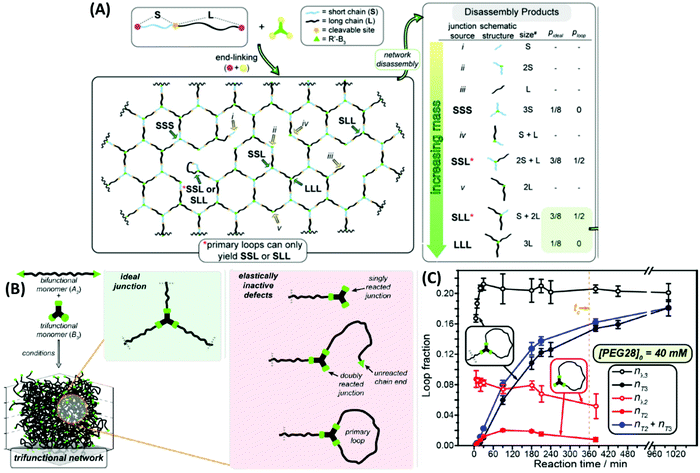Fig. 14 (A) Schematic representation of the concept of network disassembly spectroscopy (NDS). Reaction of bifucntional macromonomers with tri-functional units forms a network. Due to the non-central placement of a cleavable site along the macromonomers, junctions with different mass are formed. After disassembly of the network, the fraction of each junction can be quantified. (B) By reaction of A₂ and B₃ monomers, in addition to the elastically active ideal junctions, elastically inactive defects such as singly reacted or doubly reacted junctions as well as primary loops can be formed. (C) Fraction of each defect as a function of the gelation process as quantified by NDS. n_λ3 is the fraction of triply reacted junctions that contain a primary loop. n_λ2 is the fraction of doubly reacted junctions that contain a primary loop and a dangling chain. n_T3 is fraction of all network junctions that possess a triply reacted primary loop. n_T2 is fraction of all network junctions that are cyclic molecules. Panels A and (B, C) are reprinted from ref. 363 and 374, respectively. Copyright 2012 and 2014, National Academy of Sciences of the United States and American Chemical Society, respectively.

Johnson, Olsen and coworkers also developed a modified rate theory to describe both the topology of polymer networks and the kinetics of network formation.³⁷⁶ For networks prepared by end-linking of bifunctional PEG precursor and trifunctional junctions, they investigated all possible configurations containing two junctions (Fig. 15A). They illustrated that the fractions of primary and secondary loops depend on a dimensionless variable: cb³(M/m)^3/2, where c is the polymer concentration, b is the Kuhn length of monomer (1.1 nm for PEG), m is the molar mass of Kuhn monomer (137 g mol⁻¹), and M is the molar mass of bifunctional PEG precursors. Fig. 15B shows that the fraction of loops can be engineered by variation of the polymer concentration and precursor molar mass. Their model illustrated that the entire loop spectrum can be divided into three regions. In region 1, primary loops are dominant. In region 3, by contrast, primary loops are rare, dumbbell primary loops (short-range correlations) disappear, and tree structures dominate instead. The same theory is also able to predict the kinetics of loop formation in agreement with experimental NDS results, confirming again that the reaction time in the process of network formation is an important parameter to control different types of loop defect (Fig. 15C). Primary and secondary loops are accumulated smoothly as the conversion increases. The fraction of tree structures, however, shows a sharp increase at high conversion.

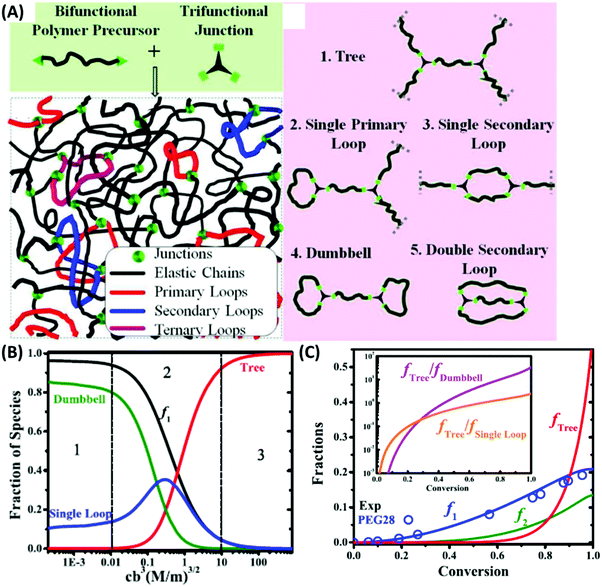Fig. 15 (A) All possible configurations containing two junctions in a network formed from A₂ and B₃ monomers. (B) Content of each configuration as a function of dimensionless parameter cb³(M/m)^3/2, where b and m are constants, c is the polymer concentration, and M is the molar mass of the A₂ (macro)monomer. (C) Content of each configuration as a function of the gelation conversion, which can be translated into the reaction time (kinetics). Reprinted from ref. 376; copyright 2016 American Physical Society.

Another strategy to control loop defects is through control of the kinetics of network formation. Gu, Johnson, and coworkers illustrated that in A₂ (bis-cyclooctyne) and B₄ (tetra-azide PEG), end-linked star polymer gel systems, if B₄ monomers are slowly added to the A₂ monomers, about 50% of 1° loops in comparison with batch-addition are depleted.³⁸¹ By measuring the fraction of 1° loops per binary reacted A₂ (φ_λ) using the NDS technique, they showed that φ_λ can be highly controlled by the B₄ addition rate. This reduction of defects is also confirmed by changing material properties. While at a specific concentration (1 mM), batch or fast semi-batch addition of B₄ cannot make solid gels, slow semi-batch addition leads to solid gels. The authors also investigated a mixed “slow then fast” approach in which 50% of the B₄ monomers is added slowly and another 50% is added in one portion to induce gelation. This method did not show further improvement in loop reduction, but was faster and more convenient in comparison to the slow, semi-batch addition.

4.4.3 Control of the network spatial inhomogeneity. As mentioned briefly before, end-linking is a classical approach to minimize structural heterogeneities and to prepare model networks.^344–346 End-linked networks formed via step-growth polymerization of A_x and B_f monomers feature a relatively homogenous structures, specifically when macromonomers with a narrow molar mass distribution are utilized. However, while the spatial distribution of strands and junctions in such networks is almost homogenous, formation of local topological defects such as loops, dangling chains, or double connection cannot be excluded. As an example, formation of loops considerably occurs if the polymer concentration is low.³⁴⁴ A strategy to prevent (or better saying: to minimize) such loop formation is to use monomers with heterocomplementary A- and B-type functional groups that selectively react with one other only, but not with their own kind. Based on that idea, in a seminal work, Sakai, Chung, and coworkers designed a network by reaction of two well-defined symmetrical tetrahedron-shaped PEG macromonomers of the same size (M_w = 10 g mol⁻¹), referred to as “terta-PEG network”.³⁸² One macromonomer had amine-terminated groups at each arm terminus, whereas the other macromonomer had succinimidyl glutarate, NHS, terminated arms. The mechanical properties (breaking stress and breaking strain in compression tests) of a hydrogel network formed from stoichiometric ratios of these two macromonomers were much stronger than those of conventional hydrogels. The authors found that the mechanical strength of this network highly depends on the polymer concentration in the hydrogel. At the overlap concentration, C* ≈ 60 mg mL⁻¹, and at its twofold 2C*, the mechanical properties show performance maxima, which is related to the formation of a homogenous and a pseudo double network structure, respectively. At concentrations below C*, between C* and 2C*, and above C*, by contrast, the mechanical properties are weaker due to the presence of defects such as dangling chains in the network structure. In their original work, Sakai and coworkers investigated the spatial inhomogeneity of these networks by dynamic light scattering. The scattering of light generally originates from the fluctuating components in a polymer-network sample as well as from its potential frozen-in spatial structural inhomogeneities introduced during the crosslinking. The latter was found to be very low in the tetra-PEG networks, with about 100% of optical transmittance, which confirms the exquisite network homogeneity. In particular, a minimum of that scattering contribution was observed at C*, which suggests a particularly homogenous structure at that concentration (Fig. 16A). Further studies on these networks and gels by small angle neutron scattering and static light scattering confirmed the lack of spatial inhomogeneity even in equilibrium swollen states.^383,384 This nearly perfect model-network structure in tetra-PEG systems can therefore be considered as a reference state in the attempt of rational engineering of defects in polymer networks.

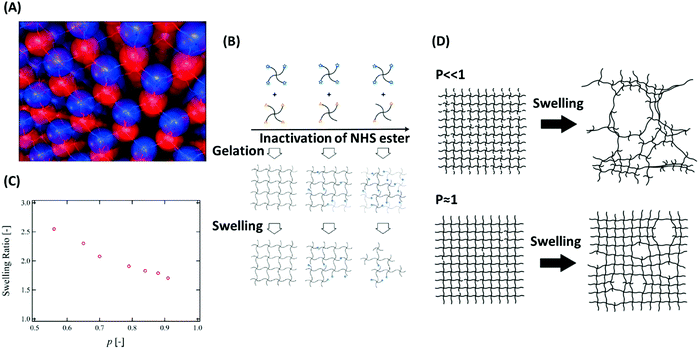Fig. 16 (A) Schematic of the diamond-like model network structure in tetra-PEG gels formed at the overlap concentration, C*. Red and blue spheres represent tetra-arm PEG with amine and succinimidyl glutarate terminated groups, respectively. (B) Experimental approach to tune the bond ratio, P, in tetra-PEG networks, resulting in (C) systematically varying swelling ratios for networks with different P. (D) The topological defects induced by a decreasing bond ratio significantly influence spatial inhomogeneities of the networks in equilibrium swollen states. Panels A and (B–D) are adopted from ref. 382 and 360, respectively. Copyright 2008 and 2014, American Chemical Society.

Later on, Lange, Saalwächter, and coworkers investigated the local microstructure of the tetra-PEG hydrogels introduced by Sakai through the use of proton multiple-quantum NMR at low magnetic field strength.³⁷³ They could identify well-separated defect fractions with distinct motional anisotropy and characterized them quantitatively due to the very homogenous structure of the tetra-PEG networks at larger scales (10–100 nm). The fraction of loops of different order was counted to be less than 1%. These researchers also measured the fraction of sol and dangling chains as a function of the macromonomer concentration, which was less than 5% when the concentration was equal to C*. Accordingly, the authors concluded that while such networks are very homogenous on length scales beyond the mesh size, their microstructure is still not quite ideal diamond-like. In the following, Shibayama and coworkers developed a computer simulation to investigate the mechanical properties of tetra-PEG gels at large deformation.³⁸⁵ To rationally unravel the relationships between structural inhomogeneity and mechanical properties, they introduced defects by randomly cutting the network chains and decreasing the bond ratio, P, from 1 to 0.4. With that approach, they found that as the defect fractions of the networks increase (by decreasing P), the stretching force decreases, whereby the Young's modulus has a strikingly linear dependency on P. Such a relationship was also observed between the gel modulus and the polymer concentration. Therefore, it can be concluded that defects in tetra-PEG gels can be controlled by variation of the macromonomer concentration. Later on, Shibayama and coworkers introduced an approach to experimentally tune the parameter P in tetra-PEG network systems.³⁶⁰ In that work, the number density of NHS groups was tuned by hydrolysis of the tetra-PEG-NHS precursor in water (Fig. 16B). The results of that study illustrated that the swelling ratio of the networks decreases by increase of the bond ratio due to the increase of the number of elastically effective chains (Fig. 16C). In addition, by studying networks in as-prepared and equilibrium swollen states with small angle neutron scattering, the authors concluded that extent of spatial inhomogeneities in the swollen state significantly depends on the local topological defects (such as dangling chains at low bond ratio) of the as-prepared gels (Fig. 16D).

4.4.4 Network–filler composites. Polymer (nano) composites have been widely studied in efforts to engineer materials with mechanical properties superior to those of the pure polymer.^386,387 The main mechanism of this enhancement is the wrapping of polymer chains around several filler particles/fibers that form a bridge structure.^386,388 It is proposed that at high nanoparticle loading, where the face-to-face distance of particles is comparable to the entanglement tube diameter of the neat polymer, nanoparticles are bridged by bound polymer segments. In such a particle-dominated network, the dynamics and mechanical properties are controlled by the nanoparticle content.³⁸⁷ Similar to linear or branched polymers, polymer networks like elastomers or hydrogels can be modified with this approach. There are numerous numbers of studies in which polymer networks are mixed with organic/inorganic fillers to form micro/nanocomposites to modify their properties and/or to induce new properties on them.^389–391 In elastomers, for example, micro-and nano fibers/particles like carbon nanotubes, graphenes, graphite derivatives, (nano) silica, (nano) metal particles, (nano) clay, or nano cellulose fibers and particles are utilized to modify their mechanical and thermal properties or to induce electrical conductivity.^392,393 Similarly, in hydrogels such modification is widely used to modify their commonly weak mechanical properties. In nature, many tissues like cartilage and cornea are fiber-reinforced gels with moduli of 10–1000 kPa.³⁹⁴ Developing synthetic hydrogels as cell scaffolding materials in soft tissue engineering highly depends on the improvement of their mechanical properties. This is one of the main areas of research on hydrogel composites.^394–402 As one example, poly(2-acrylamido-2-methylpropane sulfonic acid)/poly(acryl amide) network reinforced by silica nanopartciles with vinyl end groups is a super-tough material with fracture strength of 73 MPa and fracture strain of 0.98. Such a hydrogel resembles the network structure of the extracellular matrix in biological tissues with water content more than 60%.⁴⁰⁰

Network composites, similar to their unfilled analogs, have different types of defects in their microstructure like inhomogeneities, dangling chains, and loops. In addition to these defects, aggregation of fillers may additionally cause new volume defects in the microstructure of the enforced polymer networks.⁴⁰³ Density and size of these filler aggregates depend on the individual interactions between the fillers as well as on the interaction between the fillers and the hosting network matrix.^388,404,405 This type of defect has been extensively studied, while apparently opposite influences on the mechanical properties have been reported in different studies. In a part of these studies, filler aggregation has been introduced to be responsible for the enhancement of the mechanical properties. In such composites, fillers that have high interfacial energies with their matrixes may make a very stiff network due to the filler percolation.⁴⁰⁴ Zhang and Archer studied the microstructure and rheology of nanocomposites formed by silica particles with chemically different surfaces. The results demonstrated that surface-modified nano silica particles with a low tendency of aggregation have a very low influence on the elastic plateau modulus of the matrix. However, nano silica particles without surface modification, which have a high likelihood of aggregation, have a significant effect on the elastic plateau modulus.³⁸⁸ A similar finding has been reported by Dorigato and coworkers.⁴⁰⁶ Genix and coworkers controlled the aggregate size by variation of the grafting density in elastomer nanocomposites of styrene–butadiene rubber and silica nanocomposites.^407,408 Dynamic mechanical analysis results revealed that by increasing the grafting density of the elastomer chains on the silica nanoparticles, and with that by decreasing the size of the aggregates, the plateau modulus decreases if the nanoparticle content is above the percolation volume. Based on broadband dielectric spectroscopy and rheology, the authors proposed that by grafting of polymer chains on the nanoparticles, depercolation of aggregates occurs. Therefore, at a given nanoparticle volume fraction, a sample without grafting chains has a more percolated behavior (such as higher plateau modulus) than a sample with grafting chains.⁴⁰⁸ In opposite, it is also reported that the poor adhesion between fillers and networks, which is a driving force for aggregation, causes failure at the filler–network interface, and with that weakens the mechanical properties.⁴⁰⁹ As an example, nanocomposites formed by surface-modified carbon nanotubes with high compatibility with the matrix reveal higher enhanced mechanical properties compared to nanocomposites based on non-surface modified nanotubes with low compatibility with the matrix.⁴¹⁰ In the latter, upon strain failure, nanotubes are pulled out of the matrix instead of being broken. As highlighted precisely by Pukanszky, aggregation may have a reinforcing effect, but they act as failure interaction sites.⁴¹¹

In addition to forming aggregates, (nano)fillers also have influence on the density of other types of defects like dangling chains, loops, and spatial inhomogeneity. It has been shown that during the synthesis of polymer networks in the presence of silica particles, radical polymerization is inhibited.⁴¹² This may increase the extent of defects such as dangling chains in the vicinity of the fillers.⁴¹³ For example, in poly(ethylene glycole) hydrogels modified with poly(lactic-co-glycolic acid) particles, the viability of encapsulated liver-derived cells is improved compared to a plain hydrogel without particles.⁴¹⁴ This enhanced viability has been attributed to the numerous network defects in the vicinity of the fillers, which increases the permeability of necessary solutes. Yanagioka and Frank proposed that in hydrogel composites, there are zones with increased defect concentration in the vicinity of nanoparticles. The authors studied poly(NIPAAm) hydrogels filled with silica nanoparticles. Investigation of the lower critical solution temperature of these hydrogels and comparison of them with their unfilled analogs demonstrated that the filled ones have faster kinetics of shrinking due to the heterogeneous structure introduced by the particles. The shrinkage content of the hydrogels as a function of the volume percentage of particles revealed a percolation volume, which is about 1/20 of the expected percolation volume for spherical particles. The authors proposed that defects in these hydrogel composites are large enough to be interconnected with each other such that they form a percolated passway for water diffusion.⁴¹³ Fillers can also affect the homogeneity of crosslinking junctions in polymer networks. Chazeau, Chenal and coworkers demonstrated that in elastomer composites of natural rubber and zinc oxide, aggregates of fillers are surrounded with a high crosslinked phase, which in turn promotes spatial inhomogeneity.⁴¹⁵ In opposite to this hypothesis, it was also proposed that the presence of (nano) fillers reduces the density of defects like loops. In hydrogel composites formed from a physical association network based on poly(lactic acid)–poly(ethylene oxide)–poly(lactic acid) reinforced with nanoclay, small-angle neutron scattering studies confirmed adsorption of the midblock on the nanoclay. This adsorption forms new junctions between the polymer chains, which is responsible for an enhanced elasticity. By this strategy, some of the poly(ethylene oxide) loops become elastically effective chains in the networks, which may be considered as a kind of defect engineering in these network materials. For poly(acrylic acid) hydrogels reinforced with cellulose nanocrystals, it has been proposed that grafting of poly(acrylic acid) chains onto the surface of the cellulose nanocrystals promotes the formation of mutual entanglements, which increases the formation of cross-linked chains and conversion of loops and dangling chains to bridging chains.⁴¹⁶ Recalling the examples of Section 4.4.2 revealing the possibility of controlling loops by controlling the kinetics of network formation, it should be noted that this method is not necessarily valid in network-filled nanocomposites. Recently, it is reported that in elastomer nanocomposites based on styrene–butadiene rubber and nanosilica, variation of the vulcanization kinetics through the use of different amounts of vulcanization agents does not change the network architecture. In this study, elastomer nanocomposites with identical contents of nanosilica, but prepared by different vulcanization kinetics, demonstrated almost identical mechanical properties at low and intermediate strain, which could reflect their similar defect content.⁴¹⁷

4.4.5 Summary of defect engineering in polymer networks. The review of references of this section illustrates that especially the mechanical properties of polymer networks are significantly affected by defects. These defects can be characterized and quantified by different methods such light/X-ray/neutron scattering, MQ-NMR, NDS, and dynamic mechanical analysis or rheology. Engineering of defects in polymer network can be achieved mainly by (i) controlling the chemistry and mechanism of the gelation reaction, (ii) molecular architecture and molar mass of the (macro) monomers, (iii) concentration of (macro)monomers, and (iv) kinetics of the gelation reaction. Moreover, in network composites, defects can be engineered via the interaction of fillers and networks as well as the filler content.

5. Self-assembled amphiphiles, proteins, block copolymers and supramolecular polymers

5.1 Defects in self-assembled molecular amphiphiles

Amphiphiles are molecules that contain both hydrophilic and hydrophobic parts. The main feature of this class of materials is the ability for self-assembly in water or even non-polar solvents. Amphiphiles are very important in biology, since the self-assembly of phospholipids (as a class of amphiphilic molecules) in water can form bilayers, which resemble the unit structure of biomembranes.^418,419

As mentioned in Section 2, dispersion of amphiphiles in polar or non-polar solvents can form lytropic liquid crystals. In water, for example, hydrophilic head groups shield hydrophobic tails from the surrounding medium, which directs the self-assembly process. At low concentration, the self-assembly of amphiphiles in water leads to micelles or vesicles without orientational or positional ordering (Fig. 17A). At higher concentration, different types of lytropic liquid crystals such as cubic, hexagonal, or lamellar mesophases can be formed. The type of mesophase formed by the self-assembly of amphiphiles is defined by their molecular geometry, assessed by a packing parameter, along with concentration and/or temperature. A lamella lytropic LC consists of a planar arrangement of amphiphilic molecules, in which a bilayer structure is formed by separation of non-polar chains from polar head groups and the placement of water between the bilayer units (Fig. 17A).

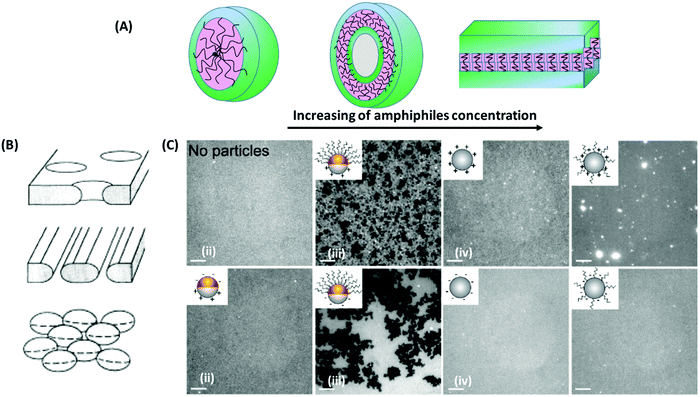Fig. 17 (A) Examples of different structures formed by the self-assembly of amphiphilic molecules in water. From left to right: micelle, vesicle, and lamellar phase. (B) The proposed defect structures in bilayers, from top to down: bilayers perforated by pores, bilayers with slits and ribbon-like aggregates, and bilayers fragmented into discrete discoidal micelles. (C) Fluorescence images showing the morphology of lipid bilayers after interaction with different types of nanoparticles. Top row: (i) a bilayer without particles, and bilayers interacted with (ii) Janus cationic/hydrophobic, (iii) uniform cationic, and (iv) uniform cationic/hydrophobic nanoparticles. Bottom row: bilayers interacted with (i) dipolar, (ii) Janus anionic/hydrophobic, (iii) uniform anionic, and (iv) uniform anionic/hydrophobic nanoparticles. The concentration of the cationic and dipolar particles is 40 pM. The concentration of the anionic particles is 150 pM. The scale bars represent 10 μm. Panel A is adapted from ref. 419; copyright 2015 Hindawi Publishing Corporation. Panels B and C are reprinted from ref. 422 and 428, respectively. Copyright 1993 and 2018, American Physical Society and American Chemical Society, respectively.

Instead of continuous, homogenous structures, the described bilayers contain defects, leading to three main types of microstructures: bilayers perforated by pores (aqueous pores as point defects), bilayers with slits and ribbon-like aggregates (aqueous slits or amphiphile ribbons as line defect), and bilayers fragmented into discrete discoidal micelles (micelles with smectic translational order containing point defects).^420–422 Since bilayers are fluid, these defects are continuously created and annihilated. The density and pattern of these lamellae defects depends on the bilayer–bilayer interaction and hence on the amphiphile concentration.⁴²⁰ Such intrinsic structural defects may affect the properties or functions of the lamellar mesophases. For biomembranes, as an example, pores crucially influence the permeation properties.⁴²³ Raghunathan and coworkers illustrated that pores and slit-type defects mediate a reversible transition between a lamellar mesophase and an isotropic phase in a specific range of amphiphile concentration and temperature.⁴²⁴ They studied an amphiphile/water system consisting of sodium dodecylsulphate and p-toluidine hydrochloride and found that when the total concentration of these two compounds in water is 30%, below 35 °C, a lamellar phase coexists with excess of solvent, entailing a sharp peak in the small angle X-ray scattering pattern. By heating to 90 °C, this pattern changes such to confirm the transition to an isotropic phase. By decreasing the temperature back, the isotropic phase re-transits to the previous mesophase structure.

Besides intrinsic defects, the addition of nanoparticles into a lipid bilayer can induce disruption and defects. Due to the importance of nanoparticles in developing biomedical applications such as drug delivery, gene therapy, cell imaging, or nanomedicine, this topic has been widely studied in last twenty years.^{423,425–435} Banaszak Holl and coworkers investigated a wide variety of cationic nanoparticles including bio-, polymeric-, and inorganic-types in combination with lipid bilayers and found that all these nanoparticles can induce disruption, including the formation of holes, membrane thinning, and/or membrane erosion.⁴²⁶ Considering the interactions between nanoparticles and lipid bilayers, they divided nanoparticles into three groups: (i) particles that aggregates around pre-existing defects without effective ability to induce new defects, (ii) particles that diffuse to existing defects and therefore expand them, and (iii) particles that are capable to directly induce defects in lipid bilayer membranes. From these results, it can be indirectly concluded that the defects in a nanoparticle/lipid bilayers system can be engineered by the type of nanoparticles. In another work, Brozik and coworkers illustrated that in a series of nanoparticle/lipid bilayer system consisting of a mixture of cationic and zwitterionic lipids and negatively charged nanoparticles or quantum dots, deposition of nanoparticles and disruption are highly controlled by the molar ratio of the cationic lipid.⁴²⁷ More recently, Lee, Yu and coworkers studied the disruption of biomembranes in presence of amphiphilic “two-faced” Janus nanoparticles.^428–430 They found that these particles can induce defects (holes) in zwitterionic lipid bilayers even at picomolar concentration. However, particles coated uniformly with hydrophobic and/or charged molecules do not show such defect formation (Fig. 17B). These results illustrate that defect formation can be engineered with the type of amphiphilic Janus particles (cationic/hydrophobic or anionic/hydrophobic), concentration of the particles, and fraction of hydrophobic part. Regards to the latter, the authors showed that cationic/hydrophobic amphiphilic nanoparticles form defects if the fraction of the hydrophobic part is above 20%. Above this threshold, the resulting defect density can be controlled by this parameter.⁴³⁰

As a short conclusion on defects in amphiphilic bilayer biomembrane/nanoparticle systems, the formation as well as the engineering of defects are highly versatile by controlling different parameters such as the chemistry of the bilayers and nanoparticles as well as the topology or concentration of the nanoparticles. Such engineering is a promising approach to tune the properties and functions of biomembranes.^423,435

5.2 Defects in self-assembled proteins

Self-assembly is a process by which an organized structure (spontaneously) forms from simple parts, usually mediated by noncovalent interactions.^436,437 The concept of self-assembly is highly interconnected with supramolecular chemistry, which refers to ordered molecular aggregates that are held together by noncovalent binding.^438–440 The term of supramolecular chemistry was introduced in 1987 by Jean-Marie Lehn who shared the Nobel prize in chemistry in 1987 with Charles J. Pedersen and Donald J. Cram for fundamental research on the chemical basis of molecular recognition.⁴⁴¹

The process of self-assembly, generally, depends on five characteristics of a system:⁴³⁷ (i) components, which are the groups of molecules or macromolecules that interact with one another, (ii) interactions, which are generally weak and noncovalent (such as Coulomb interactions, hydrophobic interactions, and hydrogen bonds), (iii) reversibility of the association, (iv) potential interactions between the components and their environment, and (v) sufficient mobility of the components to find each other. The components may have a broad range of size, among them the molecular scale, the nanoscale, and meso to macroscopic scales.⁴⁴² The formation of molecular crystals,⁴⁴³ colloidal aggregates,⁴⁴⁴ lipid bilayers,⁴⁴⁵ phase separated polymer structures (like block copolymer phases),⁴⁴⁶ and self-assembled monolayers⁴⁴⁷ as well as the folding of polypeptide chains into proteins⁴⁴⁸ or the folding of nucleic acids into their functional forms⁴⁴⁹ are examples of molecular self-assembly in synthetic and natural molecular systems.

Different types of defects may form during self-assembly processes in different systems. In folding of proteins, conflicting interactions, or frustration, can be considered as a class of defects. These defects determine how fast biomolecules can explore their configurational landscape. As a result, the speed and the mechanism of protein folding are strongly affected by the protein native structure and the density of frustrations.⁴⁵⁰ Clementi and coworkers proposed a model that demonstrates that there is a range of frustration (defect density) that lowers the barrier to fold proteins. In addition, the impact of frustration defects induced by nonnative heterogeneity on protein folding systematically depends on the native state size and topology. If a protein has a large enough absolute contact order (average sequence separation between native contacts), the influence of frustration on the protein topology is negligible. The suggested interplay between nonnative interactions and protein topology can explain the misfolding behavior of α and β proteins of similar size.⁴⁵⁰

Another type of defect in the self-assembly process of biological systems is the oppositely charged disclination. These defects have been reported in the hierarchical self-assembly of microtubular bundles. At high enough concentration, microtubules form percolated active networks. If these networks are confined within emulsion droplets, the networks adsorb onto the droplet surfaces and form active 2D nematic liquid crystals with disclination defects of charge +1/2 or −1/2.⁴⁵¹

In addition, geometrical frustration can be considered as a defect in the self-assembly of biological systems. Geometrical frustration refers to the incompatibility of local interactions with global geometric constraints, making the propagation of uniform and strain-free order impossible.⁴⁵² These defects play a crucial role in the self-assembly and aggregation of proteins or (in general) particles into fibers. Generally, in contrast to identical cubes, which can pack into dense space-filling aggregates, the aggregation of particles with other shapes tends to be frustrated.^453,454 In proteins, for example, deformed or partially denatured domains, juxtaposition of residues with unfavorable interactions, or sterically hindered hydrogen bonding can induce frustration. Due to such frustrations, the global morphology is defined by the competition between geometrical constraints, which hinders the formation of compact aggregates, and the overall attractive interactions of (protein) particles.⁴⁵⁵ This concept can be applied to understand phenomena like yeast inheritable phenotype or sickle cell hemoglobin polymerization, which are important in the sense of medical applications.^456,457

Another category of self-assembly defects can be found in highly symmetric protein nanoshells, which exist in many biological systems such as viral capsids and clathrin vesicles. Similar to shells that are constructed of spheres, these structures have icosahedral symmetry (Fig. 18A–C),⁴⁵⁸ where triangle subunits (protein trimers or triskelion molecules) self-assemble to form hexameric or pentameric units (Fig. 18D). The choice between forming a pentamer and a hexamer is based on what leads to a lower energy per triangle subunit in the growing shell. Further self-assembly of hexameric units forms a flat layer, whereas formation of a closed shell requires the inclusion of 12 defects with a local fivefold rotational symmetry (Fig. 18E).^458–461 With that, spherical capsids with different sizes can form from 12 pentamer units, so-called pentons, separated by different numbers of hexameric units, so-called hexons (Fig. 18F).⁴⁶⁰

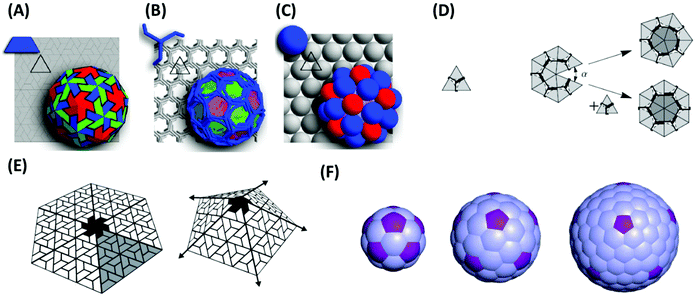Fig. 18 Scheme of (A) a viral capsid, (B) a clathrin vesicle, and (C) a shell constructed of spheres. These shells have similar symmetry (solid triangle). (D) To grow a shell, equilateral triangle subunits bond together. Two unbound edges can either bind to form a pentamer or an additional subunit can be added to form a hexamer. (E) The assembly of the hexamer units forms a flat layer, whereas the presence of pentamer units forces this layer to fold. Formation a closed shell requires 12 pentamers in the hexamer layer. (F) In symmetric closed shells, the position of these pentamers in respect to each other is precise. By increasing the numbers of the hexamer units, the size of the closed shell increases. Panels (A–D), E and F are reprinted from ref. 458, 459 and 460, respectively. Copyright 2015, 2010 and 2014, Biophysical Society, Public Library of Science, and Royal Society of Chemistry, respectively.

In biology, control over the self-assembly of supramolecular structures is crucial for living cells.⁴⁵⁵ In this view, engineering the defects that are formed in self-assembly processes is a key point to control the microstructure, and with that, the properties of biological systems. As an example, in the self-assembly of protein building blocks, the final architecture highly depends on the density of geometrical frustrations. In a model developed by Lenz and Witten, the final morphology of the architecture can be engineered by control of the frustration of the protein building blocks via their rigidity.⁴⁵⁵ In this model, to explore the competition between geometrical frustration and overall attraction of the building blocks, aggregations formed by two-dimensional, deformable polygons are considered. These polygon building blocks can be regular or irregular. Aggregations form by connecting multiple polygons via the joining of one or several of their sides. Side joining occurs when the surface tension of the corresponding sides is higher than zero. In the limit of rigid blocks, the assemblies form tree-shaped, branched polymers with a large fraction of unbound edges. By contrast, floppy blocks can deform into compatible shapes that assemble without bound in any dimension. At the boundary of these two regimes, self-assembly of blocks with intermediate rigidity forms fiber-like morphologies.⁴⁵²

5.3 Defects in the self-assembly of block copolymers

Self-assembly of block copolymers provides a particularly versatile strategy for fabricating dense, ordered structures on the scale of nanometers;^462,463 this is because there are universal rules for pattern formation in these systems, whereby the specificity of a given copolymer type at hand determines the specific set of parameters that controls this. In the case of AB diblock copolymers, this process may form ordered structures such as lamellar, hexagonally arranged cylindrical, body-centered-cubic spherical, or gyroid phases in the bulk, depending on the volume fraction of the A and B blocks (Fig. 19A). However, single-crystalline periodic microphases do typically not form by spontaneous self-assembly, instead, a rich variety of defects such as disclination, dislocation, and grain boundaries are observed that results in the formation of polycrystalline morphologies.^464–466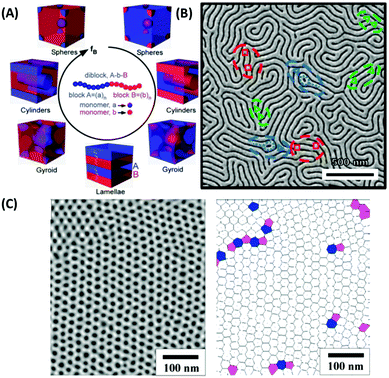

Fig. 19 (A) Morphologies of an AB diblock copolymer system. The microstructure depends on the volume fraction of the blocks A and B. Upon increase of the volume fraction of one block, the morphology of block copolymers generally changes from cubic-packed spheres to hexagonally packed cylinders, bicontinuous cubic networks (gyroids), and finally to lamellar sheets (see the guiding curved arrow). The exact volume fraction range in which a specified morphology is formed depends on the chemical dissimilarity of the blocks, as assessed by the Flory interaction parameter. (B) Defect structures in the self-assembly of a lamellar-forming symmetric copolymer in thin film. The red dashed circles with square markers inside highlight pairs of oppositely charged dislocations. The green dashed circles with triangle markers inside denote domains formed by same charged dislocations. The blue circles indicate disclination defects. (C) The left image shows a 2D hexagonal array of cylinder cores of a poly(cyclohexylethylene-b-styrene-b-cyclohexylethylene) film. The right diagram is constructed from the array of cylinder core centroid from the left image. Five- and sevenfold polygon disclinations are shown by magenta and blue color, respectively. Panel A is reprinted from ref. 466; copyright 2014 Royal Society of Chemistry. Panels B, and C are adopted from ref. 467, and 468, respectively. Copyright 2013 and 2009, American Chemical Society.

When the self-assembled block copolymers form lamellae, the ordered patterns have the same symmetry than smectic liquid crystals in the smectic A phase. Therefore, the same types of topological defects emerge, i.e., dislocations and disclinations, which are associated with bending and distortions of the domains. Two dimensional smectic structures are also observed in single-layer-thick films of asymmetric cylinder-forming block copolymers with surface interactions that are selective for the majority block, such that the cylinders align parallel to the surface (Fig. 19B). On the other hand, confinement of ultrathin cylinder-forming block copolymers or single-layer-thick films of sphere-forming block copolymers leads to the assembly of 2D hexagonal structures. These structures exhibit defects composed of dislocations and disclinations similar to 2D triangular colloidal crystals (Fig. 10A and 19C). The disclinations take the form of domains with five and seven nearest neighbors rather than the normal 6-fold coordination.^{464,467–469} For the gyroid morphology, the interface between the domains is not gyroidal, and therefore grain boundary defects form between gyroid domains. In addition, inside the domains, there are topological defects such as dislocations corresponding to the termination of a plane of unit cells.⁴⁷⁰ Furthermore, regards to the network-like structure of this morphology, defects such as node functionality and loops have been identified for poly(styrene-b-dimethylsiloxane) copolymers.⁴⁷¹

5.3.1 Defect engineering in block-copolymer self-assembly. A common approach to controlling defects in block copolymer self-assembly is to direct it by external fields such as electric fields, shear flow, and chemical guiding patterns on a supporting substrate of a thin film (like guiding lines that attract one component of the block copolymer) or geometric substrate features (like grooves)^472–477 Often, the target of such a directed self-assembly is actually to minimize the defect density, and even the fabrication of defect-free structure. Another target of this approach is the formation of device-oriented, irregular or periodic structures.⁴⁷⁸ In the pursuit of these goals, directed self-assembly of block copolymers has been widely studied in the last twenty years and extensively reviewed.^{464–466,479,480} To illustrate this approach, we focus here on two examples. In one of them, Nealey and coworkers studied the directed self-assembly of a symmetric poly(styrene-b-methyl methacrylate), Ps-b-PMMA, by using a series of chemical patterned substrates (Fig. 20A).⁴⁸¹ Considering the line width, W, the bulk period of the block copolymer, L₀, and the period of the guiding line, L_s, they set the dimension of the patterns to W ∼ 0.5–1L₀ when L_s = 2L₀ and W ∼0.5–1.5L₀ when L_s = 4L₀. They utilized a thin film of crosslinked PS or PMMA followed by a lithographic etching patterning process. The remaining crosslinked PS/PMMA constitutes the guiding lines of the chemical patterns. Then, they covered both guiding lines and interspacial regions by (PS-r-PMMA)-OH random copolymer brushes. The chemistry of the patterns was controllable by change of the PS content in the PS-r-PMMA. Analysis of the directed self-assembly of PS-b-PMMA on these substrates by scanning electron microscopy illustrated that the pattern of self-assembly can be controlled via changing the chemistry of the substrate. When crosslinked PS is used to make guiding stripes, the area fraction of assembly defects and the misalignment of the PS-b-PMMA domains increase as the content of PS increases from 43% to 73%. In the case of 73%, the alignment of the block copolymers is equivalent to self-assembled PS-b-PMMA on a homogenous, non-preferential surface. The authors illustrated that the obtained self-assembly patterns depend also on the ratio of W/L₀. In another work, Nealey and coworkers illustrated that directed self-assembly of a ternary blend of a symmetric PS-b-PMMA copolymer and PS as well as PMMA homopolymers on a silicon substrate grafted by PS forms patterns of line segments and nested arrays of lines with sharp bends (Fig. 20B).⁴⁸² The PS brush was coated with a thin film of a photoresist that can be patterned with roughly equal lines and spaces (periodic distance between 50 and 92 nm, and bend angles from 45° to 135°) using advanced lithography. On homogenous neutral wetting surfaces, the blend forms a lamellar phase with a period, L_B, of 70 nm. The self-assembly on described substrates with striped chemical nanopatterns, however, is different and highly depends on the surface period, L_S. In addition, the authors investigated the self-assembly of nested arrays of lines with different bend geometries. Their results showed that when the substrate is patterned by bending lines with an angle of 45°, the ternary blend forms defect-free lamellae on a surface pattern with 60 < L_S <85 nm. By increasing the angle, the range of L_S in which the formation of defect-free lamellae is possible, gets smaller.

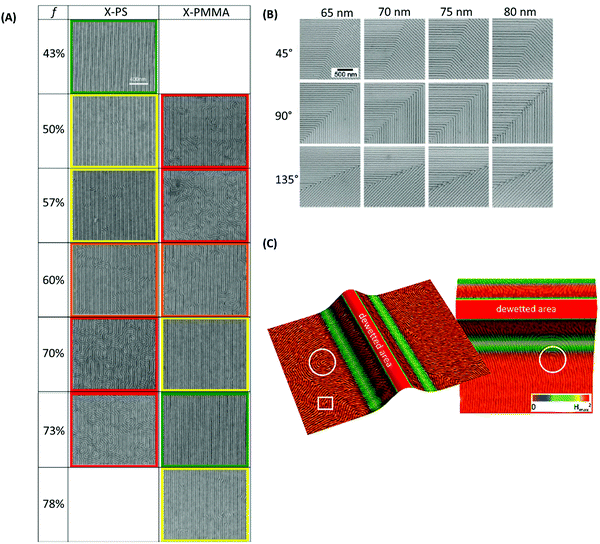Fig. 20 (A) Directed self-assembly of a symmetric PS-b-PMMA copolymer thin film on chemical patterns with guiding stripes composed of crosslinked PS or PMMA. The substrate is coated with a brush random copolymer of PS and PMMA. The PS content in this brush is varied systematically to control the self-assembly of PS-b-PMMA. The color of the border indicates density of defects (green: no defects, yellow: few defects, orang and red: many defects). (B) Directed self-assembly of a ternary blend of a PS-b-PMMA copolymer and PS as well as PMMA homopolymers on a chemical surface patterned with periodic lines at distances of 65, 70, and 80 nm and angles of 45°, 90°, and 135°. (C) AFM phase-height images of a cylinder-forming PS-b-PEP block copolymer film on a curved substrate after thermal annealing at T = 373 K for 90 min (left) and 3.5 h (right). Rectangles and circles indicate selected dislocations and disclinations with strength w = 1/2, respectively. Panels A, B, and C are reprinted from ref. 481, 482 and 484, respectively. Copyright 2013, 2005, and 2018, American Chemical Society, American Association for the Advancement of Science, and American Physical Society, respectively.

In block copolymer films and membranes, the alignment of patterns and the defect formation can also be controlled by curvature,⁴⁸³ similar to 2D liquid crystals and colloid. By depositing thin block copolymer films with smectic order onto a curved substrate and subsequent annealing, the orientation of the smectic patterns can be controlled and defects can be removed and/or confined to defined positions on the plane (Fig. 20C).⁴⁸⁴

In addition to the nature and the pattern of substrates, defects in block copolymer films can also be engineered by varying the film thickness and the molar mass of the copolymer. Stoykovich and coworkers studied these parameters in lamellar structures formed from PS-b-PMMA copolymers.⁴⁶⁷ Their results illustrated that an increase of the film thickness introduces new intermediate morphologies and may increase the driving force for defect annihilation and therefore may lead to a decrease of the defect density. On the other hand, the degree of polymerization determines the interfacial bending rigidity of the lamellar domains. Lower molar mass copolymers show higher defect annihilation, and with that, lower defect densities than higher molar mass copolymers. In addition, the blending of block copolymers with different molar masses and volume fractions of the blocks can be considered as a potential approach for the engineering of defects. Hashimoto and Yamaguchi have investigated the morphology of several mixtures of poly(styrene-b-isoprene) with different molar masses and volume fraction ratios.⁴⁸⁵ The authors have proposed a phase diagram predicting the morphology of the mixtures as a function of the mentioned parameters. The results reveal that with such an approach, a transition between different morphologies is possible.^485,486 Considering the potential of morphology transition upon mixing block copolymers, this method has the potential to be employed for control of the type and density of defects in block copolymers.

5.4 Defects in supramolecular polymers

Supramolecular polymers are produced from monomeric building blocks that self- or co-assemble based on specific, moderately strong and reversible non-covalent interactions.^487,488 A combination of hydrogen bonding, Coulomb and van der Waals forces, π–π stacking, as well as solvophobic shielding are critical to support sufficiently robust supramolecular interactions, which is particularly important for aqueous supramolecular polymers.⁴⁸⁹ This process results in high molecular weight linear polymers, even under dilute conditions, and exciting applications have been investigated for supramolecular polymers and supramolecular materials which incorporate mechanical, biological, or optoelectronic functionalities.⁴⁹⁰ Mechanistic investigations have revealed the need to differentiate between a thermodynamically controlled cooperative nucleation–elongation mechanism, a non-cooperative isodesmic self-assembly or ring-chain equilibria.⁴⁹¹ Kinetic investigations have received increased attention in recent years and revealed control over pathway selectivity.^492–494 This has led to the development of seed-induced living supramolecular polymerization, chain growth-type supramolecular polymerization, the preparation of supramolecular block copolymers and specific supramolecular polymer polymorphs.^495–497

It is clear that in order to design supramolecular polymers with similar control over polymer length, monomer sequence and random, alternating or blocked ordering, compared to the achievements in controlled covalent polymerization processes,⁴⁹⁸ it is imperative to control their intrinsic dynamics.⁴⁹⁹ Albertazzi and Meijer systematically investigated the exchange kinetics and pathways in one-dimensional (1D) supramolecular polymers using super-resolution microscopy.⁵⁰⁰ The fiber-like assemblies were based on an amphiphilic 1,3,5-benzenetricarboxamide (BTA) motif, which is well-known to from triple hydrogen bonded supramolecular polymers in dilute solution. To investigate the time-scale and mechanism of the dynamic exchange, the monomers were labeled with Cy3 and Cy5 dyes. By probing the monomer distribution using STORM imaging, the authors could quantitatively address the mechanism of BTA monomer exchange, and the findings did not support a fragmentation-fusion process or polymerization–depolymerization at the chain ends. Instead, the exchange was suggested to occur homogenously along the polymer backbone, a process which was rationalized by the presence of disordered domains inside the hydrogen-bonded ordered supramolecular polymers. In these disordered domains, the interactions between monomers were proposed to be weakened and, therefore, favor monomers to leave and enter the supramolecular polymer fiber. Pavan and coworkers have described these domains as hot spots and defects, prone to facilitate monomer exchange (Fig. 21).^499,501 In their theoretical approach, the authors used well-tempered metadynamics (WT-MetaD) simulations to investigate the monomer exchange in amphiphilic BTA supramolecular polymers at submolecular resolution. Several important findings resulted from the simulations, the exchange of monomers from the interior of the fibers is less frequent and an unfavorable event compared to exchange at the fiber surface. The monomers diffuse on the surface from one hot spot to another, demonstrating that structural defects are key for the dynamic properties of supramolecular polymers. In order to generalize their findings, the authors hypothesized that exchange in supramolecular structures originates from defects that are intrinsically dynamic, while increasingly strong supramolecular interactions or high structural perfection slows down exchange in the assemblies. As was also highlighted in the subchapters on liquid crystals, polymer networks, as well as colloidal, block copolymer and protein assemblies these structure-dynamics relationships are key for the design of soft matter materials, where defects control the dynamic properties of the end-product.

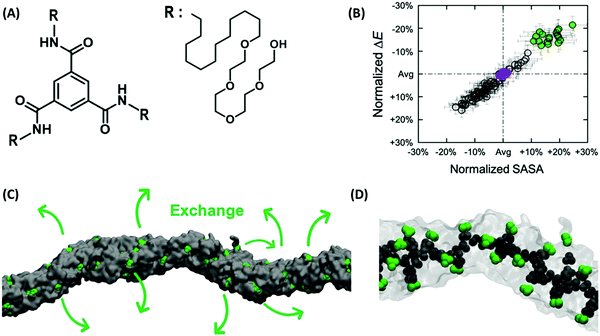Fig. 21 Defects in BTA supramolecular polymers. (A) Chemical structure of the amphiphilic BTA supramolecular monomer. (B) Heuristic analysis of the coarse-grained molecular dynamics (CG-MD) for supramolecular polymers: classification of monomers (black and green) based on their incorporation energy into the assembly (ΔE) and their solvent-accessible surface area (SASA). Exterior (C) and interior (D) snapshots of a section of the equilibrated supramolecular fiber from a CG-MD simulation; the fiber surface is colored in gray, whereas green spots (monomer cores) become visible. These are defects in the supramolecular stack, or “hot spots” from which monomer exchange. Adapted from ref. 501; copyright 2019 American Chemical Society.

In a collaborative effort, the Kudernac and Pavan groups investigated the role of defects in photoswitchable supramolecular tubules.⁵⁰² The molecular amphiphiles involved a V-shaped aromatic core in which two azobenzene photoswitches are incorporated, connected to branched hydrophilic oligoether chains.⁵⁰³ The planar trans form supports self-assembly into microtubular structures, whereas photoisomerization to the cis form disrupts planarity. The non-planar and bend cis form led to the accumulation of strain in the supramolecular tubules, and as a consequence catastrophic disassembly was observed. The suggested mechanism was further supported by all-atom,⁵⁰³ coarse-grained and WT-MetaD simulations.⁵⁰² The simulations further revealed that the trans-to-cis azobenzene isomerization is a rare event in a perfect tubular structure due to crowding effects in the assembly. Transitions become more probable/frequent in the direct proximity of an existing defect. As a result, the dynamic accumulation of the transitions under the exposure to light leads to the amplification of local defects, which promotes localized opening of the tubular structure, rather than homogeneous destabilization of the monomers along the tubes.

In the following, we further highlight examples where defects and defect engineering play a key role in tuning the properties of supramolecular polymers and materials with catalytic, electronic, and mechanical functionality. Note that similar to the previous sections for the other types of soft matter, environmental conditions, which can change the properties of supramolecular polymers,⁵⁰⁴ are excluded from being discussed as defects. In addition, we only include the engineering of molecular defects, and excluded the use of dynamic supramolecular or covalent bonds to provide energy dissipation in mechanical deformations or repair mechanisms of macroscopic defects, like cracks, notches, or other geometric discontinuities.^505–509

Conformational defects have further been investigated in the context of chirality amplification in helical 1D supramolecular polymers.⁵¹⁰ Amplification of chirality is generally referred to as the ability of a small chiral bias to fully control or dictate the helicity of polymers and assemblies,⁵¹¹ and was recently used to prepare functional helical nanostructures as asymmetric catalysts,⁵¹² or chiral stationary phases.⁵¹³

Giuseppone and coworkers have used supramolecular polymers in the gel-state to combine the electronic properties of organic materials exhibiting metallic behavior, with the mechanical properties of soft self-assembled systems.⁵¹⁴ The 1D fibres were obtained from columnar stacks of tris-amide triarylamines, which were oxidized to their radical cation by light or photodoping. These gave rise to charge-transport properties similar to metallic conducting conjugated polymers. The investigations revealed that structural defects, which are detrimental for conductivity, could be repaired due to the diffusion of so-called “supramolecular polarons” leading to an increase in the coherence length and improving conduction. The authors concluded that an optimal balance between order and mobility is able to produce functional materials with a unique combination of metallic character with soft mechanical and defect-healing properties.

Self-assembled trialkyl substituted BTAs have been used to prepare organic ferroelectric materials.⁵¹⁵ BTAs form well-ordered columns due to the threefold intermolecular hydrogen bonds.^516,517 In this structure, the carbonyl groups are able to align, whereby the individual dipole moments add up to macrodipoles along the columnar axis. The alignment of the supramolecular columns next to each other depends on the electrostatic interactions between these macrodipoles, steric restraints induced by peripheral groups that are linked to the benzene core via amides bonds, and van der Waals forces. The latter favor a dense packing of neighboring columns and induce hexagonal rod packing. However, in such a packing, the macrodipole interaction between neighboring columns becomes frustrated, since the simultaneous alignment of all dipoles in a desired direction is not possible.⁵¹⁸

The dislocation structures and examination of the defect morphologies could be used to determine elastic properties of columnar hexagonal mesophases made from amphiphilic dendritic molecules.^519,520 The hydrogen-bonded hexagonal columnar liquid crystalline phases formed by BTA derivatives can be aligned uniformly by an electric field and display switching behavior with a high remnant polarization, as shown by the Sijbesma lab and collaborators.⁵¹⁵ As pointed out by the coauthors, the extrinsic switching of polarization is an inhomogeneous process that can be initiated by defects in the phase structure or small amounts of impurities. More recently Kemerink and coworkers developed an electrostatic model that was used as basis for 3D kinetic Monte Carlo simulations in order to describe switching kinetics in these ferroelectrics.⁵²¹ The authors found that in the case of spontaneous polarization reversal, nucleation occurs at defects, which are caused by disorder. In contrast, in the field-driven reversal, nucleation occurs at the electrodes. Thus, by reducing the disorder, the retention time can be drastically increased without affecting the coercive field, which provides access to the rational design and optimization of ferroelectric devices, for example for memory-type applications.

6. Conclusion

The microstructure of hard crystalline inorganic materials contains irregularities and inhomogeneities, known as defects, which strongly affect the physical and mechanical properties of this class of materials. Therefore, controlling these defects, known as defect engineering, is a stimulating approach to tailor material properties for designing functionality, most prominently semiconduction. The classical, most well-known example of such defect engineering is doping silicon with very small amounts of atoms from the next higher or lower neighboring groups of the periodic table (n- or p-doping, respectively) to induce extra negative or positive charges into the microstructure. More recently, similar tailoring of properties via defect engineering has also been applied in organic materials⁶⁶ such as graphene layers,^522,523 metal–organic frameworks,²⁹ and nanodiamonds.⁵⁶ In analogy to these hard materials, the microstructure of soft matter inherently contains different types of defects as well, which can be classified as doping defects, topological defects, and connectivity defects. However, rational engineering of these defects is not as prominent as in hard materials, although quite a number of breakthroughs have in fact been achieved, as reviewed in here. Despite these promising advances, though, the field is still in an early stage, and the workout of general functional principles for defects in soft matter such to then develop design principles for defect engineering in this realm is desirable. Furthermore, on top of the reviewed approaches, the exploitation of environmentally sensitive features of soft matter such as phase transition of thermo-responsive polymers in solution at lower or upper critical solution temperatures offers a significant potential to be utilized for reversible and switchable defect engineering, for example, to reversibly adjust the density or patterning of defects by temperature.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank Frank Giesselmann (Stuttgart) for giving valuable feedback upon pre-submission proofreading of this article. F. Schmid and K. Kremer acknowledge partial funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) in the context of the Collaborative Research Centre/Transregio TRR 146 (Project number 233630050). S. Seiffert acknowledges partial funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) in the context of the Research Unit FOR 2811 (Project number 423791428). The authors are grateful for financial support from CINEMA (Johannes Gutenberg-University of Mainz).

References

1. W. D. Callister, Materials science and engineering: an introduction, John Wiley, 2007, pp. 90–122.
2. E. Mittemeijer, Fundamentals of Materials Science, (The Crystal Imperfection; Lattice Defects), Springer, Berlin, Heidelberg, 2011.
3. W. Truszkowski, The plastic anisotropy in single crystals and polycrystalline metals, Springer, 2001.
4. L. Mezeix and D. J. Green, Comparison of the mechanical properties of single crystal and polycrystalline yttrium aluminum garnet, Int. J. Appl. Ceram. Technol., 2006, 3, 166–176.
5. H. Richter, M. Mai, F. Kirscht and P. Gaworzewski, Defect engineering as an important factor in developing VLSI substrates, Physica B+C, 1983, 116, 162–167.
6. G. Rozgonyi, A. Salih, Z. Radzimski, R. Kola, J. Honeycutt, K. Bean and K. Lindberg, Defect engineering for VLSI epitaxial silicon, J. Cryst. Growth, 1987, 85, 300–307.
7. J. Lagowski, GaAs versus Si-hopes, challenges and defect engineering, Acta Phys. Pol., A, 1990, 77, 311–322.
8. L. C. Kimerling, Defect Engineering, MRS. Bull., 1991, 16, 42–47.
9. P. Capper, Bulk Crystal Growth of Electronic, Optical and Optoelectronic Materials, John Wiley & Sons, 2005, vol. 14.
10. J. Singh, Electronic and optoelectronic properties of semiconductor structures, Cambridge University Press, 2007.
11. T. Fennell, P. Deen, A. Wildes, K. Schmalzl, D. Prabhakaran, A. Boothroyd, R. Aldus, D. McMorrow and S. Bramwell, Magnetic Coulomb phase in the spin ice HO₂Ti₂O₇, Science, 2009, 326, 415–417.
12. E. S. Božin, C. D. Malliakas, P. Souvatzis, T. Proffen, N. A. Spaldin, M. G. Kanatzidis and S. J. Billinge, Entropically stabilized local dipole formation in lead chalcogenides, Science, 2010, 330, 1660–1663.
13. G. Xu, Z. Zhong, Y. Bing, Z.-G. Ye and G. Shirane, Electric-field-induced redistribution of polar nano-regions in a relaxor ferroelectric, Nat. Mater., 2006, 5, 134.
14. T. Damhus; R. Hartshorn and A. Hutton Nomenclature of inorganic chemistry: IUPAC recommendations 2005, Chem. Int. 2005.
15. R. J. Tilley, Defects in solids, John Wiley & Sons, 2008, vol. 4.
16. M. Radu and K. Kremer, Enhanced crystal growth in binary Lennard-Jones mixtures, Phys. Rev. Lett., 2017, 118, 055702.
17. A. Rothschild, W. Menesklou, H. L. Tuller and E. Ivers-Tiffee, Electronic structure, defect chemistry, and transport properties of SrTi_1−xFe_xO_3−y solid solutions, Chem. Mater., 2006, 18, 3651–3659.
18. H. L. Tuller and S. R. Bishop, Point defects in oxides: tailoring materials through defect engineering, Annu. Rev. Mater. Res., 2011, 41, 369–398.
19. G. S. Pomrehn, A. Zevalkink, W. G. Zeier, A. Van De Walle and G. J. Snyder, Defect-Controlled Electronic Properties in AZn2Sb2 Zintl Phases, Angew. Chem., Int. Ed., 2014, 53, 3422–3426.
20. P. Axmann, C. Stinner, M. Wohlfahrt-Mehrens, A. Mauger, F. Gendron and C. Julien, Nonstoichiometric LiFePO₄: defects and related properties, Chem. Mater., 2009, 21, 1636–1644.
21. Y. Wang, K. Duncan, E. D. Wachsman and F. Ebrahimi, The effect of oxygen vacancy concentration on the elastic modulus of fluorite-structured oxides, Solid State Ionics, 2007, 178, 53–58.
22. K. L. Duncan, Y. Wang, S. R. Bishop, F. Ebrahimi and E. D. Wachsman, Role of point defects in the physical properties of fluorite oxides, J. Am. Ceram. Soc., 2006, 89, 3162–3166.
23. M. Morales, J. J. Roa, X. Capdevila, M. Segarra and S. Piñol, Mechanical properties at the nanometer scale of GDC and YSZ used as electrolytes for solid oxide fuel cells, Acta Mater, 2010, 58, 2504–2509.
24. R. Ameloot, F. Vermoortele, J. Hofkens, F. C. De Schryver, D. E. De Vos and M. B. Roeffaers, Three-dimensional visualization of defects formed during the synthesis of metal–organic frameworks: a fluorescence microscopy study, Angew. Chem., Int. Ed., 2013, 52, 401–405.
25. J.-S. Choi, W.-J. Son, J. Kim and W.-S. Ahn, Metal–organic framework MOF-5 prepared by microwave heating: factors to be considered, Microporous Mesoporous Mater., 2008, 116, 727–731.
26. H. Wu, Y. S. Chua, V. Krungleviciute, M. Tyagi, P. Chen, T. Yildirim and W. Zhou, Unusual and highly tunable missing-linker defects in zirconium metal–organic framework UiO-66 and their important effects on gas adsorption, J. Am. Chem. Soc., 2013, 135, 10525–10532.
27. R. Chakrabarty, P. S. Mukherjee and P. J. Stang, Supramolecular coordination: self-assembly of finite two-and three-dimensional ensembles, Chem. Rev., 2011, 111, 6810–6918.
28. U. Ravon, M. Savonnet, S. Aguado, M. E. Domine, E. Janneau and D. Farrusseng, Engineering of coordination polymers for shape selective alkylation of large aromatics and the role of defects, Microporous Mesoporous Mater., 2010, 129, 319–329.
29. Z. Fang, B. Bueken, D. E. De Vos and R. A. Fischer, Defect-Engineered Metal–Organic Frameworks, Angew. Chem., Int. Ed., 2015, 54, 7234–7254.
30. U. Ravon, M. E. Domine, C. Gaudillere, A. Desmartin-Chomel and D. Farrusseng, MOFs as acid catalysts with shape selectivity properties, New. J. Chem, 2008, 32, 937–940.
31. F. X. Llabrés i Xamena, F. García Cirujano and A. Corma Canós, An unexpected bifunctional acid base catalysis in IRMOF-3 for Knoevenagel condensation reactions, Microporous Mesoporous Mater., 2012, 157, 112–117.
32. L. T. Nguyen, K. K. Le, H. X. Truong and N. T. Phan, Metal–organic frameworks for catalysis: the Knoevenagel reaction using zeolite imidazolate framework ZIF-9 as an efficient heterogeneous catalyst, Catal. Sci. Technol., 2012, 2, 521–528.
33. M. Feyand, E. Mugnaioli, F. Vermoortele, B. Bueken, J. M. Dieterich, T. Reimer, U. Kolb, D. De Vos and N. Stock, Automated Diffraction Tomography for the Structure Elucidation of Twinned, Sub-micrometer Crystals of a Highly Porous, Catalytically Active Bismuth Metal–Organic Framework, Angew. Chem., Int. Ed., 2012, 51, 10373–10376.
34. F. Vermoortele, R. Ameloot, L. Alaerts, R. Matthessen, B. Carlier, E. V. R. Fernandez, J. Gascon, F. Kapteijn and D. E. De Vos, Tuning the catalytic performance of metal–organic frameworks in fine chemistry by active site engineering, J. Mater. Chem., 2012, 22, 10313–10321.
35. S. Yang, X. Lin, W. Lewis, M. Suyetin, E. Bichoutskaia, J. E. Parker, C. C. Tang, D. R. Allan, P. J. Rizkallah and P. Hubberstey, A partially interpenetrated metal–organic framework for selective hysteretic sorption of carbon dioxide, Nat. Mater., 2012, 11, 710.
36. J. Park, Z. U. Wang, L.-B. Sun, Y.-P. Chen and H.-C. Zhou, Introduction of functionalized mesopores to metal–organic frameworks via metal–ligand–fragment coassembly, J. Am. Chem. Soc., 2012, 134, 20110–20116.
37. K. M. Choi, H. J. Jeon, J. K. Kang and O. M. Yaghi, Heterogeneity within order in crystals of a porous metal–organic framework, J. Am. Chem. Soc., 2011, 133, 11920–11923.
38. O. Kozachuk, I. Luz, F. X. Llabres i Xamena, H. Noei, M. Kauer, H. B. Albada, E. D. Bloch, B. Marler, Y. Wang and M. Muhler, Multifunctional, defect-engineered metal–organic frameworks with ruthenium centers: sorption and catalytic properties, Angew. Chem., Int. Ed., 2014, 53, 7058–7062.
39. C.-S. Tsao, M.-S. Yu, T.-Y. Chung, H.-C. Wu, C.-Y. Wang, K.-S. Chang and H.-L. Chen, Characterization of Pore Structure in Metal–Organic Framework by Small-Angle X-ray Scattering, J. Am. Chem. Soc., 2007, 129, 15997–16004.
40. C. L. Whittington, L. Wojtas and R. W. Larsen, Ruthenium(II) tris (2,2′-bipyridine)-templated zinc(II) 1,3,5-tris (4-carboxyphenyl) benzene metal organic frameworks: structural characterization and photophysical properties, Inorg. Chem., 2013, 53, 160–166.
41. Z. Fang, J. P. Dürholt, M. Kauer, W. Zhang, C. Lochenie, B. Jee, B. Albada, N. Metzler-Nolte, A. Pöppl and B. Weber, Structural complexity in metal–organic frameworks: Simultaneous modification of open metal sites and hierarchical porosity by systematic doping with defective linkers, J. Am. Chem. Soc., 2014, 136, 9627–9636.
42. L. Shen, S.-W. Yang, S. Xiang, T. Liu, B. Zhao, M.-F. Ng, J. R. Göettlicher, J. Yi, S. Li and L. Wang, Origin of long-range ferromagnetic ordering in metal–organic frameworks with antiferromagnetic dimeric-Cu(II) building units, J. Am. Chem. Soc., 2012, 134, 17286–17290.
43. J.-C. Charlier, X. Blase and S. Roche, Electronic and transport properties of nanotubes, Rev. Mod. Phys., 2007, 79, 677.
44. M. B. Nardelli, B. I. Yakobson and J. Bernholc, Mechanism of strain release in carbon nanotubes, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, R4277.
45. K. Suenaga, H. Wakabayashi, M. Koshino, Y. Sato, K. Urita and S. Iijima, Imaging active topological defects in carbon nanotubes, Nat. Nanotechnol, 2007, 2, 358.
46. Y. Lee, J. Han, I.-H. Lee and S. Im, Mobility of a 5|7 defect in carbon nanotubes, Nanotechnology, 2011, 22, 105707.
47. A. Allal, A. Lavernhe, B. Vergnes and G. Marin, Relationships between molecular structure and sharkskin defect for linear polymers, J. Non-Newtonian Fluid Mech, 2006, 134, 127–135.
48. L. Valentini, F. Mercuri, I. Armentano, C. Cantalini, S. Picozzi, L. Lozzi, S. Santucci, A. Sgamellotti and J. Kenny, Role of defects on the gas sensing properties of carbon nanotubes thin films: experiment and theory, Chem. Phys. Lett., 2004, 387, 356–361.
49. J. Kong, N. R. Franklin, C. Zhou, M. G. Chapline, S. Peng, K. Cho and H. Dai, Nanotube molecular wires as chemical sensors, Science, 2000, 287, 622–625.
50. X. Fang, J. Mao, E. Levin and K. Schmidt-Rohr, Nonaromatic core–shell structure of nanodiamond from solid-state NMR spectroscopy, J. Am. Chem. Soc., 2009, 131, 1426–1435.
51. M. Radtke, E. Bernardi, A. Slablab, R. Nelz and E. Neu, Nanoscale sensing based on nitrogen vacancy centers in single crystal diamond and nanodiamonds: achievements and challenges, Nano Futures, 2019, 3, 042004.
52. R. Schirhagl, K. Chang, M. Loretz and C. L. Degen, Nitrogen-vacancy centers in diamond: nanoscale sensors for physics and biology, Annu. Rev. Phys. Chem., 2014, 65, 83–105.
53. X. Chen and W. Zhang, Diamond nanostructures for drug delivery, bioimaging, and biosensing, Chem. Soc. Rev., 2017, 46, 734–760.
54. F. Dolde, M. W. Doherty, J. Michl, I. Jakobi, B. Naydenov, S. Pezzagna, J. Meijer, P. Neumann, F. Jelezko and N. B. Manson, Nanoscale detection of a single fundamental charge in ambient conditions using the NV-center in diamond, Phys. Rev. Lett., 2014, 112, 097603.
55. F. Dolde, H. Fedder, M. W. Doherty, T. Nöbauer, F. Rempp, G. Balasubramanian, T. Wolf, F. Reinhard, L. C. Hollenberg and F. Jelezko, Electric-field sensing using single diamond spins, Nat. Phys., 2011, 7, 459–463.
56. A. Ermakova, G. Pramanik, J.-M. Cai, G. Algara-Siller, U. Kaiser, T. Weil, Y.-K. Tzeng, H.-C. Chang, L. McGuinness and M. B. Plenio, Detection of a Few Metallo-Protein Molecules Using Color Centers in Nanodiamonds, Nano. Lett., 2013, 13, 3305–3309.
57. P. G. de Gennes, Soft Matter (Nobel lecture), Angew. Chem., Int. Ed. Engl., 1992, 31, 842–845.
58. T. A. Witten, Insights from soft condensed matter, Rev. Mod. Phys., 1999, 71, S367.
59. H. Löwen; M. Watzlawek; C. Likos; M. Schmidt; A. Jusufi; J. Dzubiella; C. von Ferber; E. Allahyarov; A. Thünemann and I. D'Amico, The hard physics of soft matter. Advances in Solid State Physics, Springer, 2000, pp. 809–817.
60. I. Hamley, Introduction to Soft Matter-Revised Edition, Wiley Online Library, 2007.
61. G. Gompper, J. K. Dhont and D. Richter, Editorial [24pt] A unified view of soft matter systems?, Eur. Phys. J. E., 2008, 26, 1–2.
62. S. Zhang, S. Ali, H. Ma, L. Zhang, Z. Wu, D. Wu and T. S. Hu, Preparation of Poly(bis(phenoxy) phosphazene) and 31P NMR Analysis of Its Structural Defects under Various Synthesis Conditions, J. Phys. Chem. B, 2016, 120, 11307–11316.
63. E. Q. Chen, G. Xue, S. Jin, S. W. Lee, I. Mann, B. S. Moon, F. W. Harris and S. Z. Cheng, Defect orientation on the chain folded surfaces of two-arm poly(ethylene oxide) lamellar crystals, Macromol. Rapid Commun., 1999, 20, 431–434.
64. A. Tintaru, R. Ungaro, X. Liu, C. Chen, L. Giordano, L. Peng and L. Charles, Structural characterization of new defective molecules in poly(amidoamide) dendrimers by combining mass spectrometry and nuclear magnetic resonance, Anal. Chim. Acta, 2015, 853, 451–459.
65. D. C. Martin and C. Viney, Defects in polymers, MRS. Bull., 1995, 20, 13–17.
66. K. Müllen, Molecular Defects in Organic Materials, Nat. Rev. Mater., 2016, 1, 15013.
67. Y. Golitsyn, M. Pulst, J. Kressler and D. Reichert, Molecular Dynamics in the Crystalline Regions of Poly(ethylene oxide) Containing a Well-Defined Point Defect in the Middle of the Polymer Chain, J. Phys. Chem. B, 2017, 121, 4620–4630.
68. M. Kleman and O. D. Laverntovich, Soft matter physics: an introduction, Springer Science & Business Media, 2007.
69. P.-G. De Gennes and J. Prost, The physics of liquid crystals, Oxford University Press, 1993, vol. 83.
70. P. Pieranski, Colloidal crystals, Contemporary Physics, 1983, 24, 25–73.
71. H. Staudinger, Über polymerisation, Berichte der deutschen chemischen Gesellschaft (A and B Series), 1920, 53, 1073–1085.
72. H. Frey and T. Johann, Celebrating 100 years of “polymer science”: Hermann Staudinger's 1920 manifesto, Polym. Chem., 2020, 11, 8–14.
73. D. Andrienko, Introduction to liquid crystals, J. Mol. Liq., 2018, 267, 520–541.
74. M. Kléman, Defects in liquid crystals, Rep. Prog. Phys., 1989, 52, 555.
75. A. Ciferri, Polymer liquid crystals, Elsevier, 2012.
76. P. J. Collings and J. W. Goodby, Introduction to liquid crystals: chemistry and physics, CRC Press, 2019.
77. F. C. Frank, I. Liquid crystals. On the theory of liquid crystals, Discuss. Faraday Soc., 1958, 25, 19–28.
78. E. Priestly, Introduction to liquid crystals, Springer Science & Business Media, 2012.
79. P. Oswald and P. Pieranski, Nematic and cholesteric liquid crystals: concepts and physical properties illustrated by experiments, CRC Press, 2005.
80. Y.-C. Yang, C.-S. Kee, J.-E. Kim, H. Y. Park, J.-C. Lee and Y.-J. Jeon, Photonic defect modes of cholesteric liquid crystals, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 60, 6852.
81. H. R. Brand, P. Cladis and H. Pleiner, Macroscopic properties of smectic liquid crystals, Eur. Phys. J. B, 1998, 6, 347–353.
82. S. Laschat, A. Baro, N. Steinke, F. Giesselmann, C. Haegele, G. Scalia, R. Judele, E. Kapatsina, S. Sauer and A. Schreivogel, Discotic liquid crystals: from tailor-made synthesis to plastic electronics, Angew. Chem., Int. Ed., 2007, 46, 4832–4887.
83. T. Wöhrle, I. Wurzbach, J. Kirres, A. Kostidou, N. Kapernaum, J. Litterscheidt, J. C. Haenle, P. Staffeld, A. Baro and F. Giesselmann, Discotic liquid crystals, Chem. Rev., 2016, 116, 1139–1241.
84. J. W. Goodby; P. J. Collings; T. Kato; H. Gleeson; C. Tschierske; V. Vill and P. Raynes, Handbook of Liquid Crystals, 8 Volume Set, John Wiley & Sons, 2014, vol. 7.
85. T. Kato, T. Yasuda, Y. Kamikawa and M. Yoshio, Self-assembly of functional columnar liquid crystals, Chem. Commun., 2009, 729–739.
86. J. Goldstone, A. Salam and S. Weinberg, Broken symmetries, Phys. Rev., 1962, 127, 965.
87. P. M. Chaikin; T. C. Lubensky and T. A. Witten, Principles of condensed matter physics, Cambridge University Press, Cambridge, 1995, vol. 10.
88. I. I. Smalyukh, Liquid crystal colloids, Annu. Rev. Condens. Matter. Phys, 2018, 9, 207–226.
89. L. M. Blinov, Structure and properties of liquid crystals. Springer Science & Business Media, 2010, vol. 123.
90. T. Araki, F. Serra and H. Tanaka, Defect science and engineering of liquid crystals under geometrical frustration, Soft Matter, 2013, 9, 8107–8120.
91. E. Putzig, G. S. Redner, A. Baskaran and A. Baskaran, Instabilities, defects, and defect ordering in an overdamped active nematic, Soft Matter, 2016, 12, 3854–3859.
92. M. Kleman, Defects in Liquid-Crystalline Polymers, MRS. Bull., 1995, 20, 23–28.
93. M. Kleman, Invited Lecture. Defects in small-molecule and polymeric nematics, Liq. Cryst., 1989, 5, 399–417.
94. W. B.-P. Cladis, Defects in liquid crystals, Phys. Today, 1982, 35, 48–54.
95. J. M. Ball, Liquid crystals and their defects, Mathematical thermodynamics of complex fluids, Springer, 2017, pp. 1–46.
96. P. J. Collings and M. Hird, Introduction to liquid crystals: chemistry and physics, CRC Press, 2017.
97. O. D. Lavrentovich; P. Pasini; C. Zannoni and S. Zumer, Defects in liquid crystals: Computer simulations, theory and experiments, Springer Science & Business Media, 2012, vol. 43.
98. R. G. Jones, Compendium of polymer terminology and nomenclature: IUPAC recommendations, 2008. Royal Society of Chemistry, Cambridge, 2009, vol. 464.
99. M. Kleman and J. Friedel, Disclinations, dislocations, and continuous defects: A reappraisal, Rev. Modern Phys., 2008, 80, 61.
100. T. Ohzono, K. Katoh, C. Wang, A. Fukazawa, S. Yamaguchi and J.-I. Fukuda, Uncovering different states of topological defects in schlieren textures of a nematic liquid crystal, Sci. Rep., 2017, 7, 16814.
101. M. Kleman and O. D. Lavrentovich, Topological point defects in nematic liquid crystals, Philos. Mag., 2006, 86, 4117–4137.
102. N. Kumar, R. Zhang, J. J. De Pablo and M. L. Gardel, Tunable structure and dynamics of active liquid crystals, Sci. Adv., 2018, 4, eaat7779.
103. M. Kléman and O. D. Lavrentovich, Grain boundaries and the law of corresponding cones in smectics, Eur. Phys. J. E, 2000, 2, 47–57.
104. D. A. Beller, M. A. Gharbi, A. Honglawan, K. J. Stebe, S. Yang and R. D. Kamien, Focal conic flower textures at curved interfaces, Phys. Rev. X, 2013, 3, 041026.
105. C. Meyer, L. Le Cunff, M. Belloul and G. Foyart, Focal conic stacking in smectic a liquid crystals: Smectic flower and Apollonius tiling, Materials, 2009, 2, 499–513.
106. N. Clark and T. Rieker, Smectic-C ‘‘chevron,’’a planar liquid-crystal defect: Implications for the surface-stabilized ferroelectric liquid-crystal geometry, Phys. Rev. A, 1988, 37, 1053.
107. N. U. Islam, N. Mottram and S. Elston, Stability of the formation of the chevron structure, Liq. Cryst., 1999, 26, 1059–1065.
108. G. McKay, Modelling smectics in confined geometries, J. Non-Newtonian Fluid Mech., 2004, 119, 115–122.
109. J. Jones, On the biaxiality of smectic C and ferroelectric liquid crystals, Liq. Cryst., 2015, 42, 732–759.
110. C. Tschierske, Mirror symmetry breaking in liquids and liquid crystals, Liq. Cryst., 2018, 45, 2221–2252.
111. C. F. Dietrich, P. Rudquist, K. Lorenz and F. Giesselmann, Chiral structures from achiral micellar lyotropic liquid crystals under capillary confinement, Langmuir, 2017, 33, 5852–5862.
112. A. Nikoubashman, D. A. Vega, K. Binder and A. Milchev, Semiflexible polymers in spherical confinement: Bipolar orientational order versus tennis ball states, Phys. Rev. Lett., 2017, 118, 217803.
113. S. S. Gandhi, M. S. Kim, J. Y. Hwang and L. C. Chien, Electro-optical Memory of a Nanoengineered Amorphous Blue-Phase-III Polymer Scaffold, Adv. Mater., 2016, 28, 8998–9005.
114. P. Poulin, H. Stark, T. Lubensky and D. Weitz, Novel colloidal interactions in anisotropic fluids, Science, 1997, 275, 1770–1773.
115. R. Barboza, U. Bortolozzo, G. Assanto, E. Vidal-Henriquez, M. Clerc and S. Residori, Harnessing optical vortex lattices in nematic liquid crystals, Phys. Rev. Lett., 2013, 111, 093902.
116. J. Kobashi, H. Yoshida and M. Ozaki, Planar optics with patterned chiral liquid crystals, Nat. Photonics, 2016, 10, 389.
117. G. Bryan-Brown; C. Brown; J. Jones; E. Wood; I. Sage; P. Brett and J. Rudin In Grating aligned bistable nematic device, SID International Symposium Digest of Technical Papers, 1997; society for information display: 1997, pp. 37–40.
118. T. Carroll, Liquid-Crystal Diffraction Grating, J. Appl. Phys., 1972, 43, 767–770.
119. B. Y. Wei, W. Hu, Y. Ming, F. Xu, S. Rubin, J. G. Wang, V. Chigrinov and Y. Q. Lu, Generating switchable and reconfigurable optical vortices via photopatterning of liquid crystals, Adv. Mater., 2014, 26, 1590–1595.
120. H. Chen, G. Tan, Y. Huang, Y. Weng, T.-H. Choi, T.-H. Yoon and S.-T. Wu, A low voltage liquid crystal phase grating with switchable diffraction angles, Sci. Rep., 2017, 7, 39923.
121. Y. Sasaki, V. Jampani, C. Tanaka, N. Sakurai, S. Sakane, K. V. Le, F. Araoka and H. Orihara, Large-scale self-organization of reconfigurable topological defect networks in nematic liquid crystals, Nat. Commun., 2016, 7, 13238.
122. M. Kim and F. Serra, Tunable Dynamic Topological Defect Pattern Formation in Nematic Liquid Crystals, Adv. Opt. Mater., 2019.
123. M. Cavallaro Jr, M. A. Gharbi, D. A. Beller, S. Čopar, Z. Shi, R. D. Kamien, S. Yang, T. Baumgart and K. J. Stebe, Ring around the colloid, Soft Matter, 2013, 9, 9099–9102.
124. A. Honglawan, D. A. Beller, M. Cavallaro, R. D. Kamien, K. J. Stebe and S. Yang, Topographically induced hierarchical assembly and geometrical transformation of focal conic domain arrays in smectic liquid crystals, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 34–39.
125. F. Serra, Curvature and defects in nematic liquid crystals, Liq. Cryst., 2016, 43, 1920–1936.
126. T. Lopez-Leon, V. Koning, K. Devaiah, V. Vitelli and A. Fernandez-Nieves, Frustrated nematic order in spherical geometries, Nat. Phys, 2011, 7, 391.
127. D. R. Nelson, Defects and geometry in condensed matter physics, Cambridge University Press, 2002.
128. T. Lopez-Leon, A. Fernandez-Nieves, M. Nobili and C. Blanc, Nematic-smectic transition in spherical shells, Phys. Rev. Lett., 2011, 106, 247802.
129. A. Darmon, M. Benzaquen, D. Seč, S. Čopar, O. Dauchot and T. Lopez-Leon, Waltzing route toward double-helix formation in cholesteric shells, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 9469–9474.
130. H.-L. Liang, R. Zentel, P. Rudquist and J. Lagerwall, Towards tunable defect arrangements in smectic liquid crystal shells utilizing the nematic–smectic transition in hybrid-aligned geometries, Soft Matter, 2012, 8, 5443–5450.
131. R. Ruhwandl and E. Terentjev, Monte Carlo simulation of topological defects in the nematic liquid crystal matrix around a spherical colloid particle, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 56, 5561.
132. H. Stark, Director field configurations around a spherical particle in a nematic liquid crystal, Eur. Phys. J. B, 1999, 10, 311–321.
133. H. Stark, Physics of colloidal dispersions in nematic liquid crystals, Phys. Rep., 2001, 351, 387–474.
134. H. Mori and H. Nakanishi, On the stability of topologically non-trivial point defects, J. Phys. Soc. Jpn., 1988, 57, 1281–1286.
135. S. Park, Q. Liu and I. I. Smalyukh, Colloidal surfaces with boundaries, apex boojums, and nested elastic self-assembly of nematic colloids, Phys. Rev. Lett., 2016, 117, 277801.
136. C. P. Lapointe, T. G. Mason and I. I. Smalyukh, Shape-controlled colloidal interactions in nematic liquid crystals, Science, 2009, 326, 1083–1086.
137. K. P. Sharma, A. K. Ganai, D. Sen, B. Prasad and G. Kumaraswamy, Exclusion from hexagonal mesophase surfactant domains drives end-to-end enchainment of rod-like particles, J. Phys. Chem. B, 2013, 117, 12661–12668.
138. K. P. Sharma, G. Kumaraswamy, I. Ly and O. Mondain-Monval, Self-assembly of silica particles in a nonionic surfactant hexagonal mesophase, J. Phys. Chem. B, 2009, 113, 3423–3430.
139. I. Muševič and M. Škarabot, Self-assembly of nematic colloids, Soft Matter, 2008, 4, 195–199.
140. I. Muševič, M. Škarabot, U. Tkalec, M. Ravnik and S. Žumer, Two-dimensional nematic colloidal crystals self-assembled by topological defects, Science, 2006, 313, 954–958.
141. M. A. Gharbi, M. Nobili and C. Blanc, Use of topological defects as templates to direct assembly of colloidal particles at nematic interfaces, J. Colloid Interface Sci., 2014, 417, 250–255.
142. A. Nych, U. Ognysta, M. Škarabot, M. Ravnik, S. Žumer and I. Muševič, Assembly and control of 3D nematic dipolar colloidal crystals, Nat. Commun., 2013, 4, 1–8.
143. H. Yoshida, K. Asakura, J. Fukuda and M. Ozaki, Three-dimensional positioning and control of colloidal objects utilizing engineered liquid crystalline defect networks, Nat. Commun., 2015, 6, 1–8.
144. I. Abdulhalim, Non-display bio-optic applications of liquid crystals, Liquid Crystals Today, 2011, 20, 44–60.
145. R. Mezzenga, J. M. Seddon, C. J. Drummond, B. J. Boyd, G. E. Schröder-Turk and L. Sagalowicz, Nature-Inspired design and application of lipidic lyotropic liquid crystals, Adv. Mater., 2019, 31, 1900818.
146. Q. Li, Liquid crystals beyond displays: chemistry, physics, and applications, John Wiley & Sons, 2012.
147. Q. Li, Nanoscience With Liquid Crystals, Springer, 2016.
148. L. Vicari, Optical applications of liquid crystals, CRC Press, 2016.
149. B. Bahadur, Liquid crystals: applications and uses, World scientific, 1990, vol. 1.
150. C. Blanc, D. Coursault and E. Lacaze, Ordering nano-and microparticles assemblies with liquid crystals, Liq. Cryst. Rev., 2013, 1, 83–109.
151. S. J. Woltman, G. D. Jay and G. P. Crawford, Liquid-crystal materials find a new order in biomedical applications, Nat. Mater., 2007, 6, 929–938.
152. Y. H. Kim, J. O. Lee, H. S. Jeong, J. H. Kim, E. K. Yoon, D. K. Yoon, J. B. Yoon and H. T. Jung, Optically Selective Microlens Photomasks Using Self-Assembled Smectic Liquid Crystal Defect Arrays, Adv. Mater., 2010, 22, 2416–2420.
153. H. Kikuchi, M. Yokota, Y. Hisakado, H. Yang and T. Kajiyama, Polymer-stabilized liquid crystal blue phases, Nat. Mater., 2002, 1, 64–68.
154. Y.-K. Kim, J. Noh, K. Nayani and N. L. Abbott, Soft matter from liquid crystals, Soft Matter, 2019, 15, 6913–6929.
155. X. Zhao, F. Pan, H. Xu, M. Yaseen, H. Shan, C. A. Hauser, S. Zhang and J. R. Lu, Molecular self-assembly and applications of designer peptide amphiphiles, Chem. Soc. Rev., 2010, 39, 3480–3498.
156. D. J. Shaw, Introduction to colloid and surface chemistry, Butterworths, 1980.
157. T. Cosgrove, Colloid science: principles, methods and applications, John Wiley & Sons, 2010.
158. G. M. Kontogeorgis and S. Kiil, Introduction to applied colloid and surface chemistry, Wiley Online Library, 2016.
159. V. N. Manoharan, Colloidal matter: Packing, geometry, and entropy, Science, 2015, 349, 1253751.
160. K. Kratz and W. Eimer, Swelling properties of colloidal poly(n-isopropylacrylamide) microgels in solution, Berichte der Bunsengesellschaft für physikalische Chemie, 1998, 102, 848–854.
161. J. Khodadadi, L. Fan and H. Babaei, Thermal conductivity enhancement of nanostructure-based colloidal suspensions utilized as phase change materials for thermal energy storage: a review, Renewable Sustainable Energy Rev., 2013, 24, 418–444.
162. A. Bausch, M. J. Bowick, A. Cacciuto, A. Dinsmore, M. Hsu, D. Nelson, M. Nikolaides, A. Travesset and D. Weitz, Grain boundary scars and spherical crystallography, Science, 2003, 299, 1716–1718.
163. U. Gasser, C. Eisenmann, G. Maret and P. Keim, Melting of crystals in two dimensions, ChemPhysChem, 2010, 11, 963–970.
164. A. Pertsinidis and X. Ling, Diffusion of point defects in two-dimensional colloidal crystals, Nature, 2001, 413, 147.
165. A. Pertsinidis and X. Ling, Equilibrium configurations and energetics of point defects in two-dimensional colloidal crystals, Phys. Rev. Lett., 2001, 87, 098303.
166. A. Pertsinidis and X. S. Ling, Video microscopy and micromechanics studies of one-and two-dimensional colloidal crystals, New J. Phys., 2005, 7, 33.
167. B. Van Der Meer, W. Qi, J. Sprakel, L. Filion and M. Dijkstra, Dynamical heterogeneities and defects in two-dimensional soft colloidal crystals, Soft Matter, 2015, 11, 9385–9392.
168. A. Libal, C. Reichhardt and C. O. Reichhardt, Point-defect dynamics in two-dimensional colloidal crystals, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 011403.
169. L. DaSilva, L. Candido, L. d. F. Costa and O. N. Oliveira, Formation energy and interaction of point defects in two-dimensional colloidal crystals, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 035441.
170. W. Lechner and C. Dellago, Point defects in two-dimensional colloidal crystals: simulation vs. elasticity theory, Soft Matter, 2009, 5, 646–659.
171. M. J. Bowick and L. Giomi, Two-dimensional matter: order, curvature and defects, Adv. Phys., 2009, 58, 449–563.
172. P. Hilton and J. Pedersen, The Euler characteristic and Pólya's dream, American mathematical monthly, 1996, 103, 121–131.
173. W. T. Irvine, V. Vitelli and P. M. Chaikin, Pleats in crystals on curved surfaces, Nature, 2010, 468, 947–951.
174. N. A. García, A. D. Pezzutti, R. A. Register, D. A. Vega and L. R. Gómez, Defect formation and coarsening in hexagonal 2D curved crystals, Soft Matter, 2015, 11, 898–907.
175. G. Meng, J. Paulose, D. R. Nelson and V. N. Manoharan, Elastic instability of a crystal growing on a curved surface, Science, 2014, 343, 634–637.
176. S. Sacanna, W. T. Irvine, P. M. Chaikin and D. J. Pine, Lock and key colloids, Nature, 2010, 464, 575–578.
177. É. Duguet, C. Hubert, C. Chomette, A. Perro and S. Ravaine, Patchy colloidal particles for programmed self-assembly, C. R. Chim., 2016, 19, 173–182.
178. S. Ravaine and E. Duguet, Synthesis and assembly of patchy particles: Recent progress and future prospects, Curr. Opin. Colloid Interface Sci., 2017, 30, 45–53.
179. Z. Zhang and S. C. Glotzer, Self-assembly of patchy particles, Nano Lett., 2004, 4, 1407–1413.
180. M. Youssef, T. Hueckel, G.-R. Yi and S. Sacanna, Shape-shifting colloids via stimulated dewetting, Nat. Commun., 2016, 7, 1–7.
181. V. Burtsev, V. Marchuk, A. Kugaevskiy, O. Guselnikova, R. Elashnikov, E. Miliutina, P. Postnikov, V. Svorcik and O. Lyutakov, Hydrophilic/hydrophobic surface modification impact on colloid lithography: Schottky-like defects, dislocation, and ideal distribution, Appl. Surf. Sci., 2018, 433, 443–448.
182. H. Staudinger, Macromolecular chemistry, Nobel Lecture, 1953, 397–419.
183. D. Braun; H. Cherdron; M. Rehahn; H. Ritter and B. Voit, Functional Polymers, Polymer Synthesis: Theory and Practice, Springer, 2013, pp 375–395.
184. D. Fournier, R. Hoogenboom and U. S. Schubert, Clicking polymers: a straightforward approach to novel macromolecular architectures, Chem. Soc. Rev., 2007, 36, 1369–1380.
185. L. J. Markoski, J. L. Thompson and J. S. Moore, Synthesis and Characterization of Linear− Dendritic Aromatic Etherimide Copolymers: Tuning Molecular Architecture To Optimize Properties and Processability, Macromolecules, 2000, 33, 5315–5317.
186. Z. H. Guo, A. N. Le, X. Feng, Y. Choo, B. Liu, D. Wang, Z. Wan, Y. Gu, J. Zhao and V. Li, Janus Graft Block Copolymers: Design of a Polymer Architecture for Independently Tuned Nanostructures and Polymer Properties, Angew. Chem., Int. Ed., 2018, 57, 8493–8497.
187. W. Sriprom, M. Néel, C. D. Gabbutt, B. M. Heron and S. Perrier, Tuning the color switching of naphthopyrans via the control of polymeric architectures, J. Mater. Chem., 2007, 17, 1885–1893.
188. A. Lederer and W. Burchard, Hyperbranched Polymers: Macromolecules in between deterministic linear chains and dendrimer structures, Royal Society of Chemistry, 2015.
189. A. Baker and A. Windle, The effects of branching and fibre drawing on the crystal structure of polyethylene, Polymer, 2001, 42, 651–665.
190. X. Zhu, Y. Zhou and D. Yan, Influence of branching architecture on polymer properties, J. Polym. Sci., Part B: Polym. Phys., 2011, 49, 1277–1286.
191. D. Mäder, J. Heinemann, P. Walter and R. Mülhaupt, Influence of n-alkyl branches on glass-transition temperatures of branched polyethylenes prepared by means of metallocene-and palladium-based catalysts, Macromolecules, 2000, 33, 1254–1261.
192. X. Luo, S. Xie, J. Liu, H. Hu, J. Jiang, W. Huang, H. Gao, D. Zhou, Z. Lü and D. Yan, The relationship between the degree of branching and glass transition temperature of branched polyethylene: experiment and simulation, Polym. Chem., 2014, 5, 1305–1312.
193. Z. Guan, P. Cotts, E. McCord and S. McLain, Chain walking: a new strategy to control polymer topology, Science, 1999, 283, 2059–2062.
194. Z. Guan, Control of Polymer Topology by Chain-Walking Catalysts, Chem. – Eur. J., 2002, 8, 3086–3092.
195. Z. Guan, Recent progress of catalytic polymerization for controlling polymer topology, Chem. – Asian J., 2010, 5, 1058–1070.
196. J. M. Rose, A. E. Cherian, J. H. Lee, L. A. Archer, G. W. Coates and L. J. Fetters, Rheological behavior of chain-straightened poly(α-olefin)s, Macromolecules, 2007, 40, 6807–6813.
197. J. M. Rose, T. H. Mourey, L. A. Slater, I. Keresztes, L. J. Fetters and G. W. Coates, Poly(ethylene-co-propylene macromonomer)s: Synthesis and Evidence for Starlike Conformations in Dilute Solution, Macromolecules, 2008, 41, 559–567.
198. P. Xiang and Z. Ye, Copolymerization of Ethylene with Sterically Hindered 3,3-Dimethyl-1-Butene Using a Chain-Walking Pd-Diimine Catalyst, Macromol. Rapid Commun., 2010, 31, 1083–1089.
199. K. S. O’Connor, A. Watts, T. Vaidya, A. M. LaPointe, M. A. Hillmyer and G. W. Coates, Controlled chain walking for the synthesis of thermoplastic polyolefin elastomers: synthesis, structure, and properties, Macromolecules, 2016, 49, 6743–6751.
200. C. Ruiz-Orta, J. P. Fernandez-Blazquez, A. M. Anderson-Wile, G. W. Coates and R. G. Alamo, Isotactic polypropylene with (3, 1) chain-walking defects: characterization, crystallization, and melting behaviors, Macromolecules, 2011, 44, 3436–3451.
201. L. A. Utracki and C. A. Wilkie, Polymer blends handbook, Springer, 2002, vol. 1.
202. L. M. Robeson, Polymer blends. A Comprehensive Review, 2007.
203. F. Siepmann, J. Siepmann, M. Walther, R. MacRae and R. Bodmeier, Polymer blends for controlled release coatings, J. Controlled Release, 2008, 125, 1–15.
204. S. Yu and B. C. Benicewicz, Synthesis and properties of functionalized polybenzimidazoles for high-temperature PEMFCs, Macromolecules, 2009, 42, 8640–8648.
205. C. Feng, Y. Li, D. Yang, J. Hu, X. Zhang and X. Huang, Well-defined graft copolymers: from controlled synthesis to multipurpose applications, Chem. Soc. Rev., 2011, 40, 1282–1295.
206. A. Gudadhe, N. Bachhar, A. Kumar, P. Andrade and G. Kumaraswamy, Three-dimensional printing with waste high-density polyethylene, ACS Appl. Polym. Mater., 2019, 1, 3157–3164.
207. A. Kulkarni, A. Lele, S. Sivaram, P. Rajamohanan, S. Velankar and A. Chatterji, Star telechelic poly(L-lactide) ionomers, Macromolecules, 2015, 48, 6580–6588.
208. A. Carlmark, C. Hawker, A. Hult and M. Malkoch, New methodologies in the construction of dendritic materials, Chem. Soc. Rev., 2009, 38, 352–362.
209. P. R. Dvornic and D. A. Tomalia, Recent advances in dendritic polymers, Curr. Opin. Colloid Interface Sci., 1996, 1, 221–235.
210. M. Seiler, Dendritic polymers–interdisciplinary research and emerging applications from unique structural properties, Chem. Eng. Technol., 2002, 25, 237–253.
211. R. Soleyman and M. Adeli, Impact of dendritic polymers on nanomaterials, Polym. Chem., 2015, 6, 10–24.
212. M. V. Walter and M. Malkoch, Simplifying the synthesis of dendrimers: accelerated approaches, Chem. Soc. Rev., 2012, 41, 4593–4609.
213. A. D. Schlüter; A. Halperin; M. Kröger; D. Vlassopoulos; G. Wegner and B. Zhang, Dendronized polymers: Molecular objects between conventional linear polymers and colloidal particles, ACS Publications, 2014.
214. S. Costanzo, L. F. Scherz, T. Schweizer, M. Kröger, G. Floudas, A. D. Schlüter and D. Vlassopoulos, Rheology and packing of Dendronized polymers, Macromolecules, 2016, 49, 7054–7068.
215. D. Yan; C. Gao and H. Frey, Hyperbranched polymers: synthesis, properties, and applications. John Wiley & Sons, 2011, vol. 8.
216. Y. H. Kim and O. W. Webster, Hyperbranched polyphenylenes, Macromolecules, 1992, 25, 5561–5572.
217. S. R. Turner, F. Walter, B. I. Voit and T. H. Mourey, Hyperbranched aromatic polyesters with carboxylic acid terminal groups, Macromolecules, 1994, 27, 1611–1616.
218. T. H. Mourey, S. Turner, M. Rubinstein, J. Fréchet, C. Hawker and K. Wooley, Unique behavior of dendritic macromolecules: intrinsic viscosity of polyether dendrimers, Macromolecules, 1992, 25, 2401–2406.
219. S. R. Turner, B. I. Voit and T. H. Mourey, All-aromatic hyperbranched polyesters with phenol and acetate end groups: synthesis and characterization, Macromolecules, 1993, 26, 4617–4623.
220. D. H. Rouvray and R. B. King, Topology in chemistry: Discrete mathematics of molecules, Elsevier, 2002.
221. P. F. Sheridan, D. B. Adolf, A. V. Lyulin, I. Neelov and G. R. Davies, Computer simulations of hyperbranched polymers: The influence of the Wiener index on the intrinsic viscosity and radius of gyration, J. Chem. Phys., 2002, 117, 7802–7812.
222. P. Lutz, M. S. Plentz, J. Kress, A. Lapp and M. Duval, Polym. Prepr., 2000, 41, 1882.
223. Z. Guan and P. Cotts, In Tuning polymer topology by late transition metal catalyst: From linear to hyperbranched to “dendritic”, Abstracts Of Papers Of The American Chemical Society, 2001; Amer Chemical Soc 1155 16th St, Nw, Washington, Dc 20036 Usa: 2001; Pp U391-U391.
224. H. Rabbel, H. Frey and F. Schmid, Statistical properties of linear-hyperbranched graft copolymers prepared via “hypergrafting” of AB m monomers from linear B-functional core chains: A molecular dynamics simulation, J. Chem. Phys., 2015, 143, 243125.
225. Y. H. Kim and R. Beckerbauer, Role of end groups on the glass transition of hyperbranched polyphenylene and triphenylbenzene derivatives, Macromolecules, 1994, 27, 1968–1971.
226. D. Astruc, E. Boisselier and C. Ornelas, Dendrimers designed for functions: from physical, photophysical, and supramolecular properties to applications in sensing, catalysis, molecular electronics, photonics, and nanomedicine, Chem. Rev., 2010, 110, 1857–1959.
227. P. Ceroni and M. Venturi, Photoactive and electroactive dendrimers: future trends and applications, Aust. J. Chem., 2011, 64, 131–146.
228. Y. Cheng, L. Zhao, Y. Li and T. Xu, Design of biocompatible dendrimers for cancer diagnosis and therapy: current status and future perspectives, Chem. Soc. Rev., 2011, 40, 2673–2703.
229. M. A. Mintzer and M. W. Grinstaff, Biomedical applications of dendrimers: a tutorial, Chem. Soc. Rev., 2011, 40, 173–190.
230. L. Röglin, E. H. Lempens and E. Meijer, A Synthetic “Tour de Force”: Well-Defined Multivalent and Multimodal Dendritic Structures for Biomedical Applications, Angew. Chem., Int. Ed., 2011, 50, 102–112.
231. S. Chatterjee and S. Ramakrishnan, Defect-free hyperbranched polydithioacetal via melt polymerization, ACS. Macro. Lett, 2012, 1, 593–598.
232. G. Mihov, D. Grebel-Koehler, A. Lübbert, G. W. Vandermeulen, A. Herrmann, H.-A. Klok and K. Müllen, Polyphenylene dendrimers as scaffolds for shape-persistent multiple peptide conjugates, Bioconjugate Chem., 2005, 16, 283–293.
233. T. Vossmeyer, B. Guse, I. Besnard, R. E. Bauer, K. Müllen and A. Yasuda, Gold nanoparticle/polyphenylene dendrimer composite films: Preparation and vapor-sensing properties, Adv. Mater., 2002, 14, 238–242.
234. N. Krasteva, I. Besnard, B. Guse, R. E. Bauer, K. Müllen, A. Yasuda and T. Vossmeyer, Self-assembled gold nanoparticle/dendrimer composite films for vapor sensing applications, Nano Lett., 2002, 2, 551–555.
235. A.-M. Caminade, D. Yan and D. K. Smith, Dendrimers and hyperbranched polymers, Chem. Soc. Rev., 2015, 44, 3870–3873.
236. B. Zhang, H. Yu, A. D. Schlüter, A. Halperin and M. Kröger, Synthetic regimes due to packing constraints in dendritic molecules confirmed by labelling experiments, Nat. Commun., 2013, 4, 1993.
237. D. K. Smith, A. R. Hirst, C. S. Love, J. G. Hardy, S. V. Brignell and B. Huang, Self-assembly using dendritic building blocks—towards controllable nanomaterials, Prog. Polym. Sci., 2005, 30, 220–293.
238. D. K. Smith, Dendritic supermolecules–towards controllable nanomaterials, Chem. Commun., 2006, 34–44.
239. C. Schüll and H. Frey, Grafting of hyperbranched polymers: From unusual complex polymer topologies to multivalent surface functionalization, Polymer, 2013, 54, 5443–5455.
240. D. Hölter, A. Burgath and H. Frey, Degree of branching in hyperbranched polymers, Acta Polym., 1997, 48, 30–35.
241. C. J. Hawker, Dendritic and hyperbranched macromolecules—precisely controlled macromolecular architectures in Macromolecular Architectures, Springer, 1999, pp. 113–160.
242. A. Hult; M. Johansson and E. Malmström, Hyperbranched polymers, In Branched Polymers II, Springer, 1999, pp. 1–34.
243. Y. H. Kim, Hyperbranched polymers 10 years after, J. Polym. Sci. Part A, Polym. Chem., 1998, 36, 1685–1698.
244. J. M. Frechet, M. Henmi, I. Gitsov, S. Aoshima, M. R. Leduc and R. B. Grubbs, Self-condensing vinyl polymerization: an approach to dendritic materials, Science, 1995, 269, 1080–1083.
245. C. J. Hawker, J. M. Frechet, R. B. Grubbs and J. Dao, Preparation of hyperbranched and star polymers by a “living”, self-condensing free radical polymerization, J. Am. Chem. Soc., 1995, 117, 10763–10764.
246. D. Yan, A. H. Müller and K. Matyjaszewski, Molecular parameters of hyperbranched polymers made by self-condensing vinyl polymerization. 2. Degree of branching, Macromolecules, 1997, 30, 7024–7033.
247. H. Mori, D. C. Seng, H. Lechner, M. Zhang and A. H. Müller, Synthesis and characterization of branched polyelectrolytes. 1. Preparation of hyperbranched poly(acrylic acid) via self-condensing atom transfer radical copolymerization, Macromolecules, 2002, 35, 9270–9281.
248. C. J. Hawker and F. Chu, Hyperbranched poly(ether ketones): manipulation of structure and physical properties, Macromolecules, 1996, 29, 4370–4380.
249. Y. Ishida, A. C. Sun, M. Jikei and M.-A. Kakimoto, Synthesis of hyperbranched aromatic polyamides starting from dendrons as AB x monomers: effect of monomer multiplicity on the degree of branching, Macromolecules, 2000, 33, 2832–2838.
250. A. Sunder, M. Krämer, R. Hanselmann, R. Mülhaupt and H. Frey, Molecular nanocapsules based on amphiphilic hyperbranched polyglycerols, Angew. Chem., Int. Ed., 1999, 38, 3552–3555.
251. D. Wilms, S.-E. Stiriba and H. Frey, Hyperbranched polyglycerols: from the controlled synthesis of biocompatible polyether polyols to multipurpose applications, Acc. Chem. Res., 2009, 43, 129–141.
252. M. Suzuki, A. Ii and T. Saegusa, Multibranching polymerization: palladium-catalyzed ring-opening polymerization of cyclic carbamate to produce hyperbranched dendritic polyamine, Macromolecules, 1992, 25, 7071–7072.
253. M. Suzuki, S. Yoshida, K. Shiraga and T. Saegusa, New ring-opening polymerization via a π-allylpalladium complex. 5. Multibranching polymerization of cyclic carbamate to produce hyperbranched dendritic polyamine, Macromolecules, 1998, 31, 1716–1719.
254. D. Holter, Degree of branching (DB) in hyperbranched polymers. Part 2. Enhancement of the DB. Scope and limitations, Acta Polym., 1997, 48, 298–309.
255. G. Maier, C. Zech, B. Voit and H. Komber, An approach to hyperbranched polymers with a degree of branching of 100%, Macromol. Chem. Phys., 1998, 199, 2655–2664.
256. Y. Fu, C. Van Oosterwijck, A. Vandendriessche, A. Kowalczuk-Bleja, X. Zhang, A. Dworak, W. Dehaen and M. Smet, Hyperbranched Poly(arylene oxindole) s with a Degree of Branching of 100% for the Construction of Nanocontainers by Orthogonal Modification, Macromolecules, 2008, 41, 2388–2393.
257. Y. Fu, A. Vandendriessche, W. Dehaen and M. Smet, Effective acid-catalyzed synthesis of 100% hyperbranched polyacenaphthenones, Macromolecules, 2006, 39, 5183–5186.
258. M. Yamada, J. Sun, Y. Suda and T. Nakaya, Synthesis of fluorenebisphenoxy derivatives by acid-sulfur compound catalyzed condensation reaction, Chem. Lett., 1998, 1055–1056.
259. W. Huang, L. Su and Z. Bo, Hyperbranched Polymers with a Degree of Branching of 100% Prepared by Catalyst Transfer Suzuki–Miyaura Polycondensation, J. Am. Chem. Soc., 2009, 131, 10348–10349.
260. M. Zolotukhin, S. Fomine, R. Salcedo and L. Khalilov, Remarkable enhancement of reactivity of carbonyl compounds for polymerizations with non-activated aromatic hydrocarbons, Chem. Commun., 2004, 1030–1031.
261. Y. Segawa, W. Sinananwanich and M. Ueda, Facile Synthesis of Poly(phenylene ether) and “in-Situ” Functionalization of Polymer Backbones, Macromolecules, 2008, 41, 8309–8311.
262. Y. Segawa, T. Higashihara and M. Ueda, Hyperbranched polymers with controlled degree of branching from 0 to 100%, J. Am. Chem. Soc., 2010, 132, 11000–11001.
263. A. Peacock, Handbook of polyethylene: structures: properties, and applications, CRC Press, 2000.
264. P. S. Chum, W. J. Kruper and M. J. Guest, Materials properties derived from INSITE metallocene catalysts, Adv. Mater., 2000, 12, 1759–1767.
265. P. Xiang, Z. Ye, S. Morgan, X. Xia and W. Liu, Tuning polyethylene chain topology via ring incorporation in chain walking ethylene polymerization, Macromolecules, 2009, 42, 4946–4949.
266. S. Morgan, Z. Ye, R. Subramanian, W.-J. Wang and G. Ulibarri, Chain walking copolymerization of ethylene with cyclopentene–Effect of ring incorporation on polymer chain topology, Polymer, 2010, 51, 597–605.
267. Q. Zhu, F. Qiu, B. Zhu and X. Zhu, Hyperbranched polymers for bioimaging, RSC Adv., 2013, 3, 2071–2083.
268. M. Krämer, J. F. Stumbé, H. Türk, S. Krause, A. Komp, L. Delineau, S. Prokhorova, H. Kautz and R. Haag, pH-responsive molecular nanocarriers based on dendritic core–shell architectures, Angew. Chem., Int. Ed., 2002, 41, 4252–4256.
269. M. Q. Slagt, S.-E. Stiriba, R. J. Klein Gebbink, H. Kautz, H. Frey and G. van Koten, Encapsulation of Hydrophilic Pincer–Platinum (II) Complexes in Amphiphilic Hyperbranched Polyglycerol Nanocapsules, Macromolecules, 2002, 35, 5734–5737.
270. H. Türk, A. Shukla, P. C. Alves Rodrigues, H. Rehage and R. Haag, Water-Soluble Dendritic Core–Shell-Type Architectures Based on Polyglycerol for Solubilization of Hydrophobic Drugs, Chem. – Eur. J., 2007, 13, 4187–4196.
271. L. A. Tziveleka, C. Kontoyianni, Z. Sideratou, D. Tsiourvas and C. M. Paleos, Novel functional hyperbranched polyether polyols as prospective drug delivery systems, Macromol. Biosci., 2006, 6, 161–169.
272. A. Garcia-Bernabé, M. Krämer, B. Olàh and R. Haag, Syntheses and Phase-Transfer Properties of Dendritic Nanocarriers That Contain Perfluorinated Shell Structures, Chem. – Eur. J., 2004, 10, 2822–2830.
273. R. Wang, L. Zhou, Y. Zhou, G. Li, X. Zhu, H. Gu, X. Jiang, H. Li, J. Wu and L. He, Synthesis and gene delivery of poly(amido amine) s with different branched architecture, Biomacromolecules, 2010, 11, 489–495.
274. H. Cheng, X. Yuan, X. Sun, K. Li, Y. Zhou and D. Yan, Effect of degree of branching on the self-assembly of amphiphilic hyperbranched multiarm copolymers, Macromolecules, 2009, 43, 1143–1147.
275. Y. Shaked, H. Dodiuk, S. Kenig and S. McCarthy, The effect of hyperbranched polymers on processing and thermal stability of biodegradable polyesters, Polym. Eng. Sci., 2009, 49, 559–566.
276. B. Milián-Medina and J. Gierschner, π-Conjugation, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 513–524.
277. A. D. McNaught and A. Wilkinson, Compendium of Chemical Terminology, Blackwell Science, Oxford, 1997, vol. 1669.
278. W. Barford, Electronic and optical properties of conjugated polymers, Oxford University Press, 2013, vol. 159.
279. A. Facchetti, π-Conjugated polymers for organic electronics and photovoltaic cell applications, Chem. Mater., 2010, 23, 733–758.
280. Y.-J. Cheng, S.-H. Yang and C.-S. Hsu, Synthesis of conjugated polymers for organic solar cell applications, Chem. Rev., 2009, 109, 5868–5923.
281. S. R. Forrest and M. E. Thompson, Introduction: organic electronics and optoelectronics, Chem. Rev., 2007, 107, 923–925.
282. X. Guo, M. Baumgarten and K. Müllen, Designing π-conjugated polymers for organic electronics, Prog. Polym. Sci., 2013, 38, 1832–1908.
283. J. R. Reynolds and T. A. Skotheim, Handbook of Conducting Polymers: Conjugated Polymers: Theory, Synthesis, Properties, and Characterization, CRC Press, 2007.
284. C. Kallinger, M. Hilmer, A. Haugeneder, M. Perner, W. Spirkl, U. Lemmer, J. Feldmann, U. Scherf, K. Müllen and A. Gombert, A flexible conjugated polymer laser, Adv. Mater., 1998, 10, 920–923.
285. A. J. Heeger, Semiconducting and metallic polymers: the fourth generation of polymeric materials (Nobel lecture), Angew. Chem., Int. Ed., 2001, 40, 2591–2611.
286. B. A. Gregg, Excitonic solar cells, ACS Publications, 2003.
287. X. F. Wang, Y. Zhou, J. J. Xu and H. Y. Chen, Signal-on electrochemiluminescence biosensors based on CdS–carbon nanotube nanocomposite for the sensitive detection of choline and acetylcholine, Adv. Funct. Mater., 2009, 19, 1444–1450.
288. P. W. Blom, V. D. Mihailetchi, L. J. A. Koster and D. E. Markov, Device physics of polymer: fullerene bulk heterojunction solar cells, Adv. Mater., 2007, 19, 1551–1566.
289. T. Huser, M. Yan and L. J. Rothberg, Single chain spectroscopy of conformational dependence of conjugated polymer photophysics, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 11187–11191.
290. D. K. Chambers, S. Karanam, D. Qi, S. Selmic, Y. B. Losovyj, L. G. Rosa and P. A. Dowben, The electronic structure of oriented poly[2-methoxy-5-(2′-ethyl-hexyloxy)-1, 4-phenylene-vinylene], Appl. Phys. A: Mater. Sci. Process., 2005, 80, 483–488.
291. A. Caruso, D. Q. Feng, Y. B. Losovyj, D. Schulz, S. Balaz, L. G. Rosa, A. Sokolov, B. Doudin and P. A. Dowben, Defect contributions to conductivity in poly(3-hexylthiophene), Phys. Status Solidi B, 2006, 243, 1321–1330.
292. D. English, A. Furube and P. Barbara, Single-molecule spectroscopy in oxygen-depleted polymer films, Chem. Phys. Lett., 2000, 324, 15–19.
293. K. Müllen and G. Wegner, What does materials science learn from conjugated oligomers, Adv. Mater., 1998, 10, 433–436.
294. B. A. Gregg, Charged defects in soft semiconductors and their influence on organic photovoltaics, Soft Matter, 2009, 5, 2985–2989.
295. W. K. Tatum, A. B. Resing, L. Q. Flagg, D. S. Ginger and C. K. Luscombe, Defect Tolerance of π-Conjugated Polymer Crystal Lattices and Their Relevance to Optoelectronic Applications, ACS Appl. Polym. Mater., 2019, 1, 1466–1475.
296. T.-Q. Nguyen, J. Wu, V. Doan, B. J. Schwartz and S. H. Tolbert, Control of energy transfer in oriented conjugated polymer-mesoporous silica composites, Science, 2000, 288, 652–656.
297. Y. Diao, L. Shaw, Z. Bao and S. C. Mannsfeld, Morphology control strategies for solution-processed organic semiconductor thin films, Energy Environ. Sci., 2014, 7, 2145–2159.
298. M. Chang, G. T. Lim, B. Park and E. Reichmanis, Control of molecular ordering, alignment, and charge transport in solution-processed conjugated polymer thin films, Polymers, 2017, 9, 212.
299. D. Hu, J. Yu, K. Wong, B. Bagchi, P. J. Rossky and P. F. Barbara, Collapse of stiff conjugated polymers with chemical defects into ordered, cylindrical conformations, Nature, 2000, 405, 1030–1033.
300. W. Salaneck, O. Inganäs, B. Themans, J. Nilsson, B. Sjögren, J. E. Österholm, J. Bredas and S. Svensson, Thermochromism in poly(3-hexylthiophene) in the solid state: a spectroscopic study of temperature-dependent conformational defects, J. Chem. Phys., 1988, 89, 4613–4619.
301. Y. Kim, D. Spiegel, S. Hotta and A. Heeger, Photoexcitation and doping studies of poly(3-hexylthienylene), Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38, 5490.
302. E. Hennebicq, C. Deleener, J.-L. Brédas, G. D. Scholes and D. Beljonne, Chromophores in phenylenevinylene-based conjugated polymers: Role of conformational kinks and chemical defects, J. Chem. Phys., 2006, 125, 054901.
303. K. F. Wong, M. S. Skaf, C.-Y. Yang, P. J. Rossky, B. Bagchi, D. Hu, J. Yu and P. F. Barbara, Structural and electronic characterization of chemical and conformational defects in conjugated polymers, J. Phys. Chem. B, 2001, 105, 6103–6107.
304. Y. Zhang, B. de Boer and P. W. Blom, Trap-free electron transport in poly(p-phenylene vinylene) by deactivation of traps with n-type doping, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 085201.
305. H. T. Nicolai, M. Kuik, G. Wetzelaer, B. De Boer, C. Campbell, C. Risko, J. Brédas and P. Blom, Unification of trap-limited electron transport in semiconducting polymers, Nat. Mater., 2012, 11, 882–887.
306. D. Abbaszadeh, A. Kunz, N. B. Kotadiya, A. Mondal, D. Andrienko, J. J. Michels, G.-J. A. Wetzelaer and P. W. Blom, Electron trapping in conjugated polymers, Chem. Mater., 2019, 31, 6380–6386.
307. J. Schafferhans, A. Baumann, A. Wagenpfahl, C. Deibel and V. Dyakonov, Oxygen doping of P3HT: PCBM blends: Influence on trap states, charge carrier mobility and solar cell performance, Org. Electro., 2010, 11, 1693–1700.
308. A. Lücke, W. Schmidt, E. Rauls, F. Ortmann and U. Gerstmann, Influence of Structural Defects and Oxidation onto Hole Conductivity in P3HT, J. Phys. Chem. B, 2015, 119, 6481–6491.
309. J. M. Lupton, P. Schouwink, P. E. Keivanidis, A. C. Grimsdale and K. Müllen, Influence of dendronization on spectral diffusion and aggregation in conjugated polymers, Adv. Funct. Mater., 2003, 13, 154–158.
310. G. Dicker, M. P. de Haas, J. M. Warman, D. M. de Leeuw and L. D. Siebbeles, The disperse charge-carrier kinetics in regioregular poly(3-hexylthiophene), J. Phys. Chem. B, 2004, 108, 17818–17824.
311. D. Hu, J. Yu, G. Padmanaban, S. Ramakrishnan and P. F. Barbara, Spatial confinement of exciton transfer and the role of conformational order in organic nanoparticles, Nano Lett., 2002, 2, 1121–1124.
312. D. Wang, N. Kopidakis, M. O. Reese and B. A. Gregg, Treating poly(3-hexylthiophene) with dimethylsulfate improves its photoelectrical properties, Chem. Mater., 2008, 20, 6307–6309.
313. B. A. Gregg, Transport in charged defect-rich π-conjugated polymers, J. Phys Chem. C, 2009, 113, 5899–5901.
314. Z. Liang, A. Nardes, D. Wang, J. J. Berry and B. A. Gregg, Defect Engineering in π-Conjugated Polymers, Chem. Mater., 2009, 21, 4914–4919.
315. Z. Liang, M. O. Reese and B. A. Gregg, Chemically Treating Poly(3-hexylthiophene) Defects to Improve Bulk Heterojunction Photovoltaics, ACS. Appl. Mater. Interfaces, 2011, 3, 2042–2050.
316. S. Schlisske, C. Rosenauer, T. Rödlmeier, K. Giringer, J. J. Michels, K. Kremer, U. Lemmer, S. Morsbach, K. C. Daoulas and G. Hernandez-Sosa, Ink Formulation for Printed Organic Electronics: Investigating Effects of Aggregation on Structure and Rheology of Functional Inks Based on Conjugated Polymers in Mixed Solvents, Adv. Mater. Technol., 2020, 2000335.
317. J. Zhang, K. Kremer, J. J. Michels and K. C. Daoulas, Exploring Disordered Morphologies of Blends and Block Copolymers for Light-Emitting Diodes with Mesoscopic Simulations, Macromolecules, 2020, 53, 523–538.
318. B.-G. Kim, M.-S. Kim and J. Kim, Ultrasonic-assisted nanodimensional self-assembly of poly-3-hexylthiophene for organic photovoltaic cells, ACS Nano, 2010, 4, 2160–2166.
319. A. R. Aiyar, J. I. Hong, R. Nambiar, D. M. Collard and E. Reichmanis, Tunable Crystallinity in Regioregular Poly(3-Hexylthiophene) Thin Films and Its Impact on Field Effect Mobility, Adv. Funct. Mater., 2011, 21, 2652–2659.
320. D. Choi, M. Chang and E. Reichmanis, Controlled Assembly of Poly(3-hexylthiophene): Managing the Disorder to Order Transition on the Nano-through Meso-Scales, Adv. Funct. Mater., 2015, 25, 920–927.
321. M. Chang, J. Lee, N. Kleinhenz, B. Fu and E. Reichmanis, Photoinduced anisotropic supramolecular assembly and enhanced charge transport of poly(3-hexylthiophene) thin films, Adv. Funct. Mater., 2014, 24, 4457–4465.
322. Y. Zhang, B. de Boer and P. W. Blom, Controllable Molecular Doping and Charge Transport in Solution-Processed Polymer Semiconducting Layers, Adv. Funct. Mater., 2009, 19, 1901–1905.
323. D. Khim, H. Han, K. J. Baeg, J. Kim, S. W. Kwak, D. Y. Kim and Y. Y. Noh, Simple Bar-Coating Process for Large-Area, High-Performance Organic Field-Effect Transistors and Ambipolar Complementary Integrated Circuits, Adv. Mater., 2013, 25, 4302–4308.
324. M. Chang, D. Choi and E. Egap, Macroscopic alignment of one-dimensional conjugated polymer nanocrystallites for high-mobility organic field-effect transistors, ACS Appl. Mater. Interfaces, 2016, 8, 13484–13491.
325. M. Chang, Z. Su and E. Egap, Alignment and charge transport of one-dimensional conjugated polymer nanowires in insulating polymer blends, Macromolecules, 2016, 49, 9449–9456.
326. M. Gross, D. C. Müller, H.-G. Nothofer, U. Scherf, D. Neher, C. Bräuchle and K. Meerholz, Improving the performance of doped π-conjugated polymers for use in organic light-emitting diodes, Nature, 2000, 405, 661–665.
327. H.-W. Chen, J.-H. Lee, B.-Y. Lin, S. Chen and S.-T. Wu, Liquid crystal display and organic light-emitting diode display: present status and future perspectives, Light: Sci. Appl., 2018, 7, 17168.
328. Y. Zhang and P. W. Blom, Enhancement of the hole injection into regioregular poly(3-hexylthiophene) by molecular doping, Appl. Phys. Lett., 2010, 97, 185.
329. P. Liu, S. Li, Y. Jin, L. Qian, N. Gao, S. Q. Yao, F. Huang, Q.-H. Xu and Y. Cao, Red-emitting DPSB-based conjugated polymer nanoparticles with high two-photon brightness for cell membrane imaging, ACS Appl. Mater. Interfaces, 2015, 7, 6754–6763.
330. B. Bonillo, R. S. Sprick and A. I. Cooper, Tuning photophysical properties in conjugated microporous polymers by comonomer doping strategies, Chem. Mater., 2016, 28, 3469–3480.
331. Y. Osada and A. Khokhlov, Polymer gels and networks, CRC Press, 2001.
332. Y. Gu, J. Zhao and J. A. Johnson, A (macro) molecular-level understanding of polymer network topology, Trends. Chem, 2019, 1, 318–334.
333. Y. Gu, J. Zhao and J. A. Johnson, Polymer Networks: From Plastics and Gels to Porous Frameworks, Angew. Chem., Int. Ed., 2020, 59, 5022–5049.
334. M. Nébouy, A. de Almeida, S. N. Brottet and G. P. Baeza, Process-oriented structure tuning of PBT/PTHF thermoplastic elastomers, Macromolecules, 2018, 51, 6291–6302.
335. S. Seiffert and J. Sprakel, Physical chemistry of supramolecular polymer networks, Chem. Soc. Rev., 2012, 41, 909–930.
336. T. Rossow and S. Seiffert, Supramolecular polymer networks: Preparation, properties, and potential, in Supramolecular Polymer Networks and Gels, Springer, 2015, pp. 1–46.
337. L. Voorhaar and R. Hoogenboom, Supramolecular polymer networks: hydrogels and bulk materials, Chem. Soc. Rev., 2016, 45, 4013–4031.
338. J. Li and D. J. Mooney, Designing hydrogels for controlled drug delivery, Nat. Rev. Mater., 2016, 1, 1–17.
339. K. Y. Lee and D. J. Mooney, Hydrogels for tissue engineering, Chem. Rev., 2001, 101, 1869–1880.
340. L. Ionov, Hydrogel-based actuators: possibilities and limitations, Mater. Today, 2014, 17, 494–503.
341. N. B. McKeown and P. M. Budd, Polymers of intrinsic microporosity (PIMs): organic materials for membrane separations, heterogeneous catalysis and hydrogen storage, Chem. Soc. Rev., 2006, 35, 675–683.
342. D. D. Díaz, D. Kühbeck and R. J. Koopmans, Stimuli-responsive gels as reaction vessels and reusable catalysts, Chem. Soc. Rev., 2011, 40, 427–448.
343. J. A. Rogers, T. Someya and Y. Huang, Materials and mechanics for stretchable electronics, Science, 2010, 327, 1603–1607.
344. J. E. Herz; P. Rempp and W. Borchard, Model networks, in Polymer Chemistry, Springer, 1978, pp. 105–135.
345. J. Mark, The use of model polymer networks to elucidate molecular aspects of rubberlike elasticity. in Polymer Networks, Springer, 1982, pp. 1–26.
346. G. Hild, Model networks based on ‘endlinking’ processes: synthesis, structure and properties, Prog. Polym. Sci., 1998, 23, 1019–1149.
347. J. Mark and J. Sullivan, Model networks of end-linked polydimethylsiloxane chains. I. Comparisons between experimental and theoretical values of the elastic modulus and the equilibrium degree of swelling, J. Chem. Phys., 1977, 66, 1006–1011.
348. J. Sullivan, J. Mark and P. Hampton Jr, Cohen, R. Model networks of end-linked polydimethylsiloxane chains. II. Viscoelastic losses, J. Chem. Phys., 1978, 68, 2010–2012.
349. J. Mark, R. Rahalkar and J. Sullivan, Model networks of end-linked polydimethylsiloxane chains. III. Effect of the functionality of the cross-links, J. Chem. Phys., 1979, 70, 1794–1797.
350. M. Llorente and J. Mark, Model networks of end-linked polydimethylsiloxane chains. IV. Elastomeric properties of the tetrafunctional networks prepared at different degrees of dilution, J. Chem. Phys., 1979, 71, 682–689.
351. E. R. Duering, K. Kremer and G. S. Grest, Structure and relaxation of end-linked polymer networks, J. Chem. Phys., 1994, 101, 8169–8192.
352. R. Everaers and K. Kremer, Topological interactions in model polymer networks, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 53, R37.
353. F. Di Lorenzo and S. Seiffert, Nanostructural Heterogeneity in Polymer Networks and Gels, Polym. Chem., 2015, 6, 5515–5528.
354. S. Seiffert, Origin of nanostructural inhomogeneity in polymer-network gels, Polym. Chem, 2017, 8, 4472–4487.
355. F. Ikkai and M. Shibayama, Inhomogeneity control in polymer gels, J. Polym. Sci. Part B, Polym. Phys., 2005, 43, 617–628.
356. S. Durmaz and O. Okay, Inhomogeneities in poly(acrylamide) gels: position-dependent elastic modulus measurements, Polym. Bull., 2001, 46, 409–418.
357. K. Dušek and W. Prins, Structure and elasticity of non-crystalline polymer networks, in Fortschritte der Hochpolymeren-Forschung, Springer, 1969, pp. 1–102.
358. C. Sayil and O. Okay, Macroporous poly(N-isopropyl) acrylamide networks: formation conditions, Polymer, 2001, 42, 7639–7652.
359. J. Bastide and L. Leibler, Large-scale heterogeneities in randomly cross-linked networks, Macromolecules, 1988, 21, 2647–2649.
360. K. Nishi, H. Asai, K. Fujii, Y.-S. Han, T.-H. Kim, T. Sakai and M. Shibayama, Small-angle neutron scattering study on defect-controlled polymer networks, Macromolecules, 2014, 47, 1801–1809.
361. S. Seiffert, Scattering Perspectives on Nanostructural Inhomogeneity in Polymer Network Gels, Prog. Polym. Sci., 2017, 66, 1–21.
362. K. Saalwächter and S. Seiffert, Dynamics-based assessment of nanoscopic polymer-network mesh structures and their defects, Soft Matter, 2018, 14, 1976–1991.
363. H. Zhou, J. Woo, A. M. Cok, M. Wang, B. D. Olsen and J. A. Johnson, Counting primary loops in polymer gels, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 19119–19124.
364. D. Chan, Y. Ding, R. H. Dauskardt and E. A. Appel, Engineering the mechanical properties of polymer networks with precise doping of primary defects, ACS. Appl. Mater. Interfaces, 2017, 9, 42217–42224.
365. J. A. Johnson, D. R. Lewis, D. D. Díaz, M. Finn, J. T. Koberstein and N. J. Turro, Synthesis of degradable model networks via ATRP and click chemistry, J. Am. Chem. Soc., 2006, 128, 6564–6565.
366. M. H. Samiullah, D. Reichert, T. Zinkevich and J. R. Kressler, NMR characterization of PEG networks synthesized by CuAAC using reactive oligomers, Macromolecules, 2013, 46, 6922–6930.
367. S. Czarnecki, T. Rossow and S. Seiffert, Hybrid polymer-network hydrogels with tunable mechanical response, Polymers, 2016, 8, 82.
368. J. K. Gooden, M. L. Gross, A. Mueller, A. D. Stefanescu and K. L. Wooley, Cyclization in hyperbranched polymer syntheses: characterization by MALDI-TOF mass spectrometry, J. Am. Chem. Soc., 1998, 120, 10180–10186.
369. H. R. Kricheldorf, Polycondensation, Springer, 2016.
370. F. J. Stadler, Quantifying primary loops in polymer gels by linear viscoelasticity, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, E1972.
371. B. D. Olsen and J. A. Johnson, Reply to Stadler: Combining network disassembly spectrometry with rheology/spectroscopy, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, E1973.
372. K. Saalwächter, F. Kleinschmidt and J.-U. Sommer, Swelling heterogeneities in end-linked model networks: a combined proton multiple-quantum NMR and computer simulation study, Macromolecules, 2004, 37, 8556–8568.
373. F. Lange, K. Schwenke, M. Kurakazu, Y. Akagi, U.-I. Chung, M. Lang, J.-U. Sommer, T. Sakai and K. Saalwächter, Connectivity and structural defects in model hydrogels: A combined proton NMR and Monte Carlo simulation study, Macromolecules, 2011, 44, 9666–9674.
374. H. Zhou, E.-M. Schön, M. Wang, M. J. Glassman, J. Liu, M. Zhong, D. Díaz Díaz, B. D. Olsen and J. A. Johnson, Crossover Experiments Applied to Network Formation Reactions: Improved Strategies for Counting Elastically Inactive Molecular Defects in PEG Gels and Hyperbranched Polymers, J. Am. Chem. Soc., 2014, 136, 9464–9470.
375. K. Kawamoto, M. Zhong, R. Wang, B. D. Olsen and J. A. Johnson, Loops Versus Branch Functionality in Model Click Hydrogels, Macromolecules, 2015, 48, 8980–8988.
376. R. Wang, A. Alexander-Katz, J. A. Johnson and B. D. Olsen, Universal Cyclic Topology in Polymer Networks, Phys. Rev. Lett., 2016, 116, 188302.
377. M. Zhong, R. Wang, K. Kawamoto, B. D. Olsen and J. A. Johnson, Quantifying the Impact of Molecular Defects on Polymer Network Elasticity, Science, 2016, 353, 1264–1268.
378. R. Wang, J. A. Johnson and B. D. Olsen, Odd–even effect of junction functionality on the topology and elasticity of polymer networks, Macromolecules, 2017, 50, 2556–2564.
379. R. Wang, T.-S. Lin, J. A. Johnson and B. D. Olsen, Kinetic Monte Carlo Simulation for Quantification of the Gel Point of Polymer Networks, ACS. Macro. Lett, 2017, 6, 1414–1419.
380. T.-S. Lin, R. Wang, J. A. Johnson and B. D. Olsen, Topological Structure of Networks Formed from Symmetric Four-Arm Precursors, Macromolecules, 2018, 51, 1224–1231.
381. Y. Gu, K. Kawamoto, M. Zhong, M. Chen, M. J. Hore, A. M. Jordan, L. T. Korley, B. D. Olsen and J. A. Johnson, Semibatch Monomer Addition as a General Method to Tune and Enhance the Mechanics of Polymer Networks via Loop-Defect Control, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 4875–4880.
382. T. Sakai, T. Matsunaga, Y. Yamamoto, C. Ito, R. Yoshida, S. Suzuki, N. Sasaki, M. Shibayama and U.-I. Chung, Design and fabrication of a high-strength hydrogel with ideally homogeneous network structure from tetrahedron-like macromonomers, Macromolecules, 2008, 41, 5379–5384.
383. T. Matsunaga, T. Sakai, Y. Akagi, U.-I. Chung and M. Shibayama, SANS and SLS studies on tetra-arm PEG gels in as-prepared and swollen states, Macromolecules, 2009, 42, 6245–6252.
384. T. Matsunaga, T. Sakai, Y. Akagi, U.-I. Chung and M. Shibayama, Structure characterization of tetra-PEG gel by small-angle neutron scattering, Macromolecules, 2009, 42, 1344–1351.
385. A. Sugimura, M. Asai, T. Matsunaga, Y. Akagi, T. Sakai, H. Noguchi and M. Shibayama, Mechanical properties of a polymer network of Tetra-PEG gel, Polym. J., 2013, 45, 300.
386. R. A. Riggleman, G. Toepperwein, G. J. Papakonstantopoulos, J.-L. Barrat and J. J. de Pablo, Entanglement network in nanoparticle reinforced polymers, J. Chem. Phys., 2009, 130, 244903.
387. G. P. Baeza, C. Dessi, S. Costanzo, D. Zhao, S. Gong, A. Alegria, R. H. Colby, M. Rubinstein, D. Vlassopoulos and S. K. Kumar, Network dynamics in nanofilled polymers, Nat. Commun., 2016, 7, 1–6.
388. Q. Zhang and L. A. Archer, Poly(ethylene oxide)/silica nanocomposites: structure and rheology, Langmuir, 2002, 18, 10435–10442.
389. P. Thoniyot, M. J. Tan, A. A. Karim, D. J. Young and X. J. Loh, Nanoparticle–hydrogel composites: Concept, design, and applications of these promising, multi-functional materials, Adv. Sci., 2015, 2, 1400010.
390. C. Dannert, B. T. Stokke and R. S. Dias, Nanoparticle-hydrogel composites: from molecular interactions to macroscopic behavior, Polymers, 2019, 11, 275.
391. M. Farshad and A. Benine, Magnetoactive elastomer composites, Polymer testing, 2004, 23, 347–353.
392. S. Thomas, A. K. Chandra and P. Visakh, Advances in Elastomers II: Composites and Nanocomposites, Springer, 2012.
393. G. Heinrich, M. Klüppel and T. A. Vilgis, Reinforcement of elastomers, Curr. Opin. Solid State Mater. Sci., 2002, 6, 195–203.
394. S. K. Agrawal, N. Sanabria-DeLong, G. N. Tew and S. R. Bhatia, Nanoparticle-reinforced associative network hydrogels, Langmuir, 2008, 24, 13148–13154.
395. W. R. Illeperuma, J.-Y. Sun, Z. Suo and J. J. Vlassak, Fiber-reinforced tough hydrogels, Extreme Mech. Lett., 2014, 1, 90–96.
396. P. Calvert, Hydrogels for soft machines, Adv. Mater., 2009, 21, 743–756.
397. Y. Chen, W. Xu, W. Liu and G. Zeng, Responsiveness, swelling, and mechanical properties of PNIPA nanocomposite hydrogels reinforced by nanocellulose, J. Mater. Res., 2015, 30, 1797.
398. J. Duan, X. Liang, J. Guo, K. Zhu and L. Zhang, Ultra-stretchable and force-sensitive hydrogels reinforced with chitosan microspheres embedded in polymer networks, Adv. Mater., 2016, 28, 8037–8044.
399. J. Han, T. Lei and Q. Wu, Facile preparation of mouldable polyvinyl alcohol-borax hydrogels reinforced by well-dispersed cellulose nanoparticles: physical, viscoelastic and mechanical properties, Cellulose, 2013, 20, 2947–2958.
400. Q. Wang, R. Hou, Y. Cheng and J. Fu, Super-tough double-network hydrogels reinforced by covalently compositing with silica-nanoparticles, Soft Matter, 2012, 8, 6048–6056.
401. K. Wei, M. Zhu, Y. Sun, J. Xu, Q. Feng, S. Lin, T. Wu, J. Xu, F. Tian and J. Xia, Robust biopolymeric supramolecular “Host− Guest Macromer” hydrogels reinforced by in situ formed multivalent nanoclusters for cartilage regeneration, Macromolecules, 2016, 49, 866–875.
402. X. Yang, E. Bakaic, T. Hoare and E. D. Cranston, Injectable polysaccharide hydrogels reinforced with cellulose nanocrystals: morphology, rheology, degradation, and cytotoxicity, Biomacromolecules, 2013, 14, 4447–4455.
403. Lake, G.; GJ, L. Aspects of fatigue and fracture of rubber, 1983.
404. Y. Bréchet, J. Y. Cavaillé, E. Chabert, L. Chazeau, R. Dendievel, L. Flandin and C. Gauthier, Polymer Based Nanocomposites: Effect of Filler-Filler and Filler-Matrix Interactions, Adv. Eng. Mater., 2001, 3, 571–577.
405. S. Mubeena and A. Chatterji, Hierarchical and synergistic self-assembly in composites of model wormlike micellar-polymers and nanoparticles results in nanostructures with diverse morphologies, Eur. Phys. J. E., 2019, 42, 50.
406. A. Dorigato, Y. Dzenis and A. Pegoretti, Filler aggregation as a reinforcement mechanism in polymer nanocomposites, Mech. Mater., 2013, 61, 79–90.
407. G. P. Baeza, A.-C. Genix, C. Degrandcourt, J. R. M. Gummel, A. Mujtaba, K. Saalwächter, T. Thurn-Albrecht, M. Couty and J. Oberdisse, Studying twin samples provides evidence for a unique structure-determining parameter in simplifed industrial nanocomposites, ACS Macro Lett., 2014, 3, 448–452.
408. G. P. Baeza, J. Oberdisse, A. Alegria, K. Saalwächter, M. Couty and A.-C. Genix, Depercolation of aggregates upon polymer grafting in simplified industrial nanocomposites studied with dielectric spectroscopy, Polymer, 2015, 73, 131–138.
409. M. Bhattacharya, Polymer nanocomposites—a comparison between carbon nanotubes, graphene, and clay as nanofillers, Materials, 2016, 9, 262.
410. G. L. Hwang, Y. T. Shieh and K. C. Hwang, Efficient load transfer to polymer-grafted multiwalled carbon nanotubes in polymer composites, Adv. Funct. Mater., 2004, 14, 487–491.
411. B. Pukanszky, Influence of interface interaction on the ultimate tensile properties of polymer composites, Composites, 1990, 21, 255–262.
412. M. Yanagioka and C. W. Frank, Effect of particle distribution on morphological and mechanical properties of filled hydrogel composites, Macromolecules, 2008, 41, 5441–5450.
413. M. Yanagioka and C. W. Frank, Defect generation surrounding nanoparticles in a cross-linked hydrogel network, Langmuir, 2009, 25, 5927–5939.
414. W. Lee, N.-J. Cho, A. Xiong, J. S. Glenn and C. W. Frank, Hydrophobic nanoparticles improve permeability of cell-encapsulating poly(ethylene glycol) hydrogels while maintaining patternability, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 20709–20714.
415. F. Grasland, L. Chazeau and J.-M. Chenal, About thermo-oxidative ageing at moderate temperature of conventionally vulcanized natural rubber, Polym. Degrad. Stab., 2019, 161, 74–84.
416. J. Yang, C.-R. Han, J.-F. Duan, M.-G. Ma, X.-M. Zhang, F. Xu, R.-C. Sun and X.-M. Xie, Studies on the properties and formation mechanism of flexible nanocomposite hydrogels from cellulose nanocrystals and poly(acrylic acid), J. Mater. Chem., 2012, 22, 22467–22480.
417. G. P. Baeza, F. Dalmas, F. Dutertre and J.-C. Majesté, Isostructural softening of vulcanized nanocomposites, Soft Matter, 2020, 16, 3180–3186.
418. C. Wang, Z. Wang and X. Zhang, Amphiphilic building blocks for self-assembly: from amphiphiles to supra-amphiphiles, Acc. Chem. Res., 2012, 45, 608–618.
419. D. Lombardo, M. A. Kiselev, S. Magazù and P. Calandra, Amphiphiles self-assembly: basic concepts and future perspectives of supramolecular approaches, Adv. Condens. Matter. Phys., 2015, 2015, 151683.
420. C. K. Bagdassarian, D. Roux, A. Ben-Shaul and W. M. Gelbart, Curvature defects in lamellar phases of amphiphile–water systems, J. Chem. Phys., 1991, 94, 3030–3041.
421. B. Halle, P.-O. Quist and I. Furó, Microstructure and dynamics in lyotropic liquid crystals. Principles and applications of nuclear spin relaxation, Liq. Cryst., 1993, 14, 227–263.
422. P.-O. Quist and B. Halle, Curvature defects in a lamellar phase revealed by nuclear-spin-relaxation anisotropy, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 47, 3374.
423. S. Pogodin, M. Werner, J.-U. Sommer and V. A. Baulin, Nanoparticle-induced permeability of lipid membranes, ACS Nano, 2012, 6, 10555–10561.
424. A. Pal, G. Pabst and V. Raghunathan, Defect-mediated lamellar–isotropic transition of amphiphile bilayers, Soft Matter, 2012, 8, 9069–9072.
425. B. Wang, L. Zhang, S. C. Bae and S. Granick, Nanoparticle-induced surface reconstruction of phospholipid membranes, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 18171–18175.
426. P. R. Leroueil, S. A. Berry, K. Duthie, G. Han, V. M. Rotello, D. Q. McNerny, J. R. Baker Jr, B. G. Orr and M. M. Banaszak Holl, Wide varieties of cationic nanoparticles induce defects in supported lipid bilayers, Nano Lett., 2008, 8, 420–424.
427. X. Xiao, G. A. Montaño, T. L. Edwards, A. Allen, K. E. Achyuthan, R. Polsky, D. R. Wheeler and S. M. Brozik, Surface charge dependent nanoparticle disruption and deposition of lipid bilayer assemblies, Langmuir, 2012, 28, 17396–17403.
428. K. Lee, L. Zhang, Y. Yi, X. Wang and Y. Yu, Rupture of lipid membranes induced by amphiphilic Janus nanoparticles, ACS Nano, 2018, 12, 3646–3657.
429. K. Lee and Y. Yu, Lipid bilayer disruption induced by amphiphilic Janus nanoparticles: the non-monotonic effect of charged lipids, Soft Matter, 2019, 15, 2373–2380.
430. K. Lee and Y. Yu, Lipid Bilayer Disruption by Amphiphilic Janus Nanoparticles: The Role of Janus Balance, Langmuir, 2018, 34, 12387–12393.
431. B. Jing and Y. Zhu, Disruption of supported lipid bilayers by semihydrophobic nanoparticles, J. Am. Chem. Soc., 2011, 133, 10983–10989.
432. B. Jing, R. C. Abot and Y. Zhu, Semihydrophobic nanoparticle-induced disruption of supported lipid bilayers: specific ion effect, J. Phys. Chem. B, 2014, 118, 13175–13182.
433. J. Chen, J. A. Hessler, K. Putchakayala, B. K. Panama, D. P. Khan, S. Hong, D. G. Mullen, S. C. DiMaggio, A. Som and G. N. Tew, Cationic nanoparticles induce nanoscale disruption in living cell plasma membranes, J. Phys. Chem. B, 2009, 113, 11179–11185.
434. S. Tatur, M. Maccarini, R. Barker, A. Nelson and G. Fragneto, Effect of functionalized gold nanoparticles on floating lipid bilayers, Langmuir, 2013, 29, 6606–6614.
435. S. Hong, A. U. Bielinska, A. Mecke, B. Keszler, J. L. Beals, X. Shi, L. Balogh, B. G. Orr, J. R. Baker Jr and M. M. Banaszak Holl, Interaction of poly(amidoamine) dendrimers with supported lipid bilayers and cells: hole formation and the relation to transport, Bioconjugate Chem., 2004, 15, 774–782.
436. D. Soloveichik and E. Winfree, Complexity of self-assembled shapes, SIAM J. Comput., 2007, 36, 1544–1569.
437. G. M. Whitesides and M. Boncheva, Beyond molecules: Self-assembly of mesoscopic and macroscopic components, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 4769–4774.
438. J. Halpern, Reaching across the sciences. National Acad Sciences, 2002.
439. L. J. Atwood; J. E. D. Davies; F. Vögtle and J.-M. Lehn, Comprehensive supramolecular chemistry, Pergamon, NY, New York, vol. 8, 1996.
440. R. Ungaro and E. Dalcanale, Supramolecular Science: Where it is and Where it is Going, Springer Science & Business Media, 2012, vol. 527.
441. J. M. Lehn, Supramolecular chemistry—scope and perspectives molecules, supermolecules, and molecular devices (Nobel Lecture), Angew. Chem., Int. Ed. Engl., 1988, 27, 89–112.
442. L. Isaacs, D. N. Chin, N. Bowden, Y. Xia and G. M. Whitesides, Self-Assembling Systems on Scales from Nanometers to Millimeters: Design and Discovery, Perspect. Supramol. Chem., 1999, 4, 1–46.
443. E. Weber; Y. Aoyama; M. Caira; G. Desiraju; J. Glusker; A. Hamilton; R. Meléndez and A. Nangia, Design of organic solids, 1998.
444. D. Fennell Evans, H. Wennerstrom and R. Rajagopalan, The colloidal domain: where physics, chemistry, biology, and technology meet, J. Colloid Interface Sci., 1995, 172, 541.
445. D. Chapman; M. N. Jones and M. Jones, Micelles, monolayers, and biomembranes, Wiley-Liss, 1995.
446. E. L. Thomas, The ABCs of self-assembly, Science, 1999, 286, 1307.
447. A. Kumar, N. L. Abbott, H. A. Biebuyck, E. Kim and G. M. Whitesides, Patterned self-assembled monolayers and meso-scale phenomena, Acc. Chem. Res., 1995, 28, 219–226.
448. V. Grantcharova, E. J. Alm, D. Baker and A. L. Horwich, Mechanisms of protein folding, Curr. Opin. Struct. Biol., 2001, 11, 70–82.
449. S. Neidle, Oxford handbook of nucleic acid structure, Oxford University Press on Demand, 1999.
450. A. Kluber, T. A. Burt and C. Clementi, Size and topology modulate the effects of frustration in protein folding, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 9234–9239.
451. T. Sanchez, D. T. Chen, S. J. DeCamp, M. Heymann and Z. Dogic, Spontaneous motion in hierarchically assembled active matter, Nature, 2012, 491, 431.
452. G. M. Grason, Self-assembly: Misfits unite, Nat. Phys, 2017, 13, 1149.
453. G. Foffi, G. D. McCullagh, A. Lawlor, E. Zaccarelli, K. A. Dawson, F. Sciortino, P. Tartaglia, D. Pini and G. Stell, Phase equilibria and glass transition in colloidal systems with short-ranged attractive interactions: application to protein crystallization, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 031407.
454. F. Cardinaux, T. Gibaud, A. Stradner and P. Schurtenberger, Interplay between spinodal decomposition and glass formation in proteins exhibiting short-range attractions, Phys. Rev. Lett., 2007, 99, 118301.
455. M. Lenz and T. A. Witten, Geometrical frustration yields fibre formation in self-assembly, Nat. Phys, 2017, 13, 1100.
456. L. Bousset, N. H. Thomson, S. E. Radford and R. Melki, The yeast prion Ure2p retains its native α-helical conformation upon assembly into protein fibrils in vitro, EMBO J., 2002, 21, 2903–2911.
457. W. A. Eaton and J. Hofrichter, Sickle cell hemoglobin polymerization, in Advances in Protein Chemistry, Elsevier: 1990, vol. 40, pp. 63–279.
458. J. Wagner and R. Zandi, The Robust Assembly of Small Symmetric Nanoshells, Biophys. J., 2015, 109, 956–965.
459. R. V. Mannige and C. L. Brooks III, Periodic table of virus capsids: implications for natural selection and design, PLoS One, 2010, 5, e9423.
460. J. G. Llorente, J. Hernandez-Rojas and J. Breton, A minimal representation of the self-assembly of virus capsids, Soft Matter, 2014, 10, 3560–3569.
461. J. Spiriti, J. F. Conway and D. M. Zuckerman, Should virus capsids assemble perfectly? Theory and observation of defects, bioRxiv, 2019, 684563.
462. T. I. Löbling, O. Borisov, J. S. Haataja, O. Ikkala, A. H. Gröschel and A. H. Müller, Rational design of ABC triblock terpolymer solution nanostructures with controlled patch morphology, Nat. Commun., 2016, 7, 12097.
463. A. P. Marencic and R. A. Register, Controlling order in block copolymer thin films for nanopatterning applications, Annu. Rev. Chem. Biomol. Eng., 2010, 1, 277–297.
464. W. Li and M. Müller, Defects in the self-assembly of block copolymers and their relevance for directed self-assembly, Annu. Rev. Chem. Biomol. Eng., 2015, 6, 187–216.
465. S. Darling, Directing the self-assembly of block copolymers, Prog. Polym. Sci., 2007, 32, 1152–1204.
466. H. Hu, M. Gopinadhan and C. O. Osuji, Directed self-assembly of block copolymers: a tutorial review of strategies for enabling nanotechnology with soft matter, Soft Matter, 2014, 10, 3867–3889.
467. I. P. Campbell, S. Hirokawa and M. P. Stoykovich, Processing approaches for the defect engineering of lamellar-forming block copolymers in thin films, Macromolecules, 2013, 46, 9599–9608.
468. M. R. Hammond, S. W. Sides, G. H. Fredrickson, E. J. Kramer, J. Ruokolainen and S. F. Hahn, Adjustment of block copolymer nanodomain sizes at lattice defect sites, Macromolecules, 2003, 36, 8712–8716.
469. U. Nagpal, M. Müller, P. F. Nealey and J. J. De Pablo, Free energy of defects in ordered assemblies of block copolymer domains, ACS Macro Lett., 2012, 1, 418–422.
470. J. Harting, M. J. Harvey, J. Chin and P. V. Coveney, Detection and tracking of defects in the gyroid mesophase, Computer physics communications, 2005, 165, 97–109.
471. X. Feng, H. Guo and E. L. Thomas, Topological defects in tubular network block copolymers, Polymer, 2019, 168, 44–52.
472. D. E. Angelescu, J. H. Waller, R. A. Register and P. M. Chaikin, Shear-induced alignment in thin films of spherical nanodomains, Adv. Mater., 2005, 17, 1878–1881.
473. S. Park, L. Tsarkova, S. Hiltl, S. Roitsch, J. Mayer and A. Böker, Guiding block copolymers into sequenced patterns via inverted terrace formation, Macromolecules, 2012, 45, 2494–2501.
474. M. Luo, D. M. Scott and T. H. Epps III, Writing highly ordered macroscopic patterns in cylindrical block polymer thin films via raster solvent vapor annealing and soft shear, ACS Macro Lett., 2015, 4, 516–520.
475. S. Ji, L. Wan, C.-C. Liu and P. F. Nealey, Directed self-assembly of block copolymers on chemical patterns: A platform for nanofabrication, Prog. Polym. Sci., 2016, 54, 76–127.
476. A. A. Abate, G. T. Vu, A. D. Pezzutti, N. A. García, R. L. Davis, F. Schmid, R. A. Register and D. A. Vega, Shear-aligned block copolymer monolayers as seeds to control the orientational order in cylinder-forming block copolymer thin films, Macromolecules, 2016, 49, 7588–7596.
477. J. Choi, J. Huh, K. R. Carter and T. P. Russell, Directed self-assembly of block copolymer thin films using minimal topographic patterns, ACS Nano, 2016, 10, 7915–7925.
478. R. A. Griffiths, A. Williams, C. Oakland, J. Roberts, A. Vijayaraghavan and T. Thomson, Directed self-assembly of block copolymers for use in bit patterned media fabrication, J. Phys. D: Appl. Phys., 2013, 46, 503001.
479. H.-C. Kim, S.-M. Park and W. D. Hinsberg, Block copolymer based nanostructures: materials, processes, and applications to electronics, Chem. Rev., 2010, 110, 146–177.
480. M. Luo and T. H. Epps III, Directed block copolymer thin film self-assembly: emerging trends in nanopattern fabrication, Macromolecules, 2013, 46, 7567–7579.
481. C.-C. Liu, A. Ramírez-Hernández, E. Han, G. S. Craig, Y. Tada, H. Yoshida, H. Kang, S. Ji, P. Gopalan and J. J. de Pablo, Chemical patterns for directed self-assembly of lamellae-forming block copolymers with density multiplication of features, Macromolecules, 2013, 46, 1415–1424.
482. M. P. Stoykovich, M. Müller, S. O. Kim, H. H. Solak, E. W. Edwards, J. J. De Pablo and P. F. Nealey, Directed assembly of block copolymer blends into nonregular device-oriented structures, Science, 2005, 308, 1442–1446.
483. E. A. Matsumoto, D. A. Vega, A. D. Pezzutti, N. A. García, P. M. Chaikin and R. A. Register, Wrinkles and splay conspire to give positive disclinations negative curvature, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 12639–12644.
484. G. T. Vu, A. A. Abate, L. R. Gómez, A. D. Pezzutti, R. A. Register, D. A. Vega and F. Schmid, Curvature as a guiding field for patterns in thin block copolymer films, Phys. Rev. Lett., 2018, 121, 087801.
485. D. Yamaguchi and T. Hashimoto, A phase diagram for the binary blends of nearly symmetric diblock copolymers. 1. Parameter space of molecular weight ratio and blend composition, Macromolecules, 2001, 34, 6495–6505.
486. G. Hadziioannou and A. Skoulios, Structural study of mixtures of styrene isoprene two-and three-block copolymers, Macromolecules, 1982, 15, 267–271.
487. R. P. Sijbesma, F. H. Beijer, L. Brunsveld, B. J. Folmer, J. K. Hirschberg, R. F. Lange, J. K. Lowe and E. Meijer, Reversible polymers formed from self-complementary monomers using quadruple hydrogen bonding, Science, 1997, 278, 1601–1604.
488. L. Brunsveld, B. Folmer, E. W. Meijer and R. Sijbesma, Supramolecular polymers, Chem. Rev., 2001, 101, 4071–4098.
489. E. Krieg, M. M. Bastings, P. Besenius and B. Rybtchinski, Supramolecular polymers in aqueous media, Chem. Rev., 2016, 116, 2414–2477.
490. T. Aida, E. Meijer and S. I. Stupp, Functional supramolecular polymers, Science, 2012, 335, 813–817.
491. T. F. De Greef, M. M. Smulders, M. Wolffs, A. P. Schenning, R. P. Sijbesma and E. Meijer, Supramolecular polymerization, Chem. Rev., 2009, 109, 5687–5754.
492. Y. Tidhar, H. Weissman, S. G. Wolf, A. Gulino and B. Rybtchinski, Pathway-dependent self-assembly of perylene diimide/peptide conjugates in aqueous medium, Chem. – Eur. J., 2011, 17, 6068–6075.
493. P. A. Korevaar, S. J. George, A. J. Markvoort, M. M. Smulders, P. A. Hilbers, A. P. Schenning, T. F. De Greef and E. Meijer, Pathway complexity in supramolecular polymerization, Nature, 2012, 481, 492–496.
494. M. Wehner and F. Würthner, Supramolecular polymerization through kinetic pathway control and living chain growth, Nat. Rev. Chem., 2019, 1–16.
495. S. Ogi, K. Sugiyasu, S. Manna, S. Samitsu and M. Takeuchi, Living supramolecular polymerization realized through a biomimetic approach, Nat. Chem., 2014, 6, 188.
496. N. M. Matsumoto, R. P. Lafleur, X. Lou, K.-C. Shih, S. P. Wijnands, C. M. Guibert, J. W. van Rosendaal, I. K. Voets, A. R. Palmans and Y. Lin, Polymorphism in benzene-1,3,5-tricarboxamide supramolecular assemblies in water: a subtle trade-off between structure and dynamics, J. Am. Chem. Soc., 2018, 140, 13308–13316.
497. J. Matern, Y. Dorca, L. Sánchez and G. Fernandez, Revising complex supramolecular polymerization under kinetic and thermodynamic control, Angew. Chem., Int. Ed., 2019, 58, 16730–16740.
498. P. Besenius, Controlling supramolecular polymerization through multicomponent self-assembly, J. Polym. Sci. Part A, Polym. Chem., 2017, 55, 34–78.
499. D. Bochicchio, M. Salvalaglio and G. M. Pavan, Into the dynamics of a supramolecular polymer at submolecular resolution, Nat. Commun., 2017, 8, 1–11.
500. L. Albertazzi, D. van der Zwaag, C. M. Leenders, R. Fitzner, R. W. van der Hofstad and E. Meijer, Probing exchange pathways in one-dimensional aggregates with super-resolution microscopy, Science, 2014, 344, 491–495.
501. P. Gasparotto, D. Bochicchio, M. Ceriotti and G. M. Pavan, Identifying and Tracking Defects in Dynamic Supramolecular Polymers, J. Phys. Chem. B, 2020, 124(3), 589–599.
502. D. Bochicchio, S. Kwangmettatam, T. Kudernac and G. M. Pavan, How defects control the out-of-equilibrium dissipative evolution of a supramolecular tubule, ACS Nano, 2019, 13, 4322–4334.
503. J. W. Fredy, A. Méndez-Ardoy, S. Kwangmettatam, D. Bochicchio, B. Matt, M. C. Stuart, J. Huskens, N. Katsonis, G. M. Pavan and T. Kudernac, Molecular photoswitches mediating the strain-driven disassembly of supramolecular tubules, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 11850–11855.
504. A. Louhichi, A. Jacob, L. Bouteiller and D. Vlassopoulos, Humidity affects the viscoelastic properties of supramolecular living polymers, J. Rheol., 2017, 61, 1173–1182.
505. P. Cordier, F. Tournilhac, C. Soulié-Ziakovic and L. Leibler, Self-healing and thermoreversible rubber from supramolecular assembly, Nature, 2008, 451, 977–980.
506. M. Burnworth, L. Tang, J. R. Kumpfer, A. J. Duncan, F. L. Beyer, G. L. Fiore, S. J. Rowan and C. Weder, Optically healable supramolecular polymers, Nature, 2011, 472, 334–337.
507. T. T. Myllymaki, L. Lemetti and O. Ikkala, Hierarchical supramolecular cross-linking of polymers for biomimetic fracture energy dissipating sacrificial bonds and defect tolerance under mechanical loading, ACS Macro Lett., 2017, 6, 210–214.
508. J. Dahlke, S. Zechel, M. D. Hager and U. S. Schubert, How to design a self-healing polymer: general concepts of dynamic covalent bonds and their application for intrinsic healable materials, Adv. Mater. Interfaces, 2018, 5, 1800051.
509. A. Campanella, D. Döhler and W. H. Binder, Self-healing in supramolecular polymers, Macromol. Rapid Commun., 2018, 39, 1700739.
510. Y. Li, A. Hammoud, L. Bouteiller and M. Raynal, Emergence of homochiral benzene-1,3,5-tricarboxamide helical assemblies and catalysts upon addition of an achiral monomer, J. Am. Chem. Soc., 2020, 142, 5676–5688.
511. A. R. Palmans and E. E. W. Meijer, Amplification of chirality in dynamic supramolecular aggregates, Angew. Chem., Int. Ed., 2007, 46, 8948–8968.
512. A. Desmarchelier, X. Caumes, M. Raynal, A. Vidal-Ferran, P. W. van Leeuwen and L. Bouteiller, Correlation between the selectivity and the structure of an asymmetric catalyst built on a chirally amplified supramolecular helical scaffold, J. Am. Chem. Soc., 2016, 138, 4908–4916.
513. K. Shimomura, T. Ikai, S. Kanoh, E. Yashima and K. Maeda, Switchable enantioseparation based on macromolecular memory of a helical polyacetylene in the solid state, Nat. Chem., 2014, 6, 429.
514. J. J. Armao IV, M. Maaloum, T. Ellis, G. Fuks, M. Rawiso, E. Moulin and N. Giuseppone, Healable supramolecular polymers as organic metals, J. Am. Chem. Soc., 2014, 136, 11382–11388.
515. C. F. Fitié, W. C. Roelofs, M. Kemerink and R. P. Sijbesma, Remnant polarization in thin films from a columnar liquid crystal, J. Am. Chem. Soc., 2010, 132, 6892–6893.
516. T. Shikata, Y. Kuruma, A. Sakamoto and K. Hanabusa, Segment sizes of supramolecular polymers of N,N′,N′′-Tris(3,7-dimethyloctyl) benzene-1,3,5-tricarboxamide in n-decane, J. Phys. Chem. B, 2008, 112, 16393–16402.
517. S. Cantekin, T. F. de Greef and A. R. Palmans, Benzene-1,3,5-tricarboxamide: a versatile ordering moiety for supramolecular chemistry, Chem. Soc. Rev., 2012, 41, 6125–6137.
518. C. S. Zehe, J. A. Hill, N. P. Funnell, K. Kreger, K. P. van der Zwan, A. L. Goodwin, H. W. Schmidt and J. Senker, Mesoscale polarization by geometric frustration in columnar supramolecular crystals, Angew. Chem., Int. Ed., 2017, 56, 4432–4437.
519. S. Hudson, H.-T. Jung, V. Percec, W.-D. Cho, G. Johansson, G. Ungar and V. Balagurusamy, Direct visualization of individual cylindrical and spherical supramolecular dendrimers, Science, 1997, 278, 449–452.
520. H.-T. Jung, S. O. Kim, S. Hudson and V. Percec, Elastic properties of hexagonal columnar mesophase self-organized from amphiphilic supramolecular columns, Appl. Phys. Lett., 2002, 80, 395–397.
521. T. D. Cornelissen, M. Biler, I. Urbanaviciute, P. Norman, M. Linares and M. Kemerink, Kinetic Monte Carlo simulations of organic ferroelectrics, Phys. Chem. Chem. Phys., 2019, 21, 1375–1383.
522. L. D. Carr and M. T. Lusk, Defect engineering: Graphene gets designer defects, Nat. Nanotechnol, 2010, 5, 316.
523. A. W. Robertson, C. S. Allen, Y. A. Wu, K. He, J. Olivier, J. Neethling, A. I. Kirkland and J. H. Warner, Spatial control of defect creation in graphene at the nanoscale, Nat. Commun., 2012, 3, 1144.

---