Open Access Article
Open Access ArticleCatalytically propelled 3D printed colloidal microswimmers†
Rachel P.
Doherty
,
Thijs
Varkevisser
,
Margot
Teunisse
,
Jonas
Hoecht
,
Stefania
Ketzetzi
,
Samia
Ouhajji
and
Daniela J.
Kraft
 *
*
Soft Matter Physics, Huygens-Kamerlingh Onnes Laboratory, Leiden University, P.O. Box 9504, 2300 RA Leiden, The Netherlands. E-mail: kraft@physics.leidenuniv.nl
First published on 12th October 2020
Abstract
Synthetic microswimmers are widely employed model systems in the studies of out-of-equilibrium phenomena. Unlike biological microswimmers which naturally occur in various shapes and forms, synthetic microswimmers have so far been limited almost exclusively to spherical shapes. Here, we exploit 3D printing to produce microswimmers with complex shapes in the colloidal size regime. We establish the flexibility of 3D printing by two-photon polymerisation to produce particles smaller than 10 microns with a high-degree of shape complexity. We further demonstrate that 3D printing allows control over the location of the active site through orienting the particles in different directions during printing. We verify that particles behave colloidally by imaging their motion in the passive and active states and by investigating their mean square displacement. In addition, we find that particles exhibit shape-dependant behavior, thereby demonstrating the potential of our method to launch a wide-range of in-depth studies into shape-dependent active motion and behaviour.
1 Introduction
Shape and motion in synthetic and biological microswimmers are intimately connected. Theoretical and numerical studies on anisotropic swimmers predicted that any breaking of the particle or patch symmetry perpendicular to the propulsion direction induces an instability and leads to chiral motion.1–3 In two dimensions such chirality results in circular motion,4,5 while in three dimensions a concho spiral has been predicted by simulations.1 Besides steering self-propulsion, a recent theoretical study proposed that the anisotropic shape of biological microswimmers may have an additional function. That is, swimmers with a non-uniaxial shape experience torques that align them in viscosity gradients, providing an alternative mechanism to active alignment by other, energy-consuming, mechanisms such as flagella.6 Anisotropy is also expected to influence the interactions and collective behaviour of microswimmers.3,7,8 For instance, the torques and alignments experienced by active rods and dumbbells have been theoretically predicted to affect9 or even suppress10,11 the fascinating motility-induced phase-separation into a dilute gas-like and dense cluster phase seen in active spheres.12–14 Moreover, anisotropic microswimmers may align or reflect upon collision, segregate, or assemble into aligned fronts and microrotors.15Synthetic colloidal microswimmers,7,16–19 also known as active particles, can be employed as model systems to test these predictions and gain quantitative insights into the motion of biological microswimmers. They self-propel at low Reynolds numbers by converting energy available in their local environment into directed motion. This is achieved by exploitation of an intrinsic asymmetry, most commonly an anisotropic platinum patch which catalyses hydrogen peroxide decomposition,20,21 introduced into the material properties of the microswimmers.
Systematic investigation of shape-dependant behaviours requires a robust method to synthesize particles with diverse and complex shapes. Currently the vast majority of synthetic microswimmers are synthesized by either chemical or evaporation techniques.16,17,19 These methods, while having advantages, also have limitations in terms of shape availability, restricting studies to predominantly spherical or rod-like colloids. The straight trajectories that are associated with a spherical shape are rather an exceptional case in view of the many possibilities for achieving other types of motion.
Already, the limited number of studies on shape-dependent motion of synthetic particles have provided interesting insights into the effect of shape. One such study showed that L-shaped particles exhibit circular trajectories.22 More recent experiments on select anisotropic shapes or patches confirmed some of the predictions in 2D23–26 and found unexpected motion patterns such as non-cylindrical helices27 in 3D. Still, the current limitations in particle design prevent a systematic comparison with theory. The lack of comparison in turn hinders the disentangling of the shape-dependent contribution to the trajectories of microswimmers, their taxis in a complex environment and their collective behaviour. These insights from active model systems are relevant for understanding the motility of biological microswimmers and for example in the prevention of the formation of bacterial colonies and biofilms.
A promising technique to overcome these limitations is two-photon polymerisation (2PP). 2PP has been established as a very powerful tool to 3D print microstructures with a great deal of flexibility in terms of shape and symmetry and allows the formation of structures with sub-micron resolution.28–31 Moreover, in addition to complex shape diversity, 3D-printing also provides freedom in terms of active patch location as the user can decide how a particle is oriented relative to the substrate on which it is printed and hence the location of the active patch during sputter coating, ultimately allowing additional control over the resulting active motion.
Despite the fields of active matter and 3D micro-printing being both fully established, the combination of these two domains has been barely touched upon. The potential of 2PP to create microswimmers with a wide range of geometries is immense, allowing the production of particles with almost any desired shape, see Fig. 1 and ref. 32 and 33. Existing publications that combine 3D micro-printing and active matter have, thus far, focused on printing active particles that are either larger than 10 microns or have relatively simple shapes.34–36 These include 3D-printed microtorii,35 bullet-shaped particles36 and particles with serrated tails.34 In addition to these studies, which use local fuel-based propulsion, other studies produced helical swimmers propelled by an external magnetic field.37–39 The use of external fields is, however, not practical in many applications which require autonomous motion of the particles themselves.
 | ||
| Fig. 1 SEM images of various 3D printed particle shapes as obtained by two-photon polymerisation. (a) A spiky sphere, (b) a starship, (c) a spiral, (d) a helix, (e) a trimer and (f) 3D benchy boat. | ||
In this paper, we will demonstrate the versatility of 3D microprinting to create microswimmers with complex shapes, overcoming the current limitations in synthesizing complex colloids and allowing the disentanglement of the shape-contribution to active motion. Answering how symmetry and shape couple to motility and motion patterns, is of significant value in understanding synthetic and biological active systems alike, individually and collectively. Additionally, from an engineering perspective, it will, ultimately, allow greater control over active systems.
2 Experimental
2.1 Particle fabrication
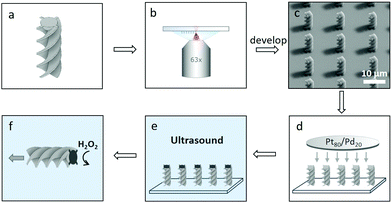
3D printed active particles were prepared by the method summarised in Fig. 2. A commercially available 3D microprinter (Photonic Professional GT, Nanoscribe GmbH) which utilises 2PP was equipped with a 63× oil-immersion objective (Zeiss, NA = 1.4) and used to print the 3D structures in dip mode. The structures were designed in Autodesk Inventor and processed by Describe. Large arrays of particles were printed onto fused-silica substrates cleaned with isopropanol using the commercial photoresist IP-Dip. This combination of photoresist, substrate and lens was chosen to give the highest possible resolution available. The number of particles that can be printed per unit area, is limited only by the size of the particle, as the user can decide where each particle is placed on the substrate. Issues of scale-up are currently being addressed by a number of groups, for example by exploiting a femtosecond projection approach40 and 3D light interference technology.41After printing, the structures were developed by submersion for 30 min in propylene glycol methylether acrylate (PGMA) followed by gently dipping into isopropanol (IPA) five times. The structures were subsequently left to dry in air. After drying, the structures were coated with a catalytically active 5 nm layer of Pt/Pd (80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20) using a Cressington 208HR sputter-coater. The sample was rotated during deposition to improve homogeneity of the resulting layer. After sputter-coating, excess Pt/Pd was removed from the substrate with a cotton bud without disturbing the printed structures. The substrate was then submerged in MilliQ water and sonicated for 10 minutes releasing the particles from the substrate. After sonication the substrate was removed and the particle solution was centrifuged and concentrated by removal of the supernatant. During this process a significant percentage of particles are lost, probably due to van der Waals interactions between particles and the container wall. We are currently looking at ways to mitigate this problem, such as by adding a stabilising agent to the particles. We have also observed that using only glass containers throughout processing leads to a significantly higher yield of particles.
20) using a Cressington 208HR sputter-coater. The sample was rotated during deposition to improve homogeneity of the resulting layer. After sputter-coating, excess Pt/Pd was removed from the substrate with a cotton bud without disturbing the printed structures. The substrate was then submerged in MilliQ water and sonicated for 10 minutes releasing the particles from the substrate. After sonication the substrate was removed and the particle solution was centrifuged and concentrated by removal of the supernatant. During this process a significant percentage of particles are lost, probably due to van der Waals interactions between particles and the container wall. We are currently looking at ways to mitigate this problem, such as by adding a stabilising agent to the particles. We have also observed that using only glass containers throughout processing leads to a significantly higher yield of particles.
2.2 Imaging
Scanning Electron Microscopy (SEM) images were taken with a Thermo-Fisher ApreoSEM either of an array, directly after printing and sputter-coating, or after removal of the particles from the substrate, in which case the resulting particle solution was deposited onto a SEM stub and allowed to dry in air.Brownian and active motion measurements were performed on a Nikon Eclipse Ti-E bright-field light microscope with a 60× long working distance objective (NA = 0.7). Measurements of Brownian motion were taken in MilliQ water and active measurements in a freshly prepared aqueous solution of 10% (v/v) hydrogen peroxide using a sample holder with an untreated borosilicate glass coverslip (VWR, 25 mm, No. 1) at the base. All active measurements were taken in the dark and during the first hour of exposure of the particles to hydrogen peroxide solution to ensure that the measurements were consistent and not significantly affected by hydrogen peroxide depletion. A 30 s movie was taken of each particle at a frame rate of 18.92 fps, unless stated otherwise.
2.3 Data analysis
Particle tracking was performed using the Trackpy algorithm42 which is a python implementation of an algorithm originally created by Crocker and Grier.43 For the spherical-like particles TrackPy was used as is. The helical particles were initially fitted with a rectangle prior to tracking with an adapted version of Trackpy. This was achieved by converting the original images into binary images, based on local intensity differences, with the adaptiveThreshold function in the OpenCV python package. A rectangle was then fitted to the contour of the helix in each frame. The centre of mass of this rectangle was then used as the particle coordinates to allow tracking.Mean-square displacement (MSD) profiles of the particles were calculated using the obtained trajectories. Translational velocities were calculated from the MSD profiles following the method outlined initially by Howse et al.20 and developed further by Bechinger et al.18 by treating the system as if it is two-dimensional. This assumption can be made because the particles quickly settled to the surface of the container and always propelled parallel to the surface. Active particles are expected to exhibit three regimes:18 A first short-term Brownian regime, where Δt ≪ τr, with τr as the inverse of the rotational diffusion constant Dr, a mid-term active regime, where Δt ≈ τr and finally a longer-term second Brownian regime, where Δt ≫ τr. For reference, τr for a sphere with a diameter of 4 μm is 49 s. The translational diffusion constant for our active particles, D, was calculated by performing a least squares fit with MSD = 4DΔt + 2V2Δt2 in the mid-term active regime, where Δt is the lag time and V is the particle velocity. Initially both V and D were left open in the fit. To ensure that the fit captured the mid-term directed motion of the particles, only lag times between Δt = 1 and 2.5 s were used. This range in lag times was determined by examining the log–log plot of the MSD. Here, we were able to observe that the active regime was established after 1 s. The weighted average of the diffusion constants from the initial fits was then used to recalculate the velocity of each particle by refitting the MSD with the above equation and the obtained value for D. We note that employing this approach for anisotropic microswimmers requires the assumption that D is isotropic for simplicity.44
3 Results and discussion
3.1 Spherical particles
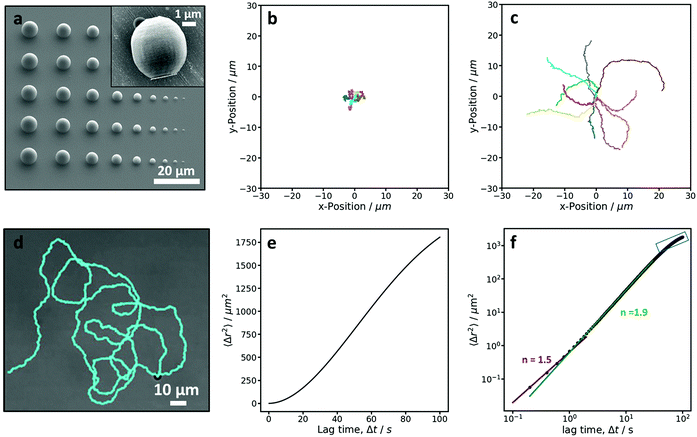
To investigate and demonstrate the feasibility of preparing active colloidal particles by 2PP, we started by printing the simplest colloidal shape, a sphere. To begin, the size limit of our 3D microprinter was investigated by printing spherical particles over a range of 1–10 μm in diameter. This allowed us to determine the smallest “spherical” size that could still be printed, see Fig. 3a. Below 4 μm, it was difficult to print particles that were even close to being spherical. This is due to the extended shape of the printing voxel in the direction along the writing beam and a slight embedding of each print into the substrate, which is necessary to connect the print to the substrate and stabilise it. A compromise between sphericity and size was made and we determined that the lower size limit for spheres printed by this method is 4 μm. A SEM image of a single sphere-like particle is shown in the inset of Fig. 3a. The brighter patch on one side of the particle is due to the platinum coating. The particles exhibit a small degree of surface roughness due to the nature of the additive printing method, which can be reduced by minimizing the distance between layers.Subsequently, a large array of 4 μm sphere-like particles were printed, coated with platinum and transferred from the substrate into water. In water, these particles exhibited Brownian motion, which can be seen from the trajectories in Fig. 3b, confirming that the particles are behaving as colloids. In 10% hydrogen peroxide the catalytic reaction at the Pt patch induces the widely employed self-propulsion of our 3D printed particles. Fig. 3c shows the trajectories of active particles. The difference between the passive trajectories in water and those in hydrogen peroxide solution show that through a simple coating procedure 3D printed colloids can be made active. The active motion is clearly seen in the longer persistence length observed for the active particles compared to the passive Brownian particles; the active particles cover greater distances during the same amount of time as the passive particles and the motion is considerably more directed.
As active colloidal motion is characterised by the interplay between propulsion and random thermal fluctuations, hence the term active Brownian motion, the activity of a particle can also be quantified by measuring the mean-squared-displacement (MSD). Active particles are initially expected to behave as Brownian particles in the short-term, move with directed motion in the mid-term, and random Brownian motion again at longer time scales, where the motion reverts to a random walk.18 The MSD curves, shown in Fig. 3e and f, of the active motion of a single 4 μm microswimmer shows behavior consistent with that of an active colloidal system. The MSD is calculated from the trajectory of a 23 minute video (see Fig. 3d) with a frame rate of 5 fps, and, as expected, shows three regimes. The log–log plot, Fig. 3f, was fitted to a powerlaw, 〈Δr2〉 = A〈Δt〉n for the different regimes, where n is the exponent and characteristic of the type of motion observed for each regime. For Brownian and active regimes exponents of 1 and 2 are expected, respectively. The short term regime exhibited an exponent of 1.51 ± 0.03, which is higher than expected18 and might be due to the limitation of the lower frame rate used in this measurement. The mid-term active regime has an exponent of 1.868 ± 0.002, confirming the active nature of this microswimmer. Finally, the beginning of the long term randomisation regime is also visible in Fig. 3f, but could not be fitted in a reliable manner. From the MSD, we also determined the average velocity of our sphere-like microswimmers and found it to be 0.5 ± 0.1 μm s−1. The value that we measure here is slightly lower than values previously measured in the same hydrogen peroxide concentration above similar glass substrates with smooth 2.7 μm TPM (3-(trimethoxysilyl)propyl methacrylate) spheres,45 in line with the inverse speed-size scaling found by Ebbens et al.46 The 2.7 μm TPM particles exhibited a speed of 1.05 ± 0.09 μm s−1. We would, therefore, expect 4 μm spheres to swim with a speed of 0.7 μm s−1 in comparison to 0.5 ± 0.1 μm s−1 which we measured here. The slight reduction in the observed speed could be the result of multiple factors such as the non-perfect particle sphericity, surface roughness,47 particle material, and Pt coating.48–50
3.2 Anisotropic particles
Once we established that active colloidal particles can be prepared by 3D printing, we printed more complex structures. Examples of potential microswimmers are shown in the SEM images in Fig. 1. Here, the true advantage of using a 3D microprinter can be seen. It becomes very simple to build complex details and anisotropy into the particles, such as spikey spheres, boats, spaceships or more conventional shapes like trimers. The boat, known as 3DBenchy51 (short for benchmark), is designed with a large array of challenging geometrical features, such as portholes and an open cabin, that provide a challenge to 3D printers with the aim of testing and benchmarking them. As can be seen in Fig. 1f our 3D microprinter successfully prints these fine details. All the examples in Fig. 1 are either below 10 microns in size or approaching this. As can be seen in the images the resolution of the fine features that can be printed by 2PP is of the order of 100 nm. We also observed a high fidelity between particles and prints, which adds another advantage to this method. This could allow more precise analysis and quantification of active motion as fine details in the data will be less obscured by broadening effects due to polydispersity in size and shape.To demonstrate shape-dependant active motion, we printed 10 μm tall and 4 μm wide helical particles. The design is shown in Fig. 2a. The helix was designed by extruding a cross that is twisted 360° in either a clockwise or anti-clockwise direction over the length of the helix. We consciously choose to print the helical particles upright, such that the active patch would be later located on the end of the particle, see Fig. 4b. A SEM image of an array of clockwise helices can be seen in Fig. 4a. Even in the absence of an active propulsion, this particle shape has a coupling term between translational diffusion along its long axis and rotational motion around it.52 An active propulsion force along the long axis should therefore lead to a pronounced rotation around the same axis.
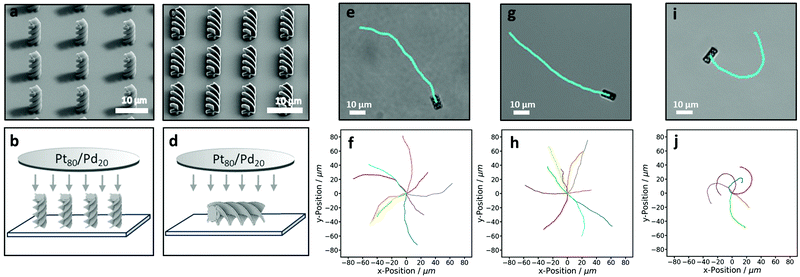 | ||
| Fig. 4 Active behaviour of 3D-printed helices. (a and c) SEM images of the helix arrays taken at a 45° tilt. (a) Upright helices and (c) lying-down helices. (b and d) Illustrate the sputter-coating direction of these particles, respectively. (e)–(j) show active trajectories of helical microswimmers of (e and f) clockwise and (g and h) anticlockwise end-coated helices, and (i and j) side-coated helices in 10% hydrogen peroxide. The top row shows an example trajectory and corresponding helix. The bottom row shows multiple trajectories of individual particles. See also Movies S1 and S2 (ESI†). | ||
We printed both clockwise and anticlockwise helices, each of which showed strongly directed motion along their long axis and a small degree of randomisation (see Movie S1, ESI†). The trajectories of active clockwise and anticlockwise helical particles, in 10% hydrogen peroxide, are shown in Fig. 4f and h, respectively. Unexpectedly, the helices also exhibit slight curvature in opposite directions. We speculate that this circular motion occurs as a result of the interaction of one side of an anisotropic helix with the underlying substrate. The substrate, parallel to which active particles swim, has been shown to have a strong effect on active motion,45,53,54 and might induce a torque in opposite directions for the different chiralities.
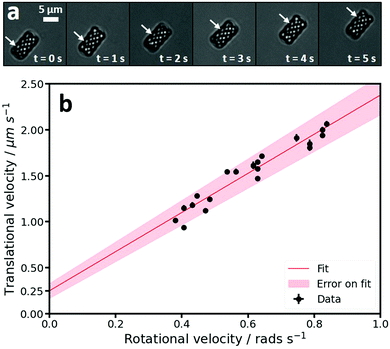
During self-propulsion, the helices not only translated but also rotated, as can be seen by a change in their scatter pattern in bright field microscopy, see Fig. 5a. To identify any coupling between the translational and rotational motion we calculated both the translational and rotational speeds around the long axis of individual active particles. The translational speeds were obtained by fitting the MSDs of individual particles for lag times between 1 and 2.5 s assuming an isotropic diffusion coefficient. The thus obtained average translational speed of the active clockwise and anti-clockwise helices agreed within error and were found to be 1.5 ± 0.3 μm s−1 and 1.5 ± 0.3 μm s−1, respectively. We speculate that the spread observed in the measured translational velocities of individual particles, see also Fig. 5b, is due to either local variations in the substrate45,53,54 or slight differences in the Pt coating.48–50 The average diffusion coefficient was D = 0.012 ± 0.011 μm2 s−1. The large spread in this value presumably stems from the domination of propulsion over diffusion at these time scales and particle sizes. It is further in line with our observation that passive helices show very little diffusion. Interestingly, the speed of spheres with equal cross section as the helices along the direction of motion was significantly lower, 0.5 ± 0.1 μm s−1, indicating a speed enhancement induced by the helical shape.
The rotational velocities around the long axis were measured directly from the videos as follows: The helical structure of the particles results in diagonal lines that are clearly visible in the bright field videos (see Fig. 5a and Movie S1, ESI†). As the helix is formed out of an extruded cross that rotates 360° over the length of the helix, see Fig. 1d and 2a, the time taken for one full rotation can be measured by measuring the time it takes for 4 diagonal lines to pass a specific point on the edge of a particle. The progression of one such diagonal line, over the course of 5 seconds, is illustrated by the arrow in Fig. 5a. When plotting the translational and rotational velocities of the active clockwise helical microswimmers, we found a coupling between the two velocities, see Fig. 5b, where each point represents an individual particle. The data was fitted with a linear function using a least squares approach, which yielded a slope of 2.13 ± 0.1 μm rad−1 and a y-intercept of 0.25 ± 0.08 μm s−1. As discussed above, this coupling is expected for the helical shape of the microswimmers, where the propulsion-induced translational motion along the long axis is coupled to a rotation around this axis. In addition, a torque around the long axis is likely to be present because the platinum inevitably coats the four angled parts of the helix at the top of the particle. When hydrogen peroxide is decomposed here, this will result in a force at a 45° angle to the long axis of the helix that causes the helix to rotate around the long axis. The shape-induced coupling between translation along and rotation around the long axis in combination with a propulsion force that not only leads to translation but also increases rotation leads to much faster speeds than were observed for spheres with the same cross section.
To illustrate the consequences of having different patch locations we printed the helical structures again but this time lying down, see SEM image in Fig. 4c. These particles are subsequently sputter-coated from above, creating an active patch on the side of the helix (see Fig. 4d). These helical particles swim very differently from the end-coated particles described in Section 3.2.1 (see Movies S1 and S2, ESI†). Firstly, they swim perpendicular instead of parallel to the long axis of the helix, see Fig. 4e, g and i. Secondly, they do not show the coupling between the translational and rotational motion seen previously. Finally, the curvature of the trajectories, see Fig. 4j, is comparatively much more pronounced. This rather well defined curvature is due to the active patch being at an approximately 45° angle to the short axis of the particle, as the coating occurs on the helical part of the particle. This means that the translational force, applied when the active patch decomposes hydrogen peroxide, is at an angle to the short axis and therefore pushes the microswimmers in circles. The average translational speeds of the side coated helices was found to be 1.4 ± 0.4 μm s−1, which is similar to the speeds found for end-coated helices. Apparently, the larger active patch area on the side-coated helices roughly compensates the higher friction terms associated with motion along the short axis.
4 Conclusions
Our results demonstrate that 3D microprinting overcomes current limitations in the fabrication of active microswimmers with complex shapes and controlled patch location. It opens the door to studying and quantifying shape-dependent motion of active microswimmers, their interactions and collective behavior, but also navigation in complex environments that rely on alignment through shape-induced torques. These particles might also be employed to gain a better understanding of the propulsion mechanism, and help in the understanding of biological microswimmers and active matter. Ultimately, it will allow a greater control and design of the behavior of synthetic microswimmers, useful for applications in therapeutic diagnostics and drug delivery.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank Jeroen Mesman and Melissa Rinaldin for help and advice with 3D printing and also Ruben Verweij and Damien Lefol for help with python. We gratefully acknowledge funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (grant agreement no. 758383).References
- R. Wittkowski and H. Löwen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 021406 CrossRef.
- F. Lugli, E. Brini and F. Zerbetto, J. Phys. Chem. C, 2012, 116, 592 CrossRef CAS.
- H. Löwen, Eur. Phys. J.: Spec. Top., 2016, 225, 2319 Search PubMed.
- S. van Teeffelen and H. Löwen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 020101 CrossRef.
- S. van Teeffelen, U. Zimmermann and H. Löwen, Soft Matter, 2009, 5, 4510 RSC.
- B. Liebchen, P. Monderkamp, B. ten Hagen and H. Löwen, Phys. Rev. Lett., 2018, 120, 208002 CrossRef CAS.
- A. Zöttl and H. Stark, J. Phys.: Condens. Matter, 2016, 28, 253001 CrossRef.
- N. H. P. Nguyen, D. Klotsa, M. Engel and S. C. Glotzer, Phys. Rev. Lett., 2014, 112, 075701 CrossRef.
- L. F. Cugliandolo, P. Digregorio, G. Gonnella and A. Suma, Phys. Rev. Lett., 2017, 119, 268002 CrossRef.
- P. Fernando, Eur. Phys. J.: Spec. Top., 2016, 225, 2301 Search PubMed.
- R. van Damme, J. Rodenburg, R. van Roij and M. Dijkstra, J. Chem. Phys., 2019, 150, 164501 CrossRef.
- G. Gonnella, D. Marenduzzo, A. Suma and A. Tiribocchi, C. R. Phys., 2015, 16, 316 CrossRef CAS.
- J. Palacci, S. Sacanna, A. Vatchinsky, P. M. Chaikin and D. J. Pine, J. Am. Chem. Soc., 2013, 135, 15978 CrossRef CAS.
- I. Buttinoni, J. Bialké, F. Kümmel, H. Löwen, C. Bechinger and T. Speck, Phys. Rev. Lett., 2013, 110, 238301 CrossRef.
- H. H. Wensink, V. Kantsler, R. E. Goldstein and J. Dunkel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 010302 CrossRef CAS.
- S. Sánchez, L. Soler and J. Katuri, Angew. Chem., Int. Ed., 2015, 54, 1414 CrossRef.
- S. Ebbens, Curr. Opin. Colloid Interface Sci., 2016, 21, 14 CrossRef CAS.
- C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe and G. Volpe, Rev. Mod. Phys., 2016, 88, 045006 CrossRef.
- M. Safdar, S. U. Khan and J. Jänis, Adv. Mater., 2018, 30, 1703660 CrossRef.
- J. R. Howse, R. A. L. Jones, A. J. Ryan, T. Gough, R. Vafabakhsh and R. Golestanian, Phys. Rev. Lett., 2007, 99, 048102 CrossRef.
- A. Brown and W. Poon, Soft Matter, 2014, 10, 4016 RSC.
- F. Kümmel, B. ten Hagen, R. Wittkowski, I. Buttinoni, R. Eichhorn, G. Volpe, H. Löwen and C. Bechinger, Phys. Rev. Lett., 2013, 110, 198302 CrossRef.
- Y. Shelke, N. Srinivasan, S. Thampi and E. Mani, Langmuir, 2019, 35, 4718 CrossRef CAS.
- D. V. Rao, N. Reddy, J. Fransaer and C. Clasen, J. Phys. D: Appl. Phys., 2018, 52, 014002 Search PubMed.
- O. Shemi and M. J. Solomon, J. Phys. Chem. B, 2018, 122, 10247 CrossRef CAS.
- Z. Wang, Z. Wang, J. Li, S. T. H. Cheung, C. Tian, S.-H. Kim, G.-R. Yi, E. Ducrot and Y. Wang, J. Am. Chem. Soc., 2019, 141, 14853 CrossRef CAS.
- J. G. Lee, A. M. Brooks, W. A. Shelton, K. J. M. Bishop and B. Bharti, Nat. Commun., 2019, 10, 2575 CrossRef.
- S. Maruo, O. Nakamura and S. Kawata, Opt. Lett., 1997, 22, 132 CrossRef CAS.
- X. Zhou, Y. Hou and J. Lin, AIP Adv., 2015, 5, 030701 CrossRef.
- S. Kawata, H.-B. Sun, T. Tanaka and K. Takada, Nature, 2001, 412, 697 CrossRef CAS.
- Y. Lin and J. Xu, Adv. Opt. Mater., 2018, 6, 1701359 CrossRef.
- T. Tigges and A. Walther, Angew. Chem., Int. Ed., 2016, 55, 11261 CrossRef CAS.
- Y. C. Saraswat, F. Ibis, L. Rossi, L. Sasso, H. B. Eral and P. Fanzio, J. Colloid Interface Sci., 2020, 564, 43 CrossRef CAS.
- D. Li, Y. Liu, Y. Yang and Y. Shen, Nanoscale, 2018, 10, 19673 RSC.
- R. D. Baker, T. Montenegro-Johnson, A. D. Sediako, M. J. Thomson, A. Sen, E. Lauga and I. S. Aranson, Nat. Commun., 2019, 10, 4932 CrossRef.
- H. Ceylan, I. C. Yasa and M. Sitti, Adv. Mater., 2017, 29, 1605072 CrossRef.
- S. Tottori, L. Zhang, F. Qiu, K. K. Krawczyk, A. Franco-Obregón and B. J. Nelson, Adv. Mater., 2012, 24, 811 CrossRef CAS.
- S. Tottori, L. Zhang, K. E. Peyer and B. J. Nelson, Nano Lett., 2013, 13, 4263 CrossRef CAS.
- K. E. Peyer, S. Tottori, F. Qiu, L. Zhang and B. J. Nelson, Chem. – Eur. J., 2013, 19, 28 CrossRef CAS.
- S. K. Saha, D. Wang, V. H. Nguyen, Y. Chang, J. S. Oakdale and S.-C. Chen, Science, 2019, 366, 105 CrossRef CAS.
- S. M. Kamali, E. Arbabi, H. Kwon and A. Faraon, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 21379 CrossRef CAS.
- D. B. Allan, T. Caswell, N. C. Keim and C. M. van der Wel, trackpy: Trackpy v0.4.1, 2018 DOI:10.5281/zenodo.1226458.
- J. C. Crocker and D. G. Grier, J. Colloid Interface Sci., 1996, 179, 298 CrossRef CAS.
- S. Ebbens, R. A. L. Jones, A. J. Ryan, R. Golestanian and J. R. Howse, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 015304 CrossRef.
- S. Ketzetzi, J. de Graaf, R. P. Doherty and D. J. Kraft, Phys. Rev. Lett., 2020, 124, 048002 CrossRef CAS.
- S. Ebbens, M.-H. Tu, J. R. Howse and R. Golestanian, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 020401 CrossRef.
- B. W. Longbottom and S. A. Bon, Sci. Rep., 2018, 8, 4622 CrossRef.
- R. J. Archer, A. J. Parnell, A. I. Campbell, J. R. Howse and S. J. Ebbens, Adv. Sci., 2018, 5, 1700528 CrossRef.
- R. J. Archer, A. I. Campbell and S. J. Ebbens, Soft Matter, 2015, 11, 6872 RSC.
- Z. Jalilvand, A. B. Pawar and I. Kretzschmar, Langmuir, 2018, 34, 15593 CrossRef CAS.
- Creative Tools, http://www.3dbenchy.com/.
- J. Happel and H. Brenner, Low Reynolds Number Hydrodynamics: With Special Applications to Particulate media, Springer, Netherlands, 1983 Search PubMed.
- M. Wei, C. Zhou, J. Tang and W. Wang, ACS Appl. Mater. Interfaces, 2018, 10, 2249 CrossRef CAS.
- A. Leeth Holterhoff, M. Li and J. G. Gibbs, J. Phys. Chem. Lett., 2018, 9, 5023 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm01320j |
| This journal is © The Royal Society of Chemistry 2020 |