DOI:
10.1039/D0SM01229G
(Paper)
Soft Matter, 2020,
16, 9347-9356
Surface pressure of liquid interfaces laden with micron-sized particles†
Received
4th July 2020
, Accepted 6th September 2020
First published on 8th September 2020
Abstract
We consider the surface pressure of a colloid–laden liquid interface. As micron-sized particles of suitable wettability can be irreversibly bound to the liquid interface on experimental timescales, we use the canonical ensemble to derive an expression for the surface pressure of a colloid–laden interface. We use this expression to show that adsorption of particles with only hard-core interactions has a negligible effect on surface pressures from typical Langmuir-trough measurements. Moreover, we show that Langmuir-trough measurements cannot be used to extract typical interparticle potentials. Finally, in the case of relatively weakly interacting sterically stabilized particles at a liquid interface, we argue that the dependence of measured surface pressure on surface fraction can be explained by particle coordination number at low to intermediate particle surface fractions. At high surface fractions, where the particles are jammed and cannot easily rearrange, we argue that contact-line sliding and/or deformations of the liquid interface at the length scale of the particles might play a pivotal role.
1 Introduction
Liquid interfaces laden with nano- and microparticles have received significant attention in the past few decades.1 One reason is that particle–laden liquid interfaces are model arrested systems in 2D. In addition, they have applications in materials science including (bicontinuous) Pickering emulsions2,3 and froth flotation.4 Moreover, studying the mechanical properties of colloid–laden interfaces provides additional insight into the mechanical properties of proteins at liquid interfaces (and vice versa).5,6 Proteins at liquid interfaces can play an important role in biofilms,7 which play a role in for example healthcare8 and shipping.9
If the colloidal particles are partially wetted by both liquid/fluid phases, they can attach to the liquid interface. The detachment free energy per particle is:
| | ΔGd = πrp2γ0(1 − |cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ|)2, θ|)2, | (1) |
in which
rp is the particle radius,
γ0 the interfacial tension of the pristine liquid interface and
θ is the three-phase contact angle.
10 For a particle of diameter 1 μm at a water–oil interface of tension 50 mN m
−1, Δ
Gd can be as large as 9.5 × 10
6kBT, where
kB is Boltzmann's constant
11 and
T is temperature (298 K in this example). Even for a particle with a contact angle as high as 150°, Δ
Gd ∼ 1.7 × 10
5kBT. This means that, under quiescent conditions, partially wetted micron-sized particles are irreversibly attached to liquid interfaces. This is markedly different from surfactants, as these can hop on and off the liquid interface due to thermal agitation.
The mechanical properties of particle–laden interfaces can be probed using interfacial rheology and are important for understanding the formation and stability of Pickering emulsions and bijels (bicontinuous Pickering emulsions).12 Interfacial shear rheology probes the response of the interface to a shape change at constant area. Several review papers have been published on interfacial shear rheology and its applications.12–17 In contrast, interfacial dilational rheology measures the response of the interface to a change in area at constant shape. In a typical interfacial dilational rheology experiment, the area available to the interfacial particles A is changed and the resulting change in surface pressure is measured.18 Surface pressure is a thermodynamic state variable and is defined as:
in which
γ is the apparent tension of the particle–laden interface.
12
In a pendant-drop set-up, the tension γ is measured by fitting the Young–Laplace equation to the measured drop profile.19 Though pendant-drop tensiometry is a popular and convenient technique, one does have to consider the potential effects of inhomogeneous particle coverage due to gravity. Moreover, the Young–Laplace equation may not apply as and when the interface becomes rigid due to compression of the particle network into a viscoelastic material.12 In a Langmuir-trough experiment, the interfacial tension γ is typically measured using a Wilhelmy plate, though probes consisting of flexible beams can be used instead.20 Notably, surface-pressure measurements using a Langmuir trough are also used as a diagnostic tool in the deposition of Langmuir–Blodget layers.21 It is worthwhile pointing out that, in a Langmuir-trough experiment, there is a small shear component to the response due to a change in shape upon compression.22 To apply pure dilation on a Langmuir-trough setup, the development of a “radial trough” has recently been reported.22
One benefit of using a Langmuir trough rather than a pendant-drop set-up for measuring the mechanical properties of colloid–laden interfaces is that the gravitational force on a single particle can typically be ignored because it is negligible compared to the interfacial-tension force. This statement can be quantified using the Bond number:
| | 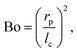 | (3) |
where
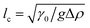
with Δ
ρ the density difference between the liquids and
g the acceleration of gravity.
23 For a 1 μm diameter sphere on a water–air interface, Bo ∼ 10
−8 ≪ 1 confirming that gravity can be ignored. Notably, this also means flotation capillary forces,
i.e. the interparticle force due to the deformation of the liquid interface caused by particle weight, can be ignored.
24 However, immersion capillary forces (for example in liquid films that are thinner than the particle diameter) or capillary forces due to contact-line undulations (for example in the case of non-spherical particles
25) cannot be ignored
a priori. In the case of pendant-drop measurements, the gravitational force has a component parallel to the interface. This leads to particles experiencing the cumulative weight of particles above them, observed experimentally as the ‘keystone’ mechanism.
26
Previous reports have highlighted that interpreting surface-pressure measurements is challenging. For example, Du et al. used pendant-drop measurements to measure the detachment energy of interfacial particles.27 They consider the change in total interfacial energy as particles adsorb from the bulk phase to derive an expression for the detachment energy in terms of surface pressure. Their model provides sensible values for ΔGd when applied to their own measurements and has been used in subsequent reports, for example ref. 28 and 29. However, the model ignores particle–particle interactions, even though the plateau value of surface pressure is used in the analysis and it is assumed that the plateau corresponds to close packing of interfacial particles; it seems unlikely that particle–particle interactions can be ignored at close packing.
Alternatively, Aveyard et al. used a model that only considers particle–particle interactions, i.e. it ignores particle detachment energies, to explain the features of their measured Langmuir-trough isotherms.30 They identify three regions (see A, B and C in Fig. 1) in their Langmuir isotherms. At large trough area (A), there is a slow rise of surface pressure upon compression due to long-range electrostatic interparticle repulsions. In region B, the surface pressure rises more rapidly until it levels off to a plateau at C, which the authors attribute to monolayer collapse at a critical surface pressure Πcvia buckling (sometimes referred to as wrinkling) rather than particle detachment. The electrostatic surface pressure model by Aveyard et al. successfully explains their own measurements. However, comparing this to the model by Du et al. raises the question whether or not the particle detachment energy contributes to the surface pressure of a particle–laden interface.
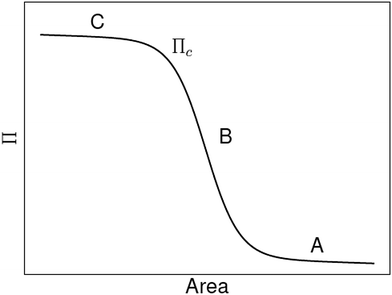 |
| | Fig. 1 Schematic of surface pressure Π vs. area for a liquid interface laden with micron-sized particles. See the main text for an explanation of the critical surface pressure Πc and the regions A, B and C (adapted from ref. 31). | |
In fact, there seems to be some confusion in the literature regarding the interpretation of surface pressure–area isotherms. For example, in their 2012 research paper, Fan and Striolo provide a brief overview of the debate on whether or not adsorbed particles can decrease interfacial tension (and hence increase surface pressure), noting that “no consensus has been reached on whether the adsorbed nanoparticles affect interfacial tension”; according to their micro-Wilhelmy plate simulations, the particle detachment energy is “not directly associated with the interfacial tension reduction”.32 In a 2017 research paper, Zhang et al. note that “despite many studies about the adsorption of particles in the interface, there appears to be no general consensus on whether simple, nonamphiphilic particles adsorbed at an interface will reduce the interfacial tension”.28 They continue to present a systematic, experimental study of the effect on surface pressure of silica particles of varying hydrophobicity, concluding that particles do reduce interfacial tension upon adsorption. Finally, a recent review on colloidal particles at fluid interfaces by Ballard et al. mentions that the “adsorption of colloidal particles can result in a lowering of the measured interfacial tension between the two liquid phases that… leads to a relation between surface tension and adsorption energy”, though they also observe that “a significant number of experimental reports show little to no change in interfacial tension upon adsorption”.33 The apparent confusion regarding the interpretation of surface-pressure data for colloid–laden interfaces led us to ask ourselves: what does surface pressure mean for liquid interfaces laden with irreversibly attached colloidal particles?
Here we start by presenting a theoretical framework for the surface pressure of particles at a liquid interface that accounts for irreversible adsorption. Given the corresponding lack of chemical equilibrium between particles at the interface and those in the bulk suspension at experimentally relevant timescales, we derive an expression for surface pressure in the canonical rather than in the grand-canonical ensemble; the latter is typically used for (reversibly adsorbed) surfactants.34 We then apply our theoretical framework to previously reported surface pressure–area measurements for sterically stabilized polymer particles at a water–oil interface. Our results demonstrate that (i) measured surface pressure should be negligible for low particle coverage (unless particle–particle interactions are strongly repulsive i.e. of the order of the particle attachment energy), (ii) surface-pressure measurements cannot be used to extract typical interparticle potentials in practice and (iii) in the case of relatively weakly interacting particles, the shape of the isotherms at low and intermediate surface coverage can be explained in terms of particle coordination number. In addition, the magnitude of measured surface pressures implies that contact-line sliding and/or deformations of the liquid interface at the scale of the particle might play a pivotal role.
2 Theory
For surfactants, the surface pressure is derived in the grand canonical ensemble, as the surfactant molecules at the interface are assumed to be in chemical equilibrium with the ones in the bulk subphase.34 As also pointed out by Hua et al.,29 this is not applicable in the case of micron-sized particles at liquid interfaces as their detachment energies are orders of magnitude larger than kBT (eqn (1)). In other words, micron-sized particles of suitable wettability are irreversibly adsorbed, which means there is no chemical equilibrium between the colloidal particles at the interface and those in the bulk (sub)phase at experimental timescales. Hence, we proceed below to derive an expression for the surface pressure of a colloid–laden liquid interface in the canonical ensemble.
2.1 Surface pressure in the canonical ensemble
We first consider the osmotic pressure Π3D of a suspension of a solute in a solvent.35 The osmotic pressure is the force per unit area that is required to hold in place a semi-permeable membrane between a volume of suspension and a volume of solvent. The surface pressure can be interpreted as the force per unit length that is required to hold in place a semi-permeable barrier between an area of particle–laden liquid interface and an area of pristine liquid interface. Hence, surface pressure is the 2D equivalent of osmotic pressure. In the canonical ensemble, the osmotic pressure can be written as:| | 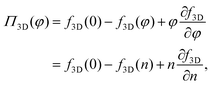 | (4) |
in which φ is the volume fraction of solute, f3D is the free energy per unit volume, and n = φ/vp is the number density in 3D, with vp the volume of a solute particle. For the surface pressure Π, we can write the 2D equivalent of eqn (4):| | | Π(ρ) = γ0 − f(ρ) + ρμ. | (5) |
Here ρ is the particle number density in 2D (equivalent to n in 3D), f is the free energy per unit area, f(0) = γ0 (at ρ = 0 the free energy per unit area is the interfacial tension of the pristine interface), and μ = (∂f/∂ρ)A,T is the chemical potential; see the ESI† for a derivation starting from the (canonical) free energy F of the particle–laden interface.
2.2 Example 1: particles with hard-core interactions
We consider the situation in which N particles from the bulk have attached to the liquid interface of fixed area A at fixed temperature T. We assume that the particles do not interact with each other, apart from that they cannot overlap, and we ignore their entropy (see eqn (12)). The free energy of the liquid interface before particle attachment is:
Each particle attaching to the interface lowers the interfacial free energy by an amount ΔGd (eqn (1)):
We can now calculate the free energy per unit area,
| | 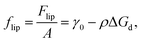 | (8) |
and the chemical potential,
| | 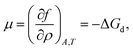 | (9) |
resulting in the following for the surface pressure:
| | 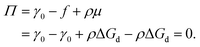 | (10) |
This result aligns with measurements at low surface fractions, where the particles are expected not to interact (see
Fig. 2).
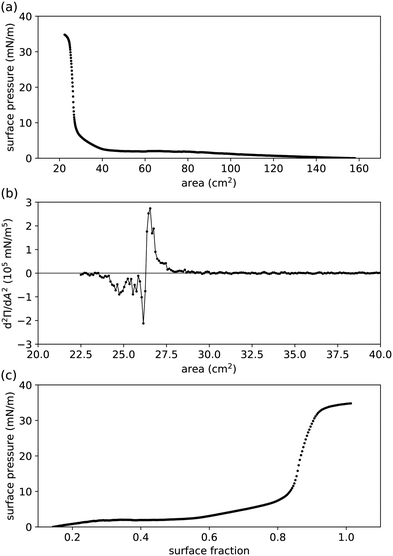 |
| | Fig. 2 Compression measurements performed in a Langmuir trough for (undried) 0.455 μm radius PMMA–PHSA particles at a water–hexadecane interface.41,44 (a) Measured surface pressure Π vs. controlled area available to the interfacial particles. (b) Second derivative of Π, determined numerically from (a), to pinpoint the area at the inflexion point Ai. The graph was smoothed by boxcar averaging to clarify where it crosses the horizontal axis (Ai ≈ 26.3 cm2). The solid line is a guide to the eye. (c) Π vs. surface fraction ϕ, extracted from (a) by setting ϕ(Ai) = 0.863.45 | |
As mentioned above, we have neglected the contribution of the entropy of the colloids to the surface pressure, as well as any entropy change due to structuring of the molecules of the dispersing medium around the colloids. Comparing to the equivalent equation for osmotic pressure in dilute suspensions of solutes in 3D:35
| | 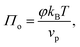 | (11) |
we can write the entropy-contribution to surface pressure at low surface fractions as:
| | 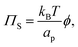 | (12) |
in which
ap = π
rp2 is the cross-sectional area per particle.
Eqn (12) predicts that
ΠS ≈ 1.3 × 10
−6ϕ mN m
−1 < 1.3 × 10
−6 mN m
−1 for
rp = 1 μm, which is negligible compared to typical values of measured interfacial tension
γ0 and surface pressure
Π (see
Fig. 2). In fact, according to
eqn (12),
ΠS is of order 1 mN m
−1 only if
rp is of order 1 nm or smaller, which is closer to the lengthscale of a typical surfactant molecule. These considerations imply that, for micron-sized colloidal particles at liquid interfaces, the contribution of their entropy to the surface pressure is negligible.
2.3 Example 2: beyond hard-core interactions
We now consider the case of particles that have interactions in addition to hard-core repulsion. Following on from eqn (7), additional interactions between the particles lead to an additional term in the free energy:| | Flip = γ0A − NΔGd + N![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) p, p, | (13) |
where ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) p is the (average) free energy per particle due to particles interacting. Note that
p is the (average) free energy per particle due to particles interacting. Note that ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) p includes the effects of pair potentials between interfacial particles but also, for example, the additional energy barrier to particle attachment caused by particles already attached to the interface. If we imagine a compression experiment in a Langmuir-trough that starts with a relatively low surface coverage, the latter contribution can be ignored.
p includes the effects of pair potentials between interfacial particles but also, for example, the additional energy barrier to particle attachment caused by particles already attached to the interface. If we imagine a compression experiment in a Langmuir-trough that starts with a relatively low surface coverage, the latter contribution can be ignored.
We can now calculate the free energy per unit area,
| | 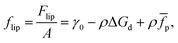 | (14) |
and the chemical potential,
| | 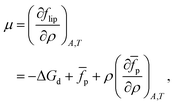 | (15) |
yielding the following for the surface pressure:
| | 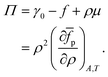 | (16) |
2.4 Comparison to Langmuir-trough experiments
The expression for surface pressure Π in eqn (16) involves partial derivatives at fixed area A and temperature T. However, typical Langmuir-trough experiments on micron-sized particles at liquid interfaces are performed at constant temperature T and number of interfacial particles N. Here, we derive an expression for surface pressure Π, at fixed T and N, as a function of surface fraction ϕ.
We start with the differential of the canonical free energy F in 2D,
| | | dF = γdA − SdT + μdN, | (17) |
in which
S is the entropy of the 2D system (see ESI
†).
34,36 Inserting
eqn (13) results in:
| | 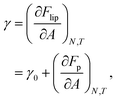 | (18) |
with
Fp the total free energy due to particles interacting. For the surface pressure
Π (
eqn (2)), we can then write:
| | 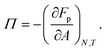 | (19) |
As the number of interfacial particles N is kept fixed, we can rewrite eqn (19) as:
| | 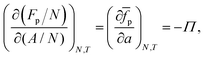 | (20) |
in which
a is the (average) interfacial area per particle. As
| | 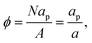 | (21) |
we can write
eqn (20) as:
| | 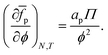 | (22) |
To obtain the average free energy per particle due to particles interacting, we can integrate eqn (22):
| | 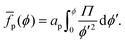 | (23) |
Note that
eqn (23) suggests that
![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) p
p can be obtained
via numerical integration of surface-pressure measurements at constant
N and
T, for example Langmuir-trough measurements.
With a few additional assumptions, we can extract interparticle potentials from Langmuir-trough measurements. First, as explained just below eqn (12), we assume that the contribution of the entropy of the particles to the surface pressure is negligible, which means eqn (22) can be written as:
| | 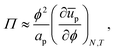 | (24) |
in which
ūp is the internal interaction energy per particle. Secondly, we will assume that particles only interact with, on average,
![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif)
(
ϕ) nearest neighbours
via an interparticle potential
![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) pp
pp(
ϕ). In that case,
| | 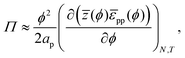 | (25) |
where the division by 2 prevents double-counting of particle–particle pairs. Integrating
eqn (25), we finally arrive at:
| | 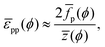 | (26) |
for which
![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) p
p can be obtained from
eqn (23). Notably,
eqn (26) provides a route, in theory, to determining interparticle potentials from Langmuir-trough measurements
via numerical integration of experimental data using
eqn (23)if z(
ϕ) is known.
2.5 Comparison with model by Du et al.
We can also compare our theoretical results to what we find with a straightforward revision of the model set out by Du et al.27 Here we consider a section of the interface with area A and number of particles N. The energy associated with this setup is given as,| | | E(A) = γ0A + Nūp − NΔGd. | (27) |
Eqn (27) is similar to eqn (13) but, following Du et al., we use energy rather than free energy here.
Consider now increasing the interfacial area by a small amount dA, while maintaining a fixed number of particles, and allowing ūp = ūp(A). We can then write the associated energy as:
| | 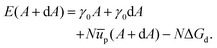 | (28) |
We can use this to find the change in energy dE upon the change in area dA,
| | 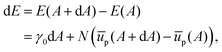 | (29) |
which, upon expansion of
ūp(
A + d
A) to first order in d
A, can be written as
| | 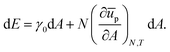 | (30) |
Following Du et al., we then write the interfacial tension of the particle laden surface as
| | 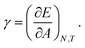 | (31) |
Combining eqn (30) and (31) leads to
| | 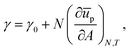 | (32) |
or equivalently (see
eqn (2)):
| | 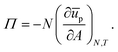 | (33) |
A change of variable from A to ρ = N/A, and then to ϕ = apρ, results in
| | 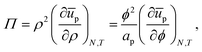 | (34) |
which is equivalent to
eqn (24), and similar to
eqn (16), if entropy is ignored.
2.6 Interparticle potentials
For poly(methyl methacrylate) (PMMA) particles stabilized by poly(12-hydroxystearic acid) (PHSA) at a water–alkane interface, as considered below, Muntz et al. have recently measured the interfacial pair potential ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) pp using fluorescence microscopy and optical tweezers. At low r,
pp using fluorescence microscopy and optical tweezers. At low r,| | 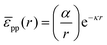 | (35) |
provides a decent fit to the measuresments.37 Here r is the distance between particles, α is a prefactor with value 4.1 × 103kBT μm and κ is the inverse Debye screening length with value 0.35 μm−1.
If we assume that the interfacial particles are arranged in a hexagonal pattern with lattice constant b, and only interact with their z nearest neighbours, we can write:
| | 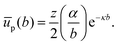 | (36) |
For the contribution of interparticle interactions to the surface pressure, following eqn (34), we can then write:
| | 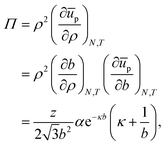 | (37) |
where we have used:
| | 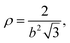 | (38) |
for a hexagonal pattern of interfacial particles.
Note that eqn (37) predicts that repulsive interactions between interfacial particles contribute to a higher surface pressure, which is in line with previous reports.29 However, even at ϕ = 0.9 i.e. b ≈ 2.008rp, Π ∼ 0.003 mN m−1 for z = 6, rp = 1 μm and T = 298 K. Hence, we would expect that these particles at a liquid interface do not lead to a substantial surface pressure until they start percolating, at which point contact forces should be considered. Given typical errors in surface-pressure measurements, this also means that extracting this colloidal pair potential from Langmuir-trough measurements does not seem feasible.
At this point, one might argue that the surface pressure could be substantially higher for charged particles at a water–oil interface. Hence, we apply a similar analysis to a system of 3.1 μm diameter polystyrene particles at a water–decane interface.38 Masschaele et al. compare the following interparticle potential:
| | 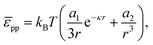 | (39) |
to a consistent set of experimental data (including from optical tweezers) using
a1 ∼ 235 m and
κ−1 = 300 nm; the experimentally determined upper bound of
a2 is of order 10
−13 m
3. For ease of comparison, we re-write
eqn (39) as:
| | 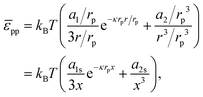 | (40) |
where
x =
r/
rp,
a1s =
a1/
rp and
a2s =
a2/
rp3. Next, we take the derivative of
eqn (40) with respect to
r (and multiply the result by −1), in order to obtain the interparticle force:
| | 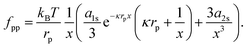 | (41) |
For example,
fpp ≈ 0.1 pN at
r = 10 μm, which compares well to the experimental measurements in Fig. 1 of
ref. 38.
If we consider that the interfacial polystyrene particles are arranged in a hexagonal pattern with lattice constant b, and only interact with their z nearest neighbours, we can write:
| | 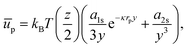 | (42) |
where
y =
b/
rp. For the contribution of interparticle interactions to the surface pressure, we can then use
eqn (34) to write:
| | 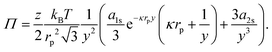 | (43) |
Hence, even at
y = 2.008 (
ϕ = 0.9),
Π ∼ 0.014 mN m
−1 for these charged 3.1 μm diameter polystyrene particles at a water–oil interface. Notably, this suggests that extracting typical colloid pair potentials from Langmuir-trough measurements does not seem feasible. It is worth noting here that reported interaction potentials measured from optical-tweezer experiments
38–40 can be several orders of magnitude smaller than those obtained from surface-pressure experiments.
30
3 Results
We apply our theoretical framework to previously reported Langmuir-trough measurements for PMMA particles, stabilized by PHSA, at a water–hexadecane interface (Fig. 2(a)).41 As expected for particles that have been reported to behave as near-hard spheres in oil,42,43 the surface pressure is practically 0 at relatively large area. At intermediate area, the surface pressure is finite but small, which has previously been attributed to long-range interparticle interactions. At low area, the surface pressure (1) rises steeply (presumably because the particles start touching) and (2) levels off as the particle–laden interface starts buckling.30 However, plotting surface pressure vs. area available to the interfacial particles is not always useful, as there is no guarantee that all particles added to the system make it to the interface, thereby making it challenging to compare Langmuir-trough measurements to other methods and/or between particle-interface combinations.
To allow comparison with other measurements, we convert area into surface fraction ϕ i.e. the area covered by all the particles as a fraction of the total area available to the particles, for which at least one value of area is needed at which the value of surface fraction is known. Fig. 2(b) shows the second derivative of the surface pressure vs. area graph in Fig. 2(a); the inflexion point Ai of the latter is where the second derivative crosses the horizontal axis. We assume that the inflexion point corresponds to the steep increase in coordination number of interfacial particles, where the surface fraction ϕ = 0.863;45 note that this does not seem too dissimilar from the procedure in, for example, ref. 46. Fig. 2(c) shows the graph of surface pressure vs. surface fraction that corresponds to Fig. 2(a). Note that the surface pressure levels off above ϕ ≈ 0.9, which aligns with the maximum surface fraction of interfacial disks in 2D being at ϕc ≈ 0.906.
Following eqn (23), we numerically integrate the data in Fig. 2(c) to obtain the free energy per particle due to the particles interacting, as ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) p is the quantity most closely related to the interparticle potential that we can extract from the data without further assumptions in our theoretical framework. Fig. 3 shows
p is the quantity most closely related to the interparticle potential that we can extract from the data without further assumptions in our theoretical framework. Fig. 3 shows ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) p as a function of surface fraction ϕ. The graph features a change in slope around ϕ ≈ 0.4, which is difficult to discern in Fig. 2(c); this is because
p as a function of surface fraction ϕ. The graph features a change in slope around ϕ ≈ 0.4, which is difficult to discern in Fig. 2(c); this is because ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) p is an integral over Π/ϕ2i.e. the integrand is Π/ϕ2 and not Π. Note that, even for moderate values of surface fraction, where surface pressure is well below 5 mN m−1,
p is an integral over Π/ϕ2i.e. the integrand is Π/ϕ2 and not Π. Note that, even for moderate values of surface fraction, where surface pressure is well below 5 mN m−1, ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) p is of order 106kBT i.e. well beyond typical values for most colloidal interactions. In fact, plotting
p is of order 106kBT i.e. well beyond typical values for most colloidal interactions. In fact, plotting ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) p in units of apγ0 (Fig. 3) implies that interactions related to deformations of the liquid interface are at play here. In principle, these could be flotation capillary interactions,24 but the Bond number for these particles is Bo ∼ 10−8 ≪ 1 i.e. flotation capillary forces are unlikely to be relevant here. Having said that, capillary forces caused by undulations of the contact line around the interfacial particles, e.g. due to uneven stabilizer coverage, could play a role. However, we would expect these to lead to attractive interactions between the particles, whereas the surface pressure is positive (Fig. 2), which points to repulsive interparticle interactions (eqn (37)); we will return to this discussion below.
p in units of apγ0 (Fig. 3) implies that interactions related to deformations of the liquid interface are at play here. In principle, these could be flotation capillary interactions,24 but the Bond number for these particles is Bo ∼ 10−8 ≪ 1 i.e. flotation capillary forces are unlikely to be relevant here. Having said that, capillary forces caused by undulations of the contact line around the interfacial particles, e.g. due to uneven stabilizer coverage, could play a role. However, we would expect these to lead to attractive interactions between the particles, whereas the surface pressure is positive (Fig. 2), which points to repulsive interparticle interactions (eqn (37)); we will return to this discussion below.
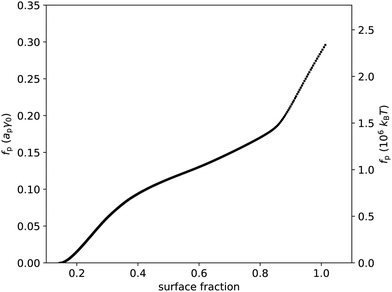 |
| | Fig. 3 Free energy per particle fp, in units of apγ0 and in units of 106kBT, vs. surface fraction ϕ. This graph was extracted from the data presented in Fig. 2 using eqn (23). | |
Even if liquid deformations could explain the order of magnitude for ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) p, it is not immediately clear how they could explain the shape of the graph in Fig. 3. To better understand that shape, we take experimentally determined values of the modal coordination number zm of (macroscopic) hard disks on an elastic sheet from Quickenden et al.45 and plot them as a function of the surface fraction of the disks (Fig. 4(a)). We interpolate between the available data points and we extropolate zm = 6 for ϕ > 0.9, as z = 6 is the maximum coordination number of (hexagonally) close-packed disks in 2D. Intriguingly, the shape of the (
p, it is not immediately clear how they could explain the shape of the graph in Fig. 3. To better understand that shape, we take experimentally determined values of the modal coordination number zm of (macroscopic) hard disks on an elastic sheet from Quickenden et al.45 and plot them as a function of the surface fraction of the disks (Fig. 4(a)). We interpolate between the available data points and we extropolate zm = 6 for ϕ > 0.9, as z = 6 is the maximum coordination number of (hexagonally) close-packed disks in 2D. Intriguingly, the shape of the (![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) p,ϕ)-graph is described remarkably well by the shape of the (zm,ϕ)-graph, especially for ϕ < 0.83 (Fig. 4(b)). This suggests that the surface-pressure behaviour at low to intermediate surface fraction can be explained by the number of particle–particle contacts. Around ϕ = 0.83, the modal coordination number zm rises rapidly from 4 to 6, whereas
p,ϕ)-graph is described remarkably well by the shape of the (zm,ϕ)-graph, especially for ϕ < 0.83 (Fig. 4(b)). This suggests that the surface-pressure behaviour at low to intermediate surface fraction can be explained by the number of particle–particle contacts. Around ϕ = 0.83, the modal coordination number zm rises rapidly from 4 to 6, whereas ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) p rises less rapidly in that regime. One explanation could be that particle rearrangements due to interparticle interactions may affect (z,ϕ), especially at high surface fraction, which is not captured by the model system of hard disks on an elastic sheet. At even higher surface fractions, surface-pressure changes can no longer be explained by changes in coordination number, as zmax = 6 has been reached.
p rises less rapidly in that regime. One explanation could be that particle rearrangements due to interparticle interactions may affect (z,ϕ), especially at high surface fraction, which is not captured by the model system of hard disks on an elastic sheet. At even higher surface fractions, surface-pressure changes can no longer be explained by changes in coordination number, as zmax = 6 has been reached.
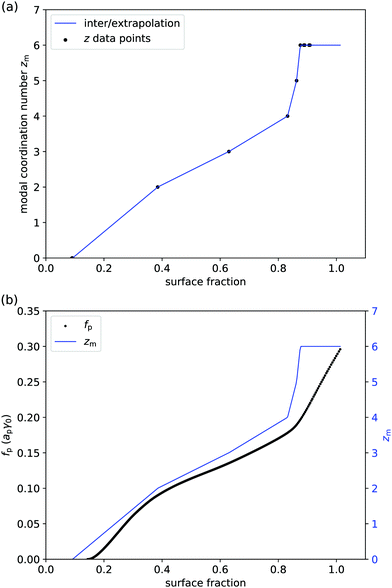 |
| | Fig. 4 (a) Modal coordination number zm of disks on an elastic sheet vs. surface fraction ϕ: solid circles are data points from ref. 45 and the solid line is a linear interpolation (apart from ϕ > 0.9 where we have set zm = 6). (b) Combined graph of the free energy per particle from Fig. 3 and the modal coordination number from panel (a); especially for ϕ < 0.83, the shapes of the two graphs are remarkably similar. | |
If we assume that particles only interact with their nearest neighbours, and that the contribution of entropy to the surface pressure is negligible for micron-sized particles, then we can attempt to extract the interparticle potential ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) pp from surface-pressure measurements (eqn (26)). Fig. 5 shows the corresponding (
pp from surface-pressure measurements (eqn (26)). Fig. 5 shows the corresponding (![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) pp,ϕ)-graph and (
pp,ϕ)-graph and (![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) pp,r/rp)-graph, where the conversion from ϕ to the particle–particle separation r has been done using a ≈ π(r/2)2 and ϕ = ap/a. As expected, the interparticle potential is negligible at large separations; it starts to increase around r = 5rpi.e. ϕ ≈ 0.16. It then rises to a plateau value for r < 3.5rp, corresponding to ϕ > 0.33. The height of this plateau, at approximately 0.09apγ0 or 7 × 105kBT, supports the idea that deformations of the liquid interface are involved, as the free energy associated with the deformation of a liquid interface is expected to be of the order of the interfacial tension times the deformed area. Approaching close-packing, i.e. near r = 2rp, the interparticle potential features an unexpected dip. However, we attribute this to artefacts of the analysis. For example, given the steepness of the (zm,ϕ) graph (Fig. 4(a)), small differences in the (z,ϕ) behavior between disks on an elastic sheet and PMMA particles at a liquid interface can cause abrupt changes in
pp,r/rp)-graph, where the conversion from ϕ to the particle–particle separation r has been done using a ≈ π(r/2)2 and ϕ = ap/a. As expected, the interparticle potential is negligible at large separations; it starts to increase around r = 5rpi.e. ϕ ≈ 0.16. It then rises to a plateau value for r < 3.5rp, corresponding to ϕ > 0.33. The height of this plateau, at approximately 0.09apγ0 or 7 × 105kBT, supports the idea that deformations of the liquid interface are involved, as the free energy associated with the deformation of a liquid interface is expected to be of the order of the interfacial tension times the deformed area. Approaching close-packing, i.e. near r = 2rp, the interparticle potential features an unexpected dip. However, we attribute this to artefacts of the analysis. For example, given the steepness of the (zm,ϕ) graph (Fig. 4(a)), small differences in the (z,ϕ) behavior between disks on an elastic sheet and PMMA particles at a liquid interface can cause abrupt changes in ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) pp(r). Moreover, near close packing, the particles are close to jamming, at which point the interfacial particles are no longer in equilibrium and our thermodynamic approach breaks down. Finally, the particle–laden interface starts buckling for ϕ > 0.9 i.e. r < 2.1rp, which has not been taken into account in this analysis.
pp(r). Moreover, near close packing, the particles are close to jamming, at which point the interfacial particles are no longer in equilibrium and our thermodynamic approach breaks down. Finally, the particle–laden interface starts buckling for ϕ > 0.9 i.e. r < 2.1rp, which has not been taken into account in this analysis.
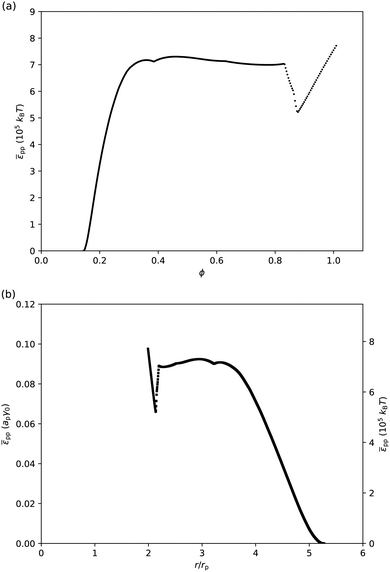 |
| | Fig. 5 (a) Interparticle potential ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) ppvs. surface fraction ϕ. (b) ppvs. surface fraction ϕ. (b) ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) pp in units of apγ0 and in units of 105kBT vs. separation r in units of particle radius rp. These graphs were extracted from the data presented in Fig. 4 using eqn (26). pp in units of apγ0 and in units of 105kBT vs. separation r in units of particle radius rp. These graphs were extracted from the data presented in Fig. 4 using eqn (26). | |
In the remainder of this section, we speculate on the origin of the repulsion of order 0.1apγ0 between the interfacial PMMA–PHSA particles considered here. One might argue that the repulsion between the particles is due to their steric stabilization. However, a repulsive interaction of order 105 to 106kBT is beyond the measured repulsive barrier of sterically stabilized PMMA–PHSA particles.47,48 It is perhaps also surprising that the interparticle potential has exceeded 105kBT at a relatively large separation of r ≈ 4.5rp. However, it should be noted that, especially at low surface fraction, the surface coverage is not necessarily homogeneous. For example, we have observed that buckling tends to start at the barriers rather than uniformly across the Langmuir trough.31 Secondly, there may be a non-uniform stress distribution across the interface i.e. a Janssen effect.49 Moreover, the barriers are typically moved at speeds and over distances that result in relatively high strain rates and total strains, for which careful constitutive modelling is required.22,50 All the same, our main claims so far are that (i) measured surface pressures should be negligible for low surface fractions and (ii) surface-pressure measurements cannot be used to extract typical colloid potentials; these claims are unaffected by these considerations.
Instead, we suggest that the following picture emerges for the surface pressure in a system of relatively weakly interacting particles at a liquid interface. At very low surface fraction, i.e. when the interfacial particles are not interacting, the surface pressure is practically negligible. At low and intermediate surface fraction, the shape of the (Π,ϕ)-graph can be explained by the particle coordination number i.e. the number of nearest neighbours of an interfacial particle. At high surface fraction, the surface pressure plateaus, which we attribute to buckling of the particle–laden liquid interface, in line with previous reports.12,30 The order of magnitude of the free energy per particle, and of the repulsive interparticle potential extracted from surface-pressure measurements, suggests that deformations of the liquid interface at the length scale of the particles are involved. We suggest that these deformations are due to interfacial particles touching: given variance in particle size and contact angle,51 particle–particle contact forces will have components in the direction perpendicular to the liquid interface, leading to particles being pushed slightly out of the plane of the liquid interface. The length scale of these deformations will be of the order of the particle radius, so the free-energy cost per particle should indeed be of order apγ0. Alternatively, it could lead to the contact line of the liquid interface sliding along the interfacial particle, but it has previously been shown that this leads to free-energy changes of a similar order of magnitude (see supplementary information of ref. 52).
Note that we have not referred to the repulsive interparticle potential ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) pp in Fig. 5 as a capillary interaction. Capillary interactions are usually considered between non-touching particles and they are almost always attractive; one has to carefully design particle shapes to observe (near field) capillary repulsion.53 Instead, we consider the situation in which a particle monolayer is compressed until particles start touching. Our suggestion is that, en route to buckling, the particles push each other out of the initially flat plane of the liquid interface while remaining attached to the liquid interface (Fig. 6). This will cause energetically unfavourable deformations of the liquid interface at the length scale of the particles, resulting in an effective capillary repulsion between the particles. Consequently, we would not expect this effective repulsion to be observed in typical optical-tweezer experiments to measure interparticle potentials: the particles are typically not made to touch in optical-tweezer experiments. In addition, we would not expect the surface-pressure graph in Fig. 2(c) to be consistent with the power-law dependence of the capillary interactions between non-touching microparticles (as considered for example by Danov et al.54) Instead, our results suggest that the surface-pressure graph in Fig. 2(c) should be consistent with z(ϕ) (Fig. 4) and the r-dependence of the contact force between interfacial particles upon compression. In the case of interfacial particles with stronger long-range interactions, the effect of that long-range interaction on z(ϕ) should also be taken into account.
pp in Fig. 5 as a capillary interaction. Capillary interactions are usually considered between non-touching particles and they are almost always attractive; one has to carefully design particle shapes to observe (near field) capillary repulsion.53 Instead, we consider the situation in which a particle monolayer is compressed until particles start touching. Our suggestion is that, en route to buckling, the particles push each other out of the initially flat plane of the liquid interface while remaining attached to the liquid interface (Fig. 6). This will cause energetically unfavourable deformations of the liquid interface at the length scale of the particles, resulting in an effective capillary repulsion between the particles. Consequently, we would not expect this effective repulsion to be observed in typical optical-tweezer experiments to measure interparticle potentials: the particles are typically not made to touch in optical-tweezer experiments. In addition, we would not expect the surface-pressure graph in Fig. 2(c) to be consistent with the power-law dependence of the capillary interactions between non-touching microparticles (as considered for example by Danov et al.54) Instead, our results suggest that the surface-pressure graph in Fig. 2(c) should be consistent with z(ϕ) (Fig. 4) and the r-dependence of the contact force between interfacial particles upon compression. In the case of interfacial particles with stronger long-range interactions, the effect of that long-range interaction on z(ϕ) should also be taken into account.
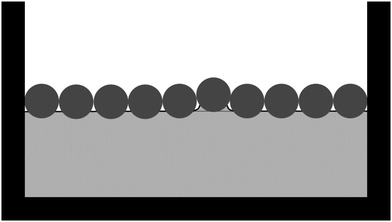 |
| | Fig. 6 Schematic of particles (dark grey) at a liquid interface (solid black line). The interfacial particles are compressed in between the vertical barriers, causing an interfacial particle to be pushed out of the plane of the initially flat liquid interface (dashed line), thereby causing a deformation of the liquid interface. | |
4 Conclusions
We have presented here a theoretical framework to understand the surface pressure of liquid interfaces laden with micron-sized particles. As the particle detachment energy is several orders of magnitude larger than kBT, and hence the particles at the liquid interface are not in chemical equilibrium with those in the bulk, we derive an expression for the surface pressure in the canonical rather than the grand-canonical ensemble. We show that the surface pressure of a (dilute) collection of particles, with hard-core repulsion only, at a liquid interface is practically negligible (and actually zero if the entropy of the particles is ignored). Moreover, typical colloidal interactions, specifically those well below 105kBT, lead to surface pressures that are small to negligible on the scale of typical (measured) surface pressures. For a system of relatively weakly interacting PMMA particles at a water–oil interface, we argue that the shape of surface pressure-surface fraction graphs can be explained by particle coordination number at low to intermediate surface fractions. The order of magnitude of the free energy per particle extracted from surface-pressure measurements suggests that contact-line sliding and/or deformations of the liquid interface at the length scale of the particles play a pivotal role; we speculate that these are caused by touching particles pushing some particles out of the initially flat plane of the liquid interface.
It is perhaps interesting to note that the system under consideration here could be considered as a 2D equivalent of the system studied by Guy et al.55 They study the role of friction in the rheology of 3D suspensions of PMMA particles. In the system considered here, the system is Brownian at low surface fraction (see Fig. 1 in Van Hooghten et al.44). At high surface fraction, i.e. when the surface pressure deviates substantially from 0, we have argued that contact forces start dominating the surface pressure, at which point the system is no longer Brownian. Hence, it would be interesting to consider what the role of friction is in Langmuir-trough experiments and our considerations here have provided an ansatz for that line of inquiry.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
RM acknowledges studentship funding from the EPSRC (EP/M506515/1) and IM acknowledges studentship funding from the EPSRC Centre for Doctoral Training in Condensed Matter Physics (CM-DTC, EP/L015110/1). The authors thank Mike Cates, Willem Boon and René van Roij for useful discussions.
Notes and references
-
Colloidal Particles at Liquid Interfaces, ed. B. P. Binks and T. S. Horozov, Cambridge University Press, Cambridge, 2006 Search PubMed.
-
J. W. Tavacoli, J. H. J. Thijssen and P. S. Clegg, in Particle-Stabilized Emulsions and Colloids: Formation and Applications, ed. T. Ngai and S. Bon, Royal Society of Chemistry, Cambridge, 2014, ch. 6, pp. 129–168 Search PubMed.
-
Bijels: Bicontinuous Particle-Stabilized Emulsions, ed. P. S. Clegg, Royal Society of Chemistry, Cambridge, 2020 Search PubMed.
-
A. V. Nguyen, R. J. Pugh and G. J. Jameson, in Colloidal Particles at Liquid interfaces, ed. B. P. Binks and T. S. Horozov, Cambridge University Press, Cambridge, 2006, ch. 9, pp. 328–382 Search PubMed.
- S. Tcholakova, N. D. Denkov and A. Lips, Phys. Chem. Chem. Phys., 2008, 10, 1608–1627 RSC.
- G. Jutz and A. Böker, J. Mater. Chem., 2010, 20, 4299–4304 RSC.
- K. M. Bromley, R. J. Morris, L. Hobley, G. Brandani, R. M. C. Gillespie, M. McCluskey, U. Zachariae, D. Marenduzzo, N. R. Stanley-Wall and C. E. MacPhee, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 5419–5424 CrossRef CAS PubMed.
- D. Lindsay and A. von Holy, J. Hosp. Infect., 2006, 64, 313–325 CrossRef CAS PubMed.
- H. C. Flemming, Appl. Microbiol. Biotechnol., 2002, 59, 629–640 CrossRef CAS PubMed.
- R. Aveyard, B. P. Binks and J. H. Clint, Adv. Colloid Interface Sci., 2003, 100–102, 503–546 CrossRef CAS.
-
CRC Handbook of Chemistry and Physics, ed. D. R. Lide, CRC Press, Boca Raton, 2001–2002 Search PubMed.
- J. H. J. Thijssen and J. Vermant, J. Phys.: Condens. Matter, 2018, 40,
023002 CrossRef PubMed.
- J. Krägel and S. R. Derkatch, Curr. Opin. Colloid Interface Sci., 2010, 15, 246–255 CrossRef.
- G. G. Fuller and J. Vermant, Soft Matter, 2011, 7, 7583–7585 RSC.
- A. J. Mendoza, E. Guzmán, F. Martínez-Pedrero, H. Ritacco, R. G. Rubio, F. Ortega, V. M. Starov and R. Miller, Adv. Colloid Interface Sci., 2014, 206, 303–319 CrossRef CAS PubMed.
- S. R. Derkach, J. Krägel and R. Miller, Colloid J., 2009, 71, 1–17 CrossRef CAS.
- R. Miller, R. Wüstneck, J. Krägel and G. Kretschmar, Colloids Surf., A, 1996, 111, 75–118 CrossRef CAS.
- P. Erni, Soft Matter, 2011, 7, 7586–7600 RSC.
- J. D. Berry, M. J. Neeson, R. R. Dagastine, D. Y. C. Chan and R. F. Tabor, J. Colloid Interface Sci., 2015, 454, 226–237 CrossRef CAS PubMed.
- P. Gijsenbergh and R. Puers, Adv. Colloid Interface Sci., 2018, 255, 26–33 CrossRef CAS PubMed.
- A. Deák, B. Bancsi, A. L. Tóth, A. L. Kovács and Z. Hórvölgyi, Colloids Surf., A, 2006, 278, 10–16 CrossRef.
- M. Pepicelli, T. Verwijlen, T. A. Tervoort and J. Vermant, Soft Matter, 2017, 13, 5977–5990 RSC.
- D. Vella, Annu. Rev. Fluid Mech., 2015, 47, 115–135 CrossRef.
- P. A. Kralchevsky and K. Nagayama, Langmuir, 1994, 10, 23–36 CrossRef CAS.
- J. C. Loudet, A. M. Alsayed, J. Zhang and A. G. Yodh, Phys. Rev. Lett., 2005, 94,
018301 CrossRef CAS PubMed.
- J. W. Tavacoli, G. Katgert, E. G. Kim, M. E. Cates and P. S. Clegg, Phys. Rev. Lett., 2012, 108,
268306 CrossRef CAS PubMed.
- K. Du, E. Glogowski, T. Emrick, T. P. Russell and A. D. Dinsmore, Langmuir, 2010, 26, 12518–12522 CrossRef CAS PubMed.
- Y. Zhang, S. Wang, J. Zhou, R. Zhao, G. Benz, S. Tcheimou, J. C. Meredith and S. H. Behrens, Langmuir, 2017, 33, 4511–4519 CrossRef CAS PubMed.
- X. Hua, M. A. Bevan and J. Frechette, Langmuir, 2016, 32, 11341–11352 CrossRef CAS PubMed.
- R. Aveyard, J. H. Clint, D. Nees and V. N. Paunov, Langmuir, 2000, 16, 1969–1979 CrossRef CAS.
-
R. Mears, PhD thesis, The University of Edinburgh, Scotland, UK, 2020.
- H. Fan and A. Striolo, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86,
051610 CrossRef PubMed.
- N. Ballard, A. D. Law and S. A. F. Bon, Soft Matter, 2019, 15, 1186–1199 RSC.
-
M. Doi, Soft Matter Physics, Oxford University Press, Oxford, 2015, ch. 4, pp. 51–73 Search PubMed.
-
M. Doi, Soft Matter Physics, Oxford University Press, Oxford, 2015, ch. 2, pp. 8–27 Search PubMed.
-
C. Kittel and H. Kroemer, Thermal Physics, W. H. Freeman and Company, New York, 1999 Search PubMed.
- I. Muntz, F. Waggett, M. Hunter, A. B. Schofield, P. Bartlett, D. Marenduzzo and J. H. J. Thijssen, Phys. Rev. Res., 2020, 2,
023388 CrossRef CAS.
- K. Masschaele, B. J. Park, E. M. Furst, J. Fransaer and J. Vermant, Phys. Rev. Lett., 2010, 105,
048303 CrossRef CAS PubMed.
- B. J. Park, J. Vermant and E. M. Furst, Soft Matter, 2010, 6, 5327–5333 RSC.
- R. Aveyard, B. P. Binks, J. H. Clint, P. D. I. Fletcher, T. S. Horozov, B. Neumann and V. N. Paunov, Phys. Rev. Lett., 2002, 88,
246102 CrossRef CAS PubMed.
-
R. Van Hooghten, V. Blair, A. Vananroye, A. Schofield, J. Vermant and J. Thijssen, Edinburgh DataShare, 2018 DOI:10.7488/ds/1997.
- G. Bosma, C. Pathmamanoharan, E. H. A. de Hoog, W. K. Kegel, A. van Blaaderen and H. N. W. Lekkerkerker, J. Colloid Interface Sci., 2002, 245, 292 CrossRef CAS PubMed.
- G. Bryant, S. R. Williams, L. Qian, I. K. Snook, E. Perez and F. Pincet, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 3 CrossRef PubMed.
- R. Van Hooghten, V. E. Blair, A. Vananroye, A. B. Schofield, J. Vermant and J. H. J. Thijssen, Langmuir, 2017, 33, 4107 CrossRef PubMed.
- T. I. Quickenden and G. K. Tan, J. Colloid Interface Sci., 1974, 48, 382–393 CrossRef CAS.
- A. Maestro, O. S. Deshmukh, F. Mugele and D. Langevin, Langmuir, 2015, 31, 6289–6297 CrossRef CAS PubMed.
- A. Doroszkowski and R. Lambourne, J. Polym. Sci., Part C: Polym. Symp., 1971, 34, 253–264 CrossRef.
- C. R. Iacovella, R. E. Rogers, S. C. Glotzer and M. J. Solomon, J. Chem. Phys., 2010, 133,
164903 CrossRef CAS PubMed.
- P. Cicuta and D. Vella, Phys. Rev. Lett., 2009, 102,
138302 CrossRef CAS PubMed.
- T. Verwijlen, L. Imperiali and J. Vermant, Adv. Colloid Interface Sci., 2014, 206, 428–436 CrossRef CAS PubMed.
- L. Isa, F. Lucas, R. Wepf and E. Reimhult, Nat. Commun., 2011, 2, 438 CrossRef PubMed.
- L. Maurice, R. A. Maguire, A. B. Schofield, M. E. Cates, P. S. Clegg and J. H. J. Thijssen, Soft Matter, 2013, 9, 7757 RSC.
- L. Yao, L. Botto, M. Cavallaro Jr, B. J. Bleier, V. Garbin and K. J. Stebe, Soft Matter, 2013, 9, 779–786 RSC.
- K. D. Danov, P. A. Kralchevsky, B. N. Naydenov and G. Brenn, J. Colloid Interface Sci., 2005, 287, 121–134 CrossRef CAS PubMed.
- B. M. Guy, M. Hermes and W. C. K. Poon, Phys. Rev. Lett., 2016, 155,
088304 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Surface-pressure derivation starting from the (canonical) free energy of the particle–laden interface, and tabular data for re-plotting Fig. 2–5. See DOI: 10.1039/d0sm01229g |
|
| This journal is © The Royal Society of Chemistry 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article and
Job H. J.
Thijssen
and
Job H. J.
Thijssen
 *
*
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ|)2,
θ|)2,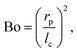
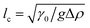 with Δρ the density difference between the liquids and g the acceleration of gravity.23 For a 1 μm diameter sphere on a water–air interface, Bo ∼ 10−8 ≪ 1 confirming that gravity can be ignored. Notably, this also means flotation capillary forces, i.e. the interparticle force due to the deformation of the liquid interface caused by particle weight, can be ignored.24 However, immersion capillary forces (for example in liquid films that are thinner than the particle diameter) or capillary forces due to contact-line undulations (for example in the case of non-spherical particles25) cannot be ignored a priori. In the case of pendant-drop measurements, the gravitational force has a component parallel to the interface. This leads to particles experiencing the cumulative weight of particles above them, observed experimentally as the ‘keystone’ mechanism.26
with Δρ the density difference between the liquids and g the acceleration of gravity.23 For a 1 μm diameter sphere on a water–air interface, Bo ∼ 10−8 ≪ 1 confirming that gravity can be ignored. Notably, this also means flotation capillary forces, i.e. the interparticle force due to the deformation of the liquid interface caused by particle weight, can be ignored.24 However, immersion capillary forces (for example in liquid films that are thinner than the particle diameter) or capillary forces due to contact-line undulations (for example in the case of non-spherical particles25) cannot be ignored a priori. In the case of pendant-drop measurements, the gravitational force has a component parallel to the interface. This leads to particles experiencing the cumulative weight of particles above them, observed experimentally as the ‘keystone’ mechanism.26

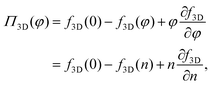
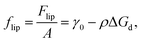
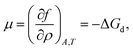
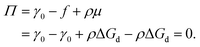

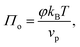
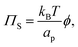
![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) p,
p,![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) p is the (average) free energy per particle due to particles interacting. Note that
p is the (average) free energy per particle due to particles interacting. Note that ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) p includes the effects of pair potentials between interfacial particles but also, for example, the additional energy barrier to particle attachment caused by particles already attached to the interface. If we imagine a compression experiment in a Langmuir-trough that starts with a relatively low surface coverage, the latter contribution can be ignored.
p includes the effects of pair potentials between interfacial particles but also, for example, the additional energy barrier to particle attachment caused by particles already attached to the interface. If we imagine a compression experiment in a Langmuir-trough that starts with a relatively low surface coverage, the latter contribution can be ignored.
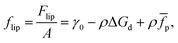
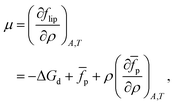
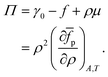
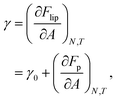
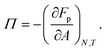
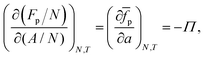
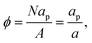
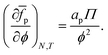
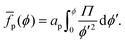
![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) p can be obtained via numerical integration of surface-pressure measurements at constant N and T, for example Langmuir-trough measurements.
p can be obtained via numerical integration of surface-pressure measurements at constant N and T, for example Langmuir-trough measurements.
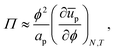
![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) (ϕ) nearest neighbours via an interparticle potential
(ϕ) nearest neighbours via an interparticle potential ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) pp(ϕ). In that case,
pp(ϕ). In that case,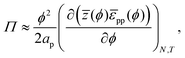
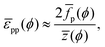
![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) p can be obtained from eqn (23). Notably, eqn (26) provides a route, in theory, to determining interparticle potentials from Langmuir-trough measurements via numerical integration of experimental data using eqn (23)if z(ϕ) is known.
p can be obtained from eqn (23). Notably, eqn (26) provides a route, in theory, to determining interparticle potentials from Langmuir-trough measurements via numerical integration of experimental data using eqn (23)if z(ϕ) is known.
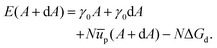
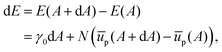
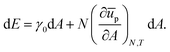
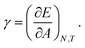
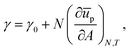
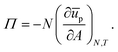
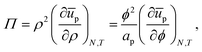
![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) pp using fluorescence microscopy and optical tweezers. At low r,
pp using fluorescence microscopy and optical tweezers. At low r,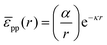
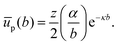
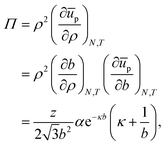
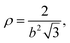
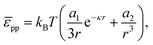
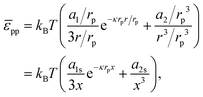
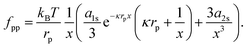
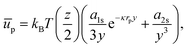
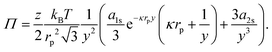
![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) p is the quantity most closely related to the interparticle potential that we can extract from the data without further assumptions in our theoretical framework. Fig. 3 shows
p is the quantity most closely related to the interparticle potential that we can extract from the data without further assumptions in our theoretical framework. Fig. 3 shows ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) p as a function of surface fraction ϕ. The graph features a change in slope around ϕ ≈ 0.4, which is difficult to discern in Fig. 2(c); this is because
p as a function of surface fraction ϕ. The graph features a change in slope around ϕ ≈ 0.4, which is difficult to discern in Fig. 2(c); this is because ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) p is an integral over Π/ϕ2i.e. the integrand is Π/ϕ2 and not Π. Note that, even for moderate values of surface fraction, where surface pressure is well below 5 mN m−1,
p is an integral over Π/ϕ2i.e. the integrand is Π/ϕ2 and not Π. Note that, even for moderate values of surface fraction, where surface pressure is well below 5 mN m−1, ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) p is of order 106kBT i.e. well beyond typical values for most colloidal interactions. In fact, plotting
p is of order 106kBT i.e. well beyond typical values for most colloidal interactions. In fact, plotting ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) p in units of apγ0 (Fig. 3) implies that interactions related to deformations of the liquid interface are at play here. In principle, these could be flotation capillary interactions,24 but the Bond number for these particles is Bo ∼ 10−8 ≪ 1 i.e. flotation capillary forces are unlikely to be relevant here. Having said that, capillary forces caused by undulations of the contact line around the interfacial particles, e.g. due to uneven stabilizer coverage, could play a role. However, we would expect these to lead to attractive interactions between the particles, whereas the surface pressure is positive (Fig. 2), which points to repulsive interparticle interactions (eqn (37)); we will return to this discussion below.
p in units of apγ0 (Fig. 3) implies that interactions related to deformations of the liquid interface are at play here. In principle, these could be flotation capillary interactions,24 but the Bond number for these particles is Bo ∼ 10−8 ≪ 1 i.e. flotation capillary forces are unlikely to be relevant here. Having said that, capillary forces caused by undulations of the contact line around the interfacial particles, e.g. due to uneven stabilizer coverage, could play a role. However, we would expect these to lead to attractive interactions between the particles, whereas the surface pressure is positive (Fig. 2), which points to repulsive interparticle interactions (eqn (37)); we will return to this discussion below.
![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) p, it is not immediately clear how they could explain the shape of the graph in Fig. 3. To better understand that shape, we take experimentally determined values of the modal coordination number zm of (macroscopic) hard disks on an elastic sheet from Quickenden et al.45 and plot them as a function of the surface fraction of the disks (Fig. 4(a)). We interpolate between the available data points and we extropolate zm = 6 for ϕ > 0.9, as z = 6 is the maximum coordination number of (hexagonally) close-packed disks in 2D. Intriguingly, the shape of the (
p, it is not immediately clear how they could explain the shape of the graph in Fig. 3. To better understand that shape, we take experimentally determined values of the modal coordination number zm of (macroscopic) hard disks on an elastic sheet from Quickenden et al.45 and plot them as a function of the surface fraction of the disks (Fig. 4(a)). We interpolate between the available data points and we extropolate zm = 6 for ϕ > 0.9, as z = 6 is the maximum coordination number of (hexagonally) close-packed disks in 2D. Intriguingly, the shape of the (![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) p,ϕ)-graph is described remarkably well by the shape of the (zm,ϕ)-graph, especially for ϕ < 0.83 (Fig. 4(b)). This suggests that the surface-pressure behaviour at low to intermediate surface fraction can be explained by the number of particle–particle contacts. Around ϕ = 0.83, the modal coordination number zm rises rapidly from 4 to 6, whereas
p,ϕ)-graph is described remarkably well by the shape of the (zm,ϕ)-graph, especially for ϕ < 0.83 (Fig. 4(b)). This suggests that the surface-pressure behaviour at low to intermediate surface fraction can be explained by the number of particle–particle contacts. Around ϕ = 0.83, the modal coordination number zm rises rapidly from 4 to 6, whereas ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) p rises less rapidly in that regime. One explanation could be that particle rearrangements due to interparticle interactions may affect (z,ϕ), especially at high surface fraction, which is not captured by the model system of hard disks on an elastic sheet. At even higher surface fractions, surface-pressure changes can no longer be explained by changes in coordination number, as zmax = 6 has been reached.
p rises less rapidly in that regime. One explanation could be that particle rearrangements due to interparticle interactions may affect (z,ϕ), especially at high surface fraction, which is not captured by the model system of hard disks on an elastic sheet. At even higher surface fractions, surface-pressure changes can no longer be explained by changes in coordination number, as zmax = 6 has been reached.
![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) pp from surface-pressure measurements (eqn (26)). Fig. 5 shows the corresponding (
pp from surface-pressure measurements (eqn (26)). Fig. 5 shows the corresponding (![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) pp,ϕ)-graph and (
pp,ϕ)-graph and (![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) pp,r/rp)-graph, where the conversion from ϕ to the particle–particle separation r has been done using a ≈ π(r/2)2 and ϕ = ap/a. As expected, the interparticle potential is negligible at large separations; it starts to increase around r = 5rpi.e. ϕ ≈ 0.16. It then rises to a plateau value for r < 3.5rp, corresponding to ϕ > 0.33. The height of this plateau, at approximately 0.09apγ0 or 7 × 105kBT, supports the idea that deformations of the liquid interface are involved, as the free energy associated with the deformation of a liquid interface is expected to be of the order of the interfacial tension times the deformed area. Approaching close-packing, i.e. near r = 2rp, the interparticle potential features an unexpected dip. However, we attribute this to artefacts of the analysis. For example, given the steepness of the (zm,ϕ) graph (Fig. 4(a)), small differences in the (z,ϕ) behavior between disks on an elastic sheet and PMMA particles at a liquid interface can cause abrupt changes in
pp,r/rp)-graph, where the conversion from ϕ to the particle–particle separation r has been done using a ≈ π(r/2)2 and ϕ = ap/a. As expected, the interparticle potential is negligible at large separations; it starts to increase around r = 5rpi.e. ϕ ≈ 0.16. It then rises to a plateau value for r < 3.5rp, corresponding to ϕ > 0.33. The height of this plateau, at approximately 0.09apγ0 or 7 × 105kBT, supports the idea that deformations of the liquid interface are involved, as the free energy associated with the deformation of a liquid interface is expected to be of the order of the interfacial tension times the deformed area. Approaching close-packing, i.e. near r = 2rp, the interparticle potential features an unexpected dip. However, we attribute this to artefacts of the analysis. For example, given the steepness of the (zm,ϕ) graph (Fig. 4(a)), small differences in the (z,ϕ) behavior between disks on an elastic sheet and PMMA particles at a liquid interface can cause abrupt changes in ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) pp(r). Moreover, near close packing, the particles are close to jamming, at which point the interfacial particles are no longer in equilibrium and our thermodynamic approach breaks down. Finally, the particle–laden interface starts buckling for ϕ > 0.9 i.e. r < 2.1rp, which has not been taken into account in this analysis.
pp(r). Moreover, near close packing, the particles are close to jamming, at which point the interfacial particles are no longer in equilibrium and our thermodynamic approach breaks down. Finally, the particle–laden interface starts buckling for ϕ > 0.9 i.e. r < 2.1rp, which has not been taken into account in this analysis.
![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) ppvs. surface fraction ϕ. (b)
ppvs. surface fraction ϕ. (b) ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) pp in units of apγ0 and in units of 105kBT vs. separation r in units of particle radius rp. These graphs were extracted from the data presented in Fig. 4 using eqn (26).
pp in units of apγ0 and in units of 105kBT vs. separation r in units of particle radius rp. These graphs were extracted from the data presented in Fig. 4 using eqn (26).![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) pp in Fig. 5 as a capillary interaction. Capillary interactions are usually considered between non-touching particles and they are almost always attractive; one has to carefully design particle shapes to observe (near field) capillary repulsion.53 Instead, we consider the situation in which a particle monolayer is compressed until particles start touching. Our suggestion is that, en route to buckling, the particles push each other out of the initially flat plane of the liquid interface while remaining attached to the liquid interface (Fig. 6). This will cause energetically unfavourable deformations of the liquid interface at the length scale of the particles, resulting in an effective capillary repulsion between the particles. Consequently, we would not expect this effective repulsion to be observed in typical optical-tweezer experiments to measure interparticle potentials: the particles are typically not made to touch in optical-tweezer experiments. In addition, we would not expect the surface-pressure graph in Fig. 2(c) to be consistent with the power-law dependence of the capillary interactions between non-touching microparticles (as considered for example by Danov et al.54) Instead, our results suggest that the surface-pressure graph in Fig. 2(c) should be consistent with z(ϕ) (Fig. 4) and the r-dependence of the contact force between interfacial particles upon compression. In the case of interfacial particles with stronger long-range interactions, the effect of that long-range interaction on z(ϕ) should also be taken into account.
pp in Fig. 5 as a capillary interaction. Capillary interactions are usually considered between non-touching particles and they are almost always attractive; one has to carefully design particle shapes to observe (near field) capillary repulsion.53 Instead, we consider the situation in which a particle monolayer is compressed until particles start touching. Our suggestion is that, en route to buckling, the particles push each other out of the initially flat plane of the liquid interface while remaining attached to the liquid interface (Fig. 6). This will cause energetically unfavourable deformations of the liquid interface at the length scale of the particles, resulting in an effective capillary repulsion between the particles. Consequently, we would not expect this effective repulsion to be observed in typical optical-tweezer experiments to measure interparticle potentials: the particles are typically not made to touch in optical-tweezer experiments. In addition, we would not expect the surface-pressure graph in Fig. 2(c) to be consistent with the power-law dependence of the capillary interactions between non-touching microparticles (as considered for example by Danov et al.54) Instead, our results suggest that the surface-pressure graph in Fig. 2(c) should be consistent with z(ϕ) (Fig. 4) and the r-dependence of the contact force between interfacial particles upon compression. In the case of interfacial particles with stronger long-range interactions, the effect of that long-range interaction on z(ϕ) should also be taken into account.
