Bridging experiments and theory: isolating the effects of metal–ligand interactions on viscoelasticity of reversible polymer networks†
Xinyue
Zhang
 a,
Yuval
Vidavsky
b,
Sinai
Aharonovich
c,
Steven J.
Yang
b,
Michael R.
Buche
b,
Charles E.
Diesendruck
a,
Yuval
Vidavsky
b,
Sinai
Aharonovich
c,
Steven J.
Yang
b,
Michael R.
Buche
b,
Charles E.
Diesendruck
 c and
Meredith N.
Silberstein
*b
c and
Meredith N.
Silberstein
*b
aDepartment of Materials Science and Engineering, Cornell University, Ithaca, New York 14853, USA
bSibley School of Mechanical and Aerospace Engineering, Cornell University, Ithaca, New York 14853, USA. E-mail: meredith.silberstein@cornell.edu
cSchulich Faculty of Chemistry, Technion – Israel Institute of Technology, Haifa 3200003, Israel
First published on 6th August 2020
Abstract
Polymer networks cross-linked by reversible metal–ligand interactions possess versatile mechanical properties achieved simply by varying the metal species and quantity. Although prior experiments have revealed the dependence of the network's viscoelastic behavior on the dynamics of metal–ligand interaction, a theoretical framework with quantitative relations that would enable efficient material design, is still lacking. One major challenge is isolating the effect of metal–ligand interaction from other factors in the polymer matrix. To address this challenge, we designed a linear precursor free from solvents, chain entanglements and polymer–metal phase separation to ensure that relaxation of the network is mainly governed by the dissociation and association of the metal–ligand cross-links. The rheological behavior of the networks was thoroughly characterized regarding the changes in cross-link density, binding stoichiometry and coordination stability, allowing quantitative comparison between experimental results and the sticky Rouse model. Through this process, we noticed that the presence of reversible cross-links increases the network modulus at high frequency compared to the linear polymer, and that the effective metal–ligand dissociation time increases dramatically with increasing the cross-link density. Informed by these findings, we modified the expression of the sticky Rouse model. For the polymer in which the metal center and ligands bond in a paired association, the relaxation follows our enhanced sticky Rouse model. For the polymer in which each reversible cross-link consists of multiple metal centers and ligands, the relaxation timescale is significantly extended due to greater restriction on the polymer chains. This systematic study bridges experiments and theory, providing deeper understanding of the mechanical properties of metallopolymers and facilitating material design.
1 Introduction
The incorporation of reversible cross-links within polymer matrices presents a revolutionary approach to engineer materials beyond the limitations of conventional polymers.1 In contrast to statically cross-linked polymers, in which the temporal and spatial features are fixed, reversibly cross-linked polymers are able to evolve through transient interactions such as hydrogen bonding,2,3 ionic interaction,4 π–π stacking,5 metal–ligand interaction,6–8 and reversible covalent bonding.9,10 The dynamic nature of these interactions enables materials that are receptive to environmental changes, which in turn facilitates a variety of fascinating properties such as stimuli-responsivity,11 self-healing,12 shape-memory,13 and recyclability.14 Therefore, reversibly cross-linked polymers are promising candidates for various fields, including drug delivery and tissue engineering,15 soft robotics,16 bio-inspired elastomers,17 and energy storage.18Reversibly cross-linked polymers exhibit unique time-dependent mechanical properties due to scission and reformation of the cross-linking sites.19 Above the glass transition, these materials behave like elastic solids at shorter timescales when cross-links remain attached, and turns into viscous liquids at longer timescales when cross-links break.20 The viscoelastic character of the network can be tuned by many factors such as interaction type and strength, the binding configuration, and cross-linking density.21,22 Studies that unveil how each of these factors influences the viscoelasticity have been performed both theoretically and experimentally.23–26 Various models have been proposed for reversible networks with different architectures. For example, Tanaka and Edwards established a transient network model to describe the dynamics of telechelic polymer gels end-functionalized with associating groups, in which the reversible junctions connecting the chains can contain an arbitrary number of stickers.27 The sticky Rouse model was first presented by Baxandall to describe the dynamics of unentangled associative polymers with multiple pairwise reversible cross-links attached to the side of the chains.28 Rubinstein and coworkers expanded the model into the entangled regime and developed the sticky reptation model.29 Semenov and Rubinstein also developed a theory describing the dynamics of micellar gels, in which sticky groups from the entangled associative polymer bind strongly and form large aggregates.30 Subsequently, material systems with different transient interactions have been utilized to corroborate these models. For example, the dynamics of unentangled and entangled ionomers made by sulfonated polystyrene were captured by the sticky Rouse model and the sticky reptation model respectively,31,32 the diffusion of protein hydrogels with coiled-coil associations showed a sticky Rouse-like behavior,33 and the linear viscoelastic properties of the entangled silk protein solution was fit to the sticky reptation model.34
Among the aforementioned interactions, polymer networks with metal–ligand interactions as reversible cross-links have received a lot of attention, because the metal–ligand bond energy spans from one order of magnitude higher than the thermal energy to nearly covalent (∼20 to ∼300 kJ mol−1) and the coordination geometry is based on the choice of metal.20,21 These metal–ligand interactions, therefore, offer the flexibility of tuning cross-linking strength, and promote a versatile change of the mechanical properties simply by varying the species and quantity of metal.19,35 Although extensive experimental studies have been performed to build understanding between the strength/kinetics of metal–ligand interactions and the dynamic properties of metallopolymer networks,19,20,36,37 a corresponding theoretical model has not been validated. In order to obtain a predictive power for rational material design, a quantitative relation is needed that can bridge the molecular-level coordination details to the macroscopic mechanical properties with experimentally proven results.
Three key challenges exist to filling the critical gap between the theoretical model and a realistic material system. First, current material systems are mostly dispersed in solutions or gels, but the rate of chain motion and the association/dissociation of the metal–ligand bond can be affected by the presence of solvent molecules. For example, hydrodynamic interactions causing extra resistance to the polymer chain need to be considered,38 and certain solvent molecules like water can also act as ligands and coordinate with metal ions.39 Second, it is hard to isolate the effect of the metal–ligand interaction when multiple interactions are involved in the relaxation process, for example: entanglements or phase separation between the metal–ligand coordination and the polymer matrix may exist in the system, and confine the chain motion with timescales overlapping those of the cross-links. Moreover, theoretical models are usually built on ideal or simplified conditions, so they are difficult to validate experimentally without considering the complexity and variation of the real material.
To overcome these three key challenges, we carefully designed a bulk polymer system with metal–ligand interactions as the interchain reversible cross-links. Critically, the linear polymer is below the entanglement length, and no phase separation is observed in these metallopolymers, so that the relaxation of the network is mainly governed by the dissociation/association of the metal–ligand bonds. Metallopolymers with different cross-linking density and different metal centers were synthesized. We first characterized the viscoelastic properties of the networks by rheological measurements, and then investigated the dynamics of the network in the framework of the sticky Rouse model. Enhancements regarding the increase of network stiffness and the extension of the effective cross-link lifetime are proposed to modify the current expression. The advantages and limitations of applying this model to quantify the viscoelastic behavior of reversible metallopolymer networks are discussed. This systematic study provides quantitative insight into the viscoelastic properties of reversible polymer networks with a range of dynamic metal–ligand bonding, which is vital for efficient polymer design.
2 Experimental results
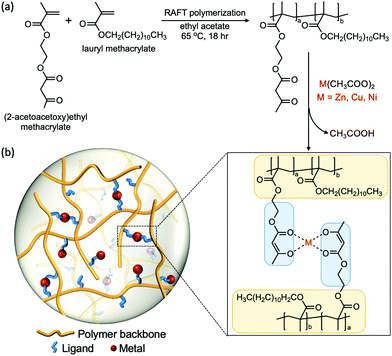
2.1 Polymer synthesis and characterization
We designed a polymeric system that enables us to study metal–ligand interactions as the key factor that governs the viscoelastic properties of the material. We used lauryl methacrylate (LM) as the main component in our system due to the high entanglement molecular weight (Me > 74 kg mol−1) and low glass transition temperature (Tg ≈ −55 °C) of its homopolymer.40–44 The high Me allows us to circumvent the influence of polymer chain entanglement, while the low Tg enables chain motion at room temperature without the addition of solvents that would affect the viscoelastic properties. The long alkyl side groups from lauryl methacrylate impart a steric effect on the chain, which suppresses the intramolecular cyclization of the polymer chains and the aggregation tendency of the associative groups. Therefore, confounding effects such as loops can be neglected.25,45 (2-acetoacetoxy)ethyl methacrylate (AAEMA) was chosen as the minor component of the copolymer because its enolate is a strong bidentate ligand which has been widely studied for its ability to coordinate with different metal cations.44The copolymer poly[(lauryl methacrylate)-co-(2-acetoacetoxy)ethyl methacrylate] (Linear), consisting of 90% lauryl methacrylate and 10% (2-acetoacetoxy)ethyl methacrylate, was synthesized by reversible addition–fragmentation chain transfer (RAFT) polymerization (Fig. 1a).46 The molecular weight of the copolymer was designed to be below the theoretical entanglement molecular weight calculated by BIOVIA Materials Studio Synthia (Table S1, ESI†) in order to avoid entanglement. Gel permeation chromatography (GPC) confirms the number-average molecular weight (Mn) is 53 kg mol−1 with polydispersity index (PDI) of 1.2 (Fig. S1, ESI†). The low polydispersity of the linear polymer facilitates fitting the rheological data into the theoretical Rouse model, which assumes the polymer is monodisperse. The 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 monomer ratio in the synthesized linear polymer was determined by 1H nuclear magnetic resonance (1H-NMR) (Fig. S2, ESI†).
1 monomer ratio in the synthesized linear polymer was determined by 1H nuclear magnetic resonance (1H-NMR) (Fig. S2, ESI†).
To obtain the metal–acetoacetate cross-linked network, complexation of the metal cation was performed by addition of metal diacetates (M(CH3COO)2, M refers to metal) to a solution of the linear polymer, followed by evaporation of solvents and acetic acid. Transition metal ions Zn(II), Cu(II) and Ni(II) were chosen as cross-linking species because the coordination complexes formed have different stabilities and geometries, which yield distinct mechanical properties.19,47 The glass transition temperature of the linear polymer and the metal cross-linked polymers were measured by differential scanning calorimetry (DSC) (Fig. S3, ESI†), which are all around −55 °C. The effect of metal–ligand coordination on Tg is insignificant, this may due to the low percentage of overall monomers (LMA + AAEMA) cross-linked in the system.
2.2 Effect of different metal concentrations
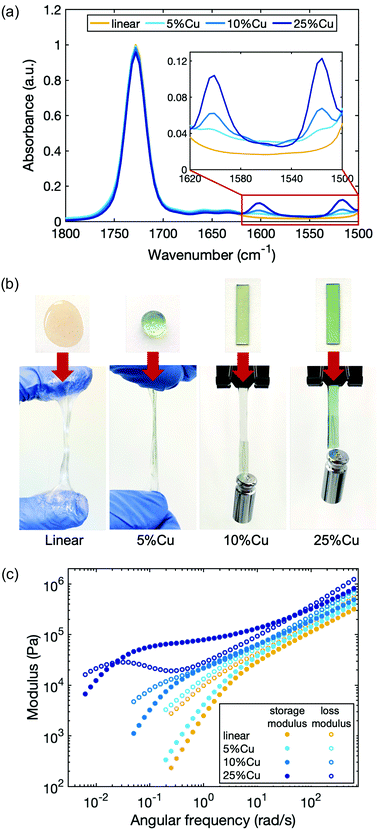
As a model system to study the influence of cross-linking density on the dynamics of the network, we chose Cu(II), which is known to form a stable complex with deprotonated 2-(acetoacetoxy)ethyl methacrylate in the polymer.48 The linear polymer was cross-linked by Cu(II) with a molar ratio of 5%, 10% and 25% compared to the total number of acetoacetate ligands (5%Cu, 10%Cu and 25%Cu). We did not use higher concentration of metal ions for two reasons. First, stiffer materials may lead to lower quality rheology tests due to the compliance effect of the rheometer. Second, in our system the metal–ligand complexes tend to precipitate out from the polymer matrices when the metal concentration is higher than that corresponding to cross-linking 40% of ligands. The tendency of phase separation is due to the polar functionality of the metal ions and nonpolar functionality of the polymer matrices.The presence of the coordination structure after adding Cu(II) was verified by infrared spectroscopy (FTIR) (Fig. 2a). The spectra were normalized to the peak at 1728 cm−1 based on the spectrum of the linear precursor, which corresponds to the absorption associated with the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibrations from both the ester groups on the backbone and the uncoordinated acetoacetate groups (keto tautomers) on the ligand. When Cu(II) coordination complexes form, two new peaks emerge at 1600 cm−1 and 1515 cm−1 due to the C
O stretching vibrations from both the ester groups on the backbone and the uncoordinated acetoacetate groups (keto tautomers) on the ligand. When Cu(II) coordination complexes form, two new peaks emerge at 1600 cm−1 and 1515 cm−1 due to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and C
O and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching vibrations of coordinated acetoacetate groups (enolate tautomers) respectively.48 The height of these two peaks increases with increasing Cu(II) cross-link ratio, indicating that more coordinated structures are present in the material.
C stretching vibrations of coordinated acetoacetate groups (enolate tautomers) respectively.48 The height of these two peaks increases with increasing Cu(II) cross-link ratio, indicating that more coordinated structures are present in the material.
The viscoelastic properties of the polymers change progressively from the linear polymer with increasing Cu(II) concentration (Fig. 2b). The linear polymer is a highly viscous liquid that flows when force is applied. When a molar ratio of 5% of total ligands in the polymer matrix are cross-linked by Cu(II), the material becomes slightly stiffer and less tacky. Increasing the cross-linking density further, yields materials with even higher stiffness. To quantify the viscoelasticity of the materials, a series of rheological experiments were performed by applying an oscillatory shear while sweeping the angular frequency (Fig. 2c). Storage G′(ω) and loss G′′(ω) moduli were measured, which capture the elasticity and viscosity of the materials respectively. The rheology curves for the linear polymer show that the storage modulus is less than the loss modulus over the entire frequency sweep, confirming the absence of entanglement.38,49 Moreover, the trend of the curves obeys the scaling law predicted by the Rouse model, which describes the viscoelastic character of unentangled ideal polymer chains: at high frequency, G′(ω) ≈ G′′(ω) ∼ ω0.5; at low frequency, G′(ω) ∼ ω2 and G′′(ω) ∼ ω.50 Without any topological confinements like entanglement or cross-links, the linear polymer chains can slide easily in response to the shear strain, therefore, the energy dissipates quickly and the material relaxes rapidly. Introducing cross-links not only results in the increase of storage and loss moduli at all measured frequencies, but also changes the shape of the curves, indicating a different relaxation progression. At sufficiently high cross-link density (25%Cu here), a plateau of the storage modulus appears at an intermediate frequency range. The characteristic relaxation time of the material (τc) can be extracted from the reciprocal of frequency at which the storage modulus becomes less than the loss modulus as frequency is decreased (Table 1). It benchmarks the timescale that viscosity overtakes elasticity to dominate the response of the network under dynamic loading. For a reversibly cross-linked network in which the breaking and reforming of cross-links is the rate determining step during the chain movement, this characteristic relaxation time can be interpreted as the timescale that the original cross-links have broken and reformed to new sites during the relaxation process as will be discussed further in the next section. The characteristic relaxation time for 10%Cu is ∼8 s, while the value extends to ∼4 min for 25%Cu. These results indicate that the more cross-links that are formed along a chain, the more difficult it is for a chain to diffuse, and thus the relaxation time is longer.
| Sample name | G′ (× 105 Pa) | G′′ (× 105 Pa) | τ c |
|---|---|---|---|
| Linear | 3.4 ± 0.1 | 5.7 ± 0.1 | — |
| 5%Cu | 4.0 ± 0.1 | 6.6 ± 0.1 | — |
| 10%Cu | 4.8 ± 0.1 | 7.6 ± 0.1 | ∼8 s |
| 25%Cu | 8.5 ± 0.2 | 12.7 ± 0.2 | ∼4 min |
| 25%Zn | 4.9 ± 0.2 | 7.6 ± 0.4 | ∼1 s |
| 25%Ni | 6.8 ± 0.2 | 9.8 ± 0.3 | >30 min |
2.3 Effect of different metal species
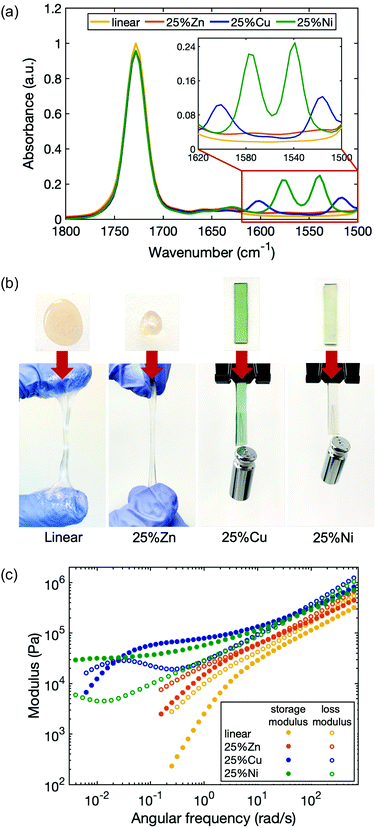
To study the dependence of network viscoelastic behavior on the choice of metal, additional metallopolymers were prepared in which 25% of the ligands were cross-linked by Zn(II) and Ni(II) (25%Zn and 25%Ni). The formation of coordination structures in each of the polymer matrices was verified by Fourier-transform infrared (FTIR) spectroscopy (Fig. 3a). In contrast to the linear polymer, 25%Zn shows two small new peaks centered at 1575 cm−1 and 1515 cm−1, corresponding to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and C
O and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching vibrations from the enolate form of the acetoacetate ligand. Similarly, for 25%Ni, new peaks are located at 1575 cm−1 and 1540 cm−1.
C stretching vibrations from the enolate form of the acetoacetate ligand. Similarly, for 25%Ni, new peaks are located at 1575 cm−1 and 1540 cm−1.
In metallopolymer networks, divalent transition metal cations form different coordination geometries with given ligands, and yield complexes with different binding modes, stoichiometry and stability.37 Zn(II) tends to form a tetrahedral structure, Cu(II) tends to be in a square planar arrangement, and Ni(II) is most stable in an octahedral geometry.51 Although Zn(II) and Cu(II) each bond with acetoacetate ligands in a binding stoichiometry of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2,48,52–54 Cu(II) has higher stability than Zn(II) according to the Irving–Williams series.55 In Ni(II), besides acetoacetate ligands, water molecules can also participate in the coordination to stabilize the octahedral geometry.56 To gain insight into how Ni(II) interacts with ligands in the polymer, we grew single crystals of Ni(II) coordinated with the ligand contributing monomer 2-(acetoacetoxy)ethyl methacrylate (NiAAEMA), and characterized the crystal structure by X-ray diffraction (Fig. S4, ESI†). Unlike Zn(II) and Cu(II), for which a paired association is formed between one metal center and two acetoacetate ligands,53,54 the crystal structure of NiAAEMA shows that in addition to coordinating with acetoacetate ligands, neighboring Ni(II) ions interact with each other, and thus each cross-linking site likely consists of multiple Ni(II) ions and ligands. To examine whether these pairs and associated metal–ligand complexes further aggregate to form a phase segmented polymer,57 SAXS and WAXS were carried out on the polymer to characterize the long-range and short-range structure respectively. The results show no observable phase separation in our system (Fig. S5, ESI†). Therefore, the viscoelastic behavior of the metallopolymer networks is governed by the breakage and reformation of the reversible cross-links arising from metal–ligand exchange.
2,48,52–54 Cu(II) has higher stability than Zn(II) according to the Irving–Williams series.55 In Ni(II), besides acetoacetate ligands, water molecules can also participate in the coordination to stabilize the octahedral geometry.56 To gain insight into how Ni(II) interacts with ligands in the polymer, we grew single crystals of Ni(II) coordinated with the ligand contributing monomer 2-(acetoacetoxy)ethyl methacrylate (NiAAEMA), and characterized the crystal structure by X-ray diffraction (Fig. S4, ESI†). Unlike Zn(II) and Cu(II), for which a paired association is formed between one metal center and two acetoacetate ligands,53,54 the crystal structure of NiAAEMA shows that in addition to coordinating with acetoacetate ligands, neighboring Ni(II) ions interact with each other, and thus each cross-linking site likely consists of multiple Ni(II) ions and ligands. To examine whether these pairs and associated metal–ligand complexes further aggregate to form a phase segmented polymer,57 SAXS and WAXS were carried out on the polymer to characterize the long-range and short-range structure respectively. The results show no observable phase separation in our system (Fig. S5, ESI†). Therefore, the viscoelastic behavior of the metallopolymer networks is governed by the breakage and reformation of the reversible cross-links arising from metal–ligand exchange.
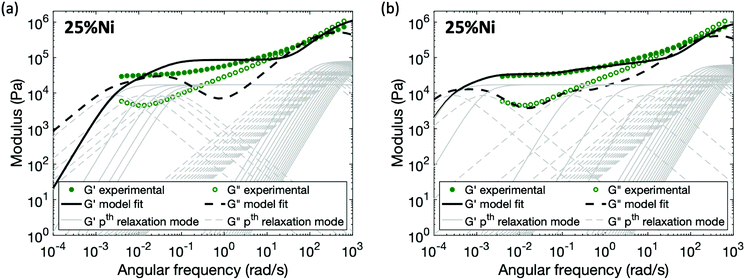
While all the metal cations enhance the elasticity of the polymer by forming temporary cross-links, each type of cation has a distinct effect. 25%Zn is stiffer and less viscous than the linear polymer, yet its stiffness increase is less dramatic than 25%Cu and 25%Ni (Fig. 3b). The viscoelasticity of the materials with each metal were quantified by rheological measurements (Fig. 3c). The storage and loss moduli of the polymers with metal–ligand coordination are all increased compared to the linear polymer. While the high frequency modulus of 25%Zn increased by only ∼30% compared to the linear polymer, those of 25%Cu and 25%Ni more than doubled, with 25%Cu slightly stiffer than 25%Ni (Table 1). Further, the characteristic relaxation times of the three samples are distinct: τZn ∼ 1 s < τCu ∼ 4 min < τNi. It is expected that 25%Zn has the shortest relaxation time due to its weaker bonding nature. According to the Irving–Williams order of stability, bivalent transition metal complexes follow Ni(II) < Cu(II),55 therefore, at first, it seems counterintuitive that 25%Ni has a longer relaxation time than 25%Cu. However, this flipped stability can be attributed to the coordination structure. As also seen in previous work, the lifetime of a multi-ion association is much longer than that of a paired association.58 For 25%Ni, stress relaxation involves consecutive scission and reformation of metal–ligand bonds associated to the same cross-linking site, so the overall relaxation process is extended. Whereas in its counterpart 25%Zn and 25%Cu, only one of the paired ligands detaching and reattaching will lead to relaxation. Since water molecules can participate in the Ni(II) coordination as substitute ligands, we found that the 25%Ni coordinated samples are sensitive to the ambient humidity, and the viscoelastic properties of the material also change accordingly (Fig. S6, ESI†). These results indicate that both the complex stability and the coordination structure are crucial to quantifying the dynamic character of polymers with metal–ligand interactions, whereas the latter is often overlooked.
3 Theoretical models and discussion
When strain is applied to a polymer, chains move to relieve the resulting stress.38 The dynamics of chain motion is dominated by the viscoelastic nature of the polymer.49 Since neither entanglement nor phase separation exists in our system, relaxation is simply governed by two stages: shorter chain segments diffuse through Brownian motion, and longer chain segments move by breaking the current cross-links and reforming to new sites. The former is theoretically studied by the Rouse model, which captures the dynamics of unentangled polymer melts.50 The sticky Rouse adaptation of the Rouse model takes account of the multiple pairwise cross-links along the side of polymer chains. So far, it has been successfully applied to the polymers with reversible hydrogen bonding and ionic interactions,31,33 but has rarely been discussed in the context of metal–ligand coordination, which contain distinct molecular level details.36 Therefore, in this section, we carefully examine the consistencies and discrepancies between our above presented experimental results and the sticky Rouse model. In order to make this discussion clear without referring to external literature, we present first the Rouse model, then the sticky Rouse model, and finally our enhanced version of the sticky Rouse model. At each stage we show quantitative comparisons of these models with our experimental results and detail how material parameters were extracted.3.1 Dynamics of linear polymers
The relaxation of an unentangled linear polymer melt is described by the Rouse model.50,59 When strain is applied to the polymer, the relaxation of a chain starts from a single Kuhn monomer length and progressively extends to the full length of the chain. Accordingly, in the Rouse model, a linear chain with N Kuhn monomers experiences a series of relaxation modes. The relaxation mode p (p = 1, 2, 3,…, N) corresponds to the relaxation involving a length of N/p monomers, with its characteristic relaxation time (τp)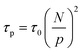 | (1) |
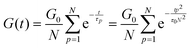 | (2) |
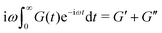 | (3) |
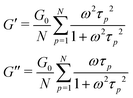 | (4) |
In order to fit the rheological data of the linear polymer to the Rouse model, we make the assumption that the chains are the same length (PDI of 1 rather than the true value of 1.2). To calculate the number of Kuhn monomers N along the chain, we use the Kuhn length of poly(lauryl methacrylate) (∼30 Å),60 since 90% of the linear polymer is composed of lauryl methacrylate. Given that the Kuhn length is equivalent to the size of ∼20 C–C bonds along the polymer backbone, which is made up of nine lauryl methacrylate molecules and one (2-acetoacetoxy)ethyl methacrylate molecule, each Kuhn monomer consists of one repeat unit. The number of Kuhn monomers on each chain (N = 21) can then be calculated by the molecular weight of the polymer. The initial modulus of the linear polymer (G0) and its Kuhn monomer relaxation time (τ0) can be obtained by fitting the rheological data to eqn (4), resulting in G0 ≈ 3.6 × 105 Pa and τ0 ≈ 10−3 s. Fig. 4 shows the experimental and Rouse model fitting results of the linear polymer. A transition is clearly present: when ω < 1/τR, G′(ω) ≈ G′′(ω) ∼ (ω)0.5; when ω > 1/τR, G′(ω) ∼ ω2 and G′′(ω) ∼ ω. Therefore, the Rouse model fits the rheological behavior of the linear polymer generally well. The deviation of the loss modulus at high frequency results from the finite number of relaxation modes. As the number of relaxation modes increases, the overlap of storage and loss moduli will be extended. A second deviation is that the loss modulus is slightly higher than the storage modulus rather than being equal as predicted by the theory; this is likely because the Rouse model ignores the intramolecular friction (internal viscosity) from the motion of submolecule junctions.49
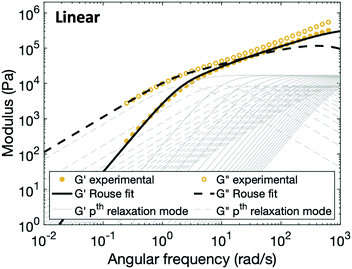 | ||
| Fig. 4 Comparison between experimental data and fitting results of the Rouse model for the linear polymer. The thin grey lines show the relaxation modes in eqn (4) (solid lines for G′ and dashed lines for G′′) that add up to form the overall simulation response. | ||
3.2 Dynamics of polymers with reversible cross-links
Built upon the Rouse model, the sticky Rouse model additionally accounts for the delay in chain relaxation due to the breaking and reforming of reversible interactions. Mathematically, it breaks down the relaxation of the network into two series of relaxation modes based on the length of the relaxing segments.31,61 The presence of dynamic cross-links slows down the relaxation modes of longer segment lengths, which involves the dissociation of cross-links. Within the length between two neighboring cross-links, the monomers relax following the Rouse model (from p = Nx + 1 to p = N, where Nx is the number of cross-links per chain). Given that the energy needed to break a cross-link is generally higher than the energy needed for the chain motion, it is assumed that breaking cross-links takes longer than these high mode chain relaxations, so the cross-links remain associated at this stage. The relaxation progression of longer chain lengths is hindered by the cross-links, and only occurs after the cross-links are broken. Consequently, the characteristic relaxation time of these modes is dominated by the lifetime of the cross-link (τx), defined as the average time a cross-link remains bonded. The cross-link lifetime is exponentially related to the activation energy of cross-link dissociation (Ea)21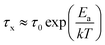 | (5) |
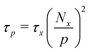 | (6) |
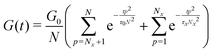 | (7) |
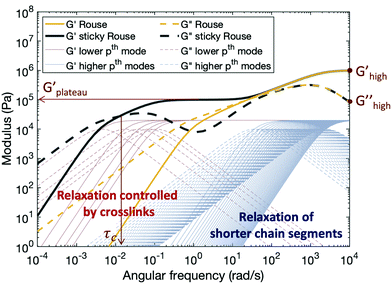
Fig. 5 shows typical storage and loss moduli curves derived from the Rouse model (eqn (4)) and the sticky Rouse model (eqn (7) in conjunction with eqn (3)). Comparing with the rheological results obtained, we can see that the sticky Rouse model captures some of the features in the stress relaxation process well, i.e., the decreasing trend of both moduli with decreasing angular frequency, a plateau storage modulus resulting from the delayed relaxation of cross-linked segments, and crossover between two moduli which gives the characteristic relaxation time. However, it was observed both in our experiments and some of other reported works that compared to the linear polymer, introducing cross-links will increase the network modulus at high frequency, and that the modulus increases as cross-link ratio increases.31,62 Whereas in Fig. 5, the storage and loss moduli at high frequency remain the same for both the linear polymer and the networks with different numbers of cross-links (e.g., Ghigh′ and Ghigh′′ in Fig. 5). This is because in the Rouse dynamics the initial modulus of the polymer only depends on the chain density: each elastically active chain contributes kT energy prior to relaxation, regardless of whether reversible cross-links are present. Below, we consider a model enhancement to address this disparity.
Compared to the linear polymer, the storage modulus of cross-linked polymers at high frequency increases with the density of metal–ligand cross-links (Fig. S7, ESI†). This stiffness increase at high frequency is rarely discussed by previous works. We hypothesize that the behavior of the reversibly cross-linked chain deviates from the purely entropic regime which underlies the Rouse dynamics. Since cross-links impose topological constraints on the chain, the rotational freedom of the chain will be affected at sufficiently high cross-link density, and thus a derivation from the ideal Gaussian behavior is expected.63 This explanation is further supported by the results published by Jangizehi et al.: the moduli difference between the linear polymer and networks at high frequency diminishes when the molar mass of the precursor is increased while keeping the cross-link molar ratios unchanged.64 Accordingly, we modify the initial modulus of a cross-linked polymer by an additional term Gx. Since this modulus correction term arises from the cross-linking, it will be released as cross-links break. For high index/short time modes (Nx + 1 < p ≤ N), which experience the cross-links as remaining closed, the modulus of the network is (G0 + Gx); while for low index/long time modes (1 ≤ p ≤ Nx + 1), the cross-links break and reform, and the apparent modulus of the network matches that of the linear polymer G0. For polymers with metal–ligand interactions acting as reversible cross-links, Gx depends on both cross-link density and metal species. Higher cross-link density yields stronger topological constraint to the chains, and thus increases the modulus of the network more, so Gx increases as increasing the cross-link density. For different metal species, Gx depends on both the coordination structure and stability of the complex: more association between the metal centers and ligands, or higher activation energy required for ligand exchange, leads to higher restriction on the chain, therefore increasing the chain stiffness.
Moreover, we noticed the cross-link lifetime in eqn (7) has different values for Cu cross-linked polymer at different cross-link ratios. According to the idea proposed by Rubinstein and Semenov for the solutions of associating polymers, a renormalized lifetime of the cross-link (τx*) rather than the actual lifetime should be applied in quantifying the stress relaxation.29 The actual lifetime is defined as the average time that a cross-link remains associated based on the binding energy (see eqn (5)), whereas the renormalized lifetime of the cross-link corresponds to the time until one end of an original cross-link connects to a new partner.29 The latter takes into account that the two ends may break and recombine with each other several times before attaching to a new partner, so the renormalized cross-link lifetime can be much longer than the actual lifetime depending on the accessibility to other open ends. Increasing cross-link density results in fewer open sites, as well as less accessible space to be explored by the open cross-link.65 Therefore, the higher the cross-link density, the longer the renormalized cross-link lifetime. This trend has been observed in some transient networks,66,67 and we next examine it in our model system.
For metallopolymers, the lifetime of metal–ligand cross-links is difficult to measure directly. However, based on eqn (6), we can calculate the renormalized lifetime of the cross-link (τx* instead of τx) from the characteristic relaxation time of a full-length chain (τp at p = 1). The value of τ1 is comparable, but not identical, to the characteristic relaxation time of the material (τc) which was extracted from the rheology curves. As listed in Table 1, τc for 10%Cu and 25%Cu is 8 s and 4 min respectively. The number of cross-links per chain is calculated in the following way: since every Kuhn monomer contains one acetoacetate ligand, each chain has 21 available cross-linking sites. When the cross-link density increases from 10% to 25%, the number of cross-links per chain increases from 2 to 5. Plugging the above-mentioned numbers into eqn (6), we get that τx* for 10%Cu is 2 s and τx* for 25%Cu is 9.6 s. These results confirm that the renormalized lifetime of a metal–ligand interaction has a strong dependence on the cross-link density.
The above discussion demonstrates the necessity of modifying the network modulus and using a renormalized lifetime of the cross-link to describe the stress relaxation of metallopolymers with dynamic metal–ligand interaction. Combining these two factors, the modified equation can be written as:
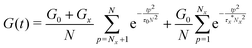 | (8) |
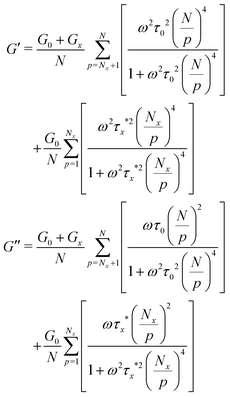 | (9) |
Applying this modified sticky Rouse model, we successfully fit the evolution of storage modulus and predicted the loss modulus for the Zn(II) and Cu(II) cross-linked polymers, fitting parameters are listed in Table 2 and methods are in the ESI.† As shown in Fig. 6, the storage and loss moduli at high frequency match the experimental results well after modifying the initial moduli of the cross-linked polymers. The trend of Gx indicates that higher metal concentration or complex stability imposes stronger constraint on the polymer backbone, and yields a stiffer network. Another observation is τx* increases dramatically as the cross-link density, τx* of 25%Cu is ∼9 times of the value at 5%Cu. This is expected since the renormalized cross-link lifetime is directly related to the accessibility of other ligands: at the gel point (5%Cu), on average there is only one ligand cross-linked per chain, so a high density of unbonded ligands are available when a cross-link breaks. Since the possibility of finding a new ligand to reform with is high, the renormalized cross-link lifetime is relatively short. In contrast, when five times as many ligands are bound (25%Cu) the local concentration of unbonded ligands is much lower, so the possibility of finding a new ligand to reform is significantly decreased. The discrepancy between the fitting curves and the experimental results is mainly observed at an intermediate frequency range. We attribute this discrepancy to a combination of the potential entanglements and polydispersity.25,31 Since the ratio between the entanglement molecular weight (Me ≈ 74 kg mol−1) and the linear chain molecular weight (Mn = 53 kg mol−1) is 1.4, it is possible that entanglements arise among the effectively longer temporary chains formed by the dynamic cross-links. These entanglements would increase both the storage and loss moduli from ∼8 rad s−1 (ω = 2π/τe, where τe is the Rouse time of an entanglement strand) until the low frequency crossover. The polydispersity of the chain segment length due to non-uniformly distributed cross-links along the chain and to dangling ends, would cause the relative heights of the relaxation modes to shift slightly, leading to a less distinct evolution of the loss modulus. In summary, from both the theoretical model and the experimental results, we can see that for the metallopolymers with pairwise metal–ligand association, increasing either cross-link density or stability of the metal–ligand bond will increase the stiffness of the network, raise the storage modulus plateau at an intermediate frequency range, and also lead to longer characteristic relaxation time of the network.
| Sample name | N x | G x (× 105 Pa) | τ x *(s) |
|---|---|---|---|
| 5%Cu | 1 | 1.4 | 0.61 |
| 10%Cu | 2 | 4.0 | 1.12 |
| 25%Cu | 5 | 16.5 | 5.43 |
| 25%Zn | 5 | 4.2 | 0.08 |
| 25%Ni | 5 | 13.1 | 13.43 |
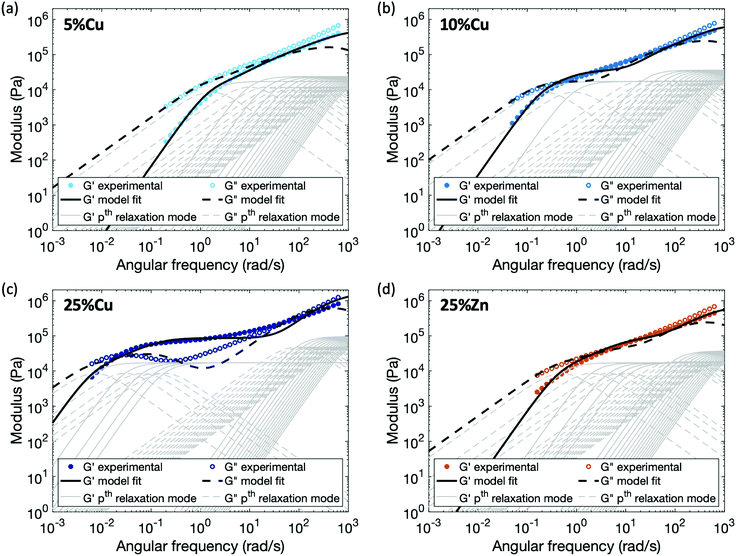 | ||
| Fig. 6 Comparison between experimental data and fitting results by applying the enhanced sticky Rouse model: (a) 5%Cu, (b) 10%Cu, (c) 25%Cu, and (d) 25%Zn. The thin grey lines show the relaxation modes in eqn (9) that add up to form the overall simulation response. | ||
For the polymers coordinated by Ni(II), in which neighboring Ni(II) ions form associated structures through the acetoacetate ligands, no set of parameters (Gx and τx*) for the enhanced sticky Rouse model (eqn (9)) exists that provides a good fit of the experimental data (Fig. 7a). The characteristic relaxation time of the material predicted by a sticky Rouse fitting is much shorter than the actual value indicated by the rheology curves. In order to fit the evolution of storage and loss moduli, the Maxwell elements representing the relaxation controlled by cross-links would need to be extended to a wider frequency range (Fig. 7b). The difference between pairwise association and multi-ion association results from the coordination number and configuration of the metal centers.37 In contrast to a monomeric metal complex, where only two ligands bond with metal, and there is a high chance that these two ligands come from different chain segment, relaxation occurs once one of the two ligands is detached from the metal centers. However, in a multi-ion association like Ni(II), a multivalency effect is in action. There is a higher chance that a chain segment is confined through multiple metal–ligand bonds. In order for a chain segment to relax, all the connected ligands need to be completely detached for this segment to relax. In addition, if only one of the ligands breaks, there is an increased chance of bond reformation to the same segment due to the cation–anion proximity. Hence, ligand exchange within the multi-ion association is in general more energetically expensive and also kinetically less favored than in a monomeric metal complex, explaining the longer relaxation time. Further study would be required to capture the mechanism of breaking and reforming within these cross-link sites.
4 Conclusions
In this work, we explored the viscoelastic properties of reversibly cross-linked metallopolymers both experimentally and in the framework of the sticky Rouse model. With a carefully designed model system, which avoids entanglement in the linear polymer, and does not have phase separation, the dynamics of the transient network is mainly governed by the dissociation/association of metal–ligand cross-links. When metal cations are incorporated within the polymer, the rheological behavior transitions from a clear Rouse relaxation to a qualitatively sticky Rouse-like relaxation. A plateau storage modulus appears at intermediate frequency with increasing the cross-link density, and the characteristic relaxation time of the material varies by orders of magnitude with choosing different metal cations. The distinct viscoelastic properties of the metallopolymers depend on cross-link density, metal–ligand bond stability, and the association structure of the complex. Upon quantitative implementation of the sticky Rouse model building upon parameters extracted from linear polymer, we noticed an increase of the network modulus at high frequency, and a cross-link density dependent extension of the cross-link lifetime, which are not inherent to the sticky Rouse model. For the metallopolymers in which the metal cation and ligands form pairwise associations, the viscoelastic properties can be quantitatively described by the sticky Rouse model enhanced by (1) a network modulus enhancement factor for the segments that relax with intact cross-links, and (2) a renormalized bond lifetime that accounts for the absence of relaxation when bonds reform in their initial pairing. For metallopolymers in which metal cations and ligands form multi-ion associations, the relaxation is extended even further due to a longer metal–ligand exchange process. These findings can be applied to metallopolymer design for mechanical properties and are readily extensible to include the effects of external stimuli to the metal centers and binding sites.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work was supported by the Office of Naval Research under Grant no. N00014-17-1-2989 under the administration of PO Dr Armistead. This work made use of the Cornell Center for Materials Research Shared Facilities which are supported through the NSF MRSEC program (DMR-1719875). It is also based in part upon research conducted at the Materials Solutions Network at CHESS (MSN-C) which is supported by the Air Force Research Laboratory under award FA8650-19-2-5220. We thank Arthur R. Woll, Louisa Smieska, and Stephanie I. Rosenbloom for the assistance in running SAXS and WAXS.References
- R. J. Wojtecki, M. A. Meador and S. J. Rowan, Nat. Mater., 2011, 10, 14–27 CrossRef CAS PubMed.
- D. K. Hohl, A.-C. Ferahian, L. Montero de Espinosa and C. Weder, ACS Macro Lett., 2019, 8, 1484–1490 CrossRef CAS.
- B. A. Lamers, M. L. Ślęczkowski, F. Wouters, T. A. Engels, E. Meijer and A. R. Palmans, Polym. Chem., 2020, 11, 2847–2854 RSC.
- Y. Peng, Y. Yang, Q. Wu, S. Wang, G. Huang and J. Wu, Polymer, 2018, 157, 172–179 CrossRef CAS.
- S. Y. Son, J.-H. Kim, E. Song, K. Choi, J. Lee, K. Cho, T.-S. Kim and T. Park, Macromolecules, 2018, 51, 2572–2579 CrossRef CAS.
- M. Burnworth, L. Tang, J. R. Kumpfer, A. J. Duncan, F. L. Beyer, G. L. Fiore, S. J. Rowan and C. Weder, Nature, 2011, 472, 334–337 CrossRef CAS PubMed.
- C.-H. Li, C. Wang, C. Keplinger, J.-L. Zuo, L. Jin, Y. Sun, P. Zheng, Y. Cao, F. Lissel and C. Linder, et al. , Nat. Chem., 2016, 8, 618 CrossRef CAS PubMed.
- L. Shi, P. Ding, Y. Wang, Y. Zhang, D. Ossipov and J. Hilborn, Macromol. Rapid Commun., 2019, 40, 1800837 CrossRef PubMed.
- G. M. Scheutz, J. J. Lessard, M. B. Sims and B. S. Sumerlin, J. Am. Chem. Soc., 2019, 141, 16181–16196 CrossRef CAS PubMed.
- P. Chakma and D. Konkolewicz, Angew. Chem., Int. Ed., 2019, 58, 9682–9695 CrossRef CAS PubMed.
- H. Sun, C. P. Kabb, M. B. Sims and B. S. Sumerlin, Prog. Polym. Sci., 2019, 89, 61–75 CrossRef CAS.
- Y. Miwa, J. Kurachi, Y. Sugino, T. Udagawa and S. Kutsumizu, Soft Matter, 2020, 16, 3384–3394 RSC.
- W. Miao, W. Zou, Y. Luo, N. Zheng, Q. Zhao and T. Xie, Polym. Chem., 2020, 11, 1369–1374 RSC.
- C. Jehanno and H. Sardon, Nature, 2019, 568, 467–469 CrossRef CAS PubMed.
- H. Wang and S. C. Heilshorn, Adv. Mater., 2015, 27, 3717–3736 CrossRef CAS PubMed.
- W. J. Zheng, N. An, J. H. Yang, J. Zhou and Y. M. Chen, ACS Appl. Mater. Interfaces, 2015, 7, 1758–1764 CrossRef CAS PubMed.
- E. Filippidi, T. R. Cristiani, C. D. Eisenbach, J. H. Waite, J. N. Israelachvili, B. K. Ahn and M. T. Valentine, Science, 2017, 358, 502–505 CrossRef CAS PubMed.
- Z. Yu, D. G. Mackanic, W. Michaels, M. Lee, A. Pei, D. Feng, Q. Zhang, Y. Tsao, C. V. Amanchukwu and X. Yan, et al. , Joule, 2019, 3, 2761–2776 CrossRef CAS.
- S. C. Grindy, R. Learsch, D. Mozhdehi, J. Cheng, D. G. Barrett, Z. Guan, P. B. Messersmith and N. Holten-Andersen, Nat. Mater., 2015, 14, 1210–1216 CrossRef CAS PubMed.
- N. S. Schauser, G. E. Sanoja, J. M. Bartels, S. K. Jain, J. G. Hu, S. Han, L. M. Walker, M. E. Helgeson, R. Seshadri and R. A. Segalman, Chem. Mater., 2018, 30, 5759–5769 CrossRef CAS.
- Z. Zhang, Q. Chen and R. H. Colby, Soft Matter, 2018, 14, 2961–2977 RSC.
- M. Golkaram and K. Loos, Macromolecules, 2019, 52, 9427–9444 CrossRef CAS PubMed.
- D. M. Loveless, S. L. Jeon and S. L. Craig, Macromolecules, 2005, 38, 10171–10177 CrossRef CAS.
- Y. Vidavsky, S. Bae and M. N. Silberstein, J. Polym. Sci., Part A: Polym. Chem., 2018, 56, 1117–1122 CrossRef CAS.
- M. Ahmadi, A. Jangizehi, E. van Ruymbeke and S. Seiffert, Macromolecules, 2019, 52, 5255–5267 CrossRef CAS.
- F. Vidal, J. Gomezcoello, R. A. Lalancette and F. Jakle, J. Am. Chem. Soc., 2019, 141, 15963–15971 CrossRef CAS PubMed.
- F. Tanaka and S. Edwards, Macromolecules, 1992, 25, 1516–1523 CrossRef CAS.
- L. Baxandall, Macromolecules, 1989, 22, 1982–1988 CrossRef CAS.
- M. Rubinstein and A. N. Semenov, Macromolecules, 2001, 34, 1058–1068 CrossRef CAS.
- A. Semenov and M. Rubinstein, Macromolecules, 2002, 35, 4821–4837 CrossRef CAS.
- Q. Chen, C. Huang, R. Weiss and R. H. Colby, Macromolecules, 2015, 48, 1221–1230 CrossRef CAS.
- X. Cao, X. Yu, J. Qin and Q. Chen, Macromolecules, 2019, 52, 8771–8780 CrossRef CAS.
- S. Tang, M. Wang and B. D. Olsen, J. Am. Chem. Soc., 2015, 137, 3946–3957 CrossRef CAS PubMed.
- C. Schaefer, P. R. Laity, C. Holland and T. C. McLeish, Macromolecules, 2020, 53, 2669–2676 CrossRef CAS PubMed.
- M. Ahmadi and S. Seiffert, Soft Matter, 2020, 16, 2332–2341 RSC.
- D. Xu and S. L. Craig, Macromolecules, 2011, 44, 5465–5472 CrossRef CAS PubMed.
- D. Mozhdehi, J. A. Neal, S. C. Grindy, Y. Cordeau, S. Ayala, N. Holten-Andersen and Z. Guan, Macromolecules, 2016, 49, 6310–6321 CrossRef CAS.
- M. Rubinstein and R. H. Colby, et al., Polymer physics, Oxford university press, New York, vol. 23, 2003 Search PubMed.
- S. Kim, A. M. Peterson and N. Holten-Andersen, Chem. Mater., 2018, 30, 3648–3655 CrossRef CAS.
- R. S. Porter and J. F. Johnson, Chem. Rev., 1966, 66, 1–27 CrossRef.
- D. P. Chatterjee and B. M. Mandal, Macromolecules, 2006, 39, 9192–9200 CrossRef CAS.
- J. L. Halary, F. Lauprêtre and L. Monnerie, Polymer materials: macroscopic properties and molecular interpretations, John Wiley & Sons, 2011 Search PubMed.
- S. Rogers and L. Mandelkern, J. Chem. Soc., 1957, 61, 985–991 CAS.
- M. Demetriou and T. Krasia-Christoforou, J. Polym. Sci., Part A: Polym. Chem., 2008, 46, 5442–5451 CrossRef CAS.
- J.-i. Ikeda, K. Fujise, H. Aota and A. Matsumoto, J. Network Polym., Jpn., 2003, 24, 97–103 CAS.
- O. Galant, M. Davidovich-Pinhas and C. E. Diesendruck, Macromol. Rapid Commun., 2018, 39, 1800407 CrossRef PubMed.
- M. E. Lamm, L. Song, Z. Wang, B. Lamm, L. Fu and C. Tang, Polym. Chem., 2019, 10, 6570–6579 RSC.
- A. Sanchez-Sanchez, A. Arbe, J. Colmenero and J. A. Pomposo, ACS Macro Lett., 2014, 3, 439–443 CrossRef CAS.
- J. D. Ferry, Viscoelastic properties of polymers, John Wiley & Sons, 1980 Search PubMed.
- P. E. Rouse Jr, J. Chem. Soc., 1953, 21, 1272–1280 Search PubMed.
- L. Rulíšek and J. Vondrášek, J. Inorg. Biochem., 1998, 71, 115–127 CrossRef.
- J. Perz and J. Mehaffey, Org. Prep. Proced. Int., 1972, 4, 299–300 CrossRef.
- R. Hayami, N. Endo, Y. Miyase, K. Yamamoto and T. Gunji, J. Sol-Gel Sci. Technol., 2019, 91, 255–260 CrossRef CAS.
- G. Barclay and A. Cooper, J. Chem. Soc., 1965, 3746–3751 RSC.
- H. Irving and R. Williams, J. Chem. Soc., 1953, 3192–3210 RSC.
- Y. Vidavsky, M. R. Buche, Z. M. Sparrow, X. Zhang, S. J. Yang, R. A. DiStasio Jr and M. N. Silberstein, Macromolecules, 2020, 53, 2021–2030 CrossRef CAS.
- A. C. Jackson, F. L. Beyer, S. C. Price, B. C. Rinderspacher and R. H. Lambeth, Macromolecules, 2013, 46, 5416–5422 CrossRef CAS.
- M. Ahmadi, L. Löser, K. Fischer, K. Saalwächter and S. Seiffert, Macromol. Chem. Phys., 2020, 221, 1900400 CrossRef CAS.
- J. D. Ferry, R. F. Landel and M. L. Williams, J. Appl. Phys., 1955, 26, 359–362 CrossRef CAS.
- S. M. Aharoni, Macromolecules, 1983, 16, 1722–1728 CrossRef CAS.
- Q. Chen, G. J. Tudryn and R. H. Colby, J. Rheol., 2013, 57, 1441–1462 CrossRef CAS.
- A. Shabbir, I. Javakhishvili, S. Cerveny, S. Hvilsted, A. L. Skov, O. Hassager and N. J. Alvarez, Macromolecules, 2016, 49, 3899–3910 CrossRef CAS.
- J. M. Charlesworth, Polym. Eng. Sci., 1988, 28, 230–236 CrossRef CAS.
- A. Jangizehi, M. Ahmadi and S. Seiffert, J. Polym. Sci., Part B: Polym. Phys., 2019, 57, 1209–1223 CrossRef CAS.
- J. Brassinne, A. Cadix, J. Wilson and E. Van Ruymbeke, J. Rheol., 2017, 61, 1123–1134 CrossRef CAS.
- S. Tang and B. D. Olsen, Macromolecules, 2016, 49, 9163–9175 CrossRef CAS.
- B. Gold, C. Hövelmann, N. Lühmann, W. Pyckhout-Hintzen, A. Wischnewski and D. Richter, J. Rheol., 2017, 61, 1211–1226 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 1986332. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0sm01115k |
| This journal is © The Royal Society of Chemistry 2020 |