Aster swarming by symmetry breaking of cortical dynein transport and coupling kinesins†
Abstract
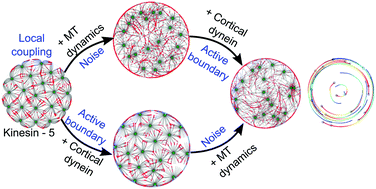
Microtubule (MT) radial arrays or asters establish the internal topology of a cell by interacting with organelles and molecular motors. We proceed to understand the general pattern forming potential of aster–motor systems using a computational model of multiple MT asters interacting with motors in cellular confinement. In this model dynein motors are attached to the cell cortex and plus-ended motors resembling kinesin-5 diffuse in the cell interior. The introduction of ‘noise’ in the form of MT length fluctuations spontaneously results in the emergence of coordinated, achiral vortex-like rotation of asters. The coherence and persistence of rotation require a threshold density of both cortical dyneins and coupling kinesins, while the onset is diffusion-limited with relation to the cortical dynein mobility. The coordinated rotational motion emerges due to the resolution of a ‘tug-of-war’ of multiple cortical dynein motors bound to MTs of the same aster by ‘noise’ in the form of MT dynamic instability. This transient symmetry breaking is amplified by local coupling by kinesin-5 complexes. The lack of widespread aster rotation across cell types suggests that biophysical mechanisms that suppress such intrinsic dynamics may have evolved. This model is analogous to more general models of locally coupled self-propelled particles (SPP) that spontaneously undergo collective transport in the presence of ‘noise’ that have been invoked to explain swarming in birds and fish. However, the aster–motor system is distinct from SPP models with regard to the particle density and ‘noise’ dependence, providing a set of experimentally testable predictions for a novel sub-cellular pattern forming system.


 Please wait while we load your content...
Please wait while we load your content...