Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Magnetorheology: a review
Jose R.
Morillas
and
Juan
de Vicente
 *
*
Biocolloid and Fluid Physics Group and Excellence Research Unit ‘Modeling Nature’ (MNat), Department of Applied Physics, Faculty of Sciences, University of Granada, C/Fuentenueva s/n, 18071 – Granada, Spain. E-mail: jvicente@ugr.es
First published on 1st September 2020
Abstract
Magnetic Soft Matter is a rapidly evolving discipline with fundamental and practical interest. This is due to the fact that its physical properties can be easily controlled through external magnetic fields. In this review paper, we revisit the most recent progress in the field (since 2010) emphasizing the rheological properties of these fascinating materials. New formulations and flow kinematics are discussed. Also, new members are integrated into the long-lived magnetorheology family and suggestions are provided for future development.
Jose R. Morillas received a BSc degree (2014) and a PhD degree (2019) in Physics from University of Granada (Spain). He was recipient of a FPU Predoctoral Fellow to complete his PhD studies on magnetorheology in the pre-yield regime. His research interests include the experimental and numerical characterization of ferrofluids and magnetorheological fluids. |
Juan de Vicente received PhD degrees in Physics from the University of Granada (Spain) and the University of Nice-Sophia Antipolis (France) in 2002. He has been FPU Predoctoral Fellow, Marie Curie Postdoc and Marie Curie ERG Fellow at the LPMC-CNRS (France), University of Twente (The Netherlands), University of Wisconsin (USA), Unilever (UK) and Imperial College London (UK). He is recipient of the “Young Investigator Award” from the Social Council and the “Physics Research Award” from the Academy of Sciences. He is presently Professor of Applied Physics at the University of Granada. His research interests include magnetorheology and soft-elasto-ferrohydrodynamic lubrication. |
1. Introduction
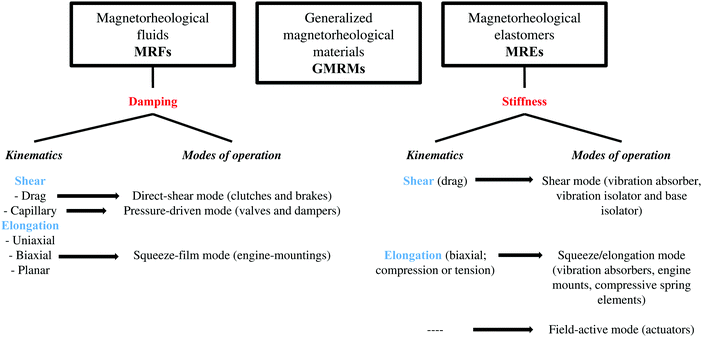
1.1. MR family
Magnetorheology is the science dealing with the rheological properties of magnetorheological (MR) materials. MR materials are magnetic field-responsive multi-phased systems. They generally consist of a magnetizable solid phase dispersed in a non-magnetic carrier that can be either a liquid (so-called MR fluids, MRFs) or an elastomer (so-called MR elastomers, MREs).1 Currently, special emphasis is given to the case of MR materials prepared in rheologically more complex media (so-called non-Newtonian fluids) such as plastics, shear thinning, shear thickening and/or viscoelastic media. These media bridge the gap between classical purely Newtonian and perfectly elastic carriers used in the formulation of MRFs and MREs, respectively. In this review paper we will refer to them as generalized MR materials (GMRMs). Apart from GMRMs, other emerging MR materials are MR foams, MRF impregnated composites and hybrid MR materials. Fig. 1 summarizes currently existing MR materials.The origins of magnetorheology are linked to MRFs (see Section 2).2 MRFs exhibit a liquid-to-solid transition under the application of a magnetic field. Their major characteristic is a field dependent yield stress (i.e. a minimum stress is needed for the MRF to flow). This property is commonly expressed by the so-called relative MR effect that is defined as the ratio between the stress increment under field and the stress value in the absence of the field. It is important to remark that the MR effect depends both on the on-state (magnetization level M and particle volume fraction ϕ) and on the off-state properties (viscous dissipation within the carrier) of the material.
Since the particles within a MRF sediment in short time scales due to the density mismatch between the particles and the carrier, the interest quickly moved toward MREs (see Section 3). In this case, the particles are entrapped within an elastomeric matrix and sedimentation is hindered. Now, the price to pay is a much smaller relative MR effect measured, in this case, as the ratio between the storage modulus increment under field and the storage modulus value in the absence of the field.3 The major characteristic of any MRE is the stiffness and loss factor (also called damping factor). Both of them are dictated by M, ϕ and the viscoelastic properties of the matrix.
More recently, novel MR materials have appeared in the intermediate region between fluids and elastomers. These novel formulations fully prevent particle settling without diminishing the MR effect (see Section 4).
Eventhough MR materials are definitely not newcomers, there is still today substantial interest in further developing these materials from practical and fundamental points of view. They already serve as interfaces between electronic and mechanical devices in multiple applications.4,5 Additionally, they serve as model systems (with easily tunable interparticle interactions) for a better understanding of directed colloidal self-assembly6 and glass transition.7
Currently there exist many review papers in this field of research8–19 as well as some books.20–23 The present review paper solely focuses in the most recent advances since 2010. In writing this review we have carefully revised upwards of 3000 publications in JCR journals. We hope that this review will allow to shed light on new directions for fundamental research and foster novel applications in this field.
1.2. Synthesis of magnetic particles
Any MR material is constituted by at least three components: particles, carrier and additives. Usually, the particles are magnetically responsive micron sized carbonyl iron powders (CIPs) and both the carrier and the additives are not magnetic. Besides CIPs, among the many methods described in the literature to synthesize magnetic particles (e.g. Singamaneni et al.24), clearly the majority of publications in the last ten years make use of hydro- and solvothermal methods. Interestingly, with these methods it is possible to easily obtain particles with controlled chemistry (magnetite,25 Ni–Zn ferrite,26 cobalt27), size28–30 and shape (spherical,25 octahedral31 and flower like27). Moreover, hydrothermal methods have also been successful in the fabrication of hollow magnetic particles.32Other methods and syntheses modifications apart from hydro- and solvothermal ones have also been reported in the formulation of MRFs. For instance, Berasategi et al.33 used the electric explosion of a wire to fabricate iron nanoparticles with a saturation magnetization larger than that of CIPs and a high production rate. Noma et al.34 used arc plasma to fabricate spherical crystalline Fe nanoparticles of 100 nm diameter and a saturation magnetization of 190 emu g−1. Arief and Mukhopadhyay used polyol methods to synthesize Co0.9Ni0.1 particles of 450 nm diameter35 and hydrothermal reduction to fabricate CoNi nanoplatelets.36 Nickel nanowires were fabricated by Xia et al.37,38 using a one-step synthesis method. Composite magnetizable polymeric particles were synthesized by Rodriguez-Lopez et al.39 using microfluidic devices and by Kim et al.40 using mini-emulsion polymerization. These composite particles consisted of micronsized polymeric particles with nanosized magnetic inclusions. Finally, magnetic carbon nanoparticles were also synthesized by Lee et al.41 through carbonization of iron-doped polypyrrole nanoparticles.
The influence of annealing temperature in the magnetic properties of the particles was investigated by Sedlacik et al.43 A larger annealing temperature resulted in a larger particle magnetization. Also, the influence of plasma treatment of CIPs in the suspension stability was reported by Sedlacik et al.42 An enhanced stability resulted from the interactions between the fluorine bonded on the CIPs surface and methyl groups of the silicone carrier oil. The influence of fatty acids (lauric, myristic, palmitic and stearic acid) on the stability and MR effect of silicone-based MRFs was investigated by Ashtiani and Hashemabadi.48 They observed an enhancement when increasing the carbon chain length of the acids. More recently, superplasticizer molecules have also been used in the formulation of MRFs in an attempt to reach extremely high particle loadings.49
2. Magnetorheological fluids (MRFs)
Magnetorheological fluids (MRFs) were the first in the big MR family to be discovered. Review papers on MRFs are those of Rankin et al.,8 Klingenberg,9 Bossis et al.,10 Bica,11 Goncalves et al.,12 Park et al.,13 de Vicente et al.,14 Ghaffari et al.16 and Felicia et al.182.1. Post-yield regime
When magnetized at rest, MRFs self-assemble forming structures oriented in the field direction. However, when a sufficiently strong stress is superimposed (above the so-called yield stress), these structures break and the MRF flows. Hence, MRFs are said to behave as solids in the pre-yield regime and as liquids in the post-yield regime. In practice, MRFs always operate in the post-yield regime.2.2. Yield stress
The mechanical behavior of MRFs is dictated by the magnetic field-induced structures and they are characterized by a single magnitude: the yield stress. Two yield stresses are generally distinguished in this field: the static and the dynamic yield stress. On the one hand, the static yield stress can be defined as the upper stress limit of the pre-yield regime, i.e. the maximum stress that the MRF can support when it is strained elastically, without implying sample flow. On the other hand, the dynamic yield stress can be seen as the stress level at the onset of the post-yield regime. In this scenario, the sample is flowing but at very small shear rate. Thus, the time scale related to particle rearrangement is totally driven by the magnetic forces but not by the hydrodynamic forces. As a result, at low shear rates the MRF stress level is independent of the shear rate, that is, there is a plateau in stress or a (dynamic) yield stress. The final goal in MRF technology is to achieve the largest MR effect possible and therefore the largest yield stress.2.3. Challenges: stability
For any MRF to be of interest in practical applications, it must exhibit a low off-state viscosity, be easily redispersable, be stable (in terms of chemical and sedimentation stability) and be resistant against chemical corrosion and/or wear.Undoubtedly, a major problem in MRFs is that the particles suffer from sedimentation instability because of the density mismatch between them and the carrier. By both increasing the viscosity of the carrier or reducing the density difference it is possible to slow down the sedimentation.
Apart from being kinetically stable, particles must also be chemically stable so that they do not (thermo)oxidize nor corrode under extreme environments. Two recent experimental papers on the importance of oxidation and corrosion are that of Plachý et al.50 and Han et al.,51 respectively. In both cases, saturation magnetization decreased when particles oxidized and/or corroded and therefore the MR performance decreased as well.
Durability is another requirement for MRFs. Desrosiers et al.52 identified base oil expansion and particle oxidation as two degradation phenomena in clutches, and proposed recirculation and expansion volume as solutions. Also, Wiehe et al.53 reported the temperature induced effects on the durability of MRFs. More recently, it has been shown that two mechanisms affect the durability of the MRF depending on its operating point. In the pre-yield regime magnetostatic forces are responsible for particle wear. In the post-yield regime, the degradation mechanism is not clear but seems to be related to thermal/chemical effects in the carrier fluid.54
For a recent review on the shortcomings of MR technology we refer to Wahid et al.55
2.4. Experimental techniques
The mechanical properties of MRFs are typically investigated using rheometry. Torsional flows are more frequently used in their rheological evaluation,10 cake formation is investigated through penetration tests with a blade56 and redispersibility is studied using vane tools57 or freeze-sampling methods.58The sedimentation stability was traditionally investigated by visual inspection first by the naked eye and then with sophisticated equipment that allowed us to track the sedimentation profile (i.e. the mudline location) as a function of time. However, by visual observation it is not possible to identify any internal stratification in the MRF although it is now well known that MRFs stratify in four sedimentation zones (supernatant zone, original concentration zone, variable concentration zone and sediment zone) in agreement with the Kynch's settling velocity model.59
A major breakthrough in the understanding of the sedimentation behavior of MRFs was the use of magnetic inductance monitoring techniques.60–62 They are based on the magnetic permeability mismatch between the particles and the carrier and the idea that the reluctance of a MRF depends on its particle loading. Hence, after calibration, it is possible to get information on the particle concentration by simply measuring the reluctance. Xie et al.63 and Choi et al.64 used a vertical axis inductance monitoring system (VAIMS) to investigate the sedimentation behavior of MRFs and the four sedimentation zones were identified. More recently, Wen et al.65 reported a refined inductance sensor with a low aspect ratio coil to localize rapid changes in concentration. However, a major disadvantage of this technique is that the results depend on the magnetic field strength and that the latter may also induce interparticle aggregation. A solution for this is the use of thermal conductivity measurements.59
2.5. Formulations
Progress in the formulation of MRFs during the last ten years can be grouped in two categories: core–shell particles and bidisperse MRFs.There is a vast amount of publications in the last ten years reporting the synthesis of core–shell magnetic particles for MR applications. Two recent review papers on polymeric coatings are those of Liu et al.76 and Seo et al.47 In Table 1 we show a summary of some of the most recent papers describing the fabrication of core–shell particles.
| Publication | Core/shell | Size, diameter (nm) | Shape | Preparation method or suppliers |
|---|---|---|---|---|
| Liu et al.66 | CIP/silica | ∼4500 | Spheres | CD grade from BASF/Stöber |
| Gao et al.67 | Magnetite/PS | ∼100 | Spheres | Coprecipitation/Shirasu porous glass (SPG) membrane emulsification technique |
| Sedlačík et al.68 | CIP/PANI | ∼3500 | Spheres | EA grade from BASF/polymerization |
| Cvek et al.69 | CIP/poly(glycidyl methacrylate) (PGMA) | ∼2000 | Spheres | SL grade from BASF/surface-initiated atom transfer radical polymerization |
| Mrlik et al.70 | CIP/cholesteryl chloroformate | ∼2000 | Spheres | ES grade from BASF/two step reaction |
| Lee et al.71 | CIP/PMMA | ∼4000 | Spheres | ISI/polymerization |
| Esmaeilzare et al.72 | CIP/cerium oxide CeO2, lanthanum oxide La2O3 and praseodymium oxide Pr2O3. | ∼2000/unknown | Spheres | CN grade from BASF/Merck, Alfa Aesar, Sigma Aldrich |
| Sim et al.73 | Magnetite/PANI | ∼800 | Spheres | Solvothermal and oxidation polymerization |
| Min et al.74 | CIP/PANI | ∼2000 | Spheres | CC grade from BASF/one step in situ oxidation polymerization process |
| Chen et al.75 | CIP/graphene oxide | ∼1000 | Spheres | CM grade from BASF/Hummers’ method |
| Dong et al.77 | Sepiolite/magnetite | Unknown | Rods | Sigma Aldrich/coprecipitation |
| Hajalilou et al.78 | CIP/Ag | ∼1000 | Spheres | Unknown/Green method |
| Kim et al.79 | CIP/polyamide 6 | ∼4500 | Spheres | CD grade from BASF/in situ polymerization method through a phase inversion method |
| Kim et al.80 | CIP/PGMA | ∼2000 | Spheres | CC grade from BASF/dispersion polymerization |
| Kwon et al.81 | CIP/xanthan gum | ∼5000 | Spheres | ISP/solvent casting method |
| Kwon et al.82 | Magnetite/PANI | Unknown | Spheres | Micelle-assisted self-assembly method |
| Nguyen et al.83 | CIP/silica | ∼4500 | Spheres | CD grade from BASF/Stöber |
| Park et al.84 | Magnetite/PMMA | ∼10 | Spheres | Coprecipitation/double miniemulsion method |
| Park et al.85 | Magnetite/polypyrrole | ∼500 | Spheres | Hydrothermal/in situ polymerization |
| Piao et al.86 | PANI/magnetite | Unknown | Fibers | Chemical oxidative polymerization/precipitation |
| Chae et al.87 | PS/magnetite | ∼500 | Spheres | Surfactant-free Pickering emulsion polymerization/Sigma Aldrich |
| Fang and Choi88 | CIP/MWCNT | ∼4500 | Spheres | CD grade from BASF/using 4-aminobenzoic acid |
| Fang et al.89 | CIP/PANI/MWCNT | ∼4500 | Spheres | CD grade from BASF/dispersion polymerization and solvent casting |
| Fang et al.90 | CIP/PS/MWCNT | ∼4500 | Spheres | CD grade from BASF/dispersion polymerization and emulsification |
| Liu et al.91 | CIP/silica | ∼4500 | Spheres | CD grade from BASF/sol–gel method based on the silane grafted CIP in two steps |
| Liu and Choi92 | PMMA/magnetite | ∼10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
Snowman | Seeded polymerization/coprecipitation |
| Liu and Choi93 | CIP/silica/MWCNT | ∼4500 | Spheres | CD grade from BASF/sol–gel/layer-by-layer |
| Pei et al.94 | Silica/magnetite | ∼200 | Spheres | Stöber/solvothermal |
First papers in this field explored mixing particles of different sizes (bimodal MRFs) with at least one particle in the micrometer range. In these references two main groups can be distinguished depending on the particle diameter ratio between the main and minority populations. In a first group, the large-to-small diameter ratio is around 10 so that both populations are non-colloidal in size. Thanks to the sample polydispersity, their main advantage is a smaller off-state viscosity in comparison to monomodal counterparts for the same solid concentration. At the same time, they show a larger on-state yield stress as small particles seem to help larger ones to get structured in more anisotropic aggregates.102,103 Previous features enhance the MR effect. However, these MRFs suffer from a high sedimentation rate due to the large size of the particles.
The tendency to sedimentation was partially overcome in a second group of works where the minority population is in the nanosized range (large-to-small diameter ratio around 1000). As a consequence, it suffers from Brownian motion interacting with the main population and hindering the sedimentation of the latter. Although these systems are also polydisperse, the fact that one of the populations is Brownian does not guarantee a reduction in the off-state viscosity. What is more, it has been seen that the yield stress in the on-state (mainly borne by the large particle structures) is not improved for any nanoparticle concentration. The reason seems to be a weakening in the primary structure due to the nanoparticles that reduce the interaction between large particles and the typical length of the structures the latter form.104,105
More recently, bimodal MRFs with a large-to-small diameter ratio of 100 have been also studied. The key of this formulation consists in the fact that the minority population has now a mean diameter around 100 nm, just in the transition between the magnetic single- and multi-domain regimes. In this boundary regime, particles exhibit a maximum coercive field and with this, superior magnetic properties in comparison to the main population. As a result, magnetic interactions and yield stress are enhanced in the on-state. At the same time, the coercivity is responsible for the formation of core–shell supraparticles with slower sedimentation rate and better redispersibility in the off-state.106
The on-state yield stress and the sedimentation profile for bimodal MRFs are plotted in Fig. 2a and b, respectively. These bimodal MRFs are mixtures of CIPs and small particles of different chemical composition in the aforementioned boundary regime. As observed, in Fig. 2a and b, an enhanced yield stress and sedimentation stability occurs for Fe-based bimodal MRFs because nano-Fe has superior magnetic properties than micro-CIP.
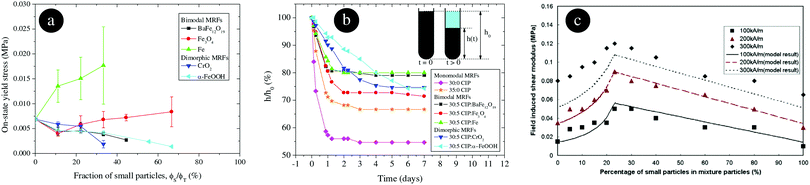 | ||
| Fig. 2 (a) Yield stress for bimodal and dimorphic MRFs based on micronsized CIP and different small particles. Small particles in bimodal MRFs are in the transition between single- and multi-domain regimes. Small particles in dimorphic MRFs are fiber nanoparticles. The applied field strength is 147 kA m−1. The total particle concentration is fixed at 45 vol%. Adapted from Fig. 4 in ref. 109 with permission from ACS, copyright 2020. (b) Sedimentation profile, in the absence of magnetic fields, for a selected large-to-small particle concentrations of the samples shown in (a). Adapted from Fig. 6 in ref. 109 with permission from ACS, copyright 2020. (c) Magnetic contribution to the storage modulus of a bimodal AMRE as a function of the small particle concentration and the applied field strength. The total particle concentration is fixed at 30 vol%. Points: shear experiments. Lines: effective permeability model prediction. From ref. 305 with permission from IOP Publishing, copyright 2020. | ||
Another particularly interesting set of bidisperse MRFs is the case of dimorphic MRFs. In a dimorphic MRF the particles differ in shape. Undoubtedly, the better understood dimorphic MRFs are those constituted by spheres and rods. In these systems, due to their shape, rod particles expose a larger wetted area that makes them aggregate to reduce surface energy and experience more contact points with other particles. Both facts give rise to a stress bearing structure that interlocks the spheres forming a secondary structure. As a result, in the off-state both yield stress and sedimentation stability (see Fig. 2b) increase with the rod concentration. In the on-state, the yield stress can be increased as well, probably due to enhanced friction forces and/or larger magnetization values provided by the particle anisotropy. Nevertheless, a limitation in the rod concentration exists due to their inferior magnetic properties (because of the nanometric size of the rods) and also because the rods interfere in the chain formation of the spherical particles (see Fig. 2a).97,107,108
There is a vast amount of publications in the last ten years reporting the preparation of bidisperse MRFs. For a recent paper we refer to Morillas et al.109 In Table 2 we show a summary of some of the most recent papers on bidisperse MRFs.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) diameter (rod) or main size for irregular shaped particles together with the synthesis method or supplier are also indicated
diameter (rod) or main size for irregular shaped particles together with the synthesis method or supplier are also indicated
| Publication | Materials | Size, diameter (nm) | Shape | Preparation method |
|---|---|---|---|---|
| Kim et al.95 | CIP/chromium dioxide | ∼4000/∼10 | Spheres/rods | CM grade from BASF/unknown |
| Gudmundsson et al.96 | CIP/CIP | ∼1000/∼1000 | Spheres | Various grades from BASF |
| Jiang et al.97 | CIP/iron | ∼3500/∼50:unknown | Spheres/rods | CN grade from BASF/reduction of Fe2+ ion with excessive sodium borohydride in aqueous solution |
| Powell et al.98 | CIP/CIP/glass | ∼2000/∼8000/∼11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
Spheres | Unknown grade from BASF/BASF/Potters Sphericel |
| Armijo et al.99 | CIP/Fe16N2 | ∼1000/∼10 | Spheres/spheres and cubes | Unknown/green process |
| Ashtiani and Hashemabadi100 | CIP/magnetite | ∼5000/∼10 | Spheres | Unknown grade from BASF/US Research Nanomaterials |
| Ashtiani and Hashemabadi100 | CIP/fumed silica | ∼5000/∼10 | Spheres | Unknown grade from BASF/Aerosil |
| Arief and Mukhopadhyay101 | Magnetite/iron | ∼300/∼800![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
Spheres/nanorod | Thermal decomposition/solvothermal |
| Morillas et al.106 | CIP/iron | 1300/100 | Sphere/irregular | EW grade from BASF/US Research Nanomaterials |
| Sedlačík et al.107 | CIP/iron | ∼750/∼590![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 135 135 |
Sphere/rod | HS grade from BASF/surfactant-controlled solvothermal method |
| Bombard et al.108 | CIP/chromium oxide | 3000/nanometric | Sphere/fiber | EW grade from BASF/Sigma Aldrich |
| Bombard et al.108 | CIP/goethite | 3000/nanometric | Sphere/fiber | EW grade from BASF/Bayer |
| Morillas et al.109 | CIP/magnetite | 1300/150 | Sphere/irregular | EW grade from BASF/Sigma Aldrich |
| Morillas et al.109 | CIP/barium ferrite | 1300/50 | Sphere/sphere | EW grade from BASF/Sigma Aldrich |
| Arief and Mukhopadhyay110 | NiCo/∼magnetite | ∼700/∼10 | Spheres | Polyol/Ferrotec |
| Esmaeilnezhad et al.111 | CIP/magnetite | ∼1000/∼10 | Spheres | CM grade from BASF/precipitation |
| Jang et al.112 | CIP/maghemite | ∼7000/∼500 | Spheres/rods | CM grade from BASF/HR-350 from Magnox |
| Jönkkäri et al.113 | CIP/maghemite | ∼1000/∼10 | Spheres | HQ grade from BASF/LFS method |
| Klingenberg and Ulicny114 | CIP/glass | ∼5000/∼10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
Spheres/hollow spheres | Unknown grade from BASF/Accumet Corp. |
| Leong et al.115 | CIP/maghemite | ∼10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000/∼10 000/∼10 |
Spheres | Sigma Aldrich/coprecipitation |
| Marins et al.116 | CIP/sepiolite | ∼1000–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000/∼20–40 000/∼20–40 |
Sphere/rod | Prolabo/Tolsa |
| Susan-Resiga and Vékás117 | Fe/magnetite | ∼2100 ± 1130/∼7 | Sphere/sphere | Merck/ROSEAL Co. (coprecipitation) |
| Susan-Resiga and Vékás118 | Fe/magnetite | ∼10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000/∼6.9 000/∼6.9 |
Sphere/sphere | Merck KGaA/coprecipitation |
| Susan-Resiga and Barvinschi119 | Fe/magnetite | ∼10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000/∼6.9 000/∼6.9 |
Sphere/sphere | Merck KGaA/coprecipitation |
| Piao et al.120 | CIP/sepiolite | ∼7000/∼10 | Sphere/rod | CM grade from BASF/Sigma Aldrich |
| Chae et al.121 | CIP/attapulgite | ∼4000/∼10 | Sphere/rod | CM grade from BASF/Fluorochem |
| Cvek et al.122 | CIP/carbon allotropes | ∼2500/∼10 | Sphere/rod | SL grade from BASF/Sigma Aldrich |
| Kwon et al.123 | CIP/halloysite | ∼4500/∼100 | Sphere/unknown | CD grade from BASF/Sigma Aldrich |
| Jonsdottir et al.124 | CIP/iron | ∼2000/∼25 and ∼2000/∼100 | Spheres | HS grade from BASF/Nanostructured & Amorphous Materials Inc. |
| Ngatu et al.125 | Iron/iron | Between 6000 and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000/230 diameter, 7500 ± 5100 length 000/230 diameter, 7500 ± 5100 length |
Sphere/nanowire | Alfa Aesar/templated assisted electrodeposition |
Of course, one can further complicate things by using tridisperse MRFs which consist of a mixture of three particles. The literature on these MRFs is very scarce. A paper in 2011 by Bombard and Teodoro,126 prepared tridisperse MRFs by mixing two CIPs and water atomized iron powder in an attempt to reach high volume fractions keeping the off-state viscosity as low as possible.
2.6. Physical properties
In the absence of magnetic fields, MRFs behave as conventional suspensions in the frontier between colloids and granular media. However, under the presence of a magnetic field, the magnetic constituents in a MR material become magnetized and interact through magnetostatic forces. In the case of MRFs at rest, these forces will promote the dynamic self-assembly of the constituents under a deterministic process if they overcome Brownian motion. This criterion is commonly assessed in the specialized literature through the coupling parameter λ defined as the ratio between magnetic and thermal energies. The dynamic self-assembly of MRFs in the absence of flow has been investigated using experiments,127,128particle level simulations (CIP,128 shifted dipoles129) and X-ray micro-computed tomography (XμCT).130 It has been demonstrated that the aggregation process (its time scale) and the aggregate morphology are dictated by the ratio between two length scales. First, the characteristic interparticle distance R0 in the absence of a magnetic field given by the particle volume fraction R0 ∼ dϕ−1/3 (d is the particle diameter). Secondly, the distance Rm where the magnetostatic energy of a pair of particles equals the thermal fluctuations: Rm ∼ dλ1/3. If Rm < R0, the aggregation process is diffusion limited while it will be deterministic in the opposite case. In addition, large Rm/R0 values imply columnar particle aggregates with defects (not aligned with the field) are more likely than perfectly linear chains.In the presence of a flow, hydrodynamic forces that try to disperse the particles apart, compete against the magnetostatic ones that promote interparticle aggregation. In fact, a dimensionless number has been documented to describe the rheological response under shearing flow. This is the so-called Mason number (Mn) commonly defined as the ratio of the aforementioned forces in the (hydrodynamic) Stokes’ drag and (magnetostatic) dipolar approximations. Under this frame, the equation of motion of the particles is solely controlled by Mn and therefore it appears as a key parameter describing the formation and breakage of the internal structures, and with this, the rheology of the MRF. For small Mn, magnetostatics are dominant. This leads to large and strong particle structures along the field direction. On the contrary, for large Mn magnetostatics is negligible in comparison to hydrodynamic forces. These leads to aggregate breaking and particles flowing.
Overall, three dimensionless numbers (λ, ϕ and Mn) dictate the flow behavior of MRFs.
Under flow and magnetic fields, MRFs essentially behave as plastic materials. For simplicity, the Bingham constitutive equation is preferred but other plastic equations (e.g. Casson and Herschel–Bulkley) can better explain the experimental observations because of the nonlinear response when the yield stress is exceeded.131
2.6.1.1. Drag flow. Undoubtedly, most of the literature under shearing flow focuses on the understanding of MRFs in drag flows (especially in plate–plate geometries) with a magnetic field oriented in the velocity gradient direction.10,132 However, other publications make use of other flow field kinematics and/or magnetic field orientations. The following are some examples. Magnetorheological investigations have recently been performed using concentric cylinders to reach high shear rates (∼30
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s−1) preventing the expulsion of MRF from the gap due to centrifugal forces that are typically observed in plate–plate configuration.133,134 In this particular geometry, the formation of Taylor vortex flows was reported by Güth and Maas.134 Furthermore, the magnetorheological behavior of MRFs when the field is oriented in the vorticity direction was investigated by Kuzhir et al.135 They reported an unexpected high MR response that was explained by stochastic fluctuations of positions and orientations of the particle aggregates. The fluctuations were modeled as a rotary diffusion process with a diffusion constant proportional to the mean square interaction torque. A quadratic dependence with the particle concentration was found.
000 s−1) preventing the expulsion of MRF from the gap due to centrifugal forces that are typically observed in plate–plate configuration.133,134 In this particular geometry, the formation of Taylor vortex flows was reported by Güth and Maas.134 Furthermore, the magnetorheological behavior of MRFs when the field is oriented in the vorticity direction was investigated by Kuzhir et al.135 They reported an unexpected high MR response that was explained by stochastic fluctuations of positions and orientations of the particle aggregates. The fluctuations were modeled as a rotary diffusion process with a diffusion constant proportional to the mean square interaction torque. A quadratic dependence with the particle concentration was found.
Most investigations under shearing flows aim to understand the yielding and flow behavior of MRFs. MRFs yield as a result of the fact that the field-induced particle-based structures break under shear. Confining surfaces (roughness, gap and magnetic character) are found to strongly affect the yielding behavior of MRFs.136,137 It has been reported that wall slip cannot always be reliably detected by comparison of the flow curves measured at different gap heights in contrast to classical colloidal suspensions.137 Also, multipolar and multibody forces were demonstrated to play a crucial role at least for perfectly aligned monomodal structures.138 Being aware of the fact that chain-like structures are not perfectly aligned with the magnetic field, Guo et al.139 proposed a yield stress model by introducing an exponential distribution for the orientation angle of the chains. Interchain interactions were neglected in their model.
Once the MRFs yield, their viscosity steadily decreases toward a constant high shear viscosity level that is achieved when the particles are randomly distributed in the carrier. The experimental viscosity (normalized by its high shear value) is plotted as a function of Mn for different applied fields in Fig. 3a. Berli and de Vicente131 demonstrated that viscosity curves are well explained by a structural viscosity model that reduces to the Casson model for very large magnetostatic interactions. More recently, Cvek et al.140 investigated the suitability of three constitutive equations to fit the flow curve of magnetized MRFs: Robertson–Stiff, Herschel–Bulkley and Mizrahi–Berk models, by comparing the correlation coefficients, sum of square errors and root mean square errors. The statistical analysis revealed that the best fitting was observed for the Robertson–Stiff model. Sherman et al.141 discussed the relationship between the Mn and the Bingham number (Bi) through a so-called critical Mn. This relationship connects the microscopic description of the particle dynamics (Mn) and the macroscopic description of the bulk MRF (Bi). Then, Ruiz-López et al.142,143 showed the functional dependence of the critical Mn on the different control parameters (magnetic field and volume fraction) for MRFs and inverse ferrofluids using experiments and simulations, and eventually provided a master curve. Finally, Jia et al.144 shed some light on how to extend the universal master curve to the case of MRFs formulated in non-Newtonian carriers (see Fig. 3b).
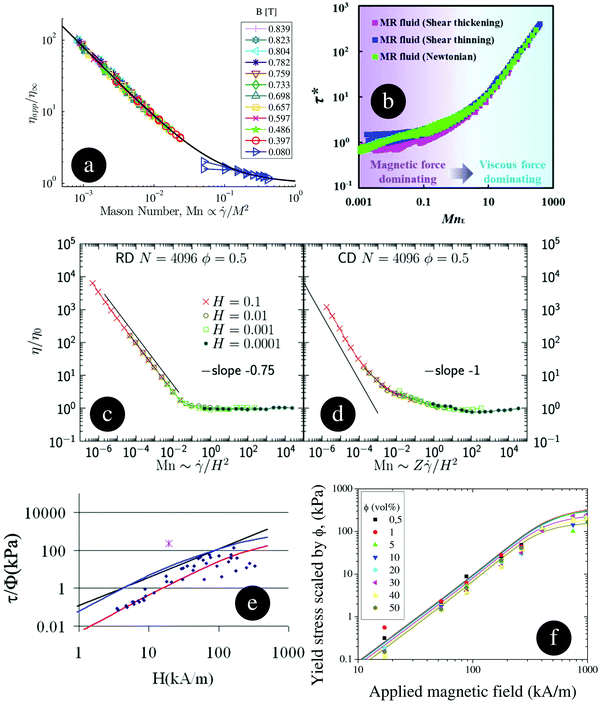 | ||
| Fig. 3 (a) Experimental viscosity, normalized by its high shear value, as a function of the Mason number Mn, for a commercial MRF (LordMRF-140CG) under different magnetic fields. The black solid line corresponds to the Bingham model equation as fitted to the experimental data. From ref. 141 with permission from Elsevier, copyright 2020. (b) Shear stress normalized by the yield stress as a function of an equivalent Mason number MnE, defined as the ratio between viscous and yield stresses. Symbols correspond to MRFs based on CIP dispersed in shear thickening (dispersion of fumed silica in ethylene glycol), shear-thinning (a methyl cellulose solution) and Newtonian (silicone oil) carriers. Adapted from Fig. 3 in ref. 144 with permission from IOP Publishing, copyright 2020. (c and d) Simulated viscosity, normalized by its high shear value, versus Mn according to 2D molecular dynamics-like simulations. Two mechanisms for energy dissipation are considered: (c) viscous dissipation due to Stokes drag law and (d) inelastic collisions between particles. Adapted from Fig. 3 in ref. 182 with permission from RSC, copyright 2020. (e) MRF yield stress, normalized by the particle volume fraction, as a function of the applied field strength. Blue points: experiments from the literature on CIP based MRFs with different concentrations. Purple star: shear stress after jamming transition in a high-concentrated (61 vol%) MRF. Red line: finite element method simulations for a pair of particles under affine motion. Black line: analytical model including particle pole saturation and affine motion. Blue line: similar to the red line but supposing that shear happens in a cutting plane. Adapted from Fig. 1 in ref. 150 with permission from Frontiers, copyright 2020. (f) MRF yield stress, normalized by the particle volume fraction, as a function of the applied field for different concentrations. Points: experiments on MRFs based on CIP. Lines: finite element method simulations for a periodic lattice of particles under affine motion. Adapted from Fig. 10 (in ref. 149 with permission from AIP, copyright 2020) and Fig. 9 (in ref. 151 with permission from RSC, copyright 2020). | ||
In most cases, the MR effect can be easily enhanced by simply increasing the magnetic field strength† and the particle concentration. The effect of the magnetic field strength was reported in the classical papers by Ginder and coworkers146 and is now better understood for homogeneous and/or saturating fields.147–149 However, the influence of particle concentration is still not well understood yet. A recent overview on the influence of particle loading is that of Bossis et al.150 They benefited from using plasticizer molecules to formulate highly concentrated CIP suspensions (ϕ > 55 vol%) that were flowable in the off-state. However, they assumed that the yield stress was linear with the particle concentration and this is not in agreement with other publications where the yield stress increases slower than linear for high concentrations.151 For comparison, in Fig. 3e and f the yield stress scaled by the particle concentration is shown using both experiments and finite element method simulations. In addition, simulations by Morillas and de Vicente152 showed that a maximum existed (with the volume fraction) in the case of monodisperse particles preassembled in a lattice under affine deformation and saturating fields.
In the last ten years there has been substantial progress on the understanding of the influence of particle size on the shearing flow behavior of MRFs. Generally speaking, the bigger the particles the larger their magnetization and hence the larger the yield stress.153,154 Nevertheless, of special interest are those particles that are in the transition between mono- and multi-domain magnetic regimes (particle diameters of around 100 nm). As already stated in Section 2.5.2, these particles exhibit a maximum coercive field and, with this, a superior magnetization and MR effect for the same applied external field than their mono- and multi-domain counterparts.154
It has also been reported the influence of particle shape. Most of the publications to date concern rod-like particles155–159 although some publications do discuss plate-like particles as well.157,160 The steady shear behavior of rod-like based MRFs has been described by Bell et al.155 and Gómez-Ramírez et al.158 and the dynamic shear behavior has been reported by de Vicente et al.156 in the linear viscoelastic (LVE) regime and by Kuzhir et al.161 in the non-linear viscoelastic regime. Experiments, simulations and theoretical developments have suggested that rod-like particles exhibit lower sedimentation rate and higher yield stress than spherical ones. Presumably these superior properties were due to a larger interparticle friction and higher magnetization level (lower demagnetization factor for rod-like particles). At present, it is not clear how important both contributions are to the yield stress and a universal explanation is still missing in the literature. Both the shape of the extremity of the rod-like particles162 and their aspect ratio159 are crucial to understand the magnetostatic contribution to the yield stress.
Apart from promoting stability, additives can also play an essential role in the shearing flow behavior of MRFs. A clear example is that of Bossis et al.49 In their paper, a superplasticizer molecule was used to coat the CIPs and concentrate them in water as much as possible. However, a discontinuous shear thickening (DST) transition appeared as a result of solid interparticle friction under the superposition of small magnetic fields (orders of 10 kA m−1) that pushed the iron particles together and expelled the molecules from the interparticle gap. The critical shear rate associated to the DST phenomena was magnetic field dependent (linearly dependent, see Fig. 3 in their paper). As the magnetic force induced by the field can be easily estimated, it may constitute an elegant approach for a better understanding of the DST phenomenon. Their approach is also useful to generate large changes in viscosity using very small fields.
Traditionally, only shear stresses were investigated in magnetized MRFs subjected to shearing flows. However, with the advent of modern rheometers that are capable to measure normal forces as well, some researchers also moved their attention to normal stresses in order to better comprehend the MR mechanism.163 An easily accessible magnitude in a plate–plate geometry is the normal force acting on the plates due to the MRF. At rest, most of the publications report a quadratic dependence of the normal force with the magnetic field strength in good agreement with the linear magnetization theory. However, contradictory observations have been reported on the shear rate and magnetic field dependence under steady shear flow.164–166 Chan et al.164 showed that the normal force increased up to a maximum and then leveled off to reach a plateau in a start-up flow test. Liu et al.166 observed a non-monotonous trend in the normal force: with the increase in the magnetic field the normal force increased first, reached a maximum and then decreased to a steady state value. When plotted as a function of the shear rate, the normal force exhibited a minimum. Yao et al.167 investigated the effects of time history, shear rate, and temperature under sweeping magnetic field on the normal force of a MRF. Normal stresses have also been measured under dynamic oscillatory shear. Guo et al.168 carried out a systematic investigation using strain amplitude sweep tests and frequency sweep tests. Three regions were identified in the strain sweep mode associated to a LVE region, a nonlinear viscoelastic region and a viscoplastic region. The frequency had little influence on the normal force evolution.
Finally, it should be said that besides rheological properties, other MRF properties have been studied. In particular, both thermal and electric conductivities increase when the MRF is magnetized in the field direction. Some recent examples on thermal studies are as follows: Ocalan and McKinley,148 Yildirim and Genç,169 Sherman et al.170 and Patel and Upadhyay.171 Very recently, Ruan et al.172 investigated the influence of oscillatory shear on the magnetic field dependent electric conductivity of MRFs. The conductivity increased about 1500 times when the field increased from 0.06 to 0.96 T. A particle–particle resistance model was also proposed to explain their experimental data.
2.6.1.2. Capillary flow. In this kind of flow, the MRF is forced to pass through a narrow channel. This particular flow kinematics is applicable in the so-called valve flow mode in the specialized literature.173 Early 2011, Kavlicoglu et al.174 proposed an analytical model to predict the pressure loss as a function of the field strength, flow rate and surface topology of the channel in terms of a non-dimensional friction factor. The importance of fluid/wall interactions in the flow behavior was corroborated by Nishiyama et al.;175 larger pressure drops were measured in grooved surfaces due to the anchoring effect. The importance of response time was investigated by Kubik et al.176 In their paper, they described the design, simulation and experimental testing of a MR valve with short response time. Both magnetostatic and hydraulic models were experimentally verified. A novel radial MR valve was described by Hu et al.177 In their design the magnetic flux was guided into the annular gap maximizing the effective area and providing larger pressure drops and response times if compared to classical radial MR valves. Also recently, Kubik et al.178 constructed a MRF shaft seal with very low friction torque under a pinch mode of operation. A lower friction torque than standard MRFs and a higher burst pressure than any ferrofluid were obtained.
2.6.1.3. Simulations. Many simulations reported in the literature have been successful in predicting experimental data (e.g. compare Fig. 3a and d). Lagger et al.179 used 3D Discrete-Element-Method (DEM) simulations to investigate the mechanisms of shear stress transmission at the particle level. Particular attention was paid to the wall roughness. In agreement with previous experiments,136 simulations with ferromagnetic walls showed no influence of wall roughness contrary to the case of non-ferromagnetic walls where the influence of roughness was important. In a subsequent paper by the same authors, an extensive DEM study was performed to elucidate the rupture mechanisms behind the yielding process in MRFs.180 They identified three different patterns: chains, sheets and columns. For each of the three structure types a corresponding failure mechanism was identified. Limitations of their model were (i) the small size of simulated boxes, (ii) that magnetic particles were modeled as magnetic dipoles and (iii) that there was force coupling from the fluid on the particles but not vice versa.
This particle–fluid coupling was studied together with the influence of the particular hydrodynamic drag force in Lagger et al.181 They investigated three models: a DEM with Stokes drag law for the hydrodynamic interaction and two coupled DEM smoothed particle hydrodynamics models with drag laws from Stokes and Dallavalle/Di Felice, respectively. Currently, this work serves as a useful guideline for the choice of the hydrodynamic interaction model in particle-based MRF simulations. In that respect, Vagberg and Tighe182 found that the viscous force law affected the existence of a true yield stress in MRFs as well. This can be appreciated in Fig. 3c and d; only in the second figure, where energy dissipation is supposed to be related to inelastic collisions between particles, viscosity diverges as Mn−1 indicating a yield stress.
Sherman et al.183 described simulations for a very large number of particles and demonstrated sheet formation at experimental volume scales. Results showed that the simulation volume had a significant effect on the structures formed. Larger volume sizes promoted the formation of thicker lamellar sheet structures due to the decreased effects of boundary conditions. Sheet formation was inhibited by increasing shear rates and aided by increasing magnetic field strength. Large particle count simulations based on CUDA by the same authors showed that even for narrow particle size distributions, the particle size distribution has a substantial effect in that it dramatically altered chain structures and substantially reduced the stress at low Mn.184 Simulations on polydisperse MRFs were also reported by Ruiz-López et al.185 In this case, the effect of polydispersity was noticeable in the resulting structure but negligible from a rheological point of view.
Aside from magnetic and hydrodynamic interactions, the importance of non-magnetic interparticle forces was investigated by Klingenberg et al.186 Non-magnetic forces played a key role in the off-state. However, they played a minor role in the on-state. Wilson and Klingenberg187 simulated mixtures of magnetic and non-magnetic particles in order to explain the yield stress enhancement of these systems as previously seen in experiments.188 In their analysis they found that non-magnetic particles did not alter the microstructure but formed, together with the magnetic particles, clusters able to transmit stress through contact repulsive forces. Typically, these clusters were aligned in the compression axis and thus they offered a larger resistance to be strained.
Outstanding simulations of rod-like magnetic particles are those of Okada and Satoh.189 They modeled magnetic sphero-cylinders using Monte Carlo techniques to investigate the structural characteristics of the aggregates and Brownian dynamics simulations to describe their magnetorheological properties.
Finally, capillary flow simulations are scarce in the recent literature. An exception is the paper by Zhang et al.190 In this study, they carried out two-phase Lattice Boltzmann Method (LBM) simulations on the yielding phenomena during start-up flow of a MRF flowing through a microchannel.
The slow squeeze flow behavior has been extensively documented in the literature. Early 2011, de Vicente et al.191 carried out experimental tests (under constant volume) and particle level simulations. A micromechanical model was proposed for dilute MRFs192 while continuum media theory predictions sufficed to explain experimental observations in highly concentrated MRFs.193 Farjoud et al.194 carried out a mathematical model using perturbation techniques. The compression behavior of MRFs was extensively investigated by Kordonski and Gorodkin.195 A significant increase in the LVE region was found as a result of column-to-column aggregation assisted by compression of the samples in the field direction. They also investigated superimposed compression and shear deformations. The squeeze flow behavior of MRFs under constant volume and uniform magnetic fields was reported by Guo et al.196 They identified two regions: elastic deformation and plastic flow regions. Horak197 presented a nonlinear model to describe the MRF behavior in the squeeze flow mode. In their work it is assumed constant area and no-slip boundary conditions.
Cyclic compression tests were carried out by Ismail et al.198 to interrogate the particle–fluid separation phenomena while Horak et al.199 performed oscillatory compression squeeze mode in a purpose-built experimental setup. A resonant method was used by Kaluvan et al.200 to determine the field dependence of the yield stress in MRFs subjected to squeeze flow. According to this method, the viscosity change was measured by the shift in the resonance frequency under a field.
During these last ten years, significant progress has been done in the understanding of the so-called squeeze-strengthening effect initially reported by Tao and coworkers.201 Hegger and Maas202 proposed a modeling approach that combined the rheological behavior with tribological effects to describe the squeeze-strengthening effect. The squeeze-strengthening of MRFs was carefully investigated by Lucking-Bigué et al.203,204 They derived a Peclet number and adapted it to the Bingham rheological model. This Peclet number well predicted the occurrence of squeeze-strengthening in highly concentrated MRFs. In the second part of their paper, they superimposed squeeze and shear at high speeds. The superimposed rotation affected the squeeze-strengthening by first reducing the radial stress which causes the filtration phenomenon and second by affecting the rate of creation/destruction of the MRF microstructure through the squeeze-to-shear-rate ratio. Horak197 investigated the squeeze flow of MRFs using simulations and taking into account that the yield stress increases due to compression.
MRFs have also been investigated under tension. Because of their tunable yield stress, MRFs can be used for variable-strength controllable adhesion to non-magnetic substrates.205 A model for the MRF adhesion under nonhomogeneous magnetic fields was reported by the authors.
Finally, Sadek et al.206 studied the uniaxial extensional flow of MRF using a CaBER device with a fixture that is capable to impose a controllable and homogeneous magnetic field over the sample volume, either parallel or perpendicular to the strain direction. Both magnets207 and coils206 have been implemented in the setup. It is shown that the filament created during the extensional flow broke earlier when the sample underwent larger Hencky strains (what promoted the capillary forces in the filament) or later when the MRF yield stress was enhanced (either increasing the applied field or particle concentration). Regarding the field direction, fields parallel to the strain made breaking times larger than the perpendicular case due to the more stable configuration of both magnetic field lines along the sample surface and particle structures.
2.7. Applications
Contrary to other members of the MR family that are still in their infancy, MRFs have successfully reached the market in several applications. A recent review on the different applications of MRFs is that of Skalski and Kalita.212 Other more specialized reviews are focused on dampers,213 MR valves214 and robotic applications.215MRFs are traditionally used in damping applications. New dampers employing permanent magnets have been constructed by Kim et al.216 and more recently by Lee and Choi.217 Dampers operating in the squeeze flow regime have also been developed by Gong et al.218 and Sapiński and Gołdasz.219 Yang et al.220 investigated the behavior of a linear damper containing MR shear thickening fluids exhibiting both MR effect and thickening effect.
Another traditional application of MRFs is their use in MR brakes. MR brakes are preferred over conventional hydraulic brakes because the stopping distance and time can be significantly reduced. Patil and Lohar221 experimentally investigated MR brakes in shear and squeeze flow modes of operation.
The durability of a MRF was investigated by Roupec et al.222 It was motivated in the classical papers by Carlson223,224 that reported an in-use-thickening meaning the damping force increases with the number of load cycles during long-term loading of a MR damper. This was found to be a result of the oxidation of the particles.225
MRFs are also of potential interest in sound propagation applications. Bramantya et al.226 analyzed the inner structure in MRFs by measuring the ultrasonic propagation velocity. Ultrasonic propagation velocity decreased as the volume fraction of the particles increased. However, when the magnetic field increased, the ultrasonic propagation velocity increased. In a later publication by the same authors, they observed significant differences in the propagation depending on the orientation and mode of application of the magnetic field.227 Nanda and Karami228 detailed the possibility of achieving one-way sound propagation using MRFs by subjecting them to a time-space varying magnetic field.
MRFs can be of interest in thermal transport applications as well. Forero-Sandoval et al.229 demonstrated that higher concentrations and field strengths led to an increase in the thermal conductivity. Rahim et al.230 explored the influence of adding copper and aluminum to MRFs in their thermal conductivity.
Making use of their adjustable viscosity, MRFs enhance oil recovery processes.231 CIPs have been incorporated to cement pastes with the intention to control their rheological properties in the fresh-state in real time232 and in the fabrication of MR electrolytes.233 More recently, MRFs have been used in the fabrication of microneedles using the so-called MR drawing lithography (MRDL) method.234
Likewise, MRFs have been used in the fabrication of field actuated grippers eliminating the need to supply vacuum.235 Zhang et al.236 compared the sealing performance of MRFs and ferrofluids. A higher sealing pressure was observed for MRFs. For those applications conceived for long operating times, Sato and Umebara237 proposed a mechanism to control the viscosity of a MRF using solenoids and permanent magnets in such a way that no current is needed in the on state while current is solely needed in the off state.
MRFs allow the generation of liquid drops with controlled size, shape and wetting characteristics.238 Majidi and Wood239 showed that surface micropatterning controlled the interfacial sliding resistance of MRF at low magnetic fields. Finally, interfacial patterns can be tuned by the superposition of magnetic fields in Hele-Shaw cells.240
In addition, MRFs are of interest in tribological applications with and without abrasive additives. Two examples are surface finishing and polishing of freeform (complex 3D) surfaces under the presence of controlled field gradients.241 A recent review on MR finishing on metals is that of Mutalib et al.242 MR finishing technology is currently commercialized by QED Technologies.243
The tribological properties of MRFs in hard contacts have been reported in the literature by using reciprocating rigs,244 wear testers,245 ball-on-three plates apparatus246,247 and four-ball tribological devices.248 Contradictory observations have been reported with no consensus on the influence of magnetic field on the friction and wear scar. Hu et al.248 suggested that the friction coefficient increased and the diameter of the wear scar decreased as the field strength was increased. In contrast, Shahrivar et al.246 observed that both friction coefficient and wear scar slightly decreased upon the application of a magnetic field. The particular magnetic field distribution at the contact seems to play a key role.
In most tribological applications, MRFs are doped with abrasive particles like cerium oxide, aluminum oxide and silicon carbide among others.249 In the presence of magnetic fields, the field-oriented structure holds the abrasive particles at place and restricts the motion of the abrasives. Then, superimposing a relative motion between the MRF and the finishing surface the abrasive particles produce the finishing action. Wang et al.250 modified the geometric shape of the magnets to improve the polishing efficiency. Currently, many variants of MR finishing process have been developed to finish different shapes. Some examples are MR abrasive flow finishing (MRAFF),251 ball end MR finishing (BEMRF),252 MR jet finishing253 and lap-MRF process.249
3. Magnetorheological elastomers (MREs)
Magnetorheological elastomers (MREs) constitute another key member in the MR family (see Fig. 1). They were created with the aim to avoid sedimentation problems in MRFs. Additionally, they exhibit a superior performance in sealing applications and are more environmentally friendly than MRFs.MREs are credited to Rigbi and Jilken.254 In their paper, they reported a pioneering work on a magnetically sensitive elastomer that aimed to exploit the MR effect. However, there seems to exist consensus that the first comprehensive investigation on MREs was conducted by Carlson and coworkers in the 90's.255
Similar to MRFs, MREs consist of at least three components: magnetizable (micronsized) particles, a non-magnetic elastomeric carrier and additives. Comprehensive review papers on MREs are those of Li et al.,15 Ubaidillah et al.17 and Cantera et al.19
The particles are typically CIPs. A high purity iron is required for better performance. In fact, a low carbon content in the particles enhances MR effect in dynamic tests.256 The larger the particle size the smaller (larger) the modulus in the absence (presence) of magnetic fields. The optimal CIP concentration is around 27 vol% in view of theoretical models by Davis.257
The elastomeric (carrier) matrix is typically made out of silicone rubber, natural rubber or thermoplastic elastomer and prevents the particles from settling. An appropriate matrix should exhibit easy processability, good aging, good thermal properties, and a low elastic modulus to maximize MR effect.
Since CIPs are hydrophilic and matrices are typically hydrophobic, coupling agents are frequently used to change the surface of the particles from hydrophilic to hydrophobic. In the off-state and when properly functionalized, CIPs act as conventional fillers reinforcing the matrix and improving its mechanical properties. In MREs, particles are often treated to remove the moisture from their surface before the curing process and to reduce the effect of oxidation on the MREs. Atom transfer radical polymerization (ATRP) techniques are frequently used for surface polymerization of iron particles with fluorinated styrene as monomer in a silicone rubber.258 A wide range of additives are incorporated in the formulation to enhance the mechanical properties of the MREs. Recently, Aziz et al.259 investigated the influence of several types of processing aids (naphthenic oil, light mineral oil and epoxidized palm oil) in the formulation of MREs.
Depending on how the particles are distributed within the matrix during the crosslinking process, one can distinguish between isotropic (unstructured) IMREs or anisotropic (structured) AMREs. Particles are homogeneously (randomly) dispersed in the matrix in the case of IMREs. On the contrary, particles are pre-arranged (aligned) in chain-like structures in the case of AMREs. Generally speaking, an anisotropic arrangement gives a better performance than an isotropic arrangement. However, minor differences have been reported between IMRE and AMRE for high-strains (about 100%) base isolation devices when the particle loading was larger than 25 vol%.260 The advantage of using IMREs instead of AMREs is that they can perform optimally for various directions of vibration. In the literature, the pre-structure process is affected by three main factors: strength of the magnetic field, time exposed and temperature.17
3.1. Pre-yield regime
Contrary to MRFs, MREs operate in the pre-yield regime. The mechanical characterization of MREs is generally performed using quasi-static or dynamic tests. Dynamic tests consist of the superposition of small oscillating forces/torques on the samples and measuring the corresponding deformation in the LVE regime. Two devices are generally used: torsional rheometers for the shear characterization and Dynamic Mechanical Analyzers or Universal Testing Machines for the compression/tension characterization.In the preyield regime there are several operation modes of interest for MREs: shear mode, squeeze/elongation mode and field-active mode (see Fig. 1). Note that the pressure mode (or valve flow mode) that works for MRFs is not applicable for MREs. However, a new mode exists which is the so-called field-active mode; MREs can change their shape by a magnetic field. For the shear mode and squeeze/elongation mode, MREs work similarly as MRFs. MREs that work in the field-active mode can be used to design various actuators. Examples of shear mode devices include vibration absorbers, vibration isolators, and base isolators. Examples of squeeze/elongation mode devices are vibration absorbers, engine mounts and compressive spring elements.15
3.2. Stiffness and damping
Contrary to MRFs that are essentially characterized by a single magnitude, the yield stress dictated by the field-induced structures, MREs are characterized by their stiffness and damping. Both features come from the viscoelastic nature of the MRE and can be easily interpreted when the MRE is studied in the LVE region during oscillatory tests. Under a small sinusoidal strain, the MRE develops a stress (also sinusoidal and with the same frequency) that can be decomposed in phase with the strain or in quadrature with the strain or, equivalently, in phase with the shear rate.The ratio between the in-phase stress component and the strain is known as the storage modulus (in shear or elongation: G′ or E′) and stands for the instant response of the MRE to a strain. It can be considered a measurement of the stiffness or elastic-solid behavior. The ratio between the in-quadrature stress component and the strain is known as the loss modulus (G′′ or E′′). Since the in-quadrature stress component is, at the same time, in phase with the shear rate, the loss modulus is a measure of the liquid-like behavior of the MRE.261
The storage and loss moduli are directly proportional to the energy stored and dissipated by the MRE, hence its damping performance (relative to the elastic stored energy) can be measured by the loss factor tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ, defined as the ratio between the two moduli (tan
δ, defined as the ratio between the two moduli (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ = G′′/G′ or tan
δ = G′′/G′ or tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ = E′′/E′).262
δ = E′′/E′).262
The final goal in MRE technology is to achieve a large increase of the storage modulus in the on-state (i.e. a large MR effect) and a controllable loss factor over a wide range of values. Specifically, in simple vibration control/isolation devices, a small loss factor is required to attenuate oscillations with frequencies above the natural frequency, while a large loss factor is required to attenuate oscillations close to the natural frequency.263,264
On the one hand, the majority of the on-state storage modulus is dictated by the field-induced structures, particle magnetization and particle concentration. However, the modulus change over its value in the off-state relies also on the viscoelastic properties of the matrix265 and particle concentration. Experimentally, the most direct way to enhance the MR response is to maximize the particle loading and minimize the storage modulus of the carrier matrix.266
On the other hand, Yang et al.267 identified three contributions to the damping properties (loss factor) of a MRE: intrinsic, interface and magneto-mechanical damping. Among them, there seems to exist consensus in that the majority of the damping properties come from the second one. At particle–matrix interfaces with a poor adhesion, the frictional sliding between the particles and the matrix is responsible for the energy dissipation. Yet, in some studies, it is stated that the loss factor of the material changes due to the magnetic field. A majority of studies conclude that a magnetic field does not have any remarkable effect on the loss factor.268–271 Therefore, the most distinctive change in the material property of MREs under a magnetic field is its storage modulus.
Overall, storage modulus and loss factor of MREs are dictated by three key ingredients: (i) magnetic field-induced structures (disposition, strength and concentration), (ii) the viscoelasticity of the matrix, and (iii) interfacial adhesion between the particles and the matrix.
In the LVE region, i.e. for small deformations typically of the order of 0.01% in torsional shear,272 both magnitudes G′ and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ remain constant with the deformation amplitude. However, G′, G′′ and tan
δ remain constant with the deformation amplitude. However, G′, G′′ and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ increase with the frequency due to the viscoelastic behavior of the elastomer in the rubbery phase (G′′,272 tan
δ increase with the frequency due to the viscoelastic behavior of the elastomer in the rubbery phase (G′′,272 tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ273). Of especial interest is that AMREs show a larger G′ and G′′ compared to IMRE and therefore a larger MR effect (assuming the field parallel to the chain axes). It has been experimentally documented that G′ increases with the magnetic field strength but there is not experimental consensus on the behavior of tan
δ273). Of especial interest is that AMREs show a larger G′ and G′′ compared to IMRE and therefore a larger MR effect (assuming the field parallel to the chain axes). It has been experimentally documented that G′ increases with the magnetic field strength but there is not experimental consensus on the behavior of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ and there exist opposite experimental results.274 A weak linear increase of tan
δ and there exist opposite experimental results.274 A weak linear increase of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ with the magnetic field has been reported by Norouzi et al.273 Lee et al.260 demonstrated that the change in tan
δ with the magnetic field has been reported by Norouzi et al.273 Lee et al.260 demonstrated that the change in tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ under an external magnetic field was almost negligible compared to the change of G′.
δ under an external magnetic field was almost negligible compared to the change of G′.
MREs deviate from the linear regime at a critical deformation that increases with the excitation frequency275 but decreases with the particle loading,276magnetic field strength (IMRE277) and temperature.276 Once the MRE deviates from the LVE region, the moduli decrease with the strain amplitude. This behavior is called the Payne effect278 and is enhanced for the more concentrated MREs.279
3.3. Challenges: interfacial adhesion
As shown in the previous section, interfacial adhesion between particles and matrix is crucial for the MRE response. A poor adhesion will allow frictional sliding at the interfaces increasing the loss factor while a good adhesion will prevent the Payne effect, extending the LVE region to larger strains,17 increasing the storage modulus and reducing the loss factor. Bodelot et al.280 stressed how important the quality of the interfacial adhesion between the filler particles and the matrix was in the mechanical behavior under large deformations.To improve dispersibility and strengthen interfacial adhesion it is convenient to perform a surface modification of the CIP.281–283 A few papers exist in the literature demonstrating how to tune the interfacial adhesion, and with it the loss factor, through the use of different additives for the matrix. Acetone has been used to prevent iron–silicone attachment and improve the loss factor284 while maleic anhydride compatibilizer in a polybutadiene matrix can reduce interfacial friction and loss factor.285 In addition, rosin glycerin in a natural rubber matrix has shown both behaviors, increasing or reducing the loss factor depending on the used concentration.286
3.4. Experimental techniques
Traditionally, Scanning Electron Micrographs (SEM) on MRE cutting planes are used to get information about particle structure and interfacial adhesion.287 More recent approaches involve the use of microrheology to monitor MREs curation process in real time288 and Atomic Force Microscopy (AFM), Magnetic Force Microscopy (MFM), Force/Distance (F/D) spectroscopy and nanoindentation to obtain information at the surface of the specimen.289 Undoubtedly, a major breakthrough during the last ten years is the use of XμCT to evaluate interfacial adhesion and structuration in MREs.Odenbach and coworkers were pioneers on the use of XμCT to investigate the 3D internal structure of MREs preserving the integrity of the sample. Some drawbacks of this technique are that, at present, the particle concentration cannot be too high (2 vol%) and the particle size must be big (of the order of tens of microns).290,291Fig. 4a shows a typical XμCT image. Using this technique, the influence of the magnetic field on the particle microscopic position and sample macroscopic shape was reported by Gundermann et al.292 Borbáth et al.291 described the structural properties of MREs fabricated at different field strengths. The average number of columns decreased with increasing the magnetic field strength. Particle distributions were obtained by Gundermann et al.293 while Borin et al.294 investigated the influence of particle concentration in the cross-linking of the elastomer. They observed a decrease in the level of crosslinking by increasing the particle concentration. The first investigation on XμCT observations under magnetic fields and a mechanical strain was reported by Schümann and Odenbach.295
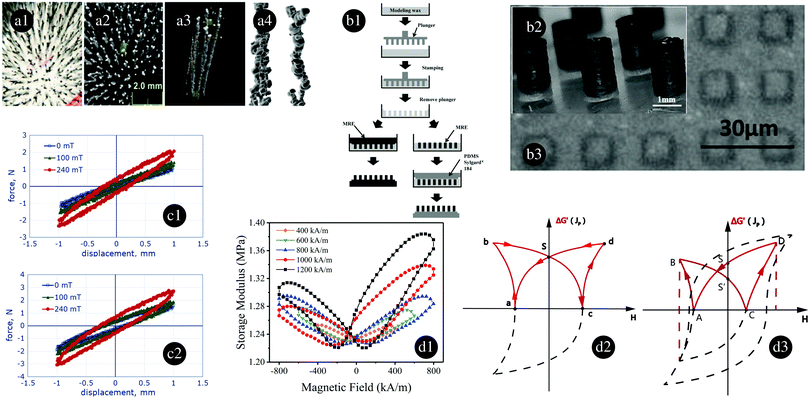 | ||
| Fig. 4 (a1) Optical microscopy image of an AMRE observed in the direction of the field-induced chains with an applied field strength of 30 kA m−1 during curing. (a2) Reconstructed image using XμCT from the same sample as in (a1). (a3) Detail of (a2). The captured box is 15 mm height and 1 × 1 mm2 cross section. (a4) Detail of chains observed with XμCT. The average particle diameter is around 35 μm. Adapted from Table 1 and Fig. 1 in ref. 291 with permission from IOP Publishing, copyright 2020. (b1) Diagram to stamp MRE patterns over MRE surfaces (left branch) or over surfaces of other materials (right branch). (b2 and b3) Examples of the resultant patterns in perspective and top view, respectively. Adapted from Fig. 2, 4 and 6 in ref. 298 with permission from Wiley Online Library, copyright 2020. (c) Force versus displacement loops obtained during tension–compression cycles over a bidisperse IMRE under different applied fields. The total magnetic particle content is 40 vol%. From this, 25% of the particles are hard magnetic: (c1) non-premagnetized sample and (c2) pre-magnetized sample at 1.5 T. Adapted from Fig. 8 and 12 in ref. 311 with permission from Springer Nature, copyright 2020. (d1) Experimental storage modulus during an applied magnetic field loop for an IMRE based on hard magnetic particles (33 vol%). The IMRE is pre-magnetized at different fields indicated in the key of the figure. The loop is asymmetric only if the pre-magnetization field is larger than the maximum applied field in the loop. (d2) and (d3) Schemes showing the loops of magnetization (Jp in this figure-dashed line) and magnetic contribution to the storage modulus (ΔG′-continuous line) when the pre-magnetization field is smaller or larger than the maximum applied field in the loop, respectively. Adapted from Fig. 8 and 10 in ref. 321 with permission from IOP Publishing, copyright 2020. | ||
3.5. Formulations
Other approaches have also been followed. For example, Forster et al.298 developed a low-cost wax-based molding technique to provide certain patterns for ultrasoft (below 40 kPa) MRE surfaces. In Fig. 4b a schematic of the manufacturing process and the resultant patterns are shown.
A strain sensor based on conductive MREs containing silver nanowires in a polyurethane sponge, CIP and PDMS matrix was developed by Hu et al.299 Prem et al.300 synthesized electro-magneto responsive elastomers by mixing magnetic CIP and electrically conductive particles. Landa et al.301 prepared Ni-based MRE with particles having spherical and rod-like shapes. Then, experiments were recorded compressing the MRE in directions parallel and perpendicular to the needles. Padalka et al.302 investigated MREs filled with Fe, Co and Ni nanowires under oscillatory compressive tests. Both the storage modulus and the dissipated energy per cycle were larger with nanowires than with spheres. Silver-coated magnetite particles were fabricated and dispersed in PDMS by Mietta et al.303 to obtain dual responsive particles. Finally, magneto-electrorheological elastomers were formulated by Borin and Stepanov.304
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) diameter (rod) or main size for irregular shaped particles together with the matrix material are also indicated. CNT: carbon nanotube. MWCNT: multiwalled carbon nanotube
diameter (rod) or main size for irregular shaped particles together with the matrix material are also indicated. CNT: carbon nanotube. MWCNT: multiwalled carbon nanotube
| Publication | Particles | Matrix | Size, diameter (nm) | Shape |
|---|---|---|---|---|
| Yu et al.264 | CIP/CIP coated with iron nanoflakes | Polyurethane | ∼6500/unknown | Spheres |
| Li and Sun265 | CIP/CNT | RTV silicone rubber | ∼15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000/∼30 000/∼30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 40 |
Sphere/fibers |
| Li and Zhang305 | CIP | Silicone rubber | ∼50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000/∼5000 000/∼5000 |
Spheres |
| Nayak et al.306 | CIP/carbon black | RTV silicone elastomer | ∼5000/unknown | Sphere/unknown |
| Kwon et al.307 | CIP/maghemite | Natural rubber | ∼5000/∼500:unknown | Sphere/rod |
| Shabdin et al.308 | CIP/graphite | Silicone rubber | ∼6000/∼16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
Sphere/unknown |
| Lu et al.309 | CIP/carbon black | Natural rubber | ∼3200/unknown | Sphere/unknown |
| Fan et al.310 | CIP/carbon black | Natural rubber | ∼3000/∼100 | Sphere/unknown |
| Borin et al.311 | CIP/NdFeB | PDMS | ∼5000/∼35000 | Spheres |
| Aziz et al.312 | CIP/MWCNT | Natural rubber | ∼6000/∼10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10 |
Sphere/fibers |
| Aziz et al.313 | CIP/MWCNT | Natural rubber | ∼6000/∼10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 20 |
Sphere/fibers |
| Poojary et al.314 | CIP/CNT | RTV silicone rubber | ∼5000/∼10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 20 |
Sphere/fibers |
| Sorokin et al.315 | Fe/magnetite | Silicon rubber | 55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000/35 000/35 |
Spheres |
| Aloui and Klüppel316 | CIP/iron oxide | Styrene–butadiene rubber | 3500/15 | Spheres/irregular |
| von Lockette et al.317 | Iron/iron | RTV silicone rubber | 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000/10 000/10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
Unknown |
Bimodal MREs were probably first investigated by Li and Zhang.305 Experiments showed that MREs with large particle sizes have lower zero-field modulus and higher field-induced modulus than MREs with small particles. Similar to some bimodal MRFs, bimodal MREs investigated in their work exhibited a much larger MR effect than similar MREs with just one kind of particle (see Fig. 2c). In their paper, they also developed an effective permeability model to describe the behavior of structured MREs.
Li and Sun265 prepared bidisperse MREs by incorporation of carbon nanotubes (CNT) to conventional MREs and demonstrated that both G′ and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ increased with the addition of CNT. The enhancement of G′ can be explained bearing in mind that a mechanical reinforcement occurs when adding CNTs. Regarding the tan
δ increased with the addition of CNT. The enhancement of G′ can be explained bearing in mind that a mechanical reinforcement occurs when adding CNTs. Regarding the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ increase, it seems that at large CNTs concentrations CIPs aggregate and weaken the bonds with the matrix and increase the loss factor.314 Indeed, Poojary et al.314 found an optimum CNT concentration below which G′ increased and tan
δ increase, it seems that at large CNTs concentrations CIPs aggregate and weaken the bonds with the matrix and increase the loss factor.314 Indeed, Poojary et al.314 found an optimum CNT concentration below which G′ increased and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ decreased. Similar observations were reported by Aziz et al.312 synthesizing MREs with pristine, carboxylated and hydroxylated multiwalled CNTs as additives below the aforementioned optimum concentration. Finally, Shabdin et al.308 investigated the rheology and resistivity of graphite based MREs.
δ decreased. Similar observations were reported by Aziz et al.312 synthesizing MREs with pristine, carboxylated and hydroxylated multiwalled CNTs as additives below the aforementioned optimum concentration. Finally, Shabdin et al.308 investigated the rheology and resistivity of graphite based MREs.
Based on its magnificent performance in the rubber industry (improving elastomers resilience, tear strength and wear resistance strength) carbon black has also been widely used in (bidisperse) MRE syntheses. The manuscript by Nayak et al.306 described the fabrication and characterization of MREs containing carbon black in a silicone elastomer. They demonstrated that the addition of carbon black improved the mechanical properties of the MREs. The MR effect was smaller in the case of a hard matrix as compared to a softer matrix. The addition of carbon black attenuated the time rate of mass loss. MREs with carbon black can operate at higher temperature compared to MREs without carbon black. E′ and G′ increased with the addition of carbon black. Lu et al.309 studied the influence of carbon black on the dynamic mechanical analysis of MREs. In particular, they investigated the storage modulus and the loss factor. They observed that the loss factor increased with the carbon black concentration. Similar results were obtained by Fan et al.310
Yu et al.264 prepared dimorphic MREs. First, CIP was modified by Fe nanoflakes using a simple method and then dimorphic MREs were fabricated by partial replacement of CIP with CIP-nano-Fe. Kwon et al.307 fabricated dimorphic MREs by addition of rod-like maghemite nanoparticles. These MREs exhibited a higher modulus, tensile strength and elongation percentage than pure CIP-based elastomers.
Most of the previous studies on MREs use soft magnetic particles so that the MRE demagnetizes in the absence of an external magnetic field (an exception is the paper by Siegfried et al.318). However, bidisperse MREs containing hard magnetic particles have received significant attention in the last ten years. Lee et al.319 described the preparation of MREs containing γ-Fe2O3 rod-shaped hard magnetic particles added to CIP to enhance the MR effect of MREs. Also, Borin et al.311 investigated the mechanical properties of MREs prepared by mixing soft and hard magnetic particles. Although the MR response is mainly governed by the (easily magnetizable) soft particles, values of E′ and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ in the on-state were larger when hard particles were pre-magnetized (see Fig. 4c). Makarova et al.320 investigated three different hard magnetic particles in the preparation of MREs. Wen et al.321 demonstrated that the storage modulus in a hard MRE can not only be increased by increasing the field but also decreased by increasing the field in the opposite direction. In Fig. 4d1 the storage modulus during applied magnetic field loops is shown. The asymmetric shape comes from the asymmetric hysteresis loops of magnetic particles when the hard MRE is pre-magnetized at a given field and then tested until a smaller applied field (compare Fig. 4d2 and d3).
δ in the on-state were larger when hard particles were pre-magnetized (see Fig. 4c). Makarova et al.320 investigated three different hard magnetic particles in the preparation of MREs. Wen et al.321 demonstrated that the storage modulus in a hard MRE can not only be increased by increasing the field but also decreased by increasing the field in the opposite direction. In Fig. 4d1 the storage modulus during applied magnetic field loops is shown. The asymmetric shape comes from the asymmetric hysteresis loops of magnetic particles when the hard MRE is pre-magnetized at a given field and then tested until a smaller applied field (compare Fig. 4d2 and d3).
3.6. Physical properties
In the absence of magnetic fields, MREs behave as conventional filled elastomers. However, in the presence of magnetic fields embedded particles become magnetized and interact increasing the MR effect. This increase is even more noticeable in the case of AMREs if compared to IMREs when the magnetic field is oriented parallel to the direction of the particle chains.322 Gorman et al.322 is probably the first publication to compare results for uniaxial and biaxial testing under high strain fatigue test conditions.The physical properties of MREs can be described using quasi-static and dynamic tests.
3.6.1.1. Shear. Liao et al.323 described the influence of shear deformation on the normal force in MREs. In the quasi-static regime, the normal force decreased with the shear strain at low magnetic field. However, it increased with the strain at high magnetic field. A similar trend was observed in oscillatory shear. However, the normal force decreased sharply when the strain amplitude exceeded 7%. Experimental results for small and large fields were explained in terms of two factors: the elastic modulus in the pre-compression direction and the magnetic torque. The sharp decrease at 7% under oscillatory shear is justified by the breakage of the field-induced structures. More recently, Kikuchi et al.324 investigated the large strain behavior of MREs in shear under uniform magnetic fields and compression under non-uniform magnetic fields. Their model was based on the previous model by Kraus.325
3.6.1.2. Tension and compression. The tensile properties of MREs have been vaguely investigated in the recent literature. Sandesh et al.326 showed that the tensile modulus of an elastomer increases by addition of CIP. However, it reduced the percentage elongation and tensile strength making the MRE brittle. The tensile properties of magnetically hard MREs were also investigated by Borin et al.327
Undoubtedly, compression tests clearly dominate over shear and tension tests. The comparison between tensile and shear moduli of MREs is missing in the literature. An attempt was carried out by Borin et al.328 using rod specimens. Ghafoorianfar et al.329 proposed a model to predict the electrical resistivity and magnetostriction of MREs under different applied magnetic fields and mechanical compressive loads. Han et al.330 proved that the dipole-interaction model failed to explain the tension/compression observed in experiments. In this paper, various filler-chain structures were studied to demonstrate the ultimate field-stiffening effect in MREs. It seems that the wavy chain structure was the key in the modulus increase. The study also foresaw the possibility of a negative MR effect. Sun et al.331 described MREs working in squeeze mode and proposed a model. Then, in a following publication they compared the shear and squeeze behavior.332 Interestingly, the squeeze MRE absorber had a larger frequency-shift range than that working in the shear mode. Suo et al.333 proposed a model for MREs. An extended fractional-order derivative model was developed to consider the Payne effect using the framework of the Kraus model.
Norouzi et al.273 described the dynamic behavior of MREs in oscillatory shear tests in terms of a modified Kelvin–Voigt model. In a later paper, Norouzi et al.336 proposed a MRE model that captures the dynamic behavior in tensile–compressive loadings and compared it with experiments. Both the equivalent storage modulus (obtained from the slope of the hysteresis loops) and loss modulus (obtained from the loop area) increased with the field. Guo et al.337 created a model using an Abel dashpot for the torsional dynamic oscillatory properties of MREs.
An alternative way to elucidate the viscoelastic character of any material is through the use of creep-recovery tests. In this sense, Qi et al.338 investigated the creep and recovery behavior of MREs based on polyurethane/epoxy resin graft interpenetrating polymer networks. Findley's, Burgers and Weibull models were used. In a following paper they investigated the stress relaxation of MREs.339
The influence of a prestress on the mechanical properties of MREs has also been investigated. Danas et al.340 found that a compressive/tensile prestress made the MRE elongate/compress itself under the presence of a magnetic field (magnetostrictive behavior). On its part, Feng et al.341 have shown that with increasing prestress, both the storage modulus and magnetoinduced modulus showed a declining trend after an initial ascent. A theoretical model was also provided in each of these works.
The temperature dependence of the dynamic properties of MREs has been reported by Wan et al.342 In their paper, the fractional Maxwell model and the generalized Maxwell model were used.
Also, exotic deformations are attracting the attention of several researchers. For instance, Schubert and Harrison346 carried out equi-biaxial tension tests on MREs. In a subsequent paper, the isotropic and anisotropic magnetic permeabilities of MREs were identified using a simple inverse modelling approach.347 MREs under impact loading conditions were investigated by Leng et al.348 They explored two influential factors: particle arrangement and magnetic field strength. The dissipated energy increased with magnetic field and is larger in the case of structured MREs.
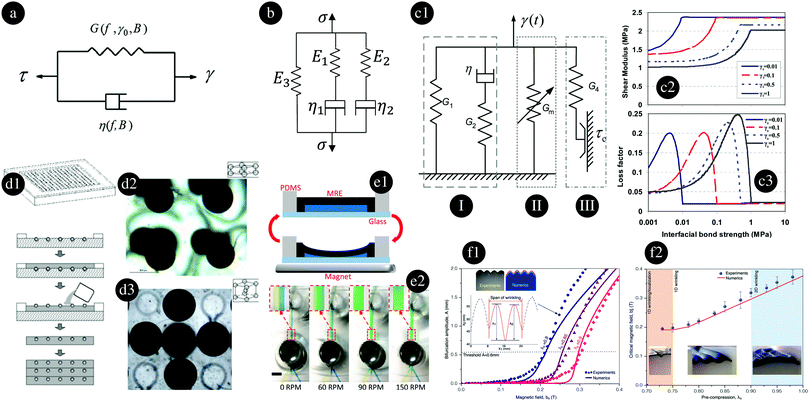 | ||
| Fig. 5 (a) Model based on stiffness and damping elements as proposed by Norouzi et al.273 to reproduce IMRE behavior in oscillatory shear tests. From ref. 273 with permission from SAGE, copyright 2020. (b) Example of model based on stiffness and damping elements proposed by Norouzi et al.336 to reproduce IMRE behavior in oscillatory compression tests. (c1) Model proposed by Chen and Jerrams349 for MREs including: (I) viscoelastic properties of the matrix, (II) magnetic contribution to mechanical properties and (III) interfacial adhesion. (c2 and c3) Represent predictions of the storage modulus and loss factor as a function of the interfacial adhesion strength, τc in (c1). Adapted from Fig. 1–3 in ref. 349 with permission from AIP, copyright 2020. (d1) Experimental layer by layer protocol to manufacture an AMRE with precise control over particle position. (d2) and (d3) are pictures of the resultant lattice (particles are 400 μm diameter) and body center cubic structures (800 μm), respectively. From ref. 356 with permission from AIP. (e1) MRE actuator implemented in a microfluidic circuit. When a permanent magnet is approached to the MRE, it deforms and squeezes the fluid within the chamber. (e2) Two channels feed the MRE chamber with different colored fluids. By increasing the frequency of approaching the magnet, the MRE induce chaotic fluid motion resulting in both fluids being mixed. Adapted from Fig. 4 in ref. 374 with permission from WILEY-VCH, copyright 2020. (f1) Amplitude of the surface deflection as a function of the applied magnetic field for different mechanical compressions. Magnetic field is applied vertically while the compression is exerted in the horizontal direction in the inset picture. (f2) For a given mechanical compression, the corresponding surface roughness appears above a critical magnetic field. From ref. 382 with permission from RSC, copyright 2020. | ||
Among macro-mechanical models, a three-parameter model has been normally used to describe the viscoelastic behavior of rubber-like material. This is typically a combination of a stiffness element and a Kelvin model (i.e. a stiffness element and damping element in parallel).15,273 Most available models in the MRE literature neglect interfacial interactions and therefore their predictions are only appropriate for the storage modulus and not the loss factor. However, as stated in Section 3.2, an appropriate viscoelastic model for MREs needs to capture not only magnetostatic forces but also the viscoelastic character of the elastomeric matrix and the interactions between the particles and the matrix. A model that includes these three contributions is that of Chen and Jerrams.349 Some of the predictions of this model are shown in Fig. 5c. In particular, it can be seen that the predicted trends for the storage modulus and the loss factor as a function of the interfacial adhesion follow the experimental trends (see Section 3.3).
At particle scale, Li and Sun274 proposed a micromechanical model that was capable of predicting the off-state stiffness and damping behavior as well as the MR effect in MREs. The dependence of the moduli on the frequency in IMREs was modeled by Agirre-Olabide and Elejabarrieta275 considering the anisotropy in the magnetic permeability of the MREs. Other theoretical developments are those of Biller et al.350,351 and Vaganov et al.352
As it happens in MRFs, particle-level simulations have become a very useful tool for MRE modeling (see Menzel353 for a recent review). With these simulations, it is possible to track each particle position bearing in mind magnetic and matrix mediated forces. An example, among many others, is the work of Pessot et al.354 where they used a simulation to calculate the frequency-dependent elastic moduli based on the decomposition of the linear response to an external stress in normal modes. Although they also compared against experiments in Pessot et al.,355 comparisons to validate previous models would be clearly favored by the manual arrangement of iron powder in lattices (e.g. Li et al.356 described the analysis, fabrication and characterization of patterned MREs, see Fig. 5d).
3.7. Applications
Commercialization of MR based devices is still limited to MRF dampers and MREs have not penetrated into commercial products.17 However, classical potential applications of MREs range from automotive357 and aerospace to civil engineering devices.291 MREs are traditionally used in mounts and shock absorbers.Since the pioneering paper by Ginder et al.,268 it was clearly demonstrated the mechanical potential of MREs to develop tuned vibration absorbers. Indeed, today, major potential applications of MREs concern vibration control (absorption and isolation). This is due to the fact that storage modulus and loss factors can be tuned by the superposition of a magnetic field. In particular, the natural frequency of the system increases together with the storage modulus. Of course, in addition to its magnetoelastic character, MREs possess other functions such as magnetoresistance, magnetostriction, piezoresistance and thermoresistance. In particular, the use or MREs in sensing devices is still in its infancy.299
The macroscale deformation of magnetized MREs has been studied extensively in the past. However, MREs have recently found another interesting application as the surface of these elastomers can be micro-deformed in a controlled way superimposing external magnetic fields. This has an impact in boundary friction, wettability and adhesion properties. Specifically, AMREs that are inherently hydrophobic can become superhydrophobic when a small magnetic field is applied.358–360 The storage modulus and the surface properties are changed. Chen et al.360 obtained an analytical model for the field-induced surface micro-deformations considering an infinite medium.
Other applications based on surface deformation involve their use as smart adaptative mirrors361 and as actuator-based hand-held devices for user interaction with touch screens. Since the touch screen is flat and featureless, the user can only interact with the virtual object under visual guidance and this is a limitation for a blind person. To enhance realism haptic devices based on MR technology are emerging.362
MREs are also used in electromagnetic (EM) protection applications. Sedlačík et al.363 investigated the EM shielding properties of MREs for the first time. MREs absorbed EM radiation in the ultra-high frequency band, namely the range from 700 MHz to 1.6 GHz. The performance was strongly dependent on the magnetic field strength with AMREs exhibiting superior EM shielding than their IMREs counterparts.364,365 Moucka et al.366 reported the dielectric properties of MREs. This is essential for applications such as piezoresistive sensors or radio-absorbing materials. It is based on the fact that AMREs exhibit higher electric conductivity when compared to their isotropic analogues. The aim of their work was to correlate the microstructure of the MRE and its dielectric response.
MREs can be applied as anisotropic thermal, electric and sound conductors/attenuators as well. Zhong et al.367 investigated the enhancement of thermal transport in AMREs with the flash method. Zhu et al.368 investigated the conductivity of MREs under pressure while their acoustical properties have been recently tested by Hasheminejad and Shabanimotlagh369 and by Korobko and coworkers.370
Apart from a controllable storage modulus and loss factor, MREs also exhibit a change in shape when placed under a magnetic field. The field-active mode originates from the magnetostrictive behavior of MREs. Therefore, they can be used in soft actuators and artificial muscles. For a recent review on this topic we refer to Elhajjar et al.371 MREs are currently used as building blocks in sensors and actuators for applications in microfluidics such as self-powered magnetic field sensors,372 mechanical actuators373,374 (see Fig. 5e), and micropumps.375 The influence of temperature in the magnetostriction was investigated by Diguet et al.376 Using digital holographic interferometry, Gong et al.377 showed that there is not consensus on whether an MRE should contract or stretch when a magnetic field is superimposed. The results demonstrated that some regions stretch while other regions contract. Isolated particles in the MRE led to contraction while grouped particles led to stretch.378 This characteristic makes it possible to control surface roughness and therefore wettability and friction as commented above.
A fast growing field of research is the use of MREs in tribological applications. Li et al.379 demonstrated that IMREs exhibit a decreasing friction coefficient with the applied magnetic field. On the other hand, the influence of magnetic field on AMREs is not monotonic. Lian et al.380 studied friction and wear properties of MREs under vibration conditions. Friction was found to decrease with magnetic field and amplitude and to increase with vibration superposition and frequency. Wear depth decreased under fields and increased with vibration. Lian et al.381 investigated the stick-slip characteristics of MRE against aluminum plate. Stick-slip is originated from the difference between the static and dynamic friction forces. Controlling stick-slip is important because it can lead to vibration, noise and wear reducing the lifetime of friction pairs. Although it was not relevant at low speeds it enhanced as the speed increased. The superposition of a magnetic field was capable to reduce the stick-slip phenomena and therefore reduce wear as well. The active control of surface roughness in MREs was also investigated by Psarra et al.382 Their experimental system consisted in an IMRE layer deposited on top of a non-magnetic elastomer that served as a substrate. By changing the applied mechanical compression and magnetic field over this system they obtained, experimentally and numerically, a phase diagram organizing the different observed surface roughness patterns (see Fig. 5f).
4. Bridging the gap between MRFs and MREs
Whenever the carrier is neither a Newtonian liquid nor a perfectly elastic material, the MR composite is said to be in the borderline between MRFs and MREs. MR materials in this region constitute a big family that grows quickly with time. We will call them generalized magnetorheological materials (GMRMs). These kinds of materials are referred in the literature as MR gels, MR plastomers, etc. (see Fig. 6a taken from Wang et al.383). | ||
| Fig. 6 (a1) Example of a GMRM consisting in CIP dispersed in a polymer matrix (silly putty) at 60 wt%. In the off-state, the GMRM exhibits the usual properties of the matrix, that is, it behaves as a brittle/soft material at large/small shear rates. (a2) Frequency dependence of the storage modulus of the GMRM shown in (a1) under different magnetic fields. The frequency to pass from soft to brittle material depends on the applied magnetic field. Adapted from Fig. 5 and 10 in ref. 383 with permission from RSC, copyright 2020. (b1) Manufacture process for an MRF impregnated polyurethane sponge. (I) Injection and immersion. (II) Oscillatory compression to guarantee homogeneous distribution of the MRF in the sponge. (III) Final MRF content is known by weighting. (IV) Joint of two specimens to perform oscillatory shear experiments (outer plates are fixed while a force/displacement is imposed in the inner one). (b2 and b3) Pictures of the polyurethane sponge without and with MRF, respectively. Inner sketch: (1) porous sponge, (2) layer of MRF, (3) empty space. Adapted from Fig. 3 and 4 in ref. 411 with permission from Elsevier, copyright 2020. (c1) Synthesis of a polyurethane sponge impregnated by a MRP. (c2 and c3) Particle disposition in the off- and on-state, respectively. As it can be seen, this composite allows particle motion as MRFs. Adapted from Fig. 2 in ref. 409 with permission from IOP Publishing, copyright 2020. (d1) Manufacture process to synthesize a hybrid material based on MRFs and a UV-curable elastomer. (d2) Cross-sectional picture of the resultant material. Adapted from Fig. 6 and 7 in ref. 418 with permission from Elsevier, copyright 2020. | ||
The motivation behind efforts filling the gap between MRFs and MREs is that both kinds of materials are complementary. MRF devices mainly possess variable damping while MRE devices mainly have variable stiffness. A difficulty that arises when working with GMRMs is that the rheological behavior is in many cases not reversible and this complicates the analysis (e.g. MR plastomers). Additionally, the rheological behavior is not linear anymore. Two recent examples exploring the large-amplitude oscillatory shear (LAOS) behavior of GMRMs are those of An et al.384 and Pang et al.385 An et al.384 prepared MR materials in self-assembled triblock copolymers. They found that the onset strain towards nonlinear rheology decreases substantially under magnetic fields. In their turn, Pang et al.385 measured the normal stress in MR materials prepared in polyurethane gels using experiments and particle level simulations. As the amplitude of the strain increased, the peak of the normal stress increased and the trough decreased. Two arguments were provided to explain the normal force evolution: the Poynting effect and the magnetic-induced normal stress.
The use of a non-Newtonian matrix, and in particular a yield stress material, has been demonstrated to be very effective in the prevention of particles from sedimentation.386,387 The paper by Rich et al.388 makes use of the fact that the process of assembling particles into organized functional structures is influenced by the rheological properties of the carrier and in particular its yield stress. Tuning these properties, for example through changes in the temperature as it was done in Wang et al.,389 represented a viable approach for controlling particle assembly. Yang et al.390 prepared MRFs by dispersion of CIP in 12-hydroxy stearic acid (12-HAS) oil solutions as carrier. These suspensions exhibited a remarkable sedimentation stability.
Available literature on this topic can be classified in two main groups: bidisperse and plastomer GMRMs. These systems are usually tested in shear and elongation modes, although some works can be found in valve flow mode as well, e.g. Whiteley et al.391
4.1. Bidisperse
Similar to MRFs and MREs, the use of bidisperse GMRMs exhibits benefits over monomodal systems, in particular, a larger storage modulus. For instance, Yang et al.392 prepared GMRMs by partial replacement of CIP with Ni-coated multi-walled CNTs. Dimorphic GMRMs were prepared by Yu et al.393 (using iron nanowires) and Yang et al.394 (using flower-like CIP). Other exotic bidisperse GMRMs have been reported by dispersing PTFE particles together with CIP in an organogel to improve frictional properties.3954.2. Plastomers
A promising GMRM in the borderline between MRFs and MREs is that of MR plastomers (MRPs) developed by Xinglong Gong and coworkers. For a recent review on MRPs we refer to Xuan et al.396Liu et al.397 investigated quasi-static loading rates (in particular, start-up tests). The non-linear properties of MRPs were investigated by Gong et al.398 using torsional rheometry. Similar to Liao et al.323 for MREs, normal stresses have also been investigated in MRPs.399 They observed an abrupt drop in the normal stress of MRPs at high fields (>491 mT) and explained it in terms of sliding. Xu et al.400 investigated compressive, tensile and oscillatory squeeze behaviors under constant volume. Three regions were distinguished in both compressive and tensile deformation modes: elastic deformation region, stress relaxation region and plastic flow region. Bidisperse MRPs have also been investigated in the literature. For instance, carbon filler-doped MRPs were synthesized by Xu et al.401 More recently, Xu et al.402 investigated the dynamic compression properties of MRPs in a modified Slit Hopkinson Pressure Bar (SHPB) device. A rate dependent stiffening performance was observed.
4.3. Other MR materials
Currently, many other MR materials exist apart from MRFs, MREs and GMRMs. Some examples are foamed MRE, impregnated MR composites and hybrid MRF-E materials.Foamed MREs are porous MREs with cells being either open or close. Major advantages are a lighter weight and also the fact that the elasticity in the off-state can be tuned changing the porosity; it typically decreases with increasing porosity. They exhibit excellent vibration and acoustic absorption performance and can be used as sensors and actuators.17 The storage modulus reduced and the loss factor increased when increasing the porosity. Stiffness and damping properties were easily controlled. Ju et al.403 fabricated a foamed silicone-based MRE using ammonium bicarbonate. More recently, Plachy et al.404 reported the synthesis of a foamed MRE using ethylene propylene diene rubber and azodicarbonamide as foaming agent.
Most MRF impregnated composites are based on sponges that serve as a scaffold for the MRF to be held in place due to capillary forces.405,406 Examples on how to synthesize these composites are shown in Fig. 6b and c. The sponge is capable to withstand a certain stress and provides the desired viscoelastic properties. In a MRF impregnated sponge the particles within the MRF have some freedom to move around a sponge scaffold and this maximizes the MR effect. Most MRF impregnated sponges reported in the recent literature are based on polyurethane with open cell matrices.407–411 An exception is the paper by Reddy et al.412 that used a CNT foam.
Another set of MRF impregnated composites uses a metal foam as a skeleton. They were discovered with the aim to improve the mechanical strength over that of MRF impregnated sponges. Liu et al.413 described the dynamic response of different metal foam MRF materials. They used three types of metal foams: Fe, Ni and Cu. They exhibit some advantages over the sponge MR materials: more wearable, longer lifetime and better damping effect. Yao et al.414 investigated the normal force generated in metal foams subjected to oscillatory shear.
Finally, hybrid MRF-E materials share the benefits of MRFs and MREs as both MRFs and MREs coexist in the same composite structure. In fact, hybrid MREs can be fabricated by encapsulating a MRF within a UV-curable silicone elastomer415–417 as it is shown in Fig. 6d. The elastic properties are provided by the MRE component while the damping properties are provided by the MRF component.
5. Conclusions and future trends
Currently, magnetorheology is a consolidated multidisciplinary field of research combining classical electromagnetism, fluid physics, mechanics and materials science. The MR family is growing fast and a number of potential applications are in development.As described above, during the last ten years, the emphasis has been focused on designing materials that result in a stronger MR response and a better stability. This includes the synthesis of core–shell magnetic particles and preparation of bidisperse MR composites. Nevertheless, there is still plenty of room for improvement with new trends and challenges.
Probably, the most direct route to enhance MR effect is maximizing the particle content. In this sense, the use of new additives such as superplasticizers was found to be of interest, particularly in low field applications. Unfortunately, the technology has been developed for water based MRFs and it seems difficult to translate it to oil-based material applications.
Other alternatives involve the use of unconventional flow/magnetic field configurations. Non-shearing (elongational) flows are vaguely understood in the literature. Moreover, it is expected that combined kinematics (i.e. superimposed flows) will generate stronger responses. Similarly, cases where a DC magnetic field is used have been widely studied. However, by employing triaxial unsteady magnetic fields, it is possible to generate self-assembled structures that are closer to the minimum energy configuration. This could be useful in the fabrication of more efficient MRFs and MREs. In addition, it should be taken into consideration that the understanding of magnetorheology in high speed and high magnetic fields is still in its infancy.
Regarding stability, new research has given rise to a wide variety of GMRMs but their fundamental understanding is far to be complete. Only time independent matrices, and in particular yield stress materials, have been explored in detail to date although their viscoelastic properties have yet to receive enough attention. In any case, before attempting the previous goal, it seems reasonable to deepen in the understanding of time dependent properties of simpler MR composites that are still vaguely understood.419,420 Even more difficult seems to be the understanding of aging effects in MR devices421 due to the large difference between time/space scales between current applications and academia investigations.
Recent progress has led to improving MR applications from different perspectives. A few of these improvements include IMREs together with AMREs in parallel and series configurations when isotropic stiffness and damping characteristics are required, mechanically deformable phases in springless damping applications422,423 or electromagnetic and permanent magnetic assemblies to reduce power consumption in applications where the MR composite operates frequently in the on-state.
Finally, it is anticipated that MR materials will be incorporated in applications related to thermal transport and heat dissipation424,425 as well as within the context of other disciplines such as Ecology (for the removal of phosphorous and lake restoration),426Biomedicine (for the fabrication of magnetic scaffolds and tissue engineering)427 or Electronics (for the fabrication of MR ionogels).428
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Matthew Terkel is acknowledged for improving the use of English in the manuscript. This work was supported by MICINN PID2019-104883GB-I00 project, Junta de Andalucía P18-FR-2465 project and European Regional Development Fund (ERDF). J. R. Morillas acknowledges FPU14/01576 fellowship.References
- M. R. Jolly, J. D. Carlson and B. C. Muñoz, Smart Mater. Struct., 1996, 5(5), 607 Search PubMed.
- J. Rabinow, AIEE Trans., 1948, 67, 1308–1315 Search PubMed.
- Y. Xu, X. Gong, S. Xuan, W. Zhang and Y. Fan, Soft Matter, 2011, 7(11), 5246–5254 Search PubMed.
- R. Ahamed, S. B. Choi and M. M. Ferdaus, J. Intell. Mater. Syst. Struct., 2018, 29(10), 2051–2095 Search PubMed.
- R. M. Andrade, A. Bento Filho, C. B. S. Vimieiro and M. Pinotti, Smart Mater. Struct., 2018, 27(10), 105031 Search PubMed.
- J. W. Swan, J. L. Bauer, Y. Liu and E. M. Furst, Soft Matter, 2014, 10(8), 1102–1109 Search PubMed.
- J. P. Segovia-Gutiérrez, J. de Vicente, A. M. Puertas and R. Hidalgo-Álvarez, Phys. Rev. E, 2017, 95(5), 052601 Search PubMed.
- P. J. Rankin, J. M. Ginder and D. J. Klingenberg, Curr. Opin. Colloid Interface Sci., 1998, 3(4), 373–381 Search PubMed.
- D. J. Klingenberg, AIChE J., 2001, 47(2), 246–249 Search PubMed.
- G. Bossis, O. Volkova, S. Lācis and A. Meunier, in Ferrofluids, ed. S. Odenbach, Springer-Verlag, Berlin Heidelberg, 2002, vol. 11, pp. 202–230 Search PubMed.
- I. Bica, J. Ind. Eng. Chem., 2006, 12(4), 501–515 Search PubMed.
- F. D. Goncalves, J. H. Koo and M. Ahmadian, Shock Vib. Dig., 2006, 38(3), 203–220 Search PubMed.
- B. J. Park, F. F. Fang and H. J. Choi, Soft Matter, 2010, 6(21), 5246–5253 Search PubMed.
- J. de Vicente, D. J. Klingenberg and R. Hidalgo-Álvarez, Soft Matter, 2011, 7(8), 3701–3710 Search PubMed.
- Y. Li, J. Li, W. Li and H. Du, Smart Mater. Struct., 2014, 23(12), 123001 Search PubMed.
- A. Ghaffari, S. H. Hashemabadi and M. Ashtiani, J. Intell. Mater. Syst. Struct., 2015, 26(8), 881–904 Search PubMed.
- Ubaidillah, J. Sutrisno, A. Purwanto and S. A. Mazlan, Adv. Eng. Mater., 2015, 17(5), 563–597 Search PubMed.
- L. J. Felicia, S. Vinod and J. Philip, J. Nanofluids, 2016, 5(1), 1–22 Search PubMed.
- M. A. Cantera, M. Behrooz, R. F. Gibson and F. Gordaninejad, Smart Mater. Struct., 2017, 26(2), 023001 Search PubMed.
- S. B. Choi and Y. M. Han, Magnetorheological fluid technology: applications in vehicle systems, CRC Press, Boca Raton, 2012 Search PubMed.
- N. M. Wereley, Magnetorheology: Advances and Applications, Royal Society of Chemistry: RSC Smart Materials, London, 2013 Search PubMed.
- A. Hajalilou, S. A. Mazlan, H. Lavvafi and K. Shameli, Field responsive fluids as smart materials, Springer, Singapore, 2016 Search PubMed.
- S. B. Choi and W. Li, Magnetorheological Materials and their Applications, The Institution of Engineering and Technology, Stevenage, 2019 Search PubMed.
- S. Singamaneni, V. N. Bliznyuk, C. Binek and E. Y. Tsymbal, J. Mater. Chem., 2011, 21(42), 16819–16845 Search PubMed.
- H. S. Chae, S. H. Piao and H. J. Choi, J. Ind. Eng. Chem., 2015, 29, 129–133 Search PubMed.
- A. V. Anupama, V. Kumaran and B. Sahoo, Powder Technol., 2018, 338, 190–196 Search PubMed.
- Y. Tong, X. Dong and M. Qi, Soft Matter, 2018, 14(18), 3504–3509 Search PubMed.
- W. Zhang, F. Shen and R. Hong, Particuology, 2011, 9(2), 179–186 Search PubMed.
- Z. Kozakova, I. Kuritka, N. E. Kazantseva, V. Babayan, M. Pastorek, M. Machovsky, P. Bazant and P. Sáha, Dalton Trans., 2015, 44(48), 21099–21108 Search PubMed.
- L. Zhuang, W. Zhang, Y. Zhao, H. Shen, H. Lin and J. Liang, Sci. Rep., 2015, 5, 9320 Search PubMed.
- H. S. Jung and H. J. Choi, J. Appl. Phys., 2015, 117(17), 17E708 Search PubMed.
- L. Pei, H. Pang, K. Chen, S. Xuan and X. Gong, Soft Matter, 2018, 14(24), 5080–5091 Search PubMed.
- J. Berasategi, A. Gómez, M. M. Bou-Ali, J. Gutiérrez, J. M. Barandiarán, I. V. Beketov, A. P. Safronov and G. V. Kurlyandskaya, Smart Mater. Struct., 2018, 27(4), 045011 Search PubMed.
- J. Noma, H. Abe, T. Kikuchi, J. Furusho and M. Naito, J. Magn. Magn. Mater., 2010, 322(13), 1868–1871 Search PubMed.
- I. Arief and P. K. Mukhopadhyay, J. Magn. Magn. Mater., 2016, 397, 57–63 Search PubMed.
- I. Arief and P. K. Mukhopadhyay, J. Magn. Magn. Mater., 2019, 479, 326–331 Search PubMed.
- Z. Xia, X. Wu, G. Peng, L. Wang, W. Li and W. Wen, Smart Mater. Struct., 2017, 26(5), 054006 Search PubMed.
- Z. Xia and W. Wen, Nanomaterials, 2016, 6(1), 19 Search PubMed.
- J. Rodríguez-López, H. C. Shum, L. Elvira, F. Montero de Espinosa and D. A. Weitz, J. Magn. Magn. Mater., 2013, 326, 220–224 Search PubMed.
- M. W. Kim, D. H. Bae, S. H. Kwon and H. J. Choi, Macromol. Res., 2018, 26(4), 353–358 Search PubMed.
- S. Lee, K. Y. Shin and J. Jang, Nanoscale, 2015, 7(21), 9646–9654 Search PubMed.
- M. Sedlačík, V. Pavlínek, M. Lehocky, A. Mracek, O. Grulich, P. Švrčinová, P. Filip and A. Vesel, Colloids Surf., A, 2011, 387(1–3), 99–103 Search PubMed.
- M. Sedlačík, V. Pavlínek, P. Sáha, P. Švrčinová and P. Filip, Mod. Phys. Lett. B, 2012, 26(03), 1150013 Search PubMed.
- H. B. Cheng, L. Zuo, J. H. Song, Q. J. Zhang and N. M. Wereley, J. Appl. Phys., 2010, 107(9), 09B507 Search PubMed.
- H. Cheng, M. Wang, C. Liu and N. M. Wereley, Smart Mater. Struct., 2018, 27(7), 075030 Search PubMed.
- M. Ashtiani, S. H. Hashemabadi and A. Ghaffari, J. Magn. Magn. Mater., 2015, 374, 716–730 Search PubMed.
- Y. P. Seo, S. Han, J. Choi, A. Takahara, H. J. Choi and Y. Seo, Adv. Mater., 2018, 30(42), 1704769 Search PubMed.
- M. Ashtiani and S. H. Hashemabadi, Colloids Surf., A, 2015, 469, 29–35 Search PubMed.
- G. Bossis, Y. Grasselli, A. Meunier and O. Volkova, Appl. Phys. Lett., 2016, 109(11), 111902 Search PubMed.
- T. Plachý, E. Kutalkova, M. Sedlačík, A. Vesel, M. Masar and I. Kuritka, J. Ind. Eng. Chem., 2018, 66, 362–369 Search PubMed.
- Y. M. Han, S. Kim, Y. D. Park, J. W. Kang and S. B. Choi, Smart Mater. Struct., 2015, 24(11), 115016 Search PubMed.
- J. F. Desrosiers, J. P. Lucking Bigué, M. Denninger, G. Julió, J. S. Plante and F. Charron, J. Phys.: Conf. Ser., 2013, 412(1), 012022 Search PubMed.
- A. Wiehe, C. Kieburg and J. Maas, J. Phys.: Conf. Ser., 2013, 412(1), 012017 Search PubMed.
- J. P. Lucking Bigué, A. Landry-Blais, A. Pin, R. Pilon, J. S. Plante, X. Chen and M. Andrews, Smart Mater. Struct., 2019, 28(9), 094003 Search PubMed.
- S. A. Wahid, I. Ismail, S. Aid and M. S. A. Rahim, IOP Conf. Ser.: Mater. Sci. Eng., 2016, 114(1), 012101 Search PubMed.
- C. Kieburg, G. Oetter, R. Lochtman, C. Gabriel, H. M. Laun, J. Pfister, G. Schober and H. Steinwender, in Proc. 10th Intl. Conf. on Electrorheological Fluids and Magnetorheological Suspensions, World Scientific, Singapore, 2007, pp. 101–107.
- J. R. Morillas, A. J. F. Bombard and J. de Vicente, Smart Mater. Struct., 2015, 25(1), 015023 Search PubMed.
- F. H. Niu, Z. D. Hu, H. Yan, J. J. Yang and H. S. Zhang, J. Magn. Magn. Mater., 2018, 465, 421–429 Search PubMed.
- H. Cheng, X. Zhang, G. Liu, W. Ma and N. M. Wereley, Smart Mater. Struct., 2016, 25(5), 055007 Search PubMed.
- S. R. Gorodkin, W. I. Kordonski, E. V. Medvedeva, Z. A. Novikova, A. B. Shorey and S. D. Jacobs, Rev. Sci. Instrum., 2000, 71(6), 2476–2480 Search PubMed.
- W. I. Kordonski, S. Gorodkin and R. Behlok, J. Magn. Magn. Mater., 2015, 382, 328–334 Search PubMed.
- J. Roupec, P. Berka, I. Mazůrek, Z. Strecker, M. Kubík, O. Macháček and M. T. Andani, Smart Mater. Struct., 2017, 26(10), 107001 Search PubMed.
- L. Xie, Y. T. Choi, C. R. Liao and N. M. Wereley, J. Appl. Phys., 2015, 117(17), 17C754 Search PubMed.
- Y. T. Choi, L. Xie and N. M. Wereley, Smart Mater. Struct., 2016, 25(4), 04LT01 Search PubMed.
- M. Wen, J. Chambers, S. G. Sherman and N. M. Wereley, Smart Mater. Struct., 2019, 28(2), 025039 Search PubMed.
- Y. D. Liu, F. F. Fang and H. J. Choi, Colloid Polym. Sci., 2011, 289(11), 1295–1298 Search PubMed.
- C. Y. Gao, M. W. Kim, D. H. Bae, Y. Z. Dong, S. H. Piao and H. J. Choi, Polymer, 2017, 125, 21–29 Search PubMed.
- M. Sedlačík, V. Pavlínek, P. Sáha, P. Švrčinová, P. Filip and J. Stejskal, Smart Mater. Struct., 2010, 19(11), 115008 Search PubMed.
- M. Cvek, M. Mrlík, M. Ilčíková, T. Plachý, M. Sedlačík, J. Mosnáček and V. Pavlínek, J. Mater. Chem. C, 2015, 3(18), 4646–4656 Search PubMed.
- M. Mrlík, M. Ilčíková, V. Pavlínek, J. Mosnáček, P. Peer and P. Filip, J. Colloid Interface Sci., 2013, 396, 146–151 Search PubMed.
- J. W. Lee, K. P. Hong, M. W. Cho, S. H. Kwon and H. J. Choi, Smart Mater. Struct., 2015, 24(6), 065002 Search PubMed.
- A. Esmaeilzare, S. M. Rezaei and B. Ramezanzadeh, Appl. Surf. Sci., 2018, 436, 1200–1212 Search PubMed.
- B. Sim, H. S. Chae and H. J. Choi, eXPRESS Polym. Lett., 2015, 9(8), 736–743 Search PubMed.
- T. H. Min, H. J. Choi, N. H. Kim, K. Park and C. Y. You, Colloids Surf., A, 2017, 531, 48–55 Search PubMed.
- K. Chen, W. L. Zhang, L. Shan, X. Zhang, Y. Meng, H. J. Choi and Y. Tian, J. Appl. Phys., 2014, 116(15), 153508 Search PubMed.
- Y. D. Liu, C. H. Hong and H. J. Choi, Macromol. Res., 2012, 20(12), 1211–1218 Search PubMed.
- Y. Z. Dong, S. H. Piao and H. J. Choi, Colloid Polym. Sci., 2018, 296(1), 11–19 Search PubMed.
- A. Hajalilou, A. Kianvash, K. Shameli and H. Lavvafi, Appl. Phys. Lett., 2017, 110(26), 261902 Search PubMed.
- G. Kim, J. E. Kim, Y. D. Liu and H. J. Choi, IEEE Trans. Magn., 2012, 48(11), 3446–3449 Search PubMed.
- S. Y. Kim, S. H. Kwon, Y. D. Liu, J. S. Lee, C. Y. You and H. J. Choi, J. Mater. Sci., 2014, 49(3), 1345–1352 Search PubMed.
- S. H. Kwon, H. J. Choi, J. W. Lee, K. P. Hong and M. W. Cho, J. Korean Phys. Soc., 2013, 62(12), 2118–2122 Search PubMed.
- S. H. Kwon, B. Sim and H. J. Choi, IEEE Trans. Magn., 2016, 52(7), 1–4 Search PubMed.
- P. B. Nguyen, X. P. Do, J. Jeon, S. B. Choi, Y. D. Liu and H. J. Choi, J. Magn. Magn. Mater., 2014, 367, 69–74 Search PubMed.
- B. O. Park, K. H. Song, B. J. Park and H. J. Choi, J. Appl. Phys., 2010, 107(9), 09A506 Search PubMed.
- D. E. Park, H. S. Chae, H. J. Choi and A. Maity, J. Mater. Chem. C, 2015, 3(13), 3150–3158 Search PubMed.
- S. H. Piao, M. Bhaumik, A. Maity and H. J. Choi, J. Mater. Chem. C, 2015, 3(8), 1861–1868 Search PubMed.
- H. S. Chae, S. H. Piao, W. J. Han and H. J. Choi, Macromol. Chem. Phys., 2018, 219(5), 1700408 Search PubMed.
- F. F. Fang and H. J. Choi, Colloid Polym. Sci., 2010, 288(1), 79–84 Search PubMed.
- F. F. Fang, H. J. Choi and W. S. Choi, Colloid Polym. Sci., 2010, 288(3), 359–363 Search PubMed.
- F. F. Fang, H. J. Choi and Y. Seo, ACS Appl. Mater. Interfaces, 2010, 2(1), 54–60 Search PubMed.
- Y. D. Liu, H. J. Choi and S. B. Choi, Colloids Surf., A, 2012, 403, 133–138 Search PubMed.
- Y. D. Liu and H. J. Choi, J. Appl. Phys., 2014, 115(17), 17B529 Search PubMed.
- Y. D. Liu and H. J. Choi, Mater. Res. Bull., 2015, 69, 92–97 Search PubMed.
- L. Pei, H. Pang, X. Ruan, X. Gong and S. Xuan, RSC Adv., 2017, 7(14), 8142–8150 Search PubMed.
- M. H. Kim, K. Choi, J. D. Nam and H. J. Choi, Smart Mater. Struct., 2017, 26(9), 095006 Search PubMed.
- K. H. Gudmundsson, F. Jonsdottir, F. Thorsteinsson and O. Gutfleisch, J. Intell. Mater. Syst. Struct., 2011, 22(15), 1763–1767 Search PubMed.
- W. Jiang, Y. Zhang, S. Xuan, C. Guo and X. Gong, J. Magn. Magn. Mater., 2011, 323(24), 3246–3250 Search PubMed.
- L. A. Powell, N. M. Wereley and J. C. Ulicny, IEEE Trans. Magn., 2012, 48(11), 3764–3767 Search PubMed.
- L. M. Armijo, L. A. Ahuré-Powell and N. M. Wereley, J. Appl. Phys., 2015, 117(17), 17C747 Search PubMed.
- M. Ashtiani and S. H. Hashemabadi, J. Intell. Mater. Syst. Struct., 2015, 26(14), 1887–1892 Search PubMed.
- I. Arief and P. K. Mukhopadhyay, J. Alloys Compd., 2017, 696, 1053–1058 Search PubMed.
- D. Kittipoomwong, D. J. Klingenberg and J. C. Ulicny, J. Rheol., 2005, 49(6), 1521–1538 Search PubMed.
- C. Ekwebelam and H. See, Rheol. Acta, 2009, 48(1), 19–32 Search PubMed.
- N. M. Wereley, A. Chaudhuri, J. H. Yoo, S. John, S. Kotha, A. Suggs, R. Radhakrishnan, B. J. Love and T. S. Sudarshan, J. Intell. Mater. Syst. Struct., 2006, 17(5), 393–401 Search PubMed.
- C. Magnet, P. Kuzhir, G. Bossis, A. Meunier, L. Suloeva and A. Zubarev, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86(1), 011404 Search PubMed.
- J. R. Morillas, A. J. F. Bombard and J. de Vicente, Smart Mater. Struct., 2018, 27(7), 07LT01 Search PubMed.
- M. Sedlačík, V. Pavlínek, R. Vyroubal, P. Peer and P. Filip, Smart Mater. Struct., 2013, 22(3), 035011 Search PubMed.
- A. J. F. Bombard, F. R. Gonçalves, J. R. Morillas and J. de Vicente, Smart Mater. Struct., 2014, 23(12), 125013 Search PubMed.
- J. R. Morillas, A. J. F. Bombard and J. de Vicente, Ind. Eng. Chem. Res., 2018, 57(40), 13427–13436 Search PubMed.
- I. Arief and P. K. Mukhopadhyay, Phys. B, 2014, 448, 73–76 Search PubMed.
- E. Esmaeilnezhad, H. J. Choi, M. Schaffie, M. Gholizadeh, M. Ranjbar and S. H. Kwon, J. Magn. Magn. Mater., 2017, 444, 161–167 Search PubMed.
- D. S. Jang, Y. D. Liu, J. H. Kim and H. J. Choi, Colloid Polym. Sci., 2015, 293(2), 641–647 Search PubMed.
- I. Jönkkäri, M. Sorvali, H. Huhtinen, E. Sarlin, T. Salminen, J. Haapanen, J. M. Mäkelä and J. Vuorinen, Smart Mater. Struct., 2017, 26(9), 095004 Search PubMed.
- D. J. Klingenberg and J. C. Ulicny, Int. J. Mod. Phys. B, 2011, 25(07), 911–917 Search PubMed.
- S. A. N. Leong, P. M. Samin, A. Idris, S. A. Mazlan and A. H. A. Rahman, Smart Mater. Struct., 2016, 25(2), 025025 Search PubMed.
- J. A. Marins, T. Plachý and P. Kuzhir, J. Rheol., 2019, 63(1), 125–139 Search PubMed.
- D. Susan-Resiga and L. Vékás, Rheol. Acta, 2014, 53(8), 645–653 Search PubMed.
- D. Susan-Resiga and L. Vékás, J. Rheol., 2017, 61(3), 401–408 Search PubMed.
- D. Susan-Resiga and P. Barvinschi, J. Rheol., 2018, 62(3), 739–752 Search PubMed.
- S. H. Piao, W. L. Zhang and H. J. Choi, IEEE Trans. Magn., 2013, 50(1), 1–4 Search PubMed.
- H. S. Chae, S. H. Piao, A. Maity and H. J. Choi, Colloid Polym. Sci., 2015, 293(1), 89–95 Search PubMed.
- M. Cvek, M. Mrlík, R. Moucka and M. Sedlačík, Colloids Surf., A, 2018, 543, 83–92 Search PubMed.
- S. H. Kwon, C. H. Hong, P. X. Do, S. B. Choi and H. J. Choi, Ind. Eng. Chem. Res., 2015, 54(16), 4655–4663 Search PubMed.
- F. Jonsdottir, K. H. Gudmundsson, T. B. Dijkman, F. Thorsteinsson and O. Gutfleisch, J. Intell. Mater. Syst. Struct., 2010, 21(11), 1051–1060 Search PubMed.
- G. T. Ngatu, N. M. Wereley, J. O. Karli and R. C. Bell, Smart Mater. Struct., 2008, 17(4), 045022 Search PubMed.
- A. J. F. Bombard and J. V. R. Teodoro, Int. J. Mod. Phys. B, 2011, 25(07), 943–946 Search PubMed.
- P. Domínguez-García, S. Melle, J. M. Pastor and M. A. Rubio, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76(5), 051403 Search PubMed.
- K. Shahrivar, E. Carreón-González, J. R. Morillas and J. de Vicente, Soft Matter, 2017, 13(14), 2677–2685 Search PubMed.
- G. I. Vega-Bellido, R. A. de la Cruz-Araujo, I. Kretzschmar and U. M. Córdova-Figueroa, Soft Matter, 2019, 15(20), 4078–4086 Search PubMed.
- T. Borbáth, I. Borbáth, S. Günther, O. Marinica, L. Vékás and S. Odenbach, Smart Mater. Struct., 2014, 23(5), 055018 Search PubMed.
- C. L. Berli and J. de Vicente, Appl. Phys. Lett., 2012, 101(2), 021903 Search PubMed.
- H. M. Laun, G. Schmidt, C. Gabriel and C. Kieburg, Rheol. Acta, 2008, 47(9), 1049–1059 Search PubMed.
- W. Hu and N. M. Wereley, Int. J. Mod. Phys. B, 2011, 25, 979–985 Search PubMed.
- D. Güth and J. Maas, J. Intell. Mater. Syst. Struct., 2016, 27(5), 689–704 Search PubMed.
- P. Kuzhir, C. Magnet, L. Rodríguez-Arco, M. T. López-López, H. Fezai, A. Meunier, A. Zubarev and G. Bossis, J. Rheol., 2014, 58(6), 1829–1853 Search PubMed.
- H. M. Laun, C. Gabriel and C. Kieburg, Rheol. Acta, 2011, 50(2), 141–157 Search PubMed.
- I. Jönkkäri, E. Kostamo, J. Kostamo, S. Syrjala and M. Pietola, Smart Mater. Struct., 2012, 21(7), 075030 Search PubMed.
- J. R. Morillas and J. de Vicente, Composites, Part B, 2019, 160, 626–631 Search PubMed.
- C. W. Guo, F. Chen, Q. R. Meng and Z. X. Dong, J. Magn. Magn. Mater., 2014, 360, 174–177 Search PubMed.
- M. Cvek, M. Mrlík and V. Pavlínek, J. Rheol., 2016, 60(4), 687–694 Search PubMed.
- S. G. Sherman, A. C. Becnel and N. M. Wereley, J. Magn. Magn. Mater., 2015, 380, 98–104 Search PubMed.
- J. A. Ruiz-López, J. C. Fernández-Toledano, R. Hidalgo-Álvarez and J. de Vicente, Soft Matter, 2016, 12(5), 1468–1476 Search PubMed.
- J. A. Ruiz-López, R. Hidalgo-Álvarez and J. de Vicente, Smart Mater. Struct., 2017, 26(5), 054001 Search PubMed.
- W. Jia, L. Shan, W. Zhang, Y. Meng and Y. Tian, Smart Mater. Struct., 2018, 27(10), 105019 Search PubMed.
- Y. Sakuda, M. Aoshima and A. Satoh, Mol. Phys., 2012, 110(13), 1429–1435 Search PubMed.
- J. M. Ginder and L. C. Davis, Appl. Phys. Lett., 1994, 65(26), 3410–3412 Search PubMed.
- H. M. Laun, C. Gabriel and C. Kieburg, J. Rheol., 2010, 54(2), 327–354 Search PubMed.
- M. Ocalan and G. H. McKinley, Rheol. Acta, 2013, 52(7), 623–641 Search PubMed.
- J. R. Morillas, J. Yang and J. de Vicente, J. Rheol., 2018, 62(6), 1485–1494 Search PubMed.
- G. Bossis, O. Volkova, Y. Grasselli and A. Ciffreo, Front. Mater., 2019, 6, 4 Search PubMed.
- J. R. Morillas and J. de Vicente, Soft Matter, 2019, 15(16), 3330–3342 Search PubMed.
- J. R. Morillas and J. de Vicente, Phys. Rev. E, 2019, 99(6), 062604 Search PubMed.
- J. Wu, L. Pei, S. Xuan, Q. Yan and X. Gong, J. Magn. Magn. Mater., 2016, 408, 18–25 Search PubMed.
- K. Shahrivar, J. R. Morillas, Y. Luengo, H. Gavilan, P. Morales, C. Bierwisch and J. de Vicente, J. Rheol., 2019, 63(4), 547–558 Search PubMed.
- R. C. Bell, J. O. Karli, A. N. Vavreck, D. T. Zimmerman, G. T. Ngatu and N. M. Wereley, Smart Mater. Struct., 2008, 17(1), 015028 Search PubMed.
- J. de Vicente, J. P. Segovia-Gutiérrez, E. Andablo-Reyes, F. Vereda and R. Hidalgo-Álvarez, J. Chem. Phys., 2009, 131(19), 194902 Search PubMed.
- J. de Vicente, F. Vereda, J. P. Segovia-Gutiérrez, M. del Puerto Morales and R. Hidalgo-Álvarez, J. Rheol., 2010, 54(6), 1337–1362 Search PubMed.
- A. Gómez-Ramírez, P. Kuzhir, M. T. López-López, G. Bossis, A. Meunier and J. D. G. Durán, J. Rheol., 2011, 55(1), 43–67 Search PubMed.
- J. R. Morillas, E. Carreón-González and J. de Vicente, Smart Mater. Struct., 2015, 24(12), 125005 Search PubMed.
- K. Shah and S. B. Choi, Smart Mater. Struct., 2014, 24(1), 015004 Search PubMed.
- P. Kuzhir, A. Gómez-Ramírez, M. T. López-López, G. Bossis and A. Zubarev, J. Non-Newtonian Fluid Mech., 2011, 166(7–8), 373–385 Search PubMed.
- G. Bossis, J. A. Marins, P. Kuzhir, O. Volkova and A. Zubarev, J. Intell. Mater. Syst. Struct., 2015, 26(14), 1871–1879 Search PubMed.
- J. de Vicente, F. González-Caballero, G. Bossis and O. Volkova, J. Rheol., 2002, 46(5), 1295–1303 Search PubMed.
- Y. T. Chan, P. Wong, K. P. Liu and W. Bullough, J. Intell. Mater. Syst. Struct., 2011, 22(6), 551–560 Search PubMed.
- J. Jiang, Y. Tian, D. Ren and Y. Meng, Smart Mater. Struct., 2011, 20(8), 085012 Search PubMed.
- X. Liu, D. Ye, X. Gao, F. Li, M. Sun, H. Zhang, T. Tu and H. Yu, J. Magn. Magn. Mater., 2016, 398, 137–140 Search PubMed.
- X. Y. Yao, M. Yu and J. Fu, Smart Mater. Struct., 2015, 24(3), 035001 Search PubMed.
- C. Guo, X. Gong, S. Xuan, L. Zong and C. Peng, J. Magn. Magn. Mater., 2012, 324(6), 1218–1224 Search PubMed.
- G. Yildirim and S. Genç, Smart Mater. Struct., 2013, 22(8), 085001 Search PubMed.
- S. G. Sherman, L. A. Powell, A. C. Becnel and N. M. Wereley, J. Appl. Phys., 2015, 117(17), 17C751 Search PubMed.
- D. M. Patel and R. V. Upadhyay, Mater. Res. Express, 2018, 6(1), 015707 Search PubMed.
- X. Ruan, Y. Wang, S. Xuan and X. Gong, Smart Mater. Struct., 2017, 26(3), 035067 Search PubMed.
- A. G. Olabi and A. Grunwald, Mater. Des., 2007, 28(10), 2658–2664 Search PubMed.
- B. Kavlicoglu, F. Gordaninejad and X. Wang, J. Appl. Mech., 2011, 78(4), 041008 Search PubMed.
- H. Nishiyama, H. Takana, K. Shinohara, K. Mizuki, K. Katagiri and M. Ohta, J. Magn. Magn. Mater., 2011, 323(10), 1293–1297 Search PubMed.
- M. Kubík, O. Macháček, Z. Strecker, J. Roupec and I. Mazůrek, Smart Mater. Struct., 2017, 26(4), 047002 Search PubMed.
- G. Hu, J. Zhang, F. Zhong and L. Yu, Smart Mater. Struct., 2019, 28(4), 047003 Search PubMed.
- M. Kubik, D. Pavliček, O. Macháček, Z. Strecker and J. Roupec, Smart Mater. Struct., 2019, 28(4), 047002 Search PubMed.
- H. G. Lagger, C. Bierwisch and M. Moseler, J. Phys.: Conf. Ser., 2013, 412(1), 012020 Search PubMed.
- H. G. Lagger, C. Bierwisch, J. G. Korvink and M. Moseler, Rheol. Acta, 2014, 53(5–6), 417–443 Search PubMed.
- H. G. Lagger, T. Breinlinger, J. G. Korvink, M. Moseler, A. Di Renzo, F. Di Maio and C. Bierwisch, J. Non-Newtonian Fluid Mech., 2015, 218, 16–26 Search PubMed.
- D. Vågberg and B. P. Tighe, Soft Matter, 2017, 13(39), 7207–7221 Search PubMed.
- S. G. Sherman, D. A. Paley and N. M. Wereley, IEEE Trans. Magn., 2012, 48(11), 3517–3520 Search PubMed.
- S. G. Sherman and N. M. Wereley, IEEE Trans. Magn., 2013, 49(7), 3430–3433 Search PubMed.
- J. A. Ruiz-López, Z. W. Wang, J. C. Fernández-Toledano, R. Hidalgo-Álvarez and J. de Vicente, Rheol. Acta, 2016, 55(3), 245–256 Search PubMed.
- D. J. Klingenberg, C. H. Olk, M. A. Golden and J. C. Ulicny, J. Phys.: Condens. Matter, 2010, 22(32), 324101 Search PubMed.
- B. T. Wilson and D. J. Klingenberg, J. Rheol., 2017, 61(4), 601–611 Search PubMed.
- J. C. Ulicny, K. S. Snavely, M. A. Golden and D. J. Klingenberg, Appl. Phys. Lett., 2010, 96(23), 231903 Search PubMed.
- K. Okada and A. Satoh, J. Magn. Magn. Mater., 2017, 437, 29–41 Search PubMed.
- S. Zhang, J. Zhou and C. Shao, Phys. Fluids, 2019, 31(2), 022005 Search PubMed.
- J. de Vicente, J. A. Ruiz-López, E. Andablo-Reyes, J. P. Segovia-Gutiérrez and R. Hidalgo-Álvarez, J. Rheol., 2011, 55(4), 753–779 Search PubMed.
- J. A. Ruiz-López, R. Hidalgo-Álvarez and J. de Vicente, Rheol. Acta, 2016, 55(3), 215–221 Search PubMed.
- J. A. Ruiz-López, R. Hidalgo-Álvarez and J. de Vicente, Rheol. Acta, 2012, 51(7), 595–602 Search PubMed.
- A. Farjoud, M. Ahmadian, N. Mahmoodi, X. Zhang and M. Craft, Smart Mater. Struct., 2011, 20(8), 085013 Search PubMed.
- W. Kordonski and S. Gorodkin, J. Rheol., 2016, 60(1), 129–139 Search PubMed.
- C. Guo, X. Gong, S. Xuan, Q. Yan and X. Ruan, Smart Mater. Struct., 2013, 22(4), 045020 Search PubMed.
- W. Horak, Smart Mater. Struct., 2018, 27(6), 065022 Search PubMed.
- I. Ismail, S. A. Mazlan, H. Zamzuri and A. G. Olabi, Jpn. J. Appl. Phys., 2012, 51(6R), 067301 Search PubMed.
- W. Horak, B. Sapiński and M. Szczęch, Acta Mech. Autom., 2017, 11(1), 64–68 Search PubMed.
- S. Kaluvan, K. Shah and S. B. Choi, Smart Mater. Struct., 2014, 23(11), 115017 Search PubMed.
- X. Tang, X. Zhang, R. Tao and Y. Rong, J. Appl. Phys., 2000, 87(5), 2634–2638 Search PubMed.
- C. Hegger and J. Maas, J. Intell. Mater. Syst. Struct., 2016, 27(14), 1895–1907 Search PubMed.
- J. P. Lucking Bigué, F. Charron and J. S. Plante, J. Intell. Mater. Syst. Struct., 2018, 29(1), 62–71 Search PubMed.
- J. P. Lucking Bigué, F. Charron and J. S. Plante, J. Intell. Mater. Syst. Struct., 2018, 29(1), 72–81 Search PubMed.
- R. H. Ewoldt, P. Tourkine, G. H. McKinley and A. E. Hosoi, Phys. Fluids, 2011, 23(7), 073104 Search PubMed.
- S. H. Sadek, H. H. Najafabadi and F. J. Galindo-Rosales, J. Rheol., 2020, 64(1), 55–65 Search PubMed.
- F. J. Galindo-Rosales, J. P. Segovia-Gutiérrez, F. T. Pinho, M. A. Alves and J. de Vicente, J. Rheol., 2015, 59(1), 193–209 Search PubMed.
- H. Wang, C. Bi, J. Kan, C. Gao and W. Xiao, J. Intell. Mater. Syst. Struct., 2011, 22(8), 811–816 Search PubMed.
- S. Rahimi and D. Weihs, Exp. Fluids, 2012, 53(5), 1577–1589 Search PubMed.
- A. K. El Wahed and C. A. McEwan, J. Intell. Mater. Syst. Struct., 2011, 22(7), 631–643 Search PubMed.
- M. Pichumani and W. González-Viñas, Soft Matter, 2013, 9(8), 2506–2511 Search PubMed.
- P. Skalski and K. Kalita, Acta Mech. Autom., 2017, 11(4), 267–274 Search PubMed.
- X. Zhu, X. Jing and L. Cheng, J. Intell. Mater. Syst. Struct., 2012, 23(8), 839–873 Search PubMed.
- A. Y. Abd Fatah, S. A. Mazlan, T. Koga, H. Zamzuri, M. Zeinali and F. Imaduddin, Int. J. Mod. Phys. B, 2015, 29(04), 1530004 Search PubMed.
- J. W. Sohn, G. W. Kim and S. B. Choi, Appl. Sci., 2018, 8(10), 1928 Search PubMed.
- W. H. Kim, J. H. Park, S. Kaluvan, Y. S. Lee and S. B. Choi, Sens. Actuators, A, 2017, 255, 104–117 Search PubMed.
- T. H. Lee and S. B. Choi, Smart Mater. Struct., 2018, 28(1), 014001 Search PubMed.
- X. Gong, X. Ruan, S. Xuan, Q. Yan and H. Deng, Adv. Mech. Eng., 2014, 6, 410158 Search PubMed.
- B. Sapiński and J. Gołdasz, Smart Mater. Struct., 2015, 24(11), 115007 Search PubMed.
- J. Yang, S. Sun, W. Li, H. Du, G. Alici and M. Nakano, J. Intell. Mater. Syst. Struct., 2015, 26(14), 1811–1817 Search PubMed.
- S. R. Patil and R. A. Lohar, J. Braz. Soc. Mech. Sci. Eng., 2018, 40(11), 546 Search PubMed.
- J. Roupec, I. Mazůrek, Z. Strecker and M. Klapka, J. Phys.: Conf. Ser., 2013, 412(1), 012024 Search PubMed.
- J. D. Carlson, J. Intell. Mater. Syst. Struct., 2002, 13(7–8), 431–435 Search PubMed.
- J. D. Carlson, Int. J. Vehicle Des., 2003, 33(1–3), 207–217 Search PubMed.
- J. C. Ulicny, M. P. Balogh, N. M. Potter and R. A. Waldo, Mater. Sci. Eng., A, 2007, 443(1–2), 16–24 Search PubMed.
- M. A. Bramantya, M. Motozawa and T. Sawada, J. Phys.: Condens. Matter, 2010, 22(32), 324102 Search PubMed.
- M. A. Bramantya and T. Sawada, J. Magn. Magn. Mater., 2011, 323(10), 1330–1333 Search PubMed.
- A. Nanda and M. A. Karami, J. Acoust. Soc. Am., 2018, 144(1), 412–420 Search PubMed.
- Y. Forero-Sandoval, A. Vega-Flick, J. J. Alvarado-Gil and R. A. Medina-Esquivel, Smart Mater. Struct., 2016, 26(2), 025010 Search PubMed.
- M. S. A. Rahim, I. Ismail, S. B. Choi, W. H. Azmi and S. N. Aqida, Smart Mater. Struct., 2017, 26(11), 115009 Search PubMed.
- E. Esmaeilnezhad, S. Le Van, H. J. Choi, B. H. Chon, M. Schaffie, M. Gholizadeh and M. Ranjbar, J. Environ. Manage., 2019, 231, 1127–1134 Search PubMed.
- S. D. Nair and R. D. Ferron, Rheol. Acta, 2016, 55(7), 571–579 Search PubMed.
- J. Ding, G. Peng, K. Shu, C. Wang, T. Tian, W. Yang, Y. Zhang, G. G. Wallace and W. Li, Sci. Rep., 2015, 5(1), 1–11 Search PubMed.
- Z. Chen, L. Ren, J. Li, L. Yao, Y. Chen, B. Liu and L. Jiang, Acta Biomater., 2018, 65, 283–291 Search PubMed.
- C. Hartzell, Y. T. Choi, N. M. Wereley and T. J. Leps, Smart Mater. Struct., 2019, 28, 035030 Search PubMed.
- Y. Zhang, D. Li, Y. Chen and Z. Li, IEEE Trans. Magn., 2018, 54(12), 1–7 Search PubMed.
- Y. Sato and S. Umebara, IEEE Trans. Magn., 2012, 48(11), 3521–3524 Search PubMed.
- V. A. Kuzmin, E. V. Korobko, V. P. Roizman, Z. A. Novikova, A. P. Dostanko and A. O. Karabko, J. Phys.: Conf. Ser., 2013, 412(1), 012021 Search PubMed.
- C. Majidi and R. J. Wood, Appl. Phys. Lett., 2010, 97(16), 164104 Search PubMed.
- P. H. Anjos, S. A. Lira and J. A. Miranda, Phys. Rev. Fluids, 2018, 3(4), 044002 Search PubMed.
- A. M. Sidpara, Opt. Eng., 2014, 53(9), 092002 Search PubMed.
- N. A. Mutalib, I. Ismail, S. M. Soffie and S. N. Aqida, IOP Conf. Ser.: Mater. Sci. Eng., 2019, 469(1), 012092 Search PubMed.
- QED Technologies, https://qedmrf.com/en/, accessed April 2020.
- P. Zhang, K. H. Lee and C. H. Lee, Chin. J. Mech. Eng., 2016, 29(1), 84–90 Search PubMed.
- P. Zhang, K. H. Lee and C. H. Lee, J. Magn. Magn. Mater., 2017, 421, 13–18 Search PubMed.
- K. Shahrivar, A. L. Ortiz and J. de Vicente, Tribol. Int., 2014, 78, 125–133 Search PubMed.
- A. J. F. Bombard, F. R. Gonçalves, K. Shahrivar, A. L. Ortiz and J. de Vicente, Tribol. Int., 2015, 81, 309–320 Search PubMed.
- Z. D. Hu, H. Yan, H. Z. Qiu, P. Zhang and Q. Liu, Wear, 2012, 278, 48–52 Search PubMed.
- T. Aravind, N. Arunachalam and A. X. Kennedy, Mater. Res. Express, 2018, 6(1), 016104 Search PubMed.
- Y. Wang, S. Yin and H. Huang, Int. J. Adv. Des. Manuf. Technol., 2017, 91(5–8), 2831–2841 Search PubMed.
- M. Das, V. K. Jain and P. S. Ghoshdastidar, Int. J. Adv. Des. Manuf. Technol., 2012, 62(1–4), 405–420 Search PubMed.
- Z. Alam and S. Jha, Wear, 2017, 374, 54–62 Search PubMed.
- J. W. Lee, S. J. Ha, Y. K. Cho, K. B. Kim and M. W. Cho, J. Mech. Sci. Technol., 2015, 29(5), 2205–2211 Search PubMed.
- Z. Rigbi and L. Jilken, J. Magn. Magn. Mater., 1983, 37(3), 267–276 Search PubMed.
- M. R. Jolly, J. D. Carlson, B. C. Muñoz and T. A. Bullions, J. Intell. Mater. Syst. Struct., 1996, 7(6), 613–622 Search PubMed.
- M. Yu, B. Ju, J. Fu, X. Liu and Q. Yang, J. Magn. Magn. Mater., 2012, 324(13), 2147–2152 Search PubMed.
- L. C. Davis, J. Appl. Phys., 1999, 85(6), 3348–3351 Search PubMed.
- A. Fuchs, J. Sutrisno, F. Gordaninejad, M. B. Caglar and L. Yanming, J. Appl. Polym. Sci., 2010, 117(2), 934–942 Search PubMed.
- S. A. A. Aziz, S. A. Mazlan, N. I. N. Ismail, S. B. Choi, N. A. Nordin and N. Mohamad, Smart Mater. Struct., 2018, 27(11), 117002 Search PubMed.
- C. W. Lee, I. H. Kim and H. J. Jung, Shock Vib., 2018, 2018, 7434536 Search PubMed.
- C. W. Macosko, Rheology: Principles, Measurements, and Applications, Wiley-VCH, New York, 1994 Search PubMed.
- B. X. Ju, M. Yu, J. Fu, Q. Yang, X. Q. Liu and X. Zheng, Smart Mater. Struct., 2012, 21(3), 035001 Search PubMed.
- X. P. Do and S. B. Choi, Shock Vib., 2015, 915859 Search PubMed.
- M. Yu, M. Zhu, J. Fu, P. A. Yang and S. Qi, Smart Mater. Struct., 2015, 24(11), 115021 Search PubMed.
- R. Li and L. Z. Sun, Appl. Phys. Lett., 2011, 99(13), 131912 Search PubMed.
- I. Agirre-Olabide, M. J. Elejabarrieta and M. M. Bou-Ali, J. Intell. Mater. Syst. Struct., 2015, 26(14), 1880–1886 Search PubMed.
- J. Yang, X. Gong, H. Deng, L. Qin and S. Xuan, Smart Mater. Struct., 2012, 21(12), 125015 Search PubMed.
- J. M. Ginder, W. F. Schlotter and M. E. Nichols, in Proc. SPIE 4331, Smart structures and materials 2001: Damping and Isolation, ed. D. J. Inman, International Society for Optics and Photonics, 2001, pp. 103–110.
- M. Kallio, PhD thesis, VTT Technical Research Centre of Finland, Helsinki Univ. of Technology, 2005.
- B. Wei, X. Gong and W. Jiang, J. Appl. Polym. Sci., 2010, 116(2), 771–778 Search PubMed.
- Y. Li, J. Li, T. Tian and W. Li, Smart Mater. Struct., 2013, 22(9), 095020 Search PubMed.
- I. Agirre-Olabide and M. J. Elejabarrieta, J. Polym. Res., 2017, 24(9), 139 Search PubMed.
- M. Norouzi, S. M. Sajjadi Alehashem, H. Vatandoost, Y. Q. Ni and M. M. Shahmardan, J. Intell. Mater. Syst. Struct., 2016, 27(8), 1121–1135 Search PubMed.
- R. Li and L. Z. Sun, Acta Mech., 2014, 225(4–5), 1347–1359 Search PubMed.
- I. Agirre-Olabide and M. J. Elejabarrieta, Polym. Test., 2018, 66, 114–121 Search PubMed.
- I. Agirre-Olabide, J. Berasategui, M. J. Elejabarrieta and M. M. Bou-Ali, J. Intell. Mater. Syst. Struct., 2014, 25(16), 2074–2081 Search PubMed.
- T. F. Tian, X. Z. Zhang, W. H. Li, G. Alici and J. Ding, J. Phys.: Conf. Ser., 2013, 412(1), 012038 Search PubMed.
- A. R. Payne, J. Appl. Polym. Sci., 1962, 6(19), 57–63 Search PubMed.
- C. Bellan and G. Bossis, Int. J. Mod. Phys. B, 2002, 16(17–18), 2447–2453 Search PubMed.
- L. Bodelot, J. P. Voropaieff and T. Pössinger, Exp. Mech., 2018, 58(2), 207–221 Search PubMed.
- T. Pössinger, C. Bolzmacher, L. Bodelot and N. Triantafyllidis, Microsyst. Technol., 2014, 20(4–5), 803–814 Search PubMed.
- S. R. Khimi and K. L. Pickering, Composites, Part B, 2016, 90, 115–125 Search PubMed.
- R. Huang, L. Wang, Y. Lin, Y. Dong and D. You, Surf. Interface Anal., 2017, 49(2), 79–84 Search PubMed.
- R. Damiani and L. Z. Sun, Int. J. Damage Mech., 2017, 26(1), 104–118 Search PubMed.
- Y. C. Fan, X. L. Gong, W. Q. Jiang, W. Zhang, B. Wei and W. H. Li, Smart Mater. Struct., 2010, 19(5), 055015 Search PubMed.
- L. Ge, X. Gong, Y. Fan and S. Xuan, Smart Mater. Struct., 2013, 22(11), 115029 Search PubMed.
- S. H. Kwon, J. H. Lee and H. J. Choi, Materials, 2018, 11(6), 1040 Search PubMed.
- C. Wu, Q. Zhang, Y. Song and Q. Zheng, AIP Adv., 2017, 7(9), 095004 Search PubMed.
- G. E. Iacobescu, M. Balasoiu and I. Bica, J. Supercond. Novel Magn., 2013, 26(4), 785–792 Search PubMed.
- D. Günther, D. Y. Borin, S. Günther and S. Odenbach, Smart Mater. Struct., 2011, 21(1), 015005 Search PubMed.
- T. Borbáth, S. Günther, D. Y. Borin, T. Gundermann and S. Odenbach, Smart Mater. Struct., 2012, 21(10), 105018 Search PubMed.
- T. Gundermann, S. Günther, D. Borin and S. Odenbach, J. Phys.: Conf. Ser., 2013, 412(1), 012027 Search PubMed.
- T. Gundermann, P. Cremer, H. Löwen, A. M. Menzel and S. Odenbach, Smart Mater. Struct., 2017, 26(4), 045012 Search PubMed.
- D. Borin, D. Günther, C. Hintze, G. Heinrich and S. Odenbach, J. Magn. Magn. Mater., 2012, 324(21), 3452–3454 Search PubMed.
- M. Schümann and S. Odenbach, J. Magn. Magn. Mater., 2017, 441, 88–92 Search PubMed.
- J. Yao, Y. Sun, Y. Wang, Q. Fu, Z. Xiong and Y. Liu, Compos. Sci. Technol., 2018, 162, 170–179 Search PubMed.
- A. Stoll, M. Mayer, G. J. Monkman and M. Shamonin, J. Appl. Polym. Sci., 2014, 131(2), 39793 Search PubMed.
- E. Forster, M. Mayer, R. Rabindranath, H. Böse, G. Schlunck, G. J. Monkman and M. Shamonin, J. Appl. Polym. Sci., 2013, 128(4), 2508–2515 Search PubMed.
- T. Hu, S. Xuan, L. Ding and X. Gong, Mater. Des., 2018, 156, 528–537 Search PubMed.
- N. Prem, J. C. Vega, V. Böhm, D. Sindersberger, G. J. Monkman and K. Zimmermann, Macromol. Chem. Phys., 2018, 219(18), 1800222 Search PubMed.
- R. A. Landa, P. Soledad Antonel, M. M. Ruiz, O. E. Pérez, A. Butera, G. Jorge, C. L. P. Oliveira and R. M. Negri, J. Appl. Phys., 2013, 114(21), 213912 Search PubMed.
- O. Padalka, H. J. Song, N. M. Wereley, J. A. Filer II and R. C. Bell, IEEE Trans. Magn., 2010, 46(6), 2275–2277 Search PubMed.
- J. L. Mietta, G. Jorge and R. M. Negri, Smart Mater. Struct., 2014, 23(8), 085026 Search PubMed.
- D. Y. Borin and G. V. Stepanov, J. Intell. Mater. Syst. Struct., 2015, 26(14), 1893–1898 Search PubMed.
- W. H. Li and X. Z. Zhang, Smart Mater. Struct., 2010, 19(3), 035002 Search PubMed.
- B. Nayak, S. K. Dwivedy and K. S. Murthy, J. Intell. Mater. Syst. Struct., 2015, 26(7), 830–839 Search PubMed.
- S. H. Kwon, C. J. Lee, H. J. Choi, K. H. Chung and J. H. Jung, Smart Mater. Struct., 2019, 28(4), 045012 Search PubMed.
- M. K. Shabdin, M. A. A. Rahman, S. A. Mazlan, Ubaidillah, N. M. Hapipi, D. Adiputra, S. A. A. Aziz, I. Bahiuddin and S. B. Choi, Materials, 2019, 12(3), 391 Search PubMed.
- H. Lu, W. Wang, F. Yang, G. Wang and X. Rui, Mater. Res. Express, 2018, 5(9), 095703 Search PubMed.
- L. Fan, G. Wang, W. Wang, H. Lu, F. Yang and X. Rui, J. Mater. Sci., 2019, 54(2), 1326–1340 Search PubMed.
- D. Borin, G. Stepanov and E. Dohmen, Arch. Appl. Mech., 2019, 89(1), 105–117 Search PubMed.
- S. A. A. Aziz, S. A. Mazlan, N. N. Ismail, M. H. A. Khairi and N. A. Yunus, J. Phys.: Conf. Ser., 2017, 795(1), 012074 Search PubMed.
- S. A. A. Aziz, S. A. Mazlan, N. I. N. Ismail and S. B. Choi, J. Mater. Sci., 2018, 53(14), 10122–10134 Search PubMed.
- U. R. Poojary, S. Hegde and K. V. Gangadharan, J. Mater. Sci., 2018, 53(6), 4229–4241 Search PubMed.
- V. V. Sorokin, G. V. Stepanov, M. Shamonin, G. J. Monkman and E. Y. Kramarenko, Smart Mater. Struct., 2017, 26(3), 035019 Search PubMed.
- S. Aloui and M. Klüppel, Smart Mater. Struct., 2014, 24(2), 025016 Search PubMed.
- P. R. von Lockette, S. E. Lofland, J. H. Koo, J. Kadlowec and M. Dermond, Polym. Test., 2008, 27(8), 931–935 Search PubMed.
- P. Siegfried, J. H. Koo and M. Pechan, Polym. Test., 2014, 37, 6–11 Search PubMed.
- C. J. Lee, S. H. Kwon, H. J. Choi, K. H. Chung and J. H. Jung, Colloid Polym. Sci., 2018, 296(9), 1609–1613 Search PubMed.
- L. A. Makarova, Y. A. Alekhina and N. S. Perov, J. Magn. Magn. Mater., 2017, 440, 30–32 Search PubMed.
- Q. Wen, Y. Wang and X. Gong, Smart Mater. Struct., 2017, 26(7), 075012 Search PubMed.
- D. Gorman, N. Murphy, R. Ekins and S. Jerrams, Polym. Test., 2016, 51, 74–81 Search PubMed.
- G. Liao, X. Gong and S. Xuan, Mater. Lett., 2013, 106, 270–272 Search PubMed.
- T. Kikuchi, Y. Kobayashi, M. Kawai and T. Mitsumata, Int. J. Mol. Sci., 2018, 19(10), 3045 Search PubMed.
- V. V. Sorokin, I. A. Belyaeva, M. Shamonin and E. Y. Kramarenko, Phys. Rev. E, 2017, 95(6), 062501 Search PubMed.
- B. Sandesh, H. Sriharsha, U. R. Sathish and G. Nikhil, MATEC Web Conf., 2018, 144, 02015 Search PubMed.
- D. Y. Borin, G. V. Stepanov and S. Odenbach, J. Phys.: Conf. Ser., 2013, 412(1), 012040 Search PubMed.
- D. Borin, N. Kolsch, G. Stepanov and S. Odenbach, Rheol. Acta, 2018, 57(3), 217–227 Search PubMed.
- N. Ghafoorianfar, X. Wang and F. Gordaninejad, Smart Mater. Struct., 2014, 23(5), 055010 Search PubMed.
- Y. Han, W. Hong and L. E. Faidley, Int. J. Solids Struct., 2013, 50(14–15), 2281–2288 Search PubMed.
- S. S. Sun, Y. Chen, J. Yang, T. F. Tian, H. X. Deng, W. H. Li, H. Du and G. Alici, Smart Mater. Struct., 2014, 23(7), 075009 Search PubMed.
- S. Sun, H. Deng, J. Yang, W. Li, H. Du and G. Alici, J. Intell. Mater. Syst. Struct., 2015, 26(14), 1757–1763 Search PubMed.
- S. Suo, Z. Xu, W. Li and Y. Gan, J. Aerosp. Eng., 2018, 31(5), 04018046 Search PubMed.
- J. H. Koo, F. Khan, D. D. Jang and H. J. Jung, Smart Mater. Struct., 2010, 19(11), 117002 Search PubMed.
- P. Małecki, M. Krolewicz, J. Krzak, J. Kaleta and J. Pigłowski, J. Intell. Mater. Syst. Struct., 2015, 26(14), 1899–1905 Search PubMed.
- M. Norouzi, M. Gilani, S. S. Alehashem and H. Vatandoost, IEEE Trans. Magn., 2017, 53(9), 1–12 Search PubMed.
- F. Guo, C. B. Du and R. P. Li, Adv. Mech. Eng., 2014, 6, 629386 Search PubMed.
- S. Qi, M. Yu, J. Fu, P. D. Li and M. Zhu, Smart Mater. Struct., 2015, 25(1), 015020 Search PubMed.
- S. Qi, M. Yu, J. Fu and M. Zhu, J. Intell. Mater. Syst. Struct., 2018, 29(2), 205–213 Search PubMed.
- K. Danas, S. V. Kankanala and N. Triantafyllidis, J. Mech. Phys. Solids, 2012, 60(1), 120–138 Search PubMed.
- J. Feng, S. Xuan, T. Liu, L. Ge, L. Yan, H. Zhou and X. Gong, Smart Mater. Struct., 2015, 24(8), 085032 Search PubMed.
- Y. Wan, Y. Xiong and S. Zhang, Compos. Struct., 2018, 202, 768–773 Search PubMed.
- Y. Tao, X. Rui, F. Yang, G. Chen, L. Bian, W. Zhu and M. Wei, J. Intell. Mater. Syst. Struct., 2018, 29(7), 1418–1429 Search PubMed.
- D. Leng, T. Wu, G. Liu, X. Wang and L. Sun, J. Intell. Mater. Syst. Struct., 2018, 29(10), 2236–2248 Search PubMed.
- H. Vatandoost, M. Norouzi, S. M. S. Alehashem and S. K. Smoukov, Smart Mater. Struct., 2017, 26(6), 065011 Search PubMed.
- G. Schubert and P. Harrison, Smart Mater. Struct., 2016, 25(1), 015015 Search PubMed.
- G. Schubert and P. Harrison, J. Magn. Magn. Mater., 2016, 404, 205–214 Search PubMed.
- D. Leng, L. Sun, J. Sun, W. Chen, F. Ma, W. Li and Y. Lin, J. Phys.: Conf. Ser., 2013, 412(1), 012029 Search PubMed.
- L. Chen and S. Jerrams, J. Appl. Phys., 2011, 110(1), 013513 Search PubMed.
- A. M. Biller, O. V. Stolbov and Y. L. Raikher, J. Appl. Phys., 2014, 116(11), 114904 Search PubMed.
- A. M. Biller, O. V. Stolbov and Y. L. Raikher, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92(2), 023202 Search PubMed.
- M. V. Vaganov, D. Y. Borin, S. Odenbach and Y. L. Raikher, J. Magn. Magn. Mater., 2018, 459, 92–97 Search PubMed.
- A. M. Menzel, Arch. Appl. Mech., 2019, 89(1), 17–45 Search PubMed.
- G. Pessot, H. Löwen and A. M. Menzel, J. Chem. Phys., 2016, 145(10), 104904 Search PubMed.
- G. Pessot, M. Schümann, T. Gundermann, S. Odenbach, H. Löwen and A. M. Menzel, J. Phys.: Condens. Matter, 2018, 30(12), 125101 Search PubMed.
- W. Li, X. Zhang, T. Tian and W. Wen, AIP Conf. Proc., 2013, 1542(1), 129–132 Search PubMed.
- S. H. Kim, Y. J. Park, A. R. Cha, G. W. Kim, J. H. Bang, C. S. Lim and S. B. Choi, IOP Conf. Ser.: Mater. Sci. Eng., 2018, 333(1), 012013 Search PubMed.
- S. Lee, C. Yim, W. Kim and S. Jeon, ACS Appl. Mater. Interfaces, 2015, 7(35), 19853–19856 Search PubMed.
- V. V. Sorokin, B. O. Sokolov, G. V. Stepanov and E. Y. Kramarenko, J. Magn. Magn. Mater., 2018, 459, 268–271 Search PubMed.
- S. Chen, S. Dong, X. Wang and W. Li, Smart Mater. Struct., 2019, 28, 045016 Search PubMed.
- J. P. Déry, D. Brousseau, M. Rochette, E. F. Borra and A. M. Ritcey, J. Appl. Polym. Sci., 2017, 134(9), 44542 Search PubMed.
- D. Chen, A. Song, X. Hu, L. Fu and Q. Ouyang, IEEE Access, 2019, 7, 15125–15139 Search PubMed.
- M. Sedlačík, M. Mrlík, V. Babayan and V. Pavlínek, Compos. Struct., 2016, 135, 199–204 Search PubMed.
- M. Cvek, R. Moucka, M. Sedlačík, V. Babayan and V. Pavlínek, Smart Mater. Struct., 2017, 26(9), 095005 Search PubMed.
- L. R. Wang, M. Yu, P. A. Yang, S. Qi and J. Fu, Smart Mater. Struct., 2019, 28(4), 044001 Search PubMed.
- R. Moucka, M. Sedlačík and M. Cvek, Appl. Phys. Lett., 2018, 112(12), 122901 Search PubMed.
- H. Zhong, Y. Pei, Z. Hu, P. Zhang, J. Guo, X. Gong and Y. Zhao, Smart Mater. Struct., 2019, 28(2), 025027 Search PubMed.
- X. Zhu, Y. Meng and Y. Tian, Smart Mater. Struct., 2010, 19(11), 117001 Search PubMed.
- S. M. Hasheminejad and M. Shabanimotlagh, Smart Mater. Struct., 2010, 19(3), 035006 Search PubMed.
- A. R. Baev, E. V. Korobko and Z. A. Novikova, J. Intell. Mater. Syst. Struct., 2015, 26(14), 1913–1919 Search PubMed.
- R. Elhajjar, C. T. Law and A. Pegoretti, Prog. Mater. Sci., 2018, 97, 204–229 Search PubMed.
- S. Qi, H. Guo, J. Chen, J. Fu, C. Hu, M. Yu and Z. L. Wang, Nanoscale, 2018, 10(10), 4745–4752 Search PubMed.
- M. Behrooz and F. Gordaninejad, Smart Mater. Struct., 2016, 25(2), 025011 Search PubMed.
- S. Y. Tang, X. Zhang, S. Sun, D. Yuan, Q. Zhao, S. Yan, L. Deng, G. Yun, J. Zhang, S. Zhang and W. Li, Adv. Funct. Mater., 2018, 28(8), 1705484 Search PubMed.
- A. Ehsani and A. Nejat, Smart Mater. Struct., 2017, 26(5), 055036 Search PubMed.
- G. Diguet, E. Beaugnon and J. Y. Cavaillé, Smart Mater. Struct., 2012, 21(2), 025016 Search PubMed.
- X. Gong, G. Liao and S. Xuan, Appl. Phys. Lett., 2012, 100(21), 211909 Search PubMed.
- O. V. Stolbov, Y. L. Raikher and M. Balasoiu, Soft Matter, 2011, 7(18), 8484–8487 Search PubMed.
- R. Li, D. Ren, X. Wang, X. Chen, S. Chen and X. Wu, J. Intell. Mater. Syst. Struct., 2018, 29(2), 160–170 Search PubMed.
- C. Lian, K. H. Lee and C. H. Lee, Tribol. Int., 2016, 98, 292–298 Search PubMed.
- C. Lian, K. H. Lee, J. W. An and C. H. Lee, Friction, 2017, 5(4), 383–391 Search PubMed.
- E. Psarra, L. Bodelot and K. Danas, Soft Matter, 2017, 13(37), 6576–6584 Search PubMed.
- S. Wang, W. Jiang, W. Jiang, F. Ye, Y. Mao, S. Xuan and X. Gong, J. Mater. Chem. C, 2014, 2(34), 7133–7140 Search PubMed.
- H. An, S. J. Picken and E. Mendes, Polymer, 2012, 53(19), 4164–4170 Search PubMed.
- H. Pang, L. Pei, C. Sun and X. Gong, J. Rheol., 2018, 62(6), 1409–1418 Search PubMed.
- P. J. Rankin, A. T. Horvath and D. J. Klingenberg, Rheol. Acta, 1999, 38(5), 471–477 Search PubMed.
- B. O. Park, B. J. Park, M. J. Hato and H. J. Choi, Colloid Polym. Sci., 2011, 289(4), 381–386 Search PubMed.
- J. P. Rich, G. H. McKinley and P. S. Doyle, Langmuir, 2012, 28(8), 3683–3689 Search PubMed.
- H. Wang, Y. Li, G. Zhang and J. Wang, Smart Mater. Struct., 2019, 28(3), 035002 Search PubMed.
- J. Yang, H. Yan, J. Dai, Z. Hu and H. Zhang, J. Rheol., 2017, 61(3), 515–524 Search PubMed.
- J. Whiteley, F. Gordaninejad and X. Wang, J. Appl. Mech., 2010, 77(4), 041011 Search PubMed.
- P. Yang, M. Yu and J. Fu, J. Nanopart. Res., 2016, 18(3), 61 Search PubMed.
- M. Yu, H. Luo, J. Fu and P. Yang, J. Intell. Mater. Syst. Struct., 2018, 29(1), 24–31 Search PubMed.
- P. Yang, M. Yu, H. Luo, J. Fu, H. Qu and Y. Xie, Appl. Surf. Sci., 2017, 416, 772–780 Search PubMed.
- H. Zhang, H. Yan, Z. Hu, J. Yang and F. Niu, J. Magn. Magn. Mater., 2018, 451, 102–109 Search PubMed.
- S. Xuan, Y. Xu, T. Liu and X. Gong, Int. J. Smart Nano Mater., 2015, 6(2), 135–148 Search PubMed.
- T. Liu, X. Gong, Y. Xu, H. Pang and S. Xuan, Smart Mater. Struct., 2014, 23(10), 105028 Search PubMed.
- X. Gong, Y. Xu, S. Xuan, C. Guo, L. Zong and W. Jiang, J. Rheol., 2012, 56(6), 1375–1391 Search PubMed.
- T. Liu, Y. Xu, X. Gong, H. Pang and S. Xuan, AIP Adv., 2013, 3(8), 082122 Search PubMed.
- Y. Xu, X. Gong, T. Liu and S. Xuan, J. Rheol., 2014, 58(3), 659–679 Search PubMed.
- J. Xu, S. Xuan, H. Pang and X. Gong, Smart Mater. Struct., 2017, 26(3), 035044 Search PubMed.
- J. Xu, P. Wang, H. Pang, Y. Wang, J. Wu, S. Xuan and X. Gong, Compos. Sci. Technol., 2018, 159, 50–58 Search PubMed.
- B. X. Ju, M. Yu, J. Fu, Q. Yang, X. Q. Liu and X. Zheng, Smart Mater. Struct., 2012, 21(3), 035001 Search PubMed.
- T. Plachý, O. Kratina and M. Sedlačík, Compos. Struct., 2018, 192, 126–130 Search PubMed.
- J. D. Carlson and M. R. Jolly, Mechatronics, 2000, 10(4-5), 555–569 Search PubMed.
- S. S. Deshmukh and G. H. McKinley, Smart Mater. Struct., 2006, 16(1), 106 Search PubMed.
- T. G. Zielinski and M. Rak, J. Intell. Mater. Syst. Struct., 2010, 21(2), 125–131 Search PubMed.
- E. Dohmen, M. Boisly, D. Borin, M. Kästner, V. Ulbricht, M. Gude, W. Hufenbach, G. Heinrich and S. Odenbach, Adv. Eng. Mater., 2014, 16(10), 1270–1275 Search PubMed.
- L. Ge, S. Xuan, G. Liao, T. Yin and X. Gong, Smart Mater. Struct., 2015, 24(3), 037001 Search PubMed.
- J. Gan, X. He, G. Zhang, C. Zhou, Q. Zheng, C. Gao and H. Wang, IOP Conf. Ser.: Mater. Sci. Eng., 2017, 231(1), 012168 Search PubMed.
- D. Bodniewicz, J. Kaleta and D. Lewandowski, Compos. Struct., 2018, 189, 177–183 Search PubMed.
- S. K. Reddy, A. Mukherjee and A. Misra, Appl. Phys. Lett., 2014, 104(26), 261906 Search PubMed.
- X. Liu, X. Gao, H. Yu and D. Ye, IEEE Trans. Magn., 2015, 51(10), 1–5 Search PubMed.
- X. Yao, C. Liu, H. Liang, H. Qin, Q. Yu and C. Li, J. Magn. Magn. Mater., 2016, 403, 161–166 Search PubMed.
- D. York, X. Wang and F. Gordaninejad, J. Intell. Mater. Syst. Struct., 2007, 18, 1221–1225 Search PubMed.
- X. Wang and F. Gordaninejad, Smart Mater. Struct., 2009, 18, 095045 Search PubMed.
- A. K. Bastola, L. Li and M. Paudel, J. Mater. Sci., 2018, 53(9), 7004–7016 Search PubMed.
- A. K. Bastola, M. Paudel and L. Li, Polymer, 2018, 149, 213–228 Search PubMed.
- J. de Vicente and C. L. Berli, Rheol. Acta, 2013, 52(5), 467–483 Search PubMed.
- L. Shan, K. Chen, M. Zhou, X. Zhang, Y. Meng and Y. Tian, Smart Mater. Struct., 2015, 24(10), 105030 Search PubMed.
- N. Caterino, M. Spizzuoco and A. Occhiuzzi, Smart Mater. Struct., 2018, 27(6), 067001 Search PubMed.
- A. Fuchs, A. Rashid, Y. Liu, B. Kavlicoglu, H. Sahin and F. Gordaninejad, J. Appl. Polym. Sci., 2010, 115(6), 3348–3356 Search PubMed.
- M. McKee, F. Gordaninejad and X. Wang, J. Intell. Mater. Syst. Struct., 2018, 29(1), 41–51 Search PubMed.
- M. C. Heine, J. de Vicente and D. J. Klingenberg, Phys. Fluids, 2006, 18(2), 023301 Search PubMed.
- G. Cha, Y. S. Ju, L. A. Ahuré and N. M. Wereley, J. Appl. Phys., 2010, 107(9), 09B505 Search PubMed.
- I. de Vicente, A. Merino-Martos, L. Cruz-Pizarro and J. de Vicente, J. Hazard. Mater., 2010, 181, 375–381 Search PubMed.
- I. Singh, C. S. Lacko, Z. Zhao, C. E. Schmidt and C. Rinaldi, J. Colloid Interface Sci., 2020, 561, 647–658 Search PubMed.
- G. Peng, Y. Ge, J. Ding, C. Wang, G. G. Wallace and W. Li, Smart Mater. Struct., 2018, 27(3), 035022 Search PubMed.
Footnote |
| † An exception is the so-called negative MR effect reported by Sakuda et al.145 on elongated particles magnetized along the short axis. |
| This journal is © The Royal Society of Chemistry 2020 |