How heat controls fracture: the thermodynamics of creeping and avalanching cracks

Abstract

While of paramount importance in material science, the dynamics of cracks still lacks a complete physical explanation. The transition from their slow creep behavior to a fast propagation regime is a notable key, as it leads to full material failure if the size of a fast avalanche reaches that of the system. We here show that a simple thermodynamics approach can actually account for such complex crack dynamics, and in particular for the non-monotonic force–velocity curves commonly observed in mechanical tests on various materials. We consider a thermally activated failure process that is coupled with the production and the diffusion of heat at the fracture tip. In this framework, the rise in temperature only affects the sub-critical crack dynamics and not the mechanical properties of the material. We show that this description can quantitatively reproduce the rupture of two different polymeric materials (namely, the mode I opening of polymethylmethacrylate (PMMA) plates, and the peeling of pressure sensitive adhesive (PSA) tapes), from the very slow to the very fast fracturing regimes, over seven to nine decades of crack propagation velocities. In particular, the fastest regime is obtained with an increase of temperature of thousands of Kelvins, on the molecular scale around the crack tip. Although surprising, such an extreme temperature is actually consistent with different experimental observations that accompany the fast propagation of cracks, namely, fractoluminescence (i.e., the emission of visible light during rupture) and a complex morphology of post-mortem fracture surfaces, which could be due to the sublimation of bubbles.

---

1 Introduction

The rupture of solids is often described by empirical observations rather than by fully understood physical models. One of the earliest formalisms is that by Griffith in 1921:¹ the propagation of cracks is described as a threshold phenomenon, only obtained when loading their encompassing matrix above a critical fracture energy. To the first order, this view matches the behavior of brittle bodies, which suddenly snap passed a certain elastic deformation. Analytical models of cracks propagating in lattices suggested^2–5 that such an instability arises from the discrete nature of matter at the atomic scale. Indeed, these models revealed a minimum propagation velocity, comparable to that of the mechanical waves in the considered material, above which the advance of a fracture tip through the network of molecular bonds can be self maintained by the emission of high frequency phonons. There, the energy binding two lattice nodes is defined as a covalence-like barrier.⁶ While this description² does not allow for slow propagation, it is acknowledged that a crack loaded well below the fast rupture threshold is still growing, but at creeping rates that are orders of magnitude below that of a ‘dynamic’ fracture (e.g., ref. 7 and 8). An approach to explain such a creep in a way that is compatible with Griffith's formalism¹ is to consider that the fracture energy is not an intrinsic material property, but is instead a particular function of the propagation velocity (e.g., ref. 9). One hence simply obtains a lower crack speed if providing a lesser mechanical load. Alternatively, the creep regime is well modelled^7,8,10–16 by thermally activated sub-critical laws such as Arrhenius-like growth rates (e.g., ref. 17), and thermodynamics has thus emerged as a framework to describe the slow failure. In such descriptions, that are sometimes referred to as ‘stress corrosion’, a variation of fracture energy with velocity is not particularly called for, as the molecular agitation allows the crack to progress at loads below an intrinsic rupture threshold.

In practice, and depending on the material being broken, both the slow and the fast propagation regimes can be observed for a same range of applied loads.^18,19 A hysteresis holds and the growth rate of a fracture is then depending on the actual mechanical history, rather than only on the instantaneous mechanical load. Maugis and Barquins^20,21 early suggested that the description of the slow and the fast regimes, as well as that of the hysteresis, could be qualitatively unified by reinterpreting Griffith's criteria,¹ if one could account for the temperature and velocity dependent viscoplasticity that occurs around crack tips.^22,23 More specifically, Marshall et al.¹⁸ and then Carbone and Persson^24,25 proposed that the induced heat associated to such a plasticity might locally soften the matter around a crack and that some thermal weakening (i.e., the abrupt transition from slow creep to fast failure due to a thermal process) arises from the related reduction of the material elastic moduli.

In this work, we propose a quantitative unifying model of the two propagation regimes that disregards such a softening effect, hence stating that some variations in the material mechanical properties are not necessarily required to obtain a slow-to-fast-crack transition. We focus instead on how the thermal dissipation, and the subsequent rise in tip temperature, affect the front sub-critical growth, as understood by statistical physics and an Arrhenius-like law. In some previous works, we indeed studied how such sub-critical laws, at fixed room temperature, well describe creep; in fibrous and polymeric materials (namely, paper sheets and polymethylmethacrylate, PMMA), they notably account for the mean kinetics of slow rupture fronts under various loading conditions.^14,15,26 When, in addition, taking into account these media structure and heterogeneities in fracture energy, such sub-critical laws also reproduce the intermittent dynamics of failure; in particular, the size distribution of crack jumps¹³ and the front roughening properties.¹⁶ Here we neglect any spatial variation of the fracture energy, but let the crack tip temperature vary as a function of the front velocity and of the applied mechanical load. Indeed, in a previous experimental and theoretical study of the tearing-induced heating in paper sheets,²⁷ we were able to relate the temperature field around moving cracks to a certain percentage of the mechanical energy which gets converted into heat as the tip advances. More recently, this rise in temperature was fed back into a sub-critical growth law and showed²⁸ that one can thus obtain a dynamics model holding numerous qualitative similarities with the observed behavior of cracks, namely, two stable phases of propagation and a critical point that is similar to a brittle-ductile transition (e.g., ref. 29). Here, this model is first reintroduced (Section 2) and then shown to quantitatively capture the fracturing dynamics of two different polymeric materials, over the full range of velocities (Section 3), namely, acrylic glass (PMMA) and pressure sensitive adhesives (PSA). In both these media, some extensive experimental work has been carried out by different groups to quantify the two rupture regimes (e.g., see ref. 9, 30–35 for PMMA and ref. 19, 36–38 for PSA) and our proposed model accounts for the experimental curves of applied load versus crack velocity, from the slowest (micrometers per second) cracks to the fastest (hundreds of meters per second) ones. Such a match suggests that the growth of cracks could be sub-critical (i.e., as stated by the model) over a far wider velocity range than what is commonly accepted, that is, even at propagation velocities approaching that of mechanical waves. Indeed, we infer that the load threshold at which cracks typically shift to the fast phase is actually smaller than the intrinsic rupture energy, as a result from the boosted thermal activation around the front. In particular, we predict that crack tips can reach thousands of degrees on the molecular scale (i.e., over a few atoms around the front), when they quickly avalanche. Although such high temperatures are today rarely considered, they have long been proposed (e.g., Rice and Levy³⁹), and we here discuss (Section 4) how they are inline with several observables that sometimes accompany the fast propagation of cracks, namely, the emission of visible light at their tips (i.e., fractoluminescence^40–42) and the existence of bubbles on their postmortem surfaces, that can nucleate secondary rupture fronts.^43,44

2 From thermal creeping to thermal weakening

2.1 The kinetics of sub-critical rupture

We here consider a refinement of the propagation model already introduced by Vincent-Dospital et al.,²⁸ that did not compare it to any actual, experimental, crack propagation. Let us start by restating the various components of this model.

We consider the velocity V of cracks to be ruled by the competition, at their tips, between breaking and healing processes⁴⁵ (or see ref. 46, chpt. 5.5.1). As many authors before us (e.g., ref. 7, 8 and 46), we propose that these processes are, at least in part, sub-critical, and are governed by some Arrhenius-type laws (e.g., ref. 17 chpt. 1.8.1). The activation energies of these laws are thus exceeded by the thermal bath according to a probabilistic Boltzmann distribution.¹⁷ The rupture activation energy can then be written as (U_c − U): the difference between the mechanical energy U that is stored in the tip bond and a critical rupture energy U_c, at which this bond fails. The latter should typically be comparable to a few electronvolts, which is a standard value for atomic covalence (e.g., see appx. E in ref. 6). Of course, depending on the studied material, U_c could also be dominated by the typically weaker binding energies of hydrogen or van der Waals bonds, and its actual value may thus lie within a few orders of magnitude. In any case, as we are here introducing a mesoscopic law for the rupture dynamics (i.e., an Arrhenius growth), U_c should be understood as a mean material property, representative of the various strengths of the links that break along a crack course. Such a statistical definition will also apply to most of the parameters that we will henceforward consider. Similarly to the rupture barrier, the activation energy to heal the atomic connections can be written as (U_h + U). There, U_h is an intrinsic repulsive energy barrier that two atoms need overcome to bond, in addition to which the thermal bath at the healing link also needs to compensate for the applied stretch U of the tip. With these considerations, the propagation velocity of a crack is then modelled by

where the first term is the forward rupture velocity of the crack and the second one is the backward healing velocity. In this equation, we denote d₀ ∼ 2 Å the inter-atomic distance, k_B is Boltzmann's constant ∼1.38 × 10⁻²³ m² kg s⁻² K⁻¹, T is the absolute temperature at the crack tip and ν is the collision frequency in the molecular bath (e.g., ref. 17 chpt. 4.1). Each exponential in eqn (1) is a probability term (i.e., the probability, challenged every 1/ν second, that the thermal bath exceeds one of the activation energies and that the crack hence advances or retreats by a step d₀). As such, these terms cannot be greater than 1 and, while the healing one always meets this condition, U ≥ U_c corresponds to an over-critical propagation regime where

The product νd₀ is a maximal velocity, that we will further denote V₀, at which a fracture front can advance, when its tip atomic bonds snap each time they are challenged and never heal. In theory,¹⁷ the frequency ν is temperature dependent, with where m is the mass of an atom or a molecule, but this dependence is small compared to that of the neighbouring exponential terms, so that we here neglect it. In our context of rupture kinetics, and more practically, it was notably proposed^5,47 that such a nominal velocity V₀ is in the order of that of the medium Rayleigh waves, as quicker fractures then propagate in a specific supersonic regime,^48,49 which is not here considered. In our description, U is the physical quantity that describes the load of a crack on the microscopic level, and that governs most of its dynamics. However, at the lab scale, U is not a measurable quantity. The energetic level at which a crack progresses is rather characterized by the macroscopic energy release rate G, which is the amount of energy that a fracture dissipates to grow by a given unit of measurable area.¹ This energy dissipation may be of diverse nature, and is to cause a relative reduction in potential energy near the tip. We will denote N > 1 the factor for this reduction, so that U ∼ d₀²G/N. More commonly, mechanical shielding is described with the introduction of a plastic process zone of radius ξ around the crack front, where the dissipation occurs. To follow this canonical framework, we define a radius ξ that is relative to the length of an atom link, such that 2ξ/d₀ = N. The intensity of the mechanical shielding (i.e., the relation between the potential energy U stored in the rupturing bond and the macroscopic energy dissipation G) then writes as

By additionally introducing G_c = 2ξU_c/d₀³ and G_h = 2ξU_h/d₀³, the respective equivalents in the energy release rate framework of U_c and U_h, one can re-write eqn (1) and (2) as functions of G:We have here also written T as T₀ + ΔT, where T₀ is the absolute room temperature (∼296 K) and ΔT is any deviation from this background value, as we will proceed to propose that the tip temperature can vary. Eqn (4) differs from that of Vincent-Dospital et al.²⁸ by the introduction of the healing term and the consideration of the over-critical regime (G > G_c). These features are necessary to fit some experimental crack dynamics (as discussed in Section 3.1). The relation linking U and G (i.e., eqn (3)), although it was discussed by Vanel et al.,¹⁴ was also absent of this previous work.²⁸

Note finally that one could also write eqn (4) as a function of the mechanical stress σ that is applied at the crack tip, using 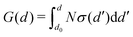, where d₀ is the nominal separation of atoms in an unloaded matrix (i.e., at G = 0) and d is the actual atom separation at the crack tip. Fig. 1 illustrates such a link between G and σ and summarizes, in a simplified atomistic view, how the thermal bath allows to overcome the surface energy barriers for breaking and healing atomic bonds, G_c − G and G_h + G, as per eqn (4).

Fig. 1 (left) Simplified atomic view of the breaking/healing site at the crack tip. (top right) Generic tip stress σ normalised by the stress shielding factor N versus atom separation for the active breaking link. (bottom right) Generic tip stress normalised by the stress shielding factor versus atom separation for the active healing link. The grey areas are the energy release rate G. At this load, d₁ and d₂ are the mean extensions of, respectively, the breaking and the healing link, while d₀ is the unstressed atom separation. On the breaking link graph: the area below the curve for d > d₀ is the intrinsic surface fracture energy G_c. The thermal agitation may overcome the remaining G_c − G barrier. Although the healing link is initially broken, an energy input is required to move the two particles closer to each other, due to the neighbouring unbroken links stretched at a load G. In addition, when the atoms separation gets smaller, the thermal agitation also needs to overcome a repulsive energy barrier G_h (the area below the atoms separation axis in this figure) before reforming the bond.

2.2 Heat dissipation and tip temperature rise

In the model we have introduced, one needs to further account for the energy which is dissipated around the running tip (G), as, even if it is mechanically lost, we will here show that it can maintain a strong effect on the crack dynamics. While the energy dissipation can be of several forms, ranging from the emission of mechanical waves⁵⁰ damped in the far field, to the nucleation of defaults in the matrix⁵¹ (i.e., crazing^9,52), we here focus on the release of heat around the fracture tip.^27,40 We thus call ϕ the percentage of G that is converted into some local rise in internal energy, and hence in temperature, and denote l the typical size over which this process occurs. As the heat, released on a production zone of area πl² close to the tip, is to diffuse in the whole bulk, the resulting temperature elevation ΔT can be modelled (e.g., ref. 27) by the standard diffusion equation:where λ is the medium's thermal conductivity, and C is the volumetric heat capacity. The last term of this equation is a source term only valid in the heat production zone. The support function f of this zone is 1 inside of it and 0 otherwise, and the thermal source term is proportional to ϕGV, that is the dissipated power per unit of crack length deposited in the advancing zone. Although governed by eqn (5), ΔT at the rupture front can approximate to far simpler expressions. It was indeed shown²⁷ that, at low propagation velocities, the temperature elevation at the centre of the heat production zone (i.e., the crack tip) is only governed by the diffusion skin depth upon the passage of the production zone of extension l within the time τ = l/V. For fast cracks however, when δ becomes smaller than l, the generated heat can barely diffuse out of its source zone and ΔT is then constrained by l. We thus haveFig. 2 shows the general evolution of ΔT at the tip with V, according to eqn (5) solved by numerically integrating the heat diffusion kernel.⁵³ Note that ΔT in eqn (5) is a temperature field as shown for instance in the inset of Fig. 3, but we are here mainly interested in its value at the centre of the heat production zone (i.e., where the rupture process occurs). Fig. 2 also shows how the two expressions of eqn (6) and (7) approximate for the tip temperature.

Fig. 2 Steady thermal elevation at a crack tip for various propagation velocities, due to the diffusion eqn (5) (plain plot). The approximations ΔT_fast and ΔT_slow, from eqn (6) and (7), are shown for comparison (dotted plots). The axes are not annotated for the sake of generality.

Fig. 3 Crack velocity V as a function of the energy release rate G as predicted by eqn (4) and (5) (plain curve) and fitted to the PMMA experimental data.³² The arrows indicate to which model parameters each part of the curve is mainly sensitive, and the main color scale specifies at which temperature the crack tip is modelled to be. The load G_a is an avalanche threshold beyond which a front can only propagate quickly and G_c is the modelled microscopic energy barrier for rupture. Below the asymptote at (G_c − G_h)/2, fronts cannot propagate forward due to some dominating healing processes. The inset shows, for a given point of the curve: V ∼ 100 m s⁻¹ and G ∼ 600 J m⁻², the associated modelled temperature field around the front. For readability, the color map is there different from the main one, and the circle corresponds to the tip of radius l, where the extra heat is emitted. ΔT of the main model curve is the value at the centre of the circle. At loads beyond G = G_c, micro-cracks begin to nucleate,³² as shown further in Fig. 4, which shows a zoom of the fast branch.

2.3 Model phase behavior

We have now derived the two constitutive equations of our fracture dynamics model: eqn (4), that gives the velocity of a crack as a function of its tip temperature, and eqn (5), that governs the thermal state around a progressing front. In a previous work,²⁸ we have simultaneously solved these two equations and, focusing on their steady state, showed that they predict two stable phases for the propagation of cracks. These two behaviors are shown by the plain curve in Fig. 3, and are there labelled ‘Slow stable phase’ and ‘Fast stable phase’. The first one, as its name suggests, is a slow one, where ΔT stays small compared to T₀, such that the growth rate is mainly governed by the medium fracture energy G_c (i.e., as indicated by eqn (4)). This slow branch ceases to exist beyond a particular load G = G_a. The second phase is reached when the generated heat (and hence ΔT) significantly overcomes the background temperature. From the Arrhenius law (4), the growth rate then significantly increases, so that the crack is said to be thermally weakened. Note, in Fig. 3, how both phases coexist for a certain range of energy release rates: a hysteresis situation holds (e.g., between G = 300 J m⁻² and G = G_a in Fig. 3). When this is the case, the model also predicts²⁸ a third phase, that is, by contrast, unstable and hence shall be difficult to be recorded experimentally.

3 Comparison to experimental results

Interestingly, this phase description in our model matches key observations of fracturing experiments. The abrupt transition, passed a load threshold, from slow cracks to fast cracks, can indeed be interpreted as a phase transition,²⁸ and the usual stick-slip of fronts is a good indicator that some hysteresis holds in the physical laws that rule the rupture dynamics.^21,28 We then proceed to test our model against two sets of experimental data, where both the energy release rate G and the velocity V of the slow creep and the fast propagation stages were well quantified, as we detail in the next section.

3.1 The rupture of PMMA

First, we look into a data set acquired when breaking polymethylmethacrylate plates (PMMA) at room temperature (T₀ = 296 K). A wedge is driven into Perspex® bodies, resulting in cracks for which two stable (G, V) branches are indeed recorded.³² These results are shown in Fig. 3. There, the fast branch, with propagation velocities above 100 m s⁻¹, was reported by Scheibert et al.,³² and the slow creeping branch is here published for the first time for this given PMMA (see the ESI† for details on how it is obtained). When forcing the rupture velocity between these two regimes (i.e., above a specific creep velocity of 4 cm s⁻¹ and below ∼100 m s⁻¹), some stick-slip is observed in the dynamics of the fronts, as reported by Hattali et al.⁵⁴

Fig. 3 then compares both experimental branches with our proposed model. We thus pursue by detailing how each parameter was fitted (i.e., how the model was calibrated to the data), based on asymptotic read-offs. We classically start by wondering how well the slow propagation phase is represented by an Arrhenius law of constant temperature. In the model, this corresponds to a linear ln(V) to G relationship that holds at low velocity, where ln is the natural logarithm. There, ΔT is negligible compared to the background T₀ and G is high enough for the healing terms of eqn (4) to be secondary (i.e., the terms involving G_h in this equation), leading to

In the data, this equation shall describe the portion of the plot lying between 10⁻⁴ and 10⁻² m s⁻¹, and the slope there, approximately 0.02 m² J⁻¹, hence constrains d₀³/(2ξk_BT₀) and so the equivalent length for the crack mechanical shielding ξ to be in the order of 50 nm. Additionally, the intercept of eqn (8) with the V axis (i.e., the second term in brackets) links V₀ and G_c. We earlier stated the former to be comparable to the medium Rayleigh velocity,³² 880 m s⁻¹ in this particular polymer, so that we can deduce the rupture threshold G_c to be about 1300 J m⁻². This value, together with that of ξ, gives a fracture energy U_c = G_cd₀³/(2ξ) comparable to 1 eV, which is satisfyingly consistent with a covalence-like barrier. Next, the healing threshold G_h can be inferred from the vertical asymptote at G = 300 J m⁻², below which healing seems to prevail as cracks do not propagate forward.⁴⁵Eqn (4) predicts this asymptote for G = (G_c − G_h)/2, when the healing term equals the breaking one, such that G_h ∼ 650 J m⁻². Let us now focus on the maximum G in the slow stable phase, denoted G_a (for ‘avalanche’) in Fig. 3, around V = 4 cm s⁻¹. It is modelled by eqn (4) once ΔT is high enough compared to T₀ to trigger a phase transition, which, as per eqn (6), mainly depends on the/ratio. By tuning this ratio, and appreciating the fit (see ESI†), we have deduced it to be around 0.9 J s⁻¹ m⁻¹ K⁻¹. As the PMMA conductivity, λ = 0.18 J s⁻¹ m⁻¹ K⁻¹, is known,⁵⁵ we can approximate ϕ ∼ 20%. Note that at this particular point (at G = G_a), the polymer suddenly breaks (e.g., ref. 20 and 56), as ∂V/∂G → +∞ and the velocity has to jump to the fast regime. Consequently, G_a is often seen as a macroscopic critical energy release rate, which in our description is less than the intrinsic microscopic energy barrier (i.e., G_a < G_c). This difference is here directly related to the thermal conductivity λ of the medium, and the avalanche to a fast rupture arises when the diffusion can no longer cope with the crack velocity, so that heat is no longer efficiently diffused away from the tip. The characteristic size l on which this heat is generated is the only parameter that remains to be determined. As, according to the model, the crack needs to be hot enough to explain some fast fronts at low mechanical load (i.e., the slower part of the fast branch in Fig. 3, around 100 m s⁻¹), we can estimate the limiting factor of ΔT_fast, Cl (see eqn (7)). Matching the data set in this area (see ESI†), and using⁵⁵C ∼ 1.5 × 10⁶ J K⁻¹ m⁻³, we have deduced l to be in the nanometer range. This magnitude happens to be in the same order as the earlier derived ξ. We thus predict that most of the induced molecular agitation is introduced on the closest atoms around the crack tip, which coincides with the length scale for the energetic shielding of the tip. Noteworthily, such a nanometer scale appears to be close to the typical entanglement scale of polymers⁵⁷ (i.e., the density of polymeric chains crossing points in the matrix).

To quantify how well the model accounts for the experimental data, we computed, for each data point, the relative orthogonal distance ε_d to the model, that is

where the subscript d stands for ‘data’ and m for ‘model’. We are thus looking at a relative fit mismatch along the G axis and a relative fit mismatch, in order of magnitude, along the V axis. For any particular measurement point below G = G_c, ε_d is at most 16%. An average error for the whole fit, [small epsilon, Greek, macron] = mean_d(ε_d), can also be inferred. To do so, we first have regularly under-sampled the experimental data onto 40 J m⁻² wide bins, keeping there only the mean G_d and the mean log₁₀(V_d). This way, and doing so separately for the two propagation branches (see ESI†), no bias is introduced on [small epsilon, Greek, macron] by the strong difference in measure density along the experimental (V_d, G_d) curve (i.e., see Fig. 3). The thus derived overall fit error computes to [small epsilon, Greek, macron] = 4%, below G = G_c. We discuss, in the next section, the fit beyond G_c and further discuss the accuracy of the inverted parameters in the ESI.†

3.2 On the fast crack velocity in PMMA

Our simple sub-critical model hence matches most of the rupture dynamics of PMMA, from slow to fast velocities. In Fig. 3 however, an increase in velocity holds in the experimental data beyond G = G_c, and is not properly accounted for. To highlight this mismatch, we display in Fig. 4 the fast branch with an optimised display scale. It has been shown³³ that, beyond a particular load, the global front velocity is impacted by the fracture instabilities that occur at high speed. Indeed, passed this threshold, fronts get more complex as micro-cracking occurs,^32,43,44 that is, as micro-cracks form and propagate in the fracture plane ahead of the main front. Such micro-cracks are shown in Fig. 4. And, at an even higher load, micro-branching also comes into play, and aborted out-of-plane secondary cracks are observed.^31,58–60 For the PMMA that is here studied, the micro-cracks were observed³² at velocities above 165 m s⁻¹, which approximately corresponds in the model to G > G_c. Beyond this threshold, the apparent macroscopic speed of the front, V, increases with the micro-cracks growing density, while the individual velocity of each micro-front, however, was inferred to stay constant,³³ around V_micro ∼ 200 ms⁻¹, as illustrated in Fig. 4.

Fig. 4 Zoom on the PMMA fast propagation branch presented in Fig. 3, and as per eqn (4) and (5). Beyond a load comparable to the modelled G_c threshold, some micro-cracks start to nucleate, impacting the overall propagation velocity as explained by Guerra et al.³³ The individual velocity of each micro-crack stays however constant at V = V_micro. The validity of our single front model is limited passed this point, although it does predict a velocity plateau V_lim, as per eqn (10), and a velocity maximum V_max, which are comparable to V_micro. Inset (a): Fractography of the secondary micro-cracks on a postmortem fracture surface. White areas mark their nucleation centres. Inset (b): Atomic force microscopy of a nucleating cavity at the centre of a micro-crack. As proposed in Section 4.4, it could derive from the sublimation of localised bubbles around the main front, due to some intense thermal effects.

Such a plateau in the propagation speed is somewhat consistent with our description (see Fig. 4). But this being said, it is clear that our unique front model shows limitations as soon as fronts complexify. We can still push this discussion on the fast regime a bit further. A question of interest about the rupture of PMMA has been why the maximal observed crack velocity was significantly lower than the theoretical Rayleigh speed³² (i.e., about 200 m s⁻¹ rather than 880 m s⁻¹). Eqn (4) gives here some insight, as it does predict a plateau velocity V_lim as the applied G gets very large. Indeed, besides preventing the crack advance at very low loads, the sub-critical healing processes significantly limit the fast growth rate, as the tip temperature is modelled to be high. More specifically, by inserting ΔT_fast (7) in eqn (4), and by looking at the high loads asymptotic regime of the healing term, we predict V to be limited by c₀ = d₀³C, the individual heat capacity of atom bounds:

In this expression, the crossed out terms are neglected in regard to the neighbouring ones. Note however that eqn (10) is mainly illustrative, as the plateau it describes occurs in a domain where our single front model does not strictly apply. Note also that the value V_lim ∼ 100 m s⁻¹ is smaller than the modelled maximum individual propagation velocity V_max ∼ 160 m s⁻¹, which is obtained for G = G_c rather than for G → +∞ (see Fig. 4).

3.3 The detachment of pressure sensitive adhesives

We now pursue the comparison with the reported rupture of another material, acrylic based pressure sensitive adhesives (PSA), that typically happens when unrolling some office tape. In particular, the peeling dynamics of Scotch® 3M 600 rolls (composed of a polyolefin rigid backing coated with a layer of synthetic acrylic adhesive) has been thoroughly studied in the last decades (e.g., ref. 19, 37 and 61); we here fit our model to two compatible (G, V) data sets that were published by Dalbe et al.³⁷ and by Barquins and Ciccotti.¹⁹ These data sets are shown in Fig. 5. Two stable modes of front detachment (i.e., a fast one and a slow one) are reported,¹⁹ similarly to those governing the rupture in PMMA. Additionally, some (unstable) stick-slip in the rupture dynamics is also observed³⁷ when peeling with an average velocity between V ∼ 15 cm s⁻¹ and V ∼ 20 m s⁻¹.

Fig. 5 Crack velocity V as a function of the energy release rate G as predicted by eqn (4) and (5) (plain curve) and fitted to the tape experimental data.^19,37 The unstable branch was not actually measured and the data points there are only averaged V versus G for a crack that undergoes stick-slip, in the given set-up, between the slow and the fast phase. The arrows indicate to which model parameters each part of the curve is mainly sensitive, and the main color scale specifies at which temperature the crack tip is modelled to be. The load G_a is an avalanche threshold beyond which peeling fronts can only propagate quickly and G_c is the modelled microscopic energy barrier for rupture. The inset shows the associated modelled temperature field around the front, at the onset of the fast to slow phase shift (G = 50 J m⁻², V = 20 m s⁻¹). For readability, the color map is there different from the main one, and the circle corresponds to the tip of radius l, where the extra heat is emitted. ΔT of the main model curve is the value at the centre of the circle.

Overlaying this experimental data, Fig. 5 also displays a calibrated version of our model. The model parameters were inverted as follows, with a similar asymptotic analysis as what was done for PMMA. As no significant healing threshold displays at low velocity, we have only assumed that G_h is high enough to completely neglect the healing processes (i.e., the healing term in eqn (4) is small if G_h is high). Of course, this absence of threshold, below which no forward propagation of the crack is observed, could also only indicate that (G_c − G_h)/2 < 0 or that this value (i.e., illustrated on the PMMA data in Fig. 3) is less than the minimum energy release rate that was investigated in the tape experiments. We discuss this particular point further in the ESI.† We now invert the length ξ, which is, again, given by the slope of the slow phase and is here about 10 nm. As no healing is now supposed to be at play, the nominal velocity V₀ is given by the highest velocity records: V₀ ∼ 30 m s⁻¹ as V₀ is the maximum value then predicted by eqn (4). Satisfyingly, this value compares well with the magnitude of a mechanical wave velocity in PSA, that is, , where μ is, for instance, the shear modulus of the adhesive,⁶² 0.1 to 1 MPa, and ρ is its volumetric mass,⁶³ about 10³ kg m⁻³. Next, from eqn (8), the intercept of the slow branch with the ordinate (zero G) axis indicates G_c ∼ 150 J m⁻². Rather logically, and with the inverted value of ξ, this again corresponds to a value of fracture energy U_c ∼ 1 eV. Note also that G_c is again higher than the transition load G_a at which a creeping front jumps to a fast regime. From this transition load, arising in the model from the temperature rise at low velocity (6), we also infer λ/ϕ to be in the order of 0.1 J s⁻¹ m⁻¹ K⁻¹. As the adhesive's conductivity λ lies in the same range,⁶⁴ a consequent portion of G should be released into heat: ϕ ∼ 1. Of course, ϕ cannot be exactly one, as other dissipating processes than heat diffusion are likely to dissipate a part of G (see the Discussion in Section 4). According to our inversion however, this part ought to be small. Finally, by varying l and by matching the coolest points of the fast phase, we estimate this parameter, which limits the highest tip temperature (i.e., eqn (7)), to be in the nanometer range. This value, for the length scale of the heat production zone, is again rather consistent with the inverted magnitude of ξ, that is, the equivalent length scale for the mechanical shielding of the tip. Note also that both ξ and l are interestingly comparable to what was obtained for PMMA, and in the order of a polymeric entanglement density.⁵⁷

As shown in Fig. 5 and with this set of parameters, the model accounts for most of the tape peeling dynamics. More quantitatively, for all the particular data points of the two stable phases, the fit error ε_d (as defined by eqn (9)) is less than 20%. We also computed a mean fit error [small epsilon, Greek, macron] = mean_d(ε_d) for the stable phases. To do so, and as done for PMMA, we first averaged the data points onto 10 J m⁻² wide bins, so that no densely populated part of the measured curve dominate the value of [small epsilon, Greek, macron] (see the ESI†). We thus computed [small epsilon, Greek, macron] = 5%.

Note that, in comparison to the fast branch for the failure of PMMA (i.e., as discussed in Section 3.2), it would be of interest to know if the critical load G = G_c also approximately corresponds to the apparition of some new rupture modes. Yet, the high velocity branch of the tape data is bound to relatively large uncertainties (the loading system of Barquins and Ciccotti¹⁹ involved dropping weights from an elevated balcony, illustrating the challenges in fast peeling measurements), so that it does not allow a more thorough analysis.

3.4 Parameter summary

In Table 1, we summarises all the parameters values, that we have inverted or supposed for the rupture of PMMA and PSA. The accuracy of these values is further discussed in the ESI.†

Table 1 Summary of all model parameters considered for the rupture of PMMA and PSA, as discussed in Section 3. A value d₀ ∼ 2 Å has been assumed in the derivation of these parameters. For completeness, the related quantities G_c/G_a = U_c/U_a, U_c = G_cd₀³/(2ξ) and the shielding factor N = 2ξ/d₀ are also specified

Parameter	PMMA	PSA	Unit
V 0	880	30	m s^−1
G c	1300	150	J m^−2
G h	650	—	J m^−2
ξ	50	10	nm
l	1	1	nm
ϕ	0.2	∼1	[−]
λ	0.1	0.18	J s^−1 m^−1 K^−1
C	1.5	1	MJ m^−3 K^−1
G c/Ga	1.8	1.6	[−]
U c	1	1	eV
N	500	100	[−]

---

4 Discussions

For two different polymeric materials, we thus have shown how a thermally activated fracture process, coupled with the dissipation and diffusion of heat, can simply explain many features of the dynamics of both creeping and fast cracks, and the shifts from one state to the other. Such novel match, over seven to nine decades of propagation velocities and with only very simple physics considerations, could shade some new light on fracture mechanics, as thermal effects are often discarded.

4.1 How hot is too hot for a crack tip? Some light from fractoluminescence

To explain the fast propagation branch, we have notably predicted the front temperature to reach several thousands of degrees. Such high values are difficult to confirm experimentally, especially as they are to stand only on a few nanometers during short avalanches. There exist however, indirect hints toward the existence of an important temperature elevation in a variety of brittle materials fracturing at high speed.

For instance, the analysis of some fracture roughness in cleaved quasi-crystals has revealed a damage zone of size anomalously large for this class of materials, and this was stated to result from a local temperature elevation of about 500 K at the moving crack tip.⁶⁵

Several experimental works in glass and quartz^40–42 also managed to indirectly measure ΔT to indeed reach thousands of degrees, by characterising the photons emission from the tips of some moving cracks and by comparing it to the blackbody radiation theory.⁶⁶ In the case of tape, when peeling fast enough to be in the stick-slip regime, a blue tribo-radiation can similarly be observed,^19,67 and it was established that this radiation only occurs during the fast propagation phases of the cycle.¹⁹ A direct example of such an emission is shown in Fig. 6, and its color could well correspond to the central wavelength λ_peak associated, via Wien's law,⁶⁶ with a blackbody temperature compatible with our model:

where b is Wien's displacement constant ∼0.0029 m K and ΔT is about 7000 K at a load just passed the stick-slip threshold G = 90 J m⁻² (see Fig. 5). The intensity of the observed light, which is visible in the dark but not under normal lightening, seems to also be consistent with the model. According to the Stefan–Boltzmann law,⁶⁶ we indeed expect a radiated power in the order of

P = s(T₀ + ΔT)⁴hl ∼ 1 mW, (12)

where s ∼ 5.67 × 10⁻⁸ W m⁻² K⁻⁴ is the Stefan–Boltzmann constant, and h the tape width (2 cm) so that hl is the total area that significantly emits light. Note that such a power only accounts for a negligible part of the energy that is dissipated as the front advances, as P/(GVh) ∼ 10⁻⁴. For a human eye at a distance D ∼ 10 cm, it corresponds to a light luminance of about eP/(4πD²) ∼ 1 cd m⁻², using a blackbody luminous efficacy⁶⁸e of 100 lumens per watt. With a pupil opening of about 10 mm², such a luminance is in the order of 10 trolands (Td),⁶⁹ which does fit that of a flickering (i.e., the front has a stick-slip motion) radiation that is only visible in the dark, as those approximately range between 0.01 and 100 Td.⁶⁹ While the eye is persistent, a camera sensor of size S ∼ 10 mm², placed at the same distance, would capture an averaged power γPS/(4πD²) ∼ 100 nW, where γ ∼ 0.1 is a typical ratio of time during which the front is in the fast phase compared to the total recording time, when peeling at a slow average velocity (i.e., ∼15 cm s⁻¹).³⁷ The magnitude of this power is interestingly close to the 10 nW that were successfully measured by Camara et al.⁶⁷ for the luminescence of another adhesive roll. For a given PMMA, Fuller et al.⁷⁰ also tried to quantify the temperature elevation around a quick fracture, both with the thermoluminescence technique and by using a liquid crystal coating on the matrix, whose color was thermosensitive.⁷¹ For cracks propagating at 400 m s⁻¹ and faster, they measured heat efficiencies of about 2000 J m⁻², which is fairly compatible with the value we have derived for ϕG (a 400 m s⁻¹ speed is obtained for G > 4000 J m⁻² in Fig. 3 and ϕ was inferred to be about 0.2). This experimental work⁷⁰ also estimated the instantaneous temperature elevation of the fractures to be about 500 K over a 0.5 mm-thick area around the front. Such a thickness for the heat source was however acknowledged to be rather uncertain, as the measure sensibility for this parameter was limited. We remark that the same energy spread on the l ∼ 10 nm thickness which we have here inferred would give a temperature rise of 10⁴ K and more, as predicted by our model (see Fig. 3).

Fig. 6 Blue radiation emitted when quickly peeling tape beyond the stick-slip threshold (i.e., at an average velocity greater than 15 cm s⁻¹, see Fig. 5). This picture was captured in the dark by a standard reflex camera (ISO: 25600, shutter speed: 1/2 s, focal length: 60 mm, aperture: f/4). The low shutter speed ensures that enough light enters the camera, but then covers many stick-slip cycles of the peeling dynamics.³⁷ Such fractoluminescence could be the mark of a very hot crack front^40–42 when unrolling tape.

Truly, fractoluminescence could emanate from other mechanisms than some hot matter radiation. It was for instance proposed^67,72 that it partly arises from the molecules excitation of the fracture in situ air, by some electrical discharges between the two crack planes. Both these phenomena could surely coincide and, in any case, the light emission is an indication that some extreme and localised phenomena are at stake during fast failure. In that way, the thermodynamics model we propose holds some compatibility with that of Slepyan,² where the abrupt advance of cracks derives from the emission of high frequency phonons, that excite atom bonds ahead of the tip, but that do not necessary thermalize.

Some relatively recent atomistic simulations⁷³ seem nonetheless to confirm that the atoms at a moving front can undergo a significant heat. In a modelled graphene, Budarapu et al.⁷³ thus inferred a 200 K temperature rise, over a 43 nm × 43 nm area surrounding a running tip. This estimation is interestingly compatible with the thermal maps presented in Fig. 3 and 5, for which the mean temperature is respectively 950 K and 350 K, when recomputed on a similar 1800 nm² surface upon the front. Note that atomistic simulations might naturally be more proper than our mesoscopic description, in particular because the small scales (l) and high excitation frequencies (V/l) at play could call for more complicated models^74,75 than plain Fourier diffusion, Arrhenius growth or blackbody radiation. Yet, atomistic simulations are by nature far heavier to run, requiring an accurate description of the atomic interactions onto femtosecond time steps.

4.2 Is a simple model too simple?

It is actually surprising that the proposed simple mesoscopic model can describe the propagation of cracks, when such a propagation, in reality, displays many complex phenomena. For instance, we have completely neglected the impact of crazing on the crack dynamics,^36,52 that is, the formation of defaults and fibrils at relatively large scales around the fracture front (i.e., a hundred of micrometers in PMMA and up to millimeters in PSA), while such large scale plasticity is often considered to have a strong effect on the growth of cracks (e.g., ref. 36 and 52). Yet, crazing is not incompatible with our thermal weakening model, which only states that a significant part of the mechanical energy should be dissipated far closer to the crack front (i.e., over a few nanometers), and that this very local dissipation should be that of a first effect on the crack dynamics. In this description, crazing is then a consequence of the front progression rather than its main cause. In a similar way, many other known failure phenomena, such as the emission of mechanical waves during rupture,⁵⁰ complicated creep laws from the corrosive interactions between the fracture fluid and the fracture tip (e.g., ref. 46 chpt. 5.4), or the complexification of fronts at high propagation velocities,⁴⁴ are not directly encompassed by eqn (4) and (5), but are not in conflict with the model either.

The simplicity of the model can actually be considered as one of its strength, as the physics that it describes could apply to many different materials and not only to polymers. Accurately testing this idea would however require the full (G, V) curves of more materials, and those are often not trivial to obtain experimentally at all velocities. Such experimental work could yet be rewarding, as we have here shown that matching the model to some (G, V) curves can give some valuable insights on the rupture of matter. Our quantification for each model parameter stays however rather approximate, and we have mainly derived their orders of magnitude. We have, in particular, assumed that they were all constant for a given material, while most could be velocity or temperature dependent.^18,24,76 For instance, the fact that PSA exhibits a larger scale viscous behavior (i.e., including fibrillation and heating over millimeters around the tip) at lower velocity³⁶ could indicate that the heat production size l decreases with the crack speed in this medium. It is especially known that the elastic moduli in PSA are strongly temperature dependent,⁶² and this was actually proposed by Maugis²¹ and Carbone and Persson²⁴ as the driving cause for failure instability in rubber-like materials. We have, besides, considered both PMMA and PSA as homogeneously tough while G_c is bound to present some quenched disorder. While such heterogeneities should not affect the stable propagation branches, as long as G and V are then understood quantities which are averaged over a few G_c correlation lengths, it could be of importance for the accuracy of the loads at which the phase transitions occur,²⁸ as slow cracks shall preferentially avalanche on weaker zones and fast cracks stop on stronger locations. In the case of PSA, we have furthermore considered that peeling was a cohesive process (i.e., that it occurs inside the adhesive), while a bi-materials interfacial model would be more appropriate, as the crack essentially propagates at the interface between the substrate and the glue.⁷⁷

These numerous limitations being stated, the parameters we have inverted are nonetheless in rather satisfying orders of magnitude, confirming the physical relevance of the model. Indeed, the intrinsic fracture energy in both materials U_c = d₀³G_c/(2ξ) is comparable to one electronvolt, which is typical for an energy that bonds atoms (e.g., see appx. E in ref. 6). Because our proposed description is statistical, one should remember that U_c is a mean material feature, for a rupture process that is made of several types of bond breaking. As a rough example, U_c ∼ 1 eV may indicate that the crack consummates in average three weak links (such as hydrogen or van der Waals bonds of respective energies⁶ ∼0.1 and ∼0.01 eV) for every stronger connection that snaps (say, one C–C link of an acrylic chain, of covalence energy⁶ ∼4 eV). The nanometric scale l for the heat generation may well correspond to the typical entanglement density in polymers⁵⁷ (the density of polymeric chains crossing points in the matrix), below which atoms have more freedom to vibrate, and which is known to affect some rupture properties (e.g., ref. 52 and 57). It is also coherent that the generation of heat was inferred to occur over a length scale comparable to ξ, the equivalent radius describing the energy shielding of the tip. We have indeed derived that the former is a strong cause for the latter, as the heat efficiency ϕ was inverted to be non negligible (i.e., ϕ ∼ 0.2–1).

4.3 Tip stress and front shielding

A nanometric scale (i.e., comparable to ξ or l) has been noteworthily observed in the rupture of other materials. One example is the length scale of a light radiating (and hence likely thermal) zone around running fracture tips in glass.⁴² In carbonate rocks, it is also the typical size of some observed nanograins that form along sliding seismic fault planes.⁷⁸ Such a nano-damage explains the glossy and reflective aspect displayed by some faults (often referred to as fault mirrors), as their typical surface roughness is then comparable to the wavelengths of visible light. The origin of this damage, however, is debated as, below 1 μm, plasticity is expected to dominate over brittleness in this material and asperities should hence deform rather than break. Noteworthily, some intense thermal effects, arising from the frictional heat, such as some fast melting and cooling or the thermal decomposition of carbonates, were proposed to solve this apparent paradox.⁷⁹

Similarly, for the materials that we have here studied, the usual predictions for the size of the shielding process zones are far larger than ξ. In PMMA, for instance, it is in the order of ξ_macro ∼ GE/σ_y²∼ 200 μm, where σ_y ∼ 100 MPa is the tensile yield stress of the bulk polymer and E ∼ 3 GPa its Young modulus.⁵⁵ However, in that description, σ_y is a stress that is averaged over a macroscopic sample, and is likely not representative of the actual energy density around the defaults of this sample. It was notably reported that a Dugdale⁸⁰ like cohesion model (i.e., σ is homogeneously equal to σ_y in a process zone of radius ξ_macro), poorly accounts for fast rupture in PMMA.⁸¹ Naturally, ξ_macro is still to bear some significance, in particular as a characteristic length scale for crazing in acrylic glass,⁵² where a portion within (1 − ϕ) of the release rate G is to be dissipated, either by the creation of dislocations,⁵¹ the emission of waves^42,50 or residual thermal effects. But ξ was inverted as an equivalent size, only defined by 2ξ/d₀ = N with N the damping of the tip potential energy U due to the energy dissipation. We solely inverted N to be around 100 and 500 for respectively PSA and PMMA, and many links might well snap and heal far away from the tip, allowing for crazing.

Still, most of the rupture is likely to occur very close to the front where the stress is to be the highest. We can estimate such a stress at the tip by considering a simplified expression for the elastic energy stored in rupturing bonds:

which, with eqn (3), is equivalent to the well known form for the limitation of an otherwise divergent stress at the tip of cracks, predicted by the general elasticity theory (e.g., ref. 46):In the case of PMMA, such a computed stress is as high as 7 GPa, and we thus predict a high atomic strain σ/E of about 200% at the onset to fast rupture (i.e., for U equal to U_c/1.8 as per Table 1). Such a strain shall be likely at a fracture tip for the strong intermolecular deformation immediately before failure. Of course, the simply linear elastic eqn (13) is unlikely to be valid at 200% strain, and we also considered describing U with a Morse potential,⁸² that iswhich, at the onset of fast rupture, predicts a strain (d − d₀)/d₀ ∼ 400%. While this dual-particles potential stays, by nature, a strong approximation in the complex rupture of a polymer, it is worth reminding that the model which we have introduced does not rely on a particular shape of the inter-atomic potentials (i.e., neither on eqn (13) or on eqn (15)), but only on their average dissociation energy U_c.

4.4 Front complexification

Overall, our derivation of ξ ≪ ξ_macro only suggests that process zones are heterogeneous objects, dissipating a higher density of energy in their centre than at their periphery. In particular, it was shown that a few tens of micrometers (i.e., a portion of ξ_macro) is a typical distance at which the secondary micro-cracks nucleate from the main front in PMMA³³ and, as shown in Fig. 4, the imaging of some postmortem rupture surfaces reveals that these micro-cracks initially grow from isolated spherical cavities at their centre, of radius about 300 nm. We here propose that such cavities could correspond to bubbles, forming by sublimation⁸³ on weak locations of the process zone, and leading to some micro-fractures once having grown to a critical size. While remaining to be confirmed, such a sublimation process would definitely require some local but very high temperatures in the crazing area. Indeed, to nucleate ahead of the main front, the observed cavities have to form during less than ξ_macro/V ∼ 1 s, and the pyrolysis of PMMA to methyl methacrylate (MMA) only reaches such a reaction rate at temperatures T_b that are beyond 1000 Kelvins.⁸³ In return, and assuming that the ideal gas law approximately applies (e.g., ref. 17 chpt. 4), some bubbles forming at this temperature would hold an internal pressure ρRT_b/M, where M = 0.1 kg mol⁻¹ is the MMA molecular mass,⁸⁴ρ = 1200 kg m⁻³ is the volumetric mass of the solid PMMA⁵⁵ and R is the ideal gas constant. This value computes to at least 100 MPa, which is comparable to the surrounding bulk compressive strength.⁵⁵ The evolution from pressurised pores to propagating micro-cracks would then be coherent.

Thus, in addition to explaining, as shown in this work, the first order dynamics of singular fronts, concentrated thermal processes could also be responsible for their complexification at high propagation velocities. In the case of acrylic glass, we have notably inferred (see Section 3.2) that the appearance of the secondary fronts approximately coincides with energy release rates that are close to the (modelled) intrinsic barrier G_c. This concomitance could be explained by the need for new dissipation processes, when cracks propagate over-critically (G > G_c) so that some extra energy is brought to the rupture system. Such an idea is notably re-enforced by the fact that the density of nucleated micro-cracks was inferred to be proportional to a value comparable to G − G_c, as shown by Guerra et al.³³

5 Conclusion and perspectives

We presented a new and general model for the kinetics of cracks. The main physical elements that were introduced in this model are, only, a sub-critical (Arrhenius-like) growth rate and the dissipation and diffusion of heat around fracture tips (where the applied mechanical stress is concentrated), an immediate consequence of the latter being the possibility for crack fronts to reach thousands of degrees temperatures. Interestingly, these different elements have, separately, long been considered or observed in the physics of rupture (e.g., ref. 7, 18, 39 and 85), but had not previously been combined for comparison with some experimental data. In doing so, we here showed that the rupture of two materials (namely, PMMA and PSA) can be quantitatively reproduced over many decades of propagation velocities, from slow creep regime to fast propagation.

Thus, we inferred that the propagation of a crack can be sub-critical, even at velocities approaching that of the mechanical waves in the surrounding matrix, due to its potentially very high tip temperature. We also suggested that the microscopic healing process around a fracture front can significantly constrain the fast velocity regime, from the strong thermal activation at such temperatures, while it is often considered that healing is only relevant for very slow cracks. The existence of thousands of degree temperatures is actually supported by many experimental works that study the visible fractoluminescence of fast fronts.^40–42,70 In some instance,⁷³ it has also been modelled by some atomistic simulations, and we additionally showed, in the present work, the existence of bubble forming in the process zones of cracks in PMMA. We proposed that these bubbles could well originate from some local sublimation of the polymer near crack tips. As they are located at the nucleation centres of secondary fracture fronts, we also suggested that the complexification of cracks at high velocities could derive, as the rest of the propagation dynamics, from some thermally activated processes. Finally, for the two materials that we have studied, we have inferred that the mechanical stress around cracks remains an increasing quantity inside the process zones up to a few nanometers from the tip. Such a nanometric scale matches the typical size over which the heat was inferred to be generated, making thermal dissipation the likely main process that shields rupture fronts from mechanical failure.

In theory, the model could be reversed, and the fast propagation of cracks under a minimum load could be triggered by a very local heating of their fronts. Related experiments could for instance be performed with localized light pulses on material that are thin or transparent enough, for the heat elevation to be controlled. Certainly, elevated ambient temperatures are known to have a strong impact on the kinetics of fractures, both in the lab (e.g., ref. 30 and 86) and in nature.⁸⁷

Noteworthily, the proposed model, and its ability to explain some actual crack dynamics, stresses the importance of the heat conductivity of materials on their macroscopic strength. A high conductivity indeed allows to evacuate the extra internal energy away from the fronts, thus delaying any thermal weakening. As a general statement, many strong materials happen to be good conductors, such as metals, graphene⁸⁸ or spider silk.⁸⁹ For the latter, it was in particular shown that, contrarily to most materials, its conductivity actually increases with deformation,⁸⁹ which could well be a natural defence mechanism for the stability of arachnid webs. Designing human-made solid matrices that can replicate such a behavior on the molecular scale could then become a new important target of material sciences.

Finally, we suggest that most of the physics that we have introduced to study mode I fractures shall also be valid for mixed-mode fracturing as well as for solid friction. The latter is actually suspected to hold some non negligible, thermal related, weakening mechanisms (e.g., ref. 90), which could notably be a key in geophysics in understanding the stability of seismic faults. Such mechanisms might be diverse, and may include the thermal pressurisation of fault fluids^91,92 or some changes in the fault planes minerals phase (i.e., such as melting or thermal decomposition).⁹³ We propose that they could also be related to a thermally boosted sub-critical slip, in the sense of statistical physics and similarly to the model we have here developed.

Contributions

T. V. D. developed and analysed the model and redacted the manuscript. R. T. proposed the physical basis of the model and its mathematical formulation. A. C. worked on its numerical implementations. D. B. and L. H. provided the PMMA data and images. S. S. and L. V. gave direct insights on the tape experiments. K. J. M. and E. G. F. contributed in the interpretation of the model in fracture mechanics applications. All authors participated to the redaction of the manuscript and agreed with the submitted version.

Conflicts of interest

The authors declare no competing interests in the publishing of this work.

Acknowledgements

We acknowledge and are grateful for the support of the IRP France-Norway D-FFRACT, of the Universities of Strasbourg and Oslo and of the CNRS INSU ALEAS program. We thank the Research Council of Norway through its Centres of Excellence funding scheme, project number 262644. We are also thankful for the support of the Russian Government, through its grant number 14.W03.31.0002. Readers are most welcome to contact the authors for discussion.

References

1. A. Griffith, Philos. Trans. R. Soc., A, 1921, 221, 163–198.
2. L. Slepyan, Phys.-Dokl., 1981, 26, 538–540.
3. S. A. Kulakhmetova, V. A. Saraikin and L. I. Slepyan, Mech. Solids, 1984, 19, 102–108.
4. M. Marder, Philos. Trans. R. Soc., A, 2019, 377(2156), 20190098.
5. M. Marder and S. Gross, J. Mech. Phys. Solids, 1995, 43, 1–48.
6. G. B. Kaufman, J. Chem. Educ., 1993, 70, A279.
7. S. S. Brenner, J. Appl. Phys., 1962, 33, 33–39.
8. S. N. Zhurkov, Int. J. Fract., 1984, 26, 295–307.
9. W. Döll and L. Könczöl, Crazing in Polymers, Springer Berlin Heidelberg, 1990, vol. 2, pp. 137–214.
10. L. Golubović and S. Feng, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 43, 5223–5227.
11. Y. Pomeau, Compte Rendu de l’Académie des Sciences Paris, 1992, 314 II, 553–556.
12. S. Roux, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2000, 62, 6164–6169.
13. S. Santucci, L. Vanel and S. Ciliberto, Phys. Rev. Lett., 2004, 93, 095505.
14. L. Vanel, S. Ciliberto, P.-P. Cortet and S. Santucci, J. Phys. D: Appl. Phys., 2009, 42, 214007.
15. O. Lengliné, R. Toussaint, J. Schmittbuhl, J. E. Elkhoury, J. P. Ampuero, K. T. Tallakstad, S. Santucci and K. J. MÅløy, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 036104.
16. A. Cochard, O. Lengliné, K. J. MÅløy and R. Toussaint, Philos. Trans. R. Soc., A, 2019, 377, 20170399.
17. G. G. Hammes, Principles of Chemical Kinetics, Academic Press, 1978.
18. G. P. Marshall, L. H. Coutts and J. G. Williams, J. Mater. Sci., 1974, 9, 1409–1419.
19. M. Barquins and M. Ciccotti, Int. J. Adhes. Adhes., 1997, 17, 65–68.
20. D. Maugis and M. Barquins, J. Phys. D: Appl. Phys., 1978, 11, 1989–2023.
21. D. Maugis, J. Mater. Sci., 1985, 20, 3041–3073.
22. E. Orowan, Energy criteria of fracture, Massachusetts institute of technology, Cambridge departement of mechanical engineering technical report, 1954.
23. G. R. Irwin, J. Appl. Mech., 1957, 24, 361–364.
24. G. Carbone and B. N. J. Persson, Phys. Rev. Lett., 2005, 95, 114301.
25. G. Carbone and B. N. J. Persson, Eur. Phys. J. E: Soft Matter Biol. Phys., 2005, 17, 261–281.
26. S. Santucci, P.-P. Cortet, S. Deschanel, L. Vanel and S. Ciliberto, Europhys. Lett., 2006, 74, 595–601.
27. R. Toussaint, O. Lengliné, S. Santucci, T. Vincent-Dospital, M. Naert-Guillot and K. J. MÅløy, Soft Matter, 2016, 12, 5563–5571.
28. T. Vincent-Dospital, R. Toussaint, A. Cochard, K. J. MÅløy and E. G. Flekkøy, Phys. Rev. Mater., 2020, 4, 023604.
29. C. H. Scholz, Geol. Rundsch., 1988, 77, 319–328.
30. A. G. Atkins, C. S. Lee and R. M. Caddell, J. Mater. Sci., 1975, 10, 1394–1404.
31. J. Fineberg, S. P. Gross, M. Marder and H. L. Swinney, Phys. Rev. Lett., 1991, 67, 457–460.
32. J. Scheibert, C. Guerra, F. Célarié, D. Dalmas and D. Bonamy, Phys. Rev. Lett., 2010, 104, 045501.
33. C. Guerra, J. Scheibert, D. Bonamy and D. Dalmas, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 390–394.
34. K. J. Måløy, S. Santucci, J. Schmittbuhl and R. Toussaint, Phys. Rev. Lett., 2006, 96, 045501.
35. K. T. Tallakstad, R. Toussaint, S. Santucci, J. Schmittbuhl and K. J. MÅløy, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 046108.
36. C. Creton and C. Ciccotti, Rep. Prog. Phys., 2016, 79, 046601.
37. M.-J. Dalbe, S. Santucci, P.-P. Cortet and L. Vanel, Soft Matter, 2014, 10, 132–138.
38. V. De Zotti, K. Rapina, P.-P. Cortet, L. Vanel and S. Santucci, Phys. Rev. Lett., 2019, 122, 068005.
39. J. R. Rice and N. Levy, Phys. Strength Plast., 1969, 277–293.
40. R. Weichert and K. Schönert, J. Mech. Phys. Solids, 1978, 26, 151–161.
41. G. N. Chapman and A. J. Walton, J. Appl. Phys., 1983, 54, 5961–5965.
42. G. Pallares, C. L. Rountree, L. Douillard, F. Charra and E. Bouchaud, Europhys. Lett., 2012, 99, 28003.
43. A. Smekal, Oesterr. Ing.-Arch., 1953, 7, 49–70.
44. K. Ravi-Chandar and B. Yang, J. Mech. Phys. Solids, 1997, 45, 535–563.
45. J. Rice, J. Mech. Phys. Solids, 1978, 26, 61–78.
46. B. Lawn, Fracture of Brittle Solids, Cambridge University Press, 2nd edn, 1993.
47. L. B. Freund, J. Mech. Phys. Solids, 1972, 20, 129–152.
48. J. L. Huang and A. V. Virkar, Eng. Fract. Mech., 1985, 21, 103–113.
49. M. J. Buehler, F. F. Abraham and H. Gao, Nature, 2003, 426, 141–146.
50. J. W. Morrissey and J. R. Rice, J. Mech. Phys. Solids, 1998, 46, 467–487.
51. J. R. Rice and D. C. Drucker, Int. J. Fract. Mech., 1967, 3, 19–27.
52. E. J. Kramer, Crazing in Polymers, Berlin, Heidelberg, 1983, pp. 1–56.
53. H. S. Carslaw and J. C. Jaeger, Conduction of Heat in Solids, Oxford, Clarendon Press, 1959.
54. M. Hattali, J. Barés, L. Ponson and D. Bonamy, THERMEC 2011, 2012, pp. 920–924.
55. Technical Information, Altuglas sheets, Arkema technical report, 2017.
56. M. Parvin, Int. J. Fract., 1979, 15, 397–404.
57. C. S. Henkee and E. J. Kramer, J. Polym. Sci., Polym. Phys. Ed., 1984, 22, 721–737.
58. K. Ravi-Chandar and W. G. Knauss, Int. J. Fract., 1984, 26, 65–80.
59. E. Sharon, S. P. Gross and J. Fineberg, Phys. Rev. Lett., 1995, 74, 5096–5099.
60. T. Goldman Boué, G. Cohen and J. Fineberg, Phys. Rev. Lett., 2015, 114, 054301.
61. V. De Zotti, K. Rapina, P.-P. Cortet, L. Vanel and S. Santucci, Phys. Rev. Lett., 2019, 122, 068005.
62. C. Creton, MRS Bull., 2003, 28, 434–439.
63. S. G. Robert, A. Morse, E. Siband, D. Dupin, S. P. Armes and J. L. Keddie, J. Colloid Interface Sci., 2015, 448, 8–16.
64. J. K. Kim, J. W. Kim, M. I. Kim and M. S. Song, Macromol. Res., 2006, 14, 517–523.
65. L. Ponson, D. Bonamy and L. Barbier, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 184205.
66. P. Jain and L. Sharma, J Appl. Sci. Southern Africa, 1998, 4, 80–101.
67. C. Camara, J. Escobar, J. R. Hird and S. J. Putterman, Nature, 2008, 455, 1089–1092.
68. V. Lampret, J. Peternelj and A. Krainer, Sol. Energy, 2002, 73, 319–326.
69. A. Stockman and L. T. Sharpe, Ophthal. Physl. Opt., 2006, 26, 225–239.
70. K. N. G. Fuller, P. G. Fox and J. E. Field, Proc. R. Soc. London, Ser. A, 1975, 341, 537–557.
71. J. L. Fergason, Appl. Opt., 1968, 7, 1729–1737.
72. H. E. Newton, Science, 1939, 89, 460–461.
73. P. R. Budarapu, B. Javvaji, V. K. Sutrakar, D. Roy Mahapatra, G. Zi and T. Rabczuk, J. Appl. Phys., 2015, 118, 064307.
74. D. W. Tang and N. Araki, Int. J. Thermophys., 1997, 18, 493.
75. S. W. S. McKeever, Thermoluminescence of Solids, Cambridge University Press, 1985.
76. K. Kitamura, Mater. Trans., 2008, 49, 643–649.
77. K. W. Allen, Polym. Int., 1996, 41, 209–210.
78. S. Siman-Tov, E. Aharonov, A. Sagy and S. Emmanuel, Geology, 2013, 41, 703–706.
79. R. Han, T. Hirose and T. Shimamoto, J. Geophys. Res.: Solid Earth, 2010, 115, B3.
80. D. Dugdale, J. Mech. Phys. Solids, 1960, 8, 100–104.
81. N. Murphy and A. A. Ivankovic, Eng. Fract. Mech., 2005, 72, 861–875.
82. P. M. Morse, Phys. Rev., 1929, 34, 57–64.
83. H. Arisawa and T. Brill, Combust. Flame, 1997, 109, 415–426.
84. S. Shaik, E. Cremades and S. Alvarez, Angew. Chem., Int. Ed., 2019, 58, 13194–13206.
85. G. Barenblatt, Advances in Applied Mechanics, Elsevier, 1962, vol. 7, pp. 55–129.
86. N. Brantut, M. J. Heap, P. G. Meredith and P. Baud, J. Struct. Geol., 2013, 52, 17–43.
87. B. D. Collins and G. M. Stock, Nat. Geosci., 2016, 9, 395–400.
88. A. Balandin, S. Ghosh, W. Bao, I. Calizo, D. Teweldebrhan, F. Miao and J. Lau, Nano Lett., 2008, 8, 902–907.
89. X. Huang, G. Liu and X. Wang, Adv. Mater., 2012, 24, 1482–1486.
90. J. R. Rice, J. Geophys. Res.: Solid Earth, 2006, 111, B5.
91. H. Noda, E. M. Dunham and J. R. Rice, J. Geophys. Res.: Solid Earth, 2009, 114, B7.
92. C. Wibberley and T. Shimamoto, Nature, 2005, 436, 689–692.
93. J. Sulem and V. Famin, J. Geophys. Res.: Solid Earth, 2009, 114, B3.

---

Footnote

† Electronic supplementary information (ESI) available: A method for the measure of crack velocity versus energy release rate in PMMA, a model parameters sensitivity study, a method to asses the goodness of fit to the experimental data and a discussion on the healing processes in tape peeling. See DOI: 10.1039/d0sm01062f

---