Fluctuation spectroscopy of giant unilamellar vesicles using confocal and phase contrast microscopy

Abstract

A widely used method to measure the bending rigidity of bilayer membranes is fluctuation spectroscopy, which analyses the thermally-driven membrane undulations of giant unilamellar vesicles recorded with either phase-contrast or confocal microscopy. Here, we analyze the fluctuations of the same vesicle using both techniques and obtain consistent values for the bending modulus. We discuss the factors that may lead to discrepancies.

---

Bending rigidity of cellular membranes plays a key role in membrane remodeling. Knowledge of its value is needed to quantify processes that involve curvature changes such as budding (as in endo- and exocytosis), tubulation and fusion. Various experimental methods have been devised to measure bending rigidity,¹e.g. micropipette aspiration,^2,3 electrodeformation,^4–7 optical tweezers,^8,9 and scattering based techniques.^10,11 One of the most popular methods is fluctuation spectroscopy, pioneered by Brochard and Lenon,¹² due to its ease of implementation.^6,13–15 In essence, a time series of vesicle contours in the focal plane (the equator of the quasi-spherical vesicle) is recorded. The quasi-circular contour is decomposed in Fourier modes. The fluctuating amplitudes have variance dependent on the membrane bending rigidity and tension. Imaging is most commonly done by phase contrast microscopy^{1,6,14,16–21} but other methods such as confocal^22–24 and light sheet microscopy²⁵ have also been employed. The increased variety of imaging methods raises the question whether they all yield the same results.

Recently, Rautu et al.²⁴ pointed out that in phase contrast imaging, projections of out-of-focus fluctuations may contribute to the contour statistics leading to systematic overestimation of the bending rigidity value when compared to other methods such as micropipette aspiration and X-ray scattering. However, comparing bending rigidity numbers obtained by different techniques is only meaningful if the same system is probed. It is known that many factors such as sugars (and gravity), salt, buffers, solution asymmetry, concentration of fluorescent lipids, preparation method or type of bilayer configuration (stacked or free-floating), influence the measured mechanical properties of bilayer membranes;^1,17,26–30 see Table S1 in the ESI† for a list of reported bending rigidity of DOPC membranes. For example, even measurements with the same method can give a wide range of values, e.g., the bending rigidity of a DOPC bilayer measured with flickering spectroscopy has been reported from 15k_BT²³ to 30k_BT,¹⁹ where k_BT is the thermal energy.

In order to compare imaging with phase contrast and confocal microscopy, which was suggested in Rautu et al.²⁴ as a better technique due to the precise control over the focal depth, we measure the bending rigidity of the same giant vesicle with both techniques. We highlight some important issues to be considered to ensure reliable measurements. We also show that results obtained with both methods are consistent.

Equilibrium fluctuations of a quasi-spherical vesicle

First, we summarize the theoretical basis of the fluctuations analysis (details are provided in ESI,† Section S6). We also correct published expressions for the relaxation frequency and cross-spectral density of the shape fluctuations.

The contour in the equatorial plane of a quasi-spherical vesicle is decomposed in Fourier modes, , where R₀ = (3V/4π)^1/3 is the radius of an equivalent sphere with the volume V of the GUV and q is the mode number. In practice, q_max is the maximum number of experimentally resolved modes. The statistical analysis of the fluctuating amplitudes u_q yields the values of membrane bending rigidity κ and the tension σ since 〈|u_q|²〉 ∼ k_BT/κ(q³ + [small sigma, Greek, macron]q), where [small sigma, Greek, macron] = σR₀²/κ.

More precisely, the statistics of the two-dimensional circular modes, u_q, is derived from the three-dimensional shape modes, f_lm, which describe the nearly-spherical shape in terms of spherical harmonics,^13,31. Here, l_max is an upper cutoff, in the order of the ratio of the GUV radius and bilayer thickness. The contour in the focal plane corresponds to the equator of the quasi-spherical vesicle, θ = π/2, i.e., , which leads to the following expression for the mean squared amplitudes

where n_lq = (2l + 1)(l − q)!/4π(l + q)! and P_lq are the associated Legendre polynomials. The short-wavelength shape fluctuations are dominated by the bending rigidity, while the long wavelengths are controlled by tension; the crossover occurs around mode .

To validate our methodology, we have simulated the thermal shape fluctuations of a GUV, see also ESI,† Section S6. We have generated a sequence of three-dimensional shapes (and their corresponding equatorial contours) using the evolution equations^31,32

where ζ_lm is the thermal noise driving the membrane undulations, η_in and η_ex are the viscosity of the solution inside and outside the vesicle. Note that the relaxation time given by eqn (2) in Rautu et al.²⁴ has incorrect dependence on the viscosities of the enclosed and suspending solutions (this mistake is unlikely to affect the reported fluctuation spectra). The simulated contours were analyzed by our code and the extracted bending rigidity and tension were compared to the input values to confirm accuracy of the contour detection, Fourier decomposition and data fitting algorithms. The time evolution of the modes also enables us to access information provided by the time correlations 〈u_q(0)u_q*(t)〉 = 〈|u_q|²〉 exp(−t/τ_q). If q ≫ 1, the correlation time tends to that of a planar membrane τ_q⁻¹ = κ(q³ + [small sigma, Greek, macron]q)/2R₀³(η_ex + η_in). If the cross-spectral density 〈|u_q(0)||u_q(t)|〉 is utilized, the correct time dependence in the exponential includes a factor of 2 and eqn (3) in Zhou et al.³³ needs to be corrected (see ESI,† Section S6, eqn (39)).

Bending rigidity obtained from confocal and phase-contrast microcopy: effect of resolution and vesicle size

Giant unilamellar vesicles (GUV) were electroformed from DOPC (99.8 mol% dioleoylphosphatidylcholine and 0.2 mol% Texas-Red 1,2-hexadecanoyl-sn-glycero-3-phosphoethanolamine, TR-DHPE) in 20 mM sucrose and subsequently diluted in 22 mM glucose, see ESI,† Section S2 for details. Low sugar concentration was used in order to minimize the effects of gravity²⁸ and effect of sugars,²⁶ but still allow the vesicles to settle to the chamber bottom for easier recording. Low dye content minimizes effects of fluorophores.²⁹

Fig. 1 shows a typical fluctuations spectrum, given by eqn (1), fitted to the experimental data for the same vesicle imaged with confocal and phase contrast microscopy using a 40× objective with 0.6 numerical aperture (NA), pinhole size of 1 Airy unit (AU) and polarization correction (see below and ESI,† Section S3). The contour was detected with sub-pixel resolution.⁶ The experimental data was fitted with eqn (1) with Levenberg–Marquardt algorithm and yielded bending rigidity κ = 23.9 ± 1.6k_BT and tension σ = 5.1 ± 1.4 × 10⁻⁹ N m⁻¹ and κ = 22.3 ± 2.1k_BT and σ = 3.1 ± 1.2 × 10⁻⁹ N m⁻¹ from the confocal and phase contrast microscopy data, respectively. The average and error in individual GUV was determined by performing fluctuation spectroscopy 2–3 times. By imaging a population of 18 vesicles with both methods, the bending rigidity obtained are 22.5 ± 2.0k_BT with confocal and 23.3 ± 1.6k_BT phase contrast microscopy; each vesicle was analyzed with both imaging techniques as in Fig. 1 and then the results were averaged over the population. Fig. 2 shows the box and whisker plot for more detailed statistics. Based on F statistics and ANOVA (analysis of variance) test, the p-value obtained is p = 0.48 for null hypothesis testing. We also performed the paired-sample t-test and obtained p = 0.43. These p-values indicate no significant difference between the two imaging techniques.

Fig. 1 Fluctuation spectrum of the same DOPC vesicle (shown in the inset) obtained with confocal and phase contrast microscopy with a 40×/NA 0.6 objective, pinhole size of 1 AU and polarization correction, see also ESI,† Movies S1 and S2. The dye concentration is 0.2 mol%. Scale bar is 15 μm. The vertical lines denote the cutoff resolution for the modes: optical resolution (solid line), phase contrast (blue dashed) and confocal (red dashed line). The theory is fitted to phase contrast data up to the mode marked by the dashed blue line. The crossover mode is 7.

Fig. 2 Imaging with phase contrast and confocal microscopy for objectives of the same numerical aperture (NA) give consistent results. Box and whisker plot comparison for a DOPC vesicle population where each vesicle was analyzed with phase contrast and confocal imaging with 40× objectives with NA 0.6 and NA 1.3. Pinhole size is 1 AU with polarization correction. The dye concentration is 0.2 mol%.

Since only modes with wavenumber are sensitive to the bending rigidity, it is desirable to have more resolved modes, i.e., modes with amplitude and wavelength greater than the optical resolution limit ≈250 nm.³⁴ The average mean fluctuation amplitude scales with the size of the vesicle , hence larger GUVs admit more spatially resolvable fluctuation modes as shown in Fig. 3. However, even for the same vesicle we find that the number of resolved modes is higher for phase contrast than for confocal imaging. Indeed, Fig. 1 shows that the noise level is higher for confocal microscopy, and on average phase contrast imaging resolves 8–10 modes more than confocal imaging does. The poorer mode resolution with confocal microscopy is likely due to poor contour recognition. The reasons for this are discussed in the next section.

Fig. 3 Larger vesicles allow resolving more fluctuation modes thus yielding more reliable determination of the bending rigidity. Data are collected on DOPC vesicles with different sizes. The dye concentration is 0.2 mol%. Regression lines are added to guide the eyes. Imaging was done with 40× objectives with different numerical aperture (NA), pinhole size of 1 AU and polarization correction.

We found that the vesicle population needs to have broad range of radii to avoid a size bias in the bending rigidity values we discovered for confocal microscopy with low resolution optics, see also ESI,† Section S4. In the case of 40×/NA 0.6 (air) objective, the mean Pearson correlation and standard deviation coefficient is 0.65 ± 0.21 (see ESI,† Section S5 for the histograms generated with bootstrapping resampling technique). Analysis of a population of similar sized vesicles with radii around 10 μm underestimates κ by roughly 6k_BT. The bias originates from out-of-plane fluorescence which worsens the contour detection. This issue is investigated in the next section and ESI,† Section S6. The size dependence is insignificant for phase contrast microscopy with a mean correlation coefficient of 0.28 ± 0.18 with 40×/NA 0.6 (air). Analyzing the same vesicle population with 40×/NA 1.3 objective in phase contrast and confocal imaging yields 21.0 ± 2.0k_BT and 21.7 ± 2.0k_BT respectively. Higher numerical aperture in phase contrast leads to negligible correlation coefficient of −0.07 ± 0.34 between bending rigidity and vesicle size and decrease in the correlation coefficient to 0.43 ± 0.14 for confocal imaging with 40×/NA 1.3 objective.

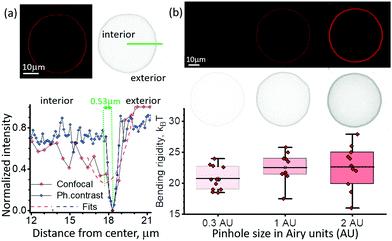
Out-of-focus fluorescence affects contour detection quality in confocal microscopy

The vesicle contour is detected from radial intensity line profiles, see ESI,† Section S2. In confocal cross sections, weak fluorescence from the vesicle membrane located above and below the focal plane may result in signal projected in the interior of the vesicle image which is higher compared to the surrounding background. The resulting asymmetry in the intensity line profile (Fig. 4a) leads to an artificial contour displacement, i.e., poor contour detection (note that such an asymmetry is absent in images acquired with phase contrast microscopy of vesicles with similar refractive indices of the internal and external solutions). This asymmetry creates a systematic error shifting the vesicle contour by 0.53 μm. The error is larger than the pixel resolution of the system, 0.252 μm, hence the higher modes are averaged out. Smaller vesicles or larger pinholes lead to higher signal inside the vesicle (see inset in Fig. 4b) corresponding to greater asymmetry which increases the error from contour fitting and introduces dependence of the bending rigidity on vesicle size. For imaging with higher numerical aperture objectives (e.g. NA 1.3), the asymmetry in the intensity line profiles is suppressed and contour detection is correct. Note that phase contrast images do not suffer from the asymmetry-induced error irrespective of the objective NA.

Fig. 4 Out-of-focus fluorescence in confocal images can result in erroneous contour detection and increased error in bending rigidity. (a) Intensity line profiles (gray-value) across the vesicle membrane (DOPC, with 0.2 mol% dye) are symmetric for phase-contrast images (blue) but asymmetric for confocal images (red, 1 AU). The asymmetry in the confocal line profile leads to incorrect detection of the contour position defined by the parabolic fit minimum, here, shifted inwards by 0.53 μm. (b) Vesicle images (and their inverted gray-value analogs) acquired with different pinhole size show increased fluorescence inside the vesicle which results in larger error in the bending rigidity. Box and whisker plot of the bending rigidity of the same DOPC vesicles imaged with confocal microscopy at three different pinhole sizes for 40×/NA 0.6 objective and polarization correction.

We investigated the impact of out-of-focus fluorescence on the fluctuations statistics by varying the pinhole size for confocal imaging on the same vesicle. The standard pinhole size in confocal microscopy is defaulted to 1 Airy unit (AU) (full width at half maximum FWHM = 1.6 μm) for 40×/NA 0.6 objective. We analyzed the same vesicles with different optical sectioning at 0.3 AU (FWHM = 0.9 μm), and 2 AU (FWHM = 2.9 μm). The mean bending rigidity did not show significant differences based on ANOVA testing, post hoc Dunnett test and paired-sample t-test (p = 0.87), however the error increases with the pinhole size. The sensitivity to the vesicle size also becomes more pronounced with higher pinhole size. At the largest pinhole size (2.0 AU) the Pearson correlation coefficient is 0.60 ± 0.22, while for 0.3 AU it becomes negligible, −0.14 ± 0.30.

Dye related artifacts: vesicle tubulation and polarization

Confocal imaging relies on fluorophores added to the membrane, and some studies have used up to 10 mol% dye.^22,23 To probe the effect of fluorophore on κ, we changed the dye concentration from 0.2 mol% to 2 mol% TR-DHPE. The bending rigidity of this population of vesicles showed non significant difference with κ = 20.09 ± 2.49k_BT with one ANOVA testing. However, it was observed that over 2–3 min of recording, around 50% of the vesicles developed inward structures such as buds or visible tubes as shown in Fig. 5. Vesicles with such defects displayed significantly higher bending rigidity, 25.01 ± 2.11k_BT.

Fig. 5 Time lapse of a DOPC vesicle with 2 mol% TR-DHPE developing inward nanotubes as a result of long exposure to laser during confocal imaging. The second and third cross sections are non-equatorial to better show the formed nanotubes.

TR-DHPE belongs to a family of polarity-sensitive fluorescent probes. As a result, the signal intensities are different at the pole and equator of the vesicle (see ESI,† Section S3). This may lead to errors in the contour detection in these regions. The polarization effect was corrected by using circular rotation plates to have even intensities across the equatorial vesicle plane. The analysis of the same vesicle with and without the polarization correction showed a 3k_BT lower bending rigidity without any correction with 40×/NA 0.6 (air) objective. This softening effect became insignificant with 40×/NA 1.3 (oil) objective (ESI,† Section S3). This is likely due to loss of signal at low intensity regions where the higher mode fluctuations intensities are averaged out with background noise due to out-of-focus fluorescence.

Effect of nearby vesicles on fluctuation spectra

The equilibrium shape fluctuations of an isolated GUV are driven by Gaussian thermal noise. Defects such as buds, nanotubes, invaginations or docked LUVs modify the vesicle fluctuations⁶ and their effect can be detected in the statistics at each point on the vesicle contour profile using the ensemble-averaged probability density function (PDF) as shown in Fig. 6a. In addition to defects attached the membrane, we also found that hydrodynamic flows and/or fluorescence signal from nearby vesicles can affect vesicle fluctuations.

Fig. 6 Nearby structures affect the fluctuation spectrum. (a) A flickering vesicle in close proximity to another vesicle bud. (b) Fluctuation density map of the vesicle in (a): the fluctuations are modified by hydrodynamic interactions of the other flickering vesicle bud. (c) Kurtosis K > 3 indicates the vesicle fluctuations have amplified meaning local softening of the membrane.

We characterized the Gaussianity of the fluctuations using the fourth PDF moment, Kurtosis, K. For a Gaussian distribution, K = 3. In Fig. 6 we demonstrate how thermal fluctuations may be modified (see ESI,† Movie S3). As shown, the majority of contours are characterized by a normal distribution. However near other flickering structures, the fluctuation map density is modified. The non-Gaussian enhanced fluctuations are observed with leptokurtic nature (K > 3). This observation serves as a caution to filter out vesicles with sub-optical structures affecting the fluctuations.

Conclusions

We compare the bending rigidity of bilayer membranes determined from flickering spectroscopy of GUVs imaged with confocal and phase contrast microscopy. Examining the same vesicle with both imaging techniques shows no significant differences in the bending modulus obtained from the two methods, in contrast to the overestimation reported by Rautu et al.²⁴ when phase contrast microscopy is used. Our analysis indicates that membrane defects such as buds and tubes induced by long laser exposure in confocal microscopy can significantly stiffen the membrane. Furthermore, we find that errors in contour detection that could impact data interpretation can arise from fluorescence signal “pollution” and dye polarization. The bending rigidity we obtain (∼22k_BT for DOPC) is in line with the values obtained with other techniques such as micropipette aspiration, X-ray scattering, electrodeformation and neutron spin echo.^3,8,10 A scatter of approximately 2k_BT is typical in the experiments and should be taken into account when comparing data from different groups and methods. Exploring the effect of various parameters, we find that optimal imaging conditions for bending rigidity measurements from confocal imaging include high magnification objective, high numerical aperture, circular polarization correction, minimum dye concentration, small pinhole size, and broad vesicle size distribution.

In conclusion, we demonstrate that phase contrast and confocal microscopy produce the same results if precautions are taken to minimize effects of the dye and improve contour detection. Our study suggests that the many published results obtained by phase contrast microscopy are likely to be unaffected by the projections of out-of-focus fluctuations onto the imaging plane in contrast to the claim by Rautu et al.²⁴ Since dye related artifacts such as laser-induced defects can compromise the data, it is advantageous to use phase contrast imaging as it does not require dyes.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was funded in part by NSF-CMMI awards 1748049 and 1740011. PV acknowledges support from the Alexander von Humboldt Foundation and HAF acknowledges financial support from Prof. Reinhard Lipowsky for visits to the Max Planck Institute of Colloids and Interfaces. VNG and RD acknowledge support of the MaxSynBio consortium which is jointly funded by the Federal Ministry of Education and Research of Germany and the Max Planck Society. We thank Paul Salipante for proofreading the manuscript and M. Turner for useful suggestions. Open Access funding provided by the Max Planck Society.

Notes and references

1. R. Dimova, Adv. Colloid Interface Sci., 2014, 208, 225–234.
2. E. Evans and W. Rawicz, Phys. Rev. Lett., 1990, 64, 2094–2097.
3. W. Rawicz, K. Olbrich, T. McIntosh, D. Needham and E. Evans, Biophys. J., 2000, 79, 328–339.
4. M. Kummrow and W. Helfrich, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 44, 8356–8360.
5. P. M. Vlahovska, R. S. Gracia, S. Aranda-Espinoza and R. Dimova, Biophys. J., 2009, 96, 4789–4803.
6. R. S. Gracia, N. Bezlyepkina, R. L. Knorr, R. Lipowsky and R. Dimova, Soft Matter, 2010, 6, 1472–1482.
7. P. F. Salipante, R. Knorr, R. Dimova and P. M. Vlahovska, Soft Matter, 2012, 8, 3810–3816.
8. A. Tian, B. R. Capraro, C. Esposito and T. Baumgart, Biophys. J., 2009, 97, 1636–1646.
9. B. Sorre, A. Callan-Jones, J.-B. Manneville, P. Nassoy, J.-F. Joanny, J. Prost, B. Goud and P. Bassereau, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 5622–5626.
10. N. Kučerka, Y. Liu, N. Chu, H. I. Petrache, S. Tristram-Nagle and J. F. Nagle, Biophys. J., 2005, 88, 2626–2637.
11. J. Pan, F. A. Heberle, S. Tristram-Nagle, M. Szymanski, M. Koepfinger, J. Katsaras and N. Kučerka, Biochim. Biophys. Acta, Biomembr., 2012, 1818, 2135–2148.
12. F. Brochard and J. F. Lennon, J. Phys., 1975, 36, 1035–1047.
13. J. Faucon, M. Mitov, P. Meleard, I. Bivas and P. Bothorel, J. Phys., 1989, 50, 2389–2414.
14. J. Pecreaux, H.-G. Dobereiner, J. Prost, J.-F. Joanny and P. Bassereau, Eur. Phys. J. E: Soft Matter Biol. Phys., 2004, 13, 277–290.
15. J. Genova, V. Vitkova and I. Bivas, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 022707.
16. P. Bassereau, B. Sorre and A. Lévy, Adv. Colloid Interface Sci., 2014, 208, 47–57.
17. H. A. Faizi, S. L. Frey, J. Steinkühler, R. Dimova and P. M. Vlahovska, Soft Matter, 2019, 15, 6006–6013.
18. H. Bouvrais, F. Cornelius, J. H. Ipsen and O. G. Mouritsen, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 18442–18446.
19. Y. Elani, S. Purushothaman, P. J. Booth, J. M. Seddon, N. J. Brooks, R. V. Law and O. Ces, Chem. Commun., 2015, 51, 6976–6979.
20. V. G. Almendro-Vedia, P. Natale, M. Mell, S. Bonneau, F. Monroy, F. Joubert and I. López-Montero, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 11291–11296.
21. P. Meleard, T. Pott, H. Bouvrais and J. H. Ipsen, Eur. Phys. J. E: Soft Matter Biol. Phys., 2011, 34, 116.
22. D. Drabik, M. Przybyłlo, G. Chodaczek, A. Iglič and M. Langner, Biochim. Biophys. Acta, Biomembr., 2016, 1858, 244–252.
23. J. B. Dahl, V. Narsimhan, B. Gouveia, S. Kumar, E. S. G. Shaqfeh and S. J. Muller, Soft Matter, 2016, 12, 3787–3796.
24. S. A. Rautu, D. Orsi, L. Di Michele, G. Rowlands, P. Cicuta and M. S. Turner, Soft Matter, 2017, 13, 3480–3483.
25. A. F. Loftus, S. Noreng, V. L. Hsieh and R. Parthasarathy, Langmuir, 2013, 29, 14588–14594.
26. V. Vitkova, J. Genova, M. D. Mitov and I. Bivas, Mol. Cryst. Liq. Cryst., 2006, 449, 95–106.
27. M. Karimi, J. Steinkühler, D. Roy, R. Dasgupta, R. Lipowsky and R. Dimova, Nano Lett., 2018, 18, 7816–7821.
28. J. R. Henriksen and J. H. Ipsen, Eur. Phys. J. E: Soft Matter Biol. Phys., 2002, 9, 365–374.
29. H. Bouvrais, T. Pott, L. A. Bagatolli, J. H. Ipsen and P. Méléard, Biochim. Biophys. Acta, Biomembr., 2010, 1798, 1333–1337.
30. H. Bouvrais, L. Duelund and J. H. Ipsen, Langmuir, 2014, 30, 13–16.
31. U. Seifert, Eur. Phys. J. B, 1999, 8, 405–415.
32. L. Miao, M. A. Lomholt and J. Kleis, Eur. Phys. J. E: Soft Matter Biol. Phys., 2002, 9, 143–160.
33. H. Zhou, B. B. Gabilondo, W. Losert and W. van de Wate, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 011905.
34. R. Lipowsky, in Structure and Dynamics of Membranes, ed. R. Lipowsky and E. Sackmann, Handbook of Biological Physics, North-Holland, 1995, vol. 1, pp. 521–602.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm00943a

---