Selective colloidal bonds via polymer-mediated interactions

Abstract

Regioselectivity in colloidal self-assembly typically requires specific chemical interactions to guide particle binding. In this paper, we describe a new method to form selective colloidal bonds that relies solely on polymer adsorption. Mixtures of polymer-coated and bare particles are initially stable due to long-ranged electrostatic repulsion. When their charge is screened, the two species can approach each other close enough for polymer bridges to form, binding the particles together. By utilizing colloidal dumbbells, where each lobe is coated with polymer brushes of differing lengths, we demonstrate that the Debye screening length serves as a selective switch for the assembly of bare tracer particles onto the two lobes. We model the interaction using numerical self-consistent field lattice computations and show how regioselectivity arises from just a few nanometers difference in polymer brush length.

---

1 Introduction

Colloidal particles are widely studied because of their display of phase behaviour that closely mimics that of atoms and molecules.¹ Like their atomic counterparts, colloids can be utilized as self-assembly building blocks that come together to form larger functional architectures and bulk materials.^2,3 Most colloids, however, are limited in their assembly behaviour because of the isotropic character of their interactions. One way to achieve control over the structure and functionality of colloidal systems is to engineer particles' shapes or decorate their surface with sticky patches capable of engaging in directional and selective interparticle bonds. Several types of “colloidal glues” have been developed to serve this purpose, from simple electrostatic charges⁴ and hydrophobic/hydrophilic interactions,⁵ to more sophisticated lock-and-key entropic forces⁶ and DNA–mediated interactions.⁷

In this article, we describe how to implement polymer-mediated interactions to program colloidal self-assembly. A polymer-mediated bond forms when a polymer-coated particle comes into contact with a polymer-free particle. The two species are initially stabilized by electrostatic repulsion, preventing them to make physical contact. By screening the charge, however, the particles reach a proximity where the polymer can form bridges and bind them together. We demonstrate selectivity by using dumbbell-shaped colloids with polymer brushes of varying lengths grafted onto each lobe. Bridging occurs at different screening lengths based on the brush length, leading to the programmable assembly of tracer particles at each lobe. We investigate polymer-mediated colloidal bonds by combining experiments and numerical self-consistent field (SCF) lattice computations, which are widely used to study polymeric and electrostatic interactions.^8–11 With SCF, the thermodynamic free energy minimum of inhomogeneous systems containing interfaces, polymers, ions and other molecules can be determined, which in turn can be used to compute interaction potentials. An advantage of SCF over full scale computer simulations is the efficiency of the computations, which makes it possible to scan a large parameter space in a short period of time.

2 Methods

In this section we provide a summary of the experimental and theoretical methods used. A detailed description of the numerical self-consistent field method is given elsewhere;^12–14 here we give a short overview of the most relevant details.

2.1 Particle synthesis and assembly

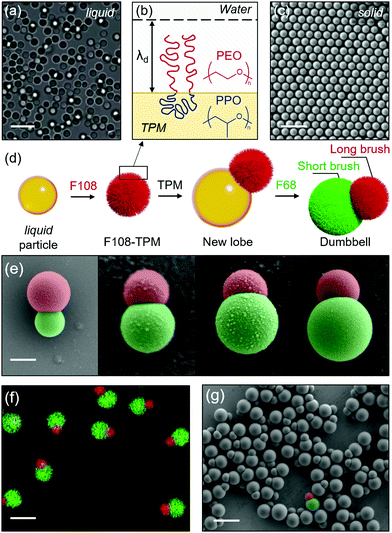
The colloidal model systems we use in this study consist of polymerizable 3-(trimethoxysilyl)propyl methacrylate (TPM) emulsions and silica particles.^15,16 Poly(ethylene oxide)–poly(propylene oxide)–poly(ethylene oxide) (PEO–PPO–PEO) triblock copolymers (Pluronic) of different lengths are used to create polymer brushes on TPM while silica remains bare, acting as tracers. The Pluronics used in this study are F108 (EO₁₃₂PO₅₆EO₁₃₂) and F68 (EO₇₆PO₂₉EO₇₆).

TPM emulsions (Fig. 1a) are synthesized by introducing 100 μL TPM oil (98% MilliporeSigma) to a 100 mL solution of water and ammonia ([NH₃] = 15 mM) and stirred magnetically at 300 rpm in a sealed beaker. After 2 hours, liquid TPM spheres are finished growing, at which point a solution of Pluronic F108 is added to form a polymer brush ([F108] = 30 μM) (Fig. 1b). The particles can then either be washed and utilized in their liquid state, or polymerized. Particles are washed by centrifuging them at 100 G for 4 hours, decanting the supernatant, resuspending the concentrated particles, and finally adding DI water. The washing process is repeated 3 times. To solidify the TPM, 20 mg of azobisisobutyronitrile (AIBN, 98% MilliporeSigma) is added to the suspension and stirred for five minutes, then the particles are heated for 4 hours at 80 °C. The polymerized particles are then washed in the manner described above (Fig. 1c).

Fig. 1 Synthesis of polymer-coated spheres and Janus dumbbells. (a) Optical micrograph of monodispersed TPM oil droplets. Scale bar 3 μm. (b) Schematic representation of the Pluronic surfactant's architecture at the TPM–water interface, with hydrophilic arms extending out into the water to form a brush and the hydrophobic core anchoring the polymer in the oil. λ_D represents the range of the electrostatic interactions from the negatively charged TPM surface. (c) SEM micrograph showing polymerized F108-TPM. Scale bar 3 μm. (d) Schematic of the dumbbell synthetic pathway. Liquid TPM particles are coated with F108 and polymerized. Solid F108-TPM is used as a seed to grow a new liquid TPM lobe. The lobe is functionalized with a shorter polymer (F68) and polymerized. The final product has two lobes with variable brush length. (e) SEM micrographs showing the tunability in the size of the second lobe, shown in green. Scale bar 1 μm. (f) Confocal micrograph of the dumbbells with different fluorescent dyes in each lobe. Scale bar 3 μm. (g) SEM micrograph showing the monodispersity of the dumbbell product. Scale bar 4 μm.

As we show in Fig. 1d, Janus dumbbell-shaped particles with two different polymer brushes are made by nucleating a secondary lobe onto polymerized F108-coated TPM particles (F108-TPM). Briefly, 100 μL TPM oil is added to a preheated (80 °C) 20 mL F108-TPM suspension (0.1 wt%) containing 15 mM NH₃. The size of the lobe directly depends on the volume of TPM oil added at this stage (Fig. 1e), while heating ensures the nucleation of a single lobe. A second Pluronic surfactant (30 μM, F68) is added to form a shorter polymer brush on the newly nucleated lobe. The dumbbells are then polymerized and purified through the processes described above (Fig. 1f and g). The silica tracers are synthesized via the Stöber process.¹⁶

Self-assembly experiments are carried out by mixing polymer-coated particles with a large excess of silica tracers (number ratio∼1 : 3000), and then adding salt to the desired final concentration. Relatively diluted NaCl stock solutions (≈25 mM) are used to avoid steep gradients during mixing. The suspension is left undisturbed for one hour to allow the particles to assemble. Unreacted silica are purified via centrifugation.

2.2 Self-consistent field calculations

Numerical self-consistent field lattice computations, developed by Scheutjens and Fleer,^17,18 were used to study colloidal interactions mediated by grafted polymers. Scheutjens–Fleer (SF) SCF is based upon mean-field lattice theory similar to Flory–Huggins theory,^19,20 but takes concentration gradients into account and can therefore be used to find equilibrium configurations of inhomogeneous systems. In SF–SCF, every component in the system is composed of segments and interactions between the different segments are taken into account by Flory–Huggins χ-parameters.²¹ A potential field is assigned to the different segment types in every lattice layer based on the interactions and local volume fractions of all different segments in the lattice layer and the neighbouring layers. Based on these potential fields, the statistical probability for a certain segment to be in a certain layer is calculated. Polymer chain conformations are approximated by the freely-jointed chain model resulting from the Edwards diffusion equation. The finite segment size and volume-filling constraint are taken into account with boundary conditions.¹³ Based on the segment probabilities a new set of volume fractions is calculated for each layer. This problem is numerically solved in a self-consistent way within the SF–SCF machinery by starting with an initial guess for the potential fields at each layer and calculating a new volume fraction profile which in turn leads to a new set of potential fields:

{ϕ_j(u_j)}_N ↔ {u_j(ϕ_j)}_N, (1)

where ϕ is the local volume fraction of segment type j and u denotes the potential field for segment type j. The braces indicate that a set of volume fractions and potential fields is obtained for all N lattice layers. This calculation is repeated until a constant solution is obtained which provides the optimized free energy of the system.

2.2.1 System parameters. The SF–SCF calculations were performed using a lattice in which all sites are filled with components. All energies are in units of k_BT and all length scales are in units of the lattice size b. Concentration gradients were taken into account in one direction and the lattice geometry used for all calculations is flat, unless indicated otherwise. The lattice constant λ, which is a measure for the fraction of contacts of a segment with a neighbouring lattice site, is set to 1/3. The water molecules are modeled as a solvent consisting of a single segment and the TPM molecules are represented as a linear chain of five segments with one extra segment connected to each side of the second segment. The Pluronic surfactants, are modeled as block copolymers consisting of a middle block with hydrophobic PO segments and two side blocks with hydrophilic EO segments. The size b of one lattice unit is considered to be equal to the Kuhn length of an ethylene oxide monomer:²² 0.8 nm. The position of a lattice site z is converted to a distance x through the relation x = bz. The number of repeating units for the EO and PO blocks in the SCF calculations is taken as n × 0.36/0.8 and m × 0.36/0.8 respectively, where 0.36 is the size of an ethylene oxide group²² and n and m are the number of repeating units of the Pluronic block copolymers.

The χ-parameters used in the calculations are shown in Table 1. The parameters χ_EO–W, χ_PO–W and χ_EO–PO are taken from Hurter et al.²³ The χ_TPM–EO and χ_TPM–PO parameters are estimated from the interaction parameters between Pluronic and benzene.²³ This is a rough approximation which is based upon the fact that benzene and TPM are both apolar molecules. However, it was found that the exact values of these interaction parameters do not have a large influence on the results since the adsorption of Pluronics at the TPM/water interface is driven by the incompatibility of TPM and PPO with water. Moreover, for simplicity we chose to model the bare tracer particles in the SF–SCF computations as TPM particles. This means that the bridging attraction between the polymer-coated particle and the bare particle is also predominantly determined by the unfavourable interaction of the bare TPM surface with the water phase. In the experimental system the bare particle is a silica particle and there is a specific attraction between the PEO chains and the silica surface due to hydrogen bonding.²⁴ However, in both cases it is the relative difference in affinity of PEO chains and water for the surface that results in a strong bridging attraction and therefore modeling the second particle as a TPM or a silica particle is not expected to lead to qualitative differences.

Table 1 χ-Parameters used for the SF–SCF computations

χ	H2O	TPM	EO	PO
H2O	0.0	3.7	0.4	2.0
TPM	3.7	0.0	0.14	0.1
EO	0.4	0.14	0.0	0.006
PO	2.0	0.1	0.006	0.0

---

The χ_TPM–W parameter is estimated by determining the interfacial tension of the TPM/water interface using SF–SCF in the absence of surfactants as a function of χ_TPM–W. The interfacial tension can be directly calculated from the grand potential of the system (Ω) which is defined as the free energy contribution of the inhomogeneities in the system, as follows from expressing the Helmholtz free energy F as:

where the first term gives the free energy contribution of the bulk, with μ_i the chemical potential of component i and n_i the number of molecules of component i. The interfacial tension of the TPM/water interface γ is then given by:with A the interfacial area, which equals b² for a flat lattice. We find that a value of χ_TPM–W = 3.7 gives an interfacial tension that matches with experimental values^25,26 which are close to 8 mN m⁻¹.

2.2.2 Block copolymer brush. In the experimental system, the polymer brushes are obtained by saturating the oil/water interface of TPM droplets with Pluronic surfactants, after which solid particles can be obtained by polymerizing the oil.²⁷ To mimic these polymeric layers with SF–SCF, we model the polymer brushes according to the following procedure. First, the critical micelle concentration (cmc) of the surfactants is determined^23,28 by computing the grand potential of a micelle as a function of the aggregation number and finding the equilibrium configuration that satisfies Ω = 0. This can be done using different lattice geometries such as flat, cylindrical and spherical ones. It was found that a spherical micelle is the preferred configuration for the block copolymers used in this study. Next, we calculate the volume fraction profile of a surfactant brush at the liquid/liquid interface that is in coexistence with a surfactant bulk concentration corresponding to the cmc of the surfactants. Finally, the adsorbed amount of surfactants at the interface is determined and this is used as input for the computation of the polymer adsorbed at a solid/liquid (TPM/water) interface. In this way, a solid particle with a polymer brush is obtained that has similar properties as the brush at the liquid/liquid interface.

Fig. 2 shows a comparison of polymer brushes adsorbed at liquid/liquid and solid/liquid interfaces. It shows that, although the profiles very close to the interface are different due to the dissimilar nature of the interface, the profiles of the brushes further away from the interface are quite similar for both cases. A key quantity needed to describe the selective adsorption process is the hydrodynamic layer thickness δ_h, which can be determined from the SF–SCF volume fraction profiles using a method described by Cohen Stuart and coworkers.^29,30 The value of δ_h is also very close for both interfaces as can be seen in Fig. 2. The adsorbed amount of Pluronics is also directly determined from the volume fraction profiles and is expressed as the excess number of surfactants at the interface:

with L, the number of segments of one Pluronic surfactant, ϕ_p(z) the local surfactant volume fraction in lattice layer z and ϕ^b_p the bulk surfactant volume fraction. The adsorbed amount is converted to real units (mg m⁻²) by the conversion factor 10³M/(N_Avb²), with M the molar mass in g mol⁻¹ and N_Av Avogadro's number. The number of lattice layers N used for the block copolymer brush calculations was chosen large enough to fulfill the condition that the volume fraction profile in the last lattice layers remained constant to make sure the equilibrium profile of an isolated brush was obtained.

Fig. 2 Self-consistent field theory results for the volume fraction profiles of an EO₁₃₂PO₅₆EO₁₃₂ polymer brush layer adsorbed at (a) the liquid–TPM/water interface and (b) at the solid–TPM/water interface, in equilibrium with a polymer solution at the cmc. The volume fraction profile in (a) is positioned such that the lattice layer where ϕ_TPM is closest to ϕ_water is taken as x = 0 nm. The adsorbed amount of polymer is equal for both interfaces.

2.2.3 Colloidal interactions. To model the double layer interactions between the particles, a certain charge density is imposed on the surface of the particles and monovalent ions consisting of one lattice site are added to the system to set the ionic strength. The non-electrostatic interactions of the ions with all other components are taken to be athermal (χ = 0). The normalized surface charge density in SF–SCF can be converted to real units (C m⁻²) with the conversion factor e/l², with e the elementary charge and l the bond length which is set to 0.3 nm in the calculations for an accurate description of the electrostatics. Due to our choice to convert the lattice size to real units using a lattice layer size of b = 0.8 nm, based on the PEO kuhn length, we slightly overestimate the range of the electrostatic interactions. The bulk salt volume fraction is converted to real units (mM) with the conversion factor ϕ^b_salt/l³N_Av.

A wall is placed at the last layer of the lattice which models the second particle. The properties of the second particle, i.e. the surface charge density and the χ-parameters, are taken to be the same as for the TPM. The relative permittivity ε used for water is 80 and for all other components ε = 10. The surface potential of the particles is affected by the grafted polymers due to their different relative perimittivity with respect to water, resulting in different surface potentials for the interacting particles. The surface potentials mentioned in this article, obtained from the SF–SCF calculations, are always the values for the bare particle. When the salt concentration is varied, the surface charge density of the particles is modified accordingly, so that the surface potential of the particles is unaffected by salt concentration.

The interaction potential is determined by calculating the difference in free energy of the system at large particle separation (no interaction) and the free energy of the system at a certain interparticle distance h as a function of this distance h. Here the system is considered to be in restricted equilibrium, where the number of polymers in between the surfaces is constant and the chemical potential is allowed to change as a function of distance. In this case the dimensionless interaction potential is given by:³¹

where N_p is the number of anchored polymers in between the surfaces (equal to Γ_p times the surface area), μ_p is the chemical potential of the polymers, and Ω(∞) and μ_p(∞) are the grand potential of the system and the polymer chemical potential in an external bulk reservoir that is in equilibrium with the system of interest. During the interaction calculations the PO segments are pinned to the ten layers closest to the TPM surface so that all Pluronic surfactants are adsorbed to the surface and there are no block copolymers in the bulk. Finally, the plate–plate interaction is converted to a sphere–sphere interaction by using the Derjaguin approximation.³²

We emphasize here that the SF–SCF calculations in this study demonstrate the proof of principle for selective assembly of bare and polymer-coated colloidal particles obtained by changing the Debye screening length. The selective assembly is solely obtained through the competition between electrostatic repulsion and bridging attraction and does not depend on specific chemical interactions. Therefore, it is expected that the exact values for the SCF parameters used in this study do not have a qualitative influence on the results but only affect the shape of the interaction curves, the screening length needed to form bonds, and the selectivity of those bonds.

3 Results and discussion

In this section the main results of the experimental and theoretical investigations are discussed and compared. First we focus on the polymer-mediated assembly of bare particles on polymer-coated spherical particles and investigate the electrostatic and polymeric interactions that are involved. Finally we investigate the selective assembly of colloidal tracers on polymeric dumbbells and discuss how to influence the selectivity of this assembly.

3.1 Polymer-mediated colloidal bonds

Polymer bridging traditionally results in random flocculation.³³ We achieve specific binding in our model system comprising F108-TPM and bare silica because polymer bridging occurs exclusively between these two species. This complementarity is enabled by the strong anchoring of the hydrophobic Pluronic core to the TPM, which keeps the water phase polymer-free and allows the silica surface to remain bare.

Electrostatic repulsion offers control over assembly. Negatively charged F108-TPM and silica are initially stable when mixed, however, when their charge is screened, the particles can come close to each other and bind (Fig. 3a). In this way, salt concentration is used to trigger the formation of polymer-mediated colloidal bonds. In Fig. 3b, for example, a mixture containing F108-TPM and silica particles remains stable when no salt is added to the system. A moderate 25 mM NaCl concentration, however, allows the particles to recognize each other and form clusters (Fig. 3c).

Fig. 3 Polymer-mediated colloidal bonds. (a) Schematic of polymer-mediated binding. Polymer-coated and bare particles are initially stable due to long-ranged electrostatic repulsion. When the charge is screened with salt, the particles can closely approach one another and the polymer can adsorb onto the bare surface to form a colloidal bond. (b and c) Optical micrographs of a mixture of F108-TPM and silica tracers at different salt concentrations. Without salt (b), the mixture is stable, and at 25 mM NaCl (c) clusters rapidly form. (b and c) Scale bars 4 μm. (d) SEM micrograph of clusters formed from a large F108-TPM core and small silica shells. (e) SEM micrograph of tetrahedral clusters formed from small F108-TPM cores and large silica shells. (d and e) Scale bars 2 μm.

Different particles can be easily combined in this fashion to generate an array of colloidal products. Various cluster geometries, for instance, are easily accessible by changing the core:shell size ratio. In Fig. 3d and e, a large core and small shells lead to a colloidosome structure, while a small core and larger shells result in tetrahedrally coordinated clusters.

3.2 Selective binding

Beyond simply triggering adhesion, salt concentration can be used to make tracers select one type of polymer-coated surface over another. For example, long brushes can form bonds at a longer Debye screening length (λ_D) than shorter brushes. Experimentally, two different polymer brushes, F108 (long) and F68 (short), are installed onto TPM surfaces. Since the polymer is grafted to the TPM surface during polymerization, F108-TPM and F68-TPM can be mixed together without polymer exchange, retaining their distinct brush lengths. The two particles begin forming bonds with bare silica at different salt concentrations, leading to selective adhesion of tracers.

Schematized in Fig. 4, a mixture of F108-TPM, F68-TPM, and silica display three assembly behaviors at varying salt concentrations. For instance, both brushes are electrostatically stabilized when λ_D is long (≈8 nm). At a λ_D of 4 nm, tracers begin adhering to F108-TPM, however the F68-TPM brush is too short to form polymer bonds. At shorter λ_D (≈2 nm), both brushes are activated, and tracers adhere indiscriminately. Shown also in Fig. 4 is an experimental example of selective assembly of silica tracers onto F108-TPM, while F68-TPM (fluorescent) remains stable.

Fig. 4 Selective bonds on polymer brushes of different lengths. An optical micrograph of a mixture of F108-TPM, F68-TPM, and tracers at λ_D = 4 nm reveals selective assembly, as tracers bind solely to F108-TPM while F68-TPM (fluorescent) remains stable. Scale bar 4 μm. Bottom left panel: F108-TPM particle coated in tracers. Bottom right panel: Stable F68-TPM particle. Inset: Schematic representation of the selection mechanism for tracers. For a large λ_D, both F108-TPM (red) and F68-TPM (green) are stable. As λ_D shrinks, F108-TPM can collect tracers, while F68-TPM remains stable. With a short λ_D both particles are able to collect tracers.

3.3 Effect of block copolymer composition

The range of screening lengths where selective adsorption of the silica tracers occurs depends on the thickness of the polymer brush. The effect of the block lengths of the Pluronic surfactants on the hydrodynamic thickness of the surfactant brush at the TPM/water interface was investigated with SCF. The hydrodynamic brush thickness δ_h and the adsorbed amount Γ for varying number of EO units n and number of PO units m are shown in Fig. 5a and b. The brush thickness δ_h increases roughly linearly as a function of the hydrophilic chain length n (Fig. 5a), which is in agreement with what is expected from scaling relations for grafted polymer chains.³⁴ There is a slight decrease in the slope of the curve due to the decrease of the adsorbed amount of polymers at the interface Γ as a function of the hydrophilic block length n (Fig. 5b). Because of this lower adsorbed amount the polymer coils can occupy more space parallel to the surface, resulting in less stretching of the polymers and therefore a slightly smaller hydrodynamic brush thickness. In contrast to the hydrophilic block length, a larger hydrophobic block length results in a slight increase of the adsorbed amount of the surfactants. As a result, the hydrodynamic brush thickness also becomes somewhat larger as a function of m due to the extra volume occupied by the PO blocks and a small increase of the stretching of the polymers. A larger hydrophobic block length of the Pluronic surfactants leads to a smaller increase in the brush thickness with respect to a larger hydrophilic block length, however it does lead to a more dense brush than a larger hydrophilic block length. Illustrative volume fraction profiles for Pluronic surfactants with different block lengths are shown in Fig. 5c–e.

Fig. 5 (a) Hydrodynamic brush thickness δ_h and (b) adsorbed amount Γ of an EO_nPO_mEO_n surfactant brush layer at the TPM/water interface as a function of n (black) and m (gray) calculated using SF–SCF theory. (c–e) Illustrative volume fraction profiles for (n = 76, m = 56), (n = 160, m = 56) and (n = 76, m = 89), respectively.

3.4 Colloidal interactions

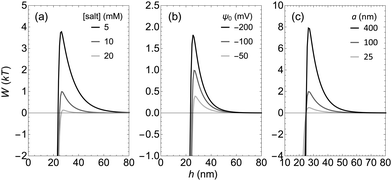
To further study the interactions involved in the selective assembly, the interaction potential between polymer-coated and bare-TPM particles is investigated. The interaction potential between a negatively charged TPM particle with an F108 polymer brush and a second negatively charged bare TPM particle is shown in Fig. 6a. At large particle separation, the interaction between the particles vanishes. A repulsion develops when the particles come closer due to the overlap of the electrostatic double layers. Below a certain separation distance h the interaction turns from repulsive to strongly attractive due to a bridging attraction. It arises due to the adsorption of the polymers on the surface onto the second bare particle. Fig. 6b shows an example of the volume fraction profile of the polymer brush at h = 24 nm where there is an attraction of roughly 2kT. At this distance the surfactant covers about 10% of the surface of the second particle, leading to a bridging attraction that is strong enough to compensate the electrostatic repulsion and induce an overall effective attraction. The range of the bridging attraction is significantly larger than the hydrodynamic thickness of the polymer brush which is 13.4 nm (see Fig. 2b) for this specific Pluronic surfactant. This is because the bridging attraction is so favourable that the polymers stretch,³⁵ reducing their configurational entropy, to adsorb at the surface of the bare particle as can be seen in the volume fraction profile of the polymer brush. It can be argued that this stretching might not occur in an experimental system since the surfactants have to cross an energy barrier to adsorb onto the surface of the second particle due to the stretching of the polymers to reach the thermodynamic energy minimum shown in Fig. 6b. However it can be expected that the range of the bridging interaction is indeed longer than the hydrodynamic brush thickness since some percentage of the surfactant tails will extend farther than the hydrodynamic thickness (as seen in Fig. 2b). Moreover, in an experimental system the polymers have a certain polydispersity and the extension of the chains is fluctuating, increasing the likelihood that the surfactants reach the second particle at distances larger then δ_h.

Fig. 6 (a) Interparticle separation distance h dependence of the interaction potential W between negatively charged F108-TPM and bare-TPM. The radius of the particles is 50 nm, the salt concentration is 10 mM and the surface charge density of both particles is 29.5 mC nm⁻² resulting in a surface potential of −100 mV for the bare particle. (b) Volume fraction profile of the polymer brush at an interparticle distance of 24 nm corresponding to the red dot in panel (a).

The height of the maximum in the interaction potential curve that represents the electrostatic repulsive barrier depends on several parameters. The effects of the salt concentration, the surface potential (ψ₀) and the radius of the particles (a) on the potential curve are shown in Fig. 7. The salt concentration tunes the range of the electrostatic repulsion, however the range of the bridging attraction is hardly affected. As a result, there is an electrostatic barrier against bridging flocculation at low salt concentrations, but at higher salt concentrations, the range of the electrostatic repulsion becomes smaller and the barrier height decreases. The strength of the electrostatic repulsion can also be tuned with the surface potential and the size of the particles. When the surface potential or the size of the particles increases, the overlap of the electrostatic double layers increases leading to a stronger repulsion and therefore a higher repulsive barrier in the interaction potential curve.

Fig. 7 Influence of salt concentration (a), surface potential ψ₀ (b) and particle radius a (c) on the interaction potential W for F108-TPM interacting with bare-TPM, determined using numerical SF–SCF lattice computations. Unless otherwise indicated, the radius of the particles is 50 nm, the salt concentration is 10 mM and the surface charge density, equal for both interacting particles, is chosen such that the surface potential of the bare particle is −100 mV. The surface charge density in the calculations for panel (b) is varied to obtain surface potentials of −50 mV, −100 mV and −200 mV for the bare particle.

3.5 Regioselectivity on Janus dumbbells

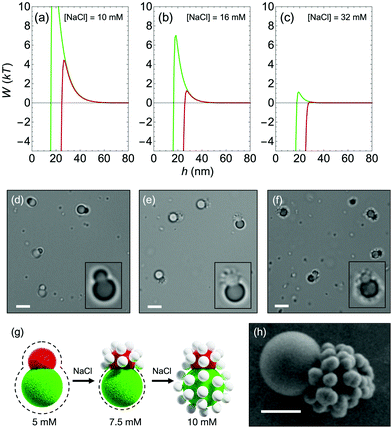
With two brushes installed on a single particle, tracers can be directed to adhere to specific areas on that particle. The binary brush particles take the form of Janus colloidal dumbbells, whose synthesis is described in Section 2.1. Using SF–SCF, we show that the dumbbells have a different activation barrier for the two lobes. In Fig. 8a–c, interaction between bare-TPM, and either F108-TPM (red) or F68-TPM (green) is plotted for different salt concentrations. Because the surface charge densities and surface potentials of the particles in the experimental system are not known, the surface charge densities in the calculations were chosen such that the surface potential of the bare particles is −100 mV, which is assumed to be a reasonable value for charged colloidal particles. Due to the different brush thicknesses of δ_h = 13.4 nm and δ_h = 8.1 nm for F108 and F68, respectively, we see that the activation barrier for F108 is lower in all cases. At low salt concentrations (Fig. 8a), however, there is still a significant electrostatic repulsive barrier for both lobes, indicating that the whole dumbbell will remain tracer free. In Fig. 8b, the increased salt concentration decreases the activation barrier for F108 to roughly 1kT, leading to tracer adhesion, while the short brush still faces a large electrostatic barrier. Finally, at high salt concentrations (Fig. 8c), both barriers are negligible and tracers will adhere everywhere on the dumbbell.

Fig. 8 Regioselectivity on Janus dumbbells. (a–c) SF–SCF interaction potential curves for F108-TPM (red) and F68-TPM (green) interacting with a bare-TPM particle. The radii of all particles is 225 nm, corresponding to the average radius of the experimental tracer particles, and the salt concentrations are 10 mM (a), 16 mM (b) and 32 mM (c). The surface charge density, equal for all interacting particles, is chosen such that the surface potential of the bare particle is −100 mV. (d–f) Optical micrographs of mixtures of Janus dumbbells and tracers at various salt concentrations. At 5 mM NaCl (d), both lobes of the dumbbell are stable. At 7.5 mM (e), the smaller F108-TPM lobe is solely decorated in tracers. At 10 mM NaCl (f), the whole dumbbell is covered in tracers. Scale bars (d–f) are 3 μm. (g) Schematic representation of regioselectivity. Without salt, both lobes have sufficient electrostatic repulsion to remain stable. With salt added, tracers can adhere first to the F108-TPM lobe (red) while the F68-TPM lobe (green) is still electrostatically stabilized. With further salt, both lobes are decorated in tracers. (h) A scanning electron micrograph of a dumbbell with tracers regioselectively adhering to the F108 lobe. Scale bar 1 μm.

Fig. 8d–f show optical micrographs of a dispersion containing negatively charged silica tracers and Janus dumbbells, verifying the adsorption trend that was expected from the theoretical SF–SCF calculations. At low salt concentrations, there is no tracer adhesion (Fig. 8d), and at high salt concentrations there are tracers on both lobes of the dumbbell (Fig. 8f). At an intermediate salt concentration, however, the silica particles selectively adsorb on the smaller F108-TPM lobe of the dumbbell, while the larger F68-TPM lobe remains bare. A schematic of the assembly behavior is shown in Fig. 8g, where the F108-TPM (red) surface is the first to become decorated with tracers as λ_D shrinks, and F68-TPM (green) is eventually decorated as well. Fig. 8h shows a SEM micrograph of a dumbbell from Fig. 8e, with tracers on the F108-TPM lobe.

The exact salt concentrations where the selective adsorption takes place in the experimental system do not match quantitatively with the theoretical predictions from Fig. 8a–c. A likely reason for this difference is that the electrostatic interactions do not correctly match with the experimental system. The surface potentials of the particles in the experimental system do not exactly match the surface potentials in the theoretical model and the size of both dumbbell lobes and the adsorbate particle in the model are taken to be equal to the size of the experimental silica particles. Also the range of the electrostatic interactions is slightly overestimated due to the value chosen for the lattice unit size as mentioned in Section 2.2.3. The bridging interactions in the calculations could also be made to resemble the experimental system more closely by modeling the adsorbate particle in the calculations specifically as a silica particle. A more realistic model of PEO adsorption on a silica surface was proposed by Postmus et al.,³⁶ here we use a general model for the proof of principle of regioselectivity through polymer brushes with different thickness. Finally, the thickness of the polymer brushes might be underestimated in the SF–SCF model due to the mean field approximation where fluctuations are not taken into account.¹² Polydispersity of the block copolymers, that can lead to an increased effective brush thickness,³⁷ is also not taken into account in our model.

Regioselectivity is determined by the difference between the height of the repulsive barriers of the dumbbell lobes interacting with a bare particle (shown in Fig. 8a–c). This difference depends mostly on the brush thickness between the two dumbbell lobes, set by the composition of the polymers. A large difference in brush thickness leads to more selective assembly by widening the range of salt concentrations where assembly can be found. Moreover, particle properties like size and surface potential affect the strength of the electrostatic repulsion, as seen in Fig. 7, and can further enhance the contrast between the energy barriers at each lobe. This can potentially lead to a system with three distinct polymer lengths for increased complexity.

4 Conclusions

We have demonstrated the possibility of polymer-mediated selective adsorption of particles on colloidal dumbbells that contain polymer brushes with a different thickness at each lobe. The method discussed here is generally applicable for surfaces that contain polymer brushes with different thickness and does not require specific interactions such as complementary DNA strands, but is obtained simply by tuning electrostatic and polymeric interactions. Currently, polymer-mediated adsorption results in irreversible and non-reconfigurable binding, preventing ordered structures such as crystals from forming, so future systems will look to achieve reversibility between polymer-coated and bare surfaces. Further, materials such as polynipam microgels are an attractive choice for polymer-mediated interactions, since properties such as brush length can be controlled by various stimuli, allowing for dynamic tuning of the interaction range. Other applications of polymer-mediated interactions include the use of more complex polymer-coated patchy particles for directional colloidal self-assembly.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the NSF CAREER award DMR-1653465. The Zeiss Merlin FESEM was acquired through the support of the NSF under award number DMR-0923251. J. O. and R. T. are grateful for financial support from the Dutch Ministry of Economic Affairs of the Netherlands via The Top-consortium Knowledge and Innovation (TKI) roadmap Chemistry of Advanced Materials (CHEMIE.PGT.2018.006).

References

1. W. Poon, Science, 2004, 304, 830–831.
2. Y. Xia, B. Gates, Y. Yin and Y. Lu, Adv. Mater., 2000, 12, 693–713.
3. Y. A. Vlasov, X.-Z. Bo, J. C. Sturm and D. J. Norris, Nature, 2001, 414, 289–293.
4. M. E. Leunissen, C. G. Christova, A.-P. Hynninen, C. P. Royall, A. I. Campbell, A. Imhof, M. Dijkstra, R. van Roij and A. van Blaaderen, Nature, 2005, 437, 235–240.
5. Q. Chen, S. C. Bae and S. Granick, Nature, 2011, 469, 381–384.
6. S. Sacanna, W. T. M. Irvine, P. M. Chaikin and D. J. Pine, Nature, 2010, 464, 575–578.
7. Y. Wang, Y. Wang, D. R. Breed, V. N. Manoharan, L. Feng, A. D. Hollingsworth, M. Weck and D. J. Pine, Nature, 2012, 491, 51–55.
8. J.-R. Roan and T. Kawakatsu, J. Chem. Phys., 2002, 116, 7295–7310.
9. R. Tuinier and G. J. Fleer, Macromolecules, 2004, 37, 8754–8763.
10. J. F. L. Duval, F. A. M. Leermakers and H. P. van Leeuwen, Langmuir, 2004, 20, 5052–5065.
11. M. Vis, R. Tuinier, B. W. M. Kuipers, A. Vrij and A. P. Philipse, Soft Matter, 2018, 14, 4702–4710.
12. G. J. Fleer, M. A. Cohen Stuart, J. M. H. M. Scheutjens, T. Cosgrove and B. Vincent, Polymers at Interfaces, Springer, Netherlands, 1998.
13. G. J. Fleer, Adv. Colloid Interface Sci., 2010, 159, 99–116.
14. G. H. Fredrickson, The Equilibrium Theory of Inhomogeneous Polymers, Oxford University Press, 2005.
15. C. van der Wel, R. K. Bhan, R. W. Verweij, H. C. Frijters, Z. Gong, A. D. Hollingsworth, S. Sacanna and D. J. Kraft, Langmuir, 2017, 33, 8174–8180.
16. W. Stöber, A. Fink and E. Bohn, J. Colloid Interface Sci., 1968, 26, 62–69.
17. J. M. H. M. Scheutjens and G. J. Fleer, J. Phys. Chem., 1979, 83, 1619–1635.
18. J. M. H. M. Scheutjens and G. J. Fleer, J. Phys. Chem., 1980, 84, 178–190.
19. P. J. Flory, J. Chem. Phys., 1942, 10, 51–61.
20. M. L. Huggins, J. Phys. Chem., 1942, 46, 151–158.
21. P. J. Flory, Principles of Polymer Chemistry, Cornell University Press, 1953.
22. B. Vincent, Colloids Surf., 1990, 50, 241–249.
23. P. N. Hurter, J. M. H. M. Scheutjens and T. A. Hatton, Macromolecules, 1993, 26, 5592–5601.
24. G. P. van der Beek, M. A. Cohen Stuart, G. J. Fleer and J. E. Hofman, Macromolecules, 1991, 24, 6600–6611.
25. S. Sacanna, W. K. Kegel and A. P. Philipse, Langmuir, 2007, 23, 10486–10492.
26. S. Sacanna, W. K. Kegel and A. P. Philipse, Phys. Rev. Lett., 2007, 98, 13–16.
27. M. Youssef, A. Morin, A. Aubret, S. Sacanna and J. Palacci, Soft Matter, 2020, 16, 4274–4282.
28. T. L. Hill, J. Chem. Phys., 1962, 36, 184111.
29. M. A. Cohen Stuart, F. H. W. H. Waajen, T. Cosgrove, B. Vincent and T. L. Crowley, Macromolecules, 1984, 17, 1825–1830.
30. J. M. H. M. Scheutjens, G. J. Fleer and M. A. Cohen Stuart, Colloids Surf., 1986, 21, 285–306.
31. G. J. Fleer and J. M. H. M. Scheutjens, Colloids Surf., 1990, 51, 281–298.
32. B. Derjaguin, Kolloid-Z., 1934, 69, 155–164.
33. R. Evans and D. H. Napper, Nature, 1973, 246, 34–35.
34. P. G. de Gennes, Macromolecules, 1980, 13, 1069–1075.
35. J. G. J. L. Lebouille, F. A. M. Leermakers, M. A. Cohen Stuart and R. Tuinier, Phys. Rev. E, 2016, 94, 1–15.
36. B. R. Postmus, F. A. M. Leermakers and M. A. Cohen Stuart, Langmuir, 2008, 24, 1930–1942.
37. W. M. de Vos and F. A. M. Leermakers, Polymer, 2009, 50, 305–316.

---

Footnote

† These authors contributed equally to this work.

---