Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Development of mechanical properties of regenerated cellulose beads during drying as investigated by atomic force microscopy†
Hailong
Li
 *a,
Katarzyna
Mystek
*a,
Katarzyna
Mystek
 a,
Lars
Wågberg
a,
Lars
Wågberg
 ab and
Torbjörn
Pettersson
ab and
Torbjörn
Pettersson
 *ab
*ab
aDepartment of Fibre- and Polymer Technology, KTH Royal Institute of Technology, Teknikringen 56, 100 44 Stockholm, Sweden. E-mail: haili@kth.se; torbj@kth.se
bWallenberg Wood Science Centre, KTH Royal Institute of Technology, Teknikringen 56, 100 44 Stockholm, Sweden
First published on 16th June 2020
Abstract
The mechanical properties as well as the size changes of swollen cellulose beads were measured in situ during solvent evaporation by atomic force microscopy (AFM) indentation measurement combined with optical microscopy. Three factors are proposed to govern the mechanical properties of the cellulose beads in the swollen state and during drying: (i) the cellulose concentration, (ii) the interaction between the cellulose entities, (iii) the heterogeneity of the network structure within the cellulose beads.
Due to its abundance, renewability, biodegradability and excellent mechanical properties, cellulose has been used as an engineering material for thousands of years.1,2 More recently, the demand for sustainable products has increased and cellulose has been used in a variety of applications including high tenacity rayon,3,4 hydrogels and aerogels,5–7 transparent films,8–10 and microspheres and beads,11 just to mention a few. Many of such products are shaped during the regeneration of the dissolved cellulose polymer and are largely used in dry environments where they maintain good strength and toughness. However, the mechanical properties of cellulose-based materials drastically change in wet or humid environments, which has been a severe drawback in many applications. While overall mechanical properties of cellulose-based materials are often lower in the wet state, it should be stressed that this is not the result of reduced stiffness of individual cellulose fibres (or cellulose nanofibrils) but specifically due to the loss of fibre/fibre and fibril/fibril interactions. Therefore, to expand the potential use of sustainable products it is important to prepare a model sample system for cellulose-based materials and to evaluate its mechanical properties in the wet state, and also the evolution of these properties during the drying process. However, the model systems must be well-defined and have very smooth surfaces to allow them to be used in model adhesion testing. In a recent development it was shown that it is indeed possible to prepare nm smooth cellulose spheres, consisting mainly of non-ordered cellulose.12 It has also been shown they are suitable for fundamental swelling studies.13,14
Atomic force microscopy (AFM) is a powerful technique that has been used to investigate the morphology and mechanical properties of a variety of materials, such as cells,15,16 enzymes,17 polymer films,18,19 among a countless number of others materials, either in dry or wet state. Using AFM, the mechanical properties (e.g. Young's modulus) of a material can be determined by measuring force as a function of indentation depth, and fitting such data with contact models, such as the Hertz model,20 the Derjaguin, Muller and Toporov (DMT) model,21 or the Johnson, Kendall and Roberts (JKR) model.22 These three different contact mechanic models were developed to suit different conditions based on the type of adhesive interactions between the probe and the sample. The Hertz model is used when no adhesion is present, the JKR model is used for large probes, soft samples and large adhesion, while the DMT model is used for small probes, stiffer samples and moderate adhesion. Thus, with AFM it is possible to perform indentation measurements and fit the captured data with the above-mentioned models to accurately evaluate the mechanical properties of materials.
Millimeter-sized and nm smooth amorphous cellulose gel beads, were used as model materials. They were successfully prepared by precipitating the solution of cellulose, dissolved in a mixture of lithium chloride and N,N-dimethylacetamide (LiCl/DMAc), into a non-solvent (ethanol or water).12–14,23,24 Apart from being used in fundamental swellings studies13,14 these cellulose gel beads have also been used as a model material to study the adhesion between cellulose surfaces and to determine influence of polymer grafting on the adhesion between modified beads on a molecular scale.12,23 Additionally, the kinetics of microstructural changes during the drying of the beads were investigated by using small/wide angle X-ray scattering (SAXS/WAXS).24 Furthermore, AFM indentation has been used to measure the elasticity of cellulose beads in the wet state as well as cellulose fibres in liquid.25–27 However, as many cellulose based materials are prepared by drying from a swollen state where cellulose fibres/fibrils are dispersed in water or other solvents, it is of outmost importance to determine how the mechanical properties of the beads, used to mimic the behavior of the fibres are developing during the removal of water or other solvents removal. Together with the adhesion between the surfaces, this behavior will determine how well the surfaces will consolidate towards each other to create a dry adhesive joint. This can be performed by AFM indentation measurements during drying of the beads.
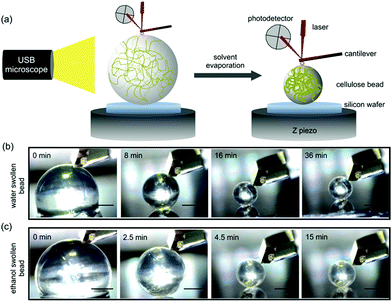
In the present work, two different cellulose beads (water swollen and ethanol swollen) were prepared according to our previous work.24 Details of the cellulose beads fabrication are summarized in the ESI.† Water swollen beads were selected since most industrial processes of cellulose today are water based. However, to evaluate differences during the drying process, based on the solvent used, ethanol swollen beads were selected since ethanol has lower surface tension and lower vapor pressure compared to water. Also, the dissociation of carboxylic acids groups, usually found in cellulose-rich materials, behave differently in ethanol and the arrangement of the solvent molecules around the hydroxyl groups will differ in ethanol compared to water as solvent. AFM indentation measurements were conducted to determine the in situ mechanical properties of these two types of cellulose beads during the solvent evaporation (Fig. 1a). The measured force vs. indentation profiles were then fitted to a linearized DMT model, due to adhesion between the indenting probe and the bead, to extract the Young's modulus for water swollen and ethanol swollen cellulose beads during the drying process.
Representative optical microscopy images of water swollen and ethanol swollen beads during different stages of drying are shown in Fig. 1b and c, respectively. The bead size decreases with evaporation time, while the spherical shape is retained throughout the evaporation process. The diameters of water swollen and ethanol swollen beads throughout the drying process at 21 °C and 24% RH are shown in Fig. 2a. It can be observed that the ethanol swollen beads have a larger initial diameter (before drying) than the water swollen beads. The most probable explanation is that cellulose chains, which are in a fully dissolved state in the cellulose/DMAc/LiCl solution, start to form small aggregated structures locally during the washing of the beads that remove the DMAc/LiCl. LiCl has a higher solubility in water than in ethanol, at room temperature,28,29 which suggests that LiCl will be more readily leached from the beads when in water. This will likely result in slightly larger aggregates inside the final water swollen beads, as suggested from the SAXS results that water and ethanol swollen beads have 2.8 nm and 2.2 nm aggregate structures, respectively.24 During drying, the diameter of the water swollen bead decreases from 1335 μm to 1040 μm during the first 6 min and then decreases faster to 550 μm over the next 7 min, following a period where the diameter stays relatively constant. These evaporation kinetics are consistent with the results in our previous work.24 For the ethanol swollen beads, the diameter decreases rapidly from 1610 μm to a constant value of 650 μm over a period of 6 min. The faster evaporation rate, compared to the water swollen beads, is due to the lower vapor pressure and overall faster evaporation of ethanol. Similar results were obtained when drying the beads under different conditions (see Fig. S2 in ESI†). The data points presented in Fig. 2 are from drying of one water swollen and one ethanol swollen bead as representative data sets. Due to experimental conditions; variation in initial diameter between different beads and different imaging capturing timing, errors for these measurements should be calculated by “binning” both for the time and the diameters. This will make a corresponding plot less clear with errors in both time and diameter. Thus, no error bars in Fig. 2 are added.
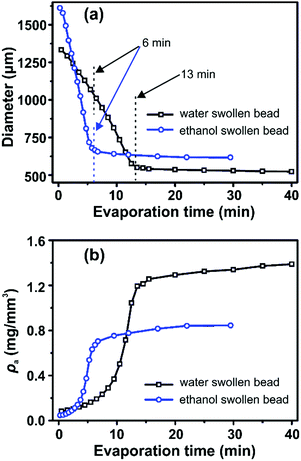 | ||
| Fig. 2 (a) The diameter and (b) cellulose apparent density (ρa) of water swollen and ethanol swollen beads during solvent evaporation estimated from optical microscopy images. | ||
The apparent density (ρa) of the cellulose inside the swollen beads was calculated as: ρa = m0/V, where m0 is the dry mass of cellulose inside of the beads and V is the volume of the bead. Using the diameter values (d) plotted in Fig. 2a, V was calculated through the equation: V = πd3/6. Thus, ρa is calculated according to: ρa = 6m0/πd3. For both water swollen and ethanol swollen beads m0 was obtained by weighing the corresponding dry beads (dried at 105 °C for 24 hours). Both water swollen and ethanol swollen beads were measured to have the same mass per bead (m0 = 0.104 mg). The calculated ρa values are shown in Fig. 2b. Following the shape of the curves in Fig. 2b, the development of ρa can be divided into three distinct drying phases; (i) initial drying during which ρa increases slowly in the first few minutes, (ii) a rapid increase in density and (iii) a plateau of near constant density in the later phases of drying.
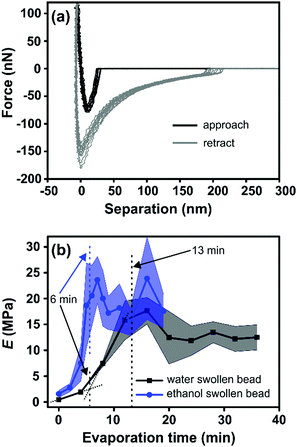
Fig. 3a shows the representative force vs. separation curve measured for a water swollen bead after an evaporation time of 16 min. The zero point in separation is arbitrary set at load zero on approach. The black line shows the force upon approach of the probe to the bead surface and the grey line displays the retraction. The force range used to calculate the elastic modulus of the bead was between 10 to 100 nN. This indentation part of the approach force curves was fitted to a linearized DMT model, taking into account the maximum attractive force on approach (e.g. force at jump-in) as the adhesive contribution to the applied load during the indentation.27 The linearized DMT model can be summarized as:27
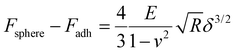 | (1) |
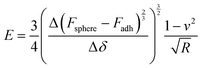 | (2) |
The Young's modulus of the swollen beads was calculated using the above linearized eqn (2), as the fitting of a linear slope of (Fsphere − Fadh)2/3vs. δ is proportional to the Young's modulus. The fitting results from representative drying series are presented in Fig. 3b. For the water swollen bead, the Young's modulus increases from 0.45 MPa to 2.60 MPa (estimated by the crossing point of the two dotted lines in Fig. 3b) during the first 6 min, and then increases to 16.3 MPa over the next 7 min. In the later stages of drying the modulus decreases and remains relatively constant near 12 MPa. Similarly, for ethanol swollen beads, the Young's modulus rapidly increases from 1.60 MPa to ca. 20.50 MPa in the first 6 min, ultimately reaching a maximum of 23.60 MPa (at 7 min), from which the modulus decreases and remains near 18 MPa. It is interesting to note that for the water swollen cellulose beads there is a close correlation to the mechanical properties of wood fibres that have been delignified to a low yield (i.e. most of the lignin and a large part of the hemicellulose have been removed) and have a wet modulus between 1 and 10 MPa as reported.32,33 This again shows that these water swollen beads are excellent models for cellulose-rich fibres.
The Young's modulus of water swollen beads before drying was measured to be 0.45 MPa (Fig. 3b). This value is one order of magnitude larger than previous results, 0.044 MPa,13,27 obtained via similar measurements. While this difference is large, it should be noted that a higher cellulose concentration was used to prepare the cellulose beads in the present work; 1.5 wt% compared to 1.0 wt% in our previous work.13,27 Thus, this shows that the Young's modulus of the swollen beads, as expected, depends on the cellulose concentration used during precipitation. This is also supported by the increase of Young's modulus for water swollen beads during drying process (Fig. 3b), in which the cellulose concentration increases with increasing evaporation time as well as the apparent density. Based on this, it could be expected that the Young's modulus of ethanol swollen beads before drying should be lower than that of water swollen beads, as the ethanol swollen beads have a lower cellulose concentration due to their larger diameter at the same mass of dry cellulose in the beads. However, contradictorily to this the Young's modulus of ethanol swollen beads, before drying, is 1.6 MPa. Previous studies using SAXS24 indicate that the microstructure of water swollen and ethanol swollen beads are similar before drying. Thus, the difference in the Young's modulus between water swollen and ethanol swollen beads is not the result of differing microstructures within the bead. Therefore, the important difference between the two swollen beads is the liquid in which they are incubated: water or ethanol. It is well known that the interaction between cellulose and water is stronger than the interactions between cellulose and ethanol, since water has better hydrogen bonding ability compared to ethanol. Additionally, the attractive van der Waals interactions between cellulose and cellulose across a liquid medium are stronger in water compared to ethanol.34 This will most probably result in a higher mobility of the cellulose entities inside the water swollen beads allowing for a higher consolidation of these structures as the water is evaporated compared with the ethanol swollen beads. For water swollen systems it is well accepted that the cellulose surfaces have at least one layer of tightly bound water molecules which is not the case for ethanol.35 This also means that the friction will be higher between the cellulose entities inside the ethanol swollen beads which means that this structure will be “locked” at a lower solids content compared with the water swollen beads. This is hence also a plausible explanation why the water swollen beads have a lower Young's modulus than the ethanol swollen beads despite having a higher cellulose concentration in the early stages of drying. Therefore, the interaction between the cellulose entities in the different solvents will have a large influence on the mechanical properties of the swollen cellulose beads.
From the TGA data (Fig. S3, ESI†), it is also shown that both water swollen and ethanol swollen beads have approximately 6 wt% of solvent remaining after 4 hours of drying, indicating that solvent is maintained inside the beads throughout the time selected for the AFM measurements (less than 40 minutes, Fig. 3b). From these results, it can hence be suggested that the mechanical properties of the beads are determined both by the cellulose concentration in the bead and the interaction between the cellulose entities which should be of similar dimensions as both types of beads were initially precipitated in ethanol.
Interestingly, both the change in apparent cellulose density, ρa, and the change in Young's modulus, E, as a function of evaporation time show a similar shape (Fig. 2b and 3b respectively). Therefore, the Young's modulus was plotted as a function of ρa for both water swollen and ethanol beads (Fig. 4). Surprisingly, the Young's modulus of ethanol swollen beads increases linearly with ρa during the early drying phase (before 6 min). After 6 min the Young's modulus stays relatively constant and the bead diameter does not significantly change (Fig. 2a). According to previously reported in situ SAXS/WAXS measurements,24 there is no significant microstructure changes and no crystalline structures formation within the ethanol swollen beads during this initial drying phase. As a result, the linear increase of the Young's modulus is largely attributed to the increase of ρa during drying. This result is consistent with the scaling law proposed by de Gennes:36E ≅ cT/N, where c is the concentration, T is the temperature, and N is the number of monomers. In this work, ρa is a measure of c and consequently E ∝ ρa is applied in the early drying phase. Similarly, for water swollen beads there is a linear increase in Young's modulus with ρa during the early drying phase (before 6 min). However, after that point the increase of the Young's modulus with ρa slows until the bead diameter plateaus (around 13 min). During this drying phase SAXS/WAXS measurements24 have shown a sharp structural transition within the water swollen beads, where cellulose II hydrate structure is formed and transformed to cellulose II structure continuously as the final solvent is removed. However, the very low degree of crystallinity will not enhance the strength of the water swollen bead. As a result, a heterogeneous network is formed, in which large cellulose II aggregated structures (10 nm) are connected by less associated cellulose chains and the formation of this heterogeneous network is potentially the reason as to why the Young's modulus does not increase linearly in this phase of the drying. This is probably also one of the reasons why water swollen beads have a smaller diameter than ethanol swollen beads (Fig. 2a) and why the water swollen beads are forming solid beads while the ethanol beads are forming porous beads in the dry state (see SEM images in Fig. S4, ESI†). Therefore, the heterogeneity of the network structure could be considered as an additional factor when describing the mechanical property of swollen cellulose beads.
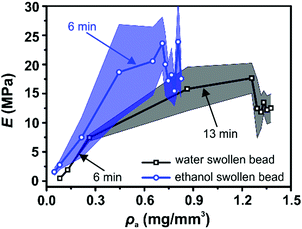 | ||
| Fig. 4 Young's modulus, E, as a function of cellulose apparent density, ρa, for water swollen (black) and ethanol swollen (blue) beads. Different evaporation times are indicated by arrows. | ||
In summary, the results presented here, in combination with previous in situ SAXS/WAXS measurements, reveal that three factors contribute to the overall mechanical properties of swollen cellulose beads: (i) the cellulose concentration within the bead, (ii) the interaction between the cellulose entities within the beads during solvent removal, (iii) the heterogeneity of the network structure formed in the cellulose beads.
Conclusions
In this work, two types of regenerated cellulose beads were prepared by precipitating 1.5 wt% cellulose/LiCl/DMAc solution into ethanol and thoroughly washing with water or ethanol, to create water swollen and ethanol swollen beads, respectively. The evolution of the mechanical properties of the beads were monitored during drying via AFM indentation measurements. The size changes of these swollen beads were simultaneously monitored by optical microscopy. The diameter of both water swollen and ethanol swollen beads decreases without changing the overall spherical shape, and the Young's moduli increase with the solvent evaporation time. The acquired results indicate that there are three factors which dominate the mechanical properties of the beads during the drying process: (i) the cellulose concentration within the bead, (ii) the interaction between the cellulose entities within the beads during solvent removal, (iii) the heterogeneity of the network structure within the cellulose bead. To the knowledge of the authors, this is the first time that mechanical property of swollen cellulose beads has been evaluated throughout the drying process. While, this work provides significant insight into the evolution of the mechanical properties of cellulose beads during drying and an initial insight into the molecular mechanisms responsible for these changes, more studies are needed to fully understand the contributions from each of the proposed mechanisms. By comparison to earlier studies, on the mechanical properties of wet, cellulose-rich fibre walls, the current results show that the beads can be used as model systems for these types of fibres. Since the beads are so much more structurally defined it will be possible to use these beads to probe the interaction between cellulose systems and to predict and explain how different treatments will affect this interaction.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
H. Li acknowledges the ForMAX pre-project by the Swedish Ministry of Enterprise and Innovation for funding. L. Wågberg acknowledges the Wallenberg Wood Science Centre at KTH for financial support.References
- M. T. Postek, A. Vladár, J. Dagata, N. Farkas, B. Ming, R. Wagner, A. Raman, R. J. Moon, R. Sabo, T. H. Wegner and J. Beecher, Meas. Sci. Technol., 2011, 22, 024005 CrossRef.
- R. J. Moon, A. Martini, J. Nairn, J. Simonsen and J. Youngblood, Chem. Soc. Rev., 2011, 40, 3941–3994 RSC.
- K. Perepelkin, Fibre Chem., 2007, 39, 163–172 CrossRef CAS.
- B. Müller, M. Gebert-Germ and A. Russler, Lenzinger Ber., 2012, 90, 64–71 Search PubMed.
- C. Chang and L. Zhang, Carbohydr. Polym., 2011, 84, 40–53 CrossRef CAS.
- W. Gindl, G. Emsenhuber, G. Maier and J. Keckes, Biomacromolecules, 2009, 10, 1315–1318 CrossRef CAS PubMed.
- J. Cai, S. Kimura, M. Wada, S. Kuga and L. Zhang, ChemSusChem, 2008, 1, 149–154 CrossRef CAS PubMed.
- H. Qi, C. Chang and L. Zhang, Green Chem., 2009, 11, 177–184 RSC.
- H. Qi, J. Cai, L. Zhang and S. Kuga, Biomacromolecules, 2009, 10, 1597–1602 CrossRef CAS PubMed.
- Q. Yang, H. Fukuzumi, T. Saito, A. Isogai and L. Zhang, Biomacromolecules, 2011, 12, 2766–2771 CrossRef CAS PubMed.
- M. Gericke, J. Trygg and P. Fardim, Chem. Rev., 2013, 113, 4812–4836 CrossRef CAS PubMed.
- C. Carrick, S. A. Pendergraph and L. Wågberg, ACS Appl. Mater. Interfaces, 2014, 6, 20928–20935 CrossRef CAS PubMed.
- R.-M. P. Karlsson, P. T. Larsson, S. Yu, S. A. Pendergraph, T. Pettersson, J. Hellwig and L. Wågberg, J. Colloid Interface Sci., 2018, 519, 119–129 CrossRef CAS PubMed.
- R.-M. P. Karlsson, P. T. Larsson, P. Hansson and L. Wågberg, Biomacromolecules, 2019, 20, 1603–1612 CrossRef CAS PubMed.
- Q. Li, G. Y. Lee, C. N. Ong and C. T. Lim, Biochem. Biophys. Res. Commun., 2008, 374, 609–613 CrossRef CAS PubMed.
- M. Sato, K. Nagayama, N. Kataoka, M. Sasaki and K. Hane, J. Biomech., 2000, 33, 127–135 CrossRef CAS PubMed.
- C. Kranz, A. Kueng, A. Lugstein, E. Bertagnolli and B. Mizaikoff, Ultramicroscopy, 2004, 100, 127–134 CrossRef CAS PubMed.
- J. Domke and M. Radmacher, Langmuir, 1998, 14, 3320–3325 CrossRef CAS.
- O. Mermut, J. Lefebvre, D. G. Gray and C. J. Barrett, Macromolecules, 2003, 36, 8819–8824 CrossRef CAS.
- H. Hertz, Z. Reine Angew. Math., 1881, 92, 156–171 Search PubMed.
- B. V. Derjaguin, V. M. Muller and Y. P. Toporov, J. Colloid Interface Sci., 1975, 53, 314–326 CrossRef CAS.
- K. L. Johnson, K. Kendall and A. Roberts, Proc. R. Soc. London, Ser. A, 1971, 324, 301–313 CAS.
- A. Träger, G. Klein, C. Carrick, T. Pettersson, M. Johansson, L. Wågberg, S. A. Pendergraph and A. Carlmark, Cellulose, 2019, 26, 1467–1477 CrossRef.
- H. Li, M. Kruteva, K. Mystek, M. Dulle, W. Ji, T. Pettersson and L. Wågberg, ACS Nano, 2020, 14, 6774–6784 CrossRef CAS PubMed.
- T. Pettersson, J. Hellwig, P.-J. Gustafsson and S. Stenström, Cellulose, 2017, 24, 4139–4149 CrossRef CAS.
- J. Hellwig, V. L. Durán and T. Pettersson, Anal. Methods, 2018, 10, 3820–3823 RSC.
- J. Hellwig, R.-M. Karlsson, L. Wågberg and T. Pettersson, Anal. Methods, 2017, 9, 4019–4022 RSC.
- D. R. Lide, CRC Handbook of Chemistry and Physics 86th Edition 2005–2006, CRC Press, Taylor & Francis, Boca Raton, FL, 2005, pp. 4–70 Search PubMed.
- M. Li, D. Constantinescu, L. Wang, A. Mohs and J. R. Gmehling, Ind. Eng. Chem. Res., 2010, 49, 4981–4988 CrossRef CAS.
- R. Roberts, R. Rowe and P. York, Int. J. Pharm., 1994, 105, 177–180 CrossRef CAS.
- E. Chanliaud, K. M. Burrows, G. Jeronimidis and M. J. Gidley, Planta, 2002, 215, 989–996 CrossRef CAS PubMed.
- B. Nilsson, L. Wågberg and D. Gray, in The science of papermaking: transactions of the XIIth Fundamental Research Symposium Oxford 2001, ed. C. F. Baker, FRC, UK, 2001, pp. 211–224 Search PubMed.
- A. Scallan and A. Tigerström, J. Pulp Pap. Sci., 1992, 18, J188–J193 Search PubMed.
- J. N. Israelachvili, Intermolecular and surface forces, Academic Press, 2011 Search PubMed.
- T.-Q. Li, U. Henriksson, T. Klason and L. Ödberg, J. Colloid Interface Sci., 1992, 154, 305–315 CrossRef CAS.
- P.-G. De Gennes and P.-G. Gennes, Scaling concepts in polymer physics, Cornell University Press, 1979 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Details of the swollen cellulose beads fabrication, atomic force microscopy indentation, scanning electron microscopy, and thermal stability of the cellulose beads after drying. See DOI: 10.1039/d0sm00866d |
| This journal is © The Royal Society of Chemistry 2020 |