Open Access Article
Open Access ArticleDetachment of giant liposomes – coupling of receptor mobility and membrane shape†
Hannes
Witt‡
 a,
Marian
Vache‡
b,
Andrea
Cordes
b and
Andreas
Janshoff
a,
Marian
Vache‡
b,
Andrea
Cordes
b and
Andreas
Janshoff
 *b
*b
aMax Planck Institute for Dynamics and Self-Organization, Am Faßberg, 37077 Göttingen, Germany
bInstitute of Physical Chemistry, Tammannstr. 6, 37077 Göttingen, Germany. E-mail: ajansho@gwdg.de; Tel: +49 551 3910633
First published on 19th June 2020
Abstract
Cellular adhesion is an intricate physical process controlled by ligand–receptor affinity, density, mobility, and external forces transmitted through the elastic properties of the cell. As a model for cellular adhesion we study the detachment of cell-sized liposomes and membrane-coated silica beads from supported bilayers using atomic force microscopy. Adhesion between the two surfaces is mediated by the interaction between the adhesive lipid anchored saccharides lactosylceramide and the ganglioside GM3. We found that force–distance curves of liposome detachment have a very peculiar, partially concave shape, reminiscent of the nonlinear extension of polymers. By contrast, detachment of membrane coated beads led to force–distance curves similar to the detachment of living cells. Theoretical modelling of the enforced detachment suggests that the non-convex force curve shape arises from the mobility of ligands provoking a switch of shapes from spherical to unduloidal during detachment.
1 Introduction
Adhesion of cells to the extracellular matrix and adjacent cells plays a pivotal role in tissue morphogenesis, migration, self-recognition, the immune response, synapse formation and embryogenesis. There have been extensive research activities towards the understanding and modelling of cell adhesion in the past decades.1–7 Cell–cell adhesion is mainly mediated by receptors and ligands anchored in apposing membranes obeying a lock-and-key mechanism.3 Non-specific interactions including electrostatic and van der Waals forces are usually negligible due to fluctuations of the cell membrane compensating these usually attractive colloidal interactions.6,8,9 Depending on the anchor-type, ligands and corresponding receptors can be still laterally mobile also within the contact area of two apposing surfaces. This can give rise to formation of clusters or domains enriched in ligand–receptor complexes in the contact zone.10A multitude of different proteins is involved in formation of focal adhesions, which might obscure the basic physical principles. Therefore, giant liposomes and membrane-coated glass beads have been established as the most frequently used model systems for cellular adhesion.8,11–17 It is convenient to use defined model systems to mimic the essential features of cellular adhesion as also found in ancient organisms or in the early onset of adhesion in oncogenesis or inflammation.6,18,19
Among the various different adhesion molecules expressed by adherent cells such as integrins, cadherins, claudins, glycolipids, etc., carbohydrate-mediated recognition is among the weakest but presumably also the most ancient one.20,21 In early metazoans, it is believed that very simple carbohydrate moieties consisting of merely 2–3 sugars played an important role in self-recognition of cells.12,21 Carbohydrate–carbohydrate interactions also occur in the specific cellular recognition between lymphoma and melanoma cells based on gangliotriaosylceramide and sialosyllactosylceramide-dependent adhesion of melanoma cells (high expressor of GM3), which led to spreading and enhancement of cell motility.22,23 There is evidence that carbohydrate–carbohydrate interactions between the ganglioside GM3 and the corresponding receptor lactosylceramide (LacCer) may provide the initial cell type-specific recognition prior to cell type-nonspecific adhesion.22 The underlying carbohydrate–carbohydrate interaction is predominately mediated by divalent cations, especially calcium ions.24
Here, we combine detachment experiments of vesicles and membrane coated glass beads with theoretical considerations to study the impact of receptor mobility of adhesive glycolipids. Both probes display the ligands (ganglioside GM3) to be recognized by the corresponding receptors (lactosylceramide) reconstituted in the apposing solid supported lipid bilayer deposited on planar glass substrates. We found that rigid probes generate convex force–distance curves as also found in contact mechanics, while deformable liposomes with mobile linkers show non-convex retraction curves with an inflection point. Using theoretical modelling we show that the shape of force–distance curves upon retraction from the surface depends on both deformability of the ligand-bearing probes and mobility of ligands and receptors.
2 Theory
2.1 Adhesion energy density of mobile receptors
Assuming that the adhesion energy density w between the vesicle and the supported membrane depends solely on the number of bonds in the contact zone we have:| w = ΓLREb | (1) |
| NL,0 = A0ΓL + AcΓLR | (2) |
Γ L is the equilibrium surface concentration of ligands, A0 = 4πR2 the area of the vesicle in suspension, with the vesicle radius R prior to deformation and Ac = πRc2 denotes the contact area between vesicle and substrate with the radius Rc. Assuming local equilibrium we obtain (see also ESI†):
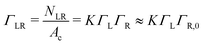 | (3) |
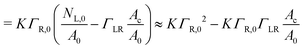 | (4) |
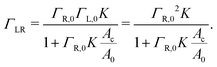 | (5) |
When the binding constant K is sufficiently large such that 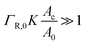 we obtain:
we obtain:
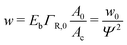 | (6) |
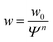 | (7) |
2.2 Analytical model for vesicle detachment with constant tension
To obtain an analytical expression for the force response during vesicle detachment we follow the approach by Brochard–Wyart.25 The contour of the vesicle is described as a surface of constant curvature (uniform pressure insight). The force balance at the contact zone is:f = 2πTRc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ) − πRc2CT sin(θ) − πRc2CT | (8) |
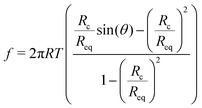 | (9) |
The adhesion energy density w and the contact angle θ are related by Young–Dupré's law:
| w = T(1 − cos(θ)) | (10) |
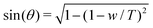 . Using the reduced contact radius
. Using the reduced contact radius 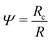 and the reduced force
and the reduced force 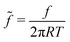 we obtain:
we obtain: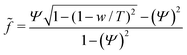 | (11) |
In the case of mobile binding partners we can use eqn (7) for the adhesion energy density w to get the force as a function of the reduced contact radius:
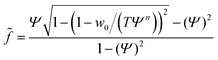 | (12) |
Examining eqn (12) we find that a point of inflection only exists if n > 2 (see ESI†). For n < 2 the force curve is convex at constant tension.
2.3 Numerical model for vesicle detachment
The analytical treatment above yields the force as a function of the reduced contact radius, which impedes comparison to experimental data. However, in order to calculate the force as a function of the vertical distance, as obtained from the experiment, we need to numerically calculate the shape of the vesicle.9,26,27 The procedure has been described in detail previously.9 In brief, the contour of the vesicle is assumed to have rotational symmetry and is parameterized by the function U(r) = sin(β) using the angle β between the normal of the contour and the normal of the substrate. It follows from the Young–Laplace law, that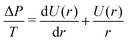 | (13) |
The tension T arises from pre-stress T0 and the relative area dilation α as T = T0 + KAα with α = (A − A0)/A0, where A is the area of the GUV.
In order to obtain the function z(r) describing the contour of the vesicle we numerically integrate 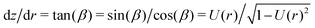 .9 From the contour we can also calculate the volume, area and height of the vesicle by describing it as a solid of revolution.9,27
.9 From the contour we can also calculate the volume, area and height of the vesicle by describing it as a solid of revolution.9,27
The geometrical parameters and the force acting on the vesicle can now be determined for a given lower contact radius by numerically solving a set of equations consisting of the Young–Dupré law (we assume the strong adhesion limit here) at the upper and lower contact (eqn (7) and (10)), the force balance at the equator of the vesicle, volume conservation, and the condition that upper and lower hemisphere of the vesicle are continuous. Then by solving these equations for different contact radii and calculating the height of the vesicle a force–distance curve is constructed. The equations were solved numerically using the Matlab function lsqnonlin. Parameters for all calculations can be found in the ESI.†
3 Results and discussion
3.1 Detachment of GUVs and colloidal probes from SSM
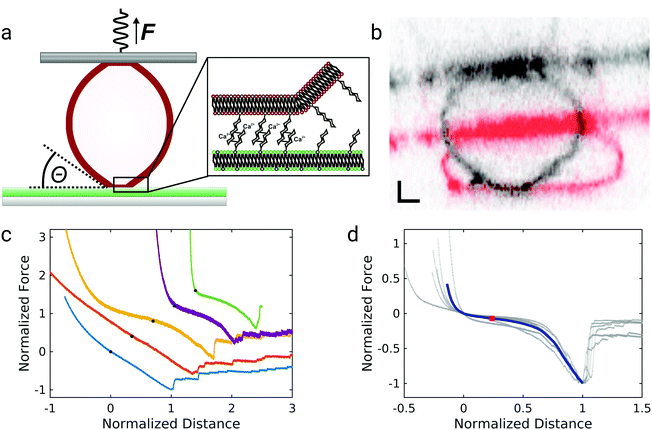
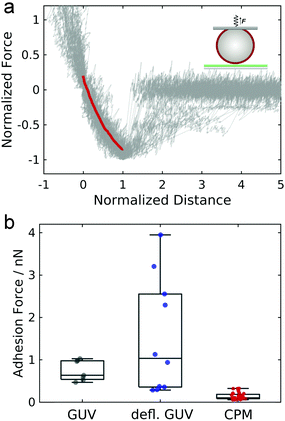
The experimental setup for GUV detachment from solid supported membranes using an atomic force microscope is shown in Fig. 1a: GUVs functionalized with biotinylated lipids and GM3 were allowed to adhere to a fluid supported lipid bilayer containing LacCer for 20 minutes (see also ESI,† Fig. S1 and S2). Firm adhesion between the GUV and the SSM was confirmed by confocal images showing a flat bottom plane of the GUVs (see also ESI,† Fig. S3). This ensures that the unbinding behaviour is not controlled by domain formation or the nucleation of a tight contact between the vesicle and the substrate.28,29 Then an avidin-functionalized AFM cantilever was brought into contact with the GUV and allowed to bind via the strong interaction between avidin and biotin. When the cantilever was retracted from the substrate, the GUV was detached from the solid-supported membrane as monitored by confocal imaging of the GUV during detachment (Fig. 1b, see also ESI†). Whereas the membrane shape apart from the adhered regions is clearly convex before the cantilever is retracted (shown in red), immediately before rupture the vesicle's shape close to the region where the GUV is adhered to the SSM is almost uncurved over a few micrometers (shown in black). Such a behavior was observed consistently for three different vesicles. Interestingly, when these experiments were performed under iso-osmotic conditions the corresponding force–distance curves obtained during the detachment process (Fig. 1c) rarely show a convex shape as expected from contact mechanics (see below). Instead the curves exhibit a linear force response at negative forces (lower two curves) or are even partly concave (non-convex) with pronounced stress stiffening (upper three curves) and an inflection point. The latter non-linear force progression was observed in all curves when the experiment was performed in hyperosmotic buffer, where the GUVs are slightly deflated. Force curves of the detachment of 6 different GUVs in hyperosmotic buffer are shown in Fig. 1d, where the forces are normalized to the maximum interaction force and set to −1 and the corresponding distance set to 1. The blue curve shows the mean of the individual curves. The curves show a characteristic inflection point at normalized distances of roughly 0.2, highlighted by a red square. The consistent results obtained from deflated GUVs suggest that the different force–distance curves observed for iso-osmolar conditions might arise due to slight differences in the membrane pretension between different GUVs – a result of mildly varying osmolarity during preparation of liposomes. After the adhesion force (the minimum of the force–distance curve) has been passed, discrete steps in the force curve beyond this point indicate that some point contacts remain between the vesicle and the substrate that permit to pull out membrane tethers.In order to assess the impact of membrane mechanics on the force curve upon detachment we compared the data to the outcome of experiments with colloidal probes. Detachment of a glass bead with a similar size as the GUV coated with a lipid bilayer of a similar composition as the GUV (without biotinylated lipids and different, but in both cases fluid-phase, matrix lipids) generates the typical convex shape as expected from standard contact mechanics (Fig. 2a).30 Since the chemical composition of the adhesive carbohydrates is kept identical for both experiments, this directly shows that the non-convex force shapes observed for GUV detachment are caused by the elastic properties of the flexible GUV. The colloidal probe experiments also showed much smaller adhesion forces: while the median adhesion force was 0.6 nN for the GUV detachment experiments (with a mean adhesion force of 0.7 nN), the median adhesion force for coated glass beads amounts only to 0.1 nN (with a mean adhesion force of also 0.1 nN). Deflated GUVs showed an increased median adhesion force of 1.0 nN (with a mean adhesion force of 1.5 nN). The large difference in adhesion forces between vesicles and colloidal probes can be explained by the different contact areas to the substrate. As can be seen in Fig. 1b, the contact area between an deflated GUV and the substrate has a radius of up to almost 6 μm, while the contact radius in case of adhesive glass beads has been estimated to be only around 100 nm based on adhesive contact theory.13 The difference in the size of the contact zone leads to a large difference in the number of bonds to the substrate and therefore to very different overall adhesion energies. Interestingly, adhesion forces are very high compared to the weak binding strength of the interaction between two carbohydrates of only few kBT.13,20 This points towards a concerted action of many carbohydrates, which is facilitated by the lateral mobility of glycolipids in the membrane.13
3.2 Impact of receptor mobility
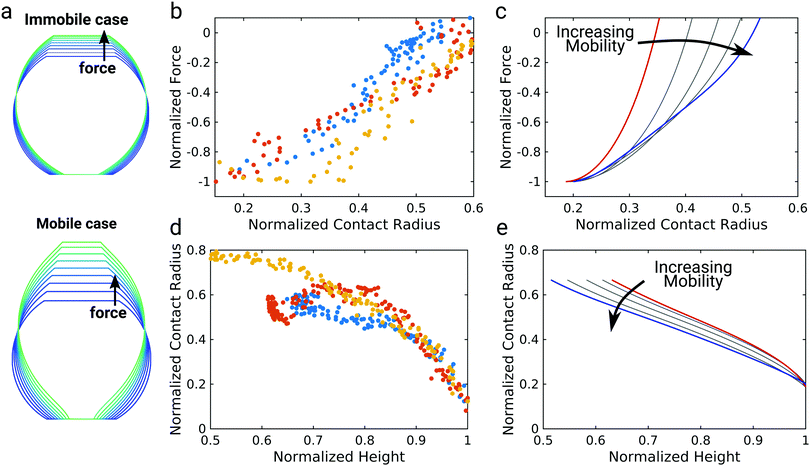
The data so far shows that the flexibility of the GUV might be responsible for the non-convex force response observed for GUV detachment contrasting the convex force curves found for non-deformable probes. To further examine the nature of the non-linear force response during GUV detachment we adopted a model put forward by Brochard–Wyart and de Gennes.25 Assuming that the vesicle can be described as a surface of constant curvature, one can derive an expression for the reduced force![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) as a function of the reduced contact radius Ψ (eqn (12)). Note that the contact radius represents here a different reaction coordinate for GUV detachment orthogonal to the distance (the z-coordinate) in the experimental force–distance curves. Mobility of the receptors is included by a non-constant adhesion energy density w = w0/Ψn (eqn (7)). Here we employ an heuristic parameter n that describes the receptor and ligand mobility with n = 0 recovering the immobile case with a constant adhesion energy density and n = 2 describing the fully mobile case as derived from the law of mass action in the limiting case of high binding affinities (eqn (6)). For n = 2 the total adhesion energy wAc does not depend on the size of the contact area Ac during detachment of the vesicle. In other words, the total number of formed bonds between the vesicle and the substrate is constant when the contact area gets smaller during detachment (Fig. 3a). Interestingly, inspection of eqn (11) shows that for n ≤ 2, it has no point of inflection in the physically relevant regime. Only when n assumes nonphysically large values of 3 to 8, the detachment curves starts to resemble the experimentally observed curve (Fig. 3b). Albeit this simple model is not sufficient to fully explain the experimental curve shape, it directly points to bond mobility as an explanation for the experimental observation – the occurrence of non-convex force curves upon detachment.
as a function of the reduced contact radius Ψ (eqn (12)). Note that the contact radius represents here a different reaction coordinate for GUV detachment orthogonal to the distance (the z-coordinate) in the experimental force–distance curves. Mobility of the receptors is included by a non-constant adhesion energy density w = w0/Ψn (eqn (7)). Here we employ an heuristic parameter n that describes the receptor and ligand mobility with n = 0 recovering the immobile case with a constant adhesion energy density and n = 2 describing the fully mobile case as derived from the law of mass action in the limiting case of high binding affinities (eqn (6)). For n = 2 the total adhesion energy wAc does not depend on the size of the contact area Ac during detachment of the vesicle. In other words, the total number of formed bonds between the vesicle and the substrate is constant when the contact area gets smaller during detachment (Fig. 3a). Interestingly, inspection of eqn (11) shows that for n ≤ 2, it has no point of inflection in the physically relevant regime. Only when n assumes nonphysically large values of 3 to 8, the detachment curves starts to resemble the experimentally observed curve (Fig. 3b). Albeit this simple model is not sufficient to fully explain the experimental curve shape, it directly points to bond mobility as an explanation for the experimental observation – the occurrence of non-convex force curves upon detachment.
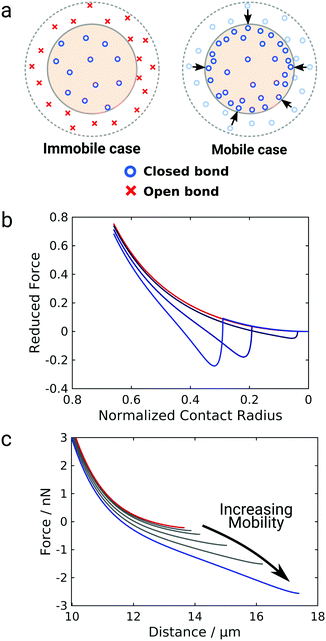 | ||
| Fig. 3 Impact of mobile bonds on the shape of theoretical detachment curves. (a) Illustration of the immobile and the mobile case. The dashed circle marks the initial contact area, the shaded area the contact area after a force is applied. In the immobile case the bond density stays constant, in case of maximal mobility (n = 2) the number of closed bonds stays constant. (b) and (c) Computational detachment curves using the analytical theory (eqn (12)) and the numerical model, respectively, for increasing values of n from the red curve (immobile case, n = 0) to the blue curve (mobile case, n = 3, 6, 8 for the analytical model and n = 2) for the numerical model. | ||
Therefore, we expand this analytical adhesion model by numerically calculating the shape of the vesicle based on the Young–Laplace law assuming volume conservation.9 Notably, in this model the restriction of constant tension is lifted and aside from pre-stress T0 the relative area dilation α as T = T0 + KAα with the area compressibility modulus KA is considered.31 We numerically calculated force–distance curves of GUV detachment for different values of the mobility parameter from immobile (n = 0, red curve) to fully mobile (n = 2, Fig. 3c, blue curve). The results generally confirm the prediction from eqn (12): while the force curve for immobile bonds is completely convex, the curves get non-convex with increasing mobility and eventually show an inflection point in accordance with the experiment. Interestingly, this effect is here more pronounced than in the analytical model and occurs at physically possible mobility, emphasizing the interplay between bond mobility and membrane shape.
In this model we use a purely deterministic description of adhesion dynamics. However, stochastic analysis has shown that finite-sized bond clusters beyond a critical force have a finite lifetime, due to stochastic fluctuation.32 Hence, the adhesion forces predicted by this model are an upper boundary for experimental adhesion forces. Both for vesicles (see Fig. 1c and d) as well as for cells,9 point contacts between the vesicle or the cell and the substrate have been observed as steps or so called tethers in the force–distance curve, even after the critical adhesion force has been reached.
It is unfortunately not possible to realize a comparable experimental setup in which both glycolipids are immobile. Using gel phase lipids would compromise our assumptions concerning the Hamiltonian (neglecting shear and bending) and introduce brittleness to the system. Along those lines Derserno and coworkers showed that gel phase bilayers do not behave like their fluid-phase counterparts.33 Besides, lateral diffusion would merely slow down and glycolipids would most-likely phase separate. We therefore used silica beads to interrupt the connection between shape and mobility (vide infra). A possible route to directly test the proposed effect might use advanced tools from synthetic biology to construct receptors with large artificial transmembrane domains to slow down their lateral mobility. These transmembrane domains might even be anchored to an artificial cytoskeleton to further restrict them.
These theoretical considerations show that the peculiar shape of the GUV detachment curve cannot be explained solely based on membrane mechanics, but additionally requires the assumption of mobile bonds.
3.3 Membrane shape
To further elucidate the interplay between the shape of the vesicle and bond mobility we compare the shape of the vesicle as observed experimentally by confocal imaging (Fig. 1b) to the numerical solution of the membrane shape (Fig. 4a).9 The calculated membrane shapes show clear differences between the immobile case with a mobility parameter of n = 0 (Fig. 4a top) and the fully mobile case with n = 2 (Fig. 4a bottom). While the vesicle membrane is strictly convex for immobile bonds, mobile bonds lead to the emergence of a more elongated shape with points of inflection close to the contact area. We will refer to this type of shape as unduloidal. Unduloids belong to the class of Delaunay surfaces with constant nonzero mean curvature and are generated as the surface of revolution of a elliptic catenary.34 This geometry is commonly used to describe liquid bridges between two surfaces.35–37 This particular shape arises due to the large adhesion energy densities for mobile bonds at small contact areas, which favor surface wetting at the cost of larger membrane deformation. This switch from spherical shapes to unduloids and concomitantly the formation of a neck in the adhesion zone goes hand in hand with the occurrence of an inflection point in the force–distance curve (see ESI,† Fig. S4). As the neck expands more and more force builds up giving rise to the observed non-linearity. The GUV shape of the mobile case at larger pulling forces agrees very well with confocal images of GUV detachment (Fig. 1b).However, due to the limited optical resolution, visual inspection is not sufficient to clearly discriminate between the immobile and the mobile case based on the experimentally observed membrane shape during detachment. Therefore, we extracted the height of the GUV and the contact radius between the GUV and the membrane for three different GUVs from the confocal images to compare them to model predictions (Fig. 4b–e). Forces and distances were normalized to the detachment force and the corresponding distance as done in Fig. 1. The contact radius was normalized to the GUV radius after detachment. This analysis revealed an almost linear dependency between pulling force and contact radius (Fig. 4b), which can be directly compared to model predictions using different mobility parameters n (Fig. 4c). For the immobile case n = 0 (red curve) the force was found to decrease sharply at higher contact radii and then less pronounced at lower contact radii. By contrast, for the fully mobile case n = 2 (blue curve) an almost linear dependency of the force on the contact radius was observed in the range of normalized contact radii from 0.2 to 0.5, which agrees excellently with the experimental observation.
Next, we consider the contact radius as a function of the height of the vesicle (Fig. 4d). In our experiments we observed a non-linear trend: the contact radius first declines slowly with increasing vesicle height, before it declines more steeply at larger heights. This experimental observation is not reproduced by the theoretical model (Fig. 4e). The mobile case (blue curve) rather displays an almost linear dependency of contact radius on vesicle height. While the immobile case (red curve) predicts a non-linear behavior the deviation from a linear dependency occurs at much higher normalized heights. This deviation between theory and experiment might be due to the finite size of the glycolipids and consequently molecular crowding in the contact zone, which is not considered in the theory. The failure of continuum theory shortly before detachment has similarly been described for the detachment of living cells.9
Since the vesicle shapes are equilibrium structures the unduloidal shape is not per se limited to mobile bonds, but might also occur for small contact angles in case of immobile bonds if the adhesion energy density is sufficiently high (see ESI,† Fig. S5). However, for larger contact areas and an adhesion energy density high enough to support the unduloidal shape, the vesicle shape cannot be solved indicating that an unduloidal shape might not be adopted with immobilie bonds.
Interestingly, a similar transition from a spherical to an unduloidal shape has been proposed for liquid bridges between solid surfaces.35–37 These studies predict that capillary bridges become unstable at contact angles approaching θ = 90°.36,38 Catenoids, where the two curvatures have opposite sign, do not support compressive forces and can be therefore ruled out as possible solutions to the problem. In experiments, purely convex capillary bridges exhibit no detectable hysteresis and show contact angles close to 100° breaking at much smaller distance or larger normalized contact radius than mathematically allowed.39 This is in accordance with our findings that once unduloids have been formed the GUVs quickly thereafter detach from the surface.
3.4 Impact of elastic parameters
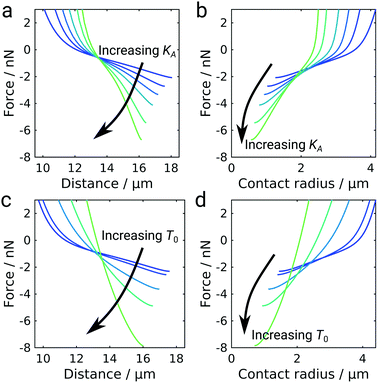
The shape of the GUV during detachment is a result of minimizing the free energy of the system. As a consequence, we expect the elastic properties of the GUV and the mobility of the ligand–receptor system to be important for the overall detachment forces and the general shape of the force curves. Besides, in the GUV detachment experiments performed at iso-osmolar conditions we already observed two qualitatively differently shaped force curves, which we attributed to differences in membrane tension (Fig. 1c). Therefore, we wanted to explore the impact of the elastic parameters, i.e., the area compressibility modulus KA and the pretension T0, on the force response employing our numerical model for GUV detachment (Fig. 5). Increasing the area compressibility modulus from 10 pN nm−1 to 500 pN nm−1 did not result in a change of the general curve shape but the vesicle stiffens as can be inferred from the distance at maximum force decreasing from almost 18 μm to 16 μm. At the same time, the detachment force increases from 2 nN to more than 6 nN. The strong dependency of the adhesion force on elastic parameters is somewhat unexpected since it differs both from the classical JKR model of adhesion and also from the Brochard–Wyart model for the adhesion of vesicles with immobile bonds (see ESI,† Fig. S6).9,25 To better understand this phenomenon we plot the force as a function of the contact radius (Fig. 5b). For immobile bonds, at a given force, a stiffer vesicle always has a smaller contact radius than a softer vesicle (see ESI,† Fig. S6), because a larger contact radius leads to a larger deviation from a perfectly spherical shape and in turn to larger areal strain. In the case of mobile bonds we can observe the same behavior at contact radii larger than 2 μm, where a crossover occurs leading to an inversion of the described effect: stiffer vesicles have larger contact radii at a given force. This is caused by the transition from the purely convex (spherical) to the unduloidal vesicle shape. The switch to the unduloidal shape is more energy costly (elastic energy rises due to areal strain) but this can be compensated by increasing the energy density of bonds formed in the contact zone. Mobile receptors accumulate in the contact zone during detachment and provide the necessary energy to permit the shape transition. The increase of w with decreasing Rc in the case of mobile linkers fosters this transition from a spheroid to an unduloid during pulling. Albeit unduloids generate larger areal strain than spheroids upon pulling they might form if a larger contact area can be established to compensate the additional elastic energy fee. In addition, a spheroidal vesicle with immobile receptors in contact with an infinitely extended support with immobile ligands but with extremely large w0 to mimic the situation of mobile linkers at small Rc is not the preferred shape at equilibrium and therefore unstable. Instead, a catenoid with zero mean curvature would form under these conditions (high w0 and pulling forces).39 However, a switch from a spheroid to a catenoid eventually requires the vesicle to cross contact angles with the substrate of 90° leading to unstable structures that lead to loss of the bridge. Notably, if fixed contact areas on both sides were realized also unduloids can arise due to the limited spreading area. This has also been experimentally shown using optical tweezers to pull out tethers from a giant liposome.40 Hence, starting off with low adhesion energy densities with stable spheroidal structures and ending with large adhesion energy densities results in stable unduloids with contact angles larger than 90°. Once the unduloid approaches contact angles of 90° the vesicle shape gets unstable and breaks off from the surface assuming again a spherical shape. Stiffer vesicles with larger KA resist the generation of larger contact angles and therefore can reach smaller Rc at lower contact angles, which in turn provides larger maximal adhesion forces (see ESI,† Fig. S7). As a consequence, the elastic energy rises during detachment of vesicles with mobile linkers causing an inflection point in the force curves (see ESI,† Fig. S8).While an increase in pretension T0 similarly leads to a stiffening of the vesicle and an increase in detachment force, the overall curve shape also changes: the characteristic inflection point is lost at high pretensions (Fig. 5c and d). This effect is presumably caused by high pretensions preventing the transition to the unduloidal vesicle shape (see ESI,† Fig. S9). The impact of pretension is in agreement with the experimental observation that the inflection point is more pronounced in deflated vesicles without pretension (Fig. 1d). At high pretensions the curve-shape resembles the shape observed for colloidal probe experiments (Fig. 2a) and also the detachment curves commonly described for living cells.9,41 While pretension in living cells arises from their contractile acto-myosin cortex,42 the incompressible membrane-coated glass bead can be considered the limiting case of an infinitely stiff entity.
It should be noted that we compare systems with the same w0, i.e., with the same initial number of bonds between the vesicle and the substrate. However, the overall number of bonds is also a function of the membrane elasticity because softer vesicles generate a larger adhesion area at the same compressive force, such that they can form a larger number of initial bonds. This was also observed in our experiments and discussed in the comparison between non-deflated and deflated GUVs (Fig. 2b). However, the general conclusion that stiffer cells or vesicles exhibit generally larger maximum adhesion forces is wrong. We find that for a given density of mobile bonds and a given force, a stiffer cell can have a larger contact radius than a softer cell only if a transition from a spherical (convex) to an unduloidal cell shape has occurred. This might explain why adherent cells prior to seeding are highly tensed but can still generate appreciable adhesion forces. In later stages, however, cortical tension is released to cover more area needed to establish more bonds.43
4 Conclusions
In conclusion, we showed that the detachment process of giant vesicles is governed by an interplay of bond mobility and membrane mechanics, that gives rise to a highly nonlinear force–distance curve reminiscent of polymer stretching. We could show that unduloids form if bonds are mobile and concomitantly the force responses also show inflection points. Thereby, our model not only predicts a transition from a more spherical (convex) vesicle shape to an unduloidal shape at larger forces but also suggests how cells might control adhesive strength through elasticity and cortical tension.These findings have interesting implications for the impact of bond mobility on biological adhesion. As an example, it was found that during the early stages of the inflammation cascade, when neutrophils roll on and start to firmly adhere to the endothelium, a switch in integrin affinity and mobility occurs. This permits to increase the strength of firm adhesions through continuous recruitment of high affinity integrin receptors to the contact site.44,45 Our results suggest that the mobility of integrins has even more dramatic consequences on cell detachment, leading to qualitatively different unbinding dynamics. Because bonds accumulate in the contact zone during detachment the average lifetime of bonds is increased allowing for stable attachment even with weak individual bonds. The view on this process needs to include also the passive mechanical properties of the cytoskeleton essentially modulating adhesion strength and lifetime as proposed here. This view is supported by findings that cytoskeletal remodeling accompanies the process of leukocyte adhesion.46 Further investigations should include a more holistic view including affinity, mobility and mechanics.
5 Experimentals
5.1 Materials
1,2-Dioleoyl-sn-glycero-3-phosphocholine (DOPC), 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine (DOPE), 1-palmitoyl-2-oleoyl-glycero-3-phosphocholine (POPC), 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine-N-biotinyl (Bio-DOPE), Ganglioside GM3 from bovine milk (GM3) and D-lactosyl-β-1,1′ N-palmitoyl-D-erythrosphingosine (LacCer) were purchased from Avanti Polar Lipids (Alabaster, AL). Fluorescently labeled lipids β-BODIPY™ 500/510 C12-HPC (Bodipy) and Texas Red™ 1,2-dihexadecanoyl-sn-glycero-3-phosphoethanolamine (TR) were supplied by Thermo Fisher Scientific (Waltham, MA). Biotinylated bovine serum albumin, avidin from egg white, 4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid (HEPES) and calcium chloride were obtained from Merck (Darmstadt, Germany) and sucrose from VWR International (Darmstadt, Germany). Sodium hydrogen carbonate and potassium chloride were purchased from Carl Roth (Karlsruhe, Germany). If not stated otherwise, phosphate buffered saline (PBS) was made from PBS Dulbecco (Biochrom, Berlin, Germany) and adjusted to pH 7.4. Water was used in ultrapure quality (18.2 MΩ cm at 25 °C) only and produced by Elix® Reference 5 (Merck, Darmstadt, Germany), Milli-Q® Advantage A10 (Merck, Darmstadt, Germany) and a membrane filter of 0.22 μm pore size (Millipak® Express 40, Merck, Darmstadt, Germany).5.2 Methods
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in chloroform was deposited onto two conductive indium tin oxide glass slides (Präzisions Glas & Optik, Iserlohn, Germany) each and distributed over an area of about 1.2 × 1.2 cm2 after evaporation of the solvent. Evaporation was completed at reduced pressure in a drying cabinet set to 35 °C for at least 2 h. An enclosed electroformation chamber was assembled by separating the two lipid films on the conductive slides apposing each other by a silicone spacer of a thickness of 1 mm. The opening of the silicone spacer was filled with a solution of sucrose (87 mosmol kg−1 as determined by freezing point osmometry (Osmomat 3000, Gonotec, Berlin, Germany)). Electroformation was performed by applying an AC voltage of 2.3 V (peak-to-peak), at a frequency of 70 Hz (33220A, Keysight Technologies, Santa Rosa, CA) to the indium tin oxide slides inside a drying cabinet set to 60 °C for 3 h.
1 in chloroform was deposited onto two conductive indium tin oxide glass slides (Präzisions Glas & Optik, Iserlohn, Germany) each and distributed over an area of about 1.2 × 1.2 cm2 after evaporation of the solvent. Evaporation was completed at reduced pressure in a drying cabinet set to 35 °C for at least 2 h. An enclosed electroformation chamber was assembled by separating the two lipid films on the conductive slides apposing each other by a silicone spacer of a thickness of 1 mm. The opening of the silicone spacer was filled with a solution of sucrose (87 mosmol kg−1 as determined by freezing point osmometry (Osmomat 3000, Gonotec, Berlin, Germany)). Electroformation was performed by applying an AC voltage of 2.3 V (peak-to-peak), at a frequency of 70 Hz (33220A, Keysight Technologies, Santa Rosa, CA) to the indium tin oxide slides inside a drying cabinet set to 60 °C for 3 h.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in chloroform, yielding a total lipid mass of 0.25 mg by evaporating the solvent in a stream of nitrogen gas at 60 °C, drying the emerging lipid film in a drying cabinet set to 60 °C for 3 h at reduced pressure, resuspending the lipids in isoosmotic HEPES-buffer (50 mm HEPES, 10 mm calcium chloride, pH 7.4) (30 min to 1 h at 60 °C) and subsequent sonication (70% of the maximum power, 0.4 s pulse followed by 0.6 s pause) for 30 min (Sonoplus HD 2070, Bandelin, Berlin, Germany). 50 μl of the vesicle dispersion were spread on glass bottom Petri dish (MatTek, Ashland, MA) in 450 μl iso- or hyperosmotic (60 mM HEPES, 10 mM calcium chloride, pH 7.4) HEPES-buffer for 30–60 min. Finally, the membranes were rinsed with fresh HEPES-buffer (5 × 2 ml) to a final volume of 2 ml.
1 in chloroform, yielding a total lipid mass of 0.25 mg by evaporating the solvent in a stream of nitrogen gas at 60 °C, drying the emerging lipid film in a drying cabinet set to 60 °C for 3 h at reduced pressure, resuspending the lipids in isoosmotic HEPES-buffer (50 mm HEPES, 10 mm calcium chloride, pH 7.4) (30 min to 1 h at 60 °C) and subsequent sonication (70% of the maximum power, 0.4 s pulse followed by 0.6 s pause) for 30 min (Sonoplus HD 2070, Bandelin, Berlin, Germany). 50 μl of the vesicle dispersion were spread on glass bottom Petri dish (MatTek, Ashland, MA) in 450 μl iso- or hyperosmotic (60 mM HEPES, 10 mM calcium chloride, pH 7.4) HEPES-buffer for 30–60 min. Finally, the membranes were rinsed with fresh HEPES-buffer (5 × 2 ml) to a final volume of 2 ml.
Solid supported membranes for colloidal probe measurements were prepared similarly, however, lipids were resuspended in phosphate buffered saline (137 mM sodium chloride, 2.7 mM potassium chloride, 8.1 mM sodium hydrogen phosphate and 1.5 mM potassium dihydrogen phosphate, pH 7.4, Biochrom, Berlin, Germany) for 10 min at 40 °C, vesicles were spread at twice the lipid concentration used in GUV adhesion experiments and buffer containing 20 mM HEPES, 20 mM potassium chloride and 10 mM calcium chloride was used for preparation and spreading of small unilamellar vesicles (pH 5.9), and for rinsing (pH 7.4).
For colloidal probe microscopy experiments, a borosilicate glass sphere (diameter 15 μm) was glued onto the bottom side of MLCT-O10 cantilevers with a nominal spring constant of 0.01 N m−1 as described elsewhere.12,48 The colloidal probes were coated with a membrane by spreading of small unilamellar vesicles of a mixture of POPC, GM3 and TR in a molar ratio of 89![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for approximately 20 min, while already being fixed to the AFM head. Afterwards, the probes were rinsed with the same buffer used for rinsing SSMs for CPM experiments (five times with 1 ml each).
1 for approximately 20 min, while already being fixed to the AFM head. Afterwards, the probes were rinsed with the same buffer used for rinsing SSMs for CPM experiments (five times with 1 ml each).
Colloidal probe measurements were performed in buffer containing 20 mM HEPES, 20 mM potassium chloride and 10 mM calcium chloride, adjusted to pH 7.4. Contact time between the two surfaces was set to 1 s and retraction speed to 1 μm s−1. For these measurements an MFP-3D (Oxford Instruments Asylum Research, Santa Barbara, CA) was utilized.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work was financially supported by the DFG (SFB937, A8) and the VW foundation (‘Living Foams’).Notes and references
- C. G. Galbraith, K. M. Yamada and M. P. Sheetz, J. Cell Biol., 2002, 159, 695–705 CrossRef CAS PubMed.
- E. Sackmann and R. F. Bruinsma, ChemPhysChem, 2002, 3, 262 CrossRef CAS PubMed.
- E. Sackmann and S. Goennenwein, Prog. Theor. Phys. Suppl., 2006, 165, 78–99 CrossRef CAS.
- B. Geiger, J. P. Spatz and A. D. Bershadsky, Nat. Rev. Mol. Cell Biol., 2009, 10, 21–33 CrossRef CAS PubMed.
- J. T. Parsons, A. R. Horwitz and M. A. Schwartz, Nat. Rev. Mol. Cell Biol., 2010, 11, 633–643 CrossRef CAS PubMed.
- U. S. Schwarz and S. A. Safran, Rev. Mod. Phys., 2013, 85, 1327–1381 CrossRef CAS.
- H. Tang, H. Chang, Y. Dong, L. Guo, X. Shi, Y. Wu, Y. Huang and Y. He, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 9246–9251 CrossRef CAS PubMed.
- E. Sackmann and A.-S. Smith, Soft Matter, 2014, 10, 1644 RSC.
- N. Kamprad, H. Witt, M. Schröder, C. T. Kreis, O. Bäumchen, A. Janshoff and M. Tarantola, Nanoscale, 2018, 10, 22504–22519 RSC.
- T. R. Weikl, M. Asfaw, H. Krobath, B. Różycki and R. Lipowsky, Soft Matter, 2009, 5, 3213–3224 RSC.
- A.-S. Smith and U. Seifert, Soft Matter, 2007, 3, 275–289 RSC.
- B. Lorenz, L. Á. de Cienfuegos, M. Oelkers, E. Kriemen, C. Brand, M. Stephan, E. Sunnick, D. Yüksel, V. Kalsani, K. Kumar, D. B. Werz and A. Janshoff, J. Am. Chem. Soc., 2012, 134, 3326–3329 CrossRef CAS PubMed.
- H. Witt, F. Savić, M. Oelkers, S. I. Awan, D. B. Werz, B. Geil and A. Janshoff, Biophys. J., 2016, 110, 1582–1592 CrossRef CAS PubMed.
- S. F. Fenz, T. Bihr, D. Schmidt, R. Merkel, U. Seifert, K. Sengupta and A.-S. Smith, Nat. Phys., 2017, 13, 906–913 Search PubMed.
- M. M. Baksh, M. Jaros and J. T. Groves, Nature, 2004, 427, 139–141 CrossRef CAS PubMed.
- J. Steinkühler, J. Agudo-Canalejo, R. Lipowsky and R. Dimova, Biophys. J., 2016, 111, 1454–1464 CrossRef PubMed.
- R. Dimova and C. Marques, The Giant Vesicle Book, CRC Press, Taylor & Francis Group, 2019 Search PubMed.
- H. F. Langer and T. Chavakis, J. Cell. Mol. Med., 2009, 13, 1211–1220 CrossRef CAS PubMed.
- R. P. McEver and C. Zhu, Annu. Rev. Cell Dev. Biol., 2010, 26, 363–396 CrossRef CAS PubMed.
- I. Bucior and M. M. Burger, Curr. Opin. Struct. Biol., 2004, 14, 631–637 CrossRef CAS PubMed.
- I. Bucior, S. Scheuring, A. Engel and M. M. Burger, J. Cell Biol., 2004, 165, 529–537 CrossRef CAS PubMed.
- N. Kojima, M. Shiota, Y. Sadahira, K. Handa and S.-I. Hakomori, J. Biol. Chem., 1992, 267, 17264–17270 CAS.
- S.-I. Hakomori and K. Handa, Glycoconjugate J., 2015, 32, 1–8 CrossRef CAS PubMed.
- P. V. Santacroce and A. Basu, Glycoconjugate J., 2004, 21, 89–95 CrossRef CAS PubMed.
- F. Brochard-Wyart and P.-G. de Gennes, C. R. Phys., 2003, 4, 281–287 CrossRef CAS.
- Y. Lin and L. Freund, Int. J. Solids Struct., 2007, 44, 1927–1938 CrossRef.
- E. Schäfer, M. Vache, T.-T. Kliesch and A. Janshoff, Soft Matter, 2015, 11, 4487–4495 RSC.
- R. Bruinsma, A. Behrisch and E. Sackmann, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 61, 4253 CrossRef CAS PubMed.
- A. Boulbitch, Z. Guttenberg and E. Sackmann, Biophys. J., 2001, 81, 2743–2751 CrossRef CAS PubMed.
- J. Israelachvili, Intermolecular and Surface Forces, Elsevier Science, 2015 Search PubMed.
- S. Sen, S. Subramanian and D. E. Discher, Biophys. J., 2005, 89, 3203–3213 CrossRef CAS PubMed.
- T. Erdmann and U. Schwarz, Phys. Rev. Lett., 2004, 92, 108102 CrossRef CAS PubMed.
- P. Diggins, Z. A. McDargh and M. Deserno, J. Am. Chem. Soc., 2015, 137, 12752–12755 CrossRef CAS PubMed.
- C. Delaunay, J. Math. Phys. Appl., 1841, 6, 309–314 Search PubMed.
- J. Bostwick and P. Steen, Annu. Rev. Fluid Mech., 2015, 47, 539–568 CrossRef.
- E. Boucher, M. Evans and S. McGarry, J. Colloid Interface Sci., 1982, 89, 154–165 CrossRef CAS.
- R. Finn and T. Vogel, Z. Anal. Anwend., 1992, 11, 3–23 CrossRef.
- M. Athanassenas, J. Reine Angew. Math., 1987, 377, 97–107 Search PubMed.
- P. V. Petkov and B. P. Radoev, Colloids Surf., A, 2014, 460, 18–27 CrossRef CAS.
- G. Koster, A. Cacciuto, I. Derényi, D. Frenkel and M. Dogterom, Phys. Rev. Lett., 2005, 94, 068101 CrossRef PubMed.
- J. Helenius, C.-P. Heisenberg, H. E. Gaub and D. J. Muller, J. Cell Sci., 2008, 121, 1785–1791 CrossRef CAS PubMed.
- B. R. Brückner, A. Pietuch, S. Nehls, J. Rother and A. Janshoff, Sci. Rep., 2015, 5, 14700 CrossRef PubMed.
- A. Pietuch and A. Janshoff, Open Biol., 2013, 3, 130084 CrossRef PubMed.
- D. F. Kucik, M. L. Dustin, J. M. Miller and E. J. Brown, J. Clin. Invest., 1996, 97, 2139–2144 CrossRef CAS PubMed.
- T. R. Gaborski, A. Clark, R. E. Waugh and J. L. McGrath, Biophys. J., 2008, 95, 4934–4947 CrossRef CAS PubMed.
- M. Vicente-Manzanares and F. Sánchez-Madrid, Nat. Rev. Immunol., 2004, 4, 110–122 CrossRef CAS PubMed.
- D. S. Dimitrov and M. I. Angelova, New Trends in Colloid Science, Springer, 1987, pp. 48–56 Search PubMed.
- H. Witt and A. Janshoff, SNAREs, Springer, 2019, pp. 145–159 Search PubMed.
- J. L. Hutter and J. Bechhoefer, Rev. Sci. Instrum., 1993, 64, 1868–1873 CrossRef CAS.
- H.-J. Butt and M. Jaschke, Nanotechnology, 1995, 6, 1 CrossRef.
- T.-T. Kliesch, PhD thesis, University of Göttingen, 2017.
- C. A. Schneider, W. S. Rasband and K. W. Eliceiri, Nat. Methods, 2012, 9, 671 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm00863j |
| ‡ Contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2020 |