Directional-dependent pockets drive columnar–columnar coexistence

Abstract

The rational design of materials requires a fundamental understanding of the mechanisms driving their self-assembly. This may be particularly challenging in highly dense and shape-asymmetric systems. Here we show how the addition of tiny non-adsorbing spheres (depletants) to a dense system of hard disc-like particles (discotics) leads to coexistence between two distinct, highly dense (liquid)-crystalline columnar phases. This coexistence emerges due to the directional-dependent free-volume pockets for depletants. Theoretical results are confirmed by simulations explicitly accounting for the binary mixture of interest. We define the stability limits of this columnar–columnar coexistence and quantify the directional-dependent depletant partitioning.

---

Compartmentalization, the distribution of components over different domains, occurs at multiple length scales. Competition for space, which grants access to resources of different kinds, leads to the emergence of patterns, for example, in the canopies of trees,¹ in crowds of humans,² and in predator-prey fish schools.³ Inside a prokaryotic cell, the shape and size of organelles influences their final distribution;⁴ this effect is termed macromolecular crowding.⁵ Therefore, understanding the fundamentals underlying the simple question ‘what goes where’ is paramount in the rational design of materials. In this Communication, we extend the concept of geometrical free volume fractions⁶ to highly dense systems containing disc-like (discotic) particles in the presence of tiny non-adsorbing spheres. For the reader who is interested in more details we refer to the ESI† and will provide our Mathematica⁷ scripts upon a reasonable request.

Size and shape asymmetry play a crucial role in the distribution of compounds in multi-component systems:³ small compounds only fit in the free volume pockets available in between the larger ones. The partitioning of non-adsorbing components (depletants) leads to a depletion zone around the bigger entities, where the depletant concentration is lower than in the bulk. This depletion zone relates to the excluded volume between the species:⁸ the space inaccessible to a second particle due to the presence of the first one.⁹ In a mixture of anisotropic particles and non-adsorbing spheres interacting solely via excluded volume, the spheres induce attraction patches between the anisotropic particles due to their optimal entropic gain upon maximun overlap of the depletion zones.¹⁰ Colloidal systems have been proposed as candidates to isolate the role of excluded volume in highly size- and shape-asymmetric, dense environments.^11–13 The role of entropy in self-assembly, termed shape-entropy,^14,15 has received substantial attention via controlled theoretical,¹⁶ simulational,^17,18 and experimental^19,20 studies. Discotic colloids are widespread in natural and human-made products spanning from blood,²¹ laquer coatings,²² clays,²³ paints,²⁴ cosmetics,²⁵ and nacre-mimetic materials²⁶ to coloration-change mechanisms.²⁷ In many of these examples, discotics are not the only compound present. Thus, a better understanding of partitioning in simple discotic–depletant mixtures will provide guidelines towards a smarter material design. Here, we quantify the distribution of tiny non-adsorbing spheres in dense discotic systems. To this end, we developed a geometrical free-volume theory (FVT) whose predictions are confirmed via direct coexistence Monte Carlo simulations accounting for the binary mixture.

We focus on the columnar phase of discotics, containing a one-dimensional stacking of hexagonally-arranged particles.^28,29 The system parameters are the disc aspect ratio (i.e., the relative thickness of the platelet) Λ ≡ L/D, where L is the platelet's thickness and D is its diameter, and the relative size of the depletant, q ≡ 2δ/D, where δ is the radius of the depletant [Fig. 1(a)]. We consider a system (S) with volume V containing N_c discotics with volume v_c at volume fraction ϕ_c = (N_cv_c)/V. The depletant volume fraction is ϕ_d = (N_dv_d)/V, where N_d is the number of depletants with volume v_d in S. We consider depletants as penetrable hard spheres (PHSs):³⁰ they do not interact with each other but are hard for the discotics. Theoretically, we account for platelets as hard cylinders;³¹ in simulations we consider oblate hard spherocylinders (OHSCs).^29,32 We apply free volume theory (FVT,³³ see ESI†) to discotic–depletant mixtures. This FVT accounts for the partitioning of depletants over the different phases present in the system.³⁴ Unless otherwise indicated, we focus on Λ = 0.1 and q = 0.01.

Fig. 1 Top panels: Representation of the inter- and intra-columnar depletion zone overlaps (purple) present when discotics (brown) are mixed with tiny depletants (green); q ≡ 2δ/D = 0.05. Depletion zones around platelets indicated in green. The effective small systems for depletants in the inter-columnar (S_⊥) and intra-columnar (S_‖) directions are shown as orange and grey boxes. Bottom panels: Snapshots of discotic–depletant mixtures in the intra- and inter-columnar directions; Λ ≡ L/D = 0.1, q = 0.01.

In Fig. 2, the free volume fraction for depletants in the columnar phase α_C is presented. Contrary to common FVT, this function is calculated on geometrical grounds by analyzing the overlap of the depletion zones within the columnar unit cell. If there is no overlap of the depletion zones, α_C is the volume unoccupied by the depletion zones and discotics over the system volume. Overlap of depletion zones leads to an increase in α_C. This overlap occurs either in the intra-r_‖ or in the inter-r_⊥ columnar direction [Fig. 1(a)]. Overlap of depletion zones in r_‖ occurs at lower ϕ_c than in r_⊥.³⁵ The kink point in α_C at ϕ_c ≈ 0.77 marks the lowest discotic volume fraction ϕ^‖_c at which depletion zone overlap in r_‖ occurs. Due to the low q-value considered, for ϕ_c<ϕ^‖_c the α_C-value calculated using the geometrical method proposed here or via the commonly applied scaled particle theory (SPT)³⁴ almost overlap. However, the SPT-derived α_C underestimates the pockets for tiny depletants in the discotic columnar phase for ϕ_c > ϕ^‖_c: the partitioning of depletants is biased towards the low-density discotic phases when using an SPT-derived α_C.

Fig. 2 Free volume fraction for depletants in the discotic columnar phase α_C with increasing ϕ_c; Λ = 0.1 and q = 0.01. Black curve is the expression used in the calculation of the binodals, orange and purple curves are the free volume fraction in the intra- and inter-columnar directions, and grey curve corresponds to weighted arithmetic mean. Dashed grey curve is the scaled particle theory (SPT) result for α_C.³¹ Arrows indicate the ϕ_c at which the overlap of the depletion zones in the intra- and inter-columnar directions occurs.

The geometrically-based α_C enables quantification of the distribution of depletants into two effective small systems: (1) in r_‖, between the flat faces of the platelets; (2) in r_⊥, from the sides of the platelets [Fig. 1(a)]. There is always room for depletants in r_⊥ (α_C > 0 ∀ ϕ_c), whilst α_C vanishes upon the overlap of the depletion zones between the flat faces of the discotics (in r_‖, α_C = 0 ∀ ϕ_c > ϕ^‖_c). A weighted arithmetic mean of the three small systems in r_‖ and of the nine ones present in r_⊥ leads to a free volume fraction close to the geometrical α_C-value. The amount of small systems present in each direction is the number of depletant-mediated discotic–discotic interactions [Fig. 1(a)].

In Fig. 3(a), we present a theoretical (equilibrium) phase diagram. All possible depletant-free phases are observed at different discotic ϕ_c and depletant ϕ_d volume fractions: isotropic (I), nematic (N), and columnar (C). Phase separation upon depletant addition is driven by partitioning of depletants and discotics over the different phases.³³ For the specified {Λ,q}, columnar–columnar (C₁–C₂) coexistence is revealed. The overall phase diagram topology and the order of the triple phase coexistences with increasing ϕ_d (N–C₁–C₂ and I–N–C₂) is in agreement with previous results.³¹ This C₁–C₂ is reminiscent of the solid–solid coexistence found in hard spheres (HSs) interacting via short-range (direct) attraction.^36–38 Here, the directionality of the attraction patches^10,39 induced by the disc-like shape drives the C₁–C₂ coexistence. Consequently, in the lower-density columnar phase (C₁) there is no overlap of the depletion zones: pockets for depletants are available in both r_⊥ and r_‖. However, in the higher-density columnar state (C₂) depletion zones overlap between the flat faces of the platelets (in r_‖), and the only pockets in the system are in r_⊥.

Fig. 3 (a) Phase diagram of discotics (L/D ≡ Λ = 0 : 1) mixed with tiny depletants (2δ/D ≡ q = 0 : 01) (tie-lines in orange). Orange stars are Monte Carlo simulations accounting for the binary mixture; tie-lines in black. Data and snapshots in (b–e) correspond to the points of the solid black tie-line. (b and c) Distribution functions in the inter- (b) g_⊥ and intra- (c) g_‖ columnar directions. Dashed curves: C1 phase; solid curves: C2 phase. The superscript 00 denotes correlation between particles in the same column, and 01 refers to correlation between particles in adjacent columns. (d–f) Simulation snapshots of discotics (brown) and depletants (green). (d) Snapshot from the (1100) plane of a direct-coexistence simulation. (e and f) Snapshots from the (0001) plane of the depletants present in the C1 (e) and C2 (f) phases.

The maximum depletion attraction W^max_AOV between discotics when q → 0 scales as W^max_AOV ∝ − ϕ^R_dq⁻², stronger than between HSs (W^max_AOV ∝ − ϕ^R_dq⁻¹). Here, ϕ^R_d is the depletant bulk concentration (see ESI†). The tendency of flat faces to align is enhanced by the presence of the depletants. Furthermore, the theoretically-predicted C₁–C₂ coexistence terminates at ϕ_c = ϕ^‖_c with ϕ_d ≈ 0, manifesting the two effective systems that tiny depletants access in the columnar phase. This vanishing depletant concentration at the C₁–C₂ critical point (CP) contrasts with the finite value obtained for solid–solid coexistence between HSs:⁶ there is no directionality for the pockets present in the HS solid. Next, the stability of this C₁–C₂ coexistence is tested against Monte Carlo (MC) simulations.

In Fig. 3(a), two equilibrium C₁–C₂ phase coexistences from direct coexistence MC computer simulations are also shown. As far as we are aware, this is the first time that direct-coexistence in highly dense discotic systems is simulated explicitly accounting for a binary mixture (OHSCs and PHSs); see ESI,† for simulation details and further results. A snapshot of an equilibrium direct C₁–C₂ coexistence of the binary mixture is shown in Fig. 3(d). The close-packing fraction for OHSCs with Λ = 0.1 is ϕ^cp_c ≈ 0.88,³² which partially explains the lower ϕ_c-values on the C₂-branch of the simulations. Due to their rounded edges, the stacking of OHSCs in the columnar phase differs from that of hard cylinders.³² Besides this offset in the C₂ branch, MC results and FVT predicted tie-lines are in remarkable agreement. Snapshots of the different plate-depletant mixtures [Fig. 1(b), and 3(e), (f)] show that the depletant partitioning is in line with theoretical predictions. More importantly, the MC simulations show that C₁–C₂ coexistence exists and is stable against fluctuations.

Next, we pay attention to discotic–discotic and discotic–depletant distribution functions g from the MC simulations [Fig. 3(b) and (c)]. The discotic–depletant distribution function in the inter-columnar direction r_⊥ is the most insightful [g^c–d_⊥]. For the C₂ phase, g^c–d_⊥ ≈ 0 for r_⊥ ≲ 0.5D: there are barely any depletants present in the intra-columnar direction in C₂. On the contrary, there is a rather constant distribution of depletants on the top and bottom of the discotic flat faces in the C₁ phase: g^c–d_⊥ ≈ 0.4 for r_⊥ ≲ 0.5D. The first peak at r_⊥ ≈ 0.5D of g^c–d_⊥, present both in C₁ and C₂, corresponds to the doughnut-like pockets. The second and third peaks of g^c–d_⊥ indicate that depletants are present in the interstices of both columnar phases. Furthermore, the g_⊥-value of these peaks is significantly higher in the C₂ phase than in the C₁ phase: the lack of pockets in r_‖ in C₂ leads to the accumulation of depletants in the interstices. In r_⊥, the discotic–discotic distribution g^c–c_⊥ shows peaks corresponding to the hexagonal (two-dimensional) arrangement.

Discotic–discotic distributions in the intra-columnar direction r_‖ are solid-like in C₂ and more fluid-like in C₁ [Fig. 3(c)]. We deduce from the discotic–discotic and discotic–depletant distributions that: (i) the C₁ phase is liquid crystalline, whereas C₂ is crystalline;²⁹ and (ii) depletants distribute according to the pockets present. In C₁, pockets are available both in r_‖ and r_⊥. Opposite to this, in C₂ pockets are only in the interstices (i.e., in r_⊥).

From our theoretical and simulation approaches we quantify how depletants partition in r_‖ and r_⊥ within each phase [Fig. 4(a)]. We define the partition coefficient of depletants in the columnar phase as:

K_C = ϕ^‖_d/ϕ^⊥_d. (1)

This coefficient along the C₁–C₂ binodal from simulations is similar as predicted from theory. From simulations K_C is computed from g^c–d_⊥ (ESI†). The genuinely fluid-like nature in r_‖ accounted for in simulations for the C₁ phase partially explains the deviation from theory at ϕ_c far from the CP.

Fig. 4 (a) Partition coefficients of depletants in the different columnar directions, K_C = ϕ^S‖_d/ϕ^S⊥_d, along the C₁–C₂ coexistence binodal for {Λ,q} = {0.1,0.01}. Circles correspond to simulations; dashed gray curve guides the eye. (b) K_C along the low-density columnar phase C₁ at fixed q/Λ; distance to the critical point is Δϕ_c ≡ ϕ^CP_c − ϕ_c(in C₁).

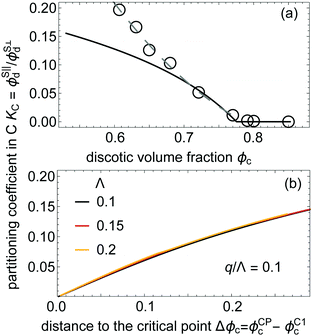
This C₁–C₂ coexistence is not unique to {Λ,q} = {0.1,0.01}. From theoretical predictions, K_C < 1: ϕ^S,⊥_d > ϕ^S,‖_d ∀ ϕ_c for any {Λ,q} (ESI†). In the denser columnar state C₂, ϕ^S,‖_d ≈ 0. Therefore, K_C ≈ 0 ∀ ϕ_c > ϕ^‖_c (above the C₁–C₂ critical point). Hence, we focus on K_C only in C₁. In Fig. 4(b) it can be appreciated that at fixed q/Λ, K_C along the C₁–C₂ binodal barely depends on Λ or on the nature of the triple-point (N–C₁–C₂ or I–C₁–C₂, see ESI†). The size of the effective system in r_‖ follows from the ratio of the depletant diameter to the thickness of the discotic, q/Λ. At fixed q, K_C increases with increasing Λ: the thicker discotics, the larger the small system size in r_‖. Thus, for smaller q the directionality of the pockets is enhanced and the C₁–C₂ coexistence spans over larger phase space (ESI†).

It is possible to assess the triple (I–N–C, N–C₁–C₂, and I–C₁–C₂) and critical C₁–C₂ points at any {Λ,q}.³¹ This provides a stability overview of the C₁–C₂ coexistence [Fig. 5(a)]. The C₁–C₂ coexistence is found for a wide range of {Λ,q}-values. The depletant-free triple point sets the reference from which the N–C₁–C₂ and I–C₁–C₂ critical-end point (CEP) curves span. The CEP marks a critical point in coexistence with a distinctive third phase;⁴⁰ hence, it constitutes a powerful tool to identify the stability limit of the C₁–C₂ phase coexistence.^6,31 A quadruple I–N–C₁–C₂ curve marks the transition from stable N–C₁–C₂ to I–C₁–C₂.³¹ Such quadruple coexistence in a two-component system is possible due to the extra field parameters Λ and q. In fact, already for the depletant-free discotic system an I–N–C coexistence is present^32,35 because Λ provides an extra field parameter; for hard spheres only two-phase fluid-solid coexistence emerges. A soft re-entrant behavior of the I–C₁–C₂ at fixed Λ is revealed.

Fig. 5 (a) Columnar coexistence overview in terms Λ and q/Λ = 2δ/L. (b) Partitioning coefficient of depletants in the nematic (solid curve) or isotropic (dotted curve) phase relative to the columnar phase at the critical end point (CEP).

For the N–(C₁C₂) CEP curve, q^cep/Λ ≈ 0.4 ∀ Λ ≲ 0.12, with q^cep the maximum depletant size at which C₁–C₂ coexistence is stable. For the I–(C₁C₂) CEP, q^cep/Λ decreases with Λ, q^cep/Λ ≈ 0.4 for Λ ≈ 0.12 and q^cep/Λ ≈ 0.3 for Λ ≈ 0.23. To understand the dependencies with Λ of the N–C₁–C₂ and of the I–C₁–C₂ CEPs, the partitioning coefficient of depletants in phase k (with k = {I,N}) relative to the columnar phase is defined:

K_k = ϕ^k_d/ϕ^C_d. (2)

As more depletants fit in the isotropic than in the nematic phase, a higher concentration of depletants is present in the columnar phases when a N–C₁–C₂ triple point occurs as compared to the I–C₁–C₂ case. Hence K_N is lower than K_I.

A simple model to understand the partitioning of tiny non-adsorbed compounds (depletants) in dense discotic systems was developed and tested against Monte Carlo simulations explicitly accounting for the binary mixture. The tiny depletants can distribute over two distinct regions, corresponding to the intra- and inter-columnar directions. Partitioning of tiny depletants in the intra-columnar direction leads to columnar–columnar coexistence, whose critical point occurs precisely at the discotic concentration at which depletants do not fit into the intra-columnar direction. A geometrically-derived free volume fraction for depletants allows understanding of not only how non-adsorbing compounds distribute in dense systems, but also the stability limits of this columnar–columnar coexistence. By considering compounds which interact solely via excluded volume interactions, the role of entropy in concentrated and highly size- and shape-asymmetric mixtures is identified. If polydispersity could be accounted for, we expect the quadruple curves to broaden as there are more possibilities for the partitioning of the depletants, but the already large simulation equilibration times would dramatically increase. We note also that we are currently working on one-to-one comparisons between FVT and experimental results for anisotropic particles, therefore moving towards a real application of the ideal FVT concepts.⁴¹

In summary, geometrical free volume fractions are a powerful tool for understanding partitioning over directional-dependent pockets in dense systems. The conceptual power of these geometrical free volume concepts has been recently exposed by applying the core of the idea here exposed to crowd control in public spaces following the new WHO regulations.⁴² Moreover, we expect this geometrical free volume to deliver further interesting insights, for example in crowded biological environments (the cell) and in photonics. Further developments could include particle interactions beyond their excluded volume, polydispersity effects, and the presence of an external field (e.g., gravity or electric fields). However, quantifying what goes where is a natural first step.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Á. G. G. and A. C. thank Prof. A. Patti for the meeting organized at Manchester University in June 2018. Prof. Lekkerkerker and the SPC-TGM participants are thanked for discussions. AC thanks the Spanish Ministerio de Ciencia Innovación y Universidades and FEDER (PGC2018-097151-B-I00) for funding and C3UPO for HPC facilities.

References

1. S. X. Meng, M. Rudnicki, V. J. Lieffers, D. E. B. Reid and U. Silins, J. Ecol., 2006, 94, 681–686.
2. J. L. Silverberg, M. Bierbaum, J. P. Sethna and I. Cohen, Phys. Rev. Lett., 2013, 110(22), 228701.
3. L. Sapir and D. Harries, Bunsen-Mag., 2017, 19, 152–162.
4. M. Hoppert and F. Mayer, Am. Sci., 1999, 87, 518–525.
5. A. P. Minton, J. Cell Sci., 2006, 119, 2863–2869.
6. Á. González García, J. Opdam, R. Tuinier and M. Vis, Chem. Phys. Lett., 2018, 709, 16–20.
7. W. R. Inc., Mathematica, Version [12.1], https://www.wolfram.com/mathematica, Champaign, IL, 2020.
8. Á. González García, H. H. Wensink, H. N. W. Lekkerkerker and R. Tuinier, Sci. Rep., 2017, 7, 17058.
9. M. Baus and C. F. Tejero, Equilibrium Statistical Physics, Springer, Berlin, Heidelberg, 1st edn, 2008.
10. A. V. Petukhov, R. Tuinier and G. J. Vroege, Curr. Opin. Colloid Interface Sci., 2017, 30, 54–61.
11. T. Sentjabrskaja, E. Zaccarelli, C. De Michele, F. Sciortino, P. Tartaglia, T. Voigtmann, S. U. Egelhaaf and M. Laurati, Nat. Commun., 2016, 7, 11133.
12. P. Struntz and M. Weiss, Phys. Chem. Chem. Phys., 2018, 20, 28910–28919.
13. N. Gnan and E. Zaccarelli, Nat. Phys., 2019, 15, 683–688.
14. G. van Anders, D. Klotsa, N. K. Ahmed, M. Engel and S. C. Glotzer, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, E4812–E4821.
15. G. van Anders, N. K. Ahmed, R. Smith, M. Engel and S. C. Glotzer, ACS Nano, 2014, 8, 931–940.
16. E. Bianchi, R. Blaak and C. N. Likos, Phys. Chem. Chem. Phys., 2011, 13, 6397–6410.
17. F. Gámez, R. D. Acemel and A. Cuetos, Mol. Phys., 2013, 111, 3136–3146.
18. M. Dijkstra, Entropy-Driven Phase Transitions in Colloids: From spheres to anisotropic particles, John Wiley & Sons, Ltd, 2014, ch. 2, pp. 35–71.
19. D. J. Kraft, R. Ni, F. Smallenburg, M. Hermes, K. Yoon, D. A. Weitz, A. van Blaaderen, J. Groenewold, M. Dijkstra and W. K. Kegel, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 10787–10792.
20. B. G. P. van Ravensteijn, M. Kamp, A. van Blaaderen and W. K. Kegel, Chem. Mater., 2013, 25, 4348–4353.
21. T. Ye, N. Phan-Thien and C. T. Lim, J. Biomech., 2016, 49, 2255–2266.
22. J. Mui, J. Ngo and B. Kim, Nanomaterials, 2016, 6(5), 90.
23. L. Bailey, H. N. W. Lekkerkerker and G. C. Maitland, Soft Matter, 2015, 11, 222–236.
24. T. Tadros, Colloids in Paints, John Wiley & Sons, Ltd, 2011.
25. T. Tadros, Colloids in Cosmetics and Personal Care, John Wiley & Sons, Ltd, 2011.
26. P. Das, J.-M. Malho, K. Rahimi, F. H. Schacher, B. Wang, D. E. Demco and A. Walther, Nat. Commun., 2015, 6, 5967.
27. J. Sun, B. Bhushan and J. Tong, RSC Adv., 2013, 3, 14862–14889.
28. H. H. Wensink, Phys. Rev. Lett., 2004, 93, 157801.
29. A. Cuetos and B. Martínez-Haya, J. Chem. Phys., 2008, 129, 214706.
30. A. Vrij, Pure Appl. Chem., 1976, 48, 471–483.
31. Á. González García, R. Tuinier, J. V. Maring, J. Opdam, H. H. Wensink and H. N. W. Lekkerkerker, Mol. Phys., 2018, 116, 2757–2772.
32. M. Marechal, A. Cuetos, B. Martínez-Haya and M. Dijkstra, J. Chem. Phys., 2011, 134, 094501.
33. H. N. W. Lekkerkerker, Colloids Surf., 1990, 51, 419–426.
34. H. N. W. Lekkerkerker and R. Tuinier, Colloids and the Depletion Interaction, Springer, Heidelberg, 2011.
35. H. H. Wensink and H. N. W. Lekkerkerker, Mol. Phys., 2009, 107, 2111–2118.
36. C. F. Tejero, A. Daanoun, H. N. W. Lekkerkerker and M. Baus, Phys. Rev. Lett., 1994, 73, 752–755.
37. P. G. Bolhuis, M. Hagen and D. Frenkel, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 50, 4880.
38. G. Foffi, G. D. McCullagh, A. Lawlor, E. Zaccarelli, K. A. Dawson, F. Sciortino, P. Tartaglia, D. Pini and G. Stell, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 031407.
39. S. C. Glotzer and M. J. Solomon, Nat. Mater., 2007, 6, 557–562.
40. J. Lang and B. Widom, Phys. A, 1975, 81, 190–213.
41. F. Dekker, Á. González García and A. P. Philipse, Eur. Phys. J. E, 2020, 43, 38,  DOI:10.1140/epje/i2020-11962-y.
42. Á. González García, J. L. Martin R and C. Alessio, Crowd Control in Plazas Constrained to Social Distancing, https://arxiv.org/abs/2005.07038.

---

Footnote

† Electronic supplementary information (ESI) available: Further theoretical and simulation details. See DOI: 10.1039/d0sm00802h

---