Open Access Article
Open Access ArticleFactors controlling the pinning force of liquid droplets on liquid infused surfaces
Muhammad Subkhi
Sadullah
 ,
Jack R.
Panter
and
Halim
Kusumaatmaja
,
Jack R.
Panter
and
Halim
Kusumaatmaja
 *
*
Department of Physics, Durham University, Durham, DH1 3LE, UK. E-mail: halim.kusumaatmaja@durham.ac.uk
First published on 24th July 2020
Abstract
Liquid infused surfaces with partially wetting lubricants have recently been exploited for numerous intriguing applications, such as for droplet manipulation, droplet collection and spontaneous motion. When partially wetting lubricants are used, the pinning force is a key factor that can strongly affect droplet mobility. Here, we derive an analytical prediction for contact angle hysteresis in the limit where the meniscus size is much smaller than the droplet, and numerically study how it is controlled by the solid fraction, the lubricant wetting angles, and the various fluid surface tensions. We further relate the contact angle hysteresis and the pinning force experienced by a droplet on a liquid infused surface, and our predictions for the critical sliding angles are consistent with existing experimental observations. Finally, we discuss why a droplet on a liquid infused surface with partially wetting lubricants typically experiences stronger pinning compared to a droplet on a classical superhydrophobic surface.
1 Introduction
Since their inception,1–3 liquid infused surfaces (LIS) have been prized for their anti-adhesive nature, which results in properties such as the high mobility of liquid droplets and anti-fouling. These properties are highly desirable in a broad range of applications, from marine and medical coatings,4,5 to non-stick packaging,6 and digital microfluidics.7LIS are formed by impregnating a rough, porous or textured surface with a lubricating liquid, which is immiscible to the mobile liquid phase introduced to LIS. The lubricant also needs to preferentially wet the solid compared to the mobile liquid phase.3 This lubricant layer imbues LIS with significant advantages over superhydrophobic surfaces, such as pressure stability2 and self healing.8
High mobility of a liquid droplet is particularly obtained when the lubricant completely wets the surface texture, as pinning of the droplet on the surface is negated by the intervening lubricant layer. However, the dependency on a fully wetting lubricant often limits the implementation of LIS, both due to the difficulty of finding the suitable lubricant for the desired applications,3,9 and due to the possibility of lubricant depletion.10–14
On the other hand, LIS with partially wetting lubricant have increasingly attracted interest, especially with a number of external stimuli shown to allow reversible change of wetting states from slippery to sticky (see for example the recent review ref. 15). Such surfaces have substantially expanded functionality compared to the purely slippery surfaces, with the ability to locally change a droplets' mobility leading to the demonstration of fog capture even in high winds,16 to introduce bidirectional motion under texture gradients,17 and recently the unprecedented manipulation of both droplets and colloids.18
It is important therefore to understand pinning from two perspectives: as a problem to be minimised, or as a functional phenomenon to be controlled. However, to the best of our knowledge, the quantitative relationship of the pinning force to both the surface roughness and fluid properties has never been systematically studied on LIS.
In this contribution, we study the pinning force and contact angle hysteresis (CAH) of a droplet on LIS. We begin by developing an analytical model for CAH based on averaged Cassie–Baxter surface properties. For simplicity, we limit our study to the case where the meniscus size is significantly smaller than the droplet size. We then observe both advancing and receding contact angles using computer simulations, showing that the simulated CAH closely matches the analytical results. We, therefore, are able to accurately quantify the hysteresis based on the surface roughness, and the set of fluid–solid and fluid–fluid surface tensions. Further, we derive the total pinning force and demonstrate that our prediction is consistent with experimental observations.
We find, similar to droplets on solid surfaces, that there is a competition between two factors which control the pinning force on LIS, (i) the droplet base perimeter and (ii) the cosine difference between the receding and the advancing angles. Our theory suggests that this competition minimises pinning when the apparent contact angle approaches θapp → 0° or θapp → 180°, but maximises it at an intermediate value of the apparent contact angle, θapp ≃ 65.5°. Since most reported values of the apparent contact angle on LIS are moderate (θapp ∼ 80°–100°), this means a small but non-zero CAH can lead to a significant critical sliding angle for droplets on LIS.
2 Method
In this work, we are interested in static wetting configurations, rather than the dynamics of LIS system. The static configurations can be obtained by minimising the total free energy. A typical LIS system consists of three fluid phases (droplet, lubricant and gas phases) and a textured solid. To simulate such systems, we need a free energy model which can describe (i) the existence of the three fluid phases and their respective interfacial tensions, and (ii) fluid–solid interactions, which in turn determines the contact angles of the fluids on the solid surface.To do this, we employ a diffuse interface approach in which the total free energy is constructed as
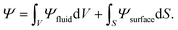 | (1) |
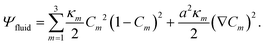 | (2) |
| γmn = a(κm + κn)/6. | (3) |
The surface free energy is given by20
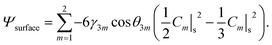 | (4) |
γgl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θgl + γld θgl + γld![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θld + γdg θld + γdg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θdg = 0. θdg = 0. | (5) |
In this work, the total free energy of the system is minimised using the L-BFGS algorithm,22 following the numerical scheme discussed in ref. 23 and 24. The L-BFGS algorithm is chosen due to its efficiency for minimisation problems with a large number of degrees of freedom, though in principle other minimisation routines may also be employed.
3 Results and discussions
3.1 Derivation of pinning force and CAH
The pinning force per unit length for a droplet on a dry (not lubricated) textured solid surface is given by25fdry = γdgΔ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, θ, | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = (cos
θ = (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θR − cos
θR − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θA) is the difference in the cosine of the receding θR and the advancing θA contact angles for the droplet–gas–solid contact line.
θA) is the difference in the cosine of the receding θR and the advancing θA contact angles for the droplet–gas–solid contact line.
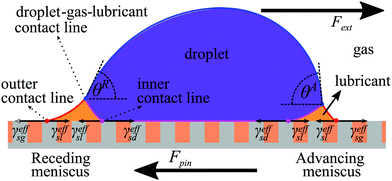
Compared to other surfaces, the distinguishing feature of LIS is the presence of the lubricant meniscus. As such, the droplet–gas–solid contact line is not present. Instead, we have to consider the compound effect of droplet–gas–lubricant, droplet–lubricant–solid and lubricant–gas–solid contact lines, as illustrated in Fig. 1. Semprebon et al. have derived an expression for the CAH on LIS using geometrical analysis of the meniscus.26 Here, we will show that the CAH can also be derived employing a simpler argument based on force balance.
Let us consider a droplet on LIS under the influence of an external force Fext, as shown in Fig. 1. Here, γeffsm denotes the effective interfacial tension of LIS with the fluid phase m, with m = d, g, l. The subscript s, d, g and l are to indicate the solid, droplet, gas and lubricant phases respectively. LIS can be considered as a composite surface where φs fraction of the surface is solid surface and the remaining (1 − φs) is the lubricant surface.27 The effective interfacial tension of the fluid phase m with the composite surface can then be written as
| γeffsm = φsγsm + (1 − φs)γlm. | (7) |
The pinning force per unit length for a droplet on LIS fLIS can be calculated from the sum of the effective interfacial tensions of this composite surface at the outer and the inner contact lines, as indicated in Fig. 1. Hence, fLIS is written as
| fLIS = ([γeffsg − γeffsl]R + [γeffsl − γeffsg]A)outer + ([γeffsl − γeffsd]R + [γeffsd − γeffsl]A)inner. | (8) |
Generally, the terms for the outer and inner contact lines cannot simply be added together since they are to be integrated over different lengths (i.e. the inner and the outer droplet base perimeters). However, in the limit where the meniscus size is small compared to the droplet, the outer and the inner droplet base perimeters can be taken to be approximately the same.26,28 In this approximation, we can introduce the effective lubricant wetting angles as
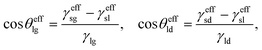 | (9) |
fLIS = ([γlg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θefflg − γld θefflg − γld![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θeffld]R − [γlg θeffld]R − [γlg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θefflg − γld θefflg − γld![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θeffld]A). θeffld]A). | (10) |
fLIS = γlg(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θeff,Rlg − cos θeff,Rlg − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θeff,Alg) − γld(cos θeff,Alg) − γld(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θeff,Rld − cos θeff,Rld − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θeff,Ald) = γlgΔ θeff,Ald) = γlgΔ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θefflg − γldΔ θefflg − γldΔ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θeffld. θeffld. | (11) |
For an advancing contact line on a dry textured surface, the front part of the droplet typically advances by bridging to the front subsequent post. For LIS, such a contact line depinning mechanism is also observed for the lubricant–droplet interface at the advancing meniscus as well as the lubricant–gas interface at the receding meniscus.30 Therefore, the effective contact angle for both interfaces are zero when they depin, [θefflg]R = 0 and [θeffld]A = 0.
There are various mechanisms for the receding contact line to depin from the post, which depend on the post geometry.24 For LIS, this is relevant for understanding the lubricant–droplet interface at the receding meniscus and the lubricant–gas interface at the advancing meniscus. Here we will focus on a square array of rectangular posts, and we can use our numerical approach to determine the relevant depinning mechanism. To do this, we start by simplifying the system studied and isolate the advancing lubricant–gas and the receding lubricant–droplet interfaces, as shown in Fig. 2(a and b). To reduce the computational cost, we concentrate our numerical study in the region close to the contact line. We have used a quasi 3D setup where only a single row of posts are explicitly simulated at the bottom surface, a smooth wall is used for the top surface, and periodic boundary condition is applied in the direction perpendicular to the row of posts. Two fluid phases are then introduced in each half of the simulation domain, and the two phases have equal pressure such that their interface is flat. The top contact angle β can be controlled to measure the depinning angles. This is performed by varying β and recording its critical angle, βmax, for the stability of the corresponding interfaces. Simple geometry then dictates that βmax is the critical depinning angle for [θefflg]A and [θeffld]R.
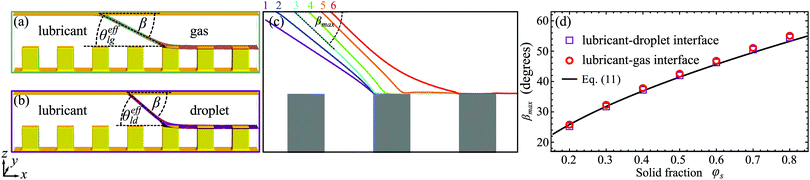 | ||
| Fig. 2 Simulations of the depinning mechanism using quasi 3D setups for (a) the advancing lubricant–gas and (b) the receding lubricant–droplet interfaces. The top contact angle β can be tuned to find θdepinlg and θdepinld. (c) The typical evolution of the contact line when β is increased. For β < βmax (purple and blue lines), the contact line is pinned. At β = βmax (cyan, green, orange and red lines), the contact line slides on top of the post. The measurement of βmax for different φs and its comparison with eqn (12) are presented in panel (d). Here, we have used θld = θlg = 60°. | ||
The typical development of a receding interface is shown in Fig. 2(c) upon varying β. The interface is initially stable and pinned at the corner of the rectangular post (purple line). Increasing β deforms the interface (blue line) until we eventually reach βmax (cyan line). Here the interface detaches from the corner and the contact line slides on top of the post (see green, orange and red lines), while maintaining a constant contact angle at the top plate. For this depinning mechanism, the critical angle is given by βmax = θCBlm, where θCBlm is the Cassie–Baxter contact angle27,31 of the composite surface:
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βmax = cos βmax = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θCBlm = φs θCBlm = φs![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θlm + (1 − φs), θlm + (1 − φs), | (12) |
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θdepinld = φs θdepinld = φs![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θld + (1 − φs), θld + (1 − φs), | (13) |
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θdepinlg = φs θdepinlg = φs![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θlg + (1 − φs). θlg + (1 − φs). | (14) |
fLIS = [γlg − γld(φs![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θld + (1 − φs))]R − [γlg(φs θld + (1 − φs))]R − [γlg(φs![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θlg + (1 − φs)) − γld]A, θlg + (1 − φs)) − γld]A, | (15) |
fLIS = φs[γlg(1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θlg) + γld(1 − cos θlg) + γld(1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θld)]. θld)]. | (16) |
fLIS = γdg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δ Δ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, θ, | (17) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = cos
θ = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θR − cos
θR − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θA, and the receding and the advancing contact angles are respectively defined as
θA, and the receding and the advancing contact angles are respectively defined as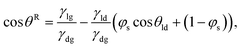 | (18) |
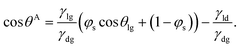 | (19) |
It is worth noting that, in this work, we have focussed on the case where the lubricant does not encapsulate the droplet. When the lubricant encapsulates the droplet, the effective droplet–gas surface tension becomes γeffdg = γlg + γld.32
3.2 The effect of changing fluid and solid properties
Eqn (18) and (19) suggest the advancing and receding angles are controlled by the surface tensions (γdg, γlg, γld), the lubricant wetting angles (θlg, θld), and the fraction of solid φs. In this subsection we will systematically test the validity and accuracy of eqn (18) and (19) for predicting the advancing and receding angles.To do this, rather than simulating the whole droplet (top panel of Fig. 3(a)), we will focus on the region around the lubricant meniscus (lower panel of Fig. 3(a)). In this simulation setup, the three fluid phases are present; and as in the setup in Fig. 2, the movement of the meniscus is controlled by the contact angle at the top plate, β. The maximum angle βmax for which the meniscus remains stable corresponds to the advancing angle θA; while the minimum angle βmin is the receding angle θR.
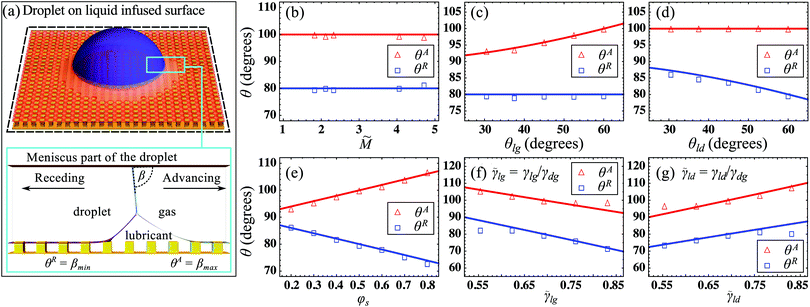 | ||
| Fig. 3 (a) Simulation setup for the advancing and the receding angles. To reduce computational costs, we focus on simulating the region around the lubricant meniscus. By varying β, we are able to investigate when the meniscus advances or recedes. The parameters studied are (b) the meniscus size, (c) the lubricant–gas wetting angle, (d) the lubricant–droplet wetting angle, (e) the solid fraction, and the ratios of (f) lubricant–gas and (g) lubricant–droplet surface tensions with the droplet–gas surface tension. In (b–g), the red and blue lines are theoretical predictions for θA and θR given in eqn (18) and (19) respectively. The default values of the parameters are θlg = 60°; θld = 60°; φs = 0.5; and γlg/γdg = γld/γdg = 0.69. | ||
We first investigate the role of meniscus size on the advancing and receding angles. The meniscus size can be controlled by tuning the volume of the lubricant phase. Here, we parameterise the meniscus size ![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) by taking the ratio of the cross sectional area of the lubricant meniscus to the unit cell of the post. The unit cell of the post is defined as the product between the centre-to-centre distance between neighbouring posts and the height of the posts. Furthermore, we set the pressure in the droplet and gas phases to be equal, such that we are always in the vanishing meniscus regime26 where the radius of the curvature of the lubricant meniscus is much smaller compared to the radius of curvature for the droplet–gas interface. From Fig. 3(b) we can see that the advancing and the receding angles are independent of the meniscus size in this limit.
by taking the ratio of the cross sectional area of the lubricant meniscus to the unit cell of the post. The unit cell of the post is defined as the product between the centre-to-centre distance between neighbouring posts and the height of the posts. Furthermore, we set the pressure in the droplet and gas phases to be equal, such that we are always in the vanishing meniscus regime26 where the radius of the curvature of the lubricant meniscus is much smaller compared to the radius of curvature for the droplet–gas interface. From Fig. 3(b) we can see that the advancing and the receding angles are independent of the meniscus size in this limit.
The effect of the lubricant wetting angles, θlg and θld, are presented in panels (c) and (d) of Fig. 3. In panel (c), we observe that θlg only affects the advancing angle but not the receding angle. This is because θlg controls the depinning angle of the lubricant–gas interface when the droplet is advancing. When the droplet is receding, the lubricant–gas interface moves by bridging the neighbouring post, which is independent from θlg. Similarly, the bridging mechanism occurs for the lubricant–droplet interface during the advancing motion. As such, θld does not affect the advancing angle, as shown in panel (d). In contrast, during the receding process, the lubricant–droplet interface moves by depinning from the post. Hence, the receding angle is affected by θld.
The influence of the solid fraction φs is shown in panel (e) of Fig. 3. Here, we vary φs = Wy/Ly by changing the post width in the direction perpendicular to the row of post (Wy). It is intuitive to foresee that Δθ increases with φs. More specifically, this is because θA increases while θR decreases with φs. This finding is aligned with the experimental results in ref. 3. In their work, although θA and θR were not measured directly, they showed that the pinning force that acts on a droplet on LIS can be reduced by employing surfaces with smaller φs.3
Next, the effect of the lubricant interfacial tensions is demonstrated in Fig. 3(f and g). Interestingly, increasing γlg decreases both the advancing and the receding angles, while for γld, the effect is reversed. This is due to the fact that increasing γlg generally makes a droplet on LIS to be more hydrophilic-like, while increasing γld makes it more hydrophobic-like, and thus the change of the contact angles follow accordingly.33,34
Finally, we have argued in eqn (15) and (16) that the pinning force of a droplet on LIS does not depend on the droplet–gas interfacial tension γdg. Indeed, while the magnitudes of the advancing and receding angles are influenced by γdg, see Fig. 4(a), the pinning force per unit length is constant regardless of γdg, as shown in Fig. 4(b).
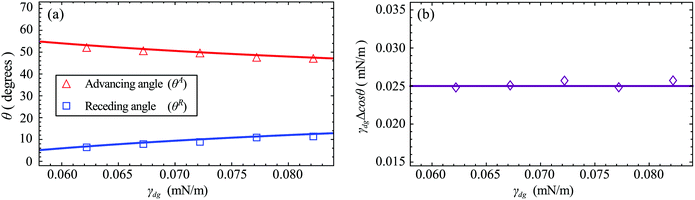 | ||
| Fig. 4 (a) The effect of γdg on θA and θR. The red and blue lines are the theoretical predictions for θA and θR as given in eqn (18) and (19) respectively. (b) The pinning force per unit length for a droplet on LIS is independent of γdg. | ||
By studying each independent variable systematically, we have therefore demonstrated that eqn (18) and (19) are an excellent model to describe the advancing and receding angles, as well as the contact angle hysteresis. All simulation results are in excellent agreement with this model.
3.3 The relationship between CAH, sliding angle and pinning force
One common practice to determine the CAH is to measure the advancing and the receding angles when a droplet is sliding as the substrate is inclined.35 The droplet starts to slide when the external body force is larger than the pinning force that holds the droplet on the surface. The sliding angle α is related to the external body force via a simple relationFext = ρVdropg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α. α. | (20) |
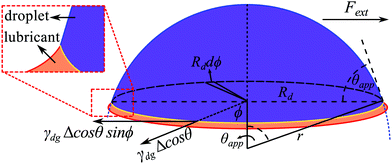
To obtain the total pinning force, we need to integrate the pinning force per unit length over the base perimeter of the droplet contact area with the solid. Consider the geometry illustrated in Fig. 5, where again we focus on the vanishing meniscus limit. The pinning force per unit length is given by γdgΔ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ; however, to balance the external force, we only need the vector component in the opposite direction of Fext. Denoting ϕ as the azimuthal angle around the droplet, this corresponds to γdgΔ
θ; however, to balance the external force, we only need the vector component in the opposite direction of Fext. Denoting ϕ as the azimuthal angle around the droplet, this corresponds to γdgΔ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ. Assuming that the droplet base is circular, the total pinning force is then
ϕ. Assuming that the droplet base is circular, the total pinning force is then
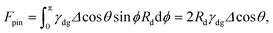 | (21) |
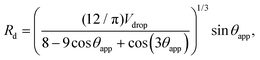 | (22) |
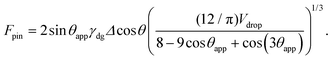 | (23) |
We can now balance the external body force eqn (20) with the pinning force eqn (21) to obtain the theoretical prediction of the sliding angle α, which is given by
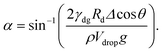 | (24) |
| φ s | Δθ (°) | α (°) | α e (°) | |α − αe| (°) |
|---|---|---|---|---|
| 0.25 | 8 | 28 | 30 | 2 |
| 0.33 | 11 | 37 | 45 | 8 |
| 0.44 | 14 | 53 | 60 | 7 |
From Table 1 we find that, on LIS, a relatively low CAH (Δθ) can still lead to a significant critical sliding angle α. This is different compared to superhydrophobic surfaces where α usually has the same magnitude as Δθ. It also suggests we should be cautious when using Δθ to characterise the mobility (and more generally, liquid repellency) of a liquid droplet on LIS.
To explain why a droplet on LIS may suffer from a large pinning force, let us now consider two key aspects in which the contact angle of a droplet can affect the pinning force in eqn (21), namely through the droplet base perimeter R and the difference in the cosine of the contact angle Δ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ. First, for LIS, the apparent contact angle θapp is relatively low such that the droplet base perimeter is large, in direct contrast to the large contact angle and small base perimeter for drops on classical superhydrophobic surfaces. This large droplet base perimeter can potentially magnify the pinning force, since Fpin ∝ R. Second, the Δ
θ. First, for LIS, the apparent contact angle θapp is relatively low such that the droplet base perimeter is large, in direct contrast to the large contact angle and small base perimeter for drops on classical superhydrophobic surfaces. This large droplet base perimeter can potentially magnify the pinning force, since Fpin ∝ R. Second, the Δ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ term has an implicit dependence on the contact angle. Even for the same value of Δθ, Δ
θ term has an implicit dependence on the contact angle. Even for the same value of Δθ, Δ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ is greater when θapp ≈ 90° than when θapp ≈ 180° or θapp ≈ 0°. Therefore, droplets on LIS are prone to large pinning forces when Δθ is large since most LIS systems reported in the literature have θapp ≈ 90°.
θ is greater when θapp ≈ 90° than when θapp ≈ 180° or θapp ≈ 0°. Therefore, droplets on LIS are prone to large pinning forces when Δθ is large since most LIS systems reported in the literature have θapp ≈ 90°.
It is useful to express the pinning force in a non-dimensionalised form, given by
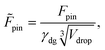 | (25) |
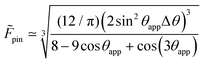 | (26) |
The effects of Δθ and θapp on the pinning force are visualised in Fig. 6. Interestingly, we find that the pinning force reaches its maximum at θapp = 65.5°, regardless of Δθ. Therefore, for LIS, it is advisable to avoid the droplet–lubricant combinations which result in θapp ≈ 65.5°. The Δ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ itself reaches its maximum at θapp = 90° for any given value of Δθ, as shown as the red plot in the inset of Fig. 6. This is an indication that Δ
θ itself reaches its maximum at θapp = 90° for any given value of Δθ, as shown as the red plot in the inset of Fig. 6. This is an indication that Δ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ is not the only factor that controls the pinning force. The shift in the maximum of
θ is not the only factor that controls the pinning force. The shift in the maximum of ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) pin to the lower θapp is due to the contribution from the droplet base perimeter. As shown in the inset (black plot), the non-dimensionalised droplet base radius Rd/(Vdrop)1/3 is larger for smaller θapp.
pin to the lower θapp is due to the contribution from the droplet base perimeter. As shown in the inset (black plot), the non-dimensionalised droplet base radius Rd/(Vdrop)1/3 is larger for smaller θapp.
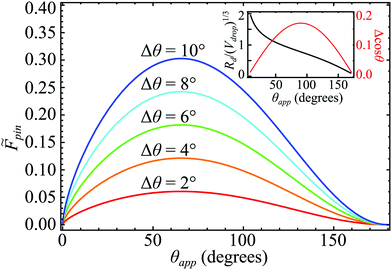 | ||
Fig. 6 Visualisation of the effects of CAH and the droplet shape on the pinning force. The inset shows the non-dimensionalised droplet base radius 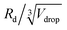 and Δ and Δ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ against θapp. θ against θapp. | ||
Consistent with our theory, Fig. 6 also rationalises why pinning force is small for superhydrophobic surfaces. This is because both Δ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ and Rd/(Vdrop)1/3 go to zero as θ → 180°.
θ and Rd/(Vdrop)1/3 go to zero as θ → 180°.
4 Conclusions
In this work, we have considered the contact angle hysteresis and pinning force of a droplet on LIS in the limit of the vanishing meniscus case. We have derived the expressions for the advancing and receding angles as well as the pinning force using a force balance argument, including how they depend on the liquid interfacial tensions, the lubricant wetting angles, and the solid fraction. Each dependency was systematically tested and verified using numerical simulations based on a diffuse interface approach. We also found that the pinning force does not depend on the droplet–gas interfacial tension.We have also derived an analytical expression for the critical droplet sliding angle, and the predictions from our theory are consistent with experimental data reported by Semprebon et al..3 Furthermore, using this theory, we assess why liquid droplets on LIS suffer from larger pinning forces compared to superhydrophobic surfaces, even for the same Δθ. We conclude this is due to two factors: both the droplet base perimeter and the magnitude of Δ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ are typically larger in LIS due to the lower (apparent) contact angle.
θ are typically larger in LIS due to the lower (apparent) contact angle.
This study helps us to carefully design LIS by providing insights into how each relevant parameter influences the pinning force. Although the example shown here is for the rectangular posts, similar derivations of the pinning force, as well as the advancing and the receding angles, can also be done for different surface geometries by following the same approach. Interestingly, the derivations rely on the depinning mechanism of each lubricant interface, which is just a binary fluid case. This shows an example where the complexity of ternary fluids systems can be broken down into their constituting binary fluids problems. It would be therefore interesting for future research to test our theory for more complex geometries, in particular for regimes where the Cassie–Baxter approximation is known to break down for contact angle hysteresis on superhydrophobic surfaces.36–38 Furthermore, we hope our theory will motivate systematic experimental verifications, harnessing recent advances in surface fabrication techniques for LIS.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
MSS is supported by an LPDP (Lembaga Pengelola Dana Pendidikan) scholarship from the Indonesian Government. JRP and HK acknowledge funding from EPSRC (grant EP/P007139/1) and Procter and Gamble. We thank to Dr Ciro Semprebon, Dr Yonas Gizaw and Dr Dan Daniel for the fruitful discussions.References
- D. Quéré, Rep. Prog. Phys., 2005, 68, 2495–2532 CrossRef
.
- T.-S. Wong, S. H. Kang, S. K. Y. Tang, E. J. Smythe, B. D. Hatton, A. Grinthal and J. Aizenberg, Nature, 2011, 477, 443–447 CrossRef CAS PubMed
.
- J. D. Smith, R. Dhiman, S. Anand, E. Reza-Garduno, R. E. Cohen, G. H. McKinley and K. K. Varanasi, Soft Matter, 2013, 9, 1772–1780 RSC
.
- I. Sotiri, J. C. Overton, A. Waterhouse and C. Howell, Exp. Biol. Med., 2016, 241, 909–918 CrossRef CAS PubMed
.
- C. S. Ware, T. Smith-Palmer, S. Peppou-Chapman, L. R. Scarratt, E. M. Humphries, D. Balzer and C. Neto, ACS Appl. Mater. Interfaces, 2018, 10, 4173–4182 CrossRef CAS PubMed
.
- P. S. Brown and B. Bhushan, J. Colloid Interface Sci., 2017, 487, 437–443 CrossRef CAS
.
- H. Geng and S. K. Cho, Lab Chip, 2019, 19, 2275–2283 RSC
.
- Q. Wei, C. Schlaich, S. Prévost, A. Schulz, C. Böttcher, M. Gradzielski, Z. Qi, R. Haag and C. A. Schalley, Adv. Mater., 2014, 26, 7358–7364 CrossRef CAS
.
- Y. Galvan, K. R. Phillips, M. Haumann, P. Wasserscheid, R. Zarraga and N. Vogel, Langmuir, 2018, 34, 6894–6902 CrossRef CAS
.
- C. Howell, T. L. Vu, C. P. Johnson, X. Hou, O. Ahanotu, J. Alvarenga, D. C. Leslie, O. Uzun, A. Waterhouse, P. Kim, M. Super, M. Aizenberg, D. E. Ingber and J. Aizenberg, Chem. Mater., 2015, 27, 1792–1800 CrossRef CAS
.
- Y. Liu, J. S. Wexler, C. Schönecker and H. A. Stone, Phys. Rev. Fluids, 2016, 1, 074003 CrossRef
.
- S. Sett, X. Yan, G. Barac, L. W. Bolton and N. Miljkovic, ACS Appl. Mater. Interfaces, 2017, 9, 36400–36408 CrossRef CAS
.
- S. Peppou-Chapman and C. Neto, ACS Appl. Mater. Interfaces, 2018, 10, 33669–33677 CrossRef CAS PubMed
.
- M. J. Kreder, D. Daniel, A. Tetreault, Z. Cao, B. Lemaire, J. V. Timonen and J. Aizenberg, Phys. Rev. X, 2018, 8, 031053 CAS
.
- X. Lou, Y. Huang, X. Yang, H. Zhu, L. Heng and F. Xia, Adv. Funct. Mater., 2020, 30, 1901130 CrossRef CAS
.
- Y. Wang, B. Qian, C. Lai, X. Wang, K. Ma, Y. Guo, X. Zhu, B. Fei and J. H. Xin, ACS Appl. Mater. Interfaces, 2017, 9, 24428–24432 CrossRef CAS PubMed
.
- M. S. Sadullah, G. Launay, J. Parle, R. Ledesma-Aguilar, Y. Gizaw, G. McHale, G. G. Wells and H. Kusumaatmaja, 2020, arXiv, 2004.10408.
- W. Wang, J. V. I. Timonen, A. Carlson, D.-M. Drotlef, C. T. Zhang, S. Kolle, A. Grinthal, T.-S. Wong, B. Hatton, S. H. Kang, S. Kennedy, J. Chi, R. T. Blough, M. Sitti, L. Mahadevan and J. Aizenberg, Nature, 2018, 559, 77–82 CrossRef CAS
.
- C. Semprebon, T. Krüger and H. Kusumaatmaja, Phys. Rev. E, 2016, 93, 033305 CrossRef
.
- T. L. K. Connington, J. Comput. Phys., 2013, 250, 601–615 CrossRef
.
- L. Girifalco and R. Good, J. Phys. Chem., 1957, 61, 904–909 CrossRef CAS
.
- D. C. Liu and J. Nocedal, Math. Program., 1989, 45, 503–528 CrossRef
.
- H. Kusumaatmaja, J. Chem. Phys., 2015, 142, 124112 CrossRef PubMed
.
- J. R. Panter, Y. Gizaw and H. Kusumaatmaja, Sci. Adv., 2019, 5, eaav7328 CrossRef CAS PubMed
.
- D. Quéré, Annu. Rev. Mater. Res., 2008, 38, 71–99 CrossRef
.
- C. Semprebon, G. McHale and H. Kusumaatmaja, Soft Matter, 2017, 13, 101–110 RSC
.
- A. Cassie and S. Baxter, Trans. Faraday Soc., 1944, 40, 546 RSC
.
- A. Keiser, L. Keiser, C. Clanet and D. Quéré, Soft Matter, 2017, 13, 6981–6987 RSC
.
- B. M. Mognetti and J. M. Yeomans, Langmuir, 2010, 26, 18162–18168 CrossRef CAS PubMed
.
- F. Schellenberger, N. Encinas, D. Vollmer and H.-J. Butt, Phys. Rev. Lett., 2016, 116, 096101 CrossRef PubMed
.
- C. Priest, R. Sedev and J. Ralston, Phys. Rev. Lett., 2007, 99, 026103 CrossRef PubMed
.
- G. McHale, B. V. Orme, G. G. Wells and R. Ledesma-Aguilar, Langmuir, 2019, 35, 4197–4204 CrossRef CAS PubMed
.
- F. Schellenberger, J. Xie, N. Encinas, A. Hardy, M. Klapper, P. Papadopoulos, H.-J. Butt and D. Vollmer, Soft Matter, 2015, 11, 7617–7626 RSC
.
- M. S. Sadullah, C. Semprebon and H. Kusumaatmaja, Langmuir, 2018, 34, 8112–8118 CrossRef CAS PubMed
.
- H. B. Eral, D. 't Mannetje and J. M. Oh, Colloid Polym. Sci., 2013, 291, 247–260 CrossRef CAS
.
- J. F. Joanny and P. G. de Gennes, J. Chem. Phys., 1984, 81, 552–562 CrossRef CAS
.
- M. Reyssat and D. Quéré, J. Phys. Chem. B, 2009, 113, 3906–3909 CrossRef CAS PubMed
.
- R. Raj, R. Enright, Y. Zhu, S. Adera and E. N. Wang, Langmuir, 2012, 28, 15777–15788 CrossRef CAS
.
| This journal is © The Royal Society of Chemistry 2020 |