Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Snapping elastic disks as microswimmers: swimming at low Reynolds numbers by shape hysteresis
Christian
Wischnewski
and
Jan
Kierfeld
 *
*
Physics Department, TU Dortmund University, 44221 Dortmund, Germany. E-mail: jan.kierfeld@tu-dortmund.de
First published on 8th July 2020
Abstract
We illustrate a concept for shape-changing microswimmers, which exploits the hysteresis of a shape transition of an elastic object, by an elastic disk undergoing cyclic localized swelling. Driving the control parameter of a hysteretic shape transition in a completely time-reversible manner gives rise to a non-time-reversible shape sequence and a net swimming motion if the elastic object is immersed into a viscous fluid. We prove this concept with a microswimmer which is a flat circular elastic disk that undergoes a transition into a dome-like shape by localized swelling of an inner disk. The control parameter of this shape transition is a scalar swelling factor of the disk material. With a fixed outer frame with an additional attractive interaction in the central region, the shape transition between flat and dome-like shape becomes hysteretic and resembles a hysteretic opening and closing of a scallop. Employing Stokesian dynamics simulations of a discretized version of the disk we show that the swimmer is effectively moving into the direction of the opening of the dome in a viscous fluid if the swelling parameter is changed in a time-reversible manner. The swimming mechanism can be qualitatively reproduced by a simple 9-bead model.
1 Introduction
Swimming on the microscale at low Reynolds numbers requires special propulsion mechanisms which are effective in the presence of dominating viscous forces. Phoretic swimmers create gradients in external fields such as concentration or temperature which in turn give rise to symmetry-breaking interfacial forces leading to propulsion if they overcome the friction force of the microswimmer.1 Besides phoretic swimmers, self-deforming or shape-changing swimmers are the largest class of microswimmers. They deform their body in a cyclic way in order to propel. This general principle has the advantage that it works independently of the environment, i.e., it does not require an external field, that eventually changes the properties of the fluid. The disadvantage of swimming by deformation is, on the other hand, that there are necessarily “moving parts” causing additional viscous flow in the fluid and forces on the swimmer. As a consequence, at low Reynolds numbers, the cyclic deformation pattern must not be invariant under time-reversal: the scallop theorem formulated by Purcell states that periodic reciprocal patterns of deformation can not lead to an effective net motion on the microscale because of the linearity of the Stokes equation.2In nature, many different examples of deformation swimmers can be found such as bacteria, algae and spermatozoa.3,4 These natural swimmers often rely on the movement of a few flagella or many cilia on their surface.5–8 Flagella employ a periodic forcing but overcome the scallop theorem by exploiting friction along the elastic flagellum to break time-reversibility. This requires a matching of driving and frictional damping time scales for efficient propulsion. Often it also requires the ability of local actuation for the periodic forcing. This makes this concept hard to reproduce or imitate in a controlled fashion in an artificial system.9,10
Another basic strategy to overcome the scallop theorem are deformation cycles that involve at least two control parameters and drive the swimmer periodically along a closed contour in this at least two-dimensional parameter space. Different shape changing artificial swimmers have been developed based on this concept starting with Purcell's three-link swimmer2 and including swimmers performing small deformations of spheres, circles, or cylinders,11–15 or shape-changing vesicles.16 The most simple shape changing microswimmer is arguably the one-dimensional linear three-bead swimmer developed by Najafi and Golestanian, where three beads change their distance in a non-time-reversible way.17,18 By extending the linear three bead arrangement to a second dimension in a triangular shape, a three bead swimmer can perform two-dimensional motions (circles)19 and steer.20 Nevertheless, despite the simplicity of the concept, this type of swimmer is difficult to implement experimentally because it requires fine control over, at least, two control parameters such as the bead positions of the three-bead swimmer.21,22
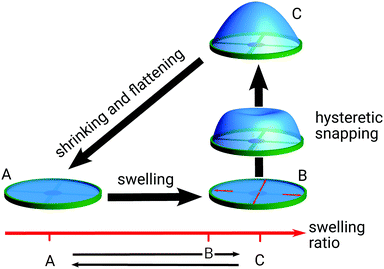
We employ a different general strategy in order to overcome the scallop theorem, which is widely applicable and only involves control of a single global and scalar control parameter, which couples, however, to a hysteretic (or bistable) shape transition of the system, see Fig. 1. If also the sequence of shapes exhibits hysteresis, this converts the time-reversible motion in one-dimensional control parameter space into a non-time-reversible motion in a higher-dimensional parameter or shape space. Hysteretic shape transitions can be realized, for example, by using the intrinsic properties of elastic materials. In this work, we will realize such a hysteretic shape transition based on a swelling process of a flat and thin circular elastic disk, where material swelling with swelling ratios of only a few percent in the central region of the disk leads to a shape transition from the flat disk shape into curved conformations, such as a dome-like shape.23–25 The snapping into an elliptic dome-like shape actually faintly resembles the opening and closing of a scallop. By further enhancing the elastic disk with a fixed frame with attractive interactions we can endow this transition with genuine hysteretic effects. These hysteresis effects allow us to break the reciprocity of the shape cycle although we employ simple cyclic and fully time-reversible oscillations of the swelling factor as single global and scalar control parameter. The main point of this paper is to give the proof of concept that this leads to net propulsion and is a viable realization of a microswimmer. The principle of exploiting a periodically driven hysteretic shape transition in order to achieve net propulsion has been introduced in ref. 26 using the buckling transition of spherical elastic shells as propulsion mechanism. The buckling of spherical shells is a subcritical hysteretic shape transition,27–29 which will turn out to be conceptually similar to the elastic instability triggered in the elastic disk by localized swelling.
Deformation cycles of elastic materials have been applied before to design artificial swimmers. In ref. 30, structured light fields were used to drive elastic deformation waves on swimmers with a homogeneous body made of a soft material. Other approaches focused on elastic double layers, where swelling of one layer can induce bending; such externally controllable swelling layers can be engineered, for example, using thermoresponsive microgels.31 These ideas were used to design swimmers with a helical structure that can be propelled by conformation changes of the helix.31–33 Here conformation changes are non-reciprocal, partly because of hysteresis effects in the heating cycle of the thermoresponsive gel.
Deformation swimmers are relatively slow in general, because the swimming distance only scales quadratically with the deformation displacement for many deformation swimmers.11,12 Therefore, a high frequency of conformation changes is needed in order to achieve a significant swimming velocity. This applies also to the concept of swimming by hysteretic shape changes. The driving frequency is, however, not limited by an additional damping time scale (as, for example, in flagellar motion) because breaking of the time-reversibility is inherent in the hysteretic shape sequence itself but, at high driving frequencies, one could leave the realm of low Reynolds numbers.
The paper is organized as follows. At first, we present a “dry” numerical analysis of the elastic deformation cycle of the elastic disk with material swelling in the interior in the absence of a surrounding fluid and corresponding hydrodynamic interactions. We quantify the hysteretic effects of the swelling transition and show that there is most likely no genuine hysteresis in experiments on simple swelling disks. We can enhance the model system by adding an additional fixed frame with an attractive interaction to the disk in order to generate a robust and genuine hysteretic shape transition. Then we perform a “wet” hydrodynamic simulation featuring a Rotne–Prager interaction in order to proof the swimming ability of this system and characterize the net propulsion. Finally, a simplified 9-bead model is presented that mimics the essence of the underlying swimming mechanism and is able to qualitatively reproduce and explain its main characteristics.
2 Swelling of a flat disk
2.1 Theory
In the following, we consider a flat circular disk with radius Rout and thickness h. The disk shall be very thin (h ≪ Rout), so we can use a two-dimensional model. We parametrize our two-dimensional disk in polar coordinates (r,φ). The basic idea is to deform the disk into a curved shape by a localized, i.e., inhomogeneous swelling process which changes the disk's metric.23–25 By swelling we mean a local isotropic swelling, where the rest lengths of fibers change by a position-dependent factor A(r,φ) independent of fiber orientation. In the following, we restrict ourselves to radially symmetric swelling functions A(r); the neutral case of the flat disk is represented by A(r) = 1, A(r) > 1 corresponds to local swelling, A(r) < 1 to local shrinking of fibers. In order to calculate the change in metric by a swelling function A(r) we re-parametrize the deformed shape using Gaussian normal coordinates. The Gaussian radial coordinate is given by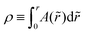 , which is the distance of a point to the origin of the coordinate system following the surface and reduces to the standard radial coordinate r for a flat disk A(r) = 1. The angular coordinate φ remains unchanged. In Gaussian coordinates a deformed fiber in radial direction has length dlρ = dρ = A(r)dr, a deformed circumferential fiber a length dlφ = rA(r)dφ. In general, the fiber length is related to the metric by dl2 = gρρdρ2 + 2gρφdρdφ + gφφdφ2 such that the metric tensor of the swollen disk can be read off as
, which is the distance of a point to the origin of the coordinate system following the surface and reduces to the standard radial coordinate r for a flat disk A(r) = 1. The angular coordinate φ remains unchanged. In Gaussian coordinates a deformed fiber in radial direction has length dlρ = dρ = A(r)dr, a deformed circumferential fiber a length dlφ = rA(r)dφ. In general, the fiber length is related to the metric by dl2 = gρρdρ2 + 2gρφdρdφ + gφφdφ2 such that the metric tensor of the swollen disk can be read off as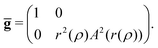 | (1) |
![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) can be deduced solely from the metric tensor. Using the Brioschi formula (with respect to the Gaussian coordinates ρ and φ of the metric) we find
can be deduced solely from the metric tensor. Using the Brioschi formula (with respect to the Gaussian coordinates ρ and φ of the metric) we find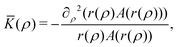 | (2) |
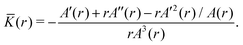 | (3) |
This is the Gaussian curvature if a shape with the metric (1) could be embedded into three-dimensional Euclidian space.
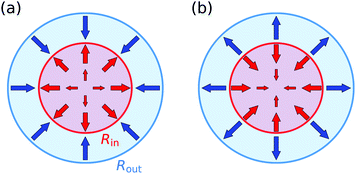
In order to deform the disk into a curved shape, we define a simple class of swelling patterns. Similar to Pezulla et al.,25 we divide the disk into two parts: An inner disk with 0 ≤ r ≤ Rin and an outer annulus with Rin < r ≤ Rout. Within these two regions, the swelling function A(r) shall be piecewise constant. To simplify things further, we define the inner disk to swell with a constant factor α, while the outer annulus shall always do the exact opposite, i.e., it shrinks with the inverse constant factor 1/α. In total, the considered swelling functions A(r) can be written as
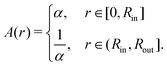 | (4) |
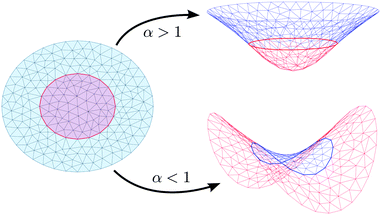
The swelling process is thus defined by two simple control parameters: the swelling factor α and the geometrical ratio Rin/Rout, which will be kept constant at Rin/Rout = 0.5 in the following so that we can focus on the influence of α. We can distinguish between two general cases: (a) α > 1 means that the material in the inner disk is swelling, while the outer annulus is shrinking, which is illustrated in Fig. 2(a). The opposite case, (b) α < 1, leads to a shrinking inner disk and a swelling annulus (Fig. 2(b)). In order to apply the Brioschi formula (3), we have to smear out the step function at r = Rin in eqn (4). For α > 1, we have A′(r) = 0 except around r = Rin, where −A′(r) is peaked. Therefore, the last term in the denominator in eqn (3) dominates and gives a positive Gaussian curvature which is peaked around r = Rin if a surface with the piecewise metric (1) could be embedded into three-dimensional space. Although the metric (1) is piecewise flat, Gaussian curvature has to be introduced because the inner disk is bonded to the outer annulus. This Gaussian curvature is positive for α > 1 and negative for α < 1. Because the metric can actually not be embedded, the Gaussian curvature will be redistributed on the entire disk to minimize the elastic energy. We thus expect a target elliptic shape with an overall positive Gaussian curvature for α > 1, and a hyperbolic target shape with a negative Gaussian curvature for α < 1.
Obviously, for α ≠ 1 the outer annulus and the inner disk are incompatible at r = Rin. Therefore, the surface described by the metric (1) has no immersion in the Euclidean three-dimensional embedding space and is an example of non-Euclidean geometry.24 The actual shape of the surface in three-dimensional space is then defined by the minimization of the elastic energy, where the elastic energy of the deformed swollen state is defined with respect to the above target metric ḡ from eqn (1). The incompatibility of the two parts and the resulting non-existence of an immersion means that there always is a residual elastic energy after minimization.24
The elastic energy contains a stretching and a bending contribution. The stretching contribution is caused by strains εij = (gij − ḡij)/2, where g is the actual metric that the deformed swollen state assumes, and given by24
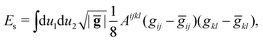 | (5) |
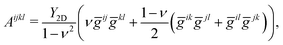 | (6) |
Likewise, the bending energy is defined with the curvature tensor L and with respect to a target curvature tensor ![[L with combining macron]](https://www.rsc.org/images/entities/b_char_004c_0304.gif) , which represents a spontaneous curvature of the material. We assume that local isotropic swelling does not introduce any spontaneous curvature to the system such that
, which represents a spontaneous curvature of the material. We assume that local isotropic swelling does not introduce any spontaneous curvature to the system such that ![[L with combining macron]](https://www.rsc.org/images/entities/b_char_004c_0304.gif) = 0. The general expression for the bending energy is24
= 0. The general expression for the bending energy is24
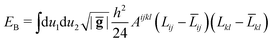 | (7) |
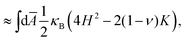 | (8) |
![[L with combining macron]](https://www.rsc.org/images/entities/b_char_004c_0304.gif) = 0, H is the mean curvature, K the Gaussian curvature, and κB = Y2Dh2/(12(1 − ν2)) the bending modulus of the disk. The bending energy penalizes deviations from the flat shape for vanishing target curvature
= 0, H is the mean curvature, K the Gaussian curvature, and κB = Y2Dh2/(12(1 − ν2)) the bending modulus of the disk. The bending energy penalizes deviations from the flat shape for vanishing target curvature ![[L with combining macron]](https://www.rsc.org/images/entities/b_char_004c_0304.gif) = 0. The last line in (8) is an approximation because we assume ḡij ≈ gij in Aijkl. Typical strains εij are ∝ (1 − α)2 such that corrections are O((1 − α)2EB) and will be small at the transition for thin disks (see eqn (17) and Fig. 6 below).
= 0. The last line in (8) is an approximation because we assume ḡij ≈ gij in Aijkl. Typical strains εij are ∝ (1 − α)2 such that corrections are O((1 − α)2EB) and will be small at the transition for thin disks (see eqn (17) and Fig. 6 below).
For numerical energy minimization the disk and its elastic energies (5) and (7) have to be suitably discretized.
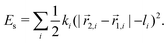 | (9) |
The vectors ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 2,i and
2,i and ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 1,i describe the positions of the vertices that define the beginning and the end of a spring. The spring constants are denoted by ki. In a hexagonal mesh, the two-dimensional Young modulus Y2D is given by the spring constant k and the Poisson ratio ν is fixed,35,36
1,i describe the positions of the vertices that define the beginning and the end of a spring. The spring constants are denoted by ki. In a hexagonal mesh, the two-dimensional Young modulus Y2D is given by the spring constant k and the Poisson ratio ν is fixed,35,36
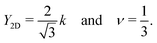 | (10) |
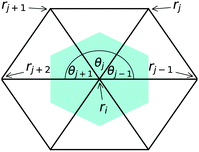
In order to evaluate the bending energy (8) on the spring mesh, the curvatures H and K have to be calculated on the mesh. The mean curvature Hi at a mesh vertex i can be expressed in terms of an area gradient:37
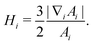 | (11) |
The quantity Ai represents the area in the mesh that is associated to the vertex i, see the colored area in Fig. 3. The gradient ∇iAi then describes derivatives of this area with respect to the coordinates of the vertex i. The Gaussian curvature K, on the other hand, can be calculated using the Gauss–Bonnet-theorem. We find
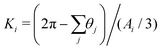 | (12) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i, see Fig. 3. Finally, the discretized bending energy (8) becomes
i, see Fig. 3. Finally, the discretized bending energy (8) becomes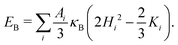 | (13) |
The total energy E = Es + EB has to be minimized with respect to all vertex coordinates in the three-dimensional embedding space. In order to overcome possible local energy minima, small fluctuations can be added to the vertex coordinates in terms of a random displacement  with
with 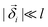 . After minimizing the global energy minimum with respect to all vertex positions, the resulting mesh represents the preferred configuration of the swollen and deformed disk, see the illustration in Fig. 4.
. After minimizing the global energy minimum with respect to all vertex positions, the resulting mesh represents the preferred configuration of the swollen and deformed disk, see the illustration in Fig. 4.
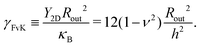 | (14) |
The Föppl–von Kármán number is large for thin disks and is the fourth and last control parameter of our system.
2.2 Results
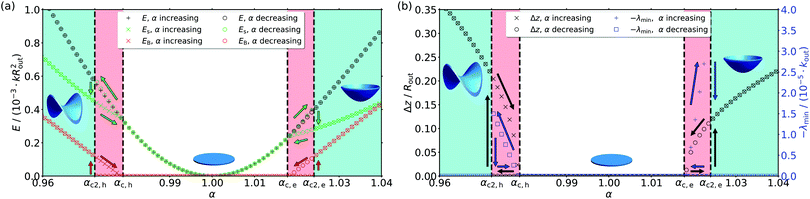
Starting with a flat disk with α = 1, we increase/decrease α in small steps Δα and minimize the energy after each step. Fig. 5(a) shows the resulting energies: the total energy, the spring energy and the bending energy (separated in mean curvature and Gaussian curvature part), as functions of α, while Fig. 5(b) shows the total height Δz of the shape. The shape can deform both into positive and negative z-direction with equal probability; we count the height Δz of the shape always as the positive absolute value of the maximal difference of z-coordinates. For small changes of α the disk stays flat at first, only the spring energy increases quadratically because of the change of the springs' rest lengths. We have E = Es in this regime. Swelling (α > 1) or shrinking (α < 1) of the interior disk imparts elastic compression or stretching energy to the flat state, which is released in the snapping transition. At a critical swelling factor αc2,e for increasing α (or αc2,h for decreasing α, respectively) a transition into a curved conformation with Δz > 0 occurs. We find two stable curved configurations: for increasing α above αc2,e > 1 the disk snaps into an elliptic (subscript “e”) dome-like shape, while it snaps into a hyperbolic (subscript “h”) saddle for decreasing α beyond αc2,h < 1 (see Fig. 4). At these transitions, Es is reduced, because the springs can relax to a certain degree. On the other hand, EB is increased because of the increased curvatures in the dome- or saddle-like shapes. Increasing (decreasing) α again in order to get back to α = 1, we do not see a transition back into the flat state at αc2,e (or αc2,h, respectively). Instead, the shape remains curved for α < αc2,e (α > αc2,h). In the following, the curved disk flattens continuously with EB and Δz decreasing until α = αc,e (or α = αc,h) is reached. There, EB and Δz vanish continuously, and the disk is flat again. In conclusion, we find an apparent hysteresis loop in the deformation behavior within the red areas between αc,e and αc2,e (or αc,h and αc2,h).We can perform a linear stability analysis of the flat compressed state of the inner disk in order to further characterize the bifurcation into an elliptic dome for increasing α above αc,e. In the limit of a small stiff outer annulus (kin/kout ≪ 1 and Rin/Rout ≈ 1), the effect of swelling the interior with a factor α > 1 is to establish a compressive homogeneous pre-stress σxx = σyy = −σ0 = −Y2D(α − 1) in the interior. We can perform a linear stability analysis of the flat state z(x,y) = 0 of an infinite plate under pre-stress −σ0 using plate theory. Expanding the Airy stress function χ(x,y) = −σ0(x2 + y2)/2 + χ1(x,y) and the normal displacement z(x,y) = z1(x,y) around the flat, homogeneously pre-stressed state we find the following plate equations to linear order in χ1 and z1:
| κB∇4z1 + σ0∇2z1 = 0, ∇4χ1 = 0. | (15) |
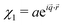 and
and 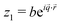 for an oscillatory instability of the flat state with a two-dimensional wave vector
for an oscillatory instability of the flat state with a two-dimensional wave vector ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) = (qx,qy) leads to the condition
= (qx,qy) leads to the condition| σ0 = Y2D(α − 1) = κBq2, | (16) |
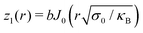 (with the Bessel function J0). The approximate boundary condition ∂rz1(Rout) = 0 for a small stiff outer annulus leads to
(with the Bessel function J0). The approximate boundary condition ∂rz1(Rout) = 0 for a small stiff outer annulus leads to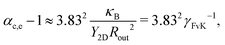 | (17) |
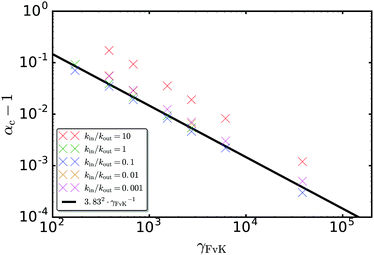 | ||
| Fig. 6 Critical swelling factor αc,e as a function of γFvK for Rin/Rout = 0.5 and different values of kin/kout. The solid black line represents the theory curve given by eqn (17). | ||
The stability analysis with the stability eqn (15) also shows that a genuine hysteresis should be absent, and the bifurcation is a supercritical pitchfork bifurcation similar to the Euler buckling bifurcation of a beam. This is in contrast to buckling of a spherical shell under pressure, which is a subcritical bifurcation.29
3 Re-establishing hysteresis
3.1 Framing the disk and additional attractive interaction
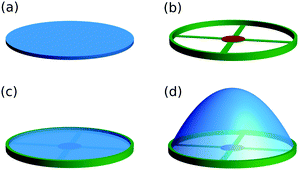
Now we want to modify the system in a way that a genuine hysteresis is re-established, which will also be present in experiments. The basic idea is to energetically penalize slightly deformed intermediate states of the disk during the transition to the curved shape resulting in an additional energy barrier for this transition. This barrier has to be overcome or decreased by additional swelling before the disk can snap into a curved state and stabilizes the flat disk.In order to realize that, the first step is to “frame the disk”: we combine our flat disk with radius Rout in the xy-plane (Fig. 7(a)) with an additional fixed, undeformable frame (Fig. 7(b)). As a result, the boundary of the disk is now fixed (Fig. 7(c)). Therefore, the piecewise constant swelling function (4) is replaced by a globally constant, homogeneous swelling factor α for the whole disk (but not for the frame); α > 1 still corresponds to swelling the interior of the disk and, accordingly, leads to a transition into a dome-like shape (Fig. 7(d)). A saddle shape can no longer be realized in this set-up. Framing is equivalent to the above limit of a very thin and stiff outer annulus.
The second step in order to create a genuine hysteresis is to introduce an additional attractive interaction between the frame and the disk. The central region of the frame Ac (red area in Fig. 7) attracts the disk leading to an additional potential energy for the disk. Inspired by an attractive van der Waals force, we choose the attractive part of a Lennard-Jones potential for the interaction,
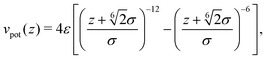 | (18) |
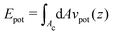 or
or 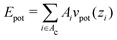 for the mesh model of the disk. The attractive potential has a finite range σ, and a potential depth −ε at z = 0; the force of this potential vanishes in the completely flat state (z = 0) improving the numerical stability. For σ ≪ Rout, on the other hand, the force nearly vanishes also in the completely deformed state because most parts of the disk are out of the potential range. In conclusion, only the transition itself is energetically penalized.
for the mesh model of the disk. The attractive potential has a finite range σ, and a potential depth −ε at z = 0; the force of this potential vanishes in the completely flat state (z = 0) improving the numerical stability. For σ ≪ Rout, on the other hand, the force nearly vanishes also in the completely deformed state because most parts of the disk are out of the potential range. In conclusion, only the transition itself is energetically penalized.
3.2 Hysteresis and short-wavelength bifurcation
In order to gain insight into the influence of an attractive potential vpot(z) onto the instability of the swelling disk, we can consider the case where the attractive potential acts over the whole area of the disk, i.e., Ac = A. Then the linear stability analysis leads to a short-wavelength instability as eqn (15) becomes modified to| κB∇4z1 + σ0∇2z1 + vpot′′(0)z1 = 0 | (19) |
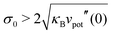 or for α > αc,f with
or for α > αc,f with 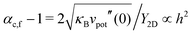 (subscript “f” for framed disk) and at the wave vector q0 = (σ0/2κB)1/2 = (vpot′′(0)/κB)1/4. This is a short-wavelength instability with q0 > 1/L if vpot′′(0) is sufficiently large. We also expect to find a subcritical bifurcation with hysteresis in analogy to buckling of a spherical shell under pressure.29
(subscript “f” for framed disk) and at the wave vector q0 = (σ0/2κB)1/2 = (vpot′′(0)/κB)1/4. This is a short-wavelength instability with q0 > 1/L if vpot′′(0) is sufficiently large. We also expect to find a subcritical bifurcation with hysteresis in analogy to buckling of a spherical shell under pressure.29
For a localized potential, i.e., if the attractive region Ac is smaller than A as in Fig. 7, we expect that the critical swelling factor is further increased such that the unstable wavelength 1/q0 = (2κB/σ0)1/2 fits into the size 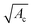 of the attractive region. This results in a condition
of the attractive region. This results in a condition 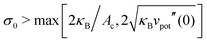 .
.
Analogously to Fig. 5, the behavior of the system including frame and attractive interaction is shown in Fig. 8. Increasing α starting at α = 1, the framed disk again stays flat at first until αc2,f is reached, where the transition into the curved, dome-like shape occurs. There, we see a significant reduction of the spring energy and an increase of the bending energy. In contrast to Fig. 5, also the total energy is reduced drastically during the transition. Decreasing α again, the behavior is qualitatively the same as before, the shape continuously flattens but stays curved until αc3,f is reached, where the disk is flat again. The significant difference to the simple set-up from above can be found by taking a look at the smallest Hessian eigenvalue λmin (Fig. 8(b), blue scale). Between αc3,f and αc,f (yellow area), there are no negative eigenvalues, which means that both the flat disk and the curved shape are (meta-)stable in this region. Only if α exceeds αc,f, λmin becomes negative signalling an unstable flat shape. In conclusion, the region between αc,f and αc2,f (red area) is again a region of pseudo-hysteresis, where we see hysteresis in the numerics but hysteresis vanishes in the presence of sufficient random fluctuations and in the experiment, while the yellow area is related to a genuine hysteresis that should also be robustly observable in an experiment in the presence of some fluctuations. This gives also rise to a shape hysteresis as indicated in Fig. 1. The intermediate states upon snapping into the dome-like shape feature a flattened region around the center, while this feature is missing when the shape continuously flattens.
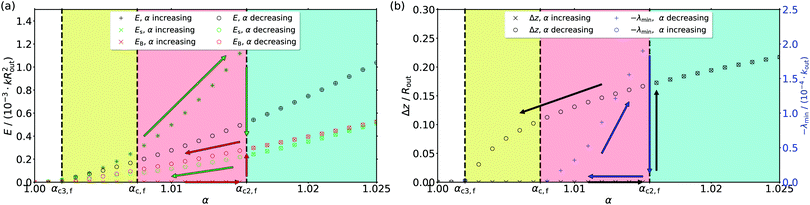 | ||
| Fig. 8 Energies (a), shape's height Δz and negative lowest Hessian eigenvalue −λmin (b) in the spring mesh of a disk in a fixed frame with attractive potential as functions of the swelling factor α. Crosses denote numerical values calculated with increasing α, while circles are related to decreasing α. The region with a genuine hysteresis is marked in yellow, while pseudo-hysteretic effects are again marked in red. The disk is always flat if it is located in the white area and always curved in the cyan region. Arrows illustrate the directions inside the hysteresis loops. The simulated system is the same system from Fig. 5 but with an additional potential energy for each vertex given by eqn (18). The simulated disk had a mesh with nB = 120 boundary vertices, γFvK = 1066 and maximum fluctuations of δmax = 10−4Rout. The parameters of the attractive potential were set to ε = 7.3 × 10−7kin and σ = 0.01Rout. The potential acted in an inner region Ac with a radius of 0.2Rout. | ||
4 Hydrodynamics
4.1 Model
In the following, we want to show that the hysteretic shape transition of the modified framed elastic disk can be exploited as a propulsion mechanism for a microswimmer under a periodic time-reversible driving of the swelling factor α. To this end, we need to model the hydrodynamic interaction between the elastic disk and a surrounding fluid. For this proof of concept we simulate the Stokesian dynamics41 and use the Rotne–Prager interaction.42,43 This interaction describes the movement of a small sphere in the flow field of another sphere. Therefore we model our disk as a sheet of small spheres and place spheres of radius a ≪ Rout on every vertex of the spring mesh, see Fig. 9. The velocity![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) i of every sphere i can then be calculated from the knowledge of the external forces
i of every sphere i can then be calculated from the knowledge of the external forces ![[f with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0066_20d1.gif) j on all spheres j via
j on all spheres j via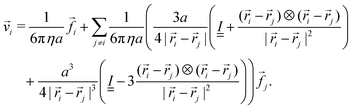 | (20) |
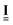 represents the three-dimensional unit matrix. In this model, we ignore torques and rotations for simplicity.
represents the three-dimensional unit matrix. In this model, we ignore torques and rotations for simplicity.
The forces ![[f with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0066_20d1.gif) i can be calculated (analytically) from the discretized stretching and bending energies (9) and (13) as gradients with respect to the vertex position
i can be calculated (analytically) from the discretized stretching and bending energies (9) and (13) as gradients with respect to the vertex position ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i at each time step, and eqn (20) gives the resulting vertex velocities. The trajectory of each sphere and the disk's center of mass as the average of all sphere positions are calculated by a simple Euler integration of the velocities with a time step Δt.
i at each time step, and eqn (20) gives the resulting vertex velocities. The trajectory of each sphere and the disk's center of mass as the average of all sphere positions are calculated by a simple Euler integration of the velocities with a time step Δt.
4.2 Simulation
To simulate the movement of the disk, the trajectories of the spheres are calculated based on the forces acting on them. For a fixed swelling factor α this dynamics will relax into the same force-free equilibrium state that we determined also by “dry” or static energy minimization in Fig. 8. Using the dynamics (20) we can, however, obtain a realistic dynamics of each sphere position and, thus, of the deformation and propulsion dynamics of the whole disk in the presence of hydrodynamic interactions in a viscous fluid.The general concept of the simulation stays basically the same. Again, α is changed in small steps Δα. After each step, the trajectories of the spheres are calculated until the forces on the spheres fall below a threshold, 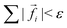 . The simulation gives, in principle, the corresponding hydrodynamic time scale Δτh on which this elastic relaxation happens. That means that there are actually two different time scales operating in this system. The swelling time scale Tsw is defined by the swelling process and is the time that the disk needs to run through a complete deformation cycle. This is the time scale that can be externally controlled in an experiment, where swelling frequencies fsw = 1/Tsw ∼ 5 Hz are possible for disks made from thermoresponsive hydrogels if plasmonic heating of embedded gold particles by laser light is utilized.31 If we divide a deformation cycle into N small changes Δαn and Δτh,n is the hydrodynamic relaxation time for each step, we obtain the second time scale
. The simulation gives, in principle, the corresponding hydrodynamic time scale Δτh on which this elastic relaxation happens. That means that there are actually two different time scales operating in this system. The swelling time scale Tsw is defined by the swelling process and is the time that the disk needs to run through a complete deformation cycle. This is the time scale that can be externally controlled in an experiment, where swelling frequencies fsw = 1/Tsw ∼ 5 Hz are possible for disks made from thermoresponsive hydrogels if plasmonic heating of embedded gold particles by laser light is utilized.31 If we divide a deformation cycle into N small changes Δαn and Δτh,n is the hydrodynamic relaxation time for each step, we obtain the second time scale 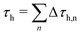 , which is the hydrodynamic relaxation time scale for one deformation cycle and determined by the interplay of elastic forces and hydrodynamic friction. In our simulation model we assume that hydrodynamic relaxation is much faster than the swelling process, τh ≪ Tsw, i.e., the disk swells slowly compared to its deformation motion caused by the swelling, and we can use quasi-equilibrated forces
, which is the hydrodynamic relaxation time scale for one deformation cycle and determined by the interplay of elastic forces and hydrodynamic friction. In our simulation model we assume that hydrodynamic relaxation is much faster than the swelling process, τh ≪ Tsw, i.e., the disk swells slowly compared to its deformation motion caused by the swelling, and we can use quasi-equilibrated forces 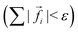 along the swelling cycle.
along the swelling cycle.
We can estimate an order of magnitude for the hydrodynamic relaxation time scale. The typical total force onto a disk with shape height Δz close to the instability is F ∼ Δzσ0 (see eqn (15), which equates areal force densities); the disk has a friction coefficient ∼ηRout, such that the typical velocity is ∂tΔz ∼ F/ηRout ∼ Δzσ0/ηRout, which leads to relaxation times
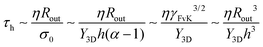 | (21) |
On the other hand, the hydrodynamical relaxation time scale τh should be large enough (the hydrodynamically damped deformation or snapping velocity of the disk slow enough) for the underlying assumption of low Reynolds number hydrodynamics to apply. This is the case if Re ∼ ρRout2/ητh < 1 or τh > ρRout2/η. Inserting τh from eqn (21) we obtain a condition on the disk geometry, h3/Rout < η2/Y3Dρ ∼ 10−1 μm2, where the last estimate is for the density and viscosity of water and moduli Y3D ∼ 10 kPa. This implies that disks have to be designed sufficiently thin (and, thus, bendable) to remain at low Reynolds numbers, which is possibly a critical point for experimental realizations. For disks of radius Rout = 30 μm, thicknesses h < 2 μm are required. As long as the low Reynolds number assumption applies, the swimming distance per deformation cycle is independent of the time scale Tsw of the swelling process and, thus, the deformation velocity. The speed of shape changes affects the swimming velocity but does not affect the swimming distance as long as shape changes remain sufficiently slow that the low Reynolds number assumption holds.
The quality of our discretization and Stokesian dynamics simulation scheme can be assessed by monitoring the fluid flow
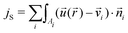 | (22) |
![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) i), which is given by the relative velocity of the fluid flow
i), which is given by the relative velocity of the fluid flow ![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) with respect to the disk vertex velocities
) with respect to the disk vertex velocities ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) i. The fluid flow field can be obtained from the Rotne–Prager interaction as
i. The fluid flow field can be obtained from the Rotne–Prager interaction as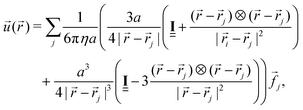 | (23) |
![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) i of vertex i is given by (20) and is essentially
i of vertex i is given by (20) and is essentially ![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i) with a regularization of the j = i term. The quality of the approximation can be measured by the dimensionless permeability |jS/jP|, where jP is the fluid stream through a theoretically perfectly permeable surface that moves with a velocity
i) with a regularization of the j = i term. The quality of the approximation can be measured by the dimensionless permeability |jS/jP|, where jP is the fluid stream through a theoretically perfectly permeable surface that moves with a velocity ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) i through the fluid (i.e., setting
i through the fluid (i.e., setting ![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) = 0 in eqn (22)). Small permeabilities indicate that discretization and Stokesian dynamics is a good approximation; ideally, we reach |jS/jP| = 0 because no fluid should pass through the surface. For a ≈ 0.1l0 (where l0 = 2πRout/nB is the typical rest length of a spring in the discretized mesh) we find surprisingly small permeabilities |jS/jP| < 20% for discretizations with nB > 100 in view of the fact that less than 5% of the surface area are covered by spheres.
) = 0 in eqn (22)). Small permeabilities indicate that discretization and Stokesian dynamics is a good approximation; ideally, we reach |jS/jP| = 0 because no fluid should pass through the surface. For a ≈ 0.1l0 (where l0 = 2πRout/nB is the typical rest length of a spring in the discretized mesh) we find surprisingly small permeabilities |jS/jP| < 20% for discretizations with nB > 100 in view of the fact that less than 5% of the surface area are covered by spheres.
4.3 Swimming motion of the snapping elastic disk
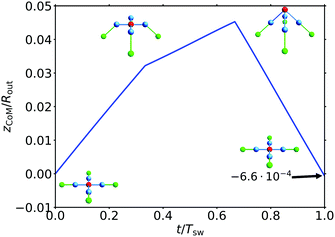
In order to quantify the swimming motion of the disk and proof the concept of a net swimming motion, we measure the movement of the disk's center of mass as a function of time over multiple swelling cycles. Because of its symmetry, the disk only moves into the direction perpendicular to its initial plane, the z-direction. Therefore, Fig. 10 shows the z-coordinate of the center of mass, zCoM, as a function of time for ten full swelling cycles. We will assume in the following that the dome-like shape always snaps downwards, i.e., the opening is in negative z-direction as shown in Fig. 7. In each swelling cycle α(t) the swelling factor α changes between αmin = 1 and αmax = 1.1 > αc2,f in 200 steps back and forth in a completely time-reversible fashion.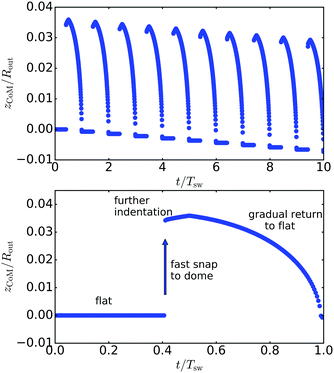 | ||
| Fig. 10 z-Coordinate zCoM of the disk's center of mass as a function of time for ten full deformation cycles. The simulated disk featured the same parameters as the disk in Fig. 8 but with nB = 60 and ε = 5 × 10−8koutRout2. The spheres in the mesh had a size of a = 2πRout/(10nB). In each swelling cycle, the swelling factor α varied between 1 and 1.1 in 200 steps. The lower graph shows a zoom into a single (the first) cycle. The net swimming motion is in the direction of the opening. | ||
Each swimming cycle consists of three phases (see Fig. 10). Beginning at α = 1 and zCoM(t = 0) = 0, the disk does not move at first as long as the disk stays flat until α > αf,c2, where the disk snaps into a dome-like shape in the numerics. The second phase starts with the short snapping process itself. During snapping into the dome-like shape, the swimmer moves into the positive z-direction (the direction of the tip of the elliptic dome, upwards in Fig. 7). This movement happens nearly instantaneously on the swelling time scale. Then, for αf,c2 < α < αmax, the height Δz of the dome-shape slowly continues to grow. Then, the swelling factor starts to shrink again, and the third phase starts. Here, the shape flattens again, and we see a movement into the negative z-direction. When the disk arrives back in its original state (α = 1), a small net motion into the negative z-direction, i.e. in the direction of the opening, remains, which results in an effective slope in the diagram over multiple swelling cycles in Fig. 10.
The effective speed of this swimmer is quite small with a net swimming distance of just below 1% of the disks radius Rout after ten deformation cycles for the parameter values given in Fig. 10. This is a consequence of the known problem of all shape-changing microswimmers that the swimming distance typically scales only quadratically with the deformation displacement.11,12 Nevertheless, this proves the principle that a the hysteretic shape transition of a flat elastic disk can be used as a propulsion mechanism for a microswimmer. Shape-changing swimmers can still be effective if the driving frequency (the swelling cycle frequency for our swimmer) is sufficiently high. At low Reynolds numbers, the resulting swimming distance ΔzCoM = zCoM(t = Tsw) is also independent of the shape of the actual swelling cycle α(t) but can only depend on the values of αmin = 1 and αmax = αf,c2 characterizing the hysteretic part of the swelling cycle.
We can use the reciprocal theorem45 in order to obtain analytical insight into the dependence of the swimming distance ΔzCoM on the deformation displacement Δz of the swimmer. We focus on the z-component as axisymmetric deformations can only lead to motion along the axis of symmetry of the disk. For a deformed disk shape A(t) with a shape deformation z = z(r,t) and a deformation velocity ż in z-direction (r is the radial coordinate in the xy-plane) the reciprocal theorem gives
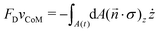 | (24) |
![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) ·σ)z the z-component of the normal stress of the fluid onto the shape A(t); these quantities are related via
·σ)z the z-component of the normal stress of the fluid onto the shape A(t); these quantities are related via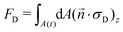 . This leads to
. This leads to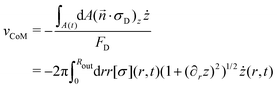 | (25) |
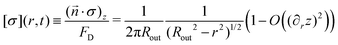 | (26) |
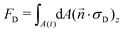 the corrections are quadratic, −O(FD(z/Rout)2). This can be shown by interpreting the weakly deformed rigid disk as perturbed flat disk and applying the reciprocal theorem.49 Because both the fluid velocity field and the pressure only vary quadratically in z close to the flat disk shape,47 boundary conditions to the flow and, thus, the fluid stresses and the drag receive only quadratic corrections. This is also supported by an exact result for the axisymmetric Stokes flow past spherical caps of opening angle β and radius R,50 which can also be interpreted as weakly bent rigid disks. The friction force FD,cap = μvCoMR(6β + 8
the corrections are quadratic, −O(FD(z/Rout)2). This can be shown by interpreting the weakly deformed rigid disk as perturbed flat disk and applying the reciprocal theorem.49 Because both the fluid velocity field and the pressure only vary quadratically in z close to the flat disk shape,47 boundary conditions to the flow and, thus, the fluid stresses and the drag receive only quadratic corrections. This is also supported by an exact result for the axisymmetric Stokes flow past spherical caps of opening angle β and radius R,50 which can also be interpreted as weakly bent rigid disks. The friction force FD,cap = μvCoMR(6β + 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β + sin(2β)) reduces in the disk limit β ≪ 1, where Rout ≈ Rβ and z/Rout ≈ β/2, to FD ≈ 16μvCoMRout(1 − (z/Rout)2/6) in the first two leading orders. Therefore, we expect to find a leading order reduction of the stress jump (26), which is quadratic in z/Rout for a weakly deformed rigid disk. This allows us to extract the scaling of the swimming velocity as a function of the deformation function z(r,t) which describes the shape hysteresis.
β + sin(2β)) reduces in the disk limit β ≪ 1, where Rout ≈ Rβ and z/Rout ≈ β/2, to FD ≈ 16μvCoMRout(1 − (z/Rout)2/6) in the first two leading orders. Therefore, we expect to find a leading order reduction of the stress jump (26), which is quadratic in z/Rout for a weakly deformed rigid disk. This allows us to extract the scaling of the swimming velocity as a function of the deformation function z(r,t) which describes the shape hysteresis.
The shape hysteresis as sketched in Fig. 1 is mainly caused by flattened shapes during snapping (ż(r) < 0, vCoM > 0), while the shape remains dome-like during re-flattening (ż(r) > 0, vCoM < 0). Expanding in the deformation z in eqn (25) and integrating over time to obtain the swimming distance, 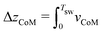 , we realize that the leading order term only depends on final and initial state. It gives the same swimming distance ΔzCoM,snap ∼ −Δz both in the snapping and re-flattening phase and cancels out exactly for a full shape cycle. The next-to-leading term, however, gives a slightly bigger contribution in the re-flattening phase, which should scale as ΔzCoM/Rout ∼ −(Δz/Rout)3. Therefore, the net swimming distance is only a third order effect in the hysteretic shape height Δz. This is even smaller than the quadratic order observed, for example, for deforming spheres11,12 and appears to be a hydrodynamic consequence of the disk geometry. This is confirmed in Fig. 11, where the net swimming distance for swimmers with different thicknesses is shown as a function of their shape height in the snapped state.
, we realize that the leading order term only depends on final and initial state. It gives the same swimming distance ΔzCoM,snap ∼ −Δz both in the snapping and re-flattening phase and cancels out exactly for a full shape cycle. The next-to-leading term, however, gives a slightly bigger contribution in the re-flattening phase, which should scale as ΔzCoM/Rout ∼ −(Δz/Rout)3. Therefore, the net swimming distance is only a third order effect in the hysteretic shape height Δz. This is even smaller than the quadratic order observed, for example, for deforming spheres11,12 and appears to be a hydrodynamic consequence of the disk geometry. This is confirmed in Fig. 11, where the net swimming distance for swimmers with different thicknesses is shown as a function of their shape height in the snapped state.
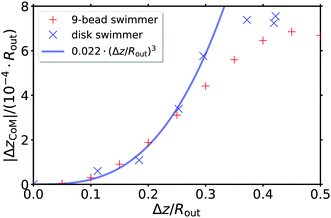 | ||
| Fig. 11 Net swimming distance |ΔzCoM/Rout| per cycle as a function of the shape height Δz/Rout both for disks and 9-bead swimmer. For the 9-bead swimmer the parameter Δz is directly prescribed. For disks the increasing shape height Δz in the snapped state is realized by increasing the thickness in the range h/Rout = 0.02 − 0.14, the other parameters are as in Fig. 8. The fit is ΔzCoM/Rout = 0.022(Δz/Rout)3. | ||
The shape height in the subcritical bifurcation with hysteresis is limited by the stretching factor α of the shape. Because a fiber along the diameter of the disk will stretch by a factor α − 1, the change in height will scale as Δz/Rout ∼ (α − 1)1/2 for a curved disk. For the hysteretic part of the deformation cycle, the relevant stretching factor is α = αc,f. This results in a net swimming distance
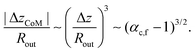 | (27) |
The swimming distance ΔzCoM per stroke can be increased by increasing αc,f − 1 and, thus, the width of the yellow hysteresis area in Fig. 8 which can be achieved, for example, by increasing the thickness and, thus, the bending modulus of the disk. This is explicitly demonstrated in Fig. 11. The thickness dependence αc,f − 1 ∝ h2 results in |ΔzCoM| ∝ h3.
The deformation of the disk into a dome-like shape resembles the deformation pattern of a scallop as envisioned by Purcell;2 our disk is, however, hysteretic, which enables swimming. Interestingly, we find swimming into negative z-direction, which is the direction away from the tip of the dome. This is the opposite swimming direction that we expect from Purcells's high Reynolds number scallop, which moves in the direction of its tip by thrusting fluid out of the opening. Our disk, on the contrary, will pull in fluid through the opening because the size of the opening is fixed by the frame. Also at high Reynolds numbers this leads to inertial thrust in the direction of the opening.
5 9-bead model
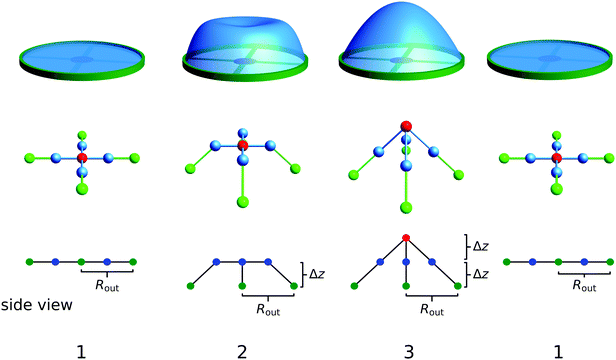
In order to further elucidate the underlying propulsion mechanism, we present a strongly simplified 9-bead model of the hysteretic scallop. In this model, the swimmer only consists of nine spheres that move on simple prescribed trajectories in relative coordinates. The 9-bead-model features three deformation phases, which mimic the above three phases of the disk swimmer; these deformation phases are visualized in Fig. 12. The sketches in the first row show the corresponding states of the full, framed disk analogously to Fig. 7. The second row shows three-dimensional illustrations of the 9-bead swimmer and the last row a two-dimensional side view.The undeformed flat state is represented in the left column. Nine spheres are aligned symmetrically in the xy-plane. The central sphere (red) is surrounded by four spheres (blue) that are placed in a symmetrical way in a distance of Rout/2. The last four spheres (green) are set in an identical way but in a distance of Rout to the central sphere. They represent the fixed frame. The connection lines between the spheres indicate the structure of the object without a direct physical meaning. The second state (second column) represents a typical transition state of the disk during the snapping transition into the dome-like shape. There, the outer regions of the disk are already close to their final position, but the central region does not show a tip yet. This is modelled by elevating the five inner spheres (red and blue) in z-direction with Δz. The third state then is the finally stable elliptic dome-like shape after the transition. Here, the central sphere is again elevated by another distance of Δz. Finally, the last state is again the flat and relaxed disk so that the cycle can be repeated. During the evolution from one state into another, the spheres move on trajectories, which simply linearly interpolate the positions of the spheres between initial and final state. Therefore, the first evolution phase (1 → 2) and the second phase (2 → 3) represent an increasing swelling factor α, while the last phase (3 → 1) is related to a decreasing α.
5.1 Swimming behavior
The swimming motion of the 9-bead model is calculated with the same hydrodynamic model as before. But now, the relative velocities of the spheres are prescribed. So the forces on them have to be calculated. The knowledge of eight relative velocities, together with the condition that the swimmer is force-free, i.e., the total force must vanish, enables us to calculate the motion of the center of mass.17,18 The results are shown in Fig. 13 for a single deformation cycle. In the first deformation phase (0 < t < 1/3Tsw), the swimmer moves upwards in positive z-direction. In the second phase, when the central sphere forms the tip (1/3Tsw < t < 2/3Tsw), there is still an upwards movement, which is simply slower than before because less spheres show a relative motion in this phase. In the final phase (t > 2/3Tsw), all spheres relax back to their original position causing a quick movement in negative direction. After one complete cycle, at t = Tsw, we see a small net movement in negative direction with ΔzCoM = −6.6 × 10−4Rout. In conclusion, we see the same qualitative behavior as for the full disk model in Fig. 10. We can state that the simplified 9-bead model is able to model the swimming mechanism of a swelling disk that has a fixed outer frame. For the 9-bead swimmer simulation results in Fig. 11 show that the swimming distance per cycle is also compatible with zCoM/Rout ∝ −(Δz/Rout)3 for small prescribed shape heights Δz and collapses onto the results for the swelling disk.We can also compare the characteristics of the resulting fluid flow field between the full disk model and the 9-bead model; Fig. 14 shows that there is good qualitative agreement between both models. In particular, the characteristic stagnation point and the vortex ring below the snapping disk are reproduced. These features are characteristic for non-convex bodies and are also observed for dragged spherical caps.50
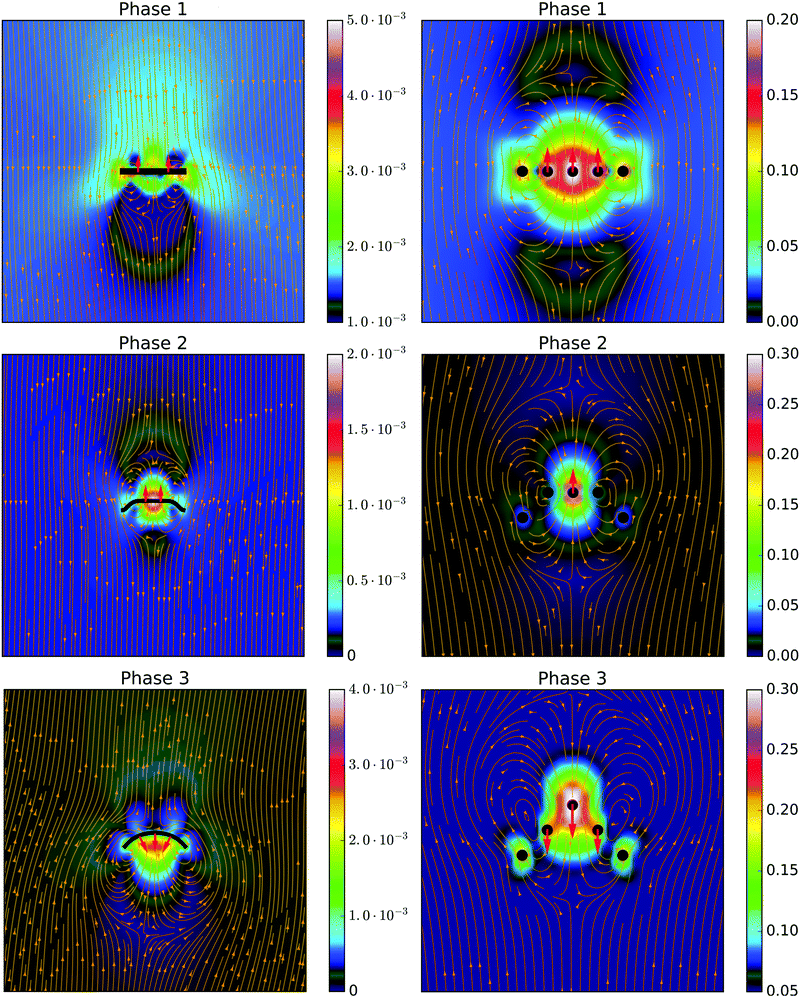 | ||
Fig. 14 Velocity field ![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) ( (![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) in the (y = 0) -plane for each deformation phase. The left side shows the disk with a fixed frame from Fig. 8 and a discretization of nB = 40. The right side shows a 9-bead swimmer with a = 0.1Rout and Δz = 0.5Rout. Colors indicate the absolute | ) in the (y = 0) -plane for each deformation phase. The left side shows the disk with a fixed frame from Fig. 8 and a discretization of nB = 40. The right side shows a 9-bead swimmer with a = 0.1Rout and Δz = 0.5Rout. Colors indicate the absolute |![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) | in units of kout/η for the disk swimmer and in units of Rout/Tsw for the 9-bead swimmer. The arrows show the direction of the fluid velocity vectors. | in units of kout/η for the disk swimmer and in units of Rout/Tsw for the 9-bead swimmer. The arrows show the direction of the fluid velocity vectors. | ||
We can expand the axisymmetric flow field in the far-field into Legendre polynomials11,12 and extract the dipole contribution p2P2(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)/r2 of the radial part ur(r,θ) of the flow field
θ)/r2 of the radial part ur(r,θ) of the flow field ![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) from eqn (23) and normalize by the center of mass velocity |vCoM| to define the dimensionless parameter
) from eqn (23) and normalize by the center of mass velocity |vCoM| to define the dimensionless parameter
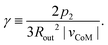 | (28) |
| Phase | γ 9-bead | γ disk |
|---|---|---|
| 1 → 2 (neutral/weakly pushing, γ small) | −0.0068 | 0.39 |
| 2 → 3 (pulling, γ < 0) | −3.63 | −10.88 |
| 3 → 1 (pushing, γ > 0) | 9.18 | 1.24 |
6 Conclusions
We pursued the concept of a low Reynolds number swimmer based on the concept of utilizing a hysteretic shape transition in order to convert a completely time-reversible oscillation of a control parameter into a directed swimming motion. We proved this concept with a flat circular elastic disk that undergoes a shape transition into curved shapes by a localized swelling of an inner disk or an exterior annulus. While swelling the inner region of the disk with a constant swelling factor α and the outer annulus with 1/α, we saw a transition into an elliptic dome-like shape for α > 1 and a transition into a hyperbolic saddle shape for α < 1. The control parameter of this shape transition is the swelling factor α. We found the transition to be a supercritical bifurcation with only numerical hysteresis, which will disappear in a real experiment in the presence of some fluctuations. We could re-establish a genuinely hysteretic shape transition by replacing the outer annulus by a fixed outer frame and by introducing an additional attractive short-range interaction in the central region. The details of this interaction are not relevant, as long as it is an attractive short-range interaction, as it arises, for example, from van der Waals forces or screened electrostatic forces. We then see a hysteretic subcritical shape transition between a flat state and a dome-like shape.Embedding this framed disk into a viscous fluid at low Reynolds numbers, a Stokesian dynamics simulation of the hydrodynamic interaction with the surrounding fluid with a time-reversible and cyclic changing of α showed that the swimmer is effectively moving into the direction of the opening of the dome. This way, a self-deforming microswimmer can be realized that uses only a single scalar control parameter, the swelling factor α. This control parameter has to be changed only by a few percent in order to trigger a drastic conformation change with the snapping transition into the curved shape. Interestingly, the snapping into an elliptic dome-like shape resembles the opening and closing of a scallop as envisioned in the scallop theorem.2 As opposed to Purcell's scallop the elastic disk swimmer actually performs directed motion at low Reynolds numbers because of the additional hysteresis. The swimming direction of the snapping elastic disk is into the direction of the opening of the dome (away from the tip). As for many shape-changing low Reynolds number microswimmers swimming is a higher order effect in the deformation displacement. For the snapping elastic disk the net swimming distance per swelling cycle is only a third order effect in the height of the dome-like shape (|ΔzCoM/Rout| ∼ −(Δz/Rout)3). The swimming mechanism by hysteretic snapping is reproduced by a simplified 9-bead model of the disk. Qualitative agreement of the resulting flow fields, its pusher/puller characteristics and the net swimming distance (see Fig. 11 and 14) show that the 9-bead model captures the essence of the swimming mechanism.
An experimental realization of the snapping disk microswimmer concept could be possible using thermoresponsive hydrogels, which have already been used for the implementation of helical microswimmers.31,32 These hydrogels can be swollen by plasmonic heating of embedded gold particles by laser light. Therefore, localized swelling is possible by embedding gold particles only in specific parts of the hydrogel, such that these hydrogels are suited to realize the proposed disk microswimmers. With hydrogel properties from the literature, an estimate of the expected swimming speed is also possible. Mourran et al. investigated the thermal swelling behavior of thermoresponsive hydrogels with the help of circular disks.31 These disks had a diameter of 30 μm and a thickness of 5 μm. They showed cyclic diameter changes of several percent caused by a pulsed laser with frequencies of 1–5 Hz. Therefore, a frequency of 5 Hz seems to be realistic for the realization of the deformation cycle of our microswimmer with comparable dimensions. With a diameter of 30 μm and a swimming distance of about 1% of the radius after ten cycles, a net velocity of 0.075 μm s−1 follows. Generally, shape-changing swimmers such as the snapping disk can only be made effective if the driving frequency (the swelling cycle frequency for our swimmer) is sufficiently high. On the one hand, we expect higher frequencies to be possible for thin disks. On the other hand, the swimming distance per swelling cycle can be increased by increasing the thickness of the disk (|ΔzCoM| ∝ h3).
One has to bear in mind that the snapping transition dynamics has to be sufficiently slow for low Reynolds number hydrodynamics to apply. We estimated the typical hydrodynamical relaxation time scale, which is the typical time scale for snapping in a viscous fluid, to be τh ∼ ηRout/σ0 ∼ γFvK3/2η/Y3D, which is of the order of τh ∼ 10−5 s for the thermoresponsive hydrogel disks from ref. 31. Then Re < 1 is equivalent to τh > ρRout2/η and restricts the low Reynolds number regime to sufficiently thin disks with h3/Rout < 10−1 μm2. At higher Reynolds numbers, we also expect swimming motion in the direction away from the tip of the dome.
The concept of a low Reynolds number swimmer based on the principle of a hysteretic shape transition can be applied to other snapping systems such as tube-like51 or shell-based snapping systems.52 All systems with a hysteretic snapping instability should give rise to a net swimming motion in a viscous fluid at low Reynolds numbers. As opposed to our disk swimmer, these tube and shell objects enclose volume and employ volume or pressure control, such that genuinely autonomous swimming is not possible because swimming requires attached devices to control volume or pressure.26 Swelling or shrinking materials as proposed in this work are an alternative to control the equilibrium area and, consequently, also equilibrium enclosed volume of these objects by swelling and shrinking, which can often trigger the same snapping transition at fixed actual volume.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge financial support by the Deutsche Forschungsgemeinschaft via SPP 1726 “Microswimmers” (KI 662/7-2).Notes and references
- P. Illien, R. Golestanian and A. Sen, Chem. Soc. Rev., 2017, 46, 5508–5518 RSC.
- E. M. Purcell, Am. J. Phys., 1977, 45, 3–11 CrossRef.
- E. Lauga and T. R. Powers, Rep. Prog. Phys., 2009, 72, 96601 CrossRef.
- J. Elgeti, R. G. Winkler and G. Gompper, Rep. Prog. Phys., 2015, 78, 056601 CrossRef CAS PubMed.
- G. Taylor, Proc. R. Soc. London, Ser. A, 1951, 209, 447–461 Search PubMed.
- H. C. Berg and R. A. Anderson, Nature, 1973, 245, 380–382 CrossRef CAS PubMed.
- R. E. Goldstein, Annu. Rev. Fluid Mech., 2015, 47, 343–375 CrossRef PubMed.
- R. Jeanneret, M. Contino and M. Polin, Eur. Phys. J.: Spec. Top., 2016, 225, 2141–2156 Search PubMed.
- R. Dreyfus, J. Baudry, M. L. Roper, M. Fermigier, H. A. Stone and J. Bibette, Nature, 2005, 437, 862–865 CrossRef CAS PubMed.
- S. Tottori and B. J. Nelson, Biomicrofluidics, 2013, 7, 061101 CrossRef PubMed.
- M. Lighthill, Commun. Pure Appl. Math., 1952, 5, 109–118 CrossRef.
- J. Blake, J. Fluid Mech., 1971, 46, 199–208 CrossRef.
- A. Shapere and F. Wilczek, Phys. Rev. Lett., 1987, 58, 2051–2054 CrossRef PubMed.
- B. U. Felderhof and R. B. Jones, Phys. A, 1994, 202, 119–144 CrossRef.
- J. E. Avron, O. Gat and O. Kenneth, Phys. Rev. Lett., 2004, 93, 1–4 CrossRef PubMed.
- A. A. Evans, S. E. Spagnolie and E. Lauga, Soft Matter, 2010, 6, 1737–1747 RSC.
- A. Najafi and R. Golestanian, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 062901 CrossRef PubMed.
- R. Golestanian and A. Ajdari, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 036308 CrossRef PubMed.
- R. Ledesma-Aguilar, H. Löwen and J. M. Yeomans, Eur. Phys. J. E: Soft Matter Biol. Phys., 2012, 35, 70 CrossRef CAS PubMed.
- M. S. Rizvi, A. Farutin and C. Misbah, Phys. Rev. E, 2018, 97, 023102 CrossRef CAS PubMed.
- M. Leoni, J. Kotar, B. Bassetti, P. Cicuta and M. C. Lagomarsino, Soft Matter, 2009, 5, 472–476 RSC.
- R. Golestanian, Phys. Rev. Lett., 2010, 105, 018103 CrossRef PubMed.
- Y. Klein, E. Efrati and E. Sharon, Science, 2007, 315, 1116–1120 CrossRef CAS PubMed.
- E. Efrati, E. Sharon and R. Kupferman, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 016602 CrossRef PubMed.
- M. Pezzulla, S. A. Shillig, P. Nardinocchi and D. P. Holmes, Soft Matter, 2015, 11, 5812–5820 RSC.
- A. Djellouli, P. Marmottant, H. Djeridi, C. Quilliet and G. Coupier, Phys. Rev. Lett., 2017, 119, 224501 CrossRef PubMed.
- S. Knoche and J. Kierfeld, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 046608 CrossRef PubMed.
- S. Knoche and J. Kierfeld, Soft Matter, 2014, 10, 8358–8369 RSC.
- L. Baumgarten and J. Kierfeld, Phys. Rev. E, 2019, 99, 022803 CrossRef CAS PubMed.
- S. Palagi, A. G. Mark, S. Y. Reigh, K. Melde, T. Qiu, H. Zeng, C. Parmeggiani, D. Martella, A. Sanchez-Castillo, N. Kapernaum, F. Giesselmann, D. S. Wiersma, E. Lauga and P. Fischer, Nat. Mater., 2016, 15, 647–653 CrossRef CAS PubMed.
- A. Mourran, H. Zhang, R. Vinokur and M. Möller, Adv. Mater., 2017, 29, 1604825 CrossRef PubMed.
- H. Zhang, A. Mourran and M. Möller, Nano Lett., 2017, 17, 2010–2014 CrossRef CAS PubMed.
- L. Koens, H. Zhang, M. Moeller, A. Mourran and E. Lauga, Eur. Phys. J. E: Soft Matter Biol. Phys., 2018, 41, 119 CrossRef CAS PubMed.
- B. Kornberger, Fade2D Delauney Trianglulation library, 2016, https://protect-eu.mimecast.com/s/iX5TC0YrLfwVDBcwyCGS?domain=geom.at.
- M. Ostoja-Starzewski, Appl. Mech. Rev., 2002, 55, 35–60 CrossRef.
- H. S. Seung and D. R. Nelson, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 1005–1018 CrossRef PubMed.
- K. A. Brakke, Exp. Math., 1992, 1, 141–165 CrossRef.
- J. W. Hutchinson, J. Appl. Mech., 1967, 34, 49 CrossRef.
- L. Baumgarten and J. Kierfeld, Phys. Rev. E, 2018, 97, 052801 CrossRef PubMed.
- Z. Y. Huang, W. Hong and Z. Suo, J. Mech. Phys. Solids, 2005, 53, 2101–2118 CrossRef CAS.
- L. Durlofsky, J. F. Brady and G. Bossis, J. Fluid Mech., 1987, 180, 21–49 CrossRef CAS.
- J. Dhont, An Introduction to Dynamics of Colloids, Elsevier Science, 1996 Search PubMed.
- J. Rotne and S. Prager, J. Chem. Phys., 1969, 50, 4831–4837 CrossRef CAS.
- T. R. Matzelle, G. Geuskens and N. Kruse, Macromolecules, 2003, 36, 2926–2931 CrossRef CAS.
- H. Stone and A. Samuel, Phys. Rev. Lett., 1996, 77, 4102–4104 CrossRef CAS.
- S. C. Gupta, Z. Angew. Math. Phys., 1957, 8, 257–261 CrossRef.
- J. P. Tanzosh and H. A. Stone, Chem. Eng. Commun., 1996, 148–150, 333–346 CrossRef CAS.
- B. U. Felderhof, J. Chem. Phys., 2012, 137, 084906 CrossRef CAS PubMed.
- H. Masoud and H. A. Stone, J. Fluid Mech., 2019, 879, P1 CrossRef.
- J. M. Dorrepaal, M. E. O'neill and K. B. Ranger, J. Fluid Mech., 1976, 75, 273–286 CrossRef.
- J. T. Overveldea, T. Kloeka, J. J. D'Haena and K. Bertoldia, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 10863–10868 CrossRef PubMed.
- B. Gorissen, D. Melancon, N. Vasios, M. Torbati and K. Bertoldi, Sci. Robot., 2020, 5, 1967 CrossRef.
| This journal is © The Royal Society of Chemistry 2020 |