Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Complexation of single stranded RNA with an ionizable lipid: an all-atom molecular dynamics simulation study†
Anastassia N.
Rissanou
 *ab,
Andreas
Ouranidis
*ab,
Andreas
Ouranidis
 a and
Kostas
Karatasos
a and
Kostas
Karatasos
 *a
*a
aDepartment of Chemical Engineering, University of Thessaloniki, P.O. BOX 420, 54124 Thessaloniki, Greece. E-mail: risanou@uoc.gr; karatas@eng.auth.gr; Fax: +30 2810393701; Fax: +30-2310996222; Tel: +30 2810393746 Tel: +30-2310995850
bDepartment of Mathematics and Applied Mathematics, University of Crete, GR-71409, Heraklion, Crete, Greece
First published on 3rd July 2020
Abstract
Complexation of a lipid-based ionizable cationic molecule (referred to as DML: see main text) with RNA in an aqueous medium was examined in detail by means of fully atomistic molecular dynamics simulations. The different stages of the DML–RNA association process were explored, while the structural characteristics of the final complex were described. The self-assembly process of the DML molecules was examined in the absence and in the presence of nucleotide sequences of different lengths. The formed DML clusters were described in detail in terms of their size and composition and were found to share common features in all the examined systems. Different timescales related to their self-assembly and their association with RNA were identified. It was found that beyond a time period of a few tens of ns, a conformationally stable DML–RNA complex was formed, characterized by DML clusters covering the entire contour of RNA. In a system with a 642-nucleotide sequence, the average size of the complex in the longest dimension was found to be close to 40 nm. The DML clusters were characterized by a rather low surface charge, while a propensity for the formation of larger size clusters close to RNA was noted. Apart from hydrophobic and electrostatic interactions, hydrogen bonding was found to play a key-role in the DML–DML and in the DML–RNA association. The information obtained regarding the structural features of the final complex, the timescales and the driving forces associated with the complexation and the self-assembly processes provide new insight towards a rational design of optimized lipid-based ionizable cationic gene delivery vectors.
1. Introduction
Gene therapies have surged as a new path towards treating diseases by addressing their genetic origins.1,2 The potential of gene-based drug formulations for targeted expression of a beneficial protein, for removal through editing or for silencing of defective genes presents also new opportunities for vaccine applications and personalized medicine.3 In such nucleic acid-based therapies, the genetic cargo is carried to the targeted sites though specialized delivery systems aiming at providing protection against enzymatic degradation, suppressing immune response and activating mechanisms for an effective intracellular delivery of the payload.4,5In this direction, recent efforts have concentrated on the development of non-viral vehicles,6–8 which are free from side-effects such as the risk of genetic integration and increased immunogenicity, which are usually met in viral vectors.9 Issues associated with relatively high toxicity levels and low potency of synthetic carriers are currently a subject of intense research efforts, towards the fabrication of systems with optimized properties.10 In this endeavor, lipid-based formulations have emerged as rapidly developing carriers in nucleic-acid therapeutics, due to their ability to accommodate long nucleic acid cargos (e.g., mRNA or pDNA), their low immunogenicity, their multiple dose capabilities and their versatility in design and fabrication.11–14 In particular, the development of pH-responsive ionizable cationic lipids, for which the surface charge can be modulated in a controllable manner, allowed efficient binding with the oppositely charged polynucleotides, prolonged significantly the circulation time of the formed complexes and increased their therapeutic efficacy by facilitating the endosomal escape and the final release of their cargo.11,15–20 Formulations based on such nanoparticles have already been FDA approved,21 or entered the clinical development phase.18
Although there are several past and ongoing efforts for rational design of ionizable lipid-based nanocarriers for gene therapy applications,14,16,19,22,23 a fundamental understanding of the physicochemical processes relevant to their association with nucleic acids, which may lead to the optimization of the formed complexes in terms of their structural characteristics and their thermodynamic stability, is still limited.23,24 To this end, computer simulations may offer a detailed description of the mechanisms involved in the complexation process, and thus shed light on the role of the different factors which control the physicochemical properties of the formed complexes.
Several simulation studies have focused on the complexation process of small-interfering RNA (siRNA) with lipid nanoparticles.23,25–28 The structure and function of liposome carriers used for siRNA delivery have been studied through all-atom27 and coarse-grained models25 as well as by using multiscale approaches.27 The role of specific sites on a siRNA molecule in its binding to a lipid bilayer surface has been explored through all-atom molecular dynamics (MD) simulations.28 Findings revealed a rather weak and unstable binding, where the siRNA adsorption is driven by the attractive interactions of overhanging terminal nucleotides with choline moieties of the lipid molecules. The complexation and dissociation of siRNA and propylamine (PMAL) has been studied using a coarse-grained model for PMAL, in order to examine the delivery efficiency of siRNA when PMAL is used as a carrier.26,27
Furthermore, since dendrimers have been widely used as cationic vectors for the transport and release of biopharmaceutical substances into the cell, many experimental29–31 and computational studies30–33 concentrated on their modification, aiming at improving their affinity for nucleic acids and their efficiency for the release of their cargo in the intracellular space. A comprehensive review by Marquez-Miranda, V. et al., presents several computational techniques developed for the study and design of dendrimers as carriers for DNA34 and RNA.35 Amongst various cationic polymers, poly(ethylene imine) (PEI)-based carriers are frequently explored for nucleic acid delivery purposes. Various simulation techniques, based on both all-atom and coarse-grained models have been used for studying the PEI-DNA and -siRNA condensation mechanism.25,29 A recent review provides an extensive description of computational methods, used to study RNA structure and dynamics.36 Heterogeneous time scales are met in the RNA processes, including very fast,37 but also very slow timescales,38 with its folding landscape involving many metastable states. For this reason, different models are used depending on the features that need to be described.39
Atomistic MD simulation is a valuable tool, which allows for a more detailed characterization of conformational, kinetic and thermodynamic properties of RNA molecules, taking always into consideration limitations of the accuracy of existing force fields used for the description of such systems. Until recently, only small- to medium-sized RNA molecules and relatively short time scales could be explored40 and enhanced sampling techniques41–44 had been employed, in order to accurately describe their properties. An alternative approach, which is based on a simplified description of molecules, is the coarse-grained models.45,46 These models can provide information at longer length and time scales and can sufficiently describe large-scale motions, mechanical properties, native structures and thermodynamics. Various coarse-grained models have been used for RNA molecules,36 with the MARTINI scheme being widely used.47
Due to the inherent difficulties related to the complexity of the models and the limited availability of powerful computational resources, only a small number of studies have so far attempted a detailed description of long RNA molecules in the all-atom representation. In the present work, we employed atomistic molecular dynamics simulations to study the associative behavior between RNA (with short and long nucleotide sequences) and a lipid-based ionizable agent in an aqueous environment and at neutral pH conditions. Our main goal was to obtain detailed information regarding the different stages involved in the complexation process and to explore the potential of the formed complex to be part of a delivery mechanism for the nucleic acid cargo. The time evolution of the system towards an energetically more stable state was recorded, whereas very fast processes, at the nanoscale, related to the complex-formation, were captured from the atomistic MD simulations. The physicochemical processes, which are described through this study, may serve as a starting point for a controlled formation of such complexes, which can be part of lipid-based formulations for gene delivery purposes.
The rest of the paper is organized as follows: Section 2 provides a description of the examined systems and the simulation method. Analysis methods and results follow in Section 3, divided into subsections according to the system and the examined properties. Finally, in Section 4, concluding remarks are presented.
2. Systems and simulation protocol
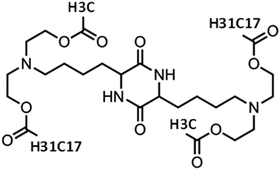
The compound that was selected as a complexation agent with the examined RNA sequences, bears a diketopiperazine core, two methyl ester end-groups and two linoleic ethyl ester end-groups (henceforth referred to as DML). Its chemical structure is shown in Fig. 1.I. Description of the system
In total, 3 systems were simulated. An aqueous solution of DML molecules, where their self-assembly propensity was examined without the presence of RNA, was used as the reference system (it will be referred to as DMLW henceforth). The other two systems were comprised of a single RNA nucleotide sequence either of 30 nucleotides (referred to as DMLRW) or of 642 nucleotides (referred to as DMLHRW), the DML complexation agent, and water. The RNA nucleotide sequence in the DMLHRW system was based on the fragment of the Herceptin antibody (light chain),48,49 while the DMLRW system was a part of this (see ESI,†). The reverse translation of the antibody, in order to obtain the nucleotide sequence of the DMLHRW system, was based on the consensus codons (see ESI†). The DMLRW system was used to collect information regarding the generic characteristics of the complexation behavior between an oligonucleotide RNA and DML particles, which was then compared to the analogous behavior in the presence of the long RNA sequence in the DMLHRW system.Details about the composition of the examined systems are given in Table 1. The ionization state of the DML molecules (due to the ionization of the backbone nitrogens, see Fig. 1) was taken to correspond to neutral pH conditions, rendering a degree of ionization50 of 0.5 for each ionizable nitrogen atom. On this basis, three kinds of DMLs, in terms of the protonation state of the two ionizable nitrogens, were considered in the simulations: electrically neutral (DML0), doubly protonated (DML2) (i.e. bearing a charge of +2|e−|, where e− symbolizes the electron charge) and singly protonated (DML1) (i.e. bearing a charge of +1|e−|). In both systems including RNA, the negative charge of the nucleotides was counterbalanced by that of the protonated DMLs, while in the DMLW system, chlorine counterions were used to ensure electrical neutrality.
| Components | DMLW (86.7 wt% water) | DMLRW (94.1 wt% water) | DMLHRW (97.6 wt% water) | |||
|---|---|---|---|---|---|---|
| Molecules | Atoms | Molecules | Atoms | Molecules | Atoms | |
| RNA | — | — | 1 | 967 | 1 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 691 691 |
| DML2 | 7 | 2520 | 12 | 2160 | 250 | 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| DML1 | 0 | 0 | 5 | 895 | 141 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 239 239 |
| DML0 | 14 | 1246 | 29 | 5162 | 641 | 114![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 098 098 |
| Water | 9138 | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 414 414 |
54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 387 387 |
163![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 161 161 |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 976 976![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 530 530 |
8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 929 929![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 590 590 |
| Cl− | 14 | 14 | — | — | — | — |
| Total atoms: | 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 180 180 |
172![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 345 345 |
9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 134 134![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 618 618 |
|||
| Simulation box (nm)3 | (6.8)3 | (12.0)3 | (65.0)3 | |||
II. Simulation method
Fully atomistic molecular dynamics simulations were performed using the GROMACS package.51 Both, RNA and DML molecules were modeled through the CHARMM3652,53 all atom force field.54 This force field has recently been used for all-atom simulations of RNA36 and lipids.55,56 For DML, charge distribution was described by the Gasteiger method.57 Solvent was described explicitly by the SPC/E model for water.58,59 Non-bonded interactions were parameterized through a spherically truncated 6-12 Lennard-Jones potential and standard Lorentz–Berthelot mixing rules. A cut-off distance of 1 nm has been applied. The particle-mesh Ewald (PME) algorithm was used for the evaluation of the electrostatic interactions. The cut-off distance for PME was 1 nm, the PME-order was 4 and 0.12 the Fourier spacing. Our choice to use the SPC/E water model, combined with a VDW cut-off of 1 nm and PME-based electrostatics was based on a previous work,60 where it was demonstrated that a combination of PME-based electrostatics with SPC/E water and a VDW cut-off of 1 nm, provided reliable results in systems interacting with Lennard-Jones pairwise potentials, in a computationally efficient manner, thus making it appropriate for large scale simulations such as those performed in the present work.Molecular dynamics simulations were performed in the isothermal–isobaric (NPT) statistical ensemble. The pressure was kept constant at P = 1 atm, using the Berendsen barostat,61 while the stochastic velocity rescaling thermostat62 was used for keeping temperature at ambient conditions (T = 300 K). The integration time step was 1 fs and the particle-mesh Ewald (PME) algorithm was used for the evaluation of the electrostatic interactions.
The initial geometry of RNA was based on a Monte Carlo procedure63 (selected as the minimum energy configuration among 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 generated), whereas lipids were uniformly distributed in the simulation box. This starting configuration was energy-minimized, while prior to the production runs all the systems were equilibrated for at least 50 ns. Within this timescale, energetic parameters and conformational properties (i.e., size distribution of the complexes, average dimensions of RNA, and average orientation of the DML molecules – see Fig. SI-1 in the ESI†) were stabilized. Ensuing the equilibration, production runs of 100–200 ns were performed. It should be noted that the secondary and tertiary structural changes of RNA and their dynamics take place at a much longer timescale than the present simulations can probe and thus possible changes in interactions with the lipid clusters formed, cannot be captured. However, as it will be described in the sections to follow, these are not expected to influence the physicochemical processes relevant to this study, since the latter take place at much shorter timescales (of the order of a few tens of ns).
000 generated), whereas lipids were uniformly distributed in the simulation box. This starting configuration was energy-minimized, while prior to the production runs all the systems were equilibrated for at least 50 ns. Within this timescale, energetic parameters and conformational properties (i.e., size distribution of the complexes, average dimensions of RNA, and average orientation of the DML molecules – see Fig. SI-1 in the ESI†) were stabilized. Ensuing the equilibration, production runs of 100–200 ns were performed. It should be noted that the secondary and tertiary structural changes of RNA and their dynamics take place at a much longer timescale than the present simulations can probe and thus possible changes in interactions with the lipid clusters formed, cannot be captured. However, as it will be described in the sections to follow, these are not expected to influence the physicochemical processes relevant to this study, since the latter take place at much shorter timescales (of the order of a few tens of ns).
3. Analysis methods and results
The hydrophobic nature of the diketopiperazine-derived lipids per se22 is expected to lead to the formation of aggregates in an aqueous environment. It is therefore interesting to explore (a) how the presence of RNA affects the clustering behavior of the DML (average number of clusters, size and composition), and (b) whether complexation with RNA takes place in a manner useful for gene delivery purposes and (c) if this is the case, what are the main driving forces for the successful complex formation.To monitor the cluster formation and to characterize the formed clusters, and to examine structural features of the formed complexes in the RNA-based systems, appropriate analysis methods were utilized. In this context, standard analysis tools of the GROMACS package51 were employed. Quantities like pair radial distribution function (rdf), density and charge distributions and hydrogen bonding were calculated. For the examination of the clustering behavior, we followed the procedure described in ref. 51 and 64 as outlined below.
Initially the center of mass of each DML molecule (CM) was determined and considered as a potential center of a cluster. The condition that was checked in order to determine whether a neighboring DML molecule belonged to a cluster centered at the selected DML was whether the CM–CM distance between the two DMLs was smaller than a critical distance (2.5 nm in our case). The selection of this critical distance was based on the separation corresponding to the first minimum in the DML–DML center of mass pair radial distribution function (see Section 3.a-III, Fig. 6a). Each time a DML molecule was found to belong in a cluster, it was excluded from the list of neighboring similar molecules and the algorithm was repeated for the remaining DML particles. This procedure ensured that each DML molecule belonged only to one cluster. The same algorithm was then repeated for all such molecules and the number of clusters, the average number of DMLs per cluster and the size of the clusters were recorded.
Since the vicinity of RNA is of particular interest, in the RNA-based systems, a “filtering” process was also applied, keeping only those DMLs for which their centers of mass were located at a distance no further than 4.0 nm from RNA. This distance was determined from the pair radial distribution function between the RNA and the DML particles (see Fig. 6b in Section 3.a-III).
In addition, to monitor the dynamics of the clustering process and the attainment of a stabilized state in the cluster formation, a series of snapshots at different time spots throughout the trajectory were analyzed.
3.a Conformational properties and static cluster analysis
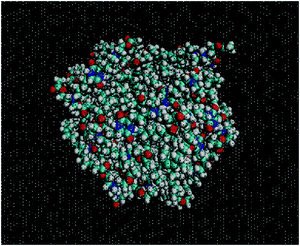
Fig. 2 shows an equilibrated configuration of a single cluster that was formed by DML molecules in the DMLW system. The timescale relevant to cluster formation was found to be less than 30 ns. An estimation of the size of the cluster can be provided by the average radius of gyration 〈Rg〉, defined by 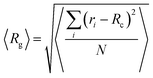 , where ri is the position of the ith atom, RC is the position of the geometric center of the cluster and N is the number of atoms. The relevant calculation rendered a value of 〈Rg〉 = 16.4 ± 0.4 Å. To further elaborate on the features of the cluster, additional analysis involving the mass and the charge distribution with respect to the geometric center of the cluster was performed. The density profile is presented in Fig. 3a and a corresponding charge profile in Fig. 3b. A peak in the density distribution is observed at 0.3 nm from the center of the cluster, which indicates a rather compact structure. A density plateau follows, up to almost 1.5 nm, beyond which the density decreases sharply. An outer surface layer of ∼1 nm width is formed (i.e., from the point at which the density starts dropping to the point at which it vanishes).
, where ri is the position of the ith atom, RC is the position of the geometric center of the cluster and N is the number of atoms. The relevant calculation rendered a value of 〈Rg〉 = 16.4 ± 0.4 Å. To further elaborate on the features of the cluster, additional analysis involving the mass and the charge distribution with respect to the geometric center of the cluster was performed. The density profile is presented in Fig. 3a and a corresponding charge profile in Fig. 3b. A peak in the density distribution is observed at 0.3 nm from the center of the cluster, which indicates a rather compact structure. A density plateau follows, up to almost 1.5 nm, beyond which the density decreases sharply. An outer surface layer of ∼1 nm width is formed (i.e., from the point at which the density starts dropping to the point at which it vanishes).
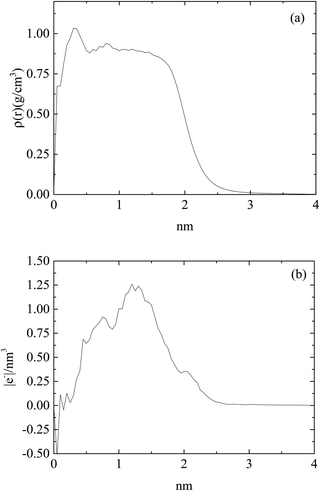 | ||
| Fig. 3 (a) Density profile and (b) charge profile, of a DML cluster as a function of the distance from the geometric center of the cluster in the DMLW system. | ||
Concerning the charge distribution, it appears that only very close to the center of mass of the cluster does a negative charge accumulate. Positive charge is distributed throughout the cluster and peaks at a distance of ∼1.23 nm, moderately lower compared to its radius of gyration. Close to the surface of the cluster (i.e., at a distance close to 〈Rg〉), only a weak positive charge, ∼0.35 |e−| is detected.
As was also observed in the DMLW system, DML molecules were found to self-assemble rapidly. A fast movement of the DML particles towards RNA was also recorded. Both processes were completed within a time period of 50–60 ns. A more detailed analysis related to the clustering kinetics will be discussed in Section 3b. A representative configuration, where DML clusters become associated with RNA, is shown in Fig. 4.
Evidently, instead of observing association of individual DML molecules with the oppositely-charged nucleotides, the former prefer to organize in clusters, which then associate with RNA. A histogram of the cluster sizes as a function of the number of DML molecules contained in each cluster is presented in Fig. 5 (it should be noted here that all DML particles in the solution were taken into account). Apart from the single-DML or double-DML state (i.e., when 1–2 DML molecules become detached for short or for longer times from a larger cluster), clusters including significantly larger numbers of DML particles are formed as well.
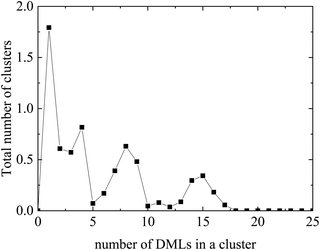 | ||
| Fig. 5 Histogram of the average cluster sizes in terms of the number of DML particles they contain in the DMLRW system. | ||
Excluding the small clusters (i.e., with occupancy <3), a weighted average rendered a mean number of DML particles per cluster equal to 8.9. The largest cluster detected included 17 DML molecules. Additional quantification of the size of the clusters is given by their mean radius of gyration, which was calculated to be 〈Rg〉 = 15.4 ± 0.1 Å. This average size is comparable to the 〈Rg〉 of the clusters formed in bulk water (see Section 3a-I). It is also worth mentioning that the surface of RNA was found to be almost entirely covered by two DML clusters, as it is illustrated in the snapshot of Fig. 4. A more comprehensive analysis of this behavior will be presented in the section to follow for the DMLHRW model.
For computational efficiency purposes (particularly for the DMLHRW system), in this work we opted for omitting the inclusion of counterions in the systems including RNA, having in mind that the presence of counterions would not play a significant role in the conditions of interest (i.e., ionic strengths of the order of 0.1 M as in the relevant experiments), since at that low salt concentration no efficient screening of electrostatic interactions between the lipids and between the lipids and RNA is expected. This effect has been demonstrated in past simulation efforts examining protein–RNA binding65 where at salt concentrations of 0.1 M no structural changes have been practically observed in an RNA–protein complex or any destabilization of the initial RNA conformation. To check this hypothesis for our models, we have also simulated a system analogous to DMLRW at an ionic strength of 0.15 M, without noticing any significant differences regarding the associative phenomena that will be described in this manuscript. A corresponding snapshot is presented in the ESI† (Fig. SI-2a), which provides a qualitative comparison, demonstrating the formation of DML clusters and the twisting of RNA around them. The comparison of radial distribution functions arising from the centers of masses, between RNA–DML and DML–DML molecules in the two systems, is presented in Fig. SI-2b in the ESI.† The similarity of the curves corroborates the aforementioned hypothesis.
To obtain information regarding the relative arrangement of the components in the studied system, we examined appropriate pair radial distribution functions between RNA and DML molecules and between only DML molecules. The radial distribution function is essentially a pair property, which is proportional to the conditional probability to find particles of one kind at a specific distance from those of the same or of another kind.66 Here, each molecule is taken as a single particle represented by its center of mass. A peak in the rdf at a distance r, indicates higher probability to find neighboring particles separated by this distance.
Fig. 6 shows the pair rdfs between DML molecules and between RNA and DML molecules, where such peaks can be observed. The intensity of the peak, which corresponds to DMLs is higher and its width is smaller compared to the analogous features of the DML–RNA rdfs. These characteristics indicate a DML–DML intermolecular arrangement with higher spatial stability, which is consistent with the cluster formation. They also imply that DML–DML interactions are more favorable than those between DML molecules and RNA. The peak in the DML–RNA rdf indicates also an associative behavior between the two molecular species and therefore implies complexation between the formed DML clusters and RNA. To check whether there was any specific trend regarding this association with respect to the protonation state of the DML particles, we computed and compared DML-specific RNA rdfs (i.e., doubly protonated, singly protonated and neutral). This comparison is shown in Fig. 6b where the DML–RNA rdf curve (shown in Fig. 6a), is also included.
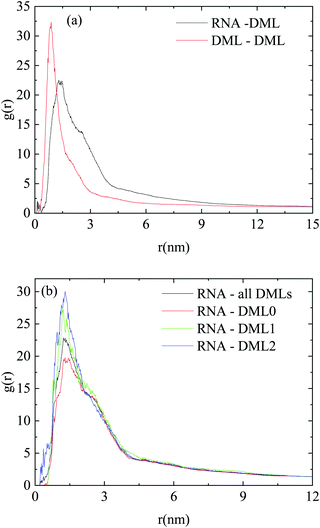 | ||
| Fig. 6 Pair radial distribution functions between the centers of mass of (a) RNA–DML and DML–DML; (b) RNA–DML0, RNA–DML1, RNA–DML2 and RNA–DML, in the DMLHRW system. | ||
Although all curves are of similar shape and width, the peak heights of the rdfs corresponding to the protonated DML particles are higher compared to that describing the neutral molecules. This can be attributed to the enhanced electrostatic interactions between RNA and the protonated DMLs, resulting in a better localization of the latter with respect to RNA. The difference in peak-height is smaller between single and doubly protonated DMLs, while the respective all-DML (i.e., non-charge-specific) rdf is an average of the charge-specific curves.
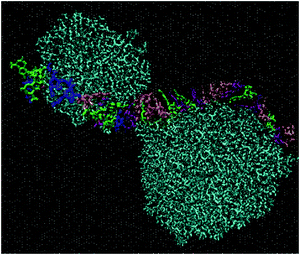
A characteristic snapshot of the DMLHRW system at an equilibrated state is presented in Fig. 7. It is shown that apart from DML clusters dispersed in the bulk aqueous phase, a significant number of DML particles have formed clusters, which practically cover the entire RNA backbone, forming thus a potentially protective layer around it. The average end-to-end distance of the RNA in the complex was found to be approximately 43.2 nm. Application of the filtering procedure described earlier, allowed the calculation of the percentage of DML molecules of the three kinds in the vicinity of RNA. It was found that this proportion ranged between 45 and 50% for all kinds of DML particles.
Fig. 8 compares the histograms of the cluster sizes resulting by analyzing either all clusters, or only those close to RNA. In the case where all the clusters are taken into account, together with the single-DML state or the doubly populated aggregates, clusters comprising a considerably larger number of DML particles are present as well. A close view of the main curve, focusing on clusters constituted by more than 3 DML molecules, is shown in the inset of Fig. 8. A broad distribution of DMLs per cluster, between 5–20 molecules, is observed. Peaks are detected at DML numbers of about 6 and between 10 and 12, while clusters of even bigger size are formed. Taking into account the values beyond 3, the total number of formed clusters in the solution is ∼55 and a weighted average on the number of DMLs in a cluster provides a mean cluster occupancy of 9, with the most populated cluster comprised of 22 DML molecules.
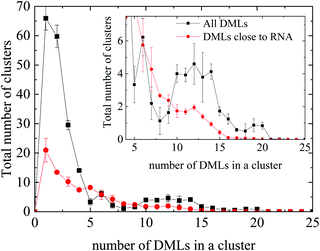 | ||
| Fig. 8 Histogram of the cluster sizes in terms of the number of DML particles they contain, for all DMLs and only for those which are close to RNA. Inset: Magnification in the range of 4–25 DMLs. | ||
Comparison to the distribution corresponding to the clusters close to RNA shows that oligomeric clusters are mostly distributed in water rather than close to RNA (note the difference in the area under the corresponding peaks). Moreover, it appears that on average, the non-oligomeric clusters, which are formed around RNA are somewhat smaller (DMLs per cluster ∼7.2) compared to their analogues in the bulk water phase (i.e., afar from RNA). Considering only clusters populated by at least 4 DML particles, integration of the distribution corresponding to the clusters close to RNA, renders a number close to 35. If we take into account the average number of DMLs per cluster, it follows that approximately 0.4 DMLs are needed to cover one nucleotide. Based on this crude estimation, the RNA backbone will be covered by 252 DMLs; the number of DML molecules was taken to be significantly larger compared to this estimation in the DMLHRW system.
A more detailed analysis is given in Fig. SI-3 of the ESI,† where sub-clusters formed by the 3 different kinds of DMLs are shown separately. In the corresponding histograms all clusters are taken into account. Qualitatively similar distributions are observed for the three kinds of sub-clusters. However, aggregations of protonated DML molecules in the formed clusters (i.e., charged sub-clusters) appear to be less populated compared to those of neutral molecules.
Fig. 9 depicts a characteristic configuration of a large cluster comprised of 21 DMLs in total, 11 of which are neutral, 4 are singly protonated and 5 are doubly protonated. The radius of gyration of such highly populated clusters (taking into account clusters comprised of 19 to 22 DMLs) was found to be 16.9 ± 0.5 Å. For comparison, the radius of gyration of an average-sized cluster (comprised of 7–10 DMLs) was found to be 14.8 ± 0.6 Å. Notably, the average occupancy of the clusters formed in the DMLHRW system, and their average dimensions (as measured by their corresponding radii of gyration) are very close to those observed in the oligonucleotide model (see Section 3a-II).
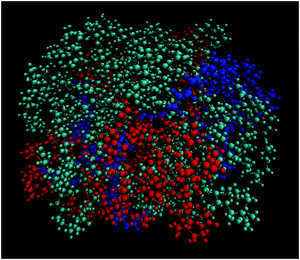 | ||
| Fig. 9 Characteristic snapshot of a highly populated cluster where the three kinds of DMLs are colored differently (DML0: cyan; DML1: red; DML2: blue). | ||
To further characterize the formed aggregates in terms of their internal structure and their charge, we have calculated the density and the charge distribution, both for a highly populated and an average sized cluster. Due to their almost spherical shape, the analysis was based on spherical shells of increasing radius, starting from the geometric center of each cluster. The so-calculated density and charge profiles are presented in Fig. 10a and b, respectively.
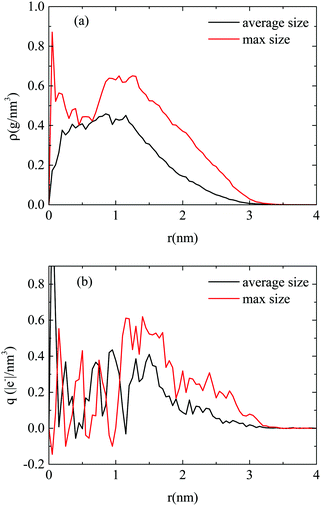 | ||
| Fig. 10 (a) Density profile and (b) charge profile, as a function of the distance from the center of the cluster, for a highly and an averagely populated cluster. Error bars are not shown for clarity reasons. A corresponding figure, which includes error bars, is given in the ESI† (Fig. SI-5). | ||
Focusing on Fig. 10a, for the large cluster a high intensity peak is observed in density at very short distances (i.e., ∼1–2 Å), which implies a rather compact core. This is followed by a broader peak around 1 nm whereas, at longer distances the density decreases gradually to zero. However, in the average-sized cluster no compact core is observed, while the density profile exhibits a more uniform distribution. This behavior is closer to that observed in the DMLW model (Fig. 3a), in terms of the existence of a plateau region of average density. In the charge profiles, intense fluctuations are present in the interior of the cluster (i.e., for distances of up to ∼1 nm) in both the clusters, with most of the minima reaching values close to 0. In addition, it can be noted that close to the exterior of the clusters a rather low positive charge is observed. Combining the information from the density and the charge profiles, it appears that there is a tendency of the highly populated clusters to grow around the protonated (and somewhat more massive) DML particles. Therefore, apart from the hydrophobic interactions, electrostatic forces play a central role in the characteristics of the formed clusters.
Along with Coulombic interactions, other interactions such as hydrogen bonding are also expected to drive the associative behavior between the clusters of the DML particles and RNA.66 To examine the propensity of the DML molecules to form hydrogen bonds with the nucleotides, we have examined hydrogen bond formation between DMLs and between DMLs and RNA. Detection of hydrogen bonding was based on the following geometric criteria associated with an acceptor A and a donor D bonded to a hydrogen (H) atom: (1) the distance r between D and A, r(D⋯A) ≤ 3.5 Å, and (2) the angle HDA ≤ 30°.
The so-estimated time-average number of hydrogen bonds are shown in Table 2. Values are statistical averages over the parts of the trajectory beyond which the system has reached a steady conformational state. The DML–DML hydrogen bonds shown in Table 2 refer to all clusters, whereas the corresponding numbers, if only clusters close to RNA are taken into account, are practically identical within the error margins. Note here that since hydrogen bonding is a dynamic process (i.e., hydrogen bonds are created and destroyed continuously), relatively large statistical errors are expected in their averages. The results in Table 2 confirm that hydrogen bonding contributes, to both the DML–DML and to the DML–RNA association.
| Pair | Number of hydrogen bonds |
|---|---|
| RNA–DML | 85.3 ± 6.5 |
| DML–DML | 72.4 ± 8.6 |
All the above analysis does not reveal any substantial difference between the clusters of DMLs, which are formed in water (DMLW system) and the ones in the aqueous solution with the RNA molecule present. It is interesting to mention that the largest clusters in the solution (where a total number of 1032 DML molecules are dispersed) are comprised of 20–22 DMLs, which is the size of the clusters in bulk water as well.
3b. Dynamic properties
Self-assembly and cluster formation by the DML molecules in the aqueous environment are processes realized at very short timescales. Due to the all-atom representation of the molecules and the time resolution afforded by fully atomistic molecular dynamics simulations, such processes can be monitored in detail. The kinetics of aggregation of the DML molecules can be recorded, by starting from an initial (out of equilibrium) configuration, as the one shown in Fig. 11, and following the time evolution of the system towards an energetically stable state. | ||
| Fig. 11 Initial configuration of the DMLHRW system. DML particles are shown in dark cyan and nucleotides are shown in different colors (water molecules are omitted for clarity). | ||
To follow the temporal evolution of this aggregation process, we have recorded appropriate measures, such as radial distribution functions at different time periods, the number of formed clusters and the extent of hydrogen bonding as a function of time.
Fig. 12a portrays the rdfs between RNA and DMLs in the DMLHRW system at different time intervals within the simulation run. An abrupt increase of the first-neighbor peak is observed between 5 ns and 15 ns from the initial state, which indicates a rapid organization of DML molecules close to RNA. At later times, a gradual enhancement of the main peak in terms of intensity and width takes place, until a convergence is observed beyond 75 ns, signifying the achievement of a stabilized conformational state. Similar stages of time-evolution are also noted in the rdf curves between DMLs, as illustrated in Fig. 12b.
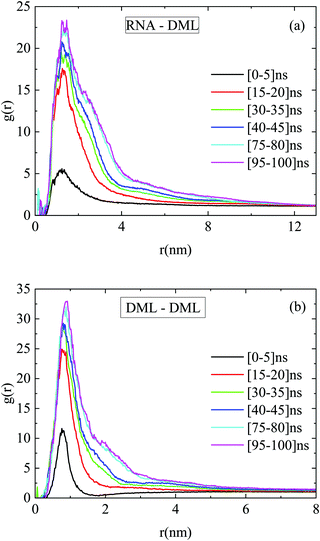 | ||
| Fig. 12 Pair radial distribution functions between the centers of mass of (a) RNA–DML and (b) DML–DML at different time intervals in the DMLHRW system. | ||
The number of hydrogen bonds formed between RNA and DMLs was also found to be an increasing function of time at short temporal scales. At later stages a stabilization of this number was observed, as shown in Fig. 13. It can be inferred that attainment of a stable average in this case was realized at a shorter timescale compared to that for the convergence of the rdf curves. In other words, hydrogen bond formation has already been completed (i.e., reached an equilibrium), while the DML aggregation process continues.
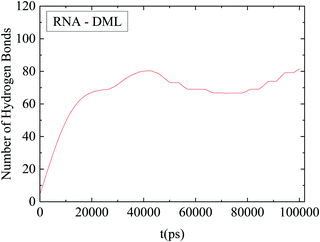 | ||
| Fig. 13 Average number of hydrogen bonds between RNA and DMLs as a function of time. The line shows an average behavior after smoothing of the data. | ||
Fig. 14 shows the time evolution of the number of formed DML clusters. Since at the starting configuration no clusters were present, the number of clusters increases initially with time, it develops a broad maximum at a timescale close to 12 ns, which is followed by a gradual decrease towards stabilization, after about 70 ns. The descent of the curve after the maximum, can be attributed to the coalescence of smaller aggregates of DMLs into larger clusters, which eventually reach an equilibrium size.
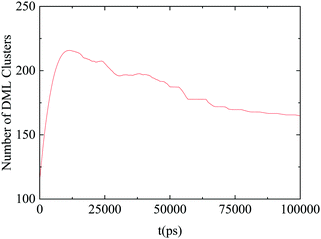 | ||
| Fig. 14 Number of DML clusters as a function of time. The line shows an average behavior after smoothing of the data. | ||
As it is described in Section 3a-III the percentage of DML molecules in the vicinity of RNA is 45–50% for all three kinds of DMLs, in the stable state. Analysis of the entire trajectory reveals that this quantity is an additional measure, which shows convergence after about 75 ns from the initial state, (data not shown here).
Summarizing the above information, it can be argued that the RNA–DML association mechanism involves many steps with different characteristic timescales. The self-assembly of DML molecules in clusters is the initial process performed within the first ∼10 ns of the simulation run, as it is revealed from the abrupt increase of the number of clusters in Fig. 14, which reaches a maximum at about 12 ns. Association of the clusters with RNA follows, as it can be inferred from the increase of the hydrogen bonding between RNA and DMLs, which reaches an almost constant value after 40–50 ns (Fig. 13). A further restructuring of the associated clusters towards an equilibrium size is the last process, which is accomplished beyond ∼70 ns, (Fig. 14).
Therefore, the characteristic timescale at which conformational equilibrium is practically reached, can be taken to be close to 75 ns. While all measures were found to have converged beyond this time window, faster processes have attained a stabilized state at even shorter timescales. All statistical analyses presented in Section 3a, involving equilibrium properties, have been performed in the trajectory beyond that characteristic timescale. The corresponding timescales in the DMLRW system for the attainment of stabilized conditions as those described in Fig. 12–14 were found to be similar.
Although the formed DML clusters seem to come to a stable state in terms of size and composition, the molecules which constitute them, may move within the cluster volume, while particle migration events between clusters cannot be excluded. Such cluster restructuring takes place within a finite timescale. To get an estimation of this timescale, one can probe the collective motion of DML molecules and estimate the time it takes for the position of the center of mass of an DML particle to become uncorrelated with that of a different DML particle. An analysis based on the distinct van Hove correlation function32 and a corresponding discussion is presented in the ESI.† This quantity indicates a gradual loss of memory of the initial local arrangement assumed by the DML molecules. It was found that internal cluster restructuring takes place at about ∼50 ns. Fig. SI-4 in the ESI,† presents distinct van Hove functions for the clusters formed by the three different kinds of DML particles for the DMLRW system. It must be noticed that this property concerns the dynamic behavior within the stabilized state (i.e., beyond 75 ns); therefore it provides another characteristic time of the system. Based on the similarity of the dynamic behavior noted between the DMLHRW and the DMLRW systems, a similar timescale is expected to characterize internal cluster restructuring in the DMLHRW model, as well.
4. Summary and conclusions
In this work we have employed fully atomistic molecular dynamics simulations, in order to explore the associative behavior between RNA fragments and a complexation agent bearing cationic ionizable sites (DML), in an aqueous environment and at neutral pH conditions. Three kinds of DML molecules, in terms of the protonation state of the two ionizable nitrogens, were considered in the simulations: electrically neutral, doubly protonated and singly protonated. Our goal was twofold. On one hand we intended to check whether such particles were capable of forming a structurally and energetically stable construct by complexing with RNA, in order to assess their potential for RNA delivery purposes. On the other hand, we aimed at understanding the role of different aspects related to the DML–DML and the DML–RNA self-assembly processes and to the equilibrium structural characteristics of the formed aggregates.Due to the computationally demanding task of simulating fully atomistic systems in high water content, with RNA fragments bearing several hundreds of nucleotides, we also constructed an oligonucleotide-based system. Our objective was to check whether this might serve as a working model, through which generic behavior can be studied using only limited computational resources. For comparison purposes, an RNA-free aqueous solution of the DML molecules was simulated as well.
In all the systems, DML particles were found to self-assemble within a few tens of ns, forming clusters with comparable average sizes and composition. A notable observation is that similar clusters of DMLs are formed in bulk water (DMLW system) and in the aqueous solutions with the RNA molecule (DMLRW and DMLHRW systems), with the largest ones to be populated by 20–22 molecules in all cases. Their internal structure, in terms of density and charge distribution varied depending on the size of the cluster. Large-sized clusters were characterized by a denser core compared to low populated aggregates. For clusters in all the systems though, it was observed that the surface charge was kept rather low (below 0.5 |e−|). This near-neutral surface charge of the clusters might result in a prolonged half-life of the DML–RNA complex in the circulation,67 mitigating at the same time against increased toxicity levels related to high-surface charge densities.68 This rather low surface charge is expected to increase at more acidic conditions (such as in the endosomal lower pH environment) due to the sufficiently high pKa (∼7) of the DML particles, and thus promote the endosomal membrane disruption and release.68 This protonation mechanism of the carrier molecules was found to be of particular importance in mRNA delivery.16,69
In the RNA-based models, electrostatic interactions and hydrogen bonding acted as the driving forces for the association of the formed DML clusters with RNA. The number of hydrogen bonds between DML molecules and between DMLs and RNA are comparable, which indicates that hydrogen bonding contributes both to the DML–DML and to the DML–RNA association. However, on average, the DML–RNA association was found to be weaker compared to the DML–DML interactions. Such a moderate RNA–DML binding strength could potentially be beneficial for the RNA release at the final stages of the delivery process. The percentage of DML molecules, which are close to RNA, is similar for all three kinds of DMLs, i.e., 45–50% of the total number for each case. The larger-sized clusters were found to be formed close to RNA, whereas those comprising 3 or less DML molecules were preferably formed in the aqueous phase afar from RNA.
The RNA–DML association mechanism involved many steps with different characteristic timescales. Analysis of various dynamic properties indicated that instead of the observed association of individual DMLs with the oppositely-charged nucleotides, self-assembly of these molecules in clusters was the initial process performed within the first ∼10 ns. Association of the clusters with RNA follows, while a further enlargement of the formed clusters towards an equilibrium size is the final process, which is realized at timescales beyond ∼70 ns. The final, conformationally stable DML–RNA complex comprised several clusters around which RNA was wrapped, in such a manner that the entire RNA contour was covered by them. This form of the RNA–DML construct might be promising for providing protection e.g., against enzymatic attack, during an actual gene-delivery process.
Although the above-described behavior was recorded for the systems including an excess of the neutral–lipid molecules (see Table 1), and with different relative lipid/water concentrations, it appears that, at least within the examined degree of variation, the lipid–lipid and the lipid–RNA associative phenomena are not very sensitive to the stoichiometry of the systems. For instance, it appears that the percentage of participation of DML0 and DML2 lipids in the clusters is somewhat lower compared to that of DML1 molecules (see Fig. SI-3, ESI†), despite the fact that in absolute numbers, DML1 lipids are well outnumbered by their DML2 analogues (see Table 1). In addition, the percentage of all different kinds of lipids close to RNA was found to lie between 45% and 50% irrespective of their charged state and of their stoichiometry (as follows from the comparison between the DMLRW and the DMLHRW systems). This also implies that the cluster composition close to RNA is not dictated solely by the stoichiometry of the lipids with different charged states, but also by the balance of the relevant interactions (in the vicinity of RNA, electrostatic and hydrogen bonding interactions come into play as well). However, this balance (and thus features of the clustering behavior and the affinity between the lipid cluster and RNA) might be affected if very different stoichiometries from those considered here are used.
It should also be noted that in all the different properties checked between the DMLRW and the DMLHRW systems, the two models exhibited similar behavior. It can therefore be inferred that smaller in size RNA fragments may serve as computationally affordable models, for examining basic aspects of the physicochemical behavior related to the association of RNA with ionizable cationic complexation agents, similar to those studied here.
Conflicts of interest
The authors declare that there is no conflict of interest regarding the publication of this article.Acknowledgements
This work was supported by a computational time granted by the Greek Research & Technology Network (GRNET) in the National HPC facility – ARIS – under project ID RNA_COMPLEX. This research has been co-financed by the European Union and Greek national funds through the Operational Program Competitiveness, Entrepreneurship and Innovation, under the call RESEARCH – CREATE – INNOVATE (project code: T1EDK-02775).References
- Y. K. Sung and S. W. Kim, Recent advances in the development of gene delivery systems, Biomater. Res., 2019, 23, 8, DOI:10.1186/s40824-019-0156-z.
- X. M. Anguela and K. A. High, Entering the Modern Era of Gene Therapy, Annu. Rev. Med., 2019, 70(1), 273–288 CrossRef CAS PubMed.
- K. A. Hajj and K. A. Whitehead, Tools for translation: non-viral materials for therapeutic mRNA delivery, Nat. Rev. Mater., 2017, 2, 17056, DOI:10.1038/natrevmats.2017.56.
- I. Lostalé-Seijo and J. Montenegro, Synthetic materials at the forefront of gene delivery, Nat. Rev. Chem., 2018, 2(10), 258–277 CrossRef.
- Z. Meng, J. O'Keeffe-Ahern, J. Lyu, L. Pierucci, D. Zhou and W. Wang, A new developing class of gene delivery: messenger RNA-based therapeutics, Biomater. Sci., 2017, 5(12), 2381–2392 RSC.
- S. Guan and J. Rosenecker, Nanotechnologies in delivery of mRNA therapeutics using nonviral vector-based delivery systems, Gene Ther., 2017, 24(3), 133–143 CrossRef CAS PubMed.
- R. Kanasty, J. R. Dorkin, A. Vegas and D. Anderson, Delivery materials for siRNA therapeutics, Nat. Mater., 2013, 12(11), 967–977 CrossRef CAS PubMed.
- H. Yin, R. L. Kanasty, A. A. Eltoukhy, A. J. Vegas, J. R. Dorkin and D. G. Anderson, Non-viral vectors for gene-based therapy, Nat. Rev. Genet., 2014, 15(8), 541–555 CrossRef CAS PubMed.
- C. E. Thomas, A. Ehrhardt and M. A. Kay, Progress and problems with the use of viral vectors for gene therapy, Nat. Rev. Genet., 2003, 4(5), 346–358 CrossRef CAS PubMed.
- A. K. Blakney, P. F. McKay, B. I. Yus, Y. Aldon and R. J. Shattock, Inside out: optimization of lipid nanoparticle formulations for exterior complexation and in vivo delivery of saRNA, Gene Ther., 2019, 26(9), 363–372 CrossRef CAS PubMed.
- K. J. Kauffman, J. R. Dorkin, J. H. Yang, M. W. Heartlein, F. DeRosa, F. F. Mir, O. S. Fenton and D. G. Anderson, Optimization of Lipid Nanoparticle Formulations for mRNA Delivery in Vivo with Fractional Factorial and Definitive Screening Designs, Nano Lett., 2015, 15(11), 7300–7306 CrossRef CAS PubMed.
- J. A. Kulkarni, P. R. Cullis and R. van der Meel, Lipid Nanoparticles Enabling Gene Therapies: From Concepts to Clinical Utility, Nucleic Acid Ther., 2018, 28(3), 146–157 CrossRef CAS PubMed.
- S. Novakowski, K. Jiang, G. Prakash and C. Kastrup, Delivery of mRNA to platelets using lipid nanoparticles, Sci. Rep., 2019, 9, 552, DOI:10.1038/s41598-018-36910-2.
- Y. Rybakova, P. S. Kowalski, Y. Huang, J. T. Gonzalez, M. W. Heartlein, F. DeRosa, D. Delcassian and D. G. Anderson, mRNA Delivery for Therapeutic Anti-HER2 Antibody Expression In Vivo, Mol. Ther., 2019, 27(8), 1415–1423 CrossRef CAS PubMed.
- J. Heyes, L. Palmer, K. Bremner and I. MacLachlan, Cationic lipid saturation influences intracellular delivery of encapsulated nucleic acids, J. Controlled Release, 2005, 107(2), 276–287 CrossRef CAS PubMed.
- S. C. Semple, A. Akinc, J. Chen, A. P. Sandhu, B. L. Mui, C. K. Cho, D. W. Y. Sah, D. Stebbing, E. J. Crosley, E. Yaworski, I. M. Hafez, J. R. Dorkin, J. Qin, K. Lam, K. G. Rajeev, K. F. Wong, L. B. Jeffs, L. Nechev, M. L. Eisenhardt, M. Jayaraman, M. Kazem, M. A. Maier, M. Srinivasulu, M. J. Weinstein, Q. Chen, R. Alvarez, S. A. Barros, S. De, S. K. Klimuk, T. Borland, V. Kosovrasti, W. L. Cantley, Y. K. Tam, M. Manoharan, M. A. Ciufolini, M. A. Tracy, A. de Fougerolles, I. MacLachlan, P. R. Cullis, T. D. Madden and M. J. Hope, Rational design of cationic lipids for siRNA delivery, Nat. Biotechnol., 2010, 28(2), 172–176 CrossRef CAS PubMed.
- A. J. Geall, A. Verma, G. R. Otten, C. A. Shaw, A. Hekele, K. Banerjee, Y. Cu, C. W. Beard, L. A. Brito, T. Krucker, D. T. O'Hagan, M. Singh, P. W. Mason, N. M. Valiante, P. R. Dormitzer, S. W. Barnett, R. Rappuoli, J. B. Ulmer and C. W. Mandl, Nonviral delivery of self-amplifying RNA vaccines, Proc. Natl. Acad. Sci. U. S. A., 2012, 109(36), 14604–14609 CrossRef CAS PubMed.
- A. Thess, S. Grund, B. L. Mui, M. J. Hope, P. Baumhof, M. Fotin-Mleczek and T. Schlake, 135. Sequence-Engineered mRNA Without Chemical Nucleoside Modifications Enables an Effective Protein Therapy in Large Animals, Mol. Ther., 2015, 23, S55 CrossRef.
- O. S. Fenton, K. J. Kauffman, R. L. McClellan, E. A. Appel, J. R. Dorkin, M. W. Tibbitt, M. W. Heartlein, F. DeRosa, R. Langer and D. G. Anderson, Bioinspired Alkenyl Amino Alcohol Ionizable Lipid Materials for Highly Potent In Vivo mRNA Delivery, Adv. Mater., 2016, 28(15), 2939–2943 CrossRef CAS PubMed.
- N. Pardi, M. J. Hogan, F. W. Porter and D. Weissman, mRNA vaccines—a new era in vaccinology, Nat. Rev. Drug Discovery, 2018, 17(4), 261–279 CrossRef CAS PubMed.
- http://investors.alnylam.com/news-releases/news-release-details/alnylam-announces-first-ever-fda-approval-rnai-therapeutic, accessed Dec 13/2019.
- O. S. Fenton, K. J. Kauffman, J. C. Kaczmarek, R. L. McClellan, S. Jhunjhunwala, M. W. Tibbitt, M. D. Zeng, E. A. Appel, J. R. Dorkin, F. F. Mir, J. H. Yang, M. A. Oberli, M. W. Heartlein, F. DeRosa, R. Langer and D. G. Anderson, Synthesis and Biological Evaluation of Ionizable Lipid Materials for the In Vivo Delivery of Messenger RNA to B Lymphocytes, Adv. Mater., 2017, 29(33), 1606944 CrossRef PubMed.
- P. P. G. Guimaraes, R. Zhang, R. Spektor, M. Tan, A. Chung, M. M. Billingsley, R. El-Mayta, R. S. Riley, L. Wang, J. M. Wilson and M. J. Mitchell, Ionizable lipid nanoparticles encapsulating barcoded mRNA for accelerated in vivo delivery screening, J. Controlled Release, 2019, 316, 404–417 CrossRef CAS PubMed.
- https://www.americanpharmaceuticalreview.com/Featured-Articles/364236-Recent-Advances-in-Lipid-Nanoparticle-Mediated-mRNA-Therapy/, accessed 10/7/2020.
- Z. Wei and E. Luijten, Systematic coarse-grained modeling of complexation between small interfering RNA and polycations, J. Chem. Phys., 2015, 143(24), 243146 CrossRef PubMed.
- Y. Lu, J. Li and D. Lu, The mechanism for the complexation and dissociation between siRNA and PMAL: a molecular dynamics simulation study based on a coarse-grained model, Mol. Simul., 2017, 43(13–16), 1385–1393 CrossRef CAS.
- J. Li, Y. Ouyang, X. Kong, J. Zhu, D. Lu and Z. Liu, A multi-scale molecular dynamics simulation of PMAL facilitated delivery of siRNA, RSC Adv., 2015, 5(83), 68227–68233 RSC.
- A. Y. Antipina and A. A. Gurtovenko, Toward Understanding Liposome-Based siRNA Delivery Vectors: Atomic-Scale Insight into siRNA–Lipid Interactions, Langmuir, 2018, 34(29), 8685–8693 CrossRef CAS PubMed.
- A. P. Pandey and K. K. Sawant, Polyethylenimine: A versatile, multifunctional non-viral vector for nucleic acid delivery, Mater. Sci. Eng., C, 2016, 68, 904–918 CrossRef CAS PubMed.
- V. Vasumathi and P. K. Maiti, Complexation of siRNA with Dendrimer: A Molecular Modeling Approach, Macromolecules, 2010, 43(19), 8264–8274 CrossRef CAS.
- P. Posocco, X. Liu, E. Laurini, D. Marson, C. Chen, C. Liu, M. Fermeglia, P. Rocchi, S. Pricl and L. Peng, Impact of siRNA Overhangs for Dendrimer-Mediated siRNA Delivery and Gene Silencing, Mol. Pharmaceutics, 2013, 10(8), 3262–3273 CrossRef CAS PubMed.
- K. Karatasos, P. Posocco, E. Laurini and S. Pricl, Poly(amidoamine)-based Dendrimer/siRNA Complexation Studied by Computer Simulations: Effects of pH and Generation on Dendrimer Structure and siRNA Binding, Macromol. Biosci., 2011, 12(2), 225–240 CrossRef PubMed.
- P. Posocco, E. Laurini, V. Dal Col, D. Marson, K. Karatasos, M. Fermeglia and S. Pricl, Tell Me Something I Do Not Know. Multiscale Molecular Modeling of Dendrimer/Dendron Organization and Self-Assembly In Gene Therapy, Curr. Med. Chem., 2012, 19(29), 5062–5087 CrossRef CAS PubMed.
- D. Kurzbach, C. Velte, P. Arnold, G. Kizilsavas and D. Hinderberger, DNA condensation with spermine dendrimers: interactions in solution, charge inversion, and morphology control, Soft Matter, 2011, 7(14), 6695–6704 RSC.
- V. Marquez-Miranda, I. Araya-Duran and F. D. Gonzalez-Nilo, Multiscale Molecular Simulations Applied to Nucleic Acid-Dendrimer Interactions Studies, Curr. Pharm. Des., 2017, 23, 21 CrossRef PubMed.
- J. Šponer, G. Bussi, M. Krepl, P. Banáš, S. Bottaro, R. A. Cunha, A. Gil-Ley, G. Pinamonti, S. Poblete, P. Jurečka, N. G. Walter and M. Otyepka, RNA Structural Dynamics As Captured by Molecular Simulations: A Comprehensive Overview, Chem. Rev., 2018, 118(8), 4177–4338 CrossRef PubMed.
- E. A. Dethoff, K. Petzold, J. Chugh, A. Casiano-Negroni and H. M. Al-Hashimi, Visualizing transient low-populated structures of RNA, Nature, 2012, 491(7426), 724–728 CrossRef CAS PubMed.
- G. Bokinsky and X. Zhuang, Single-molecule RNA folding, Acc. Chem. Res., 2005, 38(7), 566–573 CrossRef CAS PubMed.
- Computational studies of RNA and DNA, Challenges and Advances in Computational Chemistry and Physics, ed. J. Šponer and F. Lankaš, 2006 Search PubMed.
- P. T. X. Li, Formation of a metastable intramolecular RNA kissing complex by nanomanipulation, Soft Matter, 2013, 9(12), 3246–3254 RSC.
- C. Abrams and G. Bussi, Enhanced Sampling in Molecular Dynamics Using Metadynamics, Replica-Exchange, and Temperature-Acceleration, Entropy, 2013, 16(1), 163–199 CrossRef.
- D. M. Zuckerman, Equilibrium Sampling in Biomolecular Simulations, Annu. Rev. Biophys., 2011, 40(1), 41–62 CrossRef CAS PubMed.
- M. Souaille and B. T. Roux, Extension to the weighted histogram analysis method: combining umbrella sampling with free energy calculations, Comput. Phys. Commun., 2001, 135(1), 40–57 CrossRef CAS.
- O. Valsson, P. Tiwary and M. Parrinello, Enhancing Important Fluctuations: Rare Events and Metadynamics from a Conceptual Viewpoint, Annu. Rev. Phys. Chem., 2016, 67(1), 159–184 CrossRef CAS PubMed.
- Y. A. G. Fosado, D. Michieletto, J. Allan, C. A. Brackley, O. Henrich and D. Marenduzzo, A single nucleotide resolution model for large-scale simulations of double stranded DNA, Soft Matter, 2016, 12(47), 9458–9470 RSC.
- C. De Michele, L. Rovigatti, T. Bellini and F. Sciortino, Self-assembly of short DNA duplexes: from a coarse-grained model to experiments through a theoretical link, Soft Matter, 2012, 8(32), 8388–8398 RSC.
- J. J. Uusitalo, H. I. Ingólfsson, S. J. Marrink and I. Faustino, Martini Coarse-Grained Force Field: Extension to RNA, Biophys. J., 2017, 113(2), 246–256 CrossRef CAS PubMed.
- https://www.ebi.ac.uk/pdbe/entry/pdb/5tdn/protein/1, accessed 1/12/2019.
- C. Eigenbrot, M. Randal, L. Presta, P. Carter and A. A. Kossiakoff, X-ray structures of the antigen-binding domains from three variants of humanized anti-p185HER2 antibody 4D5 and comparison with molecular modeling, J. Mol. Biol., 1993, 229(4), 969–995 CrossRef CAS PubMed.
- H. N. Po and N. M. Senozan, The Henderson-Hasselbalch Equation: Its History and Limitations, J. Chem. Educ., 2001, 78(11), 1499 CrossRef CAS.
- B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, GROMACS 4:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation, J. Chem. Theory Comput., 2008, 4(3), 435–447 CrossRef CAS PubMed.
Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation, J. Chem. Theory Comput., 2008, 4(3), 435–447 CrossRef CAS PubMed. - J. Huang and A. D. MacKerell, Jr., CHARMM36 all-atom additive protein force field: validation based on comparison to NMR data, J. Comput. Chem., 2013, 34(25), 2135–2145 CrossRef CAS PubMed.
- J. Huang, S. Rauscher, G. Nawrocki, T. Ran, M. Feig, B. L. de Groot, H. Grubmüller and A. D. MacKerell, CHARMM36m: an improved force field for folded and intrinsically disordered proteins, Nat. Methods, 2017, 14(1), 71–73 CrossRef CAS PubMed.
- E. J. Denning, U. D. Priyakumar, L. Nilsson and A. D. Mackerell, Impact of 2′-hydroxyl sampling on the conformational properties of RNA: Update of the CHARMM all-atom additive force field for RNA, J. Comput. Chem., 2011, 32(9), 1929–1943 CrossRef CAS PubMed.
- T. Malaspina, G. Colherinhas, F. de Oliveira Outi and E. E. Fileti, Assessing the interaction between surfactant-like peptides and lipid membranes, RSC Adv., 2017, 7(57), 35973–35981 RSC.
- L. Zhang, Z. Zhang, J. Jasa, D. Li, R. O. Cleveland, M. Negahban and A. Jérusalem, Molecular dynamics simulations of heterogeneous cell membranes in response to uniaxial membrane stretches at high loading rates, Sci. Rep., 2017, 7, 8316, DOI:10.1038/s41598-017-06827-3.
- J. Gasteiger and M. Marsili, Iterative partial equalization of orbital electronegativity—a rapid access to atomic charges, Tetrahedron, 1980, 36(22), 3219–3228 CrossRef CAS.
- H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, The missing term in effective pair potentials, J. Phys. Chem., 1987, 91(24), 6269–6271 CrossRef CAS.
- S. Chatterjee, P. G. Debenedetti, F. H. Stillinger and R. M. Lynden-Bell, A computational investigation of thermodynamics, structure, dynamics and solvation behavior in modified water models, J. Chem. Phys., 2008, 128(12), 124511 CrossRef PubMed.
- R. E. Isele-Holder, W. Mitchell and A. E. Ismail, Development and application of a particle-particle particle-mesh Ewald method for dispersion interactions, J. Chem. Phys., 2012, 137(17), 174107 CrossRef PubMed.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, Molecular dynamics with coupling to an external bath, J. Chem. Phys., 1984, 81(8), 3684–3690 CrossRef CAS.
- G. Bussi, D. Donadio and M. Parrinello, Canonical sampling through velocity rescaling, J. Chem. Phys., 2007, 126(1), 014101 CrossRef PubMed.
- M. J. Boniecki, G. Lach, W. K. Dawson, K. Tomala, P. Lukasz, T. Soltysinski, K. M. Rother and J. M. Bujnicki, SimRNA: a coarse-grained method for RNA folding simulations and 3D structure prediction, Nucleic Acids Res., 2016, 44(7), e63 CrossRef PubMed.
- X. Daura, K. Gademann, B. Jaun, D. Seebach, W. F. van Gunsteren and A. E. Mark, Peptide Folding: When Simulation Meets Experiment, Angew. Chem., Int. Ed., 1999, 38(1-2), 236–240 CrossRef CAS.
- E. Westhof and T. Hermann, Nat. Struct. Biol., 1999, 6(6), 540–544 CrossRef PubMed.
- D. A. McQuarrie, Statistical Mechanics, University Science Books, 2000 Search PubMed.
- N. Maurer, K. F. Wong, H. Stark, L. Louie, D. McIntosh, T. Wong, P. Scherrer, S. C. Semple and P. R. Cullis, Spontaneous Entrapment of Polynucleotides upon Electrostatic Interaction with Ethanol-Destabilized Cationic Liposomes, Biophys. J., 2001, 80(5), 2310–2326 CrossRef CAS PubMed.
- I. M. Hafez, N. Maurer and P. R. Cullis, On the mechanism whereby cationic lipids promote intracellular delivery of polynucleic acids, Gene Ther., 2001, 8(15), 1188–1196 CrossRef CAS PubMed.
- K. A. Hajj, R. L. Ball, S. B. Deluty, S. R. Singh, D. Strelkova, C. M. Knapp and K. A. Whitehead, Branched-Tail Lipid Nanoparticles Potently Deliver mRNA In Vivo due to Enhanced Ionization at Endosomal pH, Small, 2019, 15(6), 1805097 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm00736f |
| This journal is © The Royal Society of Chemistry 2020 |