Open Access Article
Open Access ArticleTapered elasticæ as a route for axisymmetric morphing structures
Mingchao
Liu
,
Lucie
Domino
and
Dominic
Vella
 *
*
Mathematical Institute, University of Oxford, Oxford, OX2 6GG, UK. E-mail: dominic.vella@maths.ox.ac.uk; Tel: +44-(0) 1865 615150
First published on 17th July 2020
Abstract
Transforming flat two-dimensional (2D) sheets into three-dimensional (3D) structures by combining carefully made cuts with applied edge-loads has emerged as an exciting manufacturing paradigm in a range of applications from mechanical metamaterials to flexible electronics. In Kirigami, patterns of cuts are introduced that allow solid faces to rotate about each other, deforming in three dimensions whilst remaining planar. In other scenarios, however, the solid elements bend in one direction. In this paper, we model such bending deformations using the formulation of an elastic strip whose thickness and width are tapered (the ‘tapered elastica’). We show how this framework can be exploited to design the tapering patterns required to create planar sheets that morph into desired axisymmetric 3D shapes under a combination of horizontal and vertical edge-loads. We exhibit this technique by recreating miniature structures with positive, negative, and variable apparent Gaussian curvatures. With sheets of constant thickness, the resulting morphed shapes may leave gaps between the deformed elements. However, by tapering the thickness of the sheet too, these gaps can be closed, creating tessellated three-dimensional structures. Our theoretical approaches are verified by both numerical simulations and physical experiments.
1 Introduction
Morphing structures, which are able to change their shapes from one state to another, are finding application in scenarios as diverse as soft robotics,1,2 deployable space structures,3 aircraft drag control systems,4 biomedical devices,5 flexible electronics,6 and mechanical metamaterials.7,8 Morphing from an initial two-dimensional (2D) shape that is flat to a three-dimensional (3D) shape is a particularly popular goal since flat shapes are generally easier to manufacture (e.g. via printing or lithography) and may be stored easily by stacking.9 Designing a 2D shape that will morph into a particular desired 3D shape, however, involves confronting a series of geometrical and mechanical challenges.The primary challenge arises from a combination of geometry and mechanics: many morphing structures are thin and, as a result, prefer to bend in response to applied loads, rather than to change their length/area.10 However, Gauss’ Theorema Egregium11 states that deformations that preserve length or area (isometries) cannot change the Gaussian curvature of a surface. As a result, the range of structures that can be created from an initially flat sheet are very limited. Perhaps the most familiar example of this geometrical incompatibility of curved and flat surfaces arises in cartography: no planar (flat) map of Earth can represent areas perfectly, even for a portion of the Earth's surface, and must necessarily distort at least some distances.12 Conversely, any attempt to wrap a sphere with a thin planar sheet (as in Mozart Kügeln and other confectionery) will necessarily result in crumpling of the thin sheet.13–15
The crumpling of a thin sheet that wraps a sphere is indicative of the root of the problem. A planar sheet that tries to become curved has too much area to allow it to do so: material either needs to be removed/compressed (where the crumples form) or added/stretched elsewhere. In many applications, localized expansion in some region has become a common strategy, with many different routes used to do this, including pneumatic pressure16,17 and swelling/expansion that is induced by heat,18,19 light20,21 or chemistry.22 Such strategies rely on the use of responsive materials, such as elastomers, hydrogels, shape-memory polymers, etc., in combination with 3D/4D printing.23 All of these approaches allow true changes in Gaussian curvature to occur, and do not contradict the Theorema Egregium since the deformations are not isometries. Moreover, the inverse design problem (solving for the distribution of actuation required to achieve quite complex curvature distributions) has been solved for some of these examples.17,18,24,25
In other scenarios, however, the ability to morph without significant strain is required; for example, in inorganic flexible electronic devices26 only very small strain can be tolerated before plastic deformation and fracture occur. In such applications, approaches that allow the required changes in length to be buffered without strain are particularly desirable.27,28 One example of this is ‘buffering by buckling’:29 buckling and wrinkling instabilities allow excess length to be stored at a small scale without significant strain and can allow an ‘Apparent Gaussian Curvature’ (AGC) to develop. An alternative approach that allows changes in length/area to be buffered is to make oriented cuts/slits in a material, while leaving the area of solid to be the same as the basic sheet – Kirigami.30,31 Kirigami cut patterns can be programmed to generate different 3D shapes with different Gaussian curvature.32,33 As in the case of buffering by buckling, however, the local elements remain largely planar, so that the Gaussian curvature that develops is ‘apparent’ – at a small enough scale the elements remain planar.
Removing more material (so that the solid area is significantly decreased through cutting) is another strategy, similar to Kirigami, that has been particularly used in flexible electronics. In one family of such designs, a repeated pattern of cuts is made in a sheet around a central hub. In this way, the hub connects a series of tapered radial ‘spokes’34 that are able to bend when subject to a horizontal compressive load at their edges. Under such loads, the spokes deform to create a 3D structure that is approximately axisymmetric.35,36 As a result, the structure has an AGC that is different to that of the initially flat sheet, though again we emphasize that the Gaussian curvature of each spoke remains zero locally.29 While the inverse problem of designing three-dimensional morphing structures that use swelling and growth is well-advanced,17,18,37 the understanding of how to choose cut and tapering patterns to form axisymmetric shapes in this way is much less developed. In general, the approach used has been to develop databases of 2D patterns that deform into particular types of 3D structures. This approach largely proceeds by trial and error, though numerical optimization approaches have been used to solve the inverse design problem;38,39 a rational basis for the design of cut patterns, (i.e. determining the particular 2D flat pattern according to given 3D target shapes) is lacking. Some very recent work40 proposed a solution to this inverse design problem focussing on application to the design of flexible electronic devices at different length scales, where in-plane loads and zero moment boundary conditions are appropriate. In a similar spirit, Elishakoff40 considered the problem of how the stiffness of a vertical column might be varied along its length to give desired profiles when the column buckles under its own weight. In this paper, we show how the tapering of individual spokes in axisymmetric designs can be modelled; our approach relies on using the formalism of the ‘tapered elastica’ equation42,43 to describe the deformation of each spoke of the design under both horizontal and vertical loads applied at its edges. In this way, we investigate the axisymmetric shapes that can be formed, outlining a general strategy for the inverse design of structures and demonstrating this in particular instances. We begin by considering the theory of the tapered elastica in more detail.
2 The tapered elastica
In this section, we introduce the tapered elastica, which is the fundamental element used throughout the rest of the paper to generate morphing structures.2.1 Theoretical formulation
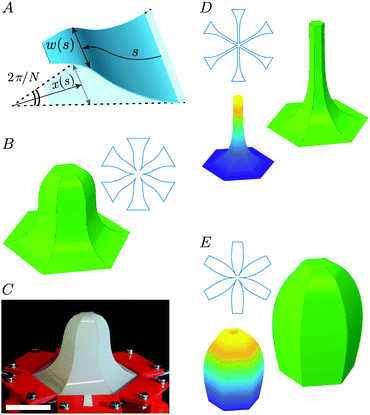
We first consider an elastic strip of length L with non-uniform cross-section, i.e. both the strip's width, w(s), and its thickness, t(s), vary with arc length, s: this is the tapered elastica43 (see Fig. 1A). The ends of the tapered elastica are subject to horizontal and vertical forces, H0 and V0, respectively, but we neglect the effect of a body force such as gravity (see later discussion). The intrinsic equation for the shape, θ(s), is determined by considering the balance of forces and torques on an infinitesimal element of the strip.44 These balances require that θ(s) satisfy the tapered elastica equation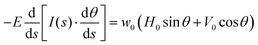 | (1) |
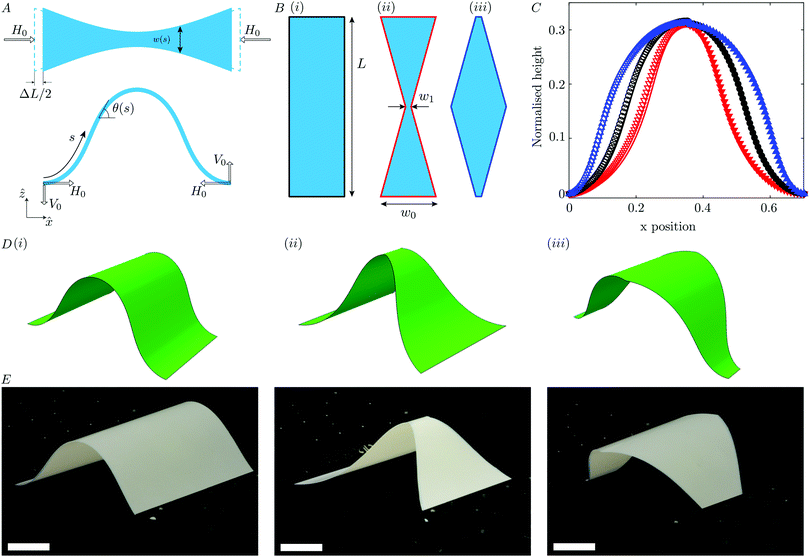 | ||
Fig. 1 The tapered elastica: (A) schematic of a tapered elastica subject to a horizontal compressive load, H0. The buckled shape is described by the intrinsic equation θ(s). (B) Representative taperings of three elasticæ with central:end width ratios (i.e., α = w1/w0): (i) α = 1 (no tapering); (ii) α = 0.1; (iii) α = 10. (C) Buckled shapes of the three elasticæ in B, subject to relative end-end compression ![[capital Delta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10b.gif) = ΔL/L = 0.3 and clamped boundary conditions. The predictions of the tapered elastica eqn (1) is shown by the solid curves, together with experimental results (empty symbols, left-hand side) and FEA predictions (filled symbols, right-hand side) with lengths normalized by the strip length, L. △ corresponds to α = 10, ○ to α = 1 and ▽ to α = 0.1. Three-dimensional snapshot of the buckled shape (again = ΔL/L = 0.3 and clamped boundary conditions. The predictions of the tapered elastica eqn (1) is shown by the solid curves, together with experimental results (empty symbols, left-hand side) and FEA predictions (filled symbols, right-hand side) with lengths normalized by the strip length, L. △ corresponds to α = 10, ○ to α = 1 and ▽ to α = 0.1. Three-dimensional snapshot of the buckled shape (again ![[capital Delta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10b.gif) = 0.3) realized in (D) FEA simulations and (E) experiments (bottom). The scale bar represents 15 mm. (Labels (i)–(iii) denote the same strip taperings as in B.) = 0.3) realized in (D) FEA simulations and (E) experiments (bottom). The scale bar represents 15 mm. (Labels (i)–(iii) denote the same strip taperings as in B.) | ||
The complete shape of the buckled elastica, [![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) (s), ẑ(s)], may be determined from the intrinsic equation θ(s) by solving the geometrical relationships
(s), ẑ(s)], may be determined from the intrinsic equation θ(s) by solving the geometrical relationships
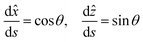 | (2) |
Typically, (1) is solved (for a given moment of inertia profile I(s)) subject to boundary conditions such as clamped boundary conditions at the edges, i.e.
| θ(0) = θ(L) = 0 | (3) |
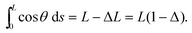 | (4) |
Note that the solution of (1) subject to boundary conditions (3) and (4) is essentially geometrical: a change in the value of the strip Young's modulus E would cause a proportionate change in the value of the horizontal force H0 required, but would not affect the deformed shape of the strip. In particular, the shapes obtained using materials with different elastic properties should be directly comparable. However, in model experiments, the effect of a strip's own weight can only be neglected if its length remains small compared to the elasto-gravitational length28![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) g = (B/ρsgt)1/3 ∝ (Et2)1/3. Because
g = (B/ρsgt)1/3 ∝ (Et2)1/3. Because ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) g increases with thickness and Young's modulus, gravity can be neglected for sufficiently stiff or thick strips.
g increases with thickness and Young's modulus, gravity can be neglected for sufficiently stiff or thick strips.
The effect of width tapering (maintaining a constant thickness) is presented in Fig. 1, where we show the results for elasticæ with three different taperings. These results show two things: firstly, that varying the width of the strip along its arc-length makes a noticeable difference to the curvature of the resulting buckled elastica. Secondly, Fig. 1 shows that the tapered elastica equation discussed above provides a satisfactory description of the deformation of a tapered strip observed in finite-element analysis (FEA) without gravity and experimentally, with the strip thickness chosen to be sufficiently large that the effects of gravity may safely be neglected. (Further details of FEA simulations and experiments are given in Appendix A and B, respectively.)
The spatial variation in curvature observed in Fig. 1 is natural: since the bending energy density is proportional to the local moment of inertia (and hence to the strip width in this constant thickness example), the strip can ‘choose’ to curve more in regions where the width is smaller, thereby minimizing the energetic cost. Indeed, according to the translation by Oldfather et al.,45 Euler even suggested that this variation in curvature may be used as a means by which to measure the width of an elastic ribbon: “… if the material of the ribbon together with its thickness be everywhere the same, but the width is variable, because the absolute elasticity is proportional to the width, the width of the ribbon at every point is learned from the form of the curve”.
Having validated the tapered elastica model for the description of the deformation of a single elastic strip, we shall shortly move on to reverse Euler's suggestion by considering how the deformed shape can be designed by an appropriate choice of the moment of inertia, I(s). First, however, we turn to discuss the appropriate non-dimensionalization.
2.2 Non-dimensionalization
We scale the coordinates s,![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) and ẑ by the length L of the elastica and the strip width and thickness by their values at s = 0, which we denote w0 and t0, respectively. We therefore introduce the dimensionless variables
and ẑ by the length L of the elastica and the strip width and thickness by their values at s = 0, which we denote w0 and t0, respectively. We therefore introduce the dimensionless variables(ξ, x, z) = (s, ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) , ẑ)/L, ω(ξ) = w(s)/w0, T(ξ) = t(s)/t0 , ẑ)/L, ω(ξ) = w(s)/w0, T(ξ) = t(s)/t0 | (5) |
| Ĩ(ξ) = I(s)/I0 | (6) |
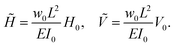 | (7) |
Combining the above non-dimensionalization with the geometrical relationships (2) to eliminate cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ and sin
θ and sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, the tapered elastica eqn (1) becomes
θ, the tapered elastica eqn (1) becomes
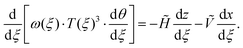 | (8) |
In a recent work,40 it was noted that a form of (8) could be used to determine the strip width and thickness profiles required to form a particular shape upon buckling under compressive forces alone (i.e. with Ṽ = 0). In our analysis, we retain the possibility of a vertical force, Ṽ, increasing the generality of our work. We note that, even with this extra term, (8) has a first integral, and so consider the properties of this first integral further.
2.3 A first integral
Eqn (8) can immediately be integrated once to give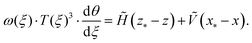 | (9) |
![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) z* + Ṽx* is a single constant of integration to be determined that is written in this way for later convenience. Writing (8) in this way also makes it clear that (8) expresses torque balance at each point of the strip, (x,z), measured relative to some point (x*,z*).46 However, by allowing x* and z*non-zero, and in contrast to the previous work of Fan et al.,40 we do not require that the domain edges are torque free (or ‘simply-supported’).
z* + Ṽx* is a single constant of integration to be determined that is written in this way for later convenience. Writing (8) in this way also makes it clear that (8) expresses torque balance at each point of the strip, (x,z), measured relative to some point (x*,z*).46 However, by allowing x* and z*non-zero, and in contrast to the previous work of Fan et al.,40 we do not require that the domain edges are torque free (or ‘simply-supported’).
To obtain a desired deformed shape, given by θ(ξ) (and the associated x and z coordinates) we note that (9) can readily be rearranged to give
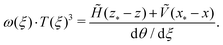 | (10) |
Eqn (10) is a key result in our analysis: it relates the shape of the deformed elastica (the right hand side of (10)) to the moment of inertia of the cross section at a particular point (the left hand side of (10)). Indeed, (10) gives, in principle, the distribution of moment of inertia that is required to generate a particular shape (the inverse design problem). We emphasize again that the inclusion of vertical applied forces, the term involving Ṽ in (10), and non-zero edge-moments, the term ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) z* + Ṽx*, goes beyond the previous analysis of Fan et al.40 which neglected both effects.
z* + Ṽx*, goes beyond the previous analysis of Fan et al.40 which neglected both effects.
In the work of Elishakoff41 to determine the tapering that will give particular buckling modes of a vertical column, the vertical stress within the column was readily determined from the stress state prior to buckling. Here, while x(ξ), z(ξ) and dθ/dξ are all known for a given target 3D structure, the constants ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) , Ṽ, x* and z* are not. These constants are related to the forces and torques that must be applied at the ends of the strip and so must be determined to allow us to calculate the required tapering. We therefore turn to consider in more detail the design of structures that, when deformed, adopt a desired shape.
, Ṽ, x* and z* are not. These constants are related to the forces and torques that must be applied at the ends of the strip and so must be determined to allow us to calculate the required tapering. We therefore turn to consider in more detail the design of structures that, when deformed, adopt a desired shape.
3 Inverse design of morphable 3D structures
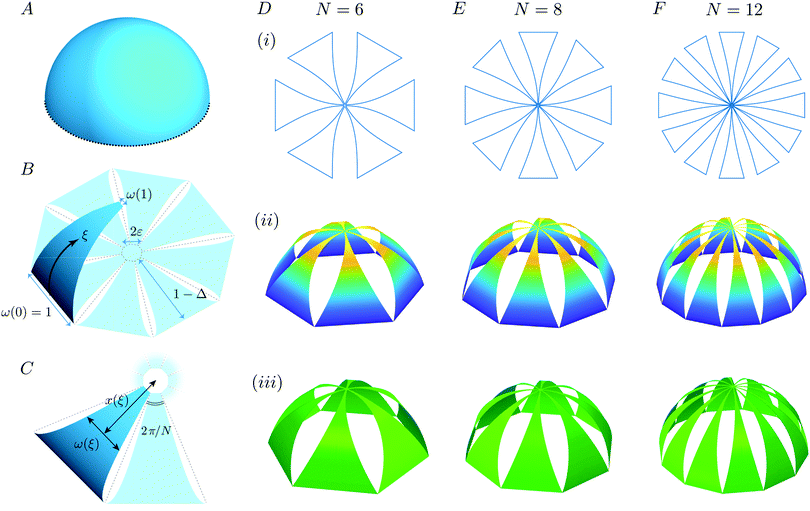
As we have just seen, the out-of-plane deformed configuration of a single elastica can be changed by modifying the cross-sectional moment of inertia (which can be achieved by tapering either the width or thickness of the strip). If N of these elasticæ (the spokes) are joined together at a central hub (of dimensional radius εL), as shown in Fig. 2, we expect that a cross section through the three-dimensional deformed shape should have the same shape as an individual tapered elastica with the same distribution of the moment of inertia. (We refer to this cross section as the ‘gross shape’ since, with many spokes used, this is the shape that would be seen at a large scale, neglecting the fine details of each individual spoke.) We also require that neighbouring spokes do not touch each other: the width profile, w(s), must be compatible with the deformation in that w(s) ≤ 2tan(π/N)x(s) or in dimensionless terms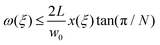 | (11) |
In this section, we focus only on the case of strips of constant thickness, T(ξ) = 1, treating (10) as an equation for the tapering ω(ξ) only. We shall see that in this way we can generate particular three-dimensional shapes, but that these shapes have large gaps. We therefore turn to generate shapes that tessellate in Section 4. Lifting the restriction of constant thickness allows us to exhibit greater control over the three-dimensional shape that can be created, as we demonstrate in Section 5.
3.1 No applied vertical load, Ṽ = 0
We begin by considering the case of no imposed vertical load at the edges, Ṽ = 0, which, combined with the constant thickness assumption T(ξ) = 1, turns (10) into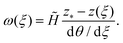 | (12) |
![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) and z*. We can also see from (12) that the technique for determining these unknown constants might change depending on whether there is any intermediate ξ* ∈ [0, 1] such that θξ(ξ*) = 0 – does the desired shape have an inflection point? (This is related to the distribution of AGC within a given 3D structure – if there is no inflection point, then the AGC has a single sign throughout, while if there is an inflection point then, in general, the AGC will also change sign there.) We therefore discuss these two cases separately.
and z*. We can also see from (12) that the technique for determining these unknown constants might change depending on whether there is any intermediate ξ* ∈ [0, 1] such that θξ(ξ*) = 0 – does the desired shape have an inflection point? (This is related to the distribution of AGC within a given 3D structure – if there is no inflection point, then the AGC has a single sign throughout, while if there is an inflection point then, in general, the AGC will also change sign there.) We therefore discuss these two cases separately.
![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) and z* can be chosen to ensure that the width at the ends of each spoke match the desired values, i.e.
and z* can be chosen to ensure that the width at the ends of each spoke match the desired values, i.e. | (13) |
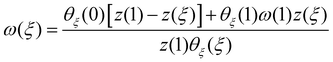 | (14) |
Given a desired 3D shape, defined by an intrinsic equation θ(ξ) and the associated shape [x(ξ),z(ξ)], (14) describes the width tapering of a strip required to generate that shape upon deformation. We note that the expression in (14) is independent of the Young's modulus of the material; this follows from the geometrical character of the (tapered) elastica equation discussed in Section 2. We also note that we have determined the values of ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) and z* required to give a particular deformed shape; as already discussed after eqn (8), this determines the edge moment required to give this shape.
and z* required to give a particular deformed shape; as already discussed after eqn (8), this determines the edge moment required to give this shape.
As a first demonstration of this strategy for the inverse design of particular 3D target structures by combining multiple such tapered elasticæ, we consider a hemispherical shell (see Fig. 2A–C). In this simple example, the curvature θξ is constant and, in particular, there are no inflection points. The tapered 2D shapes, together with the resulting 3D shapes formed after deformation (as predicted by the tapered elastica theory and FEA simulations), are shown in Fig. 2D–F. These images confirm that the deformed shape is very close to the desired hemispherical shape. We note two further features of the deformed shape: (i) large gaps are observed between the ‘spokes’ in the deformed shape and (ii) the tapered shape used is independent of the number, N, of spokes used, although the gross shape becomes ‘closer’ to the (axisymmetric) hemisphere as N increases.
Thus far, we have not considered the condition that the deformation of neighbouring spokes be compatible, i.e. is (11) satisfied for all positions ξ along the strip? In particular, since (11) must hold for all ξ it must hold at the ξ for which the ratio ω(ξ)/x(ξ) is maximized; we therefore require that
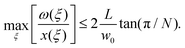 | (15) |
For many desired 3D shapes (including the hemisphere considered above), the ratio ω(ξ)/x(ξ) decays with distance from the outer edge so that all that is required for (15) to hold everywhere is that it holds at the outer edge, i.e. that w0 ≤ 2L(1 − Δ + ε)tan(π/N). Unless stated otherwise, we will take w0 to give equality in this relation. Note, however, that since w0 is used to rescale the width profile, ω(ξ), the shape of the strip that is computed through our analysis does not change as the number, N, of spokes is changed.
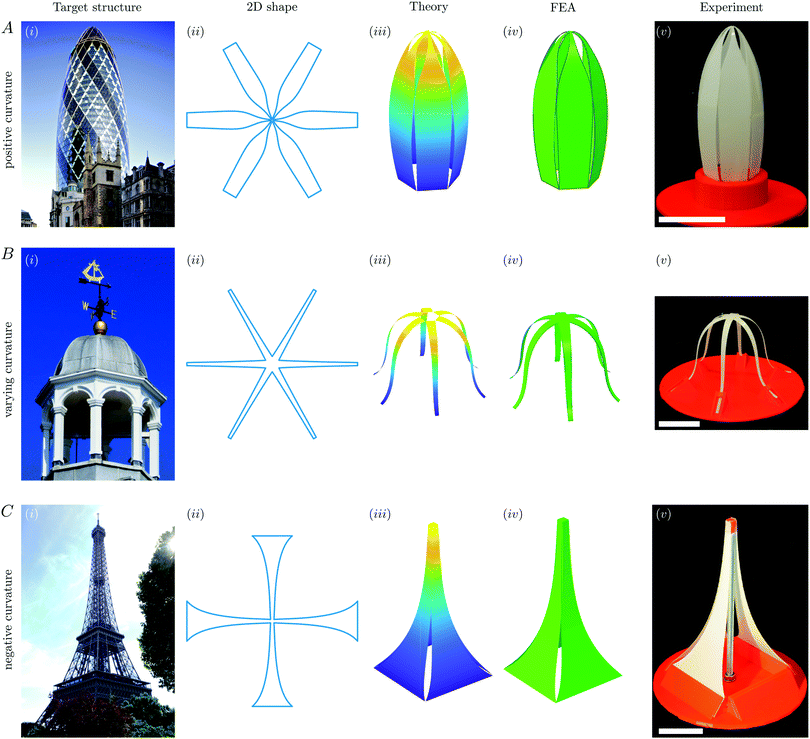
The example of a hemispherical shell highlights the ability to generate a particularly simple deformed shape through this strategy. As another, less simple example, we take ‘the Gherkin’ (30 St Mary Axe St., London). The curvature θξ in this example is again everywhere positive, but its value varies with position on the surface. Moreover, as shown in Fig. 3A, since the curvature changes very quickly in a narrow region near the tip, a very rapid change in the tapering of the elastic strip is required here.
![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) to ensure that ω(0) = 1 (which choice gives
to ensure that ω(0) = 1 (which choice gives ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) = θξ(0)/z(ξ*) with z measured from the height of the outer edge, ξ = 0) and so we have
= θξ(0)/z(ξ*) with z measured from the height of the outer edge, ξ = 0) and so we have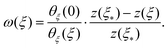 | (16) |
As should be expected from the geometrical character of the elastica equation, this result is also independent of the Young modulus of the material. Moreover, since we have now determined the available free parameters, it is clear that we cannot also specify ω(1). Instead, its value is determined by (16) according to the given target shape, and we must ensure that the size of the central portion, ε, and the width at the outer edge, w0, are chosen consistently.
As an example of the design of a structure with an inflection point, we take the cupola roof of St Thomas' Church, Lymington (UK). The shape of this cupola is such that the angle of inclination, θ, first increases away from the base, before reaching a maximum value and then decreasing again – θ reaches a maximum at an inflection point around 36.75% of the way along its length, so that ξ* ≈ 0.3675. The resulting taper shape, together with numerical simulations and experimental realization of this shape are shown in Fig. 3B. As expected, we see that the three-dimensional shape has an apparent Gaussian curvature (AGC) that changes with arc length position along the shape. Note that in this case, the required width tapering increases with distance from the outer edge, with its maximum occurring at the inner edge, i.e., ξ = 1. Furthermore, the largest value of ω(ξ)/x(ξ) also occurs at ξ = 1. To ensure that eqn (15) holds, we therefore choose w0 = 2εL·[tan(π/N)]/ω(1).
3.2 No applied horizontal load, ![[H with combining tilde]](https://www.rsc.org/images/entities/h3_i_char_0048_0303.gif) = 0
= 0
We have now seen several examples of shapes with positive, or variable, AGC that can be generated by imposing a horizontal compressive force, i.e. via buckling. To form a shape with negative AGC, we now consider the situation in which there is no load applied horizontally, ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) = 0. Instead, we envisage applying a normal load Ṽ ≠ 0, for example via a ‘poke’ at the central hub; this vertical force is balanced by shear forces acting at the base of the structure, which is clamped at a specified angle.
= 0. Instead, we envisage applying a normal load Ṽ ≠ 0, for example via a ‘poke’ at the central hub; this vertical force is balanced by shear forces acting at the base of the structure, which is clamped at a specified angle.
In this case, (10) reads
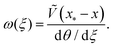 | (17) |
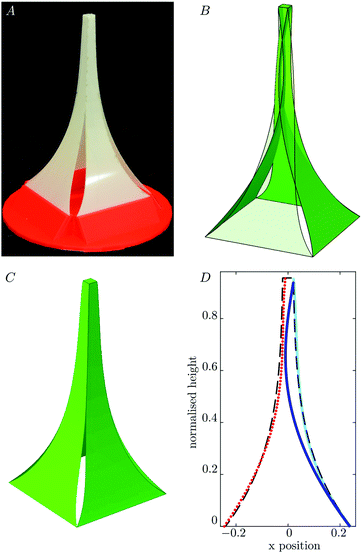
In our experiments and FEA simulations, a vertical poking force is applied at the centre by a pillar (see Fig. 3C(v) where the fourth side of the structure is removed for clarity). While including such a loading is key to this family of designs, it may be inconvenient in some situations. Nevertheless, we note that, in practice, self-contact may allow similar shapes to be achieved. For example, if the central loading point in Fig. 3C(v) is removed after the initial deformation, the shape remains very similar because the neighbouring strips ‘lock’ together (see Appendix C for more details).
4 Tessellating structures
While the 3D structures generated in Section 3 have a mid-line shape corresponding to the desired target shape (see the examples in Fig. 2 and 3), a clear limitation of this approach is that these structures all exhibit noticeable gaps in their body.In this section, we relax the constraint that the deformed shape follows a particular contour in favour of creating structures that tessellate (i.e. with no gap in the body). We shall explore and discuss the zoology of tessellating shapes that may be achieved whilst maintaining a constant sheet thickness, so that T(ξ) = 1 still. (We shall see in Section 5 that relaxing this constraint allows us to deform to a shape that both tessellates and adopts a given three-dimensional design.)
4.1 Theoretical formulation
The requirement that the deformed tapered elasticæ tessellate, that the strip edges touch throughout, introduces an additional geometrical constraint (see Fig. 4A): we must have equality in (11) for every arc length position ξ, so that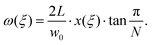 | (18) |
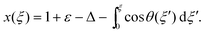 | (19) |
 | ||
| Fig. 4 Prediction of tessellating 3D structures using constant thickness spokes. (A) Illustration of the additional constraint used to determine w(s) for tessellation; with constant thickness spokes, tessellation is achieved at the expense of choice of 3D structure generated – the type of tessellating 3D structure generated in this case depends on the boundary conditions used and the position of the edges: (B) A variable AGC structure is created with clamped boundary conditions, horizontal compression and Δ = 0.5. The experimental realization of the variable AGC structure is shown in (C) (scale bar represents 4 cm). (D) A structure with negative AGC is created with free-sliding edge boundary conditions (subject to zero slope) and a central vertical indentation applied to give Δ = 0.85. (E) A structure with positive AGC is created with hinged boundary conditions, horizontal compression and Δ = 0.8. In each of panels B–E the spoke shapes, as obtained from the solution of eqn (18), are shown in the upper inset; the 3D shapes predicted by the tapered elastica analysis are shown (lower inset) together with the prediction of FEA (main panel, shown in green). | ||
We therefore have that the tapered elastica equation becomes
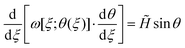 | (20) |
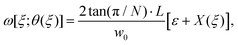 | (21) |
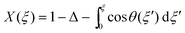 . Eqn (20), with ω(ξ) given by (21), is to be solved subject to the boundary conditions
. Eqn (20), with ω(ξ) given by (21), is to be solved subject to the boundary conditions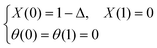 | (22) |
The resulting boundary value problem may be solved numerically using, for example, the MATLAB routine bvp4c. As in the case of the inverse problem without tessellation (Section 3), it is possible to consider combinations of horizontal and vertical loads applied at the edges, as desired.
4.2 Results
Fig. 4 shows the variety of tessellating 3D axisymmetric shapes that can be generated in this way, using different combinations of boundary conditions and horizontal or vertical forces. All these theoretical designs are validated by FEA simulations (Fig. 4B, D and E) or experiment (Fig. 4C). Crucially, while each of these shapes resembles one of the three buildings chosen for the designed structures in Fig. 3, this resemblance is not precise: the ability to design the deformed shape has been sacrificed to satisfy the constraint of tessellation. However, as we shall now show, both constraints (a designed 3D deformation and tessellation) can be satisfied by allowing both the width and strip thickness to be tapered.5 Inverse designs that tessellate
In this section we consider designs in which the strip tapering is chosen to ensure that the deformed shape will tessellate, as well as adopting a particular designed three-dimensional profile when deformed; we refer to such shapes as ‘tessellated designs’. To ensure tessellation, we first take the strip width to be given by (21). With the strip width determined in this way, we then use (10) (considering purely horizontal end forces) to give the thickness distribution required to realize a particular design as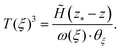 | (23) |
This equation is very similar to eqn (2) of Fan et al.40 except for the inclusion of z*, which was effectively set to vanish by their consideration of simply-supported (torque-free) edges. As was also discussed in Section 3, the presence of z* ≠ 0 allows our approach to describe shapes with an inflection point, and hence is more general than limiting to the case z* = 0. The determination of the constants ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) and z* depends on whether the shape contains such an inflection point or not; in either case, since ω(ξ) is given explicitly from (21), we use the condition T(0) = 1 as appropriate.
and z* depends on whether the shape contains such an inflection point or not; in either case, since ω(ξ) is given explicitly from (21), we use the condition T(0) = 1 as appropriate.
Fig. 5A shows the result of applying this strategy to the cupola roof presented in Fig. 3B; Fig. 6A shows that the cut pattern required to tessellate is very different to that required to generate the same shape, using constant thickness strips but without tessellating (compare the dashed and continuous curves in Fig. 6A). However, we also note that the thickness distribution required to obtain the desired shape with tessellation exhibits relatively small variations from uniform thickness: despite the large change in the portion of the shape that is filled (compare Fig. 5A and C), the thickness profile (1 ≤ T(ξ) ≤ 2.6) varies by less than a factor 3 throughout the length of each spoke (see Fig. 6A). This may seem surprising (not least since a large change in the width tapering is required to achieve tessellation) but reflects the cubic dependence of the strip's moment of inertia on its thickness: relatively small changes in thickness are able to provide the large changes in moment of inertia required to obtain the desired shape. We also note that the same strategy can be used to design a tessellating ‘Gherkin’ and Eiffel tower, but the changes in width and thickness tapering required are less dramatic, as can be seen in Fig. 6C and D for the ‘Gherkin’ and Eiffel tower, respectively – the shapes were relatively close to tessellating in any case.
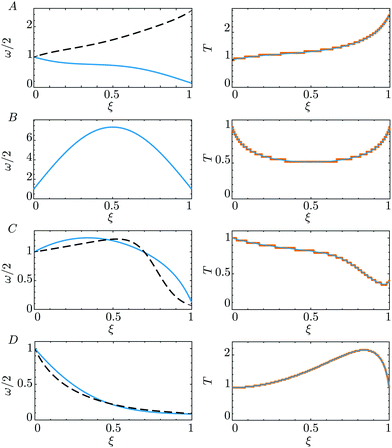 | ||
| Fig. 6 Width (left) and thickness (right) profiles required to obtain tessellated designs. In (A) and (B), we show the profiles determined by our analysis for the tessellated 3D structures of Fig. 5: (A) the cupola of St Thomas Church, Lymington and (B) a sphere. In (C) and (D) we show the profiles needed to create (C) the 'Gherkin' and (D) the Eiffel tower (though pictures of the tessellated structures are not shown in Fig. 5, for reasons of space). In each case, the left panel shows the normalized half-width profile, ω/2, for the tessellated design (solid curve) as well as for the non-tessellating, constant thickness, case (dashed curve); the right panel shows the normalized thickness profile, T, predicted by our theory (blue curve), as well as the discretization of this thickness profile used for 3D printing the samples (orange, stepped line). | ||
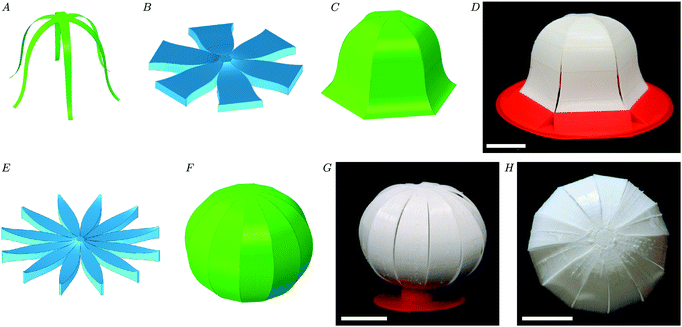
As a final example of the general strategy of designing tessellating and non-tessellating shapes, we turn to the classic example used to illustrate the strictures of Gauss' Theorema Egregium for elastic deformations: the impossibility of creating a flat map of the globe without distorting areas. Of course, our approach cannot circumvent this fundamental geometrical restriction. Nevertheless, our approach does allow us to design a cut shape that, when deformed out-of-plane, will form the arc of a circle (i.e. a line of longitude) and tessellate. The cut shape and thickness profile predicted by the theory are shown in Fig. 5E and 6B, together with FEA (Fig. 5F) and experimental realizations (Fig. 5G–H) of the resulting globe.
6 Conclusions
In this paper we have presented a model for the creation of three-dimensional shapes from a planar sheet by first removing material from the sheet in a precise way and then applying horizontal and/or vertical edge loads. The morphing strategy we presented was inspired by recent designs used in flexible electronics in which a central hub is connected to several slender spokes, each of which is tapered. Once deformed, the appearance of this arrangement of spokes around a hub is often reminiscent of a spider, and so might be referred to as a ‘spidermorph’. We studied how the tapering of the legs of a spidermorph should be chosen to produce particular desired shapes in the deformed configuration. The theoretical formulation we presented was based on the elastica equation, suitably modified to account for tapering. With this tapered elastica approach, we were able to show that arbitrary three-dimensional gross shapes could be designed by appropriately cutting a sheet of constant thickness, provided that the cross section of the desired 3D shape does not include multiple inflection points. However, this approach led to gross shapes with large gaps between deformed spokes. An alternative design goal, is to create deformed shapes that are tessellated. We have shown how cut patterns should be chosen to achieve this in sheets of uniform thickness. We further showed that designing tessellating shapes of a given gross shape is possible by tapering the sheet thickness in addition to the strip width. The geometrical nature of the elastica equation means that all of these design strategies are themselves geometrical: the Young's modulus of the material is immaterial for the required tapering, provided that the role of gravity can be neglected.We have demonstrated these design strategies with a series of examples motivated by well-known structures, the Gherkin (30 St Mary Axe, London) and the Eiffel Tower. One could also proceed analytically by considering specific functional forms, as in related previous work.40,41
Our analysis has focused on one particular design – the hub and spoke model – that can be scaled arbitrarily (though effects such as the structure's weight may need to be considered when designing structures of a particular scale, as discussed in Appendix B). Our analysis has neglected particular features of the hub-and-spoke design and has assumed that the elastica description accurately describes the deformation of each strip. This is generally expected to be the case for taperings that vary sufficiently slowly along the arc-length, but may not be valid, for example, for steep, or step-like, changes. Similarly, we have neglected the anti-clastic bending that may occur across each spoke if the thickness of the spoke is sufficiently large.47 We have also neglected the effect of deformations within the central hub region, assuming that it remains perfectly flat. Detailed FEA simulations48 show that, in fact, the hub may itself deform and, depending on its size and thickness, may modify the shape locally. We leave a detailed study of the importance of the hub, and how it should be modelled in the theoretical formulation we have presented here, for a future study.
The hub-and-spoke design could, in principle, be modified to achieve non-axisymmetric 3D structures, for example by making spokes of different lengths, which would represent a bridge to other approaches where independent elasticæ are used to generate non-axisymmetric shapes.40 A richer phenomenology may also be obtained by allowing curved spokes, which would twist upon buckling.49 Ultimately, however, we hope that the framework of the tapered elastica developed here might be implemented within more complicated kirigami designs that allow individual faces to bend, rather than remain rigid,33 or to motivate the study of grid shells50 with bending.
Conflicts of interest
There are no conflicts to declare.Appendix A: simulation details
Computational analyses were developed using the commercial finite element analysis software (ABAQUS) to simulate the deformation of both a single tapered elastica and multiple tapered elasticæ (spokes) connected to a central hub subject to either a compressive horizontal or vertical ‘poke’ load. In each case, 4-node shell elements (S4R) are used to represent the elastic strip(s), with refined meshes adopted to ensure accuracy. Each strip is modeled as a linear elastic material, with elastic modulus E = 119 GPa and Poisson' s ratio ν = 0.3. While these material parameters differ from those used experimentally, we note that the problem is essentially geometrical and so the tapering profile suggested by the inverse design procedure is dependent purely on the geometrical properties of the spokes, including its base width, w0, thickness, t0, and length, L. The mechanical properties of the material enter only to determine the magnitude of the loads required to deform a given structure, and are not, in any case, directly accessible experimentally.Most cases considered involve compressive loading; in these cases we used linear buckling analyses to determine the critical buckling strains and corresponding buckling modes of a 2D plate under compression, and used these results as initial geometric imperfections for post-buckling simulations.
Appendix B: experimental details
Materials
For experiments involving sheets with tapered width, but uniform thickness (as in Sections 2–4), Mylar sheets of thickness t0 = 0.25 mm were used. These sheets were cut to the desired tapered width profile using a laser cutter. This material and thickness were chosen so that the bending modulus B = EI0 is large enough to avoid gravity effects, but thin enough to remain within the framework of thin plate theory: for Mylar (E ∼ 5 GPa) strips to have length L ∼ 10 cm, as in the experiments presented here, whilst maintaining L ≳![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) g requires thicknesses t ≳ 100 μm, and so we use thicknesses larger than 150 μm, giving
g requires thicknesses t ≳ 100 μm, and so we use thicknesses larger than 150 μm, giving ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) g ≈ 10 cm ≳ L ≫ t. It should also be noted that the minimum width of the tapered strip within the narrow region must not be too small to avoid the possibility of plastic deformation in experiments.
g ≈ 10 cm ≳ L ≫ t. It should also be noted that the minimum width of the tapered strip within the narrow region must not be too small to avoid the possibility of plastic deformation in experiments.
For experiments involving tapered thickness profile (as in the tessellating designs of Section 5), sheets were 3-D printed to ensure that the desired thickness and width profiles were obtained. In these experiments, a flexible filament (Filaflex of hardness Shore 70, corresponding to E ≈ 5.5 MPa) was used as the printing material; this was printed with a thickness sufficiently large to have enough layers to faithfully reproduce the desired thickness profile (the z-resolution of the 3D printer is 0.06 mm), but thin enough to avoid significant anticlastic deformation when the resulting spokes were bent.47 Examples of the typical thickness profiles generated by printing are compared with the desired profiles in Fig. 6. (Fig. 6 also includes detailed plots of the tapering profiles required to generate tessellated ‘Gherkin’ and Eiffel Tower shapes, though these tessellated shapes are not shown in the paper.)
Compression
All samples (whether laser cut or 3D printed) were clamped to a solid stand designed to impose a given compression Δ and boundary condition, i.e. the angle at the base. These stands were 3D printed in hard plastic, namely polylactic acid (PLA, with Young's modulus ≃ 2 GPa). Clamping was achieved by printing a slot within the base into which additional material at the end of each spoke could be inserted, guaranteeing a particular edge inclination angle was achieved.Measurement
To obtain detailed profiles of the deformed shapes (as in, for example, Fig. 1) experiments were illuminated by a vertical laser line, aligned with a diameter of the flat shape. Side view pictures are taken to measure a profile in the central line of one of the N arms. The image resolution combined with sub-pixel detection of the laser line gives a vertical resolution of less than 0.3 mm.Appendix C: multiple equilibria for the eiffel tower
In the experimental realization of the Eiffel Tower discussed in the main text, Section 3.2, we used a central vertical pillar to impose the ‘poking’ force envisaged by the theory, as shown in Fig. 3C(v). This was included to show the potential utility of applying such vertical loads. However, our experiments also showed that the shape of the deformed structure remained very similar even if the vertical force is removed subsequently, see Fig. 7A. In this scenario, no significant vertical force can be acting on the lower edges, and so it seems that an Eiffel tower-like shape can also be obtained with the same cut pattern and horizontal, rather than vertical, applied loads. However, FEA simulations show that the cut pattern generated under the assumption of vertical loads would, if subject instead to horizontal forces, deform to an inter-penetrating shape (Fig. 7B).To rationalize the experimental observation, we hypothesize that the experimentally observed shape is stabilized by the spokes coming into contact with one another. This hypothesis is confirmed by a further FEA simulation in which a contact effect is added to avoid the inter-penetration of neighbouring spokes, thereby mimicking experiments as closely as possible. In this simulation, each spoke is clamped with the required angle at the base and then pushed up into place via the applied vertical poke force until the height at the centre reaches the required value. In the simulation, we then release the vertical load noting that the spokes fall very slightly, ultimately with self-contact between them occurring to form an equilibrium whose shape is visually indistinguishable from Fig. 3C(iv) (see Fig. 7C and D), even though in this state the clamps impose a horizontal, not vertical force on the spokes. In other words, contact effects ‘lock’ the structure in a shape that is very close to the target one. Whether this self-contact can be exploited in inverse designs is beyond the scope of the present paper.
Acknowledgements
The research leading to these results has received funding from the Royal Society through a Newton International Fellowship NIF\R1\180165 (ML), the European Research Council under the European Union's Horizon 2020 Programme/ERC Grant Agreement no. 637334 (DV) and the Leverhulme Trust through a Philip Leverhulme Prize (DV). We are grateful to J. Liu and Y. Yuan for discussions on FEA simulations.References
- T. Wallin, J. Pikul and R. Shepherd, Nat. Rev. Mater., 2018, 3, 84 CrossRef.
- A. Kotikian, C. McMahan, E. C. Davidson, J. M. Muhammad, R. D. Weeks, C. Daraio and J. A. Lewis, Sci. Robot., 2019, 4, eaax7044 CrossRef.
- A. Y. N. Sofla, D. M. Elzey and H. N. G. Wadley, Smart Mater. Struct., 2009, 18, 065012 CrossRef.
- A. Y. N. Sofla, S. A. Meguid, K. T. Tan and W. K. Yeo, Mater. Des., 2010, 31, 1284–1292 CrossRef CAS.
- A. Kirillova and L. Ionov, J. Mater. Chem. B, 2019, 7, 1597–1624 RSC.
- H. Fu, K. Nan, W. Bai, W. Huang, K. Bai, L. Lu, C. Zhou, Y. Liu, F. Liu and J. Wang, et al. , Nat. Mater., 2018, 17, 268–276 CrossRef CAS PubMed.
- B. Haghpanah, L. Salari-Sharif, P. Pourrajab, J. Hopkins and L. Valdevit, Adv. Mater., 2016, 28, 7915–7920 CrossRef CAS PubMed.
- C. Coulais, E. Teomy, K. De Reus, Y. Shokef and M. V. Hecke, Nature, 2016, 535, 529–532 CrossRef CAS PubMed.
- R. Guseinov, C. McMahan, J. Pérez, C. Daraio and B. Bickel, Nat. Commun., 2020, 11, 1–7 Search PubMed.
- L. D. Landau and E. M. Lifshitz, Theory of Elasticity, 1970 Search PubMed.
- C. F. Gauss, Disquisitiones generales circa superficies curvas, Typis Dieterichianis, 1828, vol. 1 Search PubMed.
- E. Couturier, J. Dumais, E. Cerda and E. Katifori, Soft Matter, 2013, 9, 8359–8367 RSC.
- E. D. Demaine, M. L. Demaine, J. Iacono and S. Langerman, Comput. Geom., 2009, 42, 748–757 CrossRef.
- J. D. Paulsen, Annu. Rev. Condens. Matter Phys., 2019, 10, 431–450 CrossRef CAS.
- Y.-K. Lee, Z. Xi, Y.-J. Lee, Y.-H. Kim, Y. Hao, H. Choi, M.-G. Lee, Y.-C. Joo, C. Kim and J.-M. Lien, et al. , Sci. Adv., 2020, 6, eaax6212 CrossRef PubMed.
- J. Pikul, S. Li, H. Bai, R. Hanlon, I. Cohen and R. Shepherd, Science, 2017, 358, 210–214 CrossRef CAS PubMed.
- E. Siéfert, E. Reyssat, J. Bico and B. Roman, Nat. Mater., 2019, 18, 24–28 CrossRef PubMed.
- H. Aharoni, Y. Xia, X. Zhang, R. D. Kamien and S. Yang, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 7206–7211 CrossRef CAS PubMed.
- J. W. Boley, W. M. van Rees, C. Lissandrello, M. N. Horenstein, R. L. Truby, A. Kotikian, J. A. Lewis and L. Mahadevan, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 20856–20862 CrossRef CAS PubMed.
- H. Finkelmann, E. Nishikawa, G. G. Pereira and M. Warner, Phys. Rev. Lett., 2001, 87, 015501 CrossRef CAS PubMed.
- M. Camacho-Lopez, H. Finkelmann, P. Palffy-Muhoray and M. Shelley, Nat. Mater., 2004, 3, 307–310 CrossRef CAS PubMed.
- A. Nojoomi, H. Arslan, K. Lee and K. Yum, Nat. Commun., 2018, 9, 1–11 CrossRef CAS PubMed.
- A. S. Gladman, E. A. Matsumoto, R. G. Nuzzo, L. Mahadevan and J. A. Lewis, Nat. Mater., 2016, 15, 413–418 CrossRef PubMed.
- B. A. Kowalski, C. Mostajeran, N. P. Godman, M. Warner and T. J. White, Phys. Rev. E, 2018, 97, 012504 CrossRef CAS PubMed.
- M. Warner, Annu. Rev. Condens. Matter Phys., 2020, 11, 125–145 CrossRef CAS.
- Y. Zhang, F. Zhang, Z. Yan, Q. Ma, X. Li, Y. Huang and J. A. Rogers, Nat. Rev. Mater., 2017, 2, 1–17 CAS.
- C. Modes and M. Warner, Phys. Today, 2016, 69, 32 CrossRef.
- D. P. Holmes, Curr. Opin. Colloid Interface Sci., 2019, 40, 118–137 CrossRef CAS.
- D. Vella, Nat. Rev. Phys., 2019, 1, 425–436 CrossRef.
- R. M. Neville, F. Scarpa and A. Pirrera, Sci. Rep., 2016, 6, 31067 CrossRef CAS PubMed.
- F. Wang, X. Guo, J. Xu, Y. Zhang and C. Chen, J. Appl. Mech., 2017, 84, 061007 CrossRef.
- S. J. Callens and A. A. Zadpoor, Mater. Today, 2018, 21, 241–264 CrossRef.
- G. P. T. Choi, L. H. Dudte and L. Mahadevan, Nat. Mater., 2019, 18, 999–1004 CrossRef CAS PubMed.
- Y. Zhang, Z. Yan, K. Nan, D. Xiao, Y. Liu, H. Luan, H. Fu, X. Wang, Q. Yang and J. Wang, et al. , Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 11757–11764 CrossRef CAS PubMed.
- W. Lee, Y. Liu, Y. Lee, B. K. Sharma, S. M. Shinde, S. D. Kim, K. Nan, Z. Yan, M. Han, Y. Huang, Y. Zhang, J.-H. Ahn and J. A. Rogers, Nat. Commun., 2018, 9, 1417 CrossRef PubMed.
- F. Liu, Y. Chen, H. Song, F. Zhang, Z. Fan, Y. Liu, X. Feng, J. A. Rogers, Y. Huang and Y. Zhang, Small, 2019, 15, 1804055 CrossRef PubMed.
- I. Griniasty, H. Aharoni and E. Efrati, Phys. Rev. Lett., 2019, 123, 127801 CrossRef CAS PubMed.
- Z. Xu, Z. Fan, H. Fu, Y. Liu, Y. Zi, Y. Huang and Y. Zhang, Phys. Rev. Appl., 2019, 11, 054053 CrossRef CAS.
- Z. Xu, Z. Fan, Y. Zi, Y. Zhang and Y. Huang, J. Appl. Mech., 2020, 87, 031004 CrossRef.
- Z. Fan, Y. Yang, F. Zhang, Z. Xu, H. Zhao, T. Wang, H. Song, Y. Huang, J. A. Rogers and Y. Zhang, Adv. Mater., 2020, 32, 1908424 CrossRef CAS PubMed.
- I. Elishakoff, Proc. R. Soc. A, 2000, 456, 2409–2417 Search PubMed.
- B. K. Lee and S. J. Oh, Int. J. Solids Struct., 2000, 37, 2507–2518 CrossRef.
- C. A. Stuart, C. R. Acad. Sci. I, 2000, 331, 417–421 CrossRef.
- P. Howell, G. Kozyreff and J. Ockendon, Applied Solid Mechanics, Cambridge University Press, 2008 Search PubMed.
- W. A. Oldfather, C. A. Ellis and D. M. Brown, Isis, 1933, 20, 72–160 CrossRef.
- R. Levien, The Elastica: A Mathematical History, EECS Department, University of California, Berkeley, Technical Report UCB/EECS-2008-103, 2008 Search PubMed.
- D. G. Ashwell, Aeronaut. J., 1950, 54, 708–715 CrossRef.
- L. Domino, M. Liu and D. Vella, 2020, in Preparation.
- H. Zhao, K. Li, M. Han, F. Zhu, A. Vázquez-Guardado, P. Guo, Z. Xie, Y. Park, L. Chen, X. Wang, H. Luan, Y. Yang, H. Wang, C. Liang, Y. Xue, R. D. Schaller, D. Chanda, Y. Huang, Y. Zhang and J. A. Rogers, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 13239–13248 CrossRef CAS PubMed.
- C. Baek, A. O. Sageman-Furnas, M. K. Jawed and P. M. Reis, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 75–80 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2020 |