Flip-flop asymmetry of cholesterol in model membranes induced by thermal gradients

Abstract

Lipid asymmetry is a crucial property of biological membranes and significantly influences their physical and mechanical properties. It is responsible for maintaining different chemical environments on the external and internal surfaces of cells and organelles and plays a vital role in many biological processes such as cell signalling and budding. In this work we show, using non-equilibrium molecular dynamics (NEMD) simulations, that thermal fields can induce lipid asymmetry in biological membranes. We focus our investigation on cholesterol, an abundant lipid in the plasma membrane, with a rapid flip-flop rate, significantly influencing membrane properties. We demonstrate that thermal fields induce membrane asymmetry with cholesterol showing thermophobic behaviour and therefore accumulating on the cold side of the membrane. This work highlights a possible experimental route to preparing and controlling asymmetry in synthetic membranes.

---

1 Introduction

Lipid compositional asymmetry is an important feature of many biological membranes and plays a vital role in many membrane functions.¹ The presence and degree of asymmetry directly influences various other membrane properties such as the membrane potential,² mechanical moduli,³ curvature,⁴ fluidity and phase behaviour.⁵ In turn, in biological membranes, these properties are vital for many of the functions of the membrane, including lateral organisation, stabilisation of membrane proteins, budding and fusion of membrane vesicles and cell signalling. The ability of cells to tune asymmetry is also important to adapt to external changes or mark specific cells, for example during apoptotic macrophage degradation.⁶

Asymmetry is maintained by the translocation, or “flip-flop”, of lipids from one leaflet to the other, through the membrane interior. For many lipid species, the polar, strongly hydrated head group means that spontaneous flip-flop occurs on timescales of the order of hours to days and so, in biological membranes, flip-flop is often mediated by proteins which speed up the process and control the degree of compositional asymmetry.⁷ However, for smaller, less polar molecules, such as cholesterol, flip-flop rates are considerably faster, on the order of microseconds and longer (milliseconds),^8,9 allowing cholesterol to rapidly move spontaneously between leaflets, adjusting the distribution according to the chemical potential difference across the bilayer.

Cholesterol makes up roughly 30 mol% of the lipids in mammalian plasma membranes and has a significant impact on the membrane behaviour including fluidizing the membrane, binding and stabilising membrane proteins and regulating the lateral organisation of the membrane. Despite the importance of cholesterol, the degree of cholesterol asymmetry in membranes has been an open question,¹ with recent work suggesting that cholesterol is concentrated in the inner leaflet due to negative curvature, in spite of the higher concentration of saturated lipids, usually favoured by cholesterol, in the outer leaflet.¹⁰ However, the fast, spontaneous flip-flop of cholesterol suggests that this asymmetry is likely to be strongly sensitive to differences in other membrane properties between the inner and outer leaflet and to differences in the external environment on either side of the membrane.

The ability of external, transmembrane gradients to induce membrane asymmetry has already been demonstrated. For example, transmembrane pH gradients have been shown to induce asymmetry in membranes containing lipids with different acidities.^11,12 In this work we investigate the use of thermal fields to drive asymmetry of cholesterol across model membranes.

Transient thermal gradients can occur naturally within biological cells and organelles due to localised chemical processes and the resulting heat released or absorbed. For example, metabolism occurring within mitochondria releases heat which can give rise to a thermal gradient across the mitochondrial membrane. Indeed, thermal gradients and the corresponding inhomogeneous temperature distribution have been observed experimentally within cells.¹³ Experiments using fluorescence lifetime imaging microscopy reported significant differences in temperature between the centrosome and the cytoplasm (∼0.75 degrees).¹⁴

Temperature gradients are also produced artificially by thermal therapies in which nanoparticles are injected and targeted to a specific part of the body where they are then heated to kill cancerous cells.^15–17 Previous experimental work has shown that thermal gradients do influence biological processes including cell patterning during embryo development¹⁸ and migration of bacteria.¹⁹ The presence of inhomogeneous temperature distributions and thermal gradients within cells and organelles raises the question of what effect these gradients have on the membrane composition.

Computational studies have shown that biological membranes feature a low thermal conductivity in the aliphatic region,^20,21 similar to the thermal conductivity of hydrocarbon fluids. For a given heat flux, these low thermal conductivities will lead to larger thermal gradients and therefore larger thermophoretic responses. We expect that such gradients can impart thermodiffusion in molecules embedded in the bilayer. This coupling between thermal gradients and diffusion is also known as the Soret effect and the strength of the coupling for different molecules and in different systems can be quantified by calculating the Soret coefficient. To test our hypothesis we have performed non-equilibrium molecular dynamics (NEMD) simulations on a membrane containing a 1 : 1 mixture of DPPC (1,2-dipalmitoyl-sn-glycero-3-phosphocholine) and cholesterol. At this composition, the hydrated lipid mixture forms a liquid-ordered phase, characterised by a highly-ordered conformation of the DPPC hydrocarbon chains, but with a liquid-like in-plane translational ordering of both the DPPC and the cholesterol.^22–25 Experimental studies reported a phase diagram of cholesterol–DPPC mixtures,²² hinting the existence of a critical point. At high temperatures (>320 K) there would be no coexistence between liquid crystal and liquid ordered phases. Molecular dynamics simulations are widely used to study membrane properties including lipid and cholesterol flip-flop,^26,27 helping to demonstrate the influence of different lipid compositions and to uncover the free-energy landscape. We show that the application of a thermal gradient causes compositional asymmetry, revealing the thermophobic behaviour of cholesterol as it preferentially partitions into the cold leaflet and hence, the ability of a thermal gradient to induce asymmetry in both the structure of the membrane and the flip-flop pathway is demonstrated.

2 Methods

2.1 Simulation setup

The initial system configuration for this work was taken from a previous, equilibrated NpT simulation of a single membrane at a temperature of 300 K and a pressure of 1 bar. This membrane contained an equal mixture of 256 molecules of DPPC (1,2-dipalmitoyl-sn-glycero-3-phosphocholine) and 256 molecules of cholesterol and was solvated by ∼15 500 water molecules, giving a water per lipid ‘complex’ (DPPC plus cholesterol) ratio of ∼30.3. For this work, a specific initial configuration was chosen in which the DPPC and cholesterol leaflet compositions were symmetric and 2 cholesterol molecules were situated lying horizontally between the two leaflets (see left hand side of Fig. 1), roughly half the simulation box apart in the xy plane (parallel to the membrane surface). This single membrane configuration was duplicated in the z direction to produce a simulation box containing two separate, independent membranes (see right hand side of Fig. 1).

Fig. 1 (Top-left) Structures of the united atom cholesterol (green) and DPPC (red) molecules. The head group atoms (named “O28” (cholesterol) and “PO4” (DPPC)) and the molecular axis of cholesterol used to calculate the tilt angle are highlighted. (Right) Initial simulation box configuration for boundary-driven NEMD simulations. The position-restrained water molecules which form the hot (H) and cold (C) thermostats are coloured red and light blue respectively. Other water molecules are coloured grey, DPPC molecules are drawn in blue and cholesterol are green. The zoomed in view on the left shows one of the two cholesterol molecules in each membrane which was initially positioned at the bilayer midplane lying horizontally between the two leaflets.

To generate the thermal gradient, we used the boundary driven approach (see discussion in ref. 28) in which molecules at specific regions of the simulation box are used as thermostats. In our system, the thermostat regions were placed in the middle of the water layers. 50% of the water molecules in these thermostat regions were restrained using weak position restraints (k = 100 kJ mol⁻¹) and thermostated using the velocity rescaling algorithm²⁹ with coupling constant τ = 0.2 ps. None of the other water molecules or the DPPC or cholesterol molecules were thermostated. The restrained molecules in one thermostat region were thermostated at 300 K, forming the “cold” thermostat, while molecules in the other, “hot”, thermostat region were heated to 350 K, 400 K or 450 K to produce thermal gradients of different strength, labelled TG1, TG2 and TG3 respectively. As shown in the results, the temperatures in the thermostat regions were lower than the ones set in the thermostat, showing some degree of thermal slip. A set of control simulations in which both regions were thermostated at 300 K were also run.

The simulations were performed using GROMACS-5.1³⁰ with the leap-frog integrator and a timestep of 4 fs. The cholesterol and DPPC molecules were modelled using the GROMOS 43A1-S3 united atom forcefield³¹ and the SPC/E model was used for water.³² All bonds were constrained using the LINCS algorithm.³³ Electrostatic interactions were treated using the particle-mesh Ewald method.³⁴ Initially 50 separate 50 ns simulations were run for each temperature gradient starting from the same initial configuration. One simulation at the highest temperature gradient was then extended to 7 μs to study the long time behaviour.

2.2 Analysis

To calculate the resulting temperature gradient within the simulation box, the box was divided up into slices of width δz = 0.03 nm, parallel to the xy plane. The temperature within each slice, s, is given by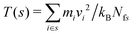 , where m_i and v_i are the mass and velocity of particle i respectively, and N_fs is the total number of degrees of freedom for all particles in slice s, taking into account the LINCS bond constraints.

To assign cholesterol molecules to one or other of the membrane leaflets, the distribution of all cholesterol oxygen atoms along the z axis of the simulation box was plotted (see ESI†). The peaks in this distribution were used to define the positions of the membrane leaflets and cholesterol molecules were assigned to the leaflet corresponding to the closest peak maximum. There was no DPPC flip-flop observed in any simulation so the assignment of DPPC molecules to leaflets did not change. The cholesterol composition of each leaflet was represented as the fractional cholesterol concentration ([CHOL]), defined as x_CHOL = [CHOL]/([DPPC] + [CHOL]), where the brackets denote the number of molecules of each type in each leaflet.

We also calculated the tilt of cholesterol molecules, defined as the angle between the rigid ring system, represented by the vector between the carbon atoms at either end of the ring structure (shown by the arrow in Fig. 1-top-left), and the z axis.

A Voronoi tessellation using the x and y coordinates of the lipid and cholesterol head groups, defined by the positions of the cholesterol oxygen and DPPC phosphate groups, was used to calculate the average area per lipid for the DPPC and cholesterol molecules in each leaflet. The Voronoi tessellation was computed using the Qhull algorithm.³⁵

The lipid tail order parameter, S_z, was used to quantify the degree of order in the DPPC hydrocarbon tails and was defined as the C–H bond order parameter, S_C–H, averaged over all tail carbon atoms in both chains for all DPPC molecules in a given leaflet. The C–H bond order parameter is defined as S_C–H = −〈3 cos²θ − 1〉/2, where θ is the angle between the C–H bond and the membrane normal (the z axis).

3 Results and discussion

3.1 Thermal gradients induce asymmetry

The temperature profiles across the simulation box are plotted in Fig. 2, overlaid over a simulation snapshot. The temperature gradients were established quickly at the start of the simulation, within the first nanosecond, and remained stable throughout the simulation.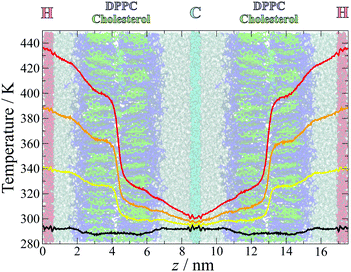

Fig. 2 Measured temperature distributions for simulations with temperature gradients TG1 (yellow), TG2 (orange), TG3 (red) and the control simulations (black). The temperatures were calculated in slices of width δt = 0.03 nm and averaged over the last 49 ns of all 50 separate simulations at each gradient, with the first 1 ns discarded to ensure that the gradient had been established and stabilised. The gradients are overlaid over a snapshot from the simulation, coloured as in Fig. 1.

Away from the thermostat regions, the temperature gradients are smooth and approximately linear, but with different slopes within different sections of the simulation box. Large slopes are observed at the water–lipid and lipid–lipid (in the middle of the bilayer) interfaces, which arise from interfacial thermal resistance. The largest difference in temperature occurs between the two leaflets, highlighting the lack of leaflet interdigitation which results in poor transfer of heat across this interface. The water–membrane interface at the hot leaflet, which is less sharply defined than the leaflet–leaflet interface due to the roughness of the membrane surface and penetration of water into the head group region, is also associated with a significant change in temperature, albeit smaller and more gradual than between the membrane leaflets.

To quantify the emergence of asymmetry in cholesterol concentration, the number of flip-flop and half-flip events were recorded. A summary of these data is reported in Table 1. Half-flips refer to the movement of the cholesterol molecules which were initially positioned lying horizontally in the middle of the bilayer (2 per membrane, see Fig. 1) to the hot (H) or cold (C) leaflet. The free energy barrier associated with the half-flip event is significantly lower than the barrier for the full flip-flop process²⁷ and therefore the movement of these cholesterols can be observed even in these relatively short 50 ns simulations, which can then be used to assess the effect of the temperature gradient.

Table 1 Total number of half-flip events (from the middle (M) of the bilayer to the hot (H) or cold (C) leaflet) and complete flip-flop events (between the hot (H) and cold (C) leaflets) in each direction from 50 separate 50 ns simulations at each temperature gradient. The percentage of half-flips which occur in a given direction is given in brackets

Thermal gradient	Half-flips		Complete flip-flops
	M → C	M → H	H → C	C → H
Control	59 (47%)	66 (53%)	0	0
TG1	84 (64%)	48 (36%)	1	0
TG2	119 (74%)	41 (26%)	34	0
TG3	119 (78%)	34 (22%)	134	0

---

The asymmetry in the number of half-flips increases with the strength of the temperature gradient, from a roughly symmetric distribution in the control simulations, to significant asymmetry for the largest gradient, with cholesterol showing a significant preference for the colder region.

The fractional cholesterol composition of each leaflet over time is plotted in Fig. 3. The development of asymmetry in response to the temperature gradient can be modelled by:³⁶

x_l(t) = (1 − e^{−(t−t₀)/τ})Δx_l,final + 1/2 (1)

where x_l(t) is the fractional cholesterol concentration at time, t, in leaflet, l ∈ {H(hot),C(cold)}, Δx_l,final is the final change in fractional cholesterol concentration in leaflet l, and τ is the time constant for the flip-flop process, τ = (k_H→C + k_C→H)⁻¹, where k are rate constants. The 1/2 term is the initial cholesterol concentration of each leaflet (x_l,initial) and indicates that the membrane is symmetric in the initial configuration.

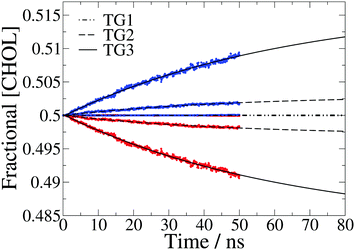Fig. 3 Fractional cholesterol concentration ([CHOL]) in the hot (red) and cold (blue) leaflet for each temperature gradient, averaged over 50 separate 50 ns simulations. The data are fit to eqn (1) and the fits plotted with dot-dashed, dashed and solid black lines for the three temperature gradients, TG1, TG2 and TG3, respectively. There is very little asymmetry for the lowest gradient so the data points for the hot and cold leaflets are on top of each other.

At the lowest temperature gradient (TG1) investigated we do not observe flip-flop events in the simulation timescale, hence these membranes remain symmetric. However, the larger gradients both show a gradual increase in asymmetry over time, with the asymmetry for the largest gradient in particular still increasing at 50 ns. We find that the time dependence of the concentration can be accurately modelled with eqn (1).

3.2 Steady-state behaviour

3.2.1 Bilayer structure. We have shown above that a thermal gradient across the membrane induces asymmetry in the cholesterol composition of the membrane leaflets. The time dependence of the fraction of cholesterol is clearly in a transient regime (see Fig. 3). To reach the stationary state we extended the trajectory corresponding to the highest thermal gradient, TG3, to 7 μs. We show in Fig. 4-top the fraction of cholesterol molecules in the hot and cold leaflets during this simulation. The composition asymmetry increases gradually from the initially symmetric membrane and reaches a constant value around 4 μs, at a fractional composition of 0.456 and 0.544 in the hot and cold leaflets respectively. This equates to a difference of 22 cholesterol molecules per membrane between the compositions of the hot and cold leaflets. This final asymmetry is also larger than that predicted from the fits to eqn (1) using the data from the 50 ns simulations (see Fig. 3). As the asymmetry develops, it causes the structures of the membrane leaflets to change, affecting the affinity of cholesterol for one or other leaflet. This explains why the final composition cannot be predicted using the transient part of the trajectory, corresponding to the first 50 ns. 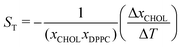To quantify the coupling between the thermal gradient and cholesterol flip-flop asymmetry, we calculate the Soret coefficient (S_T), according to, ,^37,38 where x_CHOL and x_DPPC are the number fractions of the cholesterol and lipid in the mixtures, respectively. Using the stationary fraction of cholesterol (Δx_CHOL = x_C,final − x_H,final) and the thermal gradient (ΔT = 150 K.) we estimate that the cholesterol partitioning is equivalent to a Soret coefficient of 0.0023 K⁻¹. The Soret effect was firstly observed in solutions of alkali halide salts, and the Soret coefficient obtained here is of the same order as the one observed in these salts.³⁸ We note that thermal gradients of the same magnitude as those employed in this article were used in previous studies.²⁸ This work showed that the response of the system is within the linear regime.

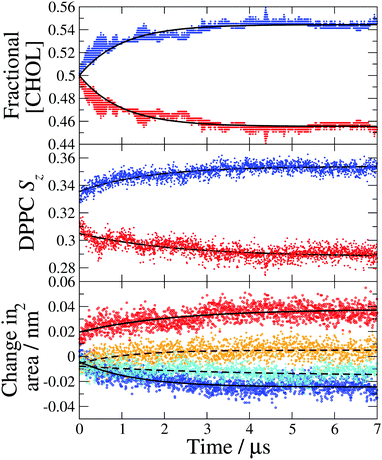Fig. 4 Leaflet compositions and structural properties calculated from a single 7 μs simulation with the largest temperature gradient (TG3). (Top) Fractional cholesterol concentration ([CHOL]) in the hot (red) and cold (blue) leaflets, the data are fit to eqn (1) (solid lines). (Middle) DPPC average chain order parameter (S_z) in the hot (red) and cold (blue) leaflets. (Bottom) Change in the average area per DPPC (solid lines) in the hot (red) and cold (blue) leaflets and the average area per cholesterol (dashed lines) in the hot (orange) and cold (cyan) leaflets. The reference areas per lipid obtained with the Voronoi method discussed in the text are A_DPPC = 0.425 nm² and A_CHOL = 0.418 nm².

We show in Fig. 4-middle and bottom, the evolution of the average DPPC tail order parameter and the change in the area per lipid, respectively, over the course of the simulation. Both of these properties for the hot and cold bilayers change with time reaching the stationary values at roughly 4 μs, the same time as the fractional cholesterol concentration. We find a significant change in the order parameter and area per lipid before a noticeable cholesterol asymmetry is achieved. These changes at the beginning of the non-equilibrium simulation reflect purely the temperature dependence of the order parameter and area per lipid. Specifically, the lipid tails become more ordered at lower temperatures and consequently the cold leaflet immediately becomes more ordered than the hot one, once the temperature gradient has been applied. The temperature gradient is established very quickly, within the first 1 ns of the simulation. This indicates that the trend in the order parameters at long times, which mirrors the increase in cholesterol asymmetry, is due to the changes in cholesterol concentration and the concomitant impact of cholesterol on the ordering of the hot and cold leaflets. The rigid, planar structure of cholesterol causes adjacent lipid tails to become more ordered to improve packing and the increase in cholesterol concentration in the cold leaflet causes an increase in the DPPC order parameter, with the opposite occurring in the hot leaflet. The changes to the ordering of the DPPC hydrocarbon tails as the asymmetry increases may further drive higher asymmetry as it has been shown that cholesterol favours membranes with more ordered lipid tails.²⁷

The change in the average area per DPPC and area per cholesterol (see Fig. 4 bottom) is a direct result of the asymmetric cholesterol concentration. The membrane remains planar, with the same surface area, throughout the simulation and there is no DPPC flip-flop, so the change in area per molecule is due to the change in the number of cholesterol molecules in each leaflet. The increase of cholesterol molecules in the cold leaflet is almost entirely accommodated for by a reduction in the area per DPPC, which occurs as the lipid tails become more ordered and closer to an all trans conformation. In the hot leaflet the disorder of the lipid tails increases the cross-sectional area of the DPPC molecules. The small change in the area per cholesterol is due to an increase in cholesterol tilt angle in the hot leaflet which increases the footprint of cholesterol molecules parallel to the membrane surface (see Fig. 5 and discussion below). The membrane thickness remains approximately constant over the course of the simulation, suggesting that the increase in leaflet thickness associated with the ordering effect of cholesterol in the cold leaflet is compensated for by the disordering of lipid chains in the hot leaflet.

Fig. 5 (a) Heat map of the negative logarithm of the population (−ln(P)) of different cholesterol configurations, defined by cholesterol head group position parallel to the z axis and molecular tilt angle (θ), visited during the steady-state portion of the simulation (from 4 μs) and sampled every 80 ns. Alongside the heat map, projections along the z and θ axes are shown and the orientation of the z axis with respect to the hot and cold thermostats is demonstrated by the red and blue bars, respectively, in the projection along z. (b) Transition matrix showing the number of transitions between different states during the steady-state portion of the simulation as a percentage of the total number of transitions. States are numbered according to the schematic in (c). (c) Schematic showing the five most populated states, arranged to mirror the positions of the corresponding states in (a) to ease comparison. The water–membrane interface of the hot and cold leaflets are illustrated by the red and blue lines, respectively, while the cholesterol head group is drawn in green and the hydrocarbon tail in black. The transition probabilities are shown next to the arrows linking different states and the size of the arrow is proportional to the logarithm of the transition probability. The transition probabilities are dimensionless, 1 referring to 100% probability.

It has been shown that cholesterol has a higher preference for membranes containing saturated lipids, and therefore more ordered bilayer structures.²⁷ In our simulations, as more cholesterol flips to the cold leaflet and the DPPC chain order increases, the affinity of cholesterol for this leaflet will also increase driving more flip-flop in this direction and further increasing the asymmetry. The increasing difference in affinity of each leaflet for cholesterol over the simulation explains why the short 50 ns simulations underestimate the final, steady-state asymmetry. In our simulations the steady-state is reached when the difference in cholesterol affinity between the two membrane leaflets is balanced by the difference in lateral pressure due to the difference in the number of molecules between the more crowded, cholesterol enriched cold leaflet and the cholesterol depleted hot leaflet. In experiments, other factors such as lipid flip-flop, compositional asymmetry of other membrane components and membrane bending or deformation are also likely to influence the response to the temperature gradient and the final steady-state asymmetry.

3.2.2 Flip-flop pathway and free energy landscape. Finally we analyse the free energy pathway for cholesterol flip-flop. This was obtained from the long (7 μs) simulation at the highest thermal gradient (TG3) by analysing the final 3 μs, corresponding to the stationary state.

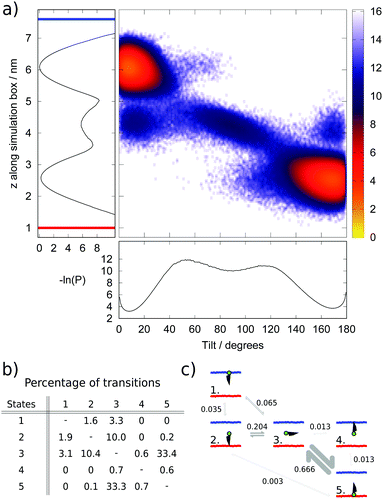
We chose as order parameters, the z coordinate of the hydroxyl group in the head group of cholesterol and the tilt angle (θ) of cholesterol with respect to the bilayer normal. We show in (Fig. 5a) a heat map illustrating the populations (P) of different tilt and z values, plotted as the negative logarithm (−ln(P)), alongside projections along the z and θ axes. Within the local equilibrium hypothesis, this parameter could be considered analogous to a free energy for an equilibrium system, however in this case the units, which are proportional to k_BT, will change in the z direction according to the local temperature profile.

The analysis of the data presented in Fig. 5a reveals the existence of five distinct populated states, illustrated and labelled in the schematic in Fig. 5c. The two most common states (labelled 1 and 5) correspond to the normal position of cholesterol within a membrane, with the cholesterol approximately aligned with the membrane normal and the hydroxyl group at, or just beneath, the membrane–water interface. The average tilt angle for these cholesterol molecules is 14° and 10° in the hot and cold leaflets respectively. This result is within the range found in previous atomistic³⁹ and coarse-grained²⁵ simulations, and close to the values reported in experimental studies.⁴⁰ The larger average tilt angle and wider distribution (denoting larger orientational freedom) observed in the hot leaflet (state 5) is connected to the less ordered structure of the hot leaflet.

The next most populated state (state 3) corresponds to cholesterol lying horizontally in the space between the two leaflets and represents a metastable intermediate state in the flip-flop pathway. This result agrees with the observation of metastable states both in equilibrium simulations²⁷ and experiments.⁴¹ Lastly, the final two states (states 2 and 4) correspond to configurations with cholesterol upside-down within a leaflet, with the hydroxyl group between the two leaflets of the membrane. This state is more common in the hot leaflet (state 2).

The numbers of transitions between these states were counted during the steady-state portion of the simulation (from 4 μs) and are shown in (Fig. 5b) as a percentage of the total number of transitions. The transition matrix is approximately symmetric as expected within a steady-state regime. Transitions between the hot leaflet and the middle of the bilayer (states 5 and 3) are the most common due to the higher temperature of this region of the simulation box, which enables more cholesterol molecules to surmount the energy barrier to reach the middle of the bilayer, and also the less ordered structure of the hot leaflet, which means cholesterol can rotate more easily during this transition.

Our results indicate that the flip-flop step corresponding to the transition of cholesterol from the middle of the membrane to the cold leaflet can occur in one step, with cholesterol simultaneously rotating and inserting into the cold leaflet (from state 3 to 1). However, we also find evidence for cholesterol reinserting into the hot leaflet, with the hydroxyl group in the centre of the bilayer. With the cholesterol in the right orientation for the cold leaflet, the cholesterol can move readily to the cold leaflet (from state 2 to 1). The thermal gradient means that transitions to and from the hot leaflet are dominated by transitions between states 3 and 5, while the equivalent pathway in the cold leaflet (between states 1 and 3) is less prevalent and the alternative route via state 2 also takes place. The presence of the thermal gradient and the resulting change in the membrane properties does therefore change the flip-flop pathway.

4 Conclusions

The presence of a temperature gradient perpendicular to the surface of a lipid membrane can induce asymmetry in cholesterol flip-flop resulting in an asymmetric cholesterol distribution between the membrane leaflets.

Cholesterol is found to be thermophobic, accumulating in the colder leaflet of the membrane due to its greater affinity for lipids with more ordered hydrocarbon tails. As the colder leaflet becomes enriched in cholesterol the ordering effect of the cholesterol further increases the lipid hydrocarbon chain order in this leaflet, with the opposite occurring in the cholesterol depleted hot leaflet. This further enhances the difference in lipid chain order between the two leaflets and increases the affinity of cholesterol for the cold leaflet over the hot leaflet, further driving asymmetry. The simulations performed here do not include DPPC flip-flop, however this would take place over a significantly longer timescale due to the much higher energy barrier associated with lipid translocation.

The average thermal gradients used in this work are between ∼ 5 and 15 K nm⁻¹, higher than those estimated in biological processes and those produced artificially in microfluidics devices, while close to gradients that can be achieved using plasmonic devices. The large gradients used here are necessary to observe the translocation of cholesterol in the simulation timescales (∼μs). Even with these large thermal gradients and the high temperatures of the hot thermostat, the membranes remained intact and were not significantly disrupted, showing only small structural changes. Therefore based on this lack of significant structural changes and existing number of simulations with similar thermal gradients, for which a linear response was observed, we expect that the behaviour described here, and the Soret coefficient, 0.0023 K⁻¹, should be representative of the behaviour at lower temperatures and smaller thermal gradients.

The thermal gradients may also drive lipid flip-flop and possibly membrane curvature. It is known that cholesterol has a higher affinity for the curvature of the inner leaflet of the plasma membrane¹⁰ and also that at higher temperatures phospholipids have a more negative curvature due to the disordering of the hydrocarbon tails which increases the average cross-sectional area of the aliphatic regions relative to the area of the head group. Therefore, we expect that thermal gradients might induce membrane curvature which in turn could also influence cholesterol asymmetry. A different configuration of thermostats to the one considered here might provide a route to investigate thermally induced curvature effects. This represents an important challenge for future simulation and experimental studies.

The response of real biological membranes to temperature gradients will be complicated by the large number of different molecules present, each with a different thermophilicity and varying ability to move in response to the gradient. The temperature sensitivity of flipase, flopase and scamblase enzymes will also influence asymmetry. Different compositions of cholesterol are expected to have an impact on the Soret coefficeint. However, considering the abundance of cholesterol in mammalian cell membranes and its rapid flip-flop rate, orders of magnitude faster than lipid flip-flop,⁴² we expect that the effect discussed in this work is likely to play a role in the response of biological membranes to thermal gradients.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge the EPSRC for grants EP/J003859/1 and EP/J017566, for a PhD Studentship to Imperial College London for JWC, and the Leverhulme Trust for grant RPG-2018-384. We thank Imperial College High Performance Computing Service for providing computational resources. MAG thanks Ayuda Juan de la Cierva-Incorporacion (IJCI-2016-27497) from Ministerio de Ciencia e Innovacion (Spain).

References

1. G. van Meer, D. D. R. Voelker and G. W. G. Feigenson, Nat. Rev. Mol. Cell Biol., 2008, 9, 112–124.
2. A. Wiese, J. O. Reiners, K. Brandenburg, K. Kawahara, U. Zähringer and U. Seydel, Biophys. J., 1996, 70, 321–329.
3. Y. Elani, S. Purushothaman, P. J. Booth, J. M. Seddon, N. J. Brooks, R. V. Law and O. Ces, Chem. Commun., 2015, 51, 6976–6979.
4. I. R. Cooke and M. Deserno, Biophys. J., 2006, 91, 487–495.
5. P. Williamson, J. Bateman, K. Kozarsky, K. Mattocks, N. Hermanowicz, H. R. Choe and R. A. Schlegel, Cell, 1982, 30, 725–733.
6. S. J. Martin, C. P. Reutelingsperger, A. J. McGahon, J. A. Rader, R. C. van Schie, D. M. LaFace and D. R. Green, J. Exp. Med., 1995, 182, 1545–1556.
7. F. J. Sharom, IUBMB Life, 2011, 63, 736–746.
8. S. Jo, H. Rui, J. B. Lim, J. B. Klauda and W. Im, J. Phys. Chem. B, 2010, 114, 13342–13348.
9. R.-X. Gu, S. Baoukina and D. P. Tieleman, J. Chem. Theory Comput., 2019, 15, 2064–2070.
10. H. Giang and M. Schick, Chem. Phys. Lipids, 2016, 199, 35–38.
11. M. J. Hope, T. E. Redelmeier, K. F. Wong, W. Rodrigueza and P. R. Cullis, Biochemistry, 1989, 28, 4181–4187.
12. P. R. Cullis, M. J. Hope, M. B. Bally, T. D. Madden, L. D. Mayer and D. B. Fenske, Biochim. Biophys. Acta, 1997, 1331, 187–211.
13. J. M. Yang, H. Yang and L. Lin, ACS Nano, 2011, 5, 5067–5071.
14. K. Okabe, N. Inada, C. Gota, Y. Harada, T. Funatsu and S. Uchiyama, Nat. Commun., 2012, 3, 705.
15. D. Jaque, L. Martínez Maestro, B. del Rosal, P. Haro-Gonzalez, A. Benayas, J. L. Plaza, E. Martín Rodríguez and J. García Solé, Nanoscale, 2014, 6, 9494–9530.
16. P. Cherukuri, E. S. Glazer and S. A. Curley, Adv. Drug Delivery Rev., 2010, 62, 339–345.
17. C. Vauthier, N. Tsapis and P. Couvreur, Nanomedicine, 2011, 6, 99–109.
18. S. Basu, Y. Gerchman, C. H. Collins, F. H. Arnold and R. Weiss, Nature, 2005, 434, 1130–1134.
19. N. Murugesan, P. Dhar, T. Panda and S. K. Das, Biomicrofluidics, 2017, 11, 024108.
20. T. Nakano, G. Kikugawa and T. Ohara, J. Chem. Phys., 2010, 133, 154705.
21. T. J. Müller and F. Müller-Plathe, Int. J. Quantum Chem., 2011, 111, 1403–1418.
22. M. R. Vist and J. H. Davis, Biochemistry, 1990, 29, 451–464.
23. S. Tristram-Nagle and J. F. Nagle, Chem. Phys. Lipids, 2004, 127, 3–14.
24. D. Marsh, Biochim. Biophys. Acta, 2010, 1798, 688–699.
25. Y. Zhang, A. Lervik, J. M. Seddon and F. Bresme, Chem. Phys. Lipids, 2015, 185, 88–98.
26. A. A. Gurtovenko and I. Vattulainen, Biophys. J., 2007, 92, 1878–1890.
27. W. F. Bennett, J. L. MacCallum, M. J. Hinner, S. J. Marrink and D. P. Tieleman, J. Am. Chem. Soc., 2009, 131, 12714–12720.
28. F. Römer, A. Lervik and F. Bresme, J. Chem. Phys., 2012, 137, 074503.
29. G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101.
30. M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1-2, 19–25.
31. S. W. Chiu, S. A. Pandit, H. L. Scott and E. Jakobsson, J. Phys. Chem. B, 2009, 113, 2748–2763.
32. H. J. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271.
33. B. Hess, H. Bekker, H. J. Berendsen and J. G. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472.
34. U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593.
35. C. B. Barber, D. P. Dobkin and H. Huhdanpaa, ACM Trans. Math Software, 1996, 22, 469–483.
36. A. Lervik and F. Bresme, Phys. Chem. Chem. Phys., 2014, 16, 13279.
37. S. R. D. Groot and P. O. Mazur, Non-Equilibrium Thermodynamics, North-Holland Pub. Co., Amsterdam, The Netherlands, 1962.
38. F. Römer, Z. Wang, S. Wiegand and F. Bresme, J. Phys. Chem. B, 2013, 117, 8209–8222.
39. J. Aittoniemi, T. Róg, P. Niemelä, M. Pasenkiewicz-Gierula, M. Karttunen and I. Vattulainen, J. Phys. Chem. B, 2006, 110, 25562–25564.
40. R. Murari, M. P. Murari and W. J. Baumann, Biochemistry, 1986, 25, 1062–1067.
41. T. A. Harroun, J. Katsaras and S. R. Wassall, Biochemistry, 2008, 47, 7090–7096.
42. J. S. Allhusen and J. C. Conboy, Acc. Chem. Res., 2017, 50, 58–65.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm00546k

‡ Present address: Departamento de Química-Física, Universidad Complutense de Madrid, Spain.

---