Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
KOBRA: a fluctuating elastic rod model for slender biological macromolecules†
Robert
Welch
 a,
Sarah A.
Harris
a,
Sarah A.
Harris
 a,
Oliver G.
Harlen
a,
Oliver G.
Harlen
 b and
Daniel J.
Read
b and
Daniel J.
Read
 *b
*b
aSchool of Physics and Astronomy, University of Leeds, Leeds, LS2 9JT, UK
bSchool of Mathematics, University of Leeds, Leeds, LS2 9JT, UK. E-mail: D.J.Read@leeds.ac.uk; Tel: +44 (0)113 343 5124
First published on 16th July 2020
Abstract
KOBRA (KirchOff Biological Rod Algorithm) is an algorithm and software package designed to perform dynamical simulations of elongated biomolecules such as those containing alpha-helices and coiled-coils. It represents these as coarsely-discretised Kirchoff rods, with linear elements that can stretch, bend and twist independently. These rods can have anisotropic and inhomogeneous parameters and bent or twisted equilibrium structures, allowing for a coarse-grained parameterisation of complex biological structures. Each element is non-inertial and subject to thermal fluctuations. The speed and simplicity of the algorithm allows KOBRA rods to easily access timescales from nanoseconds to seconds. To demonstrate this functionality, a KOBRA rod was parameterised using data from all-atom simulations of the Ndc80 protein complex, and compared against these simulations and negative-stain EM images. The distribution of bend angles and principal components were highly correlated between KOBRA, all-atom molecular dynamics, and experimental data. The properties of a hinge region, thought to be found at an unstructured loop, were studied. A C++ implementation of KOBRA is available under the GNU GPLv3 free software licence.
1 Introduction
Biomolecules often contain long elongated sections such as α-helices, coiled-coils and DNA/RNA double-helices. These motifs behave dynamically in ways that are much more complex than polymer chain models. They can have non-straight equilibrium structures, and anisotropic, inhomogeneous material parameters. Their global dynamics occur on timescales of microseconds to seconds, and they are frequently found in large, interacting, mesoscale systems, millions of atoms in size.An example of such a biomolecule is the Ndc80C protein complex (Fig. 1), which forms part of the kinetochore,1 and which anchors the microtubules of the mitotic spindle to the chromatids during cell division.2 Ndc80C is comprised mostly of an intrinsically-bent coiled-coil around 60 nm in length, with a hinge region at its centre.3 The extreme flexibility of many such elongated biomolecules means that we do not possess their fully resolved atomistic structures, however, mesoscale structural information is available from lower resolution methods, such as electron microscopy (EM).1 To build a model which will enable us to understand the full functionality of the kinetochore, we require a simulation algorithm that can capture how the various components interact.
 | ||
| Fig. 1 Schematic diagram of the kinetochore, an example of a mesoscale biological system containing many slender, rod-like structures.1 | ||
There are few existing algorithms that can help us at this scale. The large size and long timescales of the complete kinetochore system means that an all-atom simulation would be prohibitively expensive computationally. Coarse-grained MD offers a potential solution,4 however, discrete coarse-grained MD does not scale effectively to systems the size of the kinetochore. As a coarse-grained MD system gets larger, the size of the discontinuities increases, relative to its size, when in reality, the system is approaching a uniform continuum.
The Fluctuating Finite Element Analysis (FFEA) model5 addresses this problem, by treating large biomolecules as three-dimensional viscoelastic continuum objects. This approximation is valid for biological systems in which large-scale motions are more important than specific chemical interactions. While FFEA is well-suited to globular structures, such as Ndc80C's head and tail, 3D continuum methods are less well-suited to representing long, thin objects, such as Ndc80C's coiled-coil region. Creating trajectories of these objects with correct thermal fluctuations is difficult, as the length scales we need to resolve at are very small compared to the thermal fluctuations.
1.1 1-D rod models for biological objects
In this paper, we present a model specifically designed for dynamical simulations of the full variety of thin biological structures such as α-helices and coiled-coils, using a Kirchoff rod representation6 and Brownian dynamics.Elastic rod models are used as coarse-grained models for static modelling of proteins. For example, Wang et al.7 use a Cosserat model to predict the relationship between strain and chirality, and Neukirch et al.8 compute coiled-coil pitch and secondary structure. Linka et al.9 use a Cosserat representation for constitutive models of coiled-coils, but do not perform any explicit dynamics. Here, a Cosserat rod is commonly used to represent the backbone, and attempts are made to try to create a sequences of residues that matches this structure.10,11
Elastic rod models are also used to represent DNA. While these models represent DNA as Cosserat curves, they do not perform full dynamical simulations. Manning et al.12 use Cosserat rods to compute the equilibrium configuration for arbitrary DNA sequences – effectively an energy minimisation. Their more recent work has abandoned rods in favour of using interconnected 2D ‘sheets’. Smith et al.11 use a Cosserat model with anisotropic parameters, but focus almost exclusively on analytical self-contact models for supercoiling and plectoneme formation.
Kirchoff rods13 are also used for computational models of slender biological objects. Tobias et al.14 use Kirchoff rods to determine the thermodynamic properties of large ensembles of circular DNA segments. They find exact, analytical equations for the forces and energies in Kirchoff rods, but only for inextensible, uniformly-curved circular rods. Prior et al.15 develop a Kirchoff rod model for finding the bending and torsional response of helical birods from the bending and torsional responses of the constituent rods.
At larger length scales, Cosserat and Kirchoff elastic rod models are commonly used for macroscopic biological objects. An example is the STRANDS package,16 which is designed primarily for surgical simulations.
In the next section we set out a general-purpose Kirchoff rod simulation that can incorporate the properties of thin biological objects. Section 3 describes a protocol to set the physical parameters of these rods to match the dynamics of atomistic simulations. Finally, we validate these simulations against both idealised rod models and experimental and atomistic simulations for the dynamics of Ndc80C.
Our goal is to produce a model with the following specific features, in order to capture the essential dynamics of rod-like biomolecules:
• It must be able to incorporate thermodynamically-correct thermal fluctuations, which are essential to the dynamics of mesoscale biological systems.
• The rods should also be able to undergo bending, torsion and extension.
• Rods should be able to correctly represent ‘hinge regions’ in biomolecules, and so must also allow for elastic properties that are inhomogeneous and anisotropic.
• The model must allow for a non-straight equilibrium structure. Many biological objects (such as tubulin, which is found in the spindle microtubules) are bent in their equilibrium configuration, and this is integral to their function.
• It should be computationally inexpensive, allowing simulation of the equivalent of millions of atoms for timescales up to seconds.
Although, some important biopolymers, for example actin and microtubules are effectively inextensible, this limit is not straightforward because the inextensibility constraint requires that the random forces must be confined to space in which the system motion is constrained. Algorithms for achieving this have been developed by Grassia and Hinch,17 Morse18 and Liverpool.19
2 Definition of the rod model
2.1 Kirchoff and Cosserat curves
Almost all models of flexible thin rods describe their configuration in terms of the Frenet triad and Frenet–Serret relations.20,21 A rod is represented as a continuous material curve. Each point on the curve has three orthonormal vectors associated with it: the tangent vector, the normal vector, and the binormal vector (Fig. 2). A curve with normal and binormal vectors (also called director vectors) is said to be a directed curve.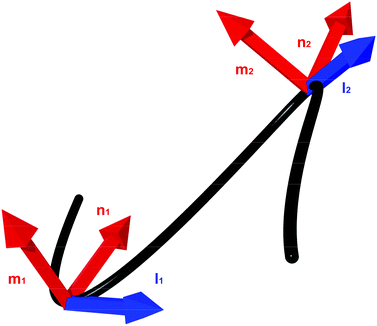 | ||
| Fig. 2 An example of a continuous framed curve. The tangent, l, and material axes represented by the normal vector m and binormal vector n are shown at two points on the curve. | ||
Most rod models use a formulation by Kirchoff,13 or by the Cosserat brothers6 to describe their energies. Elastic rods that are based on these curves are called Kirchoff or Cosserat rods.
2.2 Rod construction and notation
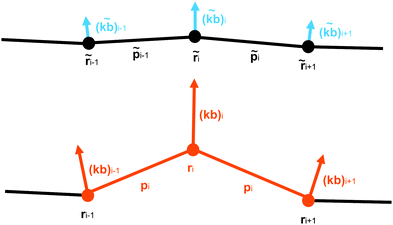
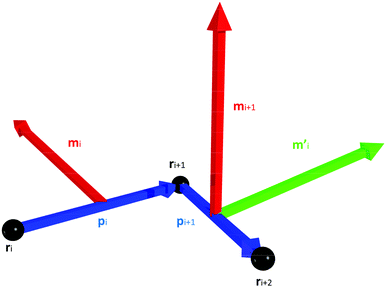
We construct a discretisation of the curve shown in Fig. 2 as a sequence of extensible straight rod sections connecting a set of discrete nodes (Fig. 3).This discretisation is based on the discretisation from Bergou et al.,22 but substantial modifications have been made in order to better support modelling of biological molecules: the addition of extension energy, the removal of inertia, the addition of viscous drag, the addition of thermal noise, changes in the bend energy formula to support hinge regions, and changes to the twist energy formula to support arbitrary equilibrium twisting. These differences will be discussed in greater detail in Section 2.4. The nodes are located at positions ri, where i ∈ {0, N − 1}, so that there are N − 1 segments, with end-to-end vectors pi = ri+1 − ri, and the unit vector along the rod li = ![[p with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0070_0302.gif) i = pi/|pi|.
i = pi/|pi|.
To represent the internal twisting of the rod, we define the material axes, mi and ni, to be perpendicular to li, such that ‖li‖ = ‖mi‖ = ‖ni‖ = 1 and li·mi = mi·ni = ni·li = 0. The choice of initial direction of mi and ni is arbitrary except that they must obey these constraints. However, these vectors are used to represent the relative twisting of rod elements, and form the basis of a local co-ordinate system which rotates as the rod rotates. The local material properties also rotate with the rod, so the directions of mi and ni are also used to define the locally anisotropic material properties. A method to initialise a rod which is untwisted at equilibrium is provided in eqn (31).
Finally, to describe rods with an arbitrary equilibrium state, we define equilibrium values  and
and  , the configuration from which the rod is deformed.
, the configuration from which the rod is deformed.
2.3 Parallel transport
We use the concept of parallel transport to distinguish between changes in the orientation of the material axes arising from the curvature of the centre line and those associated with twist about the centre line. The easiest way to find the twist between two sets of material axes is via the ‘parallel transport’ of the material axes of one element onto the other.For two unit vectors a and b we can construct a rotation matrix R that rotates a onto b:
 | (1) |
| v = a × b | (2) |
| c = a·b | (3) |
 | (4) |
To parallel transport the material axes of the ith segment onto the (i + 1)th segment, we construct the rotation matrix R, which rotates the normalised segment li onto the normalised segment li+1.23 We then apply that matrix to the material axis mi to obtain the vector mi′,
| mi′ = R(li,li+1)·mi = P(mi,li,li+1). | (5) |
The process of parallel transport is illustrated in Fig. 4, where mi′ is the result of the parallel transport of the material axis mi onto the pi+1 th segment. This allows the relative rotations of the material axes for element i and i + 1 to be compared in a manner that removes the bend between the elements.
 | ||
| Fig. 4 Parallel transport of the material axis mi from the pith segment to mi′ on the pi+1th segment. | ||
2.4 Elastic energy of deformation
We calculate the forces and torques on the rod from the gradients in the elastic energy arising from deforming the rod away from its equilibrium state. This elastic energy is composed of three components – extensional, torsional, and bending. | (6) |
![[p with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0070_0303.gif) i| is its equilibrium length (Fig. 5). The value of the spring constant ki for the ith element can be written as,
i| is its equilibrium length (Fig. 5). The value of the spring constant ki for the ith element can be written as,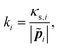 | (7) |
| Δθi = arctan2((mi+1 × mi′)·li+1,mi′·mi+1), | (8) |
 , but uses the signs of the parameters to determine which quadrant of the Euclidean plane the angle resides in, thus avoiding a potential sign error.
, but uses the signs of the parameters to determine which quadrant of the Euclidean plane the angle resides in, thus avoiding a potential sign error.
Within the linear elastic regime, the torsional energy at node i arises from the rotation between the material axes of the adjacent segments:
 | (9) |
 are the angles between the material frames in the current and equilibrium configurations, and
are the angles between the material frames in the current and equilibrium configurations, and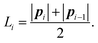 | (10) |
 . The twist energy does not account for the number of turns between two elements being >1, so the discretisation should be chosen so that Δθ is confined to the range −π < Δθ < π. By choosing a periodic function in eqn (9) we ensure that the energy remains continuous.
. The twist energy does not account for the number of turns between two elements being >1, so the discretisation should be chosen so that Δθ is confined to the range −π < Δθ < π. By choosing a periodic function in eqn (9) we ensure that the energy remains continuous.
 | (11) |
For a rod with an isotropic bending stiffness, the curvature binormal (kb)i is sufficient to calculate the bending energy. However, for a rod with an anisotropic bending stiffness, we need to resolve the components of bend with respect to the local material axes. In our discretisation, the material axes are properties of the elements, whereas the curvature binormal is defined at the node. To deal with this discrepancy, Bergou et al. average the energy arising from projecting the curvature binormal of the node onto the material axis of each the two adjacent rod elements. However, this has the effect of averaging the anisotropic bending modulus between the material directions of the two elements. Such averaging is undesirable if, for example, there is a local ‘hinge’ with strongly localised flexibility, as averaging between elements will remove the low modulus in the flexible direction. Therefore, to retain the functionality of a localised hinge, we need to define a material axis at the node. We do this by defining an intermediate segment, centred on this node, from a weighted average of the two segments on either side of this node, called the mutual segment (Fig. 8).
 | ||
| Fig. 8 A mutual rod segment lm about the ith node. The segment is weighted more towards the ith node, which it is closer to. | ||
We define the unit vector of the mutual segment as,
 | (12) |
and li and li−1 are the unit vectors of the segments on either side of the node. We use an inverse weighting of element lengths in the average so that the orientation of the mutual material frame is more affected by the shorter of the two adjacent elements (whose centre is closer to the node).
Next, we form the mutual material axis at the node by first parallel transporting the material axes of the two adjacent elements onto the mutual segment,
| m−i = P(mi−1,li−1,lm), | (13) |
| m+i = P(mi,li,lm), | (14) |
 | (15) |
By projecting the curvature binormal into the components of the material axes of the new mutual segment, we obtain the material curvature ω, the amount of bending in the local material axis frame,
| ωmi = ((kb)i·nm, −(kb)i·mm)T, | (16) |
Assuming that the material properties of the rod are such that torque and curvature are linearly related, the centreline curvature can be used to define the bending energy similarly to the previous energies – as a quadratic potential centred about ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e10f.gif) mi, the equilibrium material curvature:
mi, the equilibrium material curvature:
 | (17) |
![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) i is given by eqn (10) evaluated for the equilibrium configuration, and Bi is the bending stiffness matrix in the local material axis frame, a positive definite 2 × 2 matrix.
i is given by eqn (10) evaluated for the equilibrium configuration, and Bi is the bending stiffness matrix in the local material axis frame, a positive definite 2 × 2 matrix.
This formulation does not assume that pi−1 and pi are in similar directions, so it can account for arbitrarily large bend angles about a single element.
2.5 Dynamical equations
The changes to the configuration of the assembly of rod elements is defined by the changes of node positions, Δri and rotations Δθi, which determine the rotations of the material axes orientations (mi). The translational motion of each node is given by a stochastic equation of the formΔri = ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) i·(Fi + fi)Δt, i·(Fi + fi)Δt, | (18) |
![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) i is the mobility tensor of the rod segment in the fluid medium, Fi is the internal elastic force, and fi is the random force from stochastic thermal noise. This equation assumes that the system is overdamped, so that the inertia of the rod is negligible. We also neglect hydrodynamic interactions between the rod elements, but include a resistive (damping) force for the motion of an isolated rod element against a background fluid medium. This is therefore a Brownian equation of motion. For a general axisymmetric body the mobility tensor will be anisotropic. However, for simplicity we have approximated the mobility as being isotropic and equal to mobility of a sphere of a radius, ai equal to half the equilibrium length of each segment:25
i is the mobility tensor of the rod segment in the fluid medium, Fi is the internal elastic force, and fi is the random force from stochastic thermal noise. This equation assumes that the system is overdamped, so that the inertia of the rod is negligible. We also neglect hydrodynamic interactions between the rod elements, but include a resistive (damping) force for the motion of an isolated rod element against a background fluid medium. This is therefore a Brownian equation of motion. For a general axisymmetric body the mobility tensor will be anisotropic. However, for simplicity we have approximated the mobility as being isotropic and equal to mobility of a sphere of a radius, ai equal to half the equilibrium length of each segment:25![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) i = ζi−1I, i = ζi−1I, | (19) |
Similarly, for the rotational motion of the material axes,
 | (20) |
![[p with combining low line]](https://www.rsc.org/images/entities/b_i_char_0070_0332.gif) i|:
i|:ζθ = 8πμa2·|![[p with combining low line]](https://www.rsc.org/images/entities/b_i_char_0070_0332.gif) i|. i|. | (21) |
For a particular configuration of nodes and material axes, the forces acting on nodes (Fi) and the torques acting on material axes (τi) can be determined from the partial gradients of the energy:
 | (22) |
 | (23) |
Due to the complexity of these formulas we compute the gradient numerically using central differences,
 | (24) |
When a node is translated, the elements and the material axes on either side of that node change. The element is updated according to the discretisation given in Section 2.2. The material axis is parallel transported (Section 2.3) from the old rod direction to the new one. More details are available in Section 1 of the ESI.†
Using the drag given by eqn (19), the force acting on each node from thermal noise is given by the fluctuation dissipation theorem,26
 | (25) |
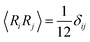 .
.
It would be possible to include hydrodynamic interactions by replacing eqn (18) for each segment with a single equation for the entire rod with a single mobility matrix including the hydrodynamic coupling between the elements. However, this would result in replacing ζi in eqn (25) with the inverse of the mobility tensor, which is computationally more expensive. If the rod remains nearly straight that the effect of hydrodynamic interactions can be approximated through a difference in the local mobility parallel and perpendicular to the rod axis.
The rotational thermal torque is given by
 | (26) |
To apply the rotation Δθ to the material axis, we use Rodrigues rotation formula:
vrot = v![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δθ + (k × v)sin Δθ + (k × v)sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δθ + k(k·v)(1 − cos Δθ + k(k·v)(1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δθ) Δθ) | (27) |
For information regarding the structure, implementation and performance of this algorithm, see Section 2 of the ESI.†
3 Parameterisation of rods from atomistic molecular dynamics
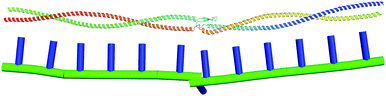
In this section, we apply the general model for rod-like biomolecules described in Section 2 to the specific case of the Ndc80 protein complex. Ndc80C is a long, flexible molecule comprised of two coiled-coil sections joined by an unstructured loop. As a consequence, this molecule has both a non-straight equilibrium shape and an inhomogeneous, anisotropic bending modulus, and so allows us to test all of the features of this model. A cartoon depiction of the Ndc80C structure is shown in Fig. 9, showing the connectivity of Ndc80C's four sub-units (Ndc80 in blue, Spc24 in purple, Nuf2 in yellow and Spc25 in green) along with the positions and residue numbers of the cross-links.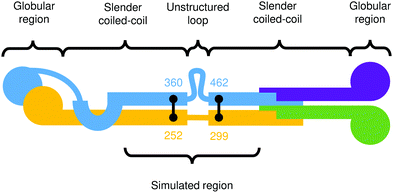 | ||
| Fig. 9 Cartoon depiction of the Ndc80C protein complex.3 The colours distinguish the four connected proteins in the complex, and the black lines denote cross-links at their respective residue numbers. | ||
First, we will construct an all-atom representation of Ndc80C. Then, we will extract coarse grained rod model parameters from the dynamics of a simulation of the all-atom Ndc80C. Finally, we will compare the results from these models to each other and to measurements acquired from negative stain EM images.27
3.1 Creation of an all-atom Ndc80C model
All-atom molecular dynamics software packages such as AMBER28 and GROMACS29 are commonly used to study the dynamics of biological molecules.30 Unlike KOBRA, these simulations consider the position and connectivity of every atom (and hence, every residue) contained within a given molecule. The dynamics are computed using a force field, from pre-computed potentials that describe every atom and bond in the system. Therefore, to run an MD simulation of Ndc80C, we need to construct a model of the structure by combining information from experimental studies.As a starting point, we use the so-called ‘Bonsai’ Ndc80C molecule3 (2VE7). This molecule contains both globular domains and heavily-truncated coiled-coil region 85 Å in length.
Ciferri et al.3 provide the positions of cross-links between the two coiled-coils and a prediction of the entire secondary structure by type: a long coiled-coil with a small, unstructured loop at the centre. They also indicate the relative residue numbers at which these features occur as shown in Fig. 9.
To construct an all-atom model of Ndc80C, we use the spatial parameters (such as the pitch and coiled-coil radius) extracted from the Bonsai Ndc80C combined with the residue sequence from the full-length molecule. We remove the globular regions at both ends and retain the central coiled-coil region. Details of the sequences are available in the ESI.† We use ISAMBARD, a software package designed for modelling, analysis and parametric design of proteins,31 to extract the coiled-coil parameters – such as pitch, radius, crick angles, and ϕCα values – from the coiled-coil present in the Bonsai molecule. The radius was found to be 7.62 ± 0.12 Å, the pitch 203 ± 26 Å. ISAMBARD is then used to create a coiled-coil backbone with these parameters out of the full Ndc80C residue sequence. This structure has no side-chains, so we recreate the side chains from the residue sequence using SCWRL4, a protein side chain predictor.32
We use the QUARK ab inito protein structure prediction server33 to create predictions of the structures in loop region from the residue sequence. These structures were peptide-bonded together with the two coiled-coils using UCSF Chimera.34 The overall length of the generated Ndc80C is 48 nm.
Finally, we refine the resulting model using ModRefiner,35 and minimise it using the YASARA minimisation server.36 This brings the protein, which has been created with somewhat arbitrary bond angles, closer to its native state. We then run simulations of this structure using AMBER28 with an implicit (GBSA) solvent, for 50 nanoseconds. The simulation trajectories and input files are available in the ESI.†
3.2 Model building
To construct a rod model for Ndc80C, we need to obtain suitable values for the physical parameters κs, β and B for each node and element. These parameters are obtained from Ndc80C's dynamics – we run an atomistic simulation of Ndc80C and aim to select rod parameters that reproduce the same local fluctuations in shape.We first map the all-atom MD trajectory directly onto a coarse-grained trajectory for an equivalent rod model. We define the position of nodes in this rod model by averaging over the positions of small clusters of atoms:
 | (28) |
Each node was averaged from a 10-atom wide cluster according to eqn (28) (see Fig. 10). This number is also system-dependent, for Ndc80C it was chosen such that there is more than a factor of 10 difference between number of atoms per rod element and the number of atoms being used to set a node position.
 | ||
| Fig. 10 To coarse-grain the atomistic Ndc80C trajectory, the co-ordinates of groups of atoms are averaged according to clusters of atom indices. | ||
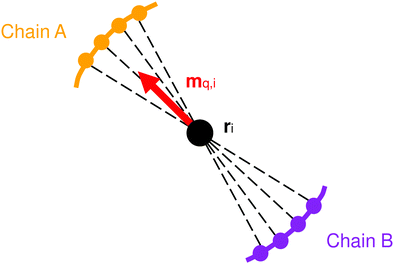
Having defined the nodes, we now need to define the material axis of each coarse-grained segment in order to measure twist. One method for doing this is to first calculate the vector qi between the opposite atoms in the two chains of the coiled-coil (Fig. 11):
 | (29) |
 | (30) |
However, the material axes of adjacent elements obtained from eqn (30) may point in quite different directions, and although the above equations for calculating deformation energy permit this, it is practically better (e.g. when defining the bending stiffness matrix) to maintain similar directions for the material axes of adjacent elements. The material axes of two adjacent elements can be considered to be in the ‘same’ direction if the material axis mi of element i, when parallel transported onto element i + 1, points in the direction of the material axis mi+1 of that element.
Consequently, we use the following procedure for calculation of material axes. We begin in the equilibrium configuration of the atomistic model. In this equilibrium configuration, we obtain the material axis m0 of the first element according to eqn (30). We then generate the material axis for all other rod elements in the equilibrium configuration by parallel transport, by iterating along the rod:
 | (31) |
 , which we then store. Then, during the subsequent dynamics of the MD trajectory, at any moment we can generate the instantaneous mq,i according to eqn (30), and calculate the instantaneous material axis mi by rotating mq,i about the rod by signed angle
, which we then store. Then, during the subsequent dynamics of the MD trajectory, at any moment we can generate the instantaneous mq,i according to eqn (30), and calculate the instantaneous material axis mi by rotating mq,i about the rod by signed angle  , using the Rodrigues rotation formula (eqn (27)).
, using the Rodrigues rotation formula (eqn (27)).
The Python script that builds this model is available in the ESI,† and as part of the FFEA software package. The model, as built, is illustrated in Fig. 12.
3.3 Model parameterisation
Having mapped the MD simulations onto a trajectory for an equivalent rod model, our strategy for model parameterisation is to select parameters such that the local mean square fluctuations in bending, twisting and extension match those observed in the equivalent rod model from the MD trajectory. From this trajectory, we therefore compute (for each rod, or node, i) the mean square fluctuations in rod length 〈(|pi| − |![[p with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0070_0303.gif) i|)2〉, and in twisting angle 〈Δθi2〉 where Δθi is the difference between instantaneous twisting angle and its time average value. Since bending is parameterised by a two-component vector ωmi (see eqn (16)), fluctuations in bending are parameterised by a covariance matrix for bending fluctuations, for node i:
i|)2〉, and in twisting angle 〈Δθi2〉 where Δθi is the difference between instantaneous twisting angle and its time average value. Since bending is parameterised by a two-component vector ωmi (see eqn (16)), fluctuations in bending are parameterised by a covariance matrix for bending fluctuations, for node i:| Ci,αβ = 〈Δωmi,αΔωmi,β〉, | (32) |
We aim to parameterise the dynamical rod model so as to match the above mean square fluctuations. As an initial estimate for the model parameters, we note that the energies defined in eqn (6), (9) and (17) are all quadratic in the respective parameters. We might expect fluctuations to be distributed normally and the equipartition theorem to apply. This produces initial estimates for the parameters as:
 | (33) |
 | (34) |
| Bi = kBTLi·Ci−1. | (35) |
We have found this problem to be especially prominent for the bending fluctuations. If we use eqn (35) for the bending stiffness matrix, then typically the mean square fluctuations in the resulting rod model do not match those expected. However, they are sufficiently close that an iterative scheme is able to rapidly converge on the correct parameterisation. For a given node i, suppose we are aiming to reproduce bending fluctuations Ctarget as measured from the all atom MD simulations. Running a KOBRA model built using the bending energy matrix Bold, given by application of eqn (35), will result in a trajectory with observed fluctuations Cold which will in general be different from Ctarget (even after reducing statistical errors by running a long trajectory). By considering the expected change in C from a small change in B, we can obtain a new guess for an optimal bending energy matrix as:
| Bnew = kBTLi(Ctarget − Cold + kBTLiBold−1)−1. | (36) |
Validation of equipartition of energy, and extraction of bending parameters from dynamical simulations, are described in more detail in Sections 3 and 4 of the ESI.†
4 Results
4.1 All-atom parameterisation results
Using the method described in Section 3.3, and the model from Section 3.1, we can determine a set of rod parameters for Ndc80C. The unstructured loop acts as a flexible hinge linking together stiffer coiled coil regions of the molecule. The average values of these constants for the entire molecule (including the flexible hinge) are given here in Table 1.| κ | (1.718 ± 0.017) × 10−11 N m−1 |
| B | (5.15 ± 0.29) × 10−31 m4 Pa |
| β | (1.32 ± 0.07) × 10−29 nm2 |
In addition to making it more flexible, Ndc80C's hinge region means that it is slightly more susceptible to bending in one axis than in the other. This hinge is localised to a small region in the centre of Ndc80C, so we need to examine the parameters extracted on a per-node basis.
Fig. 13 indicates the two eigenvalues of Bi as a function of the node number. It shows a localised region of decreased stiffness between nodes 4 and 6 in the parameterised rod model, which corresponds to the unstructured loop region (the hinge) in the atomistic model. This hinge is also observed in the negative stain EM imaging of Ndc80C,27 which will be examined in more detail in Section 4.2.1.
4.2 Comparison of dynamics with atomistic molecular dynamics and experimental data
The parameterisation from Section 4.1 was used to create a KOBRA rod model and run a simulation comprised of 2 × 107 steps, with a timestep of 10 ps, for a total simulation time of 200 μs. Note that this is more than three orders of magnitude longer than the atomistic simulations.From both the KOBRA rod and MD atomistic trajectories, the kink angles can be measured using the end-to-end vectors pa and pb of the two halves of the coiled-coil region (i.e. from one end of the coiled-coil to the loop/hinge region, and then from the loop/hinge region to the far end of the coiled-coil):
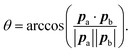 | (37) |
 | ||
| Fig. 14 Kink angles for experimental data, rod simulation and atomistic simulation. Angles are given as absolute values. | ||
The distribution of kink angles for the KOBRA rod and atomistic trajectories are very similar. Both possess a broad maximum of bend angles between 25 and 75 degrees centered on 50 degrees, that falls off rapidly for angles above 100 degrees. This occurs because of the density of states from projection of the two possible bending directions onto a single bend angle. Since the distribution of bend angles at each node from the MD trajectory was used to parameterise the KOBRA rod simulation this can be interpreted as an indication of a successful parameterisation.
The distribution of the experimental angles retains the same general features. The experimental distribution does not replicate the maximum at 50 degrees. However, this discrepancy arises in part because the experimental resolution was not able to resolve bend angles less than 30 degrees – so all angles in this range were inserted into a single bin. Otherwise, the experimental data broadly replicates the features of the distributions found from simulation although the range of the bend angles is slightly broader. It should also be noted that the experimental distribution is constructed from only 83 samples, compared to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 frames for the rod trajectory and 50
000 frames for the rod trajectory and 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 frames for the atomistic trajectory.
000 frames for the atomistic trajectory.
The rod simulation trajectories and input files are available in the ESI.†
Fig. 15 shows the dot product matrix comparing the rod and all-atom simulations. Each cell shows the dot product of the eigenvector of the rod mode with the corresponding all-atom mode. A dot product close to one means that the eigenvectors are highly correlated. The eigenvectors are sorted by eigenvalue size, so if the matrix is diagonal, it also means that the relative magnitude of the various modes of bending are in the same order. The highest correlation is between the first modes, which correspond to bending about the hinge. Although diagonal elements of the matrix dominate, there are some significant off-diagonal components, which could be evidence of mode mixture, particularly between mode 2 and 4. For reference, when assessing correlations between eigenmodes from multiple all-atom trajectories, these normally display a significantly smaller degree of diagonal correlation between PCA eigenmodes from separate runs on the same model5 than is shown in Fig. 15.
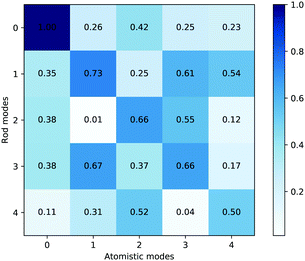 | ||
| Fig. 15 Dot product matrix of the average principal component eigenvectors. The values shown are normalised to the size of the largest dot product. | ||
To observe this mode mixture, and visualise the motion represented by the first few PCA modes, we can create ‘PCA animations’, that show the range of motion corresponding to each eigenmode. The PCA animations are created using the following formula:
| ranimi = ri + (λf)v, | (38) |
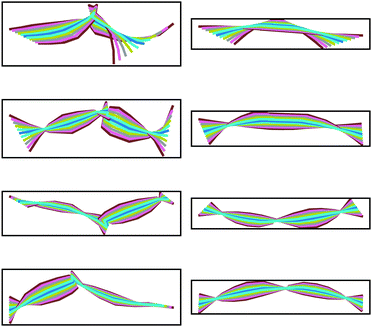
Fig. 16 compares the range of motion exhibited in the first four principal component eigenmodes obtained from the rod and the all-atom MD simulations. The first mode shows a central hinge, with similar magnitudes of bending for the rod and atomistic model. The second and third all-atom modes show the fluctuation of two different coiled-coil regions. While the second and third principal components initially look dissimilar, the dot product matrix suggests there is mixing between these modes. For example, modes 1 and 2 of the atomistic trajectory show motion on opposite sides of the hinge, whereas in the corresponding rod nodes, this motion is distributed evenly between both modes.
Together, Fig. 15 and 16 indicate a strong correlation between the motions involved in the atomistic MD simulation and the KOBRA rod trajectories. The degree of correlation is typical (and in fact good) in comparison to PCA mode correlations between similar MD simulations, or between MD and coarse grained simulations. One reason for the discrepancy in correlation is the length of the MD trajectories, which are necessarily short (due to computational constraints), and therefore do not sample a large number of different global configurations (the large scale modes) of the molecule, giving rise to a statistical sampling error. It should be noted that in deriving parameter values for the coarse grained rod model we have used local information, such as the variation in local bend and twist angles, rather than the variation in global configurations. For short MD trajectories, matching the local bend and twist variation does not necessarily translate to matching the (statistically limited) variations observed in global configurations.
Animations of each normal mode and pcz-format trajectories are available in the ESI† provided with this paper.
5 Conclusion
The KOBRA algorithm provides an efficient simulation technique for elongated biomolecules that produces dynamical rod trajectories and conformers with bend angles that closely resemble all-atom MD and experimental data. While here we have focused only on Ndc80C, KOBRA is designed to be a general model for slender biological objects such as coiled-coils and alpha helices. The current version provides a robust coarse-graining methodology designed to capture the dynamics of slender biological objects, which can have anisotropic bending moduli, inhomogeneous bending, stretch and twisting parameters, and arbitrary equilibrium configurations. In addition, it provides tools for model building and a large number of tests for validity. KOBRA is also performant enough to handle simulations of extremely large systems (of order (100 nm) over long timescales (of order 1 ms)), such as the kinetochore.In the future, we will couple the rod-like KOBRA objects with three-dimensional FFEA objects, in order to construct biomolecules comprised of both globular and filamentary structures. In particular, this will enable us to construct a model of Ndc80C featuring the globular domains at each end, and potentially larger systems including more kinetochore proteins. We will also intend to implement long range hydrodynamics.
The software implementing the KOBRA algorithm is available as part of the FFEA software package (ffea.bitbucket.io), and is free to use and modify under the conditions off the GNU GPLv3 software licence. This includes an implementation of the algorithm, the tools used to convert atomistic trajectories to rod structures, parameter extraction, all of the analysis tools, and a simple visualiser. Developer documentation is also available for those who want to add features or implement KOBRA in their own software.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Robert Welch was supported by the William Wright Scholarship at the University of Leeds. Sarah A. Harris was supported by the UK Engineering and Physical Sciences Research Council (EP/S030671/1). We also thank Tomoyuki Tanaka, Albert Solernou, and Samantha Coffey.Notes and references
- S. Gonen, B. Akiyoshi, M. G. Iadanza, D. Shi, N. Duggan, S. Biggins and T. Gonen, Nat. Struct. Mol. Biol., 2012, 19, 925–929 CrossRef CAS PubMed
.
- A. Suzuki, B. L. Badger, J. Haase, T. Ohashi, H. P. Erickson, E. D. Salmon and K. Bloom, Nat. Cell Biol., 2016, 18, 382–392 CrossRef CAS PubMed
.
- C. Ciferri, S. Pasqualato, E. Screpanti, G. Varetti, S. Santaguida, G. Dos Reis, A. Maiolica, J. Polka, J. G. De Luca and P. De Wulf,
et al.
, Cell, 2008, 133, 427–439 CrossRef CAS PubMed
.
- S. Kmiecik, D. Gront, M. Kolinski, L. Wieteska, A. E. Dawid and A. Kolinski, Chem. Rev., 2016, 116, 7898–7936 CrossRef CAS PubMed
.
- A. Solernou, B. S. Hanson, R. A. Richardson, R. Welch, D. J. Read, O. G. Harlen and S. A. Harris, PLoS Comput. Biol., 2018, 14, e1005897 CrossRef PubMed
.
- E. E. Cosserat and F. F. Cosserat, http://info:edu-jhu-library/collection/brittlebooks/id/barcode/31151000327233, 1909.
- J.-S. Wang, Y.-H. Cui, T. Shimada, H.-P. Wu and T. Kitamura, Appl. Phys. Lett., 2014, 105, 043702 CrossRef
.
- S. Neukirch, A. Goriely and A. C. Hausrath, Phys. Rev. Lett., 2008, 100, 038105 CrossRef PubMed
.
- K. Linka and M. Itskov, J. Mech. Behav. Biomed. Mater., 2016, 58, 163–172 CrossRef CAS PubMed
.
- A. Gorielyn, A. Hausrath and S. Neukirch, Biophys. Rev. Lett., 2008, 3, 77–101 CrossRef
.
- M. L. Smith and T. J. Healey, Int. J. Non Linear Mech., 2008, 43, 1020–1028 CrossRef
.
- R. S. Manning, J. H. Maddocks and J. D. Kahn, J. Chem. Phys., 1996, 105, 5626–5646 CrossRef CAS
.
- G. Kirchoff, J. Reine Angew. Math., 2009, 1859, 285–313 Search PubMed
.
- I. Tobias, B. D. Coleman and M. Lembo, J. Chem. Phys., 1996, 105, 2517–2526 CrossRef CAS
.
- C. Prior, J. Elasticity, 2014, 117, 231–277 CrossRef
.
- D. K. Pai, Comput. Graph. Forum, 2002, 21, 347–352 CrossRef
.
- P. Grassia and E. J. Hinch, J. Fluid Mech., 1996, 308, 255–288 CrossRef CAS
.
-
D. C. Morse, Advances in Chemical Physics, John Wiley & Sons, Ltd, 2004, pp. 65–189 Search PubMed
.
- T. B. Liverpool, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 021805 CrossRef PubMed
.
- F. Frenet, J. Math. Pure. Appl., 1852, 437–447 Search PubMed
.
- J.-A. Serret, J. Math. Pure. Appl., 1851, 193–207 Search PubMed
.
-
M. Bergou, M. Wardetzky, S. Robinson, B. Audoly and E. Grinspun, ACM transactions on graphics (TOG), 2008, p. 63 Search PubMed
.
- J. v. d. Berg, https://math.stackexchange.com/users/91768/jur-van-denberg, Calculate Rotation Matrix to align Vector A to Vector B in 3d?.
- A. Zhmurov, O. Kononova, R. I. Litvinov, R. I. Dima, V. Barsegov and J. W. Weisel, J. Am. Chem. Soc., 2012, 134, 20396–20402 CrossRef CAS PubMed
.
- P. Saffman, J. Fluid Mech., 1976, 73, 593–602 CrossRef
.
- H. Nyquist, Phys. Rev., 1928, 32, 110–113 CrossRef CAS
.
- H.-W. Wang, S. Long, C. Ciferri, S. Westermann, D. Drubin, G. Barnes and E. Nogales, J. Mol. Biol., 2008, 383, 894–903 CrossRef CAS PubMed
.
- D. A. Pearlman, D. A. Case, J. W. Caldwell, W. S. Ross, T. E. Cheatham, S. DeBolt, D. Ferguson, G. Seibel and P. Kollman, Comput. Phys. Commun., 1995, 91, 1–41 CrossRef CAS
.
- M. J. Abraham, T. Murtola, R. Schulz, S. Pall, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef
.
- D. J. Huggins, P. C. Biggin, M. A. Dämgen, J. W. Essex, S. A. Harris, R. H. Henchman, S. Khalid, A. Kuzmanic, C. A. Laughton, J. Michel, A. J. Mulholland, E. Rosta, M. S. P. Sansom and M. W. v. d. Kamp, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, 9, e1393 Search PubMed
.
- C. W. Wood, J. W. Heal, A. R. Thomson, G. J. Bartlett, A. Ibarra, R. L. Brady, R. B. Sessions and D. N. Woolfson, Bioinformatics, 2017, 33, 3043–3050 CrossRef CAS PubMed
.
- G. G. Krivov, M. V. Shapovalov and R. L. Dunbrack, Proteins: Struct., Funct., Bioinf., 2009, 77, 778–795 CrossRef CAS PubMed
.
- D. Xu and Y. Zhang, Proteins: Struct., Funct., Bioinf., 2012, 80, 1715–1735 CrossRef CAS PubMed
.
- E. F. Pettersen, T. D. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng and T. E. Ferrin, J. Comput. Chem., 2004, 25, 1605–1612 CrossRef CAS PubMed
.
- D. Xu and Y. Zhang, Biophys. J., 2011, 101, 2525–2534 CrossRef CAS PubMed
.
- E. Krieger, K. Joo, J. Lee, J. Lee, S. Raman, J. Thompson, M. Tyka, D. Baker and K. Karplus, Proteins, 2009, 77(Suppl 9), 114–122 CrossRef CAS PubMed
.
- K. Pearson, London, Edinburgh Dublin Philos. Mag. J. Sci., 1901, 2, 559–572 CrossRef
.
- A. Shkurti, R. Goni, P. Andrio, E. Breitmoser, I. Bethune, M. Orozco and C. A. Laughton, SoftwareX, 2016, 5, 44–50 CrossRef
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm00491j |
| This journal is © The Royal Society of Chemistry 2020 |